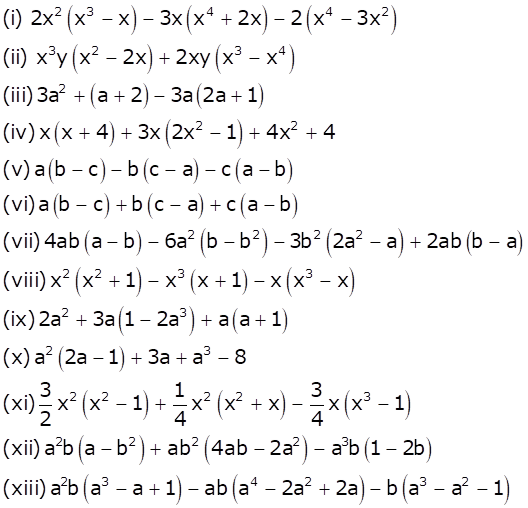
(i) 2x² (x³ – x) – 3x (x⁴ + 2x) – 2 (x⁴ – 3x²)

_{= 2x}⁵ – 2x³ – 3x⁵ – 6x² – 2x⁴ + 6x²

_{= -x}⁵ – 2x⁴ – 2x³

_{(ii) x}³y (x² – 2x) + 2xy (x³ – x⁴)

_{= x}⁵y – 2x⁴y + 2x⁴y – 2x⁵y

_{= -x}⁵y

_{(iii) 3a}² + (a + 2) – 3a (2a + 1)

_{= 3a}² + a + 2 – 6a² – 34

_{= -3a}² – 2a + 2

_{(iv) x (x + 4) + 3x (2x}² – 1) + 4x² + 4

_{= x}² + 4x + 6x³ – 3x + 4x² + 4

_{= 6x}³ + 5x² + x + 4

_{(v) a (b – c) – b (c – a) – c (a – b)}

_{= ab – ac – bc + ab – ca + bc}

_{= 2ab – 2ac}

_{(vi) a (b – c) + b (c – a) + c (a – b)}

_{= ab – ac + bc – ab + ac – bc}

_{= 0}

_{(vii) 4ab (a – b) – 6a}² (b – b²) – 3b² (2a² – a) + 2ab (b – a)

_{= 4a}²b – 4ab² – 6a²b + 6a²b² – 6a²b² + 3ab² + 2ab² – 2a²b

_{= 3ab}²

_{(viii) x}² (x² + 1) – x³ (x + 1) – x (x³ – x)

_{= x}⁴ + x² – x⁴ – x³ – x⁴ + x²

_{= 2x}² – 2x³

_{(ix) 2a}² + 3a (1 – 2a³) + a (a + 1)

_{= 2a}² + 3a – 6a⁴ + a² + a

_{= -6a}⁴ + 3a² + 4a

_{(x) a}² (2a – 1) + 3a + a³ – 8

_{= 2a}³ – a² + 3a + a³ – 8

_{= 3a}³ – a² + 3a – 8

_{(xi) x}² (x² – 1) + _x² (x² + x) - _{x (x}³ – 1)

_{= x}⁴ - _x² + _x⁴ + _x³ – _x⁴ + _x

_{= x}⁴ - _x² + _x³ + _x

_{(xii) a}²b (a – b²) + ab² (4ab – 2a²) – a³b (1 – 2b)

_{= a}³b – a²b³ + 4a²b³ – 2a³b² – a³b + 2a³b²

_{= -a}²b³ + 4a²b³

_{= 3a}²b³

_{(xiii) a}²b (a³ – a + 1) – ab (a⁴ – 2a² + 2a) – b (a³ – a² – 1)

_{= a}⁵b – a³b + a²b – a⁵b + 2a³b – 2a²b – ba³ + a²b + b

_{= b}