In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. IF OA = 20 cm, find the area of the shaded region. [Use π = 3.14]

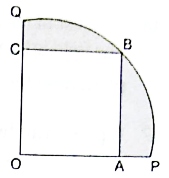
Given:

OA = Side of square OABC = 20 cm

∵ Area of square = Side × Side

∴ Area of square OABC = 20 × 20 = 400 cm²

Now,

∵ Length of diagonal of square = √2 × Side of Square

∴ Length of diagonal of square OABC = √2 × 20 = 20√2 cm

⇒ Radius of the quadrant = 20√2 cm

∵ Area of quadrant = πr²

∴ Area of quadrant OPBQ = × 3.14 × 20√2 × 20√2

= × 400 × 2

= 3.14 × 200 = 628 cm²

Area of shaded region = Area of quadrant OPBQ – Area of square OABC = 628 – 400 = 228 cm²

Hence, the area of the shaded region is 228 cm².