Table of Contents

2. Shapes and Angles
Rohini and Mohini are twin sisters. They love doing the same things. One day when they were making shapes with matchsticks, Shailagavethema challenge.
Rohini will make a shape.
Mohini has to make the same without looking at it, but she can ask questions.
Oh! That is so simple.
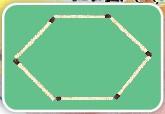
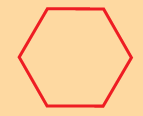
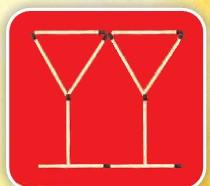
Rohini made this shape.
Mohini — Is it a closed shape or an open shape?
Rohini - It is a closed shape.
Mohini - How many sides are there?
Rohini - It has 6 sides.
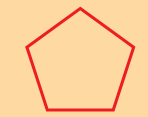
Mohini made this.
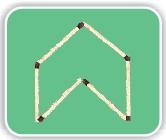
Now you give the answers.
Is it a closed shape? _____ Does it have 6 sides? _____ .
But it is not the same as the one made by Rohini So Mohini tried again.
This is what she made.

Is it a closed shape with 6 sides? _____
Is it the same as the one made by Rohini? _____
Is there some way to say in what way these shapes are different?
* Mohini tried again but got different shapes. Guess and make two more shapes Mohini could have made.
Mohini is now tired of trying and asks Shaila what to do.
If you ask for the angles that the matchsticks make at the corners, you can do it.
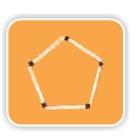
Oh! So let us look for the angles.
* Look at the angles marked in these shapes. Can you see the difference?
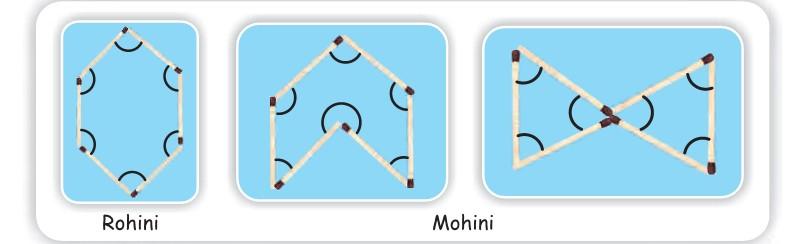
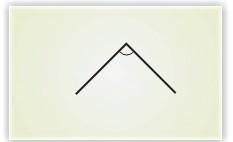
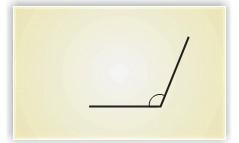
See, how the matchsticks make a small angle, a big angle, and a bigger angle.
Wow! When the angle changes the shape changes so much.
It is important to encourage children to think about the way in which shapes can differ even when the number of sides is the same. This will help them to get a sense of how angles determine the shape of a polygon.
Practice Time
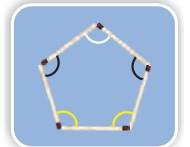
1) Look at the shape and answer.
* The angle marked in _____ colour is the biggest angle.
2(a) Are the angles marked with yellow equal? _____
b) Are the angles marked with green equal? _____
c) Are the angles marked with blue equal? _____
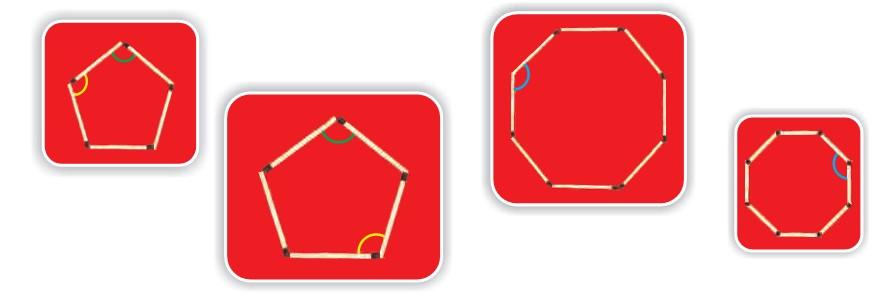
3) Four different angles are marked in four colours. Can you find other angles which are the same as the one marked in red? Mark them in red. Do this for the other colours.

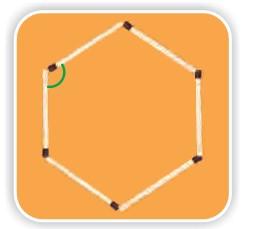

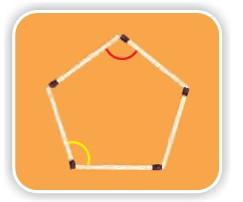
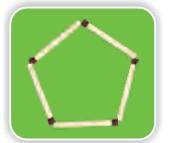
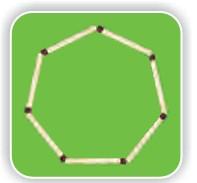
4) How many different shapes can you make by changing the angle between the matchsticks in each of these? Try.
a)

4 matchsticks
b)

8 matchsticks
c)
5 matchsticks
d)
7 matchsticks
e)
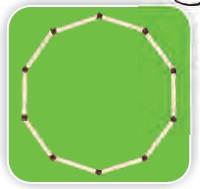
10 matchsticks
Matchstick Puzzles
1) Make 8 triangles using 6 matchsticks. Try!

2) Take 8 matchsticks and make a fish like this. Now pick up any 3 matchsticks and put them in such a way that the fish now starts swimming in the opposite direction. Did it?
3) Using 10 matchsticks make this shape. Pick up 5 matchsticks and put them in such a way that you get the shape of a house.
If you have not been able to solve these then look for the answers on page 29.
Angle Tester
How do we make equal angles?
Let us make an angle tester
You also have an angle tester in your geometry box. It is called a divider.
* Cut two strips from a cardboard sheet.
* Fix them with a drawing pin or A such that both the strips can move around easily.

Rohini and Mohini went all around with the angle tester to look for different angles in their class.
Rohini tested the angle of the Maths book and the pencil box.
Look at the tester. It has opened like the letter L.
This is a right angle. We write it as L.
* Go around with your tester and draw here those things in which the tester opens like the letter L. Are you sure they are all right angles?
Practice time
1) Look at the angles in the pictures and fill the table.
Angle | Right angle | More than a right angle | Less than a right angle |
| Right | ||
| |||
| |||
| |||
|
2) Sukhman made this picture with so many angles.

Use colour pencils to mark.
* right angles with black colour.
* angles which are more than a right angle with green.
* angles which are less than a right angle with blue.
3 Draw anything of your choice around the angle shown. Also write what kind of angle it is. The first one is done.
Less than a right angle



Activity
a) Take a square sheet of paper.

b) Fold it in half.

c) Fold it once more and press it.

d) Open the last fold so that the sheet is folded in half.

e) Take one corner and fold it to meet the dotted line.

On the paper you will find lines making a right angle, an angle less than a right angle and an angle more than a right angle.
Look for each of the angles and mark them with different colours.
Activity - Angles with your body
Can you make these angles?
a) A right angle with your hand?
b) An angle less than a right angle with your leg?
c) An angle more than a right angle with your arm?
d) An angle more than a right angle with your body?
Try them out. It's fun! Draw them in your notebook using stick drawings like these.
Angle Garden
My angle dance shows the way!
When I see flowers for making honey, I want to tell other bees. To show them the way I start dancing. My dance shows the angle between the sun and the flower.

Activity
Collect some leaves from the garden. Colour each leaf and print it. Look at the angles on the leaves. Which of them are more/less than a right angle?
Hey! Look at that bird. Its beak has an angle less than a right angle.
I am a woodpecker. My beak is sharp because it has to cut the wood.
* Look for the birds which have beaks with small angles.
* In the picture mark angles between the two branches. Which two branches have the biggest angle?
Angles in Names
You know, there are angles in the letters of our names too.
In my name there are 11 right angles. There are also 10 angles less than a right angle.
* Write 3 names using straight lines and count the angles.
Name | Number of right angles | Number of angles more than a right angle | Number of angles less than a right angle |
Activity
a) Put 10 Math-Magic books on top of each other. Keep one book slanting to make a slide.
b) Now do this with six books.
* Roll a ball from the top. From which slide does the ball roll down faster?
* Which slide has the smaller angle?

These are two slides in a park.
* Which slide has a larger angle?
* Which slide do you think is safer for the little boy? Why?
Changing Shapes
1. Things you need – used (or new) matchsticks. Piece of rubber tube used in cycle valves.
i) Clean the black end of the matchsticks.

ii) Cut small pieces of the tube (about 1 cm long).

iii) Push two matchsticks into each end of a tube piece.

iv) Add more matchsticks to form a triangle.
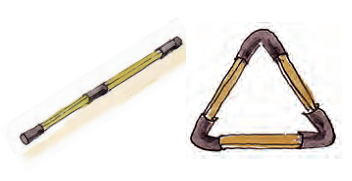
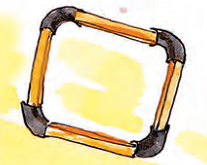
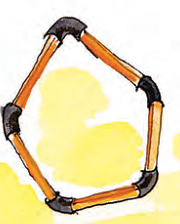
Now make these 4, 5, 6 sided shapes by using tube pieces and matchsticks.
a)
b)
c)
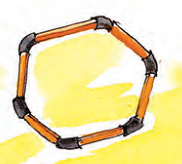
* Find out how many angles are there in each of these shapes. Mark them.
Now push each shape downwards with the tip of your finger.
Does the angle change when pushed down by the finger?
* Find out and write your results in the table given.
Shape | Change in angle Yes/No |
| |
| |
| |
|
Shapes and Towers
Look for triangles in the pictures below.



1. From the activity Changing Shapes' can you guess why triangles are used in these towers, bridges etc?
2. Look around and find out more places where triangles are used.
Angle and Time
Zeenat, your watch does not have digits. How do you read time?
I just see the angles. See, when the hands make a right angle, I know it is 9 o'clock.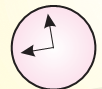
* There are many times in a day when the hands of a clock make a right angle. Now you draw some more.


Triangles are shapes which are strong and do not change easily when pressed. In fact, children can also observe how different shapes are made stronger by using diagonal beams (like in the bridge) which divide shapes into triangles.
* Write what kind of angle is made by the hands at these times. Also write the time.





* Draw the hands of the clock when they make an angle which is less than a right angle. Also write the time.



Answers: Matchstick Puzzles (page 19)
1.

2.

3.

Degree Clock
Appu and Kittu are playing carromboard. Appu hit the striker.
Hm Hm....... It comes back at the same angle.
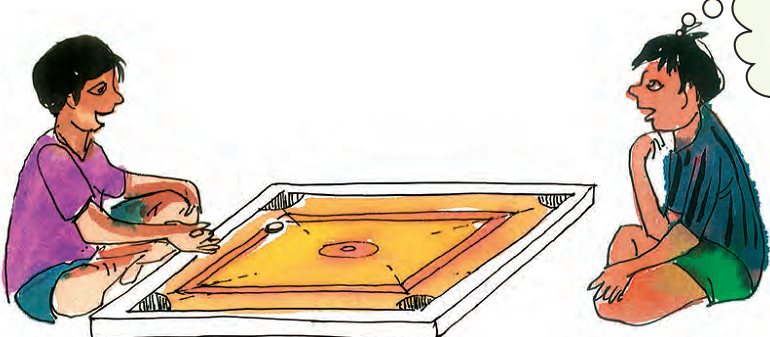
* In the picture three points A, B and C are shown. Draw a line to show from which point Kittu should hit to get the queen. _____
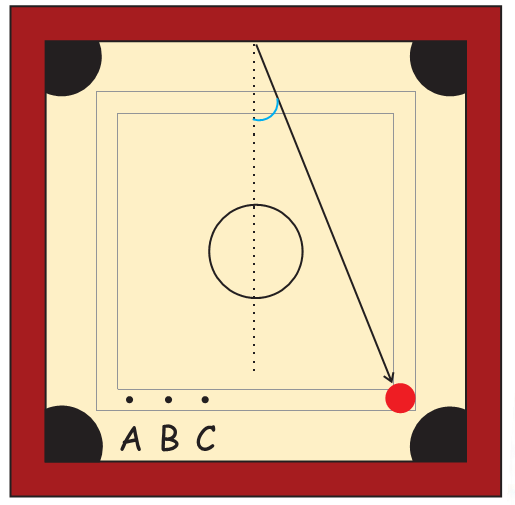
If you want, you can measure the angle in degrees using a degree clock. Degree is written as.
Activity: Making a degree clock
1. Cut a circle out of paper.
2. Fold it into half.
3. Fold it once again into a quarter.
4. Fold it once more.

5. Open the paper. You will see lines like this.
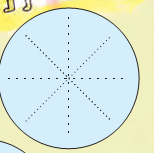
6. Now mark 0°, 45°, 90° and 180° as shown.
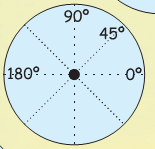
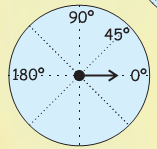
7. Paste it on an old card.
8. From the centre draw one hand.
9. Make a red hand with a thick paper and fix it to the centre with a drawing pin, so that it is free to move.
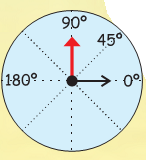
Your degree clock is ready.
* Use your degree clock to measure the right angle of your pencil box _____ is the measure of the right angle.
* Can you guess how many degrees is the angle which is -
a. 1/2 of a right angle _____
b. 1/3 of a right angle. _____
c. 2 times of a right angle _____
* Measure the angle from where Kittu should hit the striker on page 30.
90° is called of a right angle
Angles in a Paper Aeroplane
1. Take a square sheet of paper.

2. Fold it in half and open it.

3. Fold the corners to the centre. Your paper looks like this.

4. Fold the green triangle such that P touches Q.

5. Fold the top two corners of this rectangle along the dotted lines.

6. Your paper will look like this. There is a small triangle in the picture which has to be folded up.
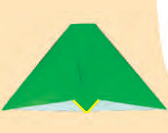
7. Turn it over and fold it in half along the dotted line.

8. Now, to make a wing fold the yellow edge over the red edge.

9. Turn it and do the same on the other side as well.

Your plane is ready to fly. How well does it fly?
* Find the angles of 45° and 90° when you open your plane.
In the aeroplane there are folds of 45°, 90° and other angles. The cut-outs of 30° and 60° are on the last page of the book. Children can be encouraged to measure various angles around them.
Angles with Yoga
Rahmat is doing Yoga. These are the pictures of different 'Asanas' he does everyday.
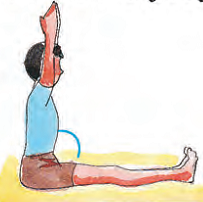
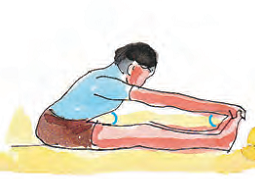
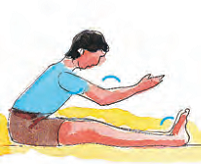
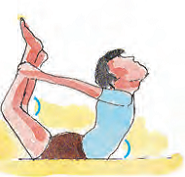
* Estimate the measure of many angles as you can made by different parts of the body while doing 'Asanas'.
The D Game
You can play the 'D' game with your friends. You draw an angle. Your friend will guess the measure of that angle. Then you use your 'D' to measure it. The difference between the measured angle and the guess will be your friend's score. The one with the lowest score will be the winner.
Come on, play!
Draw Angle | Guess | Measure | Score |
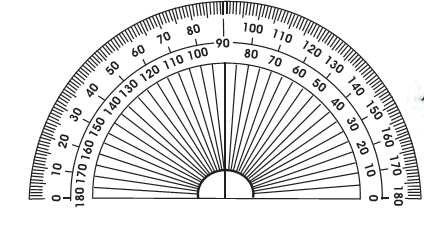
You can find this 'D' in your geometry box. Measure the angle on my head fan.
Take this opportunity to introduce the 'D' (protractor). Children will need some help to read the measure of the angle, but they need to do so only approximately.