Table of Contents

3. How Many Squares?
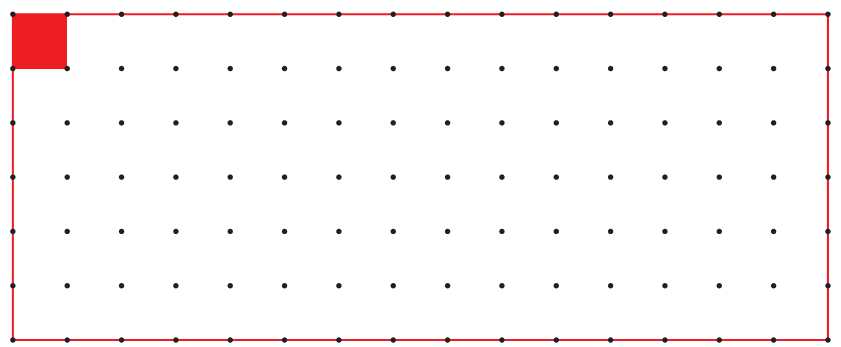
* Measure the side of the square on dotted sheet. Draw here as many rectangles as possible using such squares.
* How many rectangles could you make? _____

Here’ s one!
Each rectangle is made out of 12 equal squares, so all have the same area, but the length of the boundary will be different.
Length of the boundary is called perimeter.
* Which of these rectangles has the longest perimeter?
* Which of these rectangles has the smallest perimeter?
Children are not expected to learn the definition of the term 'area', but develop a sense of the concept through suitable examples. Give them many opportunities in the classroom to compare things in terms of area and guess which is bigger. Things like stamps, leaves, footprints, walls of the classroom etc. can be compared.
Measure Stamps
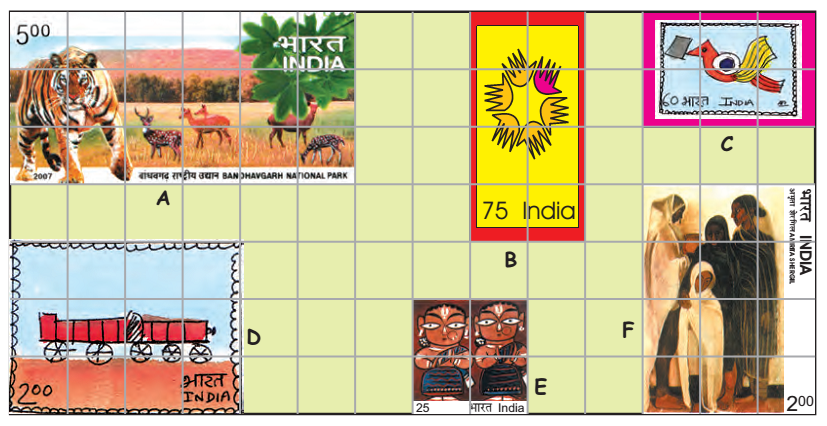
Look at these interesting stamps.
a) How many squares of one centimetre side does stamp A cover? _____
And stamp B? _____
b) Which stamp has the biggest area?
How many squares of side 1 cm does this stamp cover?
How much is the area of the biggest stamp? _____ square cm.
c) Which two stamps have the same area? _____
How much is the area of each of these stamps? _____ square cm.
d) The area of the smallest stamp is _____ square cm.
The difference between the area of the smallest and the biggest stamp is _____ square cm.
Collect some old stamps. Place them on the square grid and find their area and perimeter.
Stamp D covers 12 squares. Each square is of side 1 cm. So the area of stamp D is 12 square cm.
Guess
a) Which has the bigger area — one of your foot prints or the page of this book?
b) Which has the smaller area—two five-rupee notes together or a hundred rupee note?
c) Lookata10rupee-note. Is its area more than hundred square cm?
d) Is the area of the blue shape more than the area of the yellow shape? Why?

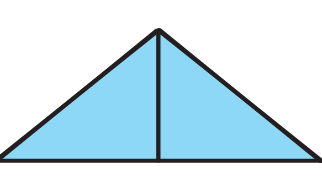

e) Is the perimeter of the yellow shape more than the perimeter of the blue shape? Why?
How Big is MY Hand?
Trace your hand on the squared sheet on the next page.

How will you decide whose hand is bigger — your hand or your friend’s hand?
What is the area of your hand? _____ square cm.
What is the area of your friend’s hand? _____ square cm.


My footprint is longer!
But my footprint is wider. So whose foot is bigger?

My Footprints
* Whose footprint is larger yours or your friend’s?
* How will you decide? Discuss.
* Is the area of both your footprints the same?
My skin has many many folds. So I have a big area! This way the air all over me keeps me cool.

What is the area of my footprint?

What is the area of my footprint?

* Guess which animal’s footprint will have the same area as yours. Discuss.
* Here are some footprints of animals — in actual sizes. Guess the area of their footprints.
Hen
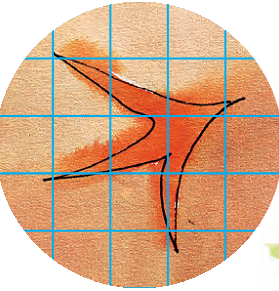

Dog

Make big squares and rectangles like this to find the area faster.

At this stage children need not count each square. Encourage them to identify the largest squares and rectangles within a footprint to know their area and then count small squares for irregular shapes. Though area of a rectangle will be done in chapter 11, some children may discover themselves that they can find the area faster through multiplication.
How Many Squares in Me?
What is the area of this triangle?
The triangle is half the rectangle of area 2 square cm.So its area is _____ square cm.

Is this shape half of the big rectangle?
Hmmm…… So its area is _____ square cm.
* Write the area (in square cm) of the shapes below.
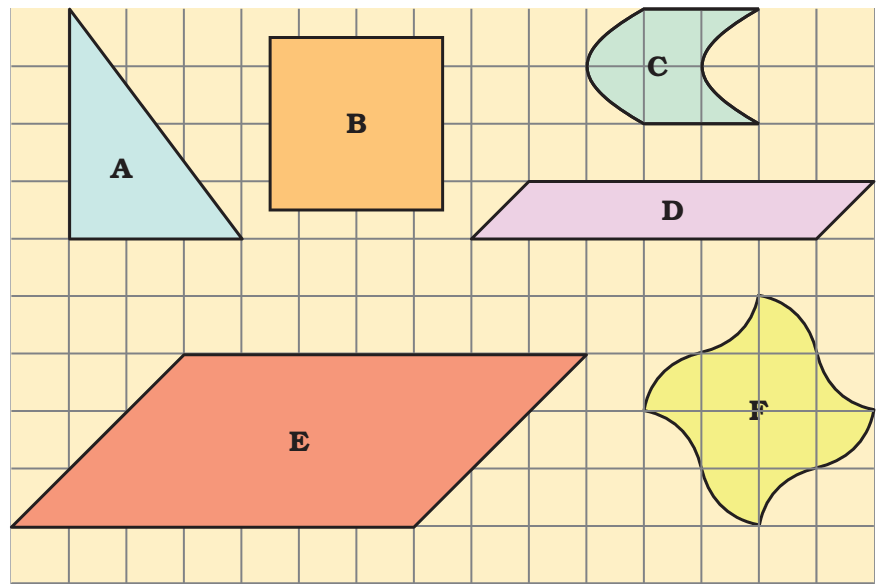
In this exercise children are expected to notice the geometrical symmetry of the shapes to find out their area. Encourage children to evolve their own strategies. Rounding off is not needed in these examples.
Try Triangles
Sameena - Both the big triangles in this rectangle have the same area.
Sadiq - But these look very different.
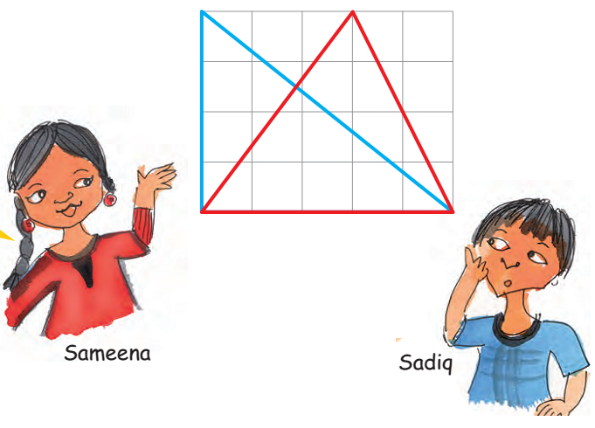
The blue triangle is half of the big rectangle. Area of the big rectangle is 20 square cm. So the area of the blue triangle is _____ square cm.
And what about the red triangle?
Ah, in it there are two halves of two different rectangles!
Now you find the area of the two rectangles Sadiq is talking about.
What is the area of the red triangle? Explain.
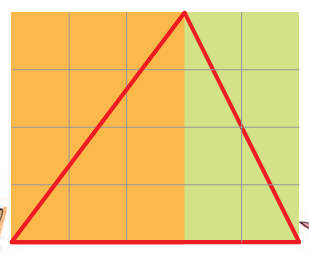
Yes you are right. And you know what!! You can draw many more triangles of area 10 square cm in this rectangle. Try drawing them.
Help Sadiq in finding some more such triangles. Draw at least 5 more.
Complete the Shape
Suruchi drew two sides of a shape. She asked Asif to complete the shape with two more sides, so that its area is 10 square cm.

He completed the shape like this.
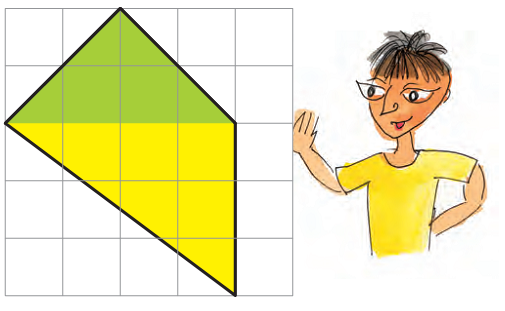
How did you do this?
Oh that's easy! If you look at the green area it is 4 square cm. Below it is the yellow area of 6 square cm. So the area of my shape is 10 square cm!
* Is he correct? Discuss.
* Explain how the green area is 4 square cm and the yellow area is 6 square cm.
Oh, I thought of doing it differently! If you draw like this, the area is still 10 square cm.
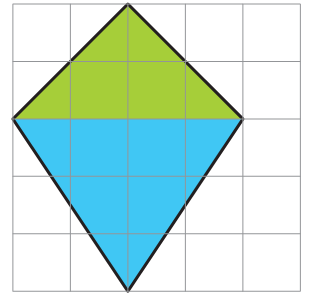
* Is Suruchi correct? How much is the blue area? Explain.
* Can you think of some other ways of completing the shape?
* Try some other ways yourself.
* Now ask your friends at home to solve these.
Every time guests come home, I ask them to do this. But why do they run away!
Practice time
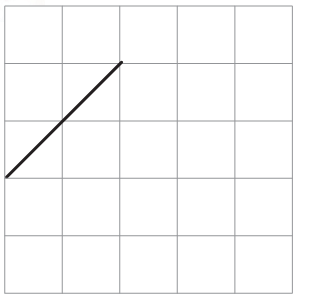
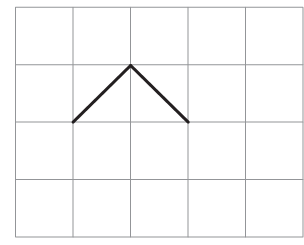
1) This is one of the sides of a shape.
Complete the shape so that its area is 4 square cm.
2) Two sides of a shape are drawn here.
Complete the shape by drawing two more sides so that its area is less than2square cm.
Children can be encouraged to make shapes with either straight edges or curved edges to cover the given area. This exercise can be extended by asking children to draw on squared paper as many shapes as they can of a given area and making guesses for the largest or the smallest perimeter. They can also be asked to check their guesses by measuring the dimensions of the shapes. In case of curved edges, thread can be used for measuring the perimeter.
3) Here is a rectangle of area 20 square cm.
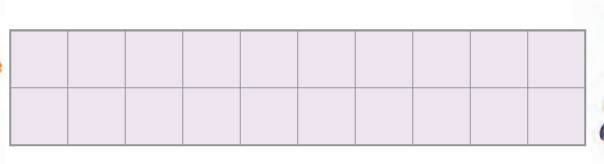
a) Draw one straight line in this rectangle to divide it into two equal triangles. What is the area of each of the triangles?
b) Draw one straight line in this rectangle to divide it into two equal rectangles. What is the area of each of the smaller rectangles?
c) Draw two straight lines in this rectangle to divide it into one rectangle and two equal triangles.

* What is the area of the rectangle?
* What is the area of each of the triangles?

Puzzles with Five Squares
Measure the side of a small square on the squared paper on page 45. Make as many shapes as possible using 5 such squares. Three are drawn for you.


a) How many different shapes can you draw? _____
b) Which shape has the longest perimeter? _____ How much? _____ cm
c) Which shape has the shortest perimeter? How much? _____ cm
d) What is the area of the shapes? _____ square cm. That’s simple!

Did you get all the 12 shapes using 5 squares?
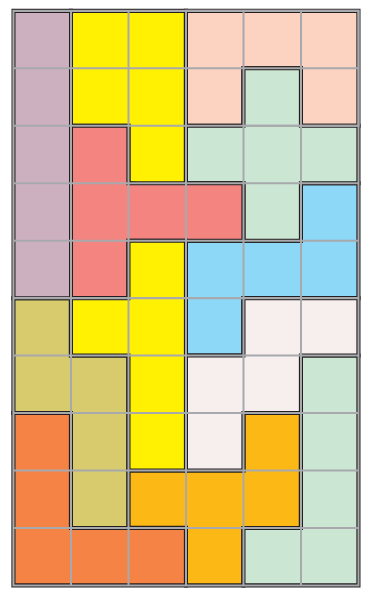
All 12 shapes are arranged here to make a rectangle.
This is a rectangle as there are 10 rows and 6 columns.
You will be surprised to know that there are more than 2000 ways in which these shapes make a 10 X 6 rectangle.
Draw all the 12 shapes on a sheet of cardboard and cut them.
Try to arrange your 12 shapes in some other way to make a rectangle. Could you do it?


Try another puzzle
You have to make a rectangle with these 12 shapes. There are more than 1000 ways to do it. If you can find even one, that’s great!
Game Time
Here is a chessboard. Play this game with your partner, with one set of 12 shapes.
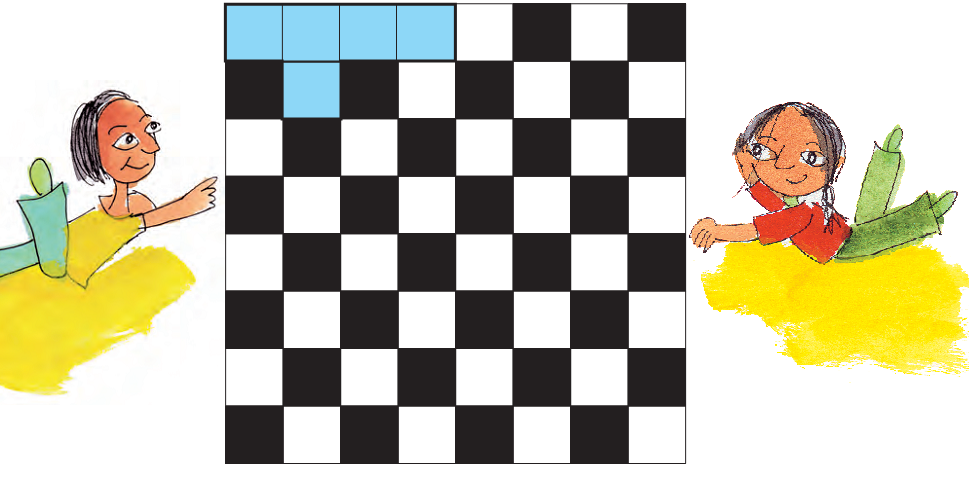
The first player picks one shape from the set and puts it on the board covering any five squares.
The other player picks another shape and puts it on the board, but it must not overlap the first shape.
Keep taking turns until one of you can’t go any further.
Whoever puts the last piece wins!
Make Your Own Tile
Remember the floor patterns in Math-Magic Book 4 (pages 117-119). You had to choose the correct tile which could be repeated to make a pattern so that there were no gaps left.
Encourage children to try to do these ‘pentomino’ puzzles at home. Such exercises can be designed for shapes with 6 squares (hexominoes) in which case there will be 35 different shapes possible.
Ziri went to a shop and was surprised to see the different designs of tiles on the floor.
Aren’t these beautiful!
* Can you find the tile which is repeated to make each of these floor patterns? Circle a tile in each pattern.



After looking at the patterns Ziri wanted to make her own yellow tile. You too make a tile this way.
Step 1: Take a piece of cardboard or thick paper. Draw a square of side 3 cm on it.

Step 2: Draw a triangle on any one of the sides of this square.
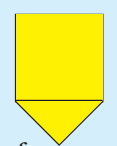
Step 3: Draw another triangle of the same size on another side of the square. But this time draw it inside the square.
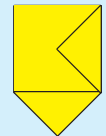
Step 4: Cut this shape from the cardboard. Your tile is ready!

What is it’s area?
Make a pattern using your tile. Trace the shape to repeat it on a page, but remember there must be no gaps between them.
Ziri made a pattern using her yellow tiles. (You know the area of her tile.)
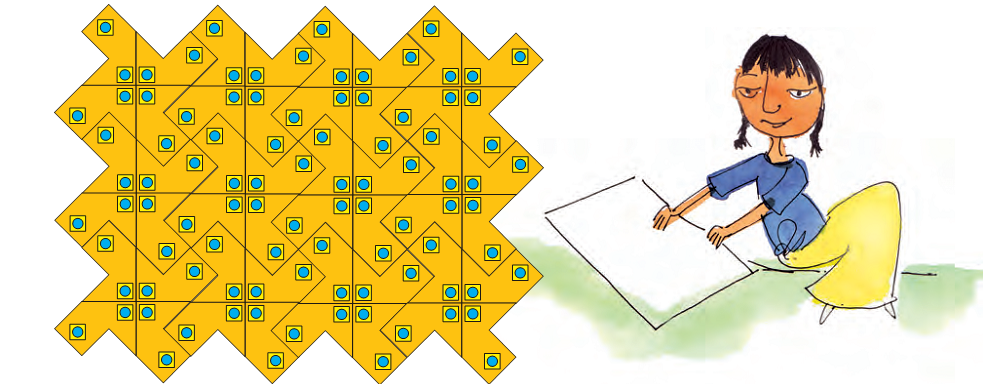
Answer these —
* How many tiles has she used?
* What is the area of the floor pattern Ziri has made here?
Practice time
Ziri tried to make some other tiles. She started with a square of 2 cm side and made shapes like these.
Look at these carefully and find out:
* Which of these shapes will tile a floor (without any gaps)? Discuss. What is the area of these shapes?
* Make designs in your copy by tiling those shapes.
* Now you create your own new tiles out of a square. Can you do the same with a triangle? Try doing it.
In Class III and IV basic shapes like squares, rectangles, hexagons, triangles, circles etc were used to examine which of those can tile and which do not tile to make floor patterns. Children must now be able to modify basic shapes to create different tiling shapes. In the exercise above they may create new shapes out of a square that do not tile even though their area remains the same as that of the square from which they are made.