Table of Contents

6. Be My Multiple, I'll be Your Factor
The Mouse and the Cat
The hungry cat is trying to catch Kunjan the mouse.
Kunjan is now on the 14th step and it can jump 2 steps at a time. The cat is on the third step. She can jump 3stepsatatime. If the mouse reaches 28 it can hide in the hole. Find out whether the mouse can get away safely!
a) The steps on which the mouse jumps —
_____
b) The steps on which the cat jumps —
_____
c) The steps on which both the cat and the mouse jump—
d) Can the mouse get away?
Find out
If the cat starts from the 5th step and jumps five steps at a time and the mouse starts from the 8th step and jumps four steps at a time, can the mouse get away?
Children should be encouraged to make similar questions with different multiples and ask each other to solve.
Who is Monto waiting for?
Monto cat is waiting for somebody. Do you know for whom he is waiting?
There is a trick to find out.
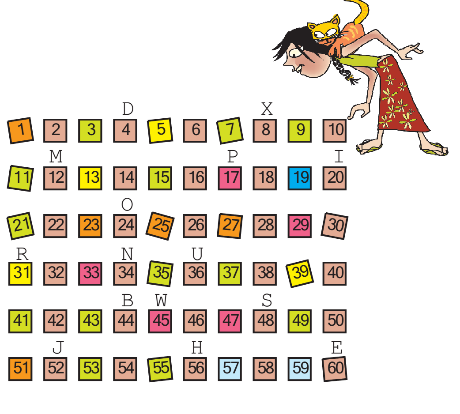
Mark with a red dot all the numbers which can be divided by 2.
Mark a yellow dot on the numbers which can be divided by 3 and a blue dot on the numbers which can be divided by 4.
Which are the boxes which have dots of all three colours?
What are the letters on top of those boxes?
Write those letters below in order.
Meow Game
To play this game, everyone stands in a circle. One player calls out ‘one’. The next player says ‘two’ and so on. A player who has to call out 3 or a number which can be divided by 3 has to say ‘Meow’ instead of the number. One who forgets to say ‘Meow’ is out of the game.
The last player left is the winner.
Which numbers did you replace with ‘Meow’?
3, 6, 9….........................

We say these numbers are the of 3.
Play the game by changing the number to 4.
Now, which numbers did you replace with ‘Meow’?
These numbers are the multiples of 4.
* Write any ten multiples of 5.
Make children play this game several times with multiples of different numbers.
Dice Game
Throw two dice together. What are the numbers that turn up on the faces of the dice? Make a two-digit number using them. If it is a multiple of any of the numbers written next to the circles, you can write it in that circle. Then it is your friend’s turn.
The one who can write more numbers in 10 rounds is the winner.


I have 3 and 2 on my dice. If I make 23, it is not the multiple of any of the numbers. So I will make 32, which is a multiple of 4, and write it in the red circle.
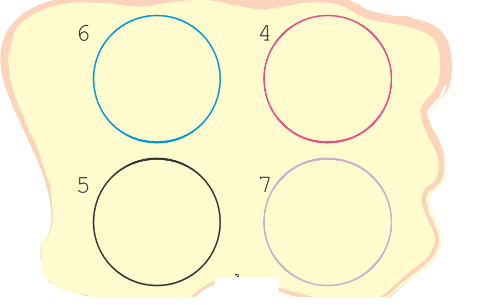
Common Multiples
Think of a number. If it is a multiple of 3 write it in the red circle. If it is a multiple of 5 write it in the blue circle.
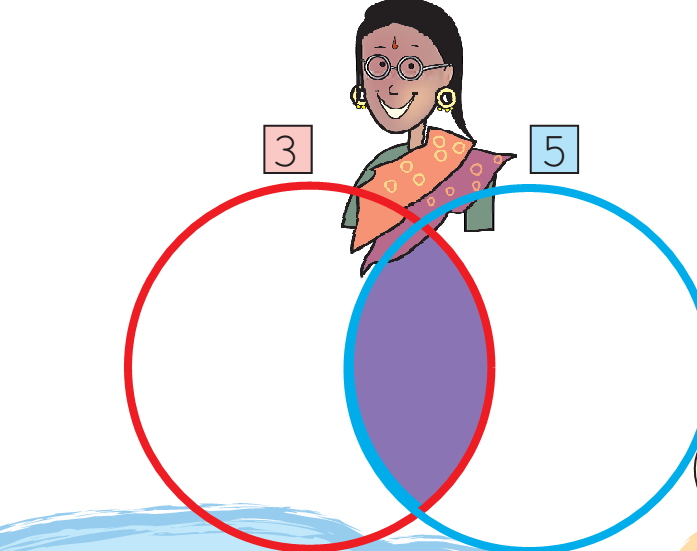
Some numbers are multiples of both 3 and 5.
So we can say that they are toboth3and 5.
Think! If you write the multiples common to 3 and 5 in the purple part, then will they still be in both the red and the blue circles?
1. Which is the smallest among these common multiples? _________
Repeat the game using the numbers 2 and 7.
2. Write the common multiples of 2 and 7.
________________________________________
Repeat the game by putting the multiples of 4,6 and 5 in the circles.
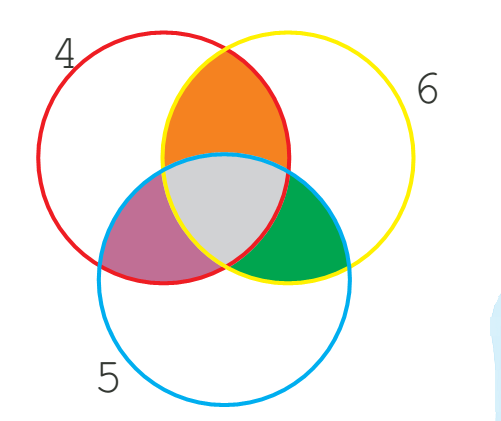
* What common multiples of 5 and 6 did you write in the green part?
* What common multiples of 4 and 6 are written in the orange part?
* In which coloured part did you write the common multiples of 4,6 and 5?
* What is the smallest common multiple of 4,6 and 5? _____
Puzzle
Tamarind seeds
Sunita took some tamarind (imli) seeds. She made groups of five with them, and found that one seed was left over. She tried making groups of six and groups of four. Each time one seed was left over. What is the smallest number of seeds that Sunita had?
Encourage children to try out themselves such activities using seeds, pebbles etc.
More tamarind seeds
Ammini is arranging 12 tamarind seeds in the form of different rectangles. Try to make more rectangles like this using 12 tamarind seeds. How many different rectangles can you make?
If there are 15 tamarind seeds how many rectangles can you make?
Colouring the Grid

In the grid here, a rectangle made of 20 boxes is drawn.
The width of this rectangle is 2 boxes.
* What is its length?
* Colour a rectangle made of 20 boxes in some other way.
* What is the length and width of the rectangle you coloured?
* In how many ways can you colour a rectangle of 20 boxes?
Colour them all in the grid, and write the length and width of each rectangle you have coloured.

Bangles
There are 18 bangles on the rod. Meena is trying to group them. She can put them in groups of 2, 3, 6, 9 and 18 — without any bangle being left.
* How many groups will she have if she makes groups of 1 bangle each? _____
Now complete the table, for different numbers of bangles. For each number see what different groups can be made.

Number of bangles | Different groups we can make |
18 | 1,2,3,6,9,18 |
24 | 1,2, … |
5 |
|
9 |
|
7 |
|
2 |
|
10 |
|
1 |
|
20 |
|
13 |
|
21 |
|
Fill the Chart
Complete the multiplication chart given here.
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
1 |
|
|
|
|
|
|
|
|
|
|
| 12 |
2 |
|
|
|
|
| 12 |
|
|
|
|
|
|
3 |
|
|
| 12 |
|
| 21 |
|
|
|
|
|
4 |
|
| 12 |
|
|
|
|
|
| 40 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
| 12 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
| 72 |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
| 66 |
|
|
|
|
|
|
12 | 12 |
|
|
|
|
|
|
|
|
|
|
|
Look at the green boxes in the chart. These show how we can get 12 by multiplying different numbers.
12 = 4 × 3, so 12 is a multiple of both 4 and 3. 12 is also a multiple of 6 and 2, as well as 12 and 1. We say 1, 2, 3, 4, 6, 12 are Factors of 12.
12
4X3
6X2
1X12
* What are the factors of 10? _____
Can you do this from the chart?
10
5X2
----
* What are the factors of 36? _____
* Find out all the factors of 36 from the multiplication chart.
* What is the biggest number for which you can find the factors from this chart?
* What can you do for numbers bigger than that?
Common factors
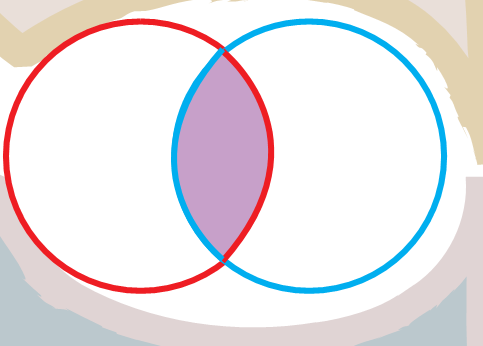
Write the factors of 25 in the red circle and the factors of 35 in the blue circle.

Which are the factors you have written in the common part (purple) of both circles? These are of 25 and 35.
Now write the factors of 40 in the red circle and 60 in the blue circle.
What are the factors written in the common (purple) part of the circle? Which is the biggest common factor of 40 and 60?
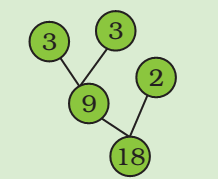
Factor Tree
Look at the factor tree. Now can you make another tree like this?
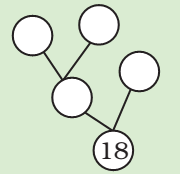
* In how many ways can you draw a factor tree for 24? Draw three of them below.

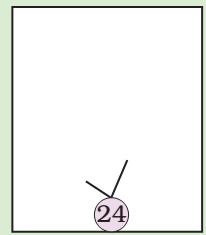
* Try drawing the factor tree using other numbers also.
Tiling Problems
1) There is a garden in Anu’s house. In the middle of the garden there is a path. They decided to tile the path using tiles of length 2 feet, 3 feet and 5 feet.
The mason tiled the first row with 2 feet tiles, the second row with 3 feet tiles and the third row with 5 feet tiles. The mason has not cut any of the tiles. Then what is the shortest length of the path?

2 Manoj has made a new house. He wants to lay tiles on the floor. The size of the room is 9 feet × 12 feet. In the market, there are three kinds of square tiles: 1 foot × 1 foot, 2 feet × 2 feet and 3 feet × 3 feet. Which size of tile should he buy for his room, so that he can lay it without cutting?
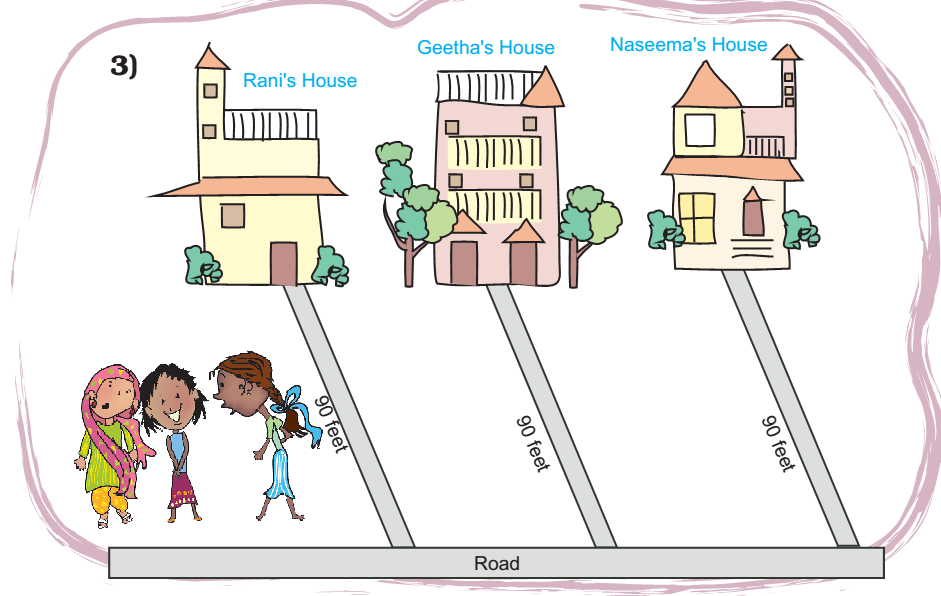
Rani, Geetha and Naseema live near each other. The distance from their house to the road is 90 feet. They decided to tile the path to road. They all bought tiles of different designs and length. Rani bought the shortest tile, Geetha bought the middle sized one and Naseema bought the longest one. If they could tile the path without cutting any of the tiles what is the size of the tiles each has bought? Suggest 3 different solutions. Explain how you get this answer.
It will be useful to have a discussion about a foot and how we use it often to talk about our own heights. Children can use their cm scale to get idea about how long a foot is.