Table of Contents

QR Code Chapter 7

7. Can You See the Pattern?

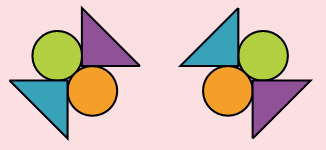
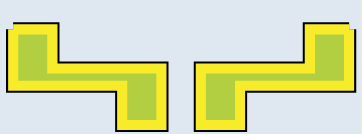
Isha, your skirt is beautiful!

A woman telling a girl that her skirt is beautiful.



My mother made this pattern

The girl is holding her skirt and saying that her mother made the pattern on the skirt.

I have seen the same block making a different pattern on a kurta.

How was it different?

A pattern in which a four sided figure is once up then down and then it is repeated.


In your skirt, the rule of the pattern is: one up, one down. Then this is repeated.

The woman is speaking.

But in my brother’s kurta, it is once up, then takes a ¼ turn every time. The rule is to repeat it with a clockwise turn.

A pattern in which a four sided figure is once up, then takes a one fourth turn and then it is repeated clockwise.

Now you use these two rules to make patterns with this block.

Also make your own rule.

In Math-Magic Class IV (page 107- 108) , children have seen how one motif is used in 3 different ways and in Class III (page 145), the same sequence of motifs is repeated. Discuss how the motif here turns clockwise.

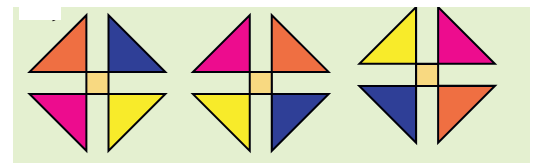
Turns and Patterns

Look at this block . We make three different rules to turn it clockwise and see the patterns.

Rule 1: Repeat it with a one-fourth turn.

A four sided figure is once up, then turns sideways, then down, then turns to he other side and up again. The pattern is then repeated.

Rule 2: Repeat it with a half turn.

A four sided figure is once up and then down and the pattern is repeated.

Rule 3: Repeat it with a three-fourth turn.

A four sided figure is once up, then turns to a side, then down, then turns to the other side and the pattern is repeated.

Practice time

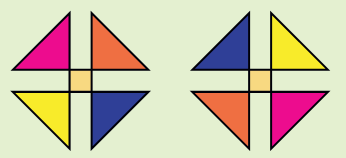
1) What should come next?

a)

A circle is divided into two parts by a line, the line is slanting to the right in the first figure, in the second figure, the line is straight and vertical and in the third figure, it is slanting to the left side, the fourth and fifth boxes are blank.

b)

In the first figure, letter N is written and in the second box, letter N is turned to look like letter Z and in the third box, again Letter N is written. The fourth and fifth boxes are blank.

Encourage children to think of other alternatives. Answers obtained by anticlockwise turns should also be accepted and discussed.

c)

In the first box, there is an inverted triangle with four dots at the base and one dot at the upper end, in the second figure, the triangle is inverted with four dots at the right side and one dot at the left corner, in the third figure, the triangle is inverted with four dots at the left side and one dot at the right corner.

d)

A circle with a four sided closed figure inside it. In the first one, the figure inside the circle is at the base of the circle, in the second one, the figure inside the circle is at the left and in the third, the figure inside the circle is at the top.

2) See this pattern

a)

Letter F is written in the first box, letter F is tilted towards the right in the second box, letter F is turned completely to the right and in the forth box, itis slightly tilted down from its position in the third box. The last box is left blank.

The of the pattern is turning by 45º each time. Which will be the next? Tick (right) the right one.

The letter F is completely sleeping towards the right side.

Letter F is tilted leftwards down from its actual position.

Letter F is now straight down from its actual position.

Using the same rule take it forward till you get back to what you started with.

b)

In the first box, letter L is written, in the second box, it is tilted slightly towards right and the next few boxes are left blank.

c)

In the first box, letter P is written, in the second box, it is tilted slightly towards right and the next few boxes are left blank.

3) Some patterns are given below on the left side of the red line. For each pattern, write the rule. Then choose what comes next from the right side of the line and tick (right) it.

a)

A figure is formed by two triangles and two circles. First it is straight, then it is slightly tilted towards the right and then completely tilted to right.

Rule: _____

he figure is first slightly tilted to right and then to the left from its actual position.

() ()

b)

Image

Rule: _____

Two figures formed by small rectangles.

() ()

c)

Image

Rule: _____

Two patterns, each looking like a level of stairs.

() ()

d)

A laterally inverted S shaped figure, then its tuned to left by forty five degrees and turned again twice similarly.

Rule: _____

A laterally inverted s shaped pattern and then its turned by ninety degrees.

() ()

Look for a Pattern

Mark that picture which is breaking the rule. Also correct it.

a)

A bird shaped pattern, then its is turned by ninety degrees and then repeated again.

b)

An umbrella tuned towards right, then down, then left and then straight and then repeated again.

c)

A flying bird shaped pattern, thrice up, then down, then up and then down again.

d)

A figure formed by a small triangle, outside it is a circle and a closed four sided figure bounds the circle. Then there is another figure formed by a triangle, inside it is a circle and inside it is a small four sided figure. The two figures are then repeated

Magic Squares

Do you remember magic triangles? Come now, let s make some magic squares.

* Fill this square using all the numbers from 46 to 54.

Rule: The total of each line is 150.

49

46

52

47

* Fill this square using all the numbers from 21 to 29.

Rule: The total of each side is 75.

25

You can see Math-Magic Class IV (page 11) for similar magic patterns.

Magic Hexagons

Look at the patterns of numbers in hexagons.

Each side has 2 circles and 1 box.

You get the number in each box by multiplying the numbers in the circles next to it.

A girl with the arms out

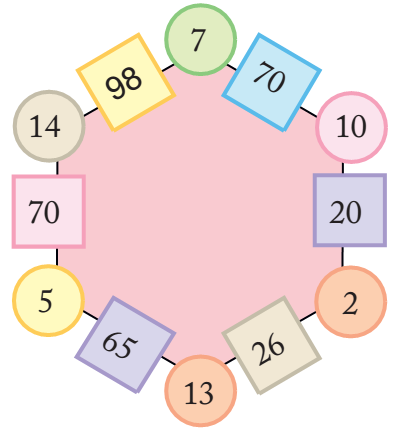
On the boundary of a six sided closed figure, some numbers are written in circles and some in squares. Numbers seven, fourteen, ten, five, thirteen and two are written in small circles and numbers ninety eight, seventy, twenty, sixty five and twenty six are written in small squares.

Capture121

Look at the number 65 in the box.

Which are the circles next to it?

Can you see how the rule works?

1. Use the same rule to fill the hexagons below.

Capture122

Now you also make your own magic hexagons.

You can discuss that a hexagon is a six-sided closed figure, but this is not to be evaluated.

Numbers and Numbers

24+19+37=37+24+19

215+120+600=600+215+120

* Are they equal?

* Fill in the blank spaces in the same way.

a) 14 + _____ + _____ = 34 + 14 + 20

b) _____ +42 + _____ = 65 + _____ + 80

c) 200 + 300 + _____ + = _____ 400 +

d) _____ + _____ + _____ = _____ + _____ +

* Now, look at this — 48 X 13 = 13 X 48

Check if it is true or not.

Left Right — Same to Same

Can you see something special about 121?

What, it’s just a number!

A girl and a boy are standing near a tree. The girl is holding a banner in her hand on which number one hundred twenty one is written.

See it is the same forward as well as backward.

Oh, yes! It is 1,2,1 from right to left also!

Discuss with students that changing the order of numbers does not make any difference to the sum.

Come, let’s see how to get such numbers.

A girl is standing

Take a number, say 43

Then add them together 77

Now turn it back to front 34

77 is one such special number.

There are many such numbers.

You have reversed the number by writing it back to front.


A boy is standing keeping his hand on his head and a bulb is lighting near his head.

Take another number 48

Now turn it back to front 84

Then add them together 132

Is this a special number? No! Why not?

OK, carry on with the number 132

Again turn it back to front 231

Then add the two together 363

Ah! 363 is a special number.

So we see that to get special numbers we sometime need more steps.

* Now you try and change these numbers into special numbers —

a) 28

b) 132

c) 273

Now let’s use words in a special way.

Its written No lemons no melons, step not on pets.

Did you notice that it reads the same from both sides — right to left and left to right?

Now try and use words in a special way.

Special words/numbers which read the same both ways are called palindromes. Help children to read them from both the ends.

Calendar Magic

Look at the calendar below.

Let us mark a 3X3 box (9 dates) on the calendar and see some magic.

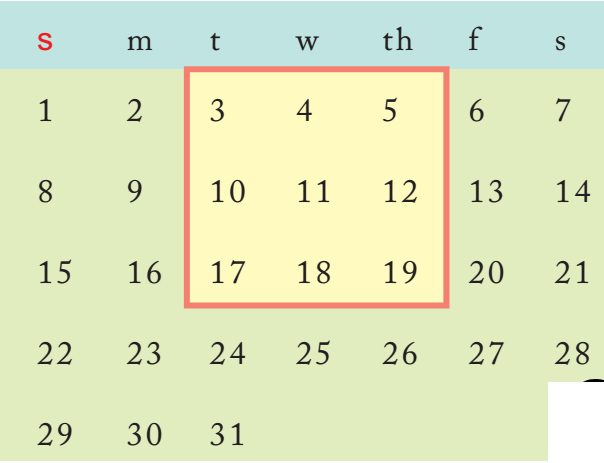
A calendar with dates marked from one to thirty one and days are also marked on the top from Sunday to Saturday. A square is highlighting digits three, four, five, ten, eleven, twelve, seventeen eighteen and nineteen.

I can quickly find the total of these numbers in the box.

A woman with a hand put out.

The total is 99.

Won't that take some time?

A girl is scratching her head.

Take the smallest number 3

Add 8 to it +8

= 11

Multiply it by 9

Total 99

A boy is sitting on the floor.

Hey! Just take the middle number and multiply it by 9. See you can get the answer even faster.


Now you choose any 3X3 box from a calendar and find the total in the same way. Play this game with your family.

You can see Math-Magic Class III (page 105 -106) for other calendar tricks.

Some more Number Patterns

1. Take any number. Now multiply it by 2, 3, 4 ..... at every step. Also add 3 to it at each step. Look at the difference in the answer. Is it the same at every step?

12 X 2 + 3 = 27

12 X 3 + 3 = 39

12 X 4 + 3 = 51

12 X 5 + 3 = 63

12 X __ + 3 = __

__ X  7 + 3 = __

__ X __ + 3 = __

__ X __ + 3 = __

__ X __ + __ = __

Now try doing it with some other number and also take a different number to add at each step .

*  Look at the numbers below. Look for the pattern. Can you take it forward?

(9 – 1) ÷ 8 = 1

(987 – 3) ÷ 8 = 123

(98 – 2) ÷ 8 = 12

(9876 – 4) ÷ 8 = ____

(98765 – 5) ÷ 8 = ____

( ________–__ ) ÷ 8 = ____

( __________–__ ) ÷ 8 = ____

Encourage children to read aloud the numbers on the left hand side, even if they can not read them correctly. Some of the numbers are large. To help children read them, recall the concept of 1 lakh or 100 thousand.

Smart Adding

What if someone gives you to add ten numbers together?

A girl wearing a spectacles.

Oh! I can find it quickly.

Smart! How can you do that?

I can get the sum without adding.

A boy is thinking something.

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55

11 + 12 + _____ + _____ + _____ + _____ + _____ + _____ + _____ +20 = 155

21 + _____ + _____ + _____ + _____ + _____ + _____ + _____ + _____ +30 = _____

31+ _____ + _____ + _____ + _____ + _____ + _____ + _____ + _____ +40 = _____

41+ _____ + _____ + _____ + _____ + _____ + _____ + _____ + _____ +50 = _____

51 + _____ + _____ + _____ + _____ + _____ + _____ + _____ + _____ + 60 = 555

61 + _____ + _____ + _____ + _____ + _____ + _____ + _____ + _____ + 70 = _____

1. Did you notice some pattern in the answers?

Fun with Odd Numbers

Take the first two odd numbers. Now add them, see what you get.

Now, at every step, add the next odd number.

1 + 3 = 4 = 2 X 2

1 + 3 + 5 = 9 = 3 X 3

1 + 3 + 5 + 7 = 16 = 4 X 4

1 + 3 + 5 + 7 + 9 = __ = __X__

1 + 3 + 5 + 7 + 9 + 11 = __ = __X__

1 + 3 + 5 + 7 + 9 + 11 + 13 = __ = __X__

How far can you go on?

When we add the first n odd numbers, we will get the sum as nXn . Children should be left free to add the numbers.

Secret Number

Banno and Binod were playing a guessing game by writing clues about a secret number. Each tried to guess the other’s secret number from the clues.

Can you guess their secret numbers?

What is my secret number? _____

1. It is larger than half of 100

2. It is more than 6 tens and less than 7 tens

3. The tens digit is one more than the ones digit

4. Together the digits have a sum of 11

What is my secret number? _____

1. It is smaller than half of 100

2. It is more than 4 tens and less than 5 tens

3. The tens digit is two more than the ones digit

4. Together the digits have a sum of 6

* Write a set of clues for a secret number of your own. Then give it to a friend to guess your secret number.

Number Surprises

a) Ask your friend rite — W down your A age. dd 5 to it. Multiply the sum by 2. Subtract 10 from it. Next divide it by 2. What do you get?

Is your friend surprised?

b) Take a number _____

Double it _______ X 2 = ______

Multiply by 5  _______ X 5 = ______

Divide your answer by 10 _______ X 10 = ______


c) Take a number _____

Double it  _________

Again double it  _______ X 2 = ______

Add the number you took first to the answer _____ + _____ = _____

Now again double it  _______ X 2 = ______

Divide by 10  _______ / 10 = ______


d) Look at this pattern of numbers and take it forward.

1 = 1 × 1

121 = 11 × 11

12321 = 111 × 111

1234321 = ?

* Now make your own number surprises.