Table of Contents

9. Boxes and Sketches
Sweet Box
Ramya went to buy sweets. The shopkeeper took a paper cut-out and quickly made a lovely pink box for the sweets!
* Look at the photo and make your own box. Use the cut-out on page 201. How fast can you fold it?
2. After coming home Ramya unfolded the box. She removed the extra flaps so the cut-out looked like this.

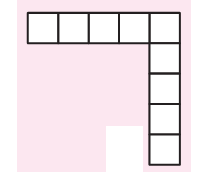
This shape makes a box. Let me see what other shapes will make a box.
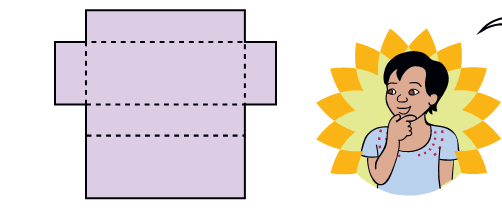
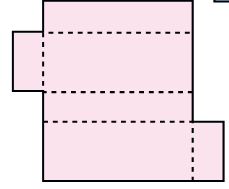
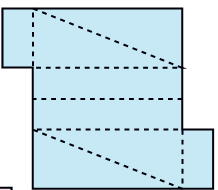
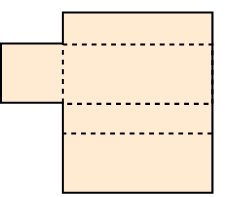
* She made four more shapes. Each is to be folded along the dotted lines. You have to find out which of these can be made into a box.
a)
b)
c)
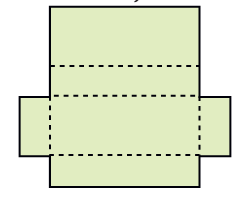
d)
This chapter focuses on visualisation of 3-dimensional shapes and how they can be represented on paper (in 2 dimensions). The representation used here are nets (like the ones above), layout plans for a house, and perspective drawings.
Shapes that Fold into a Cube
A. Buddha wants to make a paper cube using a squared sheet. He knows that all the faces of a cube are squares.
He draws two different shapes.
How many faces does the cube have? _____
* Will both these shapes fold into a cube?
* Draw at least one more shape which can fold into a cube.
* What will be the area of each face of the cube?
* Draw one shape which will not fold into a cube.
* Look around and discuss which things around you look like a cube. List a few.
Shapes for an Open Box
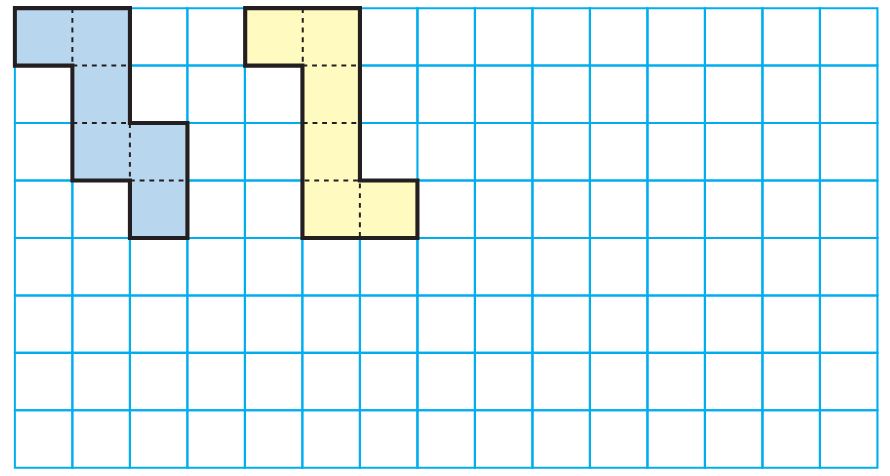
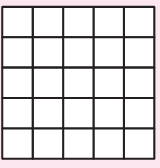
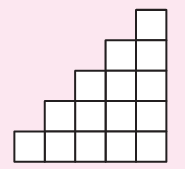
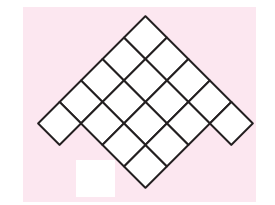
Remember the puzzles with five squares in chapter 3? You saw 12 different shapes made with five squares (page 46).
If you cut those shapes and fold them, some of those will fold into an open box (box without a top).
I can make open boxes with both these.
But with these I cannot make open boxes.
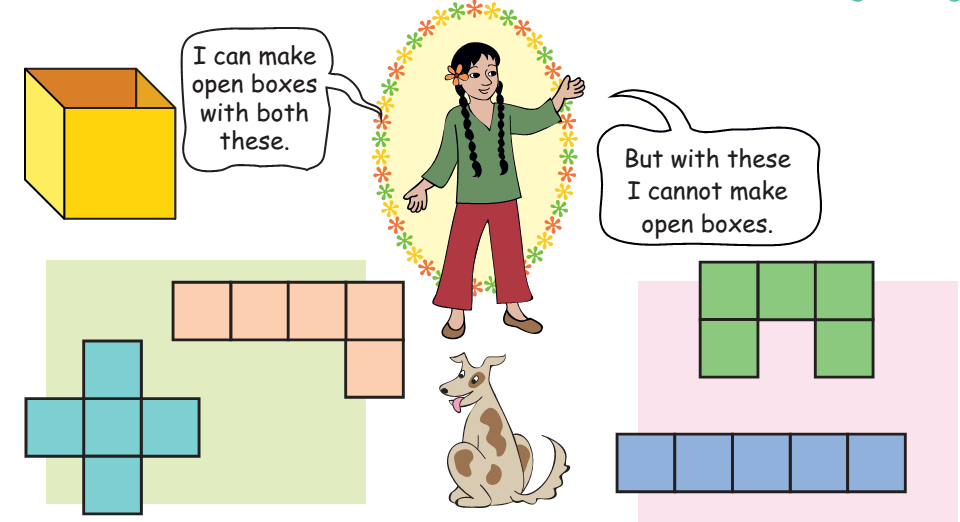
* Find out which of the other 8 shapes (on p 46) can be folded to make an open box.
* Draw more shapes which will not fold to make an open box.
Boxes and Boxes
All boxes are not cubes. Here are some different kinds of boxes.
Match the shape on the left with a box into which it will fold.
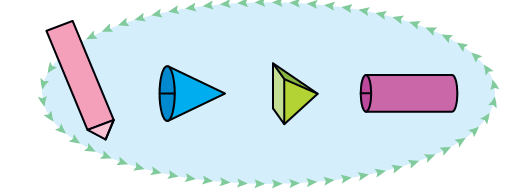
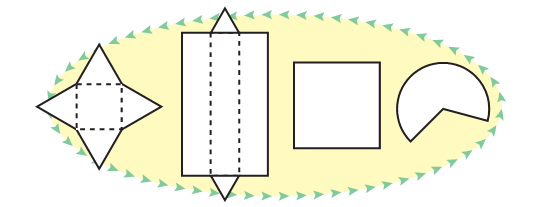
Making mental images of shapes is an important mathematical ability. Children will need many exercises to visualise the net of a box, to think of how it looks when flattened, and also to check which nets (like those on page 126) do not make a box.
Floor Maps
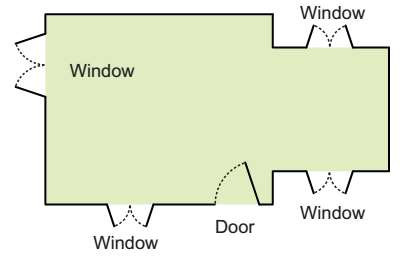
For making a house a floor map is first made. Have you ever seen a floor map? Here is a floor map of Vibha’s house. It shows where the windows and the doors are in the house.
* Which is the front side of her house? How many windows are there on the front side?
From the floor map we cannot make out what her house really looks like or how high the windows are. So we look for a special way of drawing the house which is deep — to show the length, width and height.
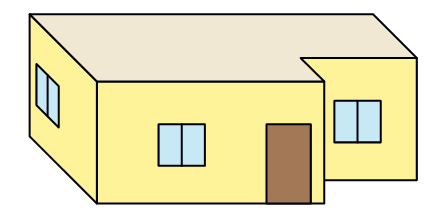
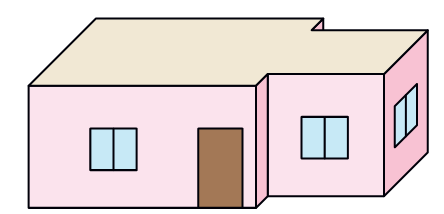
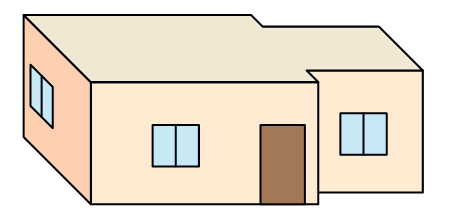
Here are four deep drawings of houses.
* Which one is Vibha’s house?
a)
b)
c)
d)
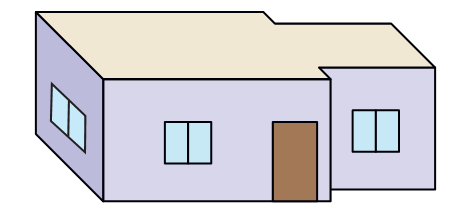
* Why do the other three deep drawings not match the floor map? Discuss.
A 3-dimensional perspective drawing has been called a 'deep drawing' so that children get a sense of the need to represent depth. They should be able to see the difference between deep drawings and layout plans.
Practice time
1. Look at this floor map of a house. Make doors and windows on the deep drawing of this house.
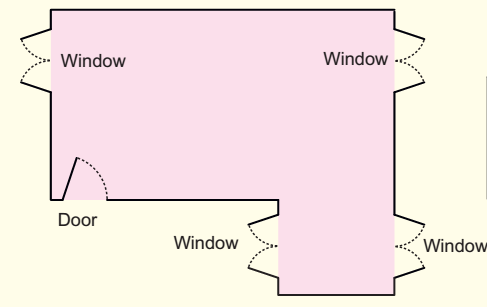
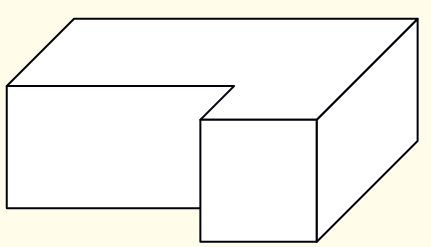
* Are there any windows you couldn’t show on the deep drawing? Circle them on the floor map.
2. Try to make a floor map of your own house.
A Deep Drawing of a Cube
Soumitro and his friends made deep drawings of a cube.
These are their drawings.
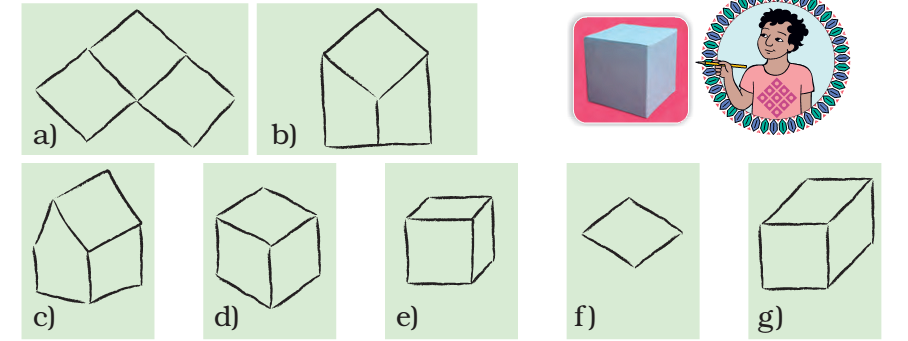
* Which of the drawings look correct to you? Discuss.
* Can you add some lines to make drawing f) into a deep drawing of the cube?
Puzzle
This cut-out is folded to make a cube.
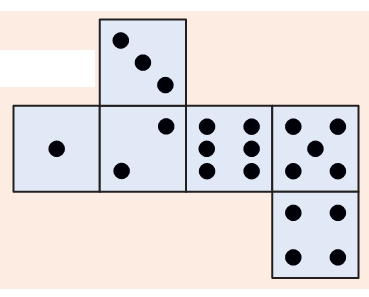
Which of these are the correct deep drawings of that cube?
a)
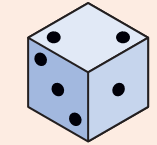
b)
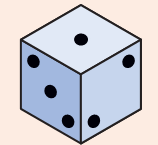
c)

d)

e)
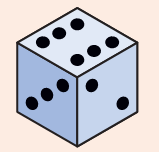
A Simple Way to Draw a Cube
Chanda wants to make a deep drawing of this cube.
She draws the cube like this.

I drew two squares like this to show the front face and the back face.
I joined the corners of the squares like this to make the deep drawing of the box.

* In the same way make a deep drawing of a box which looks like this.

The 2D representation of 3D objects is a matter of convention and is learnt by children through experience. Here the conventional way of drawing the cube is given.
Matchbox Play
Navin, Bhaskar and Pratigya made this bridge using matchboxes.

Navin and Pratigya made drawings of the bridge.
The bridge looks like this to me from where I am standing.
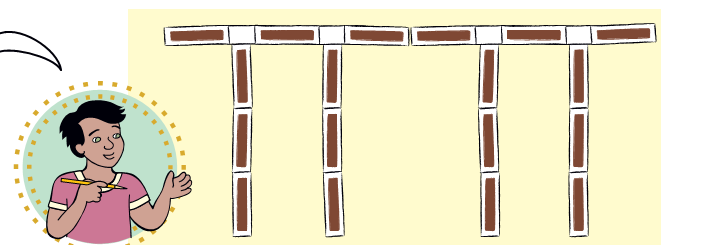
The bridge looks like this to me. My drawing shows how high our bridge is and how wide it is.
From your drawing I can make out how long and how high the bridge is. But I cannot make out how wide it is.

* If you look at the bridge from the top, how will it look? Choose the right drawing below:
a)

b)

* Look at the photo and try to make a deep drawing of this bridge.
Practice time
1) Make drawings to show how this bridge will look
* From the top
* From the front
* From the side

2) Make a matchbox model which looks like this.
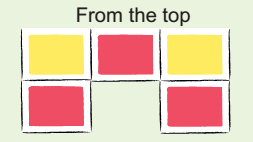
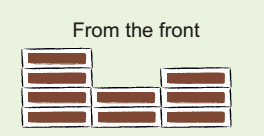
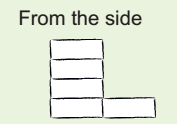
* Also make a deep drawing of the model in your notebook.
3) How many cubes are needed to make this interesting model?
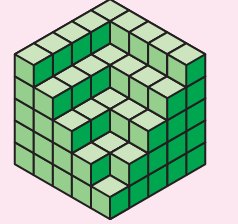
* Here are some drawings of the model. Mark the correct top view drawing with 'T' and the correct side view drawing with'S'.
a)
b)
c)
d)