Table of Contents

11. Area and its Boundary
Whose Slice is Bigger?
Parth and Gini bought aam paapad (dried mango slice) from a shop.
Their pieces looked like these.


Both could not make out whose piece was bigger.
* Suggest some ways to find out whose piece is bigger. Discuss.
A friend of Parth and Gini showed one way, using small squares.

The length of piece A is 6 cm.
So 6 squares of side 1 cm can be arranged along its length.
The width of piece A is 5 cm.
So 5 squares can be arranged along its width.
* Altogether how many squares can be arranged on it? _____
* So the area of piece A = _____ square cm

It's silly to count them all! Just multiply!
1. In the same way find the area of piece B.
2. Who had the bigger piece? How much bigger?
Cover with Stamps
This stamp has an area of 4 square cm. Guess how many such stamps will cover this big rectangle.

Encourage children to first discuss different strategies for comparing the area of things by using different tokens, stamps, etc. In Class IV they have compared irregular shapes by counting squares. In the case of rectangles they can measure the sides to see how many squares of 1 cm side will fit in the whole shape.
Check your guess
a) Measure the yellow rectangle. It is _____ cm long.
b) How many stamps can be placed along its length? _____
c) How wide is the rectangle? _____ cm
d) How many stamps can be placed along its width? _____
e) How many stamps are needed to cover the rectangle? _____
f) How close was your earlier guess? Discuss.
g) What is the area of the rectangle? _____ square cm
h) What is the perimeter of the rectangle? _____ cm
Practice time
a) Arbaz plans to tile his kitchen floor with green square tiles. Each side of the tile is 10 cm. His kitchen is 220 cm in length and 180 cm wide. How many tiles will he need?

b) The fencing of a square garden is 20 m in length. How long is one side of the garden?

c) A thin wire 20 centimetres long is formed into a rectangle. If the width of this rectangle is 4 centimetres, what is its length?
This Guess and check activity can be done in the class by making use of other things present. For example: how many postcards can be placed on the top of the mathematics book, how many charts will cover the classroom walls, etc? Children can be asked to check their guesses by tiling things wherever possible. Once they are able to make close guesses, this work can be further extended by asking them to guess the area in terms of square cm.
d) A square carrom board has a perimeter of 320 cm.
How much is its area?
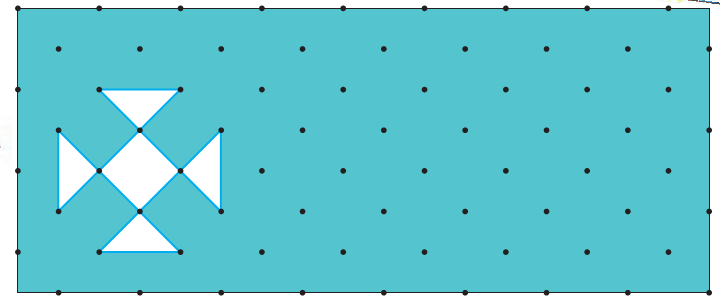
e) How many tiles like the triangle given here will fit in the white design?
This triangle is half of the cm square
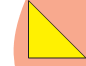
Area of design = _____ square cm

* Make your own designs of area 4 and 6 square cm.
f) Sanya, Aarushi, Manav and Kabir made greeting cards. Complete the table for their cards:
Whose card | Length | Width | Perimeter | Area |
Sanya | 10 cm | 8 cm |
|
|
Manav | 11 cm |
| 44 cm |
|
Aarushi |
| 8cm |
| 80 square cm |
Kabir |
|
| 40 cm | 100 square cm |
My Belt is Longest!
Take a thick paper sheet of length 14 cm and width 9 cm. You can also use an old postcard.
* What is its area? What is its perimeter?
* Now cut strips of equal sizes out of it.
Using tape join the strips, end to end, to make a belt.
* How long is your belt? _____
* What is its perimeter _____
* Whose belt is the longest in the class? _____
Discuss
* Why did some of your friends get longer belts than others?
* Is the area of your belt the same as the area of the postcard?
Why or why not?
* What will you do to get a longer belt next time?
This belt is for the elephant.

Look! I can pass through a postcard. I made a loop without cutting the strips.

Puzzle: Pass through a Postcard
Can you think of how to cut a postcard so that you can pass through it? (See photo.) If you have tried hard enough and still not got it… look for the answer somewhere ahead.
The aim of the belt activity is to understand that things with the same area can take different forms and also have very different perimeters. While measuring sides, lengths in mm can be rounded off for this activity.
People People Everywhere
A) You can play this game in a ground.
Make two squares of one square metre each.
Divide your class in two teams. Ready to play!
With four Math-Magic books in a line you can get the length of around one metre 9 cm.
Try these in your teams —
* How many of you can sit in one square metre? _____
* How many of you can stand in it? _____
* Which team could make more children stand in their square? How many? _____
* Which team could make more children sit in their square? How many?

B) Measure the length of the floor of your classroom in metres. Also measure the width.
* What is the area of the floor of your classroom in square metres? _____
* How many children are there in your class? _____
* So how many children can sit in one square metre? _____
* If you want to move around easily then how many children do you think should be there in one square metre? _____

Can you imagine how big a square of side 1 km is! It has an area of _____ square km.
Guess how many people can live on that.

In West Bengal there are about 900 people living in a square km.
But in Arunachal Pradesh it feels very lonely! There are less than 15 people living in a square km!
Share the Land
Nasreena is a farmer who wants to divide her land equally among her three children — Chumki, Jhumri and Imran. She wants to divide the land so that each piece of land has one tree. Her land looks like this.

Children are not expected to do conversion of sq m into sq km or vice-versa. The aim of exercise B is to develop a sense of how big or small the units of sq m and sq km are.
* Can you divide the land equally? Show how you will divide it. Remember each person has to get a tree. Colour each person’s piece of land differently.
* If each square on this page is equal to 1 square metre of land, how much land will each of her children get? _____ square m
Chumki, Jhumri and Imran need wire to make a fence.
* Who will need the longest wire for fencing? _____
* How much wire in all will the three need? _____


Practice time
A. Look at the table. If you were to write the area of each of these which column would you choose? Make a (Right).
| Square cm | Square meter | Square km |
| Right |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Total land of a city |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Land over which a river flows |
|
|
|
B. Draw a square of 9 square cm. Write A on it.
Draw another square with double the side.
Write B on it.
Answer these —
1. The perimeter of square A is _____ cm.
2. The side of square B is _____ cm.
3. The area of square B is _____ square cm.
4. The area of square B is _____ times the area of square A.
5. The perimeter of square B is _____ cm.
6. The perimeter of square B is _____ times the perimeter of square A.
Answer — Pass Through a Postcard (page 152)
1.

Make lines on a postcard like this.
2.

Cut the postcard only on the lines.
3.

So, can you pass through it!
* You know the area of the loop, don’t you? It is _____
Thread Play
Take a 15 cm long thread. Make different shapes by joining its ends on this sheet.

A) Which shape has the biggest area? How much? _____
What is the perimeter of this shape? _____
B) Which shape has the smallest area? How much? _____
What is the perimeter of this shape? _____
Also make a triangle, a square, a rectangle and a circle. Find which shape has biggest area and which has the smallest.

Save the Birds
There are two beautiful lakes near a village. People come for boating and picnics in both the lakes. The village Panchayat is worried that with the noise of the boats the birds will stop coming. The Panchayat wants motor boats in only one lake. The other lake will be saved for the birds to make their nests.

a) How many cm is the length of the boundary of lake A in the drawing? _____ (use thread to find out)
b) What is the length of the boundary of lake B in the drawing?
c) How many kilometres long is the actual boundary of lake A?
d) How many kilometres long is the actual boundary of lake B?
e) A longer boundary around the lake will help more birds to lay their eggs. So which lake should be kept for birds? Which lake should be used for boats?
f) Find the area of lake B on the drawing in square cm. What is its actual area in square km?
King's Story
The King was very happy with carpenters Cheggu and Anar. They had made a very big and beautiful bed for him. So as gifts the king wanted to give some land to Cheggu, and some gold to Anar.
Cheggu, take as much land as what comes within 100 meters of wire.

Cheggu was happy. He took 100 metres of wire and tried to make different rectangles.
He made a m rectangle. Its area was 400 square metres.
So he next made a rectangle.
* What is its area? Is it more than the first rectangle?
* What other rectangles can he make with 100 metres of wire? Discuss which of these rectangles will have the biggest area.
Cheggu’s wife asked him to make a circle with the wire. She knew it had an area of 800 square metres.
* Why did Cheggu not choose a rectangle? Explain.
Ah! I want this piece of land. It covers an area of 800 square metres.

Ok. Cheggu has taken 800 square metres of land. Anar! Now I will give you as much gold wire which can make a boundary for land with area 800 square metres.

So Anar also tried many different ways to make a boundary for 800 square metres of land.
* He made rectangles A, B and C of different sizes. Find out the length of the boundary of each. How much gold wire will he get for these rectangles?

A
40m X 20m Gold wire for A = _____ metres
B
80m X 10m Gold wire for B = _____ metres
C
800m X 1m Gold wire for C = _____ metres
But then Anar made an even longer rectangle.... See how long!
D
8000m X 0.1m So he will get _____ metres of gold wire!!
Gosh! How can I give so much gold?
Now do you understand why the king fainted!!!
Can you make a rectangle with a still longer boundary? I made a rectangle 1 cm wide and 80000 m long. Imagine how long that boundary will be!!! With that much gold wire I can become the king!
 Handkerchief
Handkerchief Sari
Sari Page of your book
Page of your book School land
School land Door of your classroom
Door of your classroom Chair seat
Chair seat Blackboard
Blackboard Indian flag
Indian flag