Table of Contents

14. How Big? How Heavy?
Sarika collects things like marbles, coins, erasers etc. She takes some water in a glass and marks the level of water as '0'.

If I drop 5 marbles in this glass, can you guess what will be the level of water?
I think this much.
She drops 5 marbles in the glass. She marks the new level of water as 5 marbles.

Oh, how did you guess! Do you know the volumeof a marble?
I just made a guess about how much water will be pushed up by the marbles. How do you find the volume?
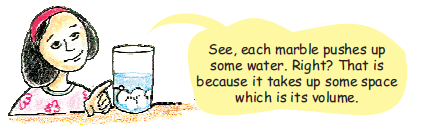
See, each marble pushes up some water. Right? That is because it takes up some space which is its volume.
Children will need more exercises to compare the volume of solid bodies by guessing and by informal measurement (using marbles, coins, matchboxes, etc.) before they begin to use formal measures such as litres and cubic centimetres.
Your Measuring Glass
Now make a guess. Do you think the volume of 10 five-rupee coins will be more than that of 10 marbles?

Guess the volume of each of these:
- A ball is nearly _____ marbles.
- An eraser is nearly _____ marbles.
- A lemon is nearly _____ marbles.
- A pencil is nearly _____ marbles.
- A potato is nearly _____ marbles.
Now make your own measuring glass using 35 marbles.
Take a glass of water and mark the level of water as ‘0’. Then put in 5 marbles and mark the level of water as 5 M.
Again drop 5 marbles and mark the level of water as 10 M. Likewise make the markings for 15 M, 20 M, 25 M, 30 M and 35 M.
Now put each thing in the measuring glass and check your guess.
Try with different things like a matchbox, a stone, etc. and fill the table.

The matchbox floats. How do I find its volume?
Let's fill it with sand or nails.
Name of the thing | Its volume (nearly how many marbles?) |
|
|
|
|
|
|
|
|
Children can paste a paper strip on the glass and mark the level of water using a pen or a pencil. The aim is to develop sense of the concept of volume through examples and hands on activities without giving a definition of volume. Comparing things on the basis of volume is more abstract then comparison in terms of length or area.
Which has More Volume?

Can you tell me the volume of 6 marbles in mL?
Yes, if we make a measuring bottle.
In Class IV you made a measuring bottle for 250 mL.
Can you think of ways for making a measuring bottle which can measure 10 mL, 20 mL, 30 mL, ………., 60 mL? Discuss with your friend.
Tariq and Mollie made their measuring bottles.
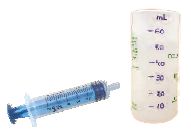
Tariq had an injection. He used it to make his measuring bottle. Mollie used an empty medicine bottle.

I took 5 mL once in my injection. I filled it twice to mark 10 mL on my bottle.
I used this bottle which measures 10 mL to make my measuring bottle.
Mollie used her measuring bottle to find the volume of five-rupee coins. She found that 9 five-rupee coins push up 10 mL of water. So you can also use 9 five-rupee coins to make your measuring bottle! Go ahead!
Use your measuring bottle to find out:
a) What is the volume of 6 marbles? _____ mL.
b) What is the volume of 16 one-rupee coins? _____ mL.
Now solve these in your mind.
c) The volume of 24 marbles is _____ mL.
d) The volume of 32 one-rupee coins? _____ mL.
e) Mollie puts some five-rupee coins in the measuring bottle.
How many coins has she put in it:
- if 30 mL water is pushed up? _____
- if 60 mL water is pushed up? _____
First guess and then use your measuring bottle to find out the volume in mL of some other things.
Thing | Its volume (in mL) |
|
|
|
|
|
|

Guess how many litres of water your body will push up?!
How Many Can Fit In?
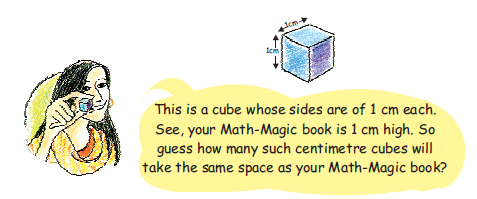
This is a cube whose sides are of 1 cm each. See, your Math-Magic book is 1 cm high. So guess how many such centimetre cubes will take the same space as your Math-Magic book?
To make a measuring bottle, make children use a wide-mouthed and transparent bottle so that markings can be made easily. The activity aims to develop measurement skills in children and involves both making and handling apparatus (such as measuring bottle) in the mathematics classroom.

Hey, my Math- Magic book is about _____ cm long. So _____ cubes will fit along its length.

And it is about cm wide. So cubes will fit along the width.
So total _____ cm cubes will fit on the Math-Magic book.
- Now if all these cubes are arranged in one line then how long will that line be? _____ cm

Practice time
1. A stage (platform) is made with 5 Math-Magic books. The volume of this stage is the same as _____ cm cubes.
2. Guess the volume of these things in cm cubes.
- A matchbox is about _____ cm cubes.
- A geometry box is about _____ cm cubes.
- An eraser is about _____ cm cubes.
How will you check your guess? Discuss.
Matchbox Play
Tanu is making a stage with matchboxes.
She first puts 14 matchboxes like this in the first layer.

The activity 'How many can fit in' requires a sense of the size of a cm cube. For finding the volume of different shapes, the teacher can make cm cubes and use matchboxes to make different models. Tanu's stage or Mohan's model are examples where children calculate volume in terms of matchboxes, which may later be converted into cm cubes.

She makes 4 such layers and her stage looks like this.
- She used _____ matchboxes to make this stage.

- The volume of one matchbox is the same as 10 cm cubes. Then the volume of this stage is same as _____ cm cubes.
- If all these cubes are arranged in a line, how long will that line be? _____ cm.
- Which has more volume — your Math-Magic book or Tanu’s platform?
With your friends, collect many empty matchboxes of the same size. Measure the sides and write here.
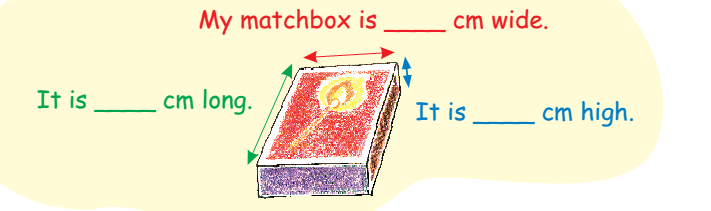
- Use 56 matchboxes to make platforms of different heights.
Fill this table.
| How high is it? | How long is it? | How wide is it? |
Platform 1 |
|
|
|
Platform 2 |
|
|
|
Platform 3 |
|
|
|
The volume of each platform is equal to ________matchboxes.
- Make deep drawings of the platforms you have made.
Practice time
Mohan arranged his matchboxes like this.

- How many matchboxes did he use to make it? What is its volume in matchboxes? _____ matchboxes.
- Collect empty matchboxes. Arrange them in an interesting way. Make a deep drawing of it.
Making a Paper Cube
Aanan and his friends are making a cube with paper. They cut a sheet of paper into a square of 19.5 cm side. They cut 6 such squares. Follow these photos to make your paper cube.
1. Fold the paper into four equal parts to make lines like this.

2. Fold the top left corner and the corner opposite to it like this.

3. Fold the top and the bottom edges to meet the centre line. Now fold corner P...

4. 4. So that the paper looks like this.

5. Fold corner Q in the same way. The paper will look like this now.

6. Lift corner P and slip it under the folded paper like this.
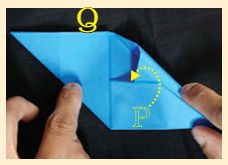
7. Do the same for corner Q. The paper will look like this.

8. Turn the paper and fold it to make lines like these.

9. Each child should make one such piece. Six children will take their pieces and put one inside another to make this paper cube.

Encourage children to make different shapes of the same volume using identical units, for example, bricks or matchboxes. To calculate the sides of the platform lengths can be rounded off to the nearest centimetr.
Note: Remember to begin with a square paper of side 19.5 cm. Also, in step 2 you must all start by folding the Left corner.
How Big is Your Cube?
a) How long is the side of your cube? _____
How many cm cubes in all do I need to make a platform as big as the paper cube?

b) How many centimetre cubes can be arranged along its:
- Length? _____
- Width? _____
- Height? _____
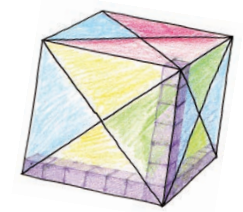
c) Answer Thimpu's questions:


To make the first layer on the table how many cm cubes will I use? _____
How many such layers will I need to make a paper cube? _____
d) So the total cm cubes = _____
e) The volume of the paper cubes is same as _____ cm cubes.
If we begin with square paper of side 19.5 cm, then we get a cube of side 7 cm.
2. Anan made a big cube having double the side of your paper cube.
How many of the your paper cubes will fit in it? Try doing it by collecting all the cubes made in your class.
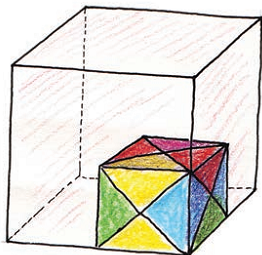
Packing Cubes
Ganesh and Dinga want to pack 4000 centimetre cubes in boxes. These are to be sent to a school. There are three different boxes available for packing.
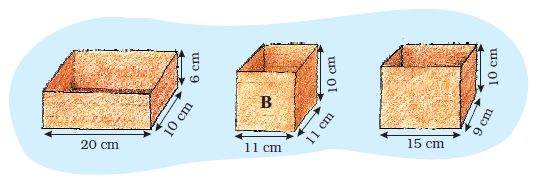
Will we be able to fit all 4000 cubes in these three boxes? I think we need one more box for it.
I think there is enough space in these boxes to pack all 4000 cubes.
- What is your guess? Who is right?
- How can Ganesh and Dinga test their guesses before packing the cubes in the boxes? Discuss with your friend.
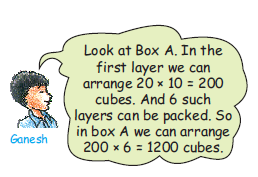
Look at Box A. In the first layer we can arrange cubes. And 6 such layers can be packed. So in box A we can arrange cubes.
Use Ganesh's method and write:
- _____ centimetre cubes can be arranged in box B.
- _____ centimetre cubes can be arranged in box C.
- So _____ centimetre cubes in all can be packed in the three boxes.
Which Pipe Fills More?
Collect some old postcards. You can also use thick paper of size .

Fold the postcard along the width to make pipe-1. Join the ends with cello tape.
Take another postcard and fold it along the length to make pipe-2. Join the ends with tape.
- Guess which pipe can take more sand inside it. Hold it on a plate and pour sand to check your guess. Was your guess correct? Discuss.

To make the triangle-shaped pipe-3, draw two lines on the postcard. Fold the postcard along the lines. Join the ends with tape.
Now make the square-shaped pipe-4.

Find out which pipe can take the most sand inside it. So which pipe has the most volume?

Remind children of the thread activity on page 155 where they may have seen that out of the shapes they made with a fixed perimeter, the circle had the biggest area. Here they will be looking for the shape with the biggest volume while they keep the area of the paper fixed.
Trek to Gangotri

The students of Class XII are going on a trek to Gangotri. They have to pack their bags for six days and keep them light.
They also have to take things that do not take too much space. So they will look for things that have both less volume and less weight. After all, they will carry their own bags while climbing the mountains!
They even dry the onions and tomatoes to make them light. One kg of onions or tomatoes becomes 100 g when the water inside dries up.

The list of food each person will need for one day:
? Rice : 100 g
? Flour (Atta): 100 g
? Pulses (Dal): 1/3 the weight of rice and flour
? Oil: 50g
? Suger: 50g
? Milk powder: 40g (for tea, porridge, and hot drink)
? Tea: Around 10g
? Dalia: 40g for breakfast.
? Salt: 5 g
? Dried onions: 10 g
? Dried tomatoes: 10 g
a) For 6 days, each person will need
? Rice and flour – _____ g
? Pulses – _____ g
? Dried onions – ______ g

b) How much of fresh tomatoes should be dried for 6 days for 10 people?
c) What is the total weight of food (for 6 days) in each person’s bag?


Even one gram extra can make the trek tough!
Guess how many of us together weigh one gram! About 100?
How Heavy am I?
Do you remember the story of how Vaidika’s daughter found the weight of an elephant? (Math-Magic Class IV Page 143)

Can you guess the weight of the heaviest animal on this earth? No, it's not me. I weigh only 5000 kg!

It is the Blue Whale. Its weight is around 35 times more than me. So how many thousand kg does it weigh?
- Guess how many children of your weight will be equal to the weight of an elephant of 5000 kg.
- At birth, a baby elephant weighs around 90 kg. How much did you weigh when you were born? Find out. How many times is a baby elephant heavier than you were at birth?
- If a grown up elephant eats 136 kg of food in a day then it will eat around _____ kg in a month.
Guess about how much it will eat in a year.
Shahid Saves the Bank!
Shahid works in a bank. He sits at the cash counter. Whenever there are too many coins he does not count them. He just weighs them.


Weighing is so much easier! The weight of a 5-rupee coin is 9 g. Tell me the weight of the sack and I will tell you the number of coins in it.

Can you hold these coins and say which is the heaviest?

My bag of 5 rupee coins weighs 9 kg. So how many coins does it have?

One kg is equal to 1000g so 9 kg is equal to 9000 g. If one coin weighs 9 g, then the bag weighing 9000 g has _____ coins in it. Easy!
- How many coins are there in a sack of 5 rupee coins if it weighs:
a) 18 kg? _____
b) 54 kg? _____
c) 4500 g? _____
d) 2 kg and 250 g? _____
e) 1 kg and 125 g? ______

2250 g can also be written as 2 kg and 250 g. Can you explain why?
- A 2 rupee coin weighs 6 g. What is the weight of a sack with:
a) 2200 coins ? _____ kg _____ g
b) 3000 coins? _____ kg
- If 100 one rupee coins weigh 485 g then how much will 10000 coins weigh? _____ kg _____ g
With your eyes closed, can you tell which is heavier — a 100-rupee note or a 50-rupee note? This may be difficult to say, but Shahid, who cannot see, has a better sense of touch than most people.
Once Shahid noticed that a bundle of notes which came to the bank felt different and heavier. He asked the manager to check. Others looked at it but found no problem. He insisted and so a machine was brought to weigh it. It showed that the notes were fake, not real ones. “Oh Shahid! You really saved the bank!” said everyone.
Find out and discuss
How do people who cannot see make out different notes and coins? (Hint: Look for a shape  etc. on notes of Rs 20, 50, 100, 500 etc. and feel it.)
etc. on notes of Rs 20, 50, 100, 500 etc. and feel it.)
- What should we look for to check if a 100-rupee note is rea lor fake?

During the discussion on checking a note as fake or real different things can be observed. A fake note may differ in size, quality of paper and printing style in which numbers are written. The watermark (the white area with Gandhi's image) and the words ‘भारत’ and 'RBI' written on the shiny security thread are to prevent people from printing fake notes.