Table of Contents
 Chapter 4
Chapter 4
Basic Geometrical Ideas
4.1 Introduction
Geometry has a long and rich history. The term ‘Geometry’ is the English equivalent of the Greek word ‘Geometron’. ‘Geo’ means Earth and ‘metron’ means Measurement. According to historians, the geometrical ideas shaped up in ancient times, probably due to the need in art, architecture and measurement. These include occasions when the boundaries of cultivated lands had to be marked without giving room for complaints. Construction of magnificent palaces, temples, lakes, dams and cities, art and architecture propped up these ideas. Even today geometrical ideas are reflected in all forms of art, measurements, architecture, engineering, cloth designing etc. You observe and use different objects like boxes, tables, books, the tiffin box you carry to your school for lunch, the ball with which you play and so on. All such objects have different shapes. The ruler which you use, the pencil with which you write are straight. The pictures of a bangle, the one rupee coin or a ball appear round.

Here, you will learn some interesting facts that will help you know more about the shapes around you.
4.2 Points
By a sharp tip of the pencil, mark a dot on the paper. Sharper the tip, thinner will be the dot. This almost invisible tiny dot will give you an idea of a point.
A point determines a location.
These are some models for a point :

The tip of a compass


The pointed end of a needle
If you mark three points on a paper, you would be required to distinguish them. For this they are denoted by a single capital letter like A,B,C.
These points will be read as point A, point B and point C.
Of course, the dots have to be invisibly thin.
1. With a sharp tip of the pencil, mark four points on a paper and name them by the letters A,C,P,H. Try to name these points in different ways. One such way could be this
2. A star in the sky also gives us an idea of a point. Identify at least five such situations in your daily life.
4.3 A Line Segment
Fold a piece of paper and unfold it. Do you see a fold? This gives the idea of a line segment. It has two end points A and B.
Take a thin thread. Hold its two ends and stretch it without a slack. It represents a line segment. The ends held by hands are the end points of the line segment.

The following are some models for a line segment :
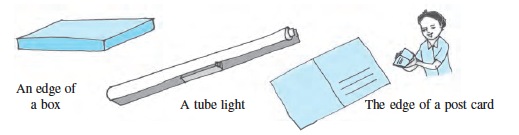
Try to find more examples for line segments from your surroundings.
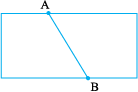
Mark any two points A and B on a sheet of paper. Try to connect A to B by all possible routes. (Fig 4.1)

What is the shortest route from A to B?
This shortest join of point A to B (including A and B) shown here is a line segment. It is denoted by  or
or  . The points A and B are called the end points of the segment.
. The points A and B are called the end points of the segment.
1. Name the line segments in the figure 4.2.
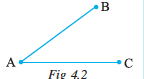
Is A, the end point of each line segment?
4.4 A Line
Imagine that the line segment from A to B (i.e.  ) is extended beyond A in one direction and beyond B in the other direction without any end (see figure). You now get a model for a line.
) is extended beyond A in one direction and beyond B in the other direction without any end (see figure). You now get a model for a line.

Do you think you can draw a complete picture of a line? No. (Why?)
A line through two points A and B is written as  . It extends indefinitely in both directions. So it contains a countless number of points. (Think about this).
. It extends indefinitely in both directions. So it contains a countless number of points. (Think about this).
Two points are enough to fix a line. We say ‘two points determine a line’.
The adjacent diagram (Fig 4.3) is that of a line PQ written as  . Sometimes a line is denoted by a letter like l, m.
. Sometimes a line is denoted by a letter like l, m.

Fig 4.3
4.5 Intersecting Lines
Look at the diagram (Fig 4.4). Two lines l1 and l2 are shown. Both the lines pass through point P. We say l1 and l2 intersect at P. If two lines have one common point, they are called intersecting lines.

Fig 4.4
The following are some models of a pair of intersecting lines (Fig 4.5) :
Try to find out some more models for a pair of intersecting lines.
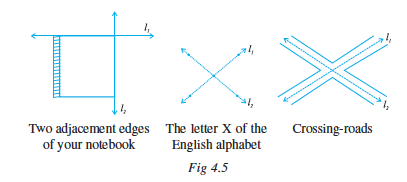
Take a sheet of paper. Make two folds (and crease them) to represent a pair of intersecting lines and discuss :
(a) Can two lines intersect in more than one point?
(b) Can more than two lines intersect in one point?
4.6 Parallel Lines
Let us look at this table (Fig 4.6). The top ABCD is flat. Are you able to see some points and line segments?
Are there intersecting line segments?
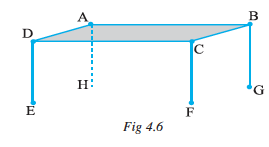
Yes, 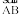 and
and 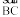 intersect at the point B.
intersect at the point B.
Which line segments intersect at A? at C? at D?
Do the lines 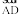 and
and  intersect?
intersect?
Do the lines  and
and  intersect?
intersect?
You find that on the table’s surface there are line segment which will not meet, however far they are extended.  and
and  form one such pair. Can you identify one more such pair of lines (which do not meet) on the top of the table?
form one such pair. Can you identify one more such pair of lines (which do not meet) on the top of the table?
Lines like these which do not meet are said to be parallel; and are called parallel lines.
Think, discuss and write
Where else do you see parallel lines? Try to find ten examples.
If two lines  and
and  are parallel, we write
are parallel, we write  ||
||  .
.
If two lines l1 and l2 are parallel, we write l1 || l2 .
Can you identify parrallel lines in the following figures?
4.7 Ray
The following are some models for a ray :
A ray is a portion of a line. It starts at one point (called starting point or initial point) and goes endlessly in a direction.
Look at the diagram (Fig 4.7) of ray shown here. Two points are shown on the ray. They are (a) A, the starting point (b) P, a point on the path of the ray.

Fig 4.7
We denote it by  .
.
Think, discuss and write
If 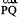 is a ray,
is a ray,
(a) What is its starting point?
(b) Where does the point Q lie on the ray?
(c) Can we say that Q is the starting point of this ray?
![]()
1. Name the rays given in this picture (Fig 4.8).
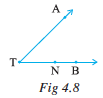
2. Is T a starting point of each of these rays?
Here is a ray  (Fig 4.9). It starts at O and passes through the point A. It also passes through the point B.
(Fig 4.9). It starts at O and passes through the point A. It also passes through the point B.
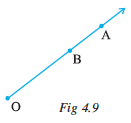
OA and OB are same here.
Can we write OA as AO ? Why or why not?
Draw five rays and write appropriate names for them.
What do the arrows on each of these rays show?
Exercise 4.1
1. Use the figure to name :
(a) Five points
(b) A line
(c) Four rays
(d) Five line segments
2. Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given.

3. Use the figure to name :
(a) Line containing point E.
(b) Line passing through A.
(c) Line on which O lies
(d) Two pairs of intersecting lines.
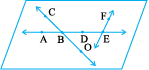
4. How many lines can pass through (a) one given point? (b) two given points?
5. Draw a rough figure and label suitably in each of the following cases:
(a) Point P lies on AB .
(b) XY and PQ intersect at M.
(c) Line l contains E and F but not D.
(d) OP and OQ meet at O
6. Consider the following figure of line  . Say whether following statements are true or false in context of the given figure.
. Say whether following statements are true or false in context of the given figure.

(a) Q, M, O, N, P are points on the line MN .
(b) M, O, N are points on a line segment MN .
(c) M and N are end points of line segment MN .
(d) O and N are end points of line segment OP .
(e) M is one of the end points of line segment QO .
(f) M is point on ray OP .
(g) Ray OP is different from ray QP .
(h) Ray OP is same as ray OM .
(i) Ray OM is not opposite to ray OP .
(j) O is not an initial point of OP .
(k) N is the initial point of NP and NM .
4.8 Curves
Have you ever taken a piece of paper and just doodled? The pictures that are results of your doodling are called curves.
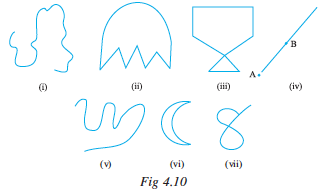
You can draw some of these drawings without lifting the pencil from the paper and without the use of a ruler. These are all curves (Fig 4.10).
‘Curve’ in everyday usage means “not straight”. In Mathematics, a curve can be straight like the one shown in fig 4.10 (iv).
Observe that the curves (iii) and (vii) in Fig 4.10 cross themselves, whereas the curves (i), (ii), (v) and (vi) in Fig 4.10 do not. If a curve does not cross itself, then it is called a simple curve.
Draw five more simple curves and five curves that are not simple.
Consider these now (Fig 4.11).
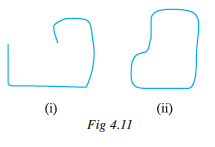
What is the difference between these two? The first i.e. Fig 4.11 (i) is an
open curve and the second i.e. Fig 4.11(ii) is a closed curve. Can you identify some closed and open curves from the figures Fig 4.10 (i), (ii), (v), (vi)? Draw five curves each that are open and closed.
Position in a figure
A court line in a tennis court divides it into three parts : inside the line, on the line and outside the line. You cannot enter inside without crossing the line.
A compound wall separates your house from the road. You talk about ‘inside’ the compound, ‘on’ the boundary of the compound and ‘outside’ the compound.
In a closed curve, thus, there are three parts.
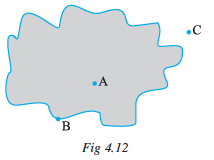
(i) interior (‘inside’) of the curve
(ii) boundary (‘on’) of the curve and
(iii) exterior (‘outside’) of the curve.
In the figure 4.12, A is in the interior, C is in the exterior and B is on the curve.
The interior of a curve together with its boundary is called its “region”.
4.9 Polygons
Look at these figures 4.13 (i), (ii), (iii), (iv), (v) and (vi).
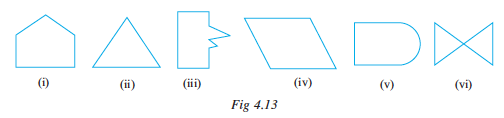
What can you say? Are they closed? How does each one of them differ from the other? (i), (ii), (iii), (iv) and (vi) are special because they are made up entirely of line segments. Out of these (i), (ii), (iii) and (iv) are also simple closed curves. They are called polygons.
So, a figure is a polygon if it is a simple closed figure made up entirely of line segments. Draw ten differently shaped polygons.
![]()
Try to form a polygonwith
1. Five matchsticks.
2. Four matchsticks.
3. Three matchsticks.
4. Two matchsticks.
In which case was it not possible? Why?
Sides, vertices and diagonals
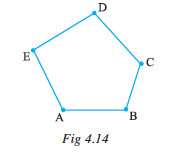
Examine the figure given here (Fig 4.14).
Give justification to call it a polygon.
The line segments forming a polygon are called its sides.
What are the sides of polygon ABCDE? (Note how the corners are named in order.)
Sides are 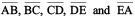 .
.
The meeting point of a pair of sides is called its vertex.
Sides 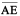 and
and 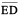 meet at E, so E is a vertex of the polygon ABCDE. Points B and C are its other vertices. Can you name the sides that meet at these points?
meet at E, so E is a vertex of the polygon ABCDE. Points B and C are its other vertices. Can you name the sides that meet at these points?
Can you name the other vertices of the above polygon ABCDE?
Any two sides with a common end point are called the adjacent sides of the polygon.
Are the sides 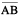 and
and 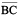 adjacent? How about
adjacent? How about 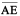 and
and 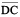 ?
?
The end points of the same side of a polygon are called the adjacent vertices. Vertices E and D are adjacent, whereas vertices A and D are not adjacent vertices. Do you see why?
Consider the pairs of vertices which are not adjacent. The joins of these vertices are called the diagonals of the polygon.
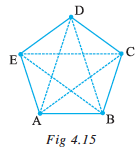
In the figure 4.15, 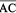 ,
,  ,
,  ,
, 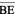 and
and 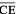 are diagonals.
are diagonals.
Is 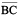 a diagonal, Why or why not?
a diagonal, Why or why not?
If you try to join adjacent vertices, will the result be a diagonal?
Name all the sides, adjacent sides, adjacent vertices of the figure ABCDE (Fig 4.15).
Draw a polygon ABCDEFGH and name all the sides, adjacent sides and vertices as well as the diagonals of the polygon.
Exercise 4.2
1. Classify the following curves as (i) Open or (ii) Closed.

2. Draw rough diagrams to illustrate the following :
(a) Open curve (b) Closed curve.
3. Draw any polygon and shade its interior.
4. Consider the given figure and answer the questions :
(a) Is it a curve? (b) Is it closed?
5. Illustrate, if possible, each one of the following with a rough diagram:

(a) A closed curve that is not a polygon.
(b) An open curve made up entirely of line segments.
(c) A polygon with two sides.
4.10 Angles
Angles are made when corners are formed.
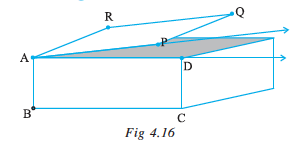
Here is a picture (Fig 4.16) where the top of a box is like a hinged lid. The edges AD of the box and AP of the door can be imagined as two rays 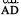 and
and  . These two rays have a common initial point A. The two rays here together are said to form an angle.
. These two rays have a common initial point A. The two rays here together are said to form an angle.
An angle is made up of two rays starting from a common initial point.
The two rays forming the angle are called the arms or sides of the angle.
The common initial point is the vertex of the angle.
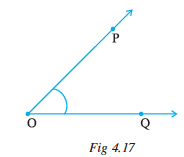
This is an angle formed by rays OP and OQ (Fig 4.17). To show this we use a small curve at the vertex. (see Fig 4.17). O is the vertex. What are the sides? Are they not OP and OQ ?
How can we name this angle? We can simply say that it is an angle at O. To be more specific we identify some two points, one on each side and the vertex to name the angle. Angle POQ is thus a better way of naming the angle. We denote this by ∠POQ .
Think, discuss and write
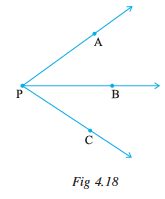
Look at the diagram (Fig 4.18).What is the name of the angle? Shall we say ? But then which one do we mean? By
? But then which one do we mean? By  what do we mean?
what do we mean?
Is naming an angle by vertex helpful here?
Why not?
By ∠P we may mean ∠APB or ∠CPB or even ∠APC ! We need more information.
Note that in specifying the angle, the vertex is always written as the middle letter.
![]()
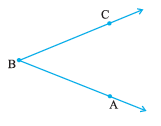
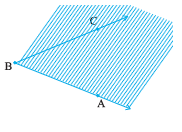
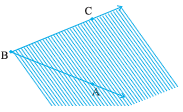
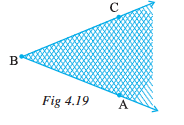
Take any angle, say ∠ABC .
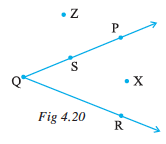
Exercise 4.3
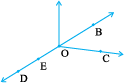
1. Name the angles in the given figure.
2. In the given diagram, name the point(s)
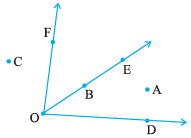
(a) In the interior of ∠DOE
(b) In the exterior of ∠EOF
(c) On ∠EOF
3. Draw rough diagrams of two angles such that they have
(a) One point in common.
(b) Two points in common.
(c) Three points in common.
(d) Four points in common.
(e) One ray in common.
4.11 Triangles
A triangle is a three-sided polygon. In fact, it is the polygon with the least number of sides.
Look at the triangle in the diagram (Fig 4.21). We write ∆ABC instead of writing “Triangle ABC”.
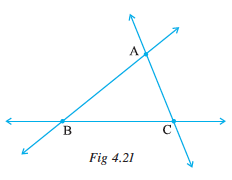
In ∆ABC, how many sides and how many angles are there?
The three sides of the triangle are AB, BC and CA. The three angles are ∠BAC, ∠BCA and ∠ABC. The points A, B and C are called the vertices of the triangle.
Exercise 4.4
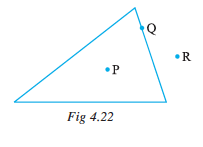
1. Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is the point A in its exterior or in its interior?
2. (a) Identify three triangles in the figure.
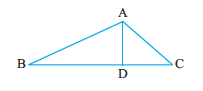
(b) Write the names of seven angles.
(c) Write the names of six line segments.
(d) Which two triangles have ∠B as common?
4.12 Quadrilaterals
A four sided polygon is a quadrilateral. It has 4 sides and 4 angles. As in the case of a triangle, you can visualise its interior too.
Note the cyclic manner in which the vertices are named.
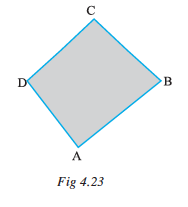
This quadrilateral ABCD (Fig 4.23) has four sides AB, BC, CD and DA. It has four angles ∠A , ∠B , ∠C and ∠D.
In any quadrilateral ABCD, AB and BC are adjacent sides. Can you write other pairs of adjacent sides?
AB and DC are opposite sides; Name the other pair of opposite sides.
∠A and ∠C are said to be opposite angles; similarly, ∠D and ∠B are opposite angles. Naturally ∠A and ∠B are adjacent angles. You can now list other pairs of adjacent angles.
Exercise 4.5
1. Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral?
(a) two pairs of opposite sides,
(b) two pairs of opposite angles,
(c) two pairs of adjacent sides,
(d) two pairs of adjacent angles.
3. Investigate :
Use strips and fasteners to make a triangle and a quadrilateral.
Try to push inward at any one vertex of the triangle. Do the same to the quadrilateral.
Is the triangle distorted? Is the quadrilateral distorted? Is the triangle rigid?
Why is it that structures like electric towers make use of triangular shapes and not quadrilaterals?
4.13 Circles
In our environment, you find many things that are round, a wheel, a bangle, a coin etc. We use the round shape in many ways. It is easier to roll a heavy steel tube than to drag it.
A circle is a simple closed curve which is not a polygon. It has some very special properties.
![]()
• Place a bangle or any round shape; trace around to get a circular shape.
• If you want to make a circular garden, how will you proceed?
Take two sticks and a piece of rope. Drive one stick into the ground. This is the centre of the proposed circle. Form two loops, one at each end of the rope. Place one loop around the stick at the centre. Put the other around the other stick. Keep the sticks vertical to the ground. Keep the rope taut all the time and trace the path. You get a circle.
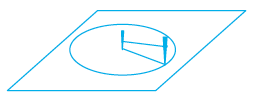
Naturally every point on the circle is at equal distance from the centre.
Parts of a circle
Here is a circle with centre C (Fig 4.24)
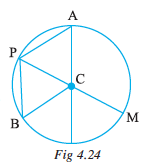
A, P, B, M are points on the circle. You will see that
CA = CP = CB = CM.
Each of the segments CA, CP, CB, CM is radius of the circle. The radius is a line segment that connects the centre to a point on the circle.CP and CM are radii (plural of ‘radius’) such that C, P, M are in a line.PM is known as diameter of the circle.
Is a diameter double the size of a radius? Yes.
PB is a chord connecting two points on a circle. Is PM also a chord?
An arc is a portion of circle.
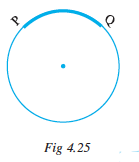
If P and Q are two points you get the arc PQ. We write it as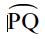 (Fig 4.25).
(Fig 4.25).
As in the case of any simple closed curve you can think of the interiorand exterior of a circle. A region in the interior of a circle enclosed by an arc on one side and a pair of radii on the other two sides is called asector (Fig 4.26).
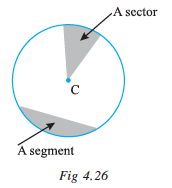
A region in the interior of a circle enclosed by a chord and an arc is called a segment of the circle.
Take any circular object. Use a thread and wrap it around the object once. The length of the thread is the distance covered to travel around the object once. What does this length denote?
The distance around a circle is its circumference.

• Take a circular sheet. Fold it into two halves. Crease the fold and open up. Do you find that the circular region is halved by the diameter?
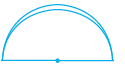
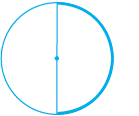
A diameter of a circle divides it into two equal parts; each part is a semi-circle. A semi-circle is half of a circle, with the end points of diameter as part of the boundary.
Exercise 4.6
1. From the figure, identify :
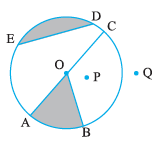
(a) the centre of circle (b) three radii
(c) a diameter (d) a chord
(e) two points in the interior (f) a point in the exterior
(g) a sector (h) a segment
2. (a) Is every diameter of a circle also a chord?
(b) Is every chord of a circle also a diameter?
3. Draw any circle and mark
(a) its centre (b) a radius
(c) a diameter (d) a sector
(e) a segment (f) a point in its interior
(g) a point in its exterior (h) an arc
4. Say true or false :
(a) Two diameters of a circle will necessarily intersect.
(b) The centre of a circle is always in its interior.
What have we discussed?
1. A point determines a location. It is usually denoted by a capital letter.
2. A line segment corresponds to the shortest distance between two points. The line segment joining points A and B is denoted by AB .
3. A line is obtained when a line segment like AB is extended on both sides indefinitely; it is denoted by AB or sometimes by a single small letter like l.
4. Two distinct lines meeting at a point are called intersecting lines.
5. Two lines in a plane are said to be parallel if they do not meet.
6. A ray is a portion of line starting at a point and going in one direction endlessly.
7. Any drawing (straight or non-straight) done without lifting the pencil may be called a curve. In this sense, a line is also a curve.
8. A simple curve is one that does not cross itself.
9. A curve is said to be closed if its ends are joined; otherwise it is said to be open.
10. A polygon is a simple closed curve made up of line segments. Here,
(i) The line segments are the sides of the polygon.
(ii) Any two sides with a common end point are adjacent sides.
(iii) The meeting point of a pair of sides is called a vertex.
(iv) The end points of the same side are adjacent vertices.
(v) The join of any two non-adjacent vertices is a diagonal.
11. An angle is made up of two rays starting from a common starting / initial point.
Two rays OA and OB make ∠AOB (or also called ∠BOA).
An angle leads to three divisions of a region:
On the angle, the interior of the angle and the exterior of the angle.
12. A triangle is a three-sided polygon.
13. A quadrilateral is a four-sided polygon. (It should be named cyclically).
In any quadrilateral ABCD, AB & DC and AD & BC are pairs of opposite sides. ∠A & ∠C and ∠B & ∠D are pairs of opposite angles. ∠A is adjacent to ∠B & ∠D ; similar relations exist for other three angles.
14. A circle is the path of a point moving at the same distance from a fixed point.
The fixed point is the centre, the fixed distance is the radius and the distance around the circle is the circumference.
A chord of a circle is a line segment joining any two points on the circle.
A diameter is a chord passing through the centre of the circle.
A sector is the region in the interior of a circle enclosed by an arc on one side and a pair of radii on the other two sides.
A segment of a circle is a region in the interior of the circle enclosed by an arc and a chord.
The diameter of a circle divides it into two semi-circles.
![]()