Table of Contents
Chapter 8
Decimals
8.1 Introduction
Savita and Shama were going to market to buy some stationary items. Savita said, “I have 5 rupees and 75 paise”. Shama said, “I have 7 rupees and 50 paise”.
They knew how to write rupees and paise using decimals.
So Savita said, I have ₹ 5.75 and Shama said,
“I have ₹ 7.50”.

Have they written correctly?
We know that the dot represents a decimal point.
In this chapter, we will learn more about working with decimals.
8.2 Tenths
Ravi and Raju measured the lengths of their pencils. Ravi’s pencil was 7 cm 5mm long and Raju’s pencil was 8 cm 3 mm long. Can you express these lengths in centimetre using decimals?
We know that 10 mm = 1 cm
Therefore, 1 mm = 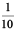 cm or one-tenth cm = 0.1 cm
cm or one-tenth cm = 0.1 cm
Now, length of Ravi’s pencil = 7cm 5mm
= 7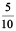 cm i.e. 7cm and 5 tenths of a cm
cm i.e. 7cm and 5 tenths of a cm
= 7.5cm
The length of Raju’s pencil = 8 cm 3 mm
= 8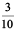 cm i.e. 8 cm and 3 tenths of a cm
cm i.e. 8 cm and 3 tenths of a cm
= 8.3 cm
Let us recall what we have learnt earlier.

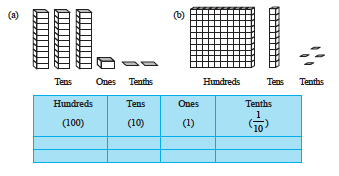
If we show units by blocks then one unit is one block, two units are two blocks and so on. One block divided into 10 equal parts means each part is 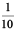 (one-tenth) of a unit, 2 parts show 2 tenths and 5 parts show 5 tenths and so on. A combination of 2 blocks and 3 parts (tenths) will be recorded as :
(one-tenth) of a unit, 2 parts show 2 tenths and 5 parts show 5 tenths and so on. A combination of 2 blocks and 3 parts (tenths) will be recorded as :
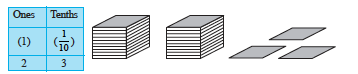
It can be written as 2.3 and read as two point three.
Let us look at another example where we have more than ‘ones’. Each tower represents 10 units. So, the number shown here is :
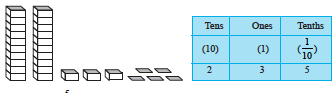
i.e. 20 + 3 + 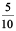 = 23.5
= 23.5
This is read as ‘twenty three point five’.
![]()
1. Can you now write the following as decimals?
2. Write the lengths of Ravi’s and Raju’s pencils in ‘cm’ using decimals.
3. Make three more examples similar to the one given in question 1 and solve them.
Representing Decimals on number line
We represented fractions on a number line. Let us now represent decimals too on a number line. Let us represent 0.6 on a number line.
We know that 0.6 is more than zero but less than one. There are 6 tenths in it. Divide the unit length between 0 and 1 into 10 equal parts and take 6 parts as shown below :

Write five numbers between 0 and 1 and show them on the number line.
Can you now represent 2.3 on a number line? Check, how many ones and tenths are there in 2.3. Where will it lie on the number line?
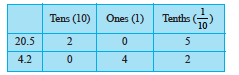
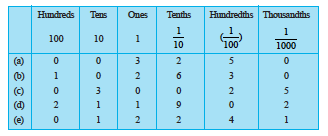
Example 1 : Write the following numbers in the place value table : (a) 20.5 (b) 4.2
Solution : Let us make a common place value table, assigning appropriate place value to the digits in the given numbers. We have,
Example 2 : Write each of the following as decimals : (a) Two ones and
five-tenths (b) Thirty and one-tenth
Solution : (a) Two ones and five-tenths = 2 + 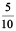 = 2.5
= 2.5
(b) Thirty and one-tenth = 30 + 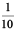 = 30.1
= 30.1
Example 3 : Write each of the following as decimals :
(a) 30 + 6 + 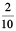 (b) 600 + 2 +
(b) 600 + 2 + 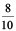
Solution : (a) 30 + 6 + 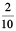
How many tens, ones and tenths are there in this number? We have
3 tens, 6 ones and 2 tenths.
Therefore, the decimal representation is 36.2.
(b) 600 + 2 + 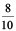
Note that it has 6 hundreds, no tens, 2 ones and 8 tenths.
Therefore, the decimal representation is 602.8
Fractions as decimals
We have already seen how a fraction with denominator 10 can be represented using decimals.
Let us now try to find decimal representation of (a) 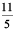 (b)
(b) 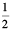
(a) We know that 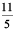 =
= 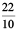 =
= 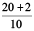 =
= 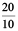 +
+ 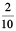 = 2 +
= 2 + 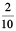 = 2.2
= 2.2
![]()
Write 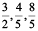 in decimal notation.
in decimal notation.
Therefore, 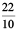 = 2.2 (in decimal notation.)
= 2.2 (in decimal notation.)
(b) In 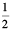 , the denominator is 2. For writing in decimal notation, the denominator should be 10. We already know
, the denominator is 2. For writing in decimal notation, the denominator should be 10. We already know
how to make an equivalent fraction. So,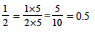
Decimals as fractions
Till now we have learnt how to write fractions with denominators 10, 2 or 5 as decimals. Can we write a decimal number like 1.2 as a fraction?
Let us see 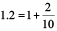
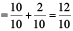
Exercise 8.1
1. Write the following as numbers in the given table.
2. Write the following decimals in the place value table.
Hundreds Tens Ones Tenths
(a) 19.4 (b) 0.3 (c) 10.6 (d) 205.9
3. Write each of the following as decimals :
(a) Seven-tenths (b) Two tens and nine-tenths
(c) Fourteen point six (d) One hundred and two ones
(e) Six hundred point eight
4. Write each of the following as decimals:
(a) 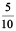 (b) 3 +
(b) 3 + 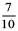 (c) 200 + 60 + 5 +
(c) 200 + 60 + 5 + 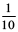 (d) 70 +
(d) 70 + 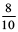 (e)
(e) 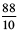
(f) 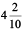 (g)
(g) 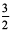 (h)
(h) 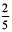 (i)
(i) 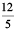 (j)
(j) 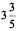 (k)
(k) 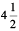
5. Write the following decimals as fractions. Reduce the fractions to lowest form.
(a) 0.6 (b) 2.5 (c) 1.0 (d) 3.8 (e) 13.7 (f) 21.2 (g) 6.4
6. Express the following as cm using decimals.
(a) 2 mm (b) 30 mm (c) 116 mm (d) 4 cm 2 mm (e) 162 mm
(f) 83 mm
7. Between which two whole numbers on the number line are the given numbers lie? Which of these whole numbers is nearer the number?
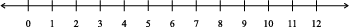
(a) 0.8 (b) 5.1 (c) 2.6 (d) 6.4 (e) 9.1 (f) 4.9
8. Show the following numbers on the number line.
(a) 0.2 (b) 1.9 (c) 1.1 (d) 2.5
9. Write the decimal number represented by the points A, B, C, D on the given number line.

10. (a) The length of Ramesh’s notebook is 9 cm 5 mm. What will be its length in cm?
(b) The length of a young gram plant is 65 mm. Express its length in cm.
8.3 Hundredths
David was measuring the length of his room. He found that the length of his room is 4 m and 25 cm.
He wanted to write the length in metres.
Can you help him? What part of a metre will be one centimetre?
1 cm = 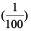 m or one-hundredth of a metre.
m or one-hundredth of a metre.
This means 25 cm = 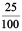 m
m
Now 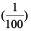 means 1 part out of 100 parts of a whole. As we have done for
means 1 part out of 100 parts of a whole. As we have done for 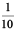 , let us try to show this pictorially.
, let us try to show this pictorially.
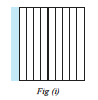
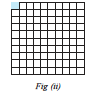
Take a square and divide it into ten equal parts.
What part is the shaded rectangle of this square?
It is 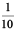 or one-tenth or 0.1, see Fig (i).
or one-tenth or 0.1, see Fig (i).
Now divide each such rectangle into ten equal parts.
We get 100 small squares as shown in Fig (ii).
Then what fraction is each small square of the whole square?
Fig (ii)
Each small square is 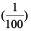 or one-hundredth of the whole square. In decimal notation, we write
or one-hundredth of the whole square. In decimal notation, we write 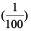 = 0.01 and read it as zero point zero one.
= 0.01 and read it as zero point zero one.
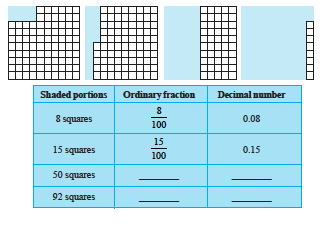
What part of the whole square is the shaded portion, if we shade 8 squares, 15 squares, 50 squares, 92 squares of the whole square?
Take the help of following figures to answer.
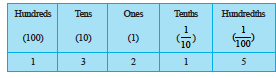
Let us look at some more place value tables.

The number shown in the table above is 2 + 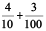 . In decimals, it is written as 2.43, which is read as ‘two point four three’.
. In decimals, it is written as 2.43, which is read as ‘two point four three’.
Example 4 : Fill the blanks in the table using ‘block’ information given below and write the corresponding number in decimal form.

Solution :
The number is 100 + 30 + 2 + 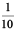 +
+ 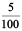 = 132.15
= 132.15
Example 5 : Fill the blanks in the table and write the corresponding number in decimal form using ‘block’ information given below.
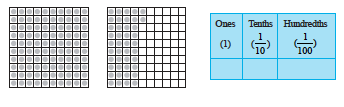
Solution :
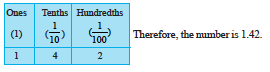
Therefore, the number is 1.42.
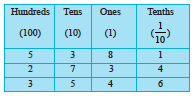
Example 6 : Given the place value table, write the number in decimal form.
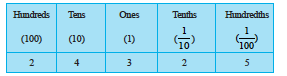
Solution : The number is 2 × 100 + 4 × 10 + 3 × 1 + 2 × 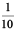 + 5 ×
+ 5 × 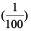
= 200 + 40 + 3 + 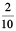 +
+ 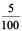 = 243.25
= 243.25
We can see that as we go from left to right, at every step the multiplying factor becomes 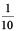 of the previous factor.
of the previous factor.
The first digit 2 is multiplied by 100; the next digit 4 is multiplied by 10 i.e. (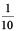 of 100); the next digit 3 is multiplied by 1. After this, the next multipling factor is
of 100); the next digit 3 is multiplied by 1. After this, the next multipling factor is 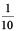 ; and then it is
; and then it is 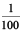 i.e. (
i.e. (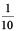 of
of 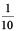 ).
).
We can see that as we go from left to right, at every step the multiplying factor becomes 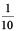 of the previous factor.
of the previous factor.
The decimal point comes between ones place and tenths place in a decimal number.
It is now natural to extend the place value table further, from hundredths to 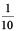 of hundredths i.e. thousandths.
of hundredths i.e. thousandths.
Let us solve some examples.
Example 7 : Write as decimals. (a) 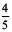 (b)
(b) 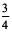 (c)
(c) 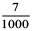
Solution : (a) We have to find a fraction equivalent to 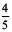 whose denominator is 10.
whose denominator is 10.
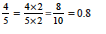
(b) Here, we have to find a fraction equivalent to 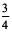 with denominator 10 or 100. There is no whole number that gives 10 on multiplying by 4, therefore, we make the demominator 100 and we have,
with denominator 10 or 100. There is no whole number that gives 10 on multiplying by 4, therefore, we make the demominator 100 and we have,
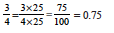
(c) Here, since the tenth and the hundredth place is zero.
Therefore, we write 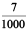 = 0.007
= 0.007
Example 8 : Write as fractions in lowest terms.
(a) 0.04 (b) 2.34 (c) 0.342
Solution : (a) 0.04 = 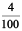 =
= 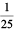
(b) 2.34 = 2 + 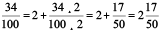
(c) 0.342 = 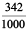 =
= 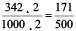
Example 9 : Write each of the following as a decimal.
(a) 200 + 30 + 5 +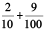 (b) 50 +
(b) 50 + 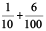
(c) 16 + 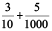
Solution : (a) 200 + 30 + 5 + 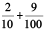
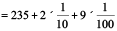 = 235.29
= 235.29
(b) 50 + 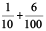 = 50 + 1 ×
= 50 + 1 × 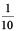 + 6 ×
+ 6 × 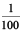 = 50.16
= 50.16
(c) 16 + 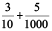 = 16 +
= 16 + 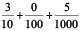
= 16 + 3 × 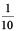 + 0 ×
+ 0 × 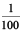 + 5 ×
+ 5 × 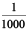 = 16.305
= 16.305
Example 10 : Write each of the following as a decimal.
(a) Three hundred six and seven-hundredths
(b) Eleven point two three five
(c) Nine and twenty five thousandths
Solution : (a) Three hundred six and seven-hundredths
= 306 + 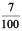 = 306 + 0 ×
= 306 + 0 × 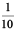 + 7 ×
+ 7 × 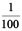 = 306.07
= 306.07
(b) Eleven point two three five = 11.235
(c) Nine and twenty five thousandths = 9 + 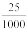
= 9 + 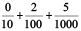 = 9.025
= 9.025
Since, 25 thousandths = 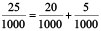 =
=  +
+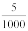
Exercise 8.2
1. Complete the table with the help of these boxes and use decimals to write the number.
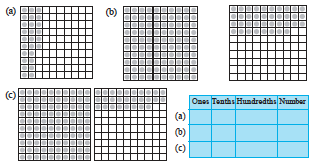
2. Write the numbers given in the following place value table in decimal form.
3. Write the following decimals in the place value table.
(a) 0.29 (b) 2.08 (c) 19.60 (d) 148.32 (e) 200.812
4. Write each of the following as decimals.
(a) 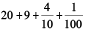 (b)
(b) 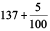 (c)
(c) 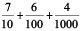
(d) 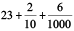 (e)
(e) 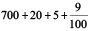
5. Write each of the following decimals in words.
(a) 0.03 (b) 1.20 (c) 108.56 (d) 10.07 (e) 0.032 (f) 5.008
6. Between which two numbers in tenths place on the number line does each of the given number lie?
(a) 0.06 (b) 0.45 (c) 0.19 (d) 0.66 (e) 0.92 (f) 0.57
7. Write as fractions in lowest terms.
(a) 0.60 (b) 0.05 (c) 0.75 (d) 0.18 (e) 0.25 (f) 0.125
(g) 0.066
8.4 Comparing Decimals
Can you tell which is greater, 0.07 or 0.1?
Take two pieces of square papers of the same size. Divide them into 100 equal parts. For 0.07 we have to shade 7 parts out of 100.
Now, 0.1 = 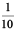 =
= 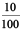 , so, for 0.1, shade 10 parts out 100.
, so, for 0.1, shade 10 parts out 100.
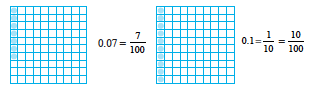
This means 0.1>0.07
Let us now compare the numbers 32.55 and 32.5. In this case , we first compare the whole part. We see that the whole part for both the nunbers is 32 and, hence, equal.
We, however, know that the two numbers are not equal. So, we now compare the tenth part. We find that for 32.55 and 32.5, the tenth part is also equal, then we compare the hundredth part.
We find,
32.55 = 32 +  +
+  and 32.5 = 32 +
and 32.5 = 32 +  +
+  , therefore, 32.55>32.5 as the hundredth part of 32.55 is more.
, therefore, 32.55>32.5 as the hundredth part of 32.55 is more.
Example 11 : Which is greater?
(a) 1 or 0.99 (b) 1.09 or 1.093
Solution : (a)  ;
; 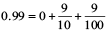
The whole part of 1 is greater than that of 0.99.
Therefore, 1 > 0.99
(b)  ;
; 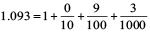
In this case, the two numbers have same parts upto hundredth.
But the thousandths part of 1.093 is greater than that of 1.09.
Therefore, 1.093 > 1.09.
Exercise 8.3
1. Which is greater?
(a) 0.3 or 0.4 (b) 0.07 or 0.02 (c) 3 or 0.8 (d) 0.5 or 0.05
(e) 1.23 or 1.2 (f) 0.099 or 0.19 (g) 1.5 or 1.50 (h) 1.431 or 1.490
(i) 3.3 or 3.300 (j) 5.64 or 5.603
2. Make five more examples and find the greater number from them.
8.5 Using Decimals
8.5.1 Money
We know that 100 paise = ₹ 1
Therefore, 1 paise = ₹ 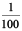 = ₹ 0.01
= ₹ 0.01
So, 65 paise = ₹  = ₹ 0.65
= ₹ 0.65
and 5 paise = ₹ 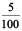 = ₹ 0.05
= ₹ 0.05
What is 105 paise? It is ₹ 1 and 5 paise = ₹ 1.05
![]()
(i) Write 2 rupees 5 paise and 2 rupees 50 paise in decimals.
(ii) Write 20 rupees 7 paise and 21 rupees 75 paise in decimals?
8.5.2 Length
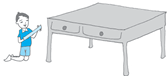
Mahesh knew that
1 cm =  m or 0.01 m
m or 0.01 m
Therefore, 56 cm = 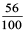 m = 0.56 m
m = 0.56 m
Thus, the length of the table top is 156 cm = 100 cm + 56 cm
= 1 m + 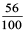 m = 1.56 m.
m = 1.56 m.
1. Can you write 4 mm in ‘cm’ using decimals?
2. How will you write 7cm 5 mm in ‘cm’ using decimals?
3. Can you now write 52 m as ‘km’ using decimals? How will you write 340 m as ‘km’ using decimals? How will you write 2008 m in ‘km’?
Mahesh also wants to represent this length pictorially. He took squared papers of equal size and divided them into 100 equal parts. He considered each small square as one cm.
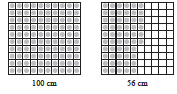
8.5.3 Weight
Nandu bought 500g potatoes, 250g capsicum, 700g onions, 500g tomatoes, 100g ginger and 300g radish. What is the total weight of the vegetables in the bag? Let us add the weight of all the vegetables in the bag.
1. Can you now write 456g as ‘kg’ using decimals?
2. How will you write 2kg 9g in ‘kg’ using decimals?
We know that 1000 g = 1 kg
Therefore, 1 g = 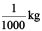 = 0.001 kg
= 0.001 kg
500 g + 250 g + 700 g + 500 g + 100 g + 300 g
= 2350 g
We know that 1000 g = 1 kg
Therefore, 1 g = 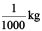 = 0.001 kg
= 0.001 kg
Thus, 2350 g = 2000 g + 350 g
= 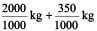
= 2 kg + 0.350 kg = 2.350 kg
i.e. 2350 g = 2 kg 350 g = 2.350 kg
Thus, the weight of vegetables in Nandu’s bag is 2.350 kg.

Exercise 8.4
1. Express as rupees using decimals.
(a) 5 paise (b) 75 paise (c) 20 paise
(d) 50 rupees 90 paise (e) 725 paise
2. Express as metres using decimals.
(a) 15 cm (b) 6 cm (c) 2 m 45 cm
(d) 9 m 7 cm (e) 419 cm
3. Express as cm using decimals.
(a) 5 mm (b) 60 mm (c) 164 mm
(d) 9 cm 8 mm (e) 93 mm
4. Express as km using decimals.
(a) 8 m (b) 88 m (c) 8888 m
(d) 70 km 5 m
5. Express as kg using decimals.
(a) 2 g (b) 100 g (c) 3750 g
(d) 5 kg 8 g (e) 26 kg 50 g
8.6 Addition of Numbers with Decimals
Add 0.35 and 0.42.
Take a square and divide it into 100 equal parts.

Mark 0.35 in this square by shading
3 tenths and colouring 5 hundredths.
Mark 0.42 in this square by shading
4 tenths and colouring 2 hundredths.
Now count the total number of tenths in the square and the total number of hundredths in the square.
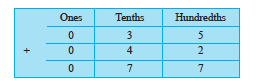
Therefore, 0.35 + 0.42 = 0.77
Thus, we can add decimals in the same way as whole numbers.
Find
(i) 0.29 + 0.36 (ii) 0.7 + 0.08
(iii) 1.54 + 1.80 (iv) 2.66 + 1.85
Can you now add 0.68 and 0.54?
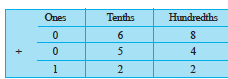
Thus, 0.68 + 0.54 = 1.22
Example 12 : Lata spent ₹ 9.50 for buying a pen and ₹ 2.50 for one pencil. How much money did she spend?
Money spent for pencil = ₹ 2.50
Total money spent = ₹ 9.50 + ₹ 2.50
Total money spent = ₹ 12.00

Example 13 : Samson travelled 5 km 52 m by bus, 2 km 265 m by car and the rest 1km 30 m he walked. How much distance did he travel in all?
Solution: Distance travelled by bus = 5 km 52 m = 5.052 km
Distance travelled by car = 2 km 265 m = 2.265 km
Distance travelled on foot = 1 km 30 m = 1.030 km
Therefore, total distance travelled is
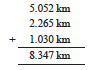
Therefore, total distance travelled = 8.347 km
Example 14 : Rahul bought 4 kg 90 g of apples, 2 kg 60 g of grapes and
5 kg 300 g of mangoes. Find the total weight of all the fruits he bought.
Solution : Weight of apples = 4 kg 90 g = 4.090 kg
Weight of grapes = 2 kg 60 g = 2.060 kg
Weight of mangoes = 5 kg 300 g = 5.300 kg
Therefore, the total weight of the fruits bought is

Total weight of the fruits bought = 11.450 kg.
Exercise 8.5
(a) 0.007 + 8.5 + 30.08
(b) 15 + 0.632 + 13.8
(c) 27.076 + 0.55 + 0.004
(d) 25.65 + 9.005 + 3.7
(e) 0.75 + 10.425 + 2
(f) 280.69 + 25.2 + 38
2. Rashid spent ₹ 35.75 for Maths book and ₹ 32.60 for Science book. Find the total amount spent by Rashid.
3. Radhika’s mother gave her ₹ 10.50 and her father gave her ₹ 15.80, find the total amount given to Radhika by the parents.
4. Nasreen bought 3 m 20 cm cloth for her shirt and 2 m 5 cm cloth for her trouser. Find the total length of cloth bought by her.
5. Naresh walked 2 km 35 m in the morning and 1 km 7 m in the evening. How much distance did he walk in all?
6. Sunita travelled 15 km 268 m by bus, 7 km 7 m by car and 500 m on foot in order to reach her school. How far is her school from her residence?
7. Ravi purchased 5 kg 400 g rice, 2 kg 20 g sugar and 10 kg 850g flour. Find the total weight of his purchases.
8.7 Subtraction of Decimals
Subtract 1.32 from 2.58
This can be shown by the table.
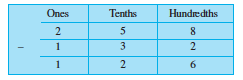
Thus, 2.58 – 1.32 = 1.26
Therefore, we can say that, subtraction of decimals can be done by subtracting hundredths from hundredths, tenths from tenths, ones from ones and so on, just as we did in addition.
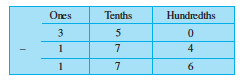
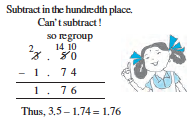
Let us subtract 1.74 from 3.5.
![]()
1. Subtract 1.85 from 5.46 ;
2. Subtract 5.25 from 8.28 ;
3. Subtract 0.95 from 2.29 ;
4. Subtract 2.25 from 5.68.
Example 15 : Abhishek had ₹ 7.45. He bought toffees for ₹ 5.30. Find the balance amount left with Abhishek.
Solution : Total amount of money = ₹ 7.45
Amount spent on toffees = ₹ 5.30
Balance amount of money = ₹ 7.45 – ₹ 5.30 = ₹ 2.15
Example 16 : Urmila’s school is at a distance of 5 km 350 m from her house. She travels 1 km 70 m on foot and the rest by bus. How much distance does she travel by bus?
Solution : Total distance of school from the house = 5.350 km
Distance travelled on foot = 1.070 km
Therefore, distance travelled by bus = 5.350 km – 1.070 km
= 4.280 km
Thus, distance travelled by bus = 4.280 km or 4 km 280 m
Example 17 : Kanchan bought a watermelon weighing 5 kg 200 g. Out of this she gave 2 kg 750 g to her neighbour. What is the weight of the watermelon left with Kanchan?
Solution : Total weight of the watermelon = 5.200 kg
Watermelon given to the neighbour = 2.750 kg
Therefore, weight of the remaining watermelon
= 5.200 kg – 2.750 kg = 2.450 kg
Exercise 8.6
1. Subtract :
(a) ₹ 18.25 from ₹ 20.75
(b) 202.54 m from 250 m
(c) ₹ 5.36 from ₹ 8.40
(d) 2.051 km from 5.206 km
(e) 0.314 kg from 2.107 kg
2. Find the value of :
(a) 9.756 – 6.28
(b) 21.05 – 15.27
(c) 18.5 – 6.79
(d) 11.6 – 9.847
4. Rani had ₹ 18.50. She bought one ice-cream for ₹ 11.75. How much money does she have now?
5. Tina had 20 m 5 cm long cloth. She cuts 4 m 50 cm length of cloth from this for making a curtain. How much cloth is left with her?
6. Namita travels 20 km 50 m every day. Out of this she travels 10 km 200 m by bus and the rest by auto. How much distance does she travel by auto?

What have we discussed?
1. To understand the parts of one whole (i.e. a unit) we represent a unit by a block. One block divided into 10 equal parts means each part is 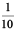 (one-tenth) of a unit. It can be written as 0.1 in decimal notation. The dot represents the decimal point and it comes between the units place and the tenths place.
(one-tenth) of a unit. It can be written as 0.1 in decimal notation. The dot represents the decimal point and it comes between the units place and the tenths place.
2. Every fraction with denominator 10 can be written in decimal notation and vice-versa.
3. One block divided into 100 equal parts means each part is 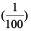 (one-hundredth) of a unit. It can be written as 0.01 in decimal notation.
(one-hundredth) of a unit. It can be written as 0.01 in decimal notation.
4. Every fraction with denominator 100 can be written in decimal notation and
vice-versa.
5. In the place value table, as we go from left to the right, the multiplying factor becomes 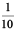 of the previous factor.
of the previous factor.
The place value table can be further extended from hundredths to 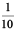 of hundredths i.e. thousandths (
of hundredths i.e. thousandths (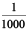
which is written as 0.001 in decimal notation.
6. All decimals can also be represented on a number line.
7. Every decimal can be written as a fraction.
8. Any two decimal numbers can be compared among themselves. The comparison can start with the whole part. If the whole parts are equal then the tenth parts can be compared and so on.
9. Decimals are used in many ways in our lives. For example, in representing units of money, length and weight.
