Table of Contents
Chapter 14
Practical Geometry
Introduction
We see a number of shapes with which we are familiar. We also make a lot of pictures. These pictures include different shapes. We have learnt about some of these shapes in earlier chapters as well. Why don’t you list those shapes that you know about alongwith how they appear?
In this chapter we shall learn to make these shapes. In making these shapes we need to use some tools. We shall begin with listing these tools, describing them and looking at how they are used.
S.No. Name and figure Description Use
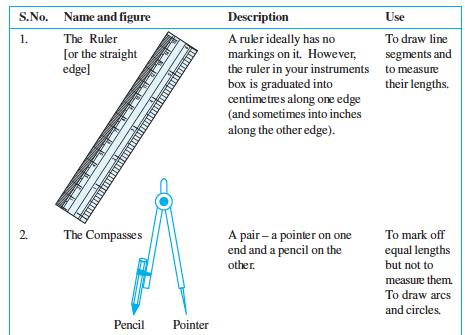
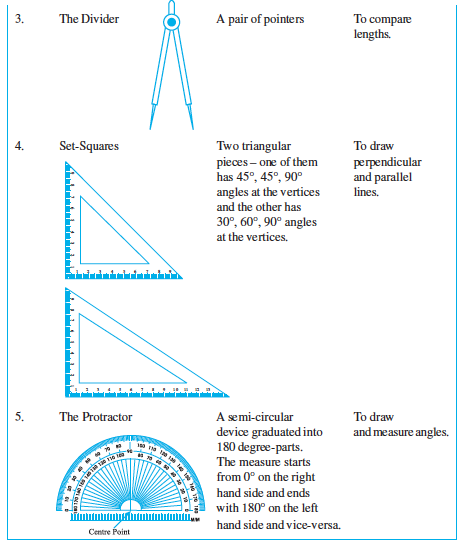
We are going to consider “Ruler and compasses constructions”, using ruler, only to draw lines, and compasses, only to draw arcs.
Be careful while doing these constructions.
Here are some tips to help you.
(a) Draw thin lines and mark points lightly.
(b) Maintain instruments with sharp tips and fine edges.
(c) Have two pencils in the box, one for insertion into the compasses and the other to draw lines or curves and mark points.
14.2 The Circle
Look at the wheel shown here. Every point on its boundary is at an equal distance from its centre. Can you mention a few such objects and draw them? Think about five such objects which have this shape.

14.2.1 Construction of a circle when its radius is known
Suppose we want to draw a circle of radius 3 cm. We need to use our compasses. Here are the steps to follow.
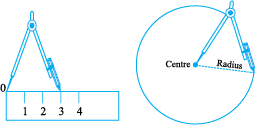
Step 1 Open the compasses for the required radius of 3cm.
Step 2 Mark a point with a sharp pencil where we want the centre of the circle to be. Name it as O.
Step 3 Place the pointer of the compasses on O.
Step 4 Turn the compasses slowly to draw the circle. Be careful to complete the movement around in one instant.
Think, discuss and write
How many circles can you draw with a given centre O and a point, say P?
Exercise 14.1
1. Draw a circle of radius 3.2 cm.
2. With the same centre O, draw two circles of radii 4 cm and 2.5 cm.
3. Draw a circle and any two of its diameters. If you join the ends of these diameters, what is the figure obtained? What figure is obtained if the diameters are perpendicular to each other? How do you check your answer?
4. Draw any circle and mark points A, B and C such that
(a) A is on the circle. (b) B is in the interior of the circle.
(c) C is in the exterior of the circle.
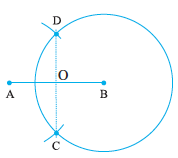
5. Let A, B be the centres of two circles of equal radii; draw them so that each one of them passes through the centre of the other. Let them intersect at C and D. Examine whether  and
and  are at right angles.
are at right angles.
14.3 A Line Segment
Remember that a line segment has two end points. This makes it possible to measure its length with a ruler.
If we know the length of a line segment, it becomes possible to represent it by a diagram. Let us see how we do this.
14.3.1 Construction of a line segment of a given length
Suppose we want to draw a line segment of length 4.7 cm. We can use our ruler and mark two points A and B which are 4.7 cm apart. Join A and B and get  . While marking the points A and B, we should look straight down at the measuring device. Otherwise we will get an incorrect value.
. While marking the points A and B, we should look straight down at the measuring device. Otherwise we will get an incorrect value.
Use of ruler and compasses
A better method would be to use compasses to construct a line segment of a given length.
Step 1 Draw a line l. Mark a point A on a line l.

Step 2 Place the compasses pointer on the zero mark of the ruler. Open it to place the pencil point upto the 4.7cm mark.
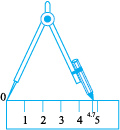
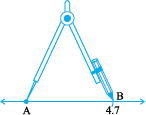
Step 3 Taking caution that the opening of the compasses has not changed, place the pointer on A and swing an arc to cut l at B.
 l
l
Step 4  is a line segment of required length.
is a line segment of required length.

Exercise 14.2
1. Draw a line segment of length 7.3 cm using a ruler.
2. Construct a line segment of length 5.6 cm using ruler and compasses.
3. Construct  of length 7.8 cm. From this, cut off
of length 7.8 cm. From this, cut off 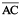 of length 4.7 cm. Measure
of length 4.7 cm. Measure 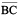 .
.
4. Given  of length 3.9 cm, construct
of length 3.9 cm, construct 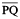 such that the length of
such that the length of 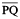 is twice that of
is twice that of  . Verify by measurement.
. Verify by measurement.

(Hint : Construct  such that length of
such that length of  = length of
= length of  ; then cut off
; then cut off 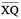 such that
such that 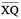 also has the length of
also has the length of  .)
.)
5. Given  of length 7.3 cm and
of length 7.3 cm and 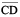 of length 3.4 cm, construct a line segment
of length 3.4 cm, construct a line segment 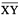 such that the length of
such that the length of 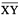 is equal to the difference between the lengths of
is equal to the difference between the lengths of  and
and 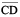 . Verify by measurement.
. Verify by measurement.
14.3.2 Constructing a copy of a given line segment
Suppose you want to draw a line segment whose length is equal to that of a given line segment  .
.
A quick and natural approach is to use your ruler (which is marked with centimetres and millimetres) to measure the length of  and then use the same length to draw another line segment
and then use the same length to draw another line segment 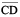 .
.
A second approach would be to use a transparent sheet and trace  onto another portion of the paper. But these methods may not always give accurate results.
onto another portion of the paper. But these methods may not always give accurate results.
A better approach would be to use ruler and compasses for making this construction.
To make a copy of  .
.
Step 1 Given  whose length is not known.
whose length is not known.
Step 2 Fix the compasses pointer on A and the pencil end on B. The opening of the instrument now gives the length of  .
.
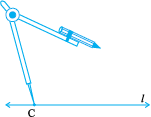
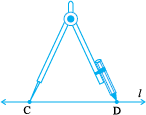
Step 3 Draw any line l. Choose a point C
on l. Without changing the compasses setting, place the pointer on C.
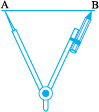
Step 4 Swing an arc that cuts l at a point, say,D. Now 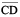 is a copy of
is a copy of  .
.
Exercise 14.3
1. Draw any line segment 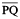 . Without measuring
. Without measuring 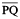 , construct a copy of
, construct a copy of 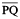 .
.
2. Given some line segment  , whose length you do not know, construct
, whose length you do not know, construct 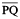 such that the length of
such that the length of 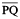 is twice that of
is twice that of  .
.
14.4 Perpendiculars
You know that two lines (or rays or segments) are said to be perpendicular if they intersect such that the angles formed between them are right angles.

In the figure, the lines l and m are perpendicular.
The corners of a foolscap paper or your notebook indicate lines meeting at right angles.

Where else do you see perpendicular lines around you?
Take a piece of paper. Fold it down the middle and make the crease. Fold the paper once again down the middle in the other direction. Make the crease and open out the page. The two creases are perpendicular to each other.


14.4.1 Perpendicular to a line through a point on it
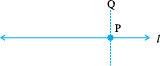
Given a line l drawn on a paper sheet and a point P lying on the line. It is easy to have a perpendicular to l through P.
We can simply fold the paper such that the lines on both sides of the fold overlap each other.
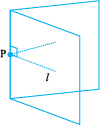
Tracing paper or any transparent paper could be better for this activity. Let us take such a paper and draw any line l on it. Let us mark a point P anywhere on l.
Fold the sheet such that l is reflected on itself; adjust the fold so that the crease passes through the marked point P. Open out; the crease is perpendicular to l.
Think, discuss and write
How would you check if it is perpendicular? Note that it passes through P as required.
A challenge : Drawing perpendicular using ruler and a set-square (An optional activity).
Step 1 A line l and a point P are given. Note that P is on the line l.

Step 2 Place a ruler with one of its edges along l. Hold this firmly.

Step 3 Place a set-square with one of its edges along the already aligned edge of the ruler such that the right angled corner is in contact with the ruler.

Step 4 Slide the set-square along the edge of ruler until its right angled corner coincides with P.

Step 5 Hold the set-square firmly in this position. Draw  along the edge of the set-square.
along the edge of the set-square.
 is perpendicular to l. (How do you use the
is perpendicular to l. (How do you use the  symbol to say this?).
symbol to say this?).
Verify this by measuring the angle at P.
Can we use another set-square in the place of the ‘ruler’? Think about it.
Method of ruler and compasses
As is the preferred practice in Geometry, the dropping of a perpendicular can be achieved through the “ruler-compasses” construction as follows :
Step 1 Given a point P on a line l.

Step 2 With P as centre and a convenient radius, construct an arc intersecting the line l at two points A and B.
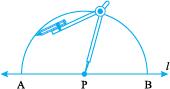
Step 3 With A and B as centres and a radius greater than AP construct two arcs, which cut each other at Q.
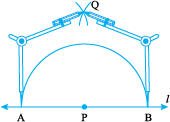
Step 4 Join PQ. Then  is perpendicular to l. We write
is perpendicular to l. We write 
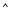 l.
l.
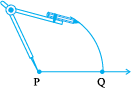
14.4.2 Perpendicular to a line through a point not on it
![]()
(Paper folding)
If we are given a line l and a point P not lying on it and we want to draw a perpendicular to l through P, we can again do it by a simple paper folding as before.
Take a sheet of paper (preferably transparent).
Draw any line l on it.
Mark a point P away from l.
Fold the sheet such that the crease passes through P. The parts of the line l on both sides of the fold should overlap each other.
Open out. The crease is perpendicular to l and passes through P.
Method using ruler and a set-square (An optional activity)
Step 1 Let l be the given line and P be a point outside l.

Step 2 Place a set-square on l such that one arm of its right angle aligns along l.

Step 3 Place a ruler along the edge opposite to the right angle of the set-square.
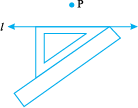
Step 4 Hold the ruler fixed. Slide the set-square along the ruler till the point P touches the other arm of the set-square.
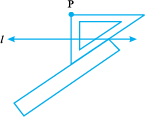
Step 5 Join PM along the edge through P,
meeting l at M.
Now ⊥ l.
⊥ l.
Method using ruler and compasses
A more convenient and accurate method, of course, is the ruler-compasses method.
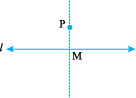
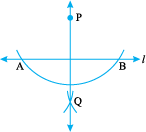
Step 1 Given a line l and a point P not on it.

Step 2 With P as centre, draw an arc which intersects line l at two points A and B.
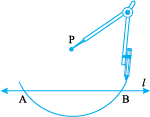
Step 3 Using the same radius and with A and B as centres, construct two arcs that intersect at a point, say Q, on the other side.
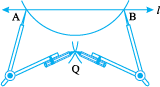
Step 4 Join PQ. Thus,  is perpendicular to l.
is perpendicular to l.
Exercise 14.4
1. Draw any line segment  . Mark any point M on it. Through M, draw a perpendicular to
. Mark any point M on it. Through M, draw a perpendicular to  . (use ruler and compasses)
. (use ruler and compasses)
2. Draw any line segment  . Take any point R not on it. Through R, draw a perpendicular to
. Take any point R not on it. Through R, draw a perpendicular to 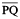 . (use ruler and set-square)
. (use ruler and set-square)
3. Draw a line l and a point X on it. Through X, draw a line segment 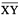 perpendicular to l.
perpendicular to l.
Now draw a perpendicular to 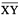 at Y. (use ruler and compasses)
at Y. (use ruler and compasses)
14.4.3 The perpendicular bisector of a line segment
Fold a sheet of paper. Let  be the fold. Place an ink-dot X, as shown, anywhere. Find the image X’ of X, with
be the fold. Place an ink-dot X, as shown, anywhere. Find the image X’ of X, with  as the mirror line.
as the mirror line.

Let  and
and 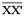 intersect at O.
intersect at O.
Is OX = OX’? Why?
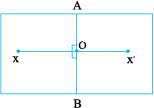
This means that  divides
divides 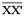 into two parts of equal length.
into two parts of equal length.  bisects
bisects 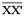 or
or  is a bisector of
is a bisector of 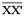 . Note also that
. Note also that 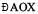 and
and 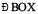 are right angles. (Why?).
are right angles. (Why?).
Hence,  is the perpendicular bisector of
is the perpendicular bisector of 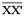 . We see only a part of
. We see only a part of  in the figure. Is the perpendicular bisector of a line joining two points the same as the axis of symmetry?
in the figure. Is the perpendicular bisector of a line joining two points the same as the axis of symmetry?
![]()
(Transparent tapes)
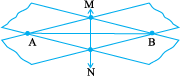
Step 1 Draw a line segment  .
.

Step 2 Place a strip of a transparent rectangular tape diagonally across  with the edges of the tape on the end points A and B, as shown in the figure.
with the edges of the tape on the end points A and B, as shown in the figure.

Step 3 Repeat the process by placing another tape over A and B just diagonally across the previous one. The two strips cross at M and N.

Step 4 Join M and N. Is  a bisector of
a bisector of  ? Measure and verify. Is it also the perpendicular bisector of
? Measure and verify. Is it also the perpendicular bisector of  ? Where is the mid point of
? Where is the mid point of  ?
?
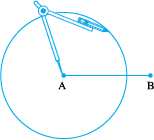
Construction using ruler and compasses
Step 1 Draw a line segment  of any length.
of any length.

Step 2 With A as centre, using compasses, draw a circle. The radius of your circle should be more than half the length of  .
.
Step 3 With the same radius and with B as centre, draw another circle using compasses. Let it cut the previous circle at C and D.
Step 4 Join 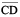 . It cuts
. It cuts  at O. Use your divider to verify that O is the midpoint of
at O. Use your divider to verify that O is the midpoint of  . Also verify that
. Also verify that 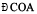 and
and  are right angles. Therefore,
are right angles. Therefore,  is the perpendicular bisector of
is the perpendicular bisector of  .
.
In the above construction, we needed the two points C and D to determine  . Is it necessary to draw the whole circle to find them? Is it not enough if we draw merely small arcs to locate them? In fact, that is what we do in practice!
. Is it necessary to draw the whole circle to find them? Is it not enough if we draw merely small arcs to locate them? In fact, that is what we do in practice!
![]()
In Step 2 of the construction using ruler and compasses, what would happen if we take the length of radius to be smaller than half the length of  ?
?
Exercise 14.5
1. Draw  of length 7.3 cm and find its axis of symmetry.
of length 7.3 cm and find its axis of symmetry.
2. Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
3. Draw the perpendicular bisector of 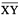 whose length is 10.3 cm.
whose length is 10.3 cm.
(a) Take any point P on the bisector drawn. Examine whether PX = PY.
(b) If M is the mid point of 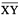 , what can you say about the lengths MX and XY?
, what can you say about the lengths MX and XY?
4. Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
In Step 2 of the construction using ruler and compasses, what would happen if we take the length of radius to be smaller than half the length of  ?
?
5. With 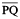 of length 6.1 cm as diameter, draw a circle.
of length 6.1 cm as diameter, draw a circle.
6. Draw a circle with centre C and radius 3.4 cm. Draw any chord  . Construct the perpendicular bisector of
. Construct the perpendicular bisector of  and examine if it passes through C.
and examine if it passes through C.
7. Repeat Question 6, if  happens to be a diameter.
happens to be a diameter.
8. Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?
9. Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of 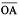 and
and 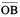 . Let them meet at P. Is PA = PB ?
. Let them meet at P. Is PA = PB ?
14.5 Angles
14.5.1 Constructing an angle of a given measure
Suppose we want an angle of measure 40°.
Here are the steps to follow :
Step 1 Draw  of any length.
of any length.

Step 2 Place the centre of the protractor at A and the zero edge along  .
.

Step 3 Start with zero near B. Mark point C at 40°.

Step 4 Join AC. 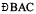 is the required angle.
is the required angle.

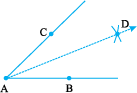
14.5.2 Constructing a copy of an angle of unknown measure
Suppose an angle (whose measure we do not know) is given and we want to make a copy of this angle. As usual, we will have to use only a straight edge and the compasses.
Given 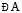 , whose measure is not known.
, whose measure is not known.

Step 1 Draw a line l and choose a point P on it.

Step 2 Place the compasses at A and draw an arc to cut the rays of 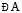 at B and C.
at B and C.

Step 3 Use the same compasses setting to draw an arc with P as centre, cutting l in Q.
 l
lStep 4 Set your compasses to the length BC with the same radius.
Step 5 Place the compasses pointer at Q and draw the arc to cut the arc drawn earlier in R.
 l
lStep 6 Join PR. This gives us 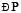 . It has the same measure as
. It has the same measure as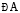 .
.
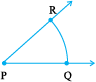 l
l
This means  has same measure as
has same measure as  .
.
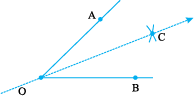
14.5.3 Bisector of an angle
Take a sheet of paper. Mark a point O on it. With O as initial point, draw two rays  and
and  . You get
. You get 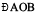 . Fold the sheet through O such that the rays
. Fold the sheet through O such that the rays 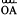 and
and  coincide. Let OC be the crease of paper which is obtained after unfolding the paper.
coincide. Let OC be the crease of paper which is obtained after unfolding the paper.
OC is clearly a line of symmetry for 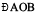 .
.
Measure 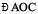 and
and 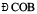 . Are they equal? OC the line of symmetry, is therefore known as the angle bisector of
. Are they equal? OC the line of symmetry, is therefore known as the angle bisector of 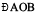 .
.
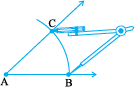
Construction with ruler and compasses
Let an angle, say, 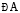 be given.
be given.
Step 1 With A as centre and using compasses, draw an arc that cuts both rays of  . Label the points of intersection as B and C.
. Label the points of intersection as B and C.
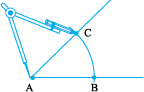
Step 2 With B as centre, draw (in the interior of  ) an arc whose radius is more than half the length BC.
) an arc whose radius is more than half the length BC.

Step 3 With the same radius and with C as centre, draw another arc in the interior of 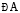 . Let the two arcs intersect at D. Then
. Let the two arcs intersect at D. Then 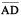 is the required bisector of
is the required bisector of 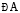 .
.
In Step 2 above, what would happen if we take radius to be smaller than half the length BC?
14.5.4 Angles of special measures
There are some elegant and accurate methods to construct some angles of special sizes which do not require the use of the protractor. We discuss a few here.
Constructing a 60° angle
Step 1 Draw a line l and mark a point O on it.

Step 2 Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line  at a point say, A.
at a point say, A.

Step 3 With the pointer at A (as centre), now draw an arc that passes through O.

In Step 2 above, what would happen if we take radius to be smaller than half the length BC?
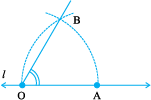
Step 4 Let the two arcs intersect at B. Join OB. We get 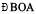 whose measure is 60°.
whose measure is 60°.
Constructing a 30° angle
Construct an angle of 60° as shown earlier. Now, bisect this angle. Each angle is 30°, verify by using a protractor.
How will you construct a 15° angle?
Constructing a 120° angle
An angle of 120° is nothing but twice of an angle of 60°. Therefore, it can be constructed as follows :
Step 1 Draw any line PQ and take a point O on it.

Step 2 Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line at A.

Step 3 Without disturbing the radius on the compasses, draw an arc with A as centre which cuts the first arc at B.
Step 4 Again without disturbing the radius on the compasses and with B as centre, draw an arc which cuts the first arc at C.

How will you construct a 15° angle?
Step 5 Join OC, 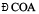 is the required angle whose measure is 120°.
is the required angle whose measure is 120°.

![]()
How will you construct a 150° angle?
Constructing a 90° angle
Construct a perpendicular to a line from a point lying on it, as discussed earlier. This is the required 90° angle.
![]()
How will you construct a 45° angle?
Exercise 14.6
1. Draw 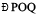 of measure 75° and find its line of symmetry.
of measure 75° and find its line of symmetry.
2. Draw an angle of measure 147° and construct its bisector.
3. Draw a right angle and construct its bisector.
4. Draw an angle of measure 153° and divide it into four equal parts.
5. Construct with ruler and compasses, angles of following measures:
(a) 60° (b) 30° (c) 90° (d) 120° (e) 45° (f) 135°
6. Draw an angle of measure 45° and bisect it.
7. Draw an angle of measure 135° and bisect it.
8. Draw an angle of 70o. Make a copy of it using only a straight edge and compasses.
9. Draw an angle of 40o. Copy its supplementary angle.
What have we discussed ?
This chapter deals with methods of drawing geometrical shapes.
1. We use the following mathematical instruments to construct shapes:
(i) A graduated ruler (ii) The compasses
(iii) The divider (iv) Set-squares (v) The protractor
2. Using the ruler and compasses, the following constructions can be made:
(i) A circle, when the length of its radius is known.
(ii) A line segment, if its length is given.
(iii) A copy of a line segment.
(iv) A perpendicular to a line through a point
(a) on the line (b) not on the line.
(v) The perpendicular bisector of a line segment of given length.
(vi) An angle of a given measure.
(vii) A copy of an angle.
(viii) The bisector of a given angle.
(ix) Some angles of special measures such as
(a) 90° (b) 45° (c) 60° (d) 30° (e) 120° (f) 135°
