Table of Contents
There was a general discussion among the children in Paheli and Boojho’s class about the places they had visited during the summer vacations. Someone had gone to their native village by a train, then a bus, and finally a bullock cart. One student had travelled by an aeroplane. Another spent many days of his holidays going on fishing trips in his uncle’s boat.
The teacher then asked them to read newspaper articles that mentioned about small wheeled vehicles that moved on the soil of Mars and conducted experiments. These vehicles were taken by spacecraft all the way to Mars!
Meanwhile, Paheli had been reading stories about ancient India and wanted to know how people travelled from one place to another in earlier times.
10.1 Story of Transport
Long ago people did not have any means of transport. They used to move only on foot and carry goods on their back. Later on they began to use animals for transportation.
For transport through water, routes, boats were used from ancient times. To begin with, boats were simple logs of wood in which a hollow cavity could be made. Later, people learnt to put together different pieces of wood and give shapes to the boats. These shapes imitated the shapes of the animals living in water. Recall our discussions of this streamlined shape of fish in Chapters 8 and 9.
Invention of the wheel made a great change in modes of transport. The design of the wheel was improved over thousands of years. Animals were used to pull carts that moved on wheels.

Until the beginning of the 19th century, people still depended on animals, boats and ships to transport them from place to place. The invention of steam engine led to the development of new means of transport. Railroads were made for steam engine driven carriages and wagons. Later came automobiles such as motor cars, trucks and buses. Motorised boats and ships were used as means of transport on water. The early years of 1900 saw the development of aeroplanes. These were later improved to carry passengers and goods. Electric trains, monorail, supersonic aeroplanes and spacecraft are some of the contributions of the 20th century.
Fig. 10.1 shows some of the different modes of transport. Place them in the correct order — from the earliest modes of transport to the most recent.
Are there any of the early modes of transport that are not in use today?
10.2 How Wide is this Desk?
How did people know how far they have travelled?
How will you know whether you can walk all the way to your school or whether you will need to take a bus or a rickshaw to reach your school? When you need to purchase something, is it possible for you to walk to the market? How will you know the answers to these questions?
It is often important to know how far a place is, so that we can have an idea how we are going to reach that place — walk, take a bus or a train, a ship, an aeroplane or even a spacecraft!
Sometimes, there are objects whose length or width we need to know.
In Paheli and Boojho’s classroom, there are large desks which are to be shared by two students. Paheli and Boojho share one desk, but, frequently end up objecting that the other is using a larger share of the desk.
On the teacher’s suggestion, they decided to measure the length of the desk, make a mark exactly in the middle of it and draw a line to separate the two halves of the desk.
Both Paheli and Boojho are very fond of playing gilli danda with their friends. Boojho brought a set of gilli and danda with him.
Here is how they tried to measure the length of the desk using the danda and the gilli (Fig. 10.2).
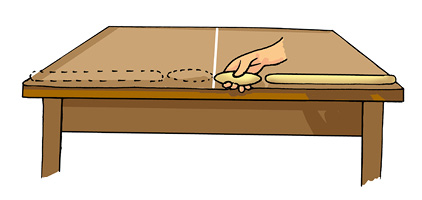
Fig. 10.2 Measuring the length of a desk with gilli and danda
The desk seems to be having a length equal to two danda lengths and two lengths of the gilli. Drawing a line in the middle of the desk leaves each of them happy with a half of the desk equal to a danda and a gilli in length. After a few days, the marked line gets wiped out. Boojho now has a new set of gilli and danda as he lost his old one. Here is how, the length of the desk seems to measure using the gilli and danda (Fig. 10.3).
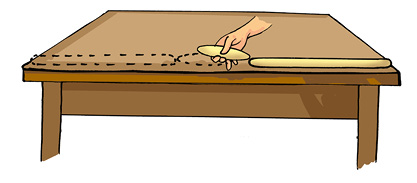
Fig. 10.3 Measuring the length of the desk with a different set of gilli and danda
Hello! Now, when measured with the new set of gilli and danda, the desk length seems to be about two danda lengths, one gilli length with a small length still left out. This is less than one gilli length. Now what?
What would you suggest Paheli and Boojho do, to measure the length of the whole desk? Can they use a cricket wicket and bails to measure the length or do you think that this might create the similar problem?
One thing they could do is to take a small length of string and mark two points on it. This will be a string length. They can measure the width of the desk in string lengths (Fig. 10.4). How can they use the string to measure distances less than the length of a string? They can fold the string and mark it into1/2, 1/4 and 1/8 ‘string lengths’. Now, perhaps Paheli and Boojho can measure the exact length of the desk using the string.
You would say that they should use the scale in their geometry box and solve their problem? Yes, Of course!

Fig. 10.4 Measuring the length of the desk with string lengths
Boojho has been reading about the way people used to measure distances before such standard scales were made and he has been trying to follow different methods of measuring distances.
There are so many occasions when we come across a need to measure lengths and distances. The tailor needs to measure the length of the cloth to know if it is enough to stitch a kurta. A carpenter needs to measure the height and width of a cupboard to know how much wood he would need to make its door. The farmer needs to know the length and breadth or the area of his land to know how much seed he can sow and how much water would be needed for his crops.
Suppose, you are asked how tall you are? You want to tell the length of a straight line from the top of your head to the heel of your feet.
How long is this room?
How wide is this desk?
How far is it from Delhi to Lucknow?
How far away is the Moon from the Earth?
All these questions have one thing in common. They all concern distance between two places. The two places may be close enough, like the two ends of a table or they may be far apart, like Jammu and Kanyakumari.
Let us do a few measurements to see what exactly we need to do, when we measure distances or lengths.
10.3 Some Measurements
Activity 1
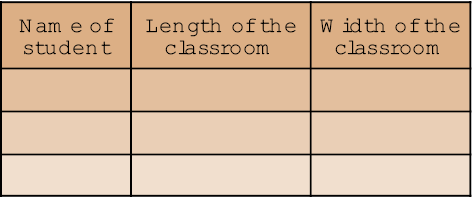
Work in groups and each of you do this activity one by one. Using your foot as a unit of length, measure the length and breadth of the classroom. It is possible that while measuring these you may find some part remains to be measured as it is smaller than your foot. Use a string to measure the length of a part of your foot as you did before. Record your observations in Table 10.1.
Table 10.1 Measuring length and breadth of classroom
Activity 2
Fig. 10.5 Measuring the width of a table with a handspan
Table 10.2 Measuring width of a table
Here too, you may find that you need string lengths equal to your handspan and then fractions of this string length to make the measurement. Record all observations in Table 10.2.
We see that, measurement means the comparison of an unknown quantity with some known quantity. This known fixed quantity is called a unit. The result of a measurement is expressed in two parts. One part is a number. The other part is the unit of the measurement. For example, if in Activity 1, the length of the room is found to be 12 lengths of your foot, then 12 is the number and ‘foot length’ is the unit selected for the measurement.
Now, study all the measurements recorded in Table 10.1 and 10.2. Are all the measurements for the room using everybody’s foot, equal? Are everybody’s measurement, by handspan, of the width of the table equal? Perhaps the results could be different as the length of your handspan and that of your friends may not be the same. Similarly, the length of the foot may be slightly different for all the students. Therefore, when you tell your measurement using your handspan or length of foot as a unit to others, they will not be able to understand how big the actual length is, unless they know the length of your handspan or foot.
We see therefore, that some standard units of measurement are needed, that do not change from person to person.
10.4 Standard Units of Measurements
In ancient times, the length of a foot, the width of a finger, and the distance of a step were commonly used as different units of measurements.
The people of the Indus valley civilisation must have used very good measurements of length because we see evidence in excavations of perfectly geometrical constructions.
A cubit as the length from the elbow to the finger tips was used in ancient Egypt and was also accepted as a unit of length in other parts of the world.
People also used the “foot” as a unit of length in different parts of the world. The length of the foot used varied slightly from region to region.
People measured a “yard” of cloth by the distance between the end of the outstretched arm and their chin. The Romans measured with their pace or steps.
In ancient India, small length measurements used were an angul (finger) or a mutthi (fist). Even today, we can see flower sellers using their forearm as a unit of length for garlands in many towns of India. Many such body parts continue to be in use as unit of length, when convenient.
However, everyone’s body parts could be of slightly different sizes. This must have caused confusion in measurement. In 1790, the French created a standard unit of measurement called the metric system.
For the sake of uniformity, scientists all over the world have accepted a set of standard units of measurement. The system of units now used is known as the International System of Units (SI units). The SI unit of length is a metre. A metre scale is shown in Fig.10.6. Also shown is the 15 cm scale in your geometry box.

Fig.10.6 A metre scale and a 15 cm scale
Each metre (m) is divided into 100 equal divisions, called centimetre (cm). Each centimetre has ten equal divisions, called millimetre (mm). Thus,
1 m = 100 cm
1 cm = 10 mm
For measuring large distances, metre is not a convenient unit. We define a larger unit of length. It is called kilometre (km).
1 km = 1000 m
Now, we can repeat all our measurement activities using a standard scale and measure in SI units. Before we do that, we do need to know the correct way of measuring lengths and distances.
10.5 Correct Measurement of Length
In our daily life we use various types of measuring devices. We use a metre scale for measuring length. A tailor uses a tape, whereas a cloth merchant uses a metre rod. For measuring the length of an object, you must choose a suitable device. You cannot measure the girth of a tree or the size of your chest using a metre scale, for instance. Measuring tape is more suitable for this. For small measurements, such as the length of your pencil, you can use a 15 cm scale from your geometry box.
In taking measurement of a length, we need to take care of the following:
1. Place the scale in contact with the object along its length as shown in Fig.10.7.
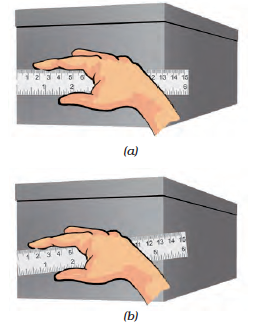
Fig. 10.7 Method of placing the scale along the length to be measured (a) correct and (b) incorrect
2. In some scales, the ends may be broken. You may not be able to see the zero mark clearly (Fig.10.8 (a)]. In such cases, you should avoid taking measurements from the zero mark of the scale. You can use any other full mark of the scale, say, 1.0 cm [Fig.10.8 (b)]. Then you must subtract the reading of this mark from the reading at the other end. For example, in Fig.10.8 (b) the reading at one end is 1.0 cm and at the other end it is 14.3 cm. Therefore, the length of the object is (14.3-1.0) cm = 13.3 cm.

Fig. 10.8 (a) Incorrect and (b) correct method of placing the scale with broken edge
3. Correct position of the eye is also important for taking measurement. Your eye must be exactly in front of the point where the measurement is to be taken as shown in Fig.10.9. Position ‘B’ is the correct position of the eye. Note that from position ‘B’, the reading is 7.5 cm. From positions ‘A’ and ‘C’, the readings may be different.
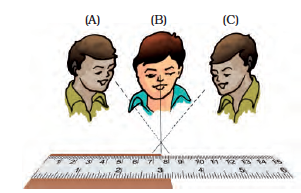
Fig. 10.9 B is the proper position of the eye for taking reading of the scale
Activity 3
Measure the height of your classmate using hand span and then by using a metre scale. For this, ask your classmate to stand with his back against a wall. Make a mark on the wall exactly above his head. Now, measure the distance from the floor to this mark on the wall with your handspan and then with a metre scale. Let all other students measure this length in a similar way. Record all observations in Table 10.3.
Table 10.3 Measurement of height
Study carefully results obtained by different students. The results in column 2 may be different from each other as the length of the handspan may be different for different students. Look at the results in column 3 where the measurements are done using a standard scale. The results may be close to each other now, but, are they exactly equal? If not, why do you think there is a difference? After all, everybody is using the same scale and not different hand spans. This could be due to small errors in taking observations. In higher classes we will learn about the importance of knowing and handling such errors in measurement.
10.6 Measuring the Length of a Curved Line
We cannot measure the length of a curved line directly by using a metre scale. We can use a thread to measure the length of a curved line.
Activity 4
Use a thread to measure the length of the curved line AB (Fig.10.10). Put a knot on the thread near one of its ends. Place this knot on the point A. Now, place a small portion of the thread along the line, keeping it taut using your fingers and thumb. Hold the thread at this end point with one hand. Using the other hand, stretch a little more portion of the thread along the curved line. Go on repeating this process till the other end B of the curved line is reached. Make a mark on the thread where it touches the end B. Now stretch the thread along a metre scale. Measure the length between the knot in the beginning and the final mark on the thread. This gives the length of the curved line AB.
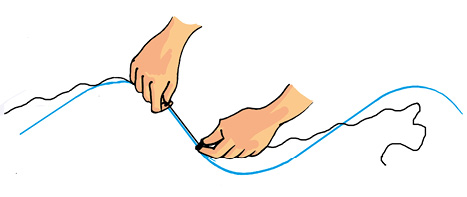
We see that we need a lot of care to ensure that we are measuring distances and lengths correctly. And, we need some standard units and devices with which we measure these distances and can convey our results to others.
10.7 Moving Things Around us
Activity 5
Think of some objects you have seen recently. List them in Table 10.4. These may include a school bag, a mosquito, a table, people sitting on chairs or people moving about. The list may also have a butterfly, a dog, a cow, your hands, a small baby, a fish in water, a house, a factory, a piece of stone, a horse, a ball, a bat, a moving train, a sewing machine, a wall clock or the hands of a clock. Make your list as large as you can.
Which of these are moving? Which are at rest?
How did you decide whether an object is in motion or at rest?
Table10. 4 Objects at rest and in motion
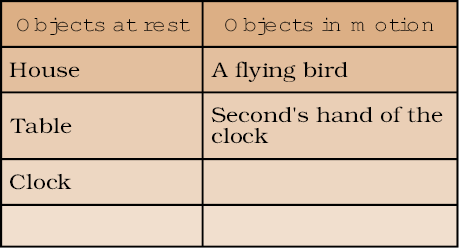
You might have noticed that the bird is not at the same place after some time, while the table is at the same place. On this basis, you may have decided whether an object is at rest or in motion.
Let us look at the motion of an ant closely.
Activity 6
Select a place where you find ants. Spread a large sheet of white paper on the ground and keep a little sugar on it. Ants are likely to be attracted to the sugar and you will find many ants crawling on the sheet of paper soon. For any one ant, try and make a small mark with a pencil near its position when it has just crawled on to the sheet of paper (Fig. 10.11). Keep marking its position after a few seconds as it moves along on the sheet of paper. After some time, shake the paper free of the sugar and the ants. Connect the different points you have marked, with arrows, to show the direction in which the ant was moving. Each point you have marked shows where the ant moved to, in intervals of a few seconds.

Fig. 10.11 Motion of an ant
Motion seems to be some kind of a change in the position of an object with time, isn’t it?
In Activity 5, where did you place objects like a clock, a sewing machine or an electric fan in your grouping of objects? Are these objects moving from one place to other? No? Do you notice movement in any of their parts? The blades of the fan or the hands of a clock— how are they moving? Is their movement similar to that of an ant or a train? Let us now look at some types of motion to help us understand these differences.
10.8 Types of Motion
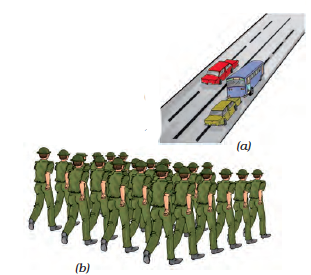
You may have observed the motion of a vehicle on a straight road, march-past of soldiers in a parade or the falling of a stone (Fig. 10.12). What kind of motion is this? Sprinters in a
100-metre race also move along a straight track. Can you think of more such examples from your surroundings?
In all these examples we see that the objects move along a straight line. This type of motion is called rectilinear motion.
Activity 7
Take a stone, tie a thread to it and whirl it with your hand. Observe the motion of the stone. We see that the stone moves along a circular path.
In this motion, the distance of the stone from your hand remains the same. This type of motion is called circular motion.
The motion of a point marked on the blade of an electric fan or the hands of a clock are examples of circular motion (Fig. 10.13).
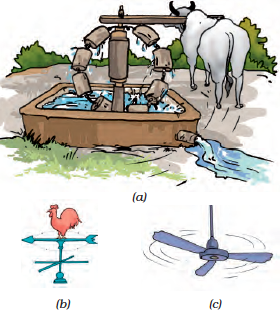
Fig. 10.13 Some objects in circular motion.

The electric fan or the clock by themselves are not moving from one place to another. But, the blades of the fan rotate and so do the hands of a clock. If we mark a point anywhere on the blades of a fan or on the hands of a clock, the distance of this point from the centre of the fan or the clock, will remain the same as they rotate.

In some cases, an object repeats its motion after some time. This type of motion is called periodic motion. Take the stone tied with a string that you used in Activity 7. Now, hold the string in your hand and let the stone hang from it. This is a pendulum. Pull the stone to one side with the other hand and let it go. Now the pendulum is in motion. It is an example of periodic motion. A branch of a tree moving to and fro, motion of a child on a swing, strings of a guitar or the membrane of drums (tabla) being played, are all examples of periodic motion where an object or a part of it repeats its motion after a fixed interval of time (Fig. 10.14).
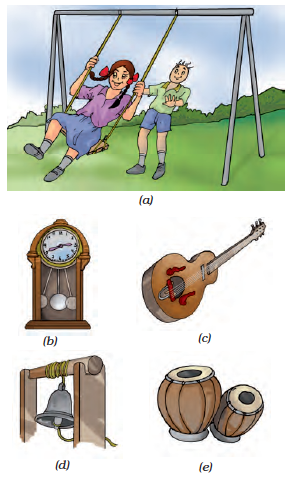
Fig. 10.14 Examples of periodic motion
Did you observe a sewing machine as a part of Activity 5? You must have observed that it remains at the same location while any point on its wheel moves with a circular motion. It also has a needle that moves up and down continuously, as long as the wheel rotates, isn’t it? This needle is undergoing a periodic motion.
Have you observed closely, the motion of a ball along the ground? Here, the ball is rolling on the ground – rotating as well as moving forward along the ground. Thus, the ball undergoes a rectilinear motion as well as rotational motion. Can you think of other examples where objects undergo combinations of different types of motion?
We did many measurement activities and discussed some kinds of motion. We saw that motion is a change in the position of an object with time. The change in this position can
be determined through distance measurements. This allows us to know how fast or slow a motion is. The movement of a snail on the ground, a butterfly flitting from flower to flower, a river flowing, an aeroplane flying, moon going around the Earth and blood flowing inside our bodies show that there is motion everywhere around us!
KeyWords

Circular motion
Summary
- Different modes of transport are used to go from one place to another.
- In ancient times, people used length of a foot, the width of a finger, the distance of a step as units of measurement. This caused confusion and a need to develop a uniform system of measurement arose.
- Now, we use International System of Units ( SI units). This is accepted all over the world.
- Metre is the unit of length in SI unit.
- Motion in a straight line is called rectilinear motion.
- In circular motion an object moves such that its distance from a fixed point remains the same.
- Motion that repeats itself after some period of time is called periodic motion.
Exercises
1. Give two examples each, of modes of transport used on land, water and air.
2. Fill in the blanks:
(i) One metre is ______________ cm.
(ii) Five kilometre is ______________ m.
(iii) Motion of a child on a swing is ______________.
(iv) Motion of the needle of a sewing machine is ______________.
(v) Motion of wheel of a bicycle is______________.
3. Why can a pace or a footstep not be used as a standard unit of length?
4. Arrange the following lengths in their increasing magnitude:
1 metre, 1 centimetre, 1 kilometre,1 millimetre.
5. The height of a person is 1.65 m. Express it into cm and mm.
6. The distance between Radha’s home and her school is 3250 m. Express this distance into km.
7. While measuring the length of a knitting needle, the reading of the scale at one end is 3.0 cm and at the other end is 33.1 cm. What is the length of the needle?
8. Write the similarities and differences between the motion of a bicycle and a ceiling fan that has been switched on.
9. Why would you not like to use a measuring tape made of an elastic material like rubber to measure distance? What would be some of the problems you would meet in telling someone about a distance you measured with such a tape?
10. Give two examples of periodic motion.
Suggested projects and Activities
1. Draw a map of your classroom. Roll a ball on the floor. In your map mark the points where the ball started and where it stopped. Show also the path it moved along. Did the ball move along a straight line?
2. Using string and a scale, let each student measure the length of his/her foot. Prepare a bar graph of the foot length measurements that have been obtained for the whole class.
