Table of Contents
अपनी संख्याओं की जानकारी
1.1 भूमिका
वस्तुओं को गिनना अब हमारे लिए सरल है। अब हम वस्तुओं को बड़ी संख्याओं में गिन सकते हैं, जैसे कि एक स्कूल के विद्यार्थियों की संख्या, और इन संख्याओं को संख्यांकों (numerals) द्वारा निरूपित कर सकते हैं। हम उपयुक्त संख्या नामों (number names) का प्रयोग करके बड़ी संख्याओं से संबंधित सूचनाएँ भी दे सकते हैं।
एेसा नहीं है कि हम हमेशा से ही बड़ी राशियों के बारे में वार्तालाप या संकेतों द्वारा सूचना देना जानते थे। कई हज़ार वर्ष पहले, लोग केवल छोटी संख्याओं के बारे में ही जानते थे। धीरे-धीरे उन्होंने बड़ी संख्याओं के साथ कार्य करना सीखा। उन्होंने बड़ी संख्याओं को संकेतों से व्यक्त करना भी सीखा। यह सब मानव प्राणियों के सामूहिक प्रयासों के कारण संभव हो सका। उनका रास्ता सरल नहीं था और उन्हें इस पूरे रास्ते में संघर्ष करना पड़ा। वास्तव में, संपूर्ण गणित के विकास को इसी रूप में समझा जा सकता है। जैसे-जैसे मानव ने उन्नति की, वैसे-वैसे गणित के विकास की आवशयकता बढ़ती गई और इसके परिणामस्वरूप गणित में विकास और तेज़ी से हुआ।
हम संख्याओं का प्रयोग करते हैं और उनके बारे में अनेक बातें जानते हैं। संख्याएँ प्रत्यक्ष वस्तुओं को गिनने में हमारी सहायता करती हैं। संख्याएँ हमारी सहायता यह बताने में करती हैं कि वस्तुओं का कौन-सा संग्रह (collection) बड़ा है और वस्तुओं को पहले, दूसरे इत्यादि क्रम में व्यवस्थित करने में भी सहायता करती हैं। संख्याओं का विभिन्न संदर्भों में और अनेक प्रकार से प्रयोग किया जाता है। विभिन्न स्थितियों के बारे में सोचिए जहाँ हम संख्याओं का प्रयोग करते हैं। भिन्न पाँच स्थितियों को लिखिए जिनमें हम संख्याओं का प्रयोग करते हैं।
हम संख्याओं के साथ कार्य करने का आनंद प्राप्त कर चुके हैं। हम इनके साथ योग, व्यवकलन (घटाने), गुणा और भाग की संक्रियाएँ भी कर चुके हैं। हम संख्या अनुक्रमों (sequences) में प्रतिरूपों (patterns) को देख चुके हैं और संख्याओं के साथ अनेक रुचिपूर्ण बातें कर चुके हैं। इस अध्याय में, हम कुछ समीक्षा और पुनरावलोकन के साथ इन रुचिपूर्ण बातों पर और आगे कदम बढ़ाएँगे।
1.2 संख्याओं की तुलना
चूँकि हम संख्याओं की तुलना पहले भी बहुत कर चुके हैं, आइए देखें कि क्या हमें याद है कि दी गई संख्याओं में कौन सी संख्या सबसे बड़ी है?
(i) 92, 392, 4456, 89742 
(ii) 1902, 1920, 9201, 9021, 9210
तो, हम यहाँ उत्तर जानते हैं।
अपने मित्रों में चर्चा कीजिए और पता कीजिए कि किसी संख्या समूह में वे सबसे बड़ी संख्या किस प्रकार ज्ञात करते हैं।

क्या आप तुरंत ज्ञात कर सकते हैं कि प्रत्येक पंक्ति में कौन सी संख्या सबसे बड़ी है और कौन सी संख्या सबसे छोटी है?
1. 382, 4972, 18, 59785, 750 उत्तर: 59785 सबसे बड़ी है और 18 सबसे छोटी है।
2. 1473, 89423, 100, 5000, 310 उत्तर: ____________________
3. 1834, 75284, 111, 2333, 450 उत्तर: ____________________
4. 2853, 7691, 9999, 12002, 124 उत्तर: ____________________
क्या यह सरल था? यह सरल क्यों था?
यहाँ हमने केवल अंकों की संख्या को देखकर ही उत्तर ज्ञात कर लिया। सबसे बड़ी संख्या में अधिकतम हज़ार थे और सबसे छोटी संख्या सैकड़ों (सौ) अथवा दहाइयों (दस) में थी।
इसी प्रकार के पाँच और प्रशन बनाइए और उन्हें हल करने के लिए अपने मित्रों को दीजिए।
हम 4875 और 3542 की तुलना किस प्रकार करते हैं? यहाँ यह अधिक कठिन नहीं है।
इन दोनों संख्याओं में अंकों की संख्या समान है। ये दोनों हज़ारों में हैं। परंतुु 4875 में हज़ार के स्थान पर अंक, 3542 के हज़ार के स्थान के अंक से बड़ा है। अत: 3542 से 4875 बड़ी है।
अब बताइए कि कौन सी संख्या बड़ी है; 4875 या 4542? यहाँ भी दोनों संख्याओं में अंकों की संख्या समान (बराबर) है। साथ ही, दोनों में हज़ार के स्थान पर समान अंक हैं। अब हम क्या करते हैं? हम अगले अंक की ओर बढ़ते हैं, अर्थात् सौ के स्थान पर आने वाले अंकों को देखते हैं। 4875 में सौवें स्थान वाला अंक 4542 के सौवें स्थान वाले अंक से बड़ा है। अत: संख्या 4542 से संख्या 4875 बड़ी है।
यदि दोनों संख्याओं में सौ के स्थान वाले अंक भी समान होते, तो हम क्या करते?
4875 और 4889 की तुलना कीजिए।
4875 और 4879 की तुलना कीजिए।

प्रत्येक समूह में सबसे बड़ी और सबसे छोटी संख्याएँ ज्ञात कीजिए:
(a) 4536, 4892, 4370, 4452
(b) 15623, 15073, 15189, 15800
(c) 25286, 25245, 25270, 25210
(d) 6895, 23787, 24569, 24659
इसी प्रकार के पाँच प्रशन और बनाइए और हल करने के लिए अपने मित्रों को दीजिए।
1.2.1 आप कितनी संख्याएँ बना सकते हैं?
मान लीजिए हमारे पास अंक 7, 8, 3 और 5 हैं। हमें इन अंकों से चार अंकों वाली भिन्न-भिन्न एेसी संख्याएँ बनाने को कहा जाता है कि एक संख्या में कोई भी अंक दोबारा न आए (अर्थात् किसी भी अंक की पुनरावृत्ति न हो)। इस प्रकार, संख्या 7835 तो बनाई जा सकती है, परंतुु 7735 नहीं। इन 4 अंकों से जितनी संख्याएँ बना सकते हैं, बनाइए।
आपको सबसे बड़ी और सबसे छोटी संख्या कौन सी प्राप्त होती है? यहाँ सबसे बड़ी संख्या 8753 है और सबसे छोटी संख्या 3578 है। दोनों में अंकों के क्रम के बारे में सोचिए। क्या आप बता सकते हैं कि दिए गए अंकों से सबसे बड़ी संख्या किस प्रकार ज्ञात की जा सकती है? अपनी प्रक्रिया को लिखिए।

1. बिना पुनरावृत्ति किए, दिए हुए अंकों का प्रयोग करके चार अंकों की सबसे बड़ी और सबसे छोटी संख्याएँ बनाइए:
(a) 2, 8, 7, 4
(b) 9, 7, 4, 1
(c) 4, 7, 5, 0
(d) 1, 7, 6, 2
(e) 5, 4, 0, 3
(संकेत : 0754 तीन अंकों की संख्या है।)
2. किसी एक अंक का दो बार प्रयोग करके चार अंकों की सबसे बड़ी और सबसे छोटी संख्याएँ बनाइए:
(a) 3, 8, 7
(b) 9, 0, 5
(c) 0, 4, 9
(d) 8, 5, 1
(संकेत : प्रत्येक स्थिति में सोचिए कि आप किस अंक का दो बार प्रयोग करेंगे।)
3. दिए हुए प्रतिबंधों के साथ, किन्हीं चार अंकों का प्रयोग करके, 4 अंकों की सबसे बड़ी और सबसे छोटी संख्याएँ बनाइए:
(a) अंक 7 सदैव इकाई के स्थान पर रहे।
सबसे बड़ी
सबसे छोटी
(ध्यान दीजिए, अंक 0 से संख्या प्रारंभ नहीं हो सकती। क्यों?)
(b) अंक 4 सदैव दहाई के स्थान पर रहे। 
सबसे बड़ी
सबसे छोटी
(c) अंक 9 सदैव सौ के स्थान पर रहे। 
(d) अंक 1 सदैव हज़ार के
स्थान पर रहे।
4. मान लीजिए, आप दो अंक 2 और 3 लेते हैं।इन अंकों को समान बार दोहराते हुए, चार अंकों की संख्याएँ बनाइए। कौन सी संख्या सबसे बड़ी है? कौन सी संख्या सबसे छोटी है? आप एेसी कुल कितनी संख्याएँ बना सकते हैं?
उचित क्रम में खड़े होना:
1. इनमें कौन सबसे लंबा है?
2. इनमें कौन सबसे छोटा है?
(a) क्या आप इन्हें इनकी लंबाइयों के बढ़ते हुए क्रम में खड़ा कर सकते हैं?
(b) क्या आप इन्हें इनकी लंबाइयों के घटते हुए क्रम में खड़ा कर सकते हैं?

क्या खरीदें?
सोहन और रीता एक अलमारी खरीदने गए। वहाँ कई अलमारियाँ उपलब्ध थीं जिन पर उनके मूल्यों की पर्चियाँ लगी हुई थीं।
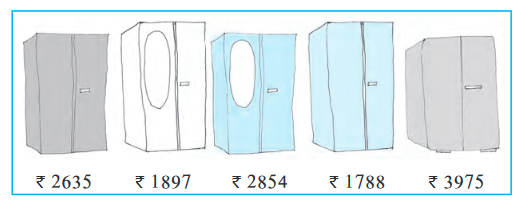
(a) क्या आप इनके मूल्यों को बढ़ते हुए क्रम में व्यवस्थित कर सकते हैं?
(b) क्या आप इनके मूल्यों को घटते हुए क्रम में व्यवस्थित कर सकते हैं?
इसी प्रकार की पाँच और स्थितियों को सोचिए जहाँ आप तीन या अधिक राशियों की तुलना करते हैं।
आरोही क्रम (Ascending order): आरोही या बढ़ते हुए क्रम का अर्थ है सबसे छोटे से प्रारंभ कर सबसे बड़े तक व्यवस्थित करना।
अवरोही क्रम (Descending order): अवरोही क्रम या घटते हुए क्रम का अर्थ है सबसे बड़े से प्रारंभ कर सबसे छोटे तक व्यवस्थित करना।

1. निम्नलिखित संख्याओं को आरोही क्रम में व्यवस्थित कीजिए:
(a) 847, 9754, 8320, 571
(b) 9801, 25751, 36501, 38802
2. निम्नलिखित संख्याओं को अवरोही क्रम में व्यवस्थित कीजिए:
(a) 5000, 7500, 85400, 7861
(b) 1971, 45321, 88715, 92547
आरोही/अवरोही क्रमों के एेसे ही दस उदाहरण और बनाइए और उन्हें आरोही/अवरोही क्रम में व्यवस्थित कीजिए।
1.2.2 अंकों का स्थानांतरण
क्या आपने सोचा है कि यदि किसी संख्या के अंकों के स्थान परस्पर बदल दिए जाएँ तो क्या होगा?
सोचिए कि 182 क्या बन जाएगा। यह 821 जैसी बड़ी हो सकती है अथवा 128 जैसी छोटी। यही प्रक्रिया 391 के साथ करके देखिए।
अब आगे दिए हुए प्रशनों पर ध्यान दीजिए। तीन भिन्न-भिन्न अंकों की कोई संख्या लीजिए और सौ के स्थान के अंक को इकाई के स्थान के अंक से बदलिए।
(a) क्या नयी संख्या पहली संख्या से बड़ी है?
(b) क्या नयी संख्या पहली संख्या से छोटी है?
इस प्रकार बनने वाली संख्याओं को आरोही और अवरोही दोनों क्रमों में लिखिए।
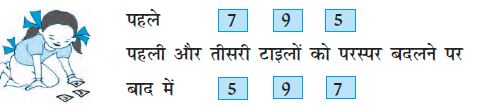
विभिन्न अंक लेकर यदि आप पहली और तीसरी टाइलों (अंकों) को परस्पर बदलते हैं, तो
किस स्थिति में संख्या बड़ी हो जाती है?
किस स्थिति में संख्या छोटी हो जाती है?
यह प्रक्रिया चार अंकों की कोई संख्या लेकर दोहराइए।
1.2.3 संख्या 10000 का प्रवेशा
हम जानते हैं कि 99 से आगे दो अंकों वाली कोई संख्या नहीं है। 99 दो अंकों की सबसे बड़ी संख्या है। इसी प्रकार 999 तीन अंकों की सबसे बड़ी संख्या है और चार अंकों की सबसे बड़ी संख्या 9999 है। यदि हम 9999 में 1 जोड़ें, तो हमें क्या प्राप्त होगा?
इस प्रतिरूप को देखिए
9 + 1 = 10 = 10 × 1
99 + 1 = 100 = 10 × 10
999 + 1 = 1000 = 10 × 100
हम देखते हैं कि
एक अंक की सबसे बड़ी संख्या + 1 = दो अंकों की सबसे छोटी संख्या,
दो अंकों की सबसे बड़ी संख्या + 1 = तीन अंकों की सबसे छोटी संख्या,
तीन अंकों की सबसे बड़ी संख्या + 1 = चार अंकों की सबसे छोटी संख्या।
तब हम क्या यह नहीं सोच सकते कि चार अंकों की सबसे बड़ी संख्या में 1 जोड़ने पर, हमें पाँच अंकों की सबसे छोटी संख्या प्राप्त होगी, अर्थात् 9999 +1= 10000 होगा। इस प्रकार, 9999 से ठीक आगे आने वाली संख्या 10000 है। इसे दस हज़ार कहते हैं। साथ ही, हम सोच सकते हैं कि 10000 = 10 × 1000 होगा।
1.2.4 स्थानीय मान पर पुनदृष्टि
आप स्थानीय मान के बारे में बहुत पहले पढ़ चुके हैं तथा 78 जैसी दो अंकों की संख्या का प्रसारित रूप आपको अवशय याद होगा। यह इस प्रकार है:
78 = 70 + 8
= 7 × 10 + 8
इसी प्रकार, आपको तीन अंकों की संख्या जैसे 278 का प्रसारित रूप भी याद होगा। यह इस प्रकार है:
278 = 200 + 70 + 8
= 2 × 100 + 7 × 10 + 8
हम कहते हैं कि 8 इकाई के स्थान पर है, 7 दहाई के स्थान पर है और 2 सौ के स्थान पर है।
बाद में, हमने इसी अवधारणा को चार अंकों की संख्या के लिए भी लागू कर लिया था।
उदाहरणार्थ, 5278 का प्रसारित रूप है:
5278 = 5000 + 200 + 70 + 8
= 5 × 1000 + 2 × 100 + 7 × 10 + 8
यहाँ, इकाई के स्थान पर 8, दहाई के स्थान पर 7, सौ के स्थान पर 2 और हज़ार के स्थान पर 5 है।
संख्या 10000 ज्ञात हो जाने पर, हम इस अवधारणा को और आगे लागू कर सकते हैं। हम पाँच अंकों की संख्या जैसे 45278 को इस प्रकार लिख सकते हैं:
45278 = 4 × 10000 + 5 × 1000 + 2 × 100 + 7 × 10 + 8
यहाँ हम कहते हैं कि इकाई के स्थान पर 8, दहाई के स्थान पर 7, सौ के स्थान पर 2, हज़ार के स्थान पर 5 और दस हज़ार के स्थान पर 4 है। इस संख्या को पैंतालीस हज़ार दो सौ अठहत्तर पढ़ा जाता है। क्या अब आप 5 अंकों की सबसे छोटी और सबसे बड़ी संख्याएँ लिख सकते हैं?

संख्याओं को पढ़िए और जहाँ-जहाँ रिक्त स्थान हैं उनके नाम लिखिए और प्रसारित रूप में लिखिए:
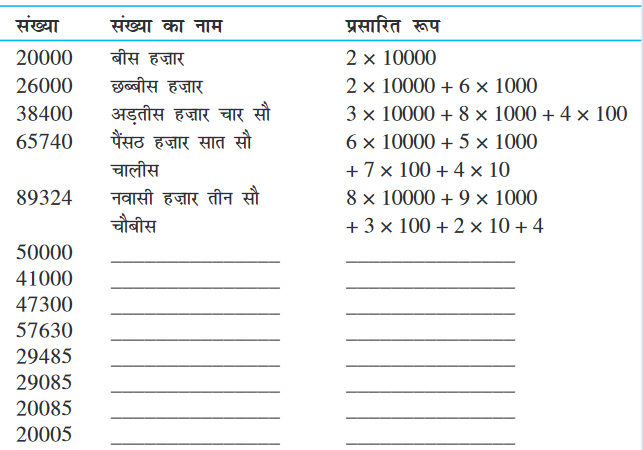
पाँच अंकों वाली पाँच और संख्याएँ लिखिए, उन्हें पढ़िए और उनको प्रसारित रूप में लिखिए।
1.2.5 संख्या 100000 का प्रवेशा
पाँच अंकों की सबसे बड़ी संख्या कौन सी है? पाँच अंकों की सबसे बड़ी संख्या में 1 जोड़ने पर छ: अंकों की सबसे छोटी संख्या प्राप्त होनी चाहिए। अर्थात्
99,999 + 1 = 1,00,000
इस संख्या को एक लाख नाम दिया जाता है। एक लाख 99999 के ठीक आगे आने वाली संख्या है।
साथ ही, 10,000 × 10 = 1,00,000
अब हम 6 अंकों की संख्याएँ और उनके प्रसारित रूप लिख सकते हैं। जैसे:
2,46,853 = 2 × 1,00,000 + 4 × 10,000 + 6 × 1,000 + 8 × 100+ 5 × 10 +3 × 1
इस संख्या में, इकाई के स्थान पर 3, दहाई के स्थान पर 5, सौ के स्थान पर 8, हज़ार के स्थान पर 6, दस हज़ार के स्थान पर 4 और लाख के स्थान पर 2 है। इस संख्या का नाम दो लाख छियालीस हज़ार आठ सौ तिरपन है।

संख्याओं को पढ़कर उन्हें रिक्त स्थानों में प्रसारित रूप में और उनके नाम लिखिए:
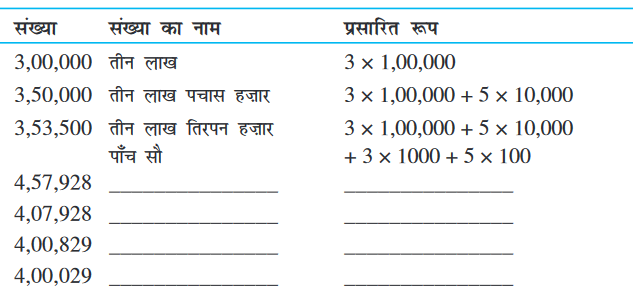
1.2.6 बड़ी संख्याएँ

यदि हम 6 अंकों की सबसे बड़ी संख्या में 1 जोड़ें, तो हमें 7 अंकों की सबसे छोटी संख्या प्राप्त होती है, जिसे दस लाख कहते हैं।
6 अंकों की सबसे बड़ी संख्या और 7 अंकों की सबसे छोटी संख्या लिखिए।
7 अंकों की सबसे बड़ी संख्या और 8 अंकों की सबसे छोटी संख्या लिखिए।
8 अंकों की सबसे छोटी संख्या एक करोड़ है।
प्रतिरूप को पूरा कीजिए: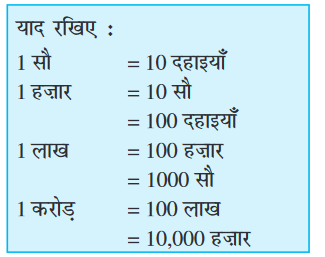
9 + 1 = 10
99 + 1 = 100
999 + 1 = _______
9,999 + 1 = _______
99,999 + 1 = _______
9,99,999 + 1 = _______
99,99,999 + 1 = 1,00,00,000

1. 10 – 1 क्या है?
2. 100 – 1 क्या है?
3. 10,000 – 1 क्या है?
4. 1,00,000 – 1 क्या है?
5. 1,00,00,000 – 1 क्या है?
(संकेत: प्रतिरूप को पहचानिए)
अनेक विभिन्न स्थितियों में हमारे सम्मुख बड़ी संख्याएँ आती हैं। उदाहरणार्थ, आपकी कक्षा के बच्चों की संख्या दो अंकों की होगी, जबकि आपके स्कूल के कुल बच्चों की संख्या 3 या 4 अंकों की होगी। पास के शहर में रहने वाले लोगों की संख्या और अधिक बड़ी होगी।
क्या यह 5 या 6 या 7 अंकों की संख्या है? क्या आप अपने राज्य में रहने वाले लोगों की संख्या के बारे में जानते हैं?
इस संख्या में कितने अंक होंगे?
गेहूँ से भरी एक बोरी में दानों (grains) की संख्या क्या होगी? यह एक 5 अंकों की संख्या या 6 अंकों की संख्या या और बड़ी संख्या होगी?

1. एेसे पाँच उदाहरण दीजिए जहाँ गिनी जाने वाली वस्तुओं की संख्या 6 अंकों की संख्या से अधिक होगी।
2. 6 अंकों की सबसे बड़ी संख्या से प्रारंभ करते हुए, अवरोही क्रम में पिछली पाँच संख्याएँ लिखिए।
3. 8 अंकों की सबसे छोटी संख्या से प्रारंभ करते हुए, आरोही क्रम में अगली पाँच संख्याएँ लिखिए और उन्हें पढ़िए।
1.2.7 बड़ी संख्याएँ पढ़ने और लिखने में एक सहायता
निम्नलिखित संख्याओं को पढ़ने का प्रयत्न कीजिए:
(a) 279453
(b) 5035472
(c) 152700375
(d) 40350894
क्या आपको कुछ कठिनाई हुई?
आपको एेसा करने में क्या कठिनाई हुई?
कभी-कभी बड़ी संख्याओं के पढ़ने और लिखने में कुछ सूचक (indicators) लगे होते हैं। शगुफ्ता भी सूचकों का प्रयोग करती है जो उसे बड़ी संख्याओं को पढ़ने और लिखने में सहायता करते हैं। उसके ये सूचक, संख्याओं को प्रसारित रूप में लिखने में भी सहायक होते हैं। उदाहरणार्थ, वह 257 में इकाई के स्थान, दहाई के स्थान और सौ के स्थान पर अंकों को ज्ञात करके उन्हें सारणी में O, T और H के नीचे निम्न प्रकार से लिखती है:
H T O प्रसारित रूप
2 5 7 2 × 100 + 5 × 10 + 7 × 1
इसी प्रकार, 2902 के लिए वह प्राप्त करती है:
Th H T O प्रसारित रूप
2 9 0 2 2 × 1000 + 9 × 100 + 0 × 10 + 2 × 1
वह इस अवधारणा को लाखों तक की संख्याओं के लिए लागू करती है, जैसा कि नीचे दी हुई सारणी में देखा जा सकता है। (हम इन्हें शगुफ्ता के खाने या बॉक्स (Boxes) कहेंगे)। ध्यान से देखिए और रिक्त स्थानों पर छूटी हुई प्रविज़्टियों को भरिए:
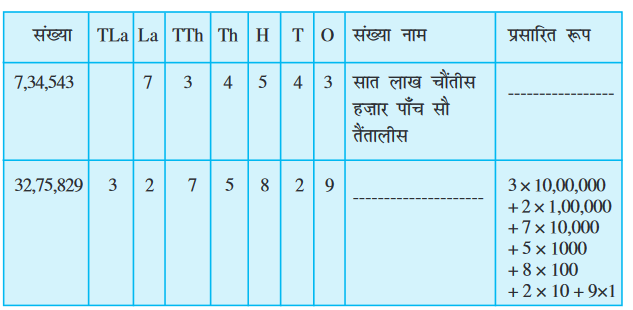
इसी प्रकार, हम करोड़ों तक की संख्याओं को सम्मिलित कर सकते हैं, जैसा कि नीचे दिखाया गया है:
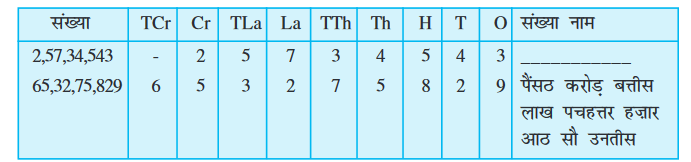
आप संख्याओं को प्रसारित रूप में लिखने के लिए अन्य तालिकाओं का प्रारूप भी बना सकते हैं।
अल्प विरामों (commas) का प्रयोग
आपने ध्यान दिया होगा कि उपरोक्त तालिकाओं में बड़ी संख्याओं के लिखने में हमने अल्प विरामों का प्रयोग किया है। बड़ी संख्याओं को पढ़ने और लिखने में अल्प विराम हमारी बड़ी सहायता करते हैं। संख्यांकन की भारतीय पद्धति (Indian system of numeration) में हम इकाई, दहाई, सौ (सैकड़ा), हज़ारों का प्रयोग करते हैं तथा आगे लाखों और करोड़ों का प्रयोग करते हैं। हज़ारों, लाखों और करोड़ों को प्रदर्शित करने के लिए अल्प विरामों का प्रयोग किया जाता है। पहला अल्प विराम सौ के स्थान (दाएँ से चलते हुए तीसरे अंक) के बाद आता है और हज़ारों को प्रदर्शित करता है। दूसरा अल्प विराम अगले दो अंकों (दाएँ से पाँचवें अंक) के बाद आता है। यह दस हज़ार के स्थान के बाद आता है और लाखों को प्रदर्शित करता है। तीसरा अल्प विराम अन्य दो अंकों (दाएँ से सातवें अंक) के बाद आता है। यह दस लाख के स्थान के बाद आता है और करोड़ों को प्रदर्शित करता है।
उदाहरणार्थ,
5, 08, 01, 592
3, 32, 40, 781
7, 27, 05, 062
संख्याओं के नाम लिखते समय, हम अल्प विरामों का प्रयोग नहीं करते हैं।
ऊपर दी हुई संख्याओं को पढ़ने का प्रयत्न कीजिए। इसी रूप में पाँच और संख्याओं को लिखिए और फिर उन्हें पढ़िए।
अंतराष्ट्रीय संख्यांकन पद्धति
संख्यांकन की अंतराष्ट्रीय (International) पद्धति में, इकाई, दहाई, सौ, हज़ारों और आगे मिलियनों (millions) का प्रयोग किया जाता है। हज़ारों और मिलियनों को प्रदर्शित करने के लिए अल्प विरामों का प्रयोग किया जाता है। अल्प विराम दाएँ से प्रत्येक तीसरे अंक के बाद आता है। पहला अल्प विराम हज़ारों को प्रदर्शित करता है और दूसरा अल्प विराम मिलियनों को प्रदर्शित करता है। उदाहरणार्थ, संख्या 50, 801, 592 को अंतराष्ट्रीय पद्धति में पचास मिलियन आठ सौ एक हज़ार पाँच सौ बानवे पढ़ा जाता है। भारतीय पद्धति में, यह पाँच करोड़ आठ लाख एक हज़ार पाँच सौ बानवे है।
कितने लाख से एक मिलियन बनता है?
कितने मिलियन से एक करोड़ बनता है?
तीन बड़ी संख्याओं को लीजिए। इन्हें भारतीय और अंतराष्ट्रीय दोनों संख्यांकन पद्धतियों में व्यक्त कीजिए।
इसमें आपकी रुचि हो सकती है:
सौ मिलियनों से बड़ी संख्याओं को व्यक्त करने के लिए, अंतराष्ट्रीय पद्धति में बिलियनों (Billions) का प्रयोग किया जाता है।
1 बिलियन = 1000 मिलियन
1991–2001 के अंतराल में कितनी वृद्धि हुई। इस जानकारी को प्राप्त करने का प्रयत्न कीजिए। क्या आप जानते हैं कि इस समय भारत की जनसंख्या कितनी है? पता करने का प्रयत्न कीजिए।
क्या आप जानते हैं?
भारत की जनसंख्या में इस प्रकार वृद्धि हुई है:
1921-1931 के अंतराल में करीब 27 मिलियन;
1931-1941 के अंतराल में करीब 37 मिलियन;
1941-1951 के अंतराल में करीब 44 मिलियन;
1951-1961 के अंतराल में करीब 78 मिलियन;

1. इन संख्याओं को बक्सों का प्रयोग करते हुए लिखिए और फिर प्रसारित रूप में लिखिए:
(i) 475320
(ii) 9847215
(iii) 97645310
(iv) 30458094
(a) इनमें कौन-सी संख्या सबसे छोटी है?
(b) इनमें कौन-सी संख्या सबसे बड़ी है?
(c) इन संख्याओं को आरोही और अवरोही क्रमों में व्यवस्थित कीजिए।
2. निम्नलिखित संख्याओं को देखिए:
(i) 527864
(ii) 95432
(iii) 18950049
(iv) 70002509
(a) इन संख्याओं को बक्सों का प्रयोग करते हुए लिखिए और फिर अल्प विरामों का प्रयोग करते हुए लिखिए।
(b) इन संख्याओं को आरोही और अवरोही क्रमों में व्यवस्थित कीजिए।
3. एेसी ही तीन और बड़ी संख्याएँ लेकर इस प्रक्रिया को दोहराइए।
क्या आप संख्यांक लिखने में मेरी सहायता कर सकते हैं?
एक संख्या के संख्यांक लिखने के लिए आप पुन: बक्सों का प्रयोग कर सकते हैं:
(a) बयालीस लाख सत्तर हज़ार आठ।
(b) दो करोड़ नब्बे लाख पचपन हज़ार आठ सौ।
(c) सात करोड़ साठ हज़ार पचपन।

1. आपके पास 4, 5, 6, 0, 7 और 8 के अंक हैं। इनका प्रयोग करते हुए 6 अंकों की पाँच संख्याएँ बनाइए।
(a) पढ़ने में सरलता के लिए अल्प विराम लगाइए।
(b) इन्हें आरोही और अवरोही क्रमों में व्यवस्थित कीजिए।
2. अंकों 4, 5, 6, 7, 8 और 9 का प्रयोग कर 8 अंकों की कोई तीन संख्याएँ बनाइए। पढ़ने में सरलता के लिए, अल्प विरामों का प्रयोग कीजिए।
3. अंकों 3, 0 और 4 का प्रयोग कर 6 अंकों की पाँच संख्याएँ बनाइए। अल्प विरामों का भी प्रयोग कीजिए।
प्रशनावली 1.1
1. रिक्त स्थानों को भरिए:
(a) 1 लाख = _______ दस हज़ार
(b) 1 मिलियन = _______ सौ हज़ार
(c) 1 करोड़ = _______ दस लाख
(d) 1 करोड़ = _______ मिलियन
(e) 1 मिलियन = _______ लाख
2. सही स्थानों पर अल्प विराम लगाते हुए, संख्यांकों को लिखिए:
(a) तिहत्तर लाख पचहत्तर हज़ार तीन सौ सात
(b) नौ करोड़ पाँच लाख इकतालीस
(c) सात करोड़ बावन लाख इक्कीस हज़ार तीन सौ दो
(d) अट्ठावन मिलियन चार सौ तेईस हज़ार दो सौ दो
(e) तेईस लाख तीस हज़ार दस
3. उपयुक्त स्थानों पर अल्प विराम लगाइए और संख्या नामों को भारतीय संख्यांकन पद्धति में लिखिए:
(a) 87595762
(b) 8546283
(c) 99900046
(d) 98432701
4. उपयुक्त स्थानों पर अल्प विराम लगाइए और संख्या नामों को अंतराष्ट्रीय संख्यांकन पद्धति में लिखिए:
(a) 78921092
(b) 7452283
(c) 99985102
(d) 48049831
1.3 व्यावहारिक प्रयोग में बड़ी संख्याएँ
पिछली कक्षाओं में, हम पढ़ चुके हैं कि लंबाई के एक मात्रक (या इकाई) (unit) के लिए सेंटीमीटर (सेमी) का प्रयोग किया जाता है। पेंसिल की लंबाई, अपनी पुस्तक या अभ्यास-पुस्तिका की चौड़ाई इत्यादि मापने के लिए हम सेंटीमीटर का प्रयोग करते हैं। हमारे रूलर पर सेंटीमीटर के चिह्न अंकित होते हैं। परंतुु, एक पेंसिल की मोटाई मापने के लिए हम पाते हैं कि सेंटीमीटर एक बड़ा मात्रक है। अत: पेंसिल की मोटाई दर्शाने के लिए, हम एक छोटे मात्रक मिलीमीटर (मिमी) का प्रयोग करते हैं।
(a) 10 मिलीमीटर = 1 सेंटीमीटर
अपनी कक्षा के कमरे की लंबाई या स्कूल के भवन की लंबाई मापने के लिए, हम पाते हैं कि सेंटीमीटर एक बहुत छोटा मात्रक है। अत: इस कार्य के लिए हम मीटर का प्रयोग करते हैं।
(b) 1 मीटर = 100 सेंटीमीटर = 1000 मिलीमीटर
यदि हमें दो शहरों, जैसे – दिल्ली-मुंबई या दिल्ली-कोलकाता के बीच की दूरियाँ बतानी हों, तो मीटर भी एक बहुत छोटा मात्रक होता है। इसके लिए हम एक बड़े मात्रक किलोमीटर (किमी) का प्रयोग करते हैं।
(c) 1 किलोमीटर = 1000 मीटर
कितने मिलीमीटरों से 1 किलोमीटर बनता है?
चूँकि 1 मीटर = 1000 मिमी, इसलिए
1 किमी = 1000 मी = 1000 × 1000 मिमी = 10,00,000 मिमी

1. कितने सेंटीमीटरों से एक किलोमीटर बनता है?
2. भारत के पाँच बड़े शहरों के नाम लिखिए। उनकी जनसंख्या पता कीजिए। इन शहरों में से प्रत्येक युग्म शहरों के बीच की दूरी भी किलोमीटरों में पता कीजिए।
हम बाज़ार में गेहूँ या चावल खरीदने जाते हैं। हम इन्हें किलोग्राम (किग्रा) में खरीदते हैं। परंतु अदरक या मिर्च जैसी वस्तुओं की हमें अधिक मात्रा में आवशयकता नहीं होती है। हम इन्हें ग्राम (ग्रा) में खरीदते हैं। हम जानते हैं कि
1 किलोग्राम = 1000 ग्राम
बीमार पड़ने पर जो दवाई की गोली ली जाती है, क्या उसके भार पर कभी आपने ध्यान दिया है? यह बहुत कम होता है। यह भार मिलीग्राम (मिग्रा) में होता है।
1 ग्राम = 1000 मिलीग्राम

1. कितने मिलीग्राम से एक किलोग्राम बनता है?
2. दवाई की गोलियों के एक बक्से में 2,00,000 गोलियाँ हैं, जिनमें प्रत्येक का भार 20 मिग्रा है। इस बक्से में रखी सभी गोलियों का कुल भार ग्रामों में कितना है और किलोग्रामों में कितना है?
पानी वाली एक साधारण बाल्टी की धारिता (capacity) प्राय: कितनी होती है? यह प्राय: 20 लीटर होती है। धारिता को लीटर में दर्शाया जाता है, परंतुु कभी-कभी हमें एक छोटे मात्रक की भी आवशयकता पड़ती है। यह मात्रक मिलीलीटर है। बालों के तेल, सफ़ाई करने वाले द्रव या एक सॉफ्ट ड्रिंक (पेय) की बोतलों पर जो मात्रा लिखी होती है वह उनके अंदर भरे द्रव की मात्रा को मिलीलीटर में दर्शाती है।
1 लीटर = 1000 मिलीलीटर
ध्यान दीजिए कि इन सभी मात्रकों में, हम कुछ सर्वनिज़्ठ शब्दों जैसे किलो, मिली और सेंटी को पाते हैं। आपको याद रखना चाहिए कि किलो का अर्थ है हज़ार और यह इनमें सबसे बड़ा है और मिली का अर्थ है हज़ारवाँ भाग और यह सबसे छोटा है। किलो 1000 गुना दर्शाता है, जबकि मिली हज़ारवाँ भाग दर्शाता है। अर्थात् 1 किलोग्राम = 1000 ग्राम और 1 ग्राम = 1000 मिलीग्राम है।
इसी प्रकार, सेंटी सौवाँ भाग दर्शाता है। अर्थात् 1 मीटर = 100 सेंटीमीटर है।

एक बस ने अपनी यात्रा प्रारंभ की और 60 किमी/घंटा की चाल से विभिन्न स्थानों पर पहुँची। इस यात्रा को नीचे दर्शाया गया है।
(i) A से D तक जाने में बस द्वारा तय की गई कुल दूरी ज्ञात कीजिए।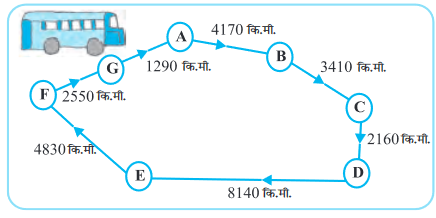
(ii) D से G तक जाने में बस द्वारा तय की गई कुल दूरी ज्ञात कीजिए।
(iii) बस द्वारा तय की गई कुल दूरी ज्ञात कीजिए।
(iv) क्या आप C से D तक और D से E तक की दूरियों का अंतर ज्ञात कर सकते हैं?
(v) बस द्वारा निम्नलिखित यात्रा में लिया समय ज्ञात कीजिए:
(a) A से B तक
(b) C से D तक
(c) E से G तक
(d) कुल यात्रा
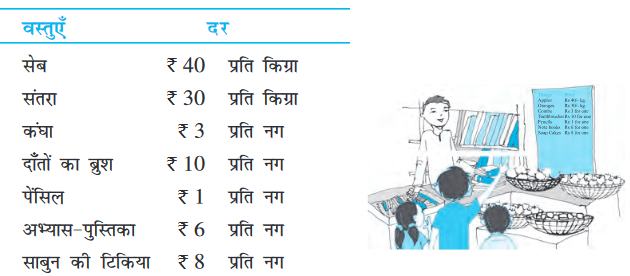
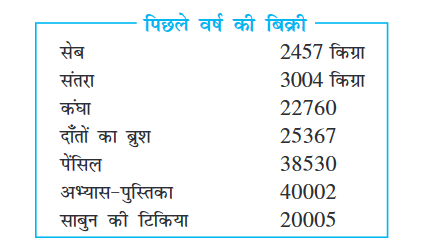
(a) क्या आप रमन द्वारा पिछले वर्ष बेचे गए सेब और संतरों का कुल भार ज्ञात कर
सकते हैं?
सेबों का भार = __________ किग्रा
संतरों का भार = __________ किग्रा
अत:, कुल भार = __________ किग्रा + _____ किग्रा = _____किग्रा
उत्तर: संतरों और सेबों का कुल भार = _________
(b) क्या आप रमन द्वारा सेबों को बेचने से प्राप्त कुल धनराशि ज्ञात कर सकते हैं?
(c) क्या आप रमन द्वारा सेबों और संतरों को बेचने से प्राप्त कुल धनराशि ज्ञात कर
सकते हैं?
(d) रमन द्वारा प्रत्येक वस्तु के बेचने से प्राप्त धनराशियों को दर्शाने वाली एक सारणी बनाइए। धनराशियों की इन प्रविज़्टियों को अवरोही क्रम में व्यवस्थित कीजिए। वह कौन-सी वस्तु है जिससे रमन को सबसे अधिक धनराशि प्राप्त हुई? यह धनराशि क्या है?
जोड़, घटा, गुणा और भाग पर हम अनेक प्रशन कर चुके हैं। यहाँ हम एेसे कुछ और प्रशन करेंगे। प्रारंभ करने से पहले निम्नलिखित उदाहरणों को देखिए तथा प्रशनों के विशलेज़ण का अनुसरण कीजिए और देखिए कि इन्हें किस प्रकार हल किया गया है।
उदाहरण 1 : वर्ष 1991 में सुंदरनगर की जनसंख्या 2,35,471 थी। वर्ष 2001 में पता चला कि जनसंख्या में 72,958 की वृद्धि हो गई। वर्ष 2001 में इस शहर की जनसंख्या क्या थी?
हल : 2001 में इस शहर की जनसंख्या
= 1991 में जनसंख्या + जनसंख्या में वृद्धि
= 2,35,471 + 72,958
अब,
235471
+ 72958
308429
सलमा ने इन संख्याओं को इस प्रकार जोड़ा : 235471 = 200000 +
35000 + 471, 72958 = 72000 + 958 और फिर 200000 + 107000 + 1429 = 308429 तथा मेरी ने इस जोड़ को इस प्रकार किया: 200000 + 35000 + 400 + 71 + 72000 + 900 + 58 = 308429
उत्तर: 2001 में शहर की जनसंख्या 3,08,429 थी।
तीनों विधियाँ सही हैं।
उदाहरण 2 : किसी राज्य में, वर्ष 2002-2003 में 7,43,000 साइकिलें बेची गईं। वर्ष 2003-04 में बेची गई साइकिलों की संख्या 8,00,100 थी। किस वर्ष में अधिक साइकिलें बेची गईं और कितनी अधिक बेची गईं?
हल : स्पष्ट है कि संख्या 8,00,100 संख्या 7,43,000 से अधिक है। अत:, उस 
राज्य में वर्ष 2003-04 में वर्ष 2002-03 से अधिक साइकिलें बेची गईं। अब,
800100
- 743000
057100
जोड़ कर उत्तर की जाँच कीजिए:
743000
+ 57100
800100 (उत्तर सही है)
क्या आप इसे करने के और भी तरीके सोच सकते हैं?
उत्तर: वर्ष 2003-04 में 57,100 साइकिलें अधिक बेची गईं।
उदाहरण 3 : एक शहर में समाचार पत्र प्रतिदिन छपता है। एक प्रति में 12 पृष्ट होते हैं। प्रतिदिन इस समाचार पत्र की 11,980 प्रतियाँ छपती हैं। प्रतिदिन सभी प्रतियों के लिए कितने पृष्ट छपते हैं?
हल : प्रत्येक प्रति में 12 पृष्ट हैं।
अत:, 11,980 प्रतियों में 12 × 11,980 पृष्ट होंगे।
यह संख्या क्या होगी? 1,00,000 से अधिक या कम।
अब,
11980
× 12
23960
+ 119800
143760
उत्तर: प्रतिदिन सभी प्रतियों के लिए 1,43,760 पृष्ट छपते हैं।
उदाहरण 4 : अभ्यास-पुस्तिकाएँ बनाने के लिए कागज़ की 75,000 शीट (sheet) उपलब्ध हैं। प्रत्येक शीट से अभ्यास-पुस्तिका के 8 पृष्ट बनते हैं। प्रत्येक अभ्यास-पुस्तिका में 200 पृष्ट हैं। उपलब्ध कागज़ से कितनी अभ्यास-पुस्तिकाएँ बनाई जा सकती हैं?
हल : प्रत्येक शीट से 8 पृष्ट बनते हैं।
अत:, 75,000 शीटों से 8 × 75,000
पृष्ट बनेंगे।
75000
× 8
600000
इस प्रकार, अभ्यास-पुस्तिका बनाने के लिए 6,00,000 पृष्ट उपलब्ध हैं।
अब, 200 पृष्टों से एक अभ्यास-पुस्तिका बनती है।

अत:, 6,00,000 पृष्टों से 6,00,000 ÷ 200 अभ्यास-पुस्तिकाएँ बनेंगी।
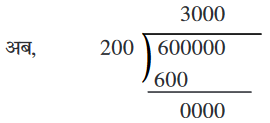
उत्तर: 3,000 अभ्यास-पुस्तिकाएँ।
प्रशनावली 1.2
1. किसी स्कूल में चार दिन के लिए एक पुस्तक प्रदर्शनी आयोजित की गई। पहले, दूसरे, तीसरे और अंतिम दिन खिड़की पर क्रमशा: 1094, 1812, 2050 और 2751 टिकट बेचे गए। इन चार दिनों में बेचे गए टिकटों की कुल संख्या ज्ञात कीजिए।
2. शेखर एक प्रसिद्ध क्रिकेट खिलाड़ी है। वह टैस्ट मैचों में अब तक 6980 रन बना चुका है। वह 10,000 रन पूरे करना चाहता है। उसे कितने और रनों की आवशयकता है?
3. एक चुनाव में, सफल प्रत्याशाी ने 5,77,500 मत प्राप्त किए, जबकि उसके निकटतम प्रतिद्वंद्वी ने 3,48,700 मत प्राप्त किए। सफल प्रत्याशाी ने चुनाव कितने मतों से जीता?
4. कीर्ति बुक-स्टोर ने जून के प्रथम सप्ताह में ₹ 2,85,891 मूल्य की पुस्तकें बेचीं। इसी माह के दूसरे सप्ताह में ₹ 4,00,768 मूल्य की पुस्तकें बेची गईं। दोनों सप्ताहों में कुल मिलाकर कितनी बिक्री हुई? किस सप्ताह में बिक्री अधिक हुई और कितनी अधिक?
5. अंकों 6, 2, 7, 4 और 3 में से प्रत्येक का केवल एक बार प्रयोग करते हुए, पाँच अंकों की बनाई जा सकने वाली सबसे बड़ी और सबसे छोटी संख्याओं का अंतर ज्ञात कीजिए।
6. एक मशाीन औसतन एक दिन में 2,825 पेंच बनाती है। जनवरी 2006 में उस मशाीन ने कितने पेंच बनाए?
7. एक व्यापारी के पास ₹78,592 थे। उसने 40 रेडियो खरीदने का अॉर्डर दिया तथा प्रत्येक रेडियो का मूल्य ₹1200 था। इस खरीदारी के बाद उसके पास कितनी धनराशि शेज़ रह जाएगी?
8. एक विद्यार्थी ने 7236 को 56 के स्थान पर 65 से गुणा कर दिया। उसका उत्तर सही उत्तर से कितना अधिक था? (संकेत: दोनों गुणा करना आवशयक नहीं)।
9. एक कमीज़ सीने के लिए 2 मी 15 सेमी कपड़े की आवशयकता है। 40 मी कपड़े में से कितनी कमीज़ें सी जा सकती हैं और कितना कपड़ा शेष बच जाएगा?
10. दवाइयों को बक्सों में भरा गया है और एेसे प्रत्येक बक्स का भार 4 किग्रा 500ग्रा है। एक वैन (Van) में जो 800 किग्रा से अधिक का भार नहीं ले जा सकती, एेसे कितने बक्से लादे जा सकते हैं?
11. एक स्कूल और किसी विद्यार्थी के घर के बीच की दूरी 1 किमी 875 मी है। प्रत्येक दिन यह दूरी दो बार तय की जाती है। 6 दिन में उस विद्यार्थी द्वारा तय की गई कुल दूरी ज्ञात कीजिए।
12. एक बर्तन में 4 ली 500 मिली दही है। 25 मिली धारिता वाले कितने गिलासों में इसे भरा जा सकता है?
1.3.1 आकलन
समाचार
1. भारत और पाकिस्तान के बीच हुए एक हॉकी मैच को जिसे स्टेडियम में लगभग 51,000 दर्शकों ने देखा और विशव-भर में 40 मिलियन लोगों ने टेलीविज़न पर देखा, हार-जीत का फ़ैसला न हो सका।
2. भारत और बंगलादेशा के तटवर्तीय क्षेत्रों में आए एक चक्रवाती तूफ़ान में लगभग 2000 व्यक्तियों की मृत्यु हो गई और 50000 से अधिक घायल हुए।
3. रेलवे द्वारा प्रतिदिन 63,000 किलोमीटर से अधिक रेलपथ पर 13 मिलियन से अधिक यात्री यात्रा करते हैं।
क्या हम विशवास के साथ कह सकते हैं कि इन समाचारों में जितने व्यक्ति कहे गए हैं वहाँ ठीक उतने ही व्यक्ति थे? उदाहरणार्थ,
(1) में, क्या स्टेडियम में ठीक 51,000 दर्शक थे? अथवा
 क्या टेलीविज़न पर ठीक 40 मिलियन लोगों ने मैच देखा?
क्या टेलीविज़न पर ठीक 40 मिलियन लोगों ने मैच देखा?
स्पष्टत:, नहीं। शब्द लगभग स्वयं यह दर्शाता है कि व्यक्तियों की संख्याएँ इन संख्याओं के निकटतम थीं। स्पष्ट रूप से, 51000 संख्याओं 50800 या 51300 में से कोई भी संख्या हो सकती है, परंतु 70000 नहीं होगी। इसी प्रकार, 40 मिलियन का अर्थ 39 मिलियन से बहुत अधिक और 41 मिलियन से कुछ कम हो सकता है। परंतु निशचय ही इसका अर्थ 50 मिलियन नहीं है।
इसी प्रकार, भारतीय रेलवे द्वारा यात्रा करने वाले यात्रियों की वास्तविक संख्या दी हुई संख्या के बराबर नहीं हो सकती है, परंतुु इससे कुछ अधिक या कम हो सकती है।
इन उदाहरणों में दी गई संख्याओं को ठीक-ठीक गिनकर (या यथार्थ रूप से) नहीं लिखा गया है, बल्कि ये उस संख्या के बारे में अनुमान देने वाले आकलन (estimate) हैं।
चर्चा कीजिए कि इनसे क्या सुझाव मिलते हैं।
हम सन्निकट (approximate) मान कहाँ निकालते हैं? अपने घर पर होने वाले एक बड़े उत्सव की कल्पना कीजिए। पहला काम जो आप करेंगे वह यह होगा कि आप यह पता करेंगे कि आपके घर पर लगभग कितने मेहमान आ सकते हैं। क्या आप मेहमानों की ठीक (exact) संख्या का विचार लेकर प्रारंभ कर सकते हैं? व्यावहारिक रूप से यह असंभव है।
हमारे देशा के वित्त मंत्री प्रति वर्ष बजट पेशा करते हैं। मंत्री महोदय ‘शिक्षा’ मद के अंतर्गत कुछ राεशा का प्रावधान रखते हैं। क्या यह राεशा यथार्थ रूप से सही होगी? यह उस वर्ष देशा में शिक्षा पर व्यय होने वाली आवशयक धनराशि का केवल एक विवेकसंगत अच्छा अनुमान या आकलन (estimate) हो सकता है।
उन स्थितियों के बारे में सोचिए जहाँ आपको ठीक-ठीक संख्याओं की आवशयकता पड़ती है तथा इनकी उन स्थितियों से तुलना कीजिए जहाँ आप केवल एक सन्निकट आकलित (estimated) संख्या से ही काम चला लेते हैं। एेसी स्थितियों के तीन उदाहरण दीजिए।
1.3.2 सन्निकटन द्वारा निकटतम दहाई तक आकलन
निम्नलिखित चित्र को देखिए :

(a) ज्ञात कीजिए कि कौन-से झंडे 270 की तुलना में 260 के अधिक समीप हैं।
(b) ज्ञात कीजिए कि कौन-से झंडे 260 की तुलना में 270 के अधिक समीप हैं।
पटरी की संख्याओं 10, 17 और 20 के स्थानों को देखिए। क्या संख्या 17 संख्या 10 के अधिक निकट है या 20 के? 17 और 20 के बीच का रिक्त स्थान 17 और 10 के बीच के रिक्त स्थान की तुलना में कम है। इसलिए, हम 17 को निकटतम दहाई तक 20 के रूप में सन्निकटित करते हैं।

अब 12 को लीजिए। यह भी 10 और 20 के बीच स्थित है। परंतुु 12 संख्या 20 की तुलना में 10 से अधिक निकट है। इसलिए हम 12 को निकटतम दहाई तक 10 के रूप में सन्निकटित करते हैं।
आप 76 को निकटतम दहाई तक किस प्रकार सन्निकटित करेंगे? क्या यह 80 नहीं है?
हम देखते हैं कि संख्याएँ 1,2,3 और 4 संख्या 10 की तुलना में संख्या 0 के अधिक निकट हैं। इसलिए हम इन्हें 0 के रूप में सन्निकटित करते हैं। संख्याएँ 6, 7, 8 और 9 संख्या 10 के अधिक निकट हैं। इसलिए हम इन्हें 10 के रूप में सन्निकटित करते हैं। संख्या 5, संख्याओं 0 और 10 से बराबर की दूरी पर है। यह सामान्य परिपाटी है कि इसे 10 के रूप में सन्निकटित किया जाता है।

इन संख्याओं को निकटतम दहाई तक सन्निकटित कीजिए:
28 32 52 41 39 48
64 59 99 215 1453 2936
1.3.3 सन्निकटन द्वारा निकटतम सैकड़े तक आकलन
संख्या 410 संख्या 400 के अधिक निकट है या 500 के अधिक निकट है?
410, संख्या 400 के अधिक निकट (समीप) है, इसलिए इसे निकटतम सौ तक 400 के रूप में सन्निकटित किया जाता है।
संख्या 889, संख्याओं 800 और 900 के बीच में है।
यह 900 के अधिक निकट है। इसलिए, इसे निकटतम सौ तक 900 के रूप में सन्निकटित किया जाता है।
संख्याएँ 1 से 49, संख्या 100 की तुलना में, संख्या 0 के अधिक निकट हैं। इसलिए, इन्हें 0 के रूप में सन्निकटित किया जाता है। 51 से 99 तक की संख्याएँ 0 की तुलना में 100 से अधिक निकट हैं। इसलिए, इन्हें 100 के रूप में सन्निकटित किया जाता है। संख्या 50 संख्याओं 0 और 100 से बराबर दूरी पर है। सामान्य परिपाटी के अनुसार, इसे 100 के रूप में सन्निकटित किया जाता है।
जाँच कीजिए कि निम्नलिखित सन्निकटन (सैकड़े तक) सही हैं या नहीं:
841  800;
800;
9537  9500;
9500;
49730  49700;
49700;
2546 2500;
2500;
286  300;
300;
5750  5800;
5800;
168  200;
200;
149  100;
100;
9870  9800.
9800.
उन्हें सही कीजिए जो गलत हैं।
1.3.4 सन्निकटन द्वारा निकटतम हज़ार तक आकलन
हम जानते हैं कि 1 से 499 तक की संख्याएँ 1000 की तुलना में 0 के अधिक निकट हैं। इसलिए, इन्हें 0 के रूप में सन्निकटित करते हैं। 501 से 999 तक की संख्याएँ 0 की तुलना में 1000 के अधिक निकट हैं। इसलिए, इन्हें 1000 के रूप में सन्निकटित किया जाता है।
संख्या 500 को भी 1000 के रूप में सन्निकटित किया जाता है।
निम्नलिखित सन्निकटनों की जाँच कीजिए और उन्हें सही कीजिए जो गलत हैं।
2573  3000;
3000;
53552  53000;
53000;
6404  6000;
6000;
65437  65000;
65000;
7805  7000;
7000;
3499  4000
4000

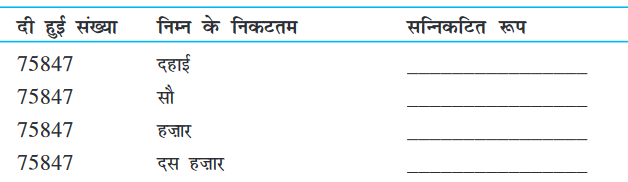
दी हुई संख्या को निकटतम दहाई, सौ, हज़ार और दस हज़ार तक सन्निकटित कीजिए:
1.3.5 संख्या संक्रियाओं के परिणामों का आकलन
हम संख्याओं को किस प्रकार जोड़ते हैं? हम संख्याओं को एक एल्गोरिथ्म (algorithm) (दी हुई विधि) का चरणबद्ध रूप से प्रयोग करते हुए जोड़ते हैं। हम संख्याओं को यह ध्यान रखते हुए लिखते हैं कि एक ही स्थान (इकाई, दहाई, सौ इत्यादि) के अंक एक ही स्तंभ (Column) में रहें। उदाहरणार्थ, 3946 + 6579 + 2050 को निम्न रूप में लिखते हैं:
TTh Th H T O
3 9 4 6
6 5 7 9
+ 2 0 5 0
फिर हम इकाई वाले स्तंभ की संख्याओं को जोड़ते हैं। यदि आवशयक हो, तो हम एक उचित संख्या को हासिल के रूप में दहाई के स्थान पर ले जाते हैं, जैसे कि इस स्थिति में है। फिर हम इसी प्रकार दहाई के स्तंभ की संख्याओं को जोड़ते हैं और एेसा आगे चलता रहता है। आप शेष प्रशन को स्वयं पूर्ण कर सकते हैं। इस प्रक्रिया में स्पष्टत: समय लगता है।
अनेक स्थितियों में, हमें उत्तरों को अधिक तीव्रता से ज्ञात करने की आवशयकता होती है। उदाहरणार्थ, जब आप किसी मेले या बाज़ार में कुछ धनराशि लेकर जाते हैं, तो आकर्ज़क वस्तुओं की किस्मों और मात्राओं को देखकर वहाँ आप सोचते हैं कि सभी को खरीद लिया जाए। आपको तुरंत यह निर्णय लेने की आवशयकता होती है कि आप किन-किन वस्तुओं को खरीद सकते हैं। इसके लिए आपको आवशयक धनराशि का आकलन करने की आवशयकता पड़ती है, जो उन वस्तुओं के मूल्यों का योग होती है जिन्हें आप खरीदना चाहते हैं।
किसी विशोज़ दिन, एक व्यापारी को दो स्थानों से धनराशि प्राप्त होनी है। एक स्थान से प्राप्त होने वाली धनराशि ₹ 13,569 है और अन्य स्थान से प्राप्त होने वाली धनराशि ₹ 26,785 है। उसे शाम तक किसी अन्य व्यक्ति को ₹ 37,000 देने हैं। वह संख्याओं को उनके निकटतम हज़ारों तक सन्निकटित करता है और तुरंत कच्चा या रफ (rough) उत्तर निकाल लेता है। वह खुशा हो जाता है कि उसके पास पर्याप्त धनराशि है।
क्या आप सोचते हैं कि उसके पास पर्याप्त धनराशि होगी? क्या आप बिना यथार्थ योग किए यह बता सकते हैं?
शीला और मोहन को अपना मासिक बजट बनाना है उन्हें परिवहन, स्कूल की आवशयकताओं, किराने का सामान, दूध और कपड़ों पर होने वाले अपने मासिक व्यय के बारे में भी जानकारी है तथा अन्य नियमित व्ययों की भी जानकारी है। इस महीने में उन्हें घूमने भी जाना है और उपहार भी खरीदने हैं। वे इन सभी पर होने वाले व्ययों का आकलन करते हैं और उन्हें जोड़कर देखते हैं कि जो राεशा उनके पास है वह पर्याप्त है या नहीं।
क्या वे हज़ारों तक सन्निकटित करेंगे, जैसा कि व्यापारी ने किया था?
एेसी पाँच और स्थितियों के बारे में सोचिए और चर्चा कीजिए, जहाँ हमें योग या अंतरों का आकलन करना पड़ता है।
क्या हम इन सभी में एक ही स्थान तक सन्निकट मान ज्ञात करते हैं?
जब आप संख्याओं के परिणामों का आकलन करते हैं, तो उसके लिए कोई निεशचत नियम नहीं है। यह विधि इस पर निर्भर करती है कि परिशाुद्धता की वांछित मात्रा कितनी है, आकलन कितनी जल्दी चाहिए तथा सबसे महत्त्वपूर्ण बात है कि अनुमानित उत्तर कितना अर्थपूर्ण होगा।
1.3.6 योग अथवा अंतर का आकलन
जैसा कि हमने ऊपर देखा, हम एक संख्या को किसी भी स्थान तक सन्निकटित कर सकते हैं। व्यापारी ने धनराशि को निकटतम हज़ारों तक सन्निकटित किया और संतुज़्ट हो गया कि उसके पास पर्याप्त धनराशि है। इसलिए जब आपको किसी योग अथवा अंतर का आकलन करना है, तो आपको यह पता होना चाहिए कि आप क्यों सन्निकटित कर रहे हैं और इसलिए किस स्थान तक आपको सन्निकटित करना है। निम्नलिखित उदाहरणों को देखिए:
उदाहरण 5 : 5,290 + 17,986 का आकलन कीजिए।
हल : हम देखते हैं कि 17,986 > 5,290 है।
हम निकटतम हज़ारों तक सन्निकटित करते हैं।
17,986 सन्निकटित होता है 18,000
+5,290 सन्निकटित होता है + 5,000
आकलित योग = 23,000
क्या यह विधि काम करती है? आप यथार्थ उत्तर ज्ञात करके जाँच कर सकते हैं कि यह आकलन विवेकपूर्ण है या नहीं।
उदाहरण 6 : 5,673 – 436 का आकलन कीजिए।
हल : प्रारंभ में, हम हज़ारों तक सन्निकटित करते हैं। (क्यों?)
5,673 सन्निकटित होता है 6,000
– 436 सन्निकटित होता है – 0
आकलित अंतर = 6,000
यह विवेकपूर्ण आकलन नहीं है। यह विवेकपूर्ण क्यों नहीं है? निकटतम आकलन प्राप्त करने के लिए, आइए प्रत्येक संख्या को निकटतम सौ तक सन्निकटित करने का प्रयत्न करें।
5,673 सन्निकटित होता है 5,700
– 436 सन्निकटित होता है – 400
आकलित अंतर = 5,300
यह एक अच्छा और अधिक अर्थपूर्ण आकलन है।
1.3.7 आकलन करना: गुणनफल
हम गुणनफल का किस प्रकार आकलन करते हैं?
19 × 78 के लिए आकलन क्या है?
स्पष्ट है कि यह गुणनफल 2000 से कम है। क्यों? यदि हम 19 का निकटतम दहाई तक मान निकालें, तो हमें 20 प्राप्त होता है और फिर 78 का निकटतम दहाई तक मान निकालें, तो 80 प्राप्त होता है। अब 20 × 80 = 1600 है।
63 × 182 को देखिए।
यदि हम दोनों संख्याओं का निकटतम सौ तक का मान निकालें, तो हमें 100 × 200 = 20,000 प्राप्त होता है। यह वास्तविक गुणनफल से बहुत अधिक है। इसलिए अब हम क्या करें? एक अधिक विवेकपूर्ण आकलन ज्ञात करने के लिए हम 63 और 182 दोनों को निकटतम दहाई तक सन्निकटित करते हैं। ये क्रमशा: 60 और 180 हैं। इसे हम60 × 180 अर्थात् 10,800 प्राप्त करते हैं। यह एक अच्छा आकलन है, परंतु यह इतनी जल्दी प्राप्त नहीं होता है। यदि हम 63 को निकटतम दहाई तक 60 लें और 182 को निकटतम सौ तक 200 लें, तो हमें 60 × 200 = 12,000 प्राप्त होता है, यह गुणनफल का एक अच्छा आकलन है और जल्दी भी प्राप्त हो जाता है।
सन्निकटन का व्यापक नियम यह है कि प्रत्येक गुणा की जाने वाली संख्या को उसके सबसे बड़े स्थान तक सन्निकटित कीजिए और सन्निकटित संख्याओं को गुणा कर दीजिए। इस प्रकार, उपरोक्त उदाहरण में हमने 63 को दहाई तक और 182 को सौ तक सन्निकटित किया है।
अब उपरोक्त नियम का प्रयोग करके, 81 × 479 का आकलन कीजिए।
479 सन्निकटित होता है 500 के (सौ तक सन्निकटित)
81 सन्निकटित होता है 80 के (दहाई तक सन्निकटित)
अत:, आकलित गुणनफल = 500 × 80 = 40,000 है।

निम्नलिखित गुणनफलों का आकलन कीजिए:
(a) 87 × 313
(b) 9 × 795
(c) 898 × 785
(d) 958 × 387
एेसे ही पाँच और प्रशन बनाइए और उन्हें हल कीजिए।
आपके लिए आकलनों का एक महत्त्वपूर्ण उपयोग यह है कि आप अपने उत्तरों की जाँच कर सकते हैं। मान लीजिए आपने 37 × 1889 ज्ञात किया है, परंतुु आप निεशचत नहीं हैं कि उत्तर सही है या नहीं। इस गुणनफल का एक तुरंत (जल्दी) प्राप्त होने वाला और विवेकपूर्ण आकलन 40 × 2000 = 80000 है। यदि आपका उत्तर 80,000 के निकट है, तो संभवत: आपका उत्तर सही है। दूसरी ओर, यदि यह 8000 या 8,00,000 के निकट है, तो आपके गुणा करने में अवशय ही कुछ गलती हुई है।
प्रशनावली 1.3
1. व्यापक नियम का प्रयोग करते हुए, निम्नलिखित में से प्रत्येक का आकलन कीजिए:
(a) 730 + 998 (b) 796 – 314
(c) 12,904 + 2,888 (d) 28,292 – 21,496
जोड़ने, घटाने और उनके परिणामों के आकलन के दस और उदाहरण बनाइए।
2. एक मोटेतौर पर (Rough) आकलन (सौ तक सन्निकटन) और एक निकटतम आकलन (दस तक सन्निकटन) दीजिए:
(a) 439 + 334 + 4,317 (b) 1,08,734 – 47,599
(c) 8325 – 491 (d) 4,89,348 – 48,365
एेसे चार और उदाहरण बनाइए।
3. व्यापक नियम का प्रयोग करते हुए, निम्नलिखित गुणनफलों का आकलन कीजिए:
(a) 578 × 161 (b) 5281 × 3491
(c) 1291 × 592 (d) 9250 × 29
एेसे चार और उदाहरण बनाइए।
1.4 कोष्ठकों का प्रयोग
मीरा ने बाज़ार से 6 अभ्यास-पुस्तिकाएँ खरीदीं जिनका मूल्य ₹10 प्रति पुस्तिका था। उसकी बहन सीमा ने इसी प्रकार की 7 अभ्यास-पुस्तिकाएँ खरीदीं। उनके द्वारा दी गई कुल धनराशि ज्ञात कीजिए।

आप देख सकते हैं कि सीमा और मीरा के उत्तर प्राप्त करने की विधियों में कुछ अंतर है, परंतु दोनों के उत्तर समान हैं और प्राप्त परिणाम सही है। क्यों?
सीमा ने कहा कि मीरा ने 7 + 6 × 10 करके उत्तर प्राप्त किया है।
अप्पू बताता है कि 7 + 6 × 10 = 7 + 60 = 67 है। लेकिन मीरा ने जो उत्तर प्राप्त किया है वह यह नहीं है। बस तीनों विद्यार्थी उलझन में पड़ जाते हैं।
एेसी स्थितियों में उलझन दूर करने के लिए हम कोष्ठकों (brackets) का प्रयोग कर सकते हैं। हम कोष्ठकों का प्रयोग करके 6 और 7 को मिलाकर एक समूह बना सकते हैं, जो दर्शाएगा कि इस समूह को एक अकेली संख्या समझा जाए। जिससे उत्तर इस प्रकार प्राप्त होता है:
(6 + 7) × 10 = 13 × 10
यह वही है जो मीरा ने किया है। उसने पहले 6 और 7 को जोड़ा और फिर प्राप्त योग को 10 से गुणा कर दिया।
कोष्ठकों का प्रयोग यह स्पष्ट रूप में हमें बताता है कि पहले कोज़्ठकों ( ) के अंदर दी हुई संख्याओं को एक अकेली संख्या के रूप में बदलिए और फिर बाहर दी हुई संक्रिया कीजिए जो यहाँ 10 से गुणा करना है।

1. कोष्ठकों का प्रयोग करते हुए, निम्नलिखित में से प्रत्येक के लिए व्यंजक लिखिए:
(a) नौ और दो के योग की चार से गुणा।
(b) अठारह और छ: के अंतर को चार से भाग।
(c) पैंतालीस को तीन और दो के योग के तिगुने से भाग देना।
2. (5 + 8) × 6 के लिए तीन विभिन्न स्थितियाँ लिखिए।
(एेसी एक स्थिति है: सोहनी और रीता ने 6 दिन कार्य किया। सोहनी 5 घंटे प्रतिदिन कार्य करती है और रीता 6 घंटे प्रतिदिन कार्य करती है। दोनों ने एक सप्ताह में कुल कितने घंटे कार्य किया?)
3. निम्नलिखित के लिए पाँच स्थितियाँ लिखिए, जहाँ कोष्ठकों का प्रयोग आवशयक हो:
(a) 7(8 – 3) (b) (7 + 2) (10 – 3)
1.4.1 कोष्ठकों का प्रसार (खोलना) (हटाना)
अब देखिए कि किस प्रकार कोष्ठकों के प्रयोग और उनके प्रसार (खोलने या हटाने) से, हमें अपने कार्य को क्रमबद्ध रूप से करने में सहायता मिलती है। क्या आप सोचते हैं कि कोष्ठकों का बिना प्रयोग किए जिन चरणों का हम पालन कर रहे हैं उन्हें समझ पाएँगे?
(i) 7 × 109 = 7 × (100 + 9) = 7 × 100 + 7 × 9 = 700 + 63 = 763
(ii) 102 × 103 = (100 + 2) × (100 + 3)
= 100 × 100 + 2 × 100 + 100 × 3 + 2 × 3
= 10,000 + 200 + 300 + 6 = 10,000 + 500 + 6
= 10,506
(iii) 17 × 109 = (10 + 7) × 109 = 10 × 109 + 7 × 109
= 10 × (100 + 9) + 7 × (100 + 9)
= 10 × 100 + 10 × 9 + 7 × 100 + 7 × 9
= 1000 + 90 + 700 + 63 = 1,790 + 63 = 1,853
1.5 रोमन संख्यांक
अभी तक हम हिंदू-अरेबिक संख्यांकों (Hindu Arabic Numerals) की पद्धति का ही प्रयोग करते रहे हैं। यह एकमात्र संख्यांक पद्धति नहीं है। संख्यांक लिखने की पुरानी पद्धतियों में से एक पद्धति रोमन संख्यांकों (Roman Numerals) की पद्धति है। यह पद्धति अभी भी अनेक स्थानों पर प्रयोग की जाती है। उदाहरणार्थ, हम घड़ियों में रोमन संख्यांकों का प्रयोग देख सकते हैं। इनका प्रयोग स्कूल की समय-सारणी में कक्षाओं के लिए भी किया जाता है, इत्यादि।
यह एकमात्र संख्यांक पद्धति नहीं है। संख्यांक लिखने की पुरानी पद्धतियों में से एक पद्धति रोमन संख्यांकों (Roman Numerals) की पद्धति है। यह पद्धति अभी भी अनेक स्थानों पर प्रयोग की जाती है। उदाहरणार्थ, हम घड़ियों में रोमन संख्यांकों का प्रयोग देख सकते हैं। इनका प्रयोग स्कूल की समय-सारणी में कक्षाओं के लिए भी किया जाता है, इत्यादि।
एेसे तीन और उदाहरण ज्ञात कीजिए जहाँ रोमन संख्यांकों का प्रयोग होता है।
रोमन संख्यांक
I, II, III, IV, V, VI, VII, VIII, IX, X
क्रमशा: संख्याएँ 1,2,3,4,5,6,7,8,9 और 10 व्यक्त करते हैं। इसके बाद 11 के लिए XI और 12 के लिए XII,... 20 के लिए XX का प्रयोग होता है।
इस पद्धति के कुछ और संख्यांक संगत हिंदू-अरेबिक संख्यांकों के साथ इस प्रकार हैं:

(a) यदि किसी संकेत की पुनरावृत्ति होती है, तो जितनी बार वह आता है उसका मान उतनी ही बार जोड़ दिया जाता है। अर्थात् II बराबर 2 है, XX बराबर 20 है और XXX बराबर 30 है।
(b) कोई संकेत तीन से अधिक बार नहीं आता है। परंतु संकेतों V, L और D की कभी पुनरावृत्ति नहीं होती है।
(c) यदि छोटे मान वाला कोई संकेत एक बड़े मान वाले संकेत के दाईं ओर जाता है, तो बड़े मान में छोटे मान को जोड़ दिया जाता है। जैसे:
VI = 5 + 1 = 6 XII = 10 + 2 = 12
LXV = 50 + 10 + 5 = 65
(d) यदि छोटे मान वाला कोई संकेत बड़े मान वाले किसी संकेत के बाईं ओर आता है, तो बड़े मान में से छोटे मान को घटा दिया जाता है। जैसे:
IV = 5 – 1 = 4 IX = 10 – 1 = 9
XL = 50 – 10 = 40 XC = 100 – 10 = 90
(e) संकेतों V, L और D को कभी भी बड़े मान वाले संकेत के बाईं ओर नहीं लिखा जाता है। अर्थात् V, L और D के मानों को कभी भी घटाया नहीं जाता है।
संकेत I को केवल V और X में से घटाया जा सकता है। संकेत X को केवल L, M और C में से ही घटाया जा सकता है।
इन नियमों का पालन करने से, हमें प्राप्त होता है:
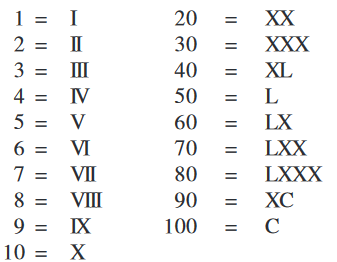
(a) उपरोक्त सारणी में छूटी हुई संख्याओं को रोमन पद्धति में लिखिए।
(b) XXXX, VX, IC, XVV ... इत्यादि, नहीं लिखे जाते हैं। क्या आप बता सकते हैं क्यों?
उदाहरण 7 : निम्नलिखित को रोमन संख्यांकों में लिखिए:
(a) 69 (b) 98
हल : (a) 69 = 60 + 9
= (50 + 10) + 9
= LX + IX
(b) 98 = 90 + 8
= (100 – 10) + 8
= XC + VIII
इसलिए 69 = LX IX इसलिए 98 = XCVIII

रोमन पद्धति में लिखिए
1. 73
2. 92
हमने क्या चर्चा की?
1. दो संख्याओं में वही संख्या बड़ी होती है, जिसमें अंकों की संख्या अधिक होती है। यदि दोनों में अंकों की संख्या समान है, तब हम उनके सबसे बाएँ स्थित अंकों की तुलना करते हैं और जिस संख्या में यह अंक बड़ा होगा वही बड़ी भी होगी। अगर ये अंक भी समान हैं, तब हम इसी प्रकार अंकों की तुलना करते जाते हैं।
2. दिए गए अंकों से संख्या बनाते समय, ध्यान रखना चाहिए कि संख्या को किन प्रतिबंधों के साथ बनाना है। जैसे अंकों 7, 8, 3 व 5 से, किसी भी अंक को बिना दोहराए, चार अंकों की बड़ी से बड़ी संख्या बनाने के लिए सबसे बड़े अंक 8 को सबसे बाईं ओर रखना होगा और फिर उससे छोटे अंक रखते जाएँगे।
3. चार अंकों की सबसे छोटी संख्या 1000 है। जिसका अर्थ है कि तीन अंकों की सबसे बड़ी संख्या 999 होगी। पाँच अंकों की सबसे बड़ी संख्या 10,000 (दस हज़ार) है, जिसका अर्थ है कि चार अंकों की बड़ी से बड़ी संख्या 9999 है।
इसी प्रकार आगे, छ: अंकों की छोटी से छोटी संख्या 1,00,000 (एक लाख) है जिसका अर्थ है कि पाँच अंकों की बड़ी से बड़ी संख्या 99999 है। यही क्रम और बड़ी संख्याओं के लिए भी लागू होता है।
4. अल्पविरामों का प्रयोग, संख्याओं के लिखने तथा पढ़ने में सहायता करता है। भारतीय संख्यांकन पद्धति में पहला अल्पविराम दाईं ओर से प्रारंभ कर तीन अंकों बाद और बाकी दो-दो अंकों बाद लगाए जाते हैं और ये अल्पविराम क्रमशा: हज़ार, लाख व करोड़ को अलग-अलग करते हैं। अंतराष्ट्रीय संख्यांकन पद्धति में अल्पविराम दाईं ओर से प्रारंभ कर तीन-तीन अंकों के बाद लगाए जाते हैं। तीन और छ: अंकों के बाद अल्पविराम क्रमशा: हज़ार व मिलियन को अलग-अलग करते हैं।
5. दैनिक जीवन में अनेक स्थानों पर हमें बड़ी-बड़ी संख्याओं की भी आवशयकता होती है। जैसे किसी विद्यालय में विद्यार्थियों की संख्या, गाँव या शहर की जनसंख्या बड़े-बड़े लेन-देन में धन तथा दो बड़े शहरों के बीच की दूरी।
6. याद रखिए किलो का अर्थ है–हज़ार, सेंटी का अर्थ है–सौवाँ भाग तथा मिली का अर्थ है–हज़ारवाँ भाग, इस प्रकार 1 किलोमीटर = 1000 मीटर, 1 मीटर = 100 सेंटीमीटर = 1000 मिलीमीटर
7. अनेक स्थितियों में हमें पूर्णतया सही-सही संख्याओं की आवशयकता नहीं होती बल्कि एक उपयुक्त आकलन से ही काम चल सकता है। जैसे एक अंतराष्ट्रीय हॉकी मैच के दर्शकों की संख्या बताने के लिए कह देते हैं कि लगभग 51,000 दर्शकों ने मैच देखा। यहाँ हमें दर्शकों की सही संख्या की आवशयकता नहीं है।
8. आकलन में किसी संख्या को एक वांछित मात्रा तक परिशाुद्ध करना होता है। जैसे 4117 का सन्निकटन, हज़ारों में 4000 तथा सैकड़ों में 4100 किया जा सकता है, जो आवशयकता पर निर्भर करता है।
9. अनेक स्थितियों में हमें संख्याओं पर संक्रियाओं के फलस्वरूप प्राप्त परिणामों का भी आकलन उपयोगी सिद्ध होता है। एेसे आकलनों में हम पहले प्रयोग होने वाली संख्याओं को सन्निकटित कर शीघ्रता से परिणाम प्राप्त कर लेते हैं।