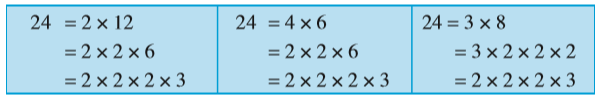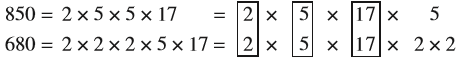Table of Contents
संख्याओं के साथ खेलना
3.1 भूमिका
रमेश के पास 6 कंचे (काँच की गोलियाँ) हैं। वह इन्हें पंक्तियों में इस प्रकार व्यवस्थित करना चाहता है कि प्रत्येक पंक्ति में कंचों की संख्या समान हो। वह उन्हें निम्न विधियों से व्यवस्थित करता है और कंचों की कुल संख्या परिकलित करता है :
(i) प्रत्येक पंक्ति में 1 कंचा।

पंक्तियों की संख्या = 6
कंचों की कुल संख्या = 1 × 6 = 6
(ii) प्रत्येक पंक्ति में 2 कंचे।

पंक्तियों की संख्या = 3
कंचों की कुल संख्या = 2 × 3 = 6
(iii) प्रत्येक पंक्ति में 3 कंचे।
पंक्तियों की संख्या = 2
कंचों की कुल संख्या = 3 × 2 = 6
(iv) वह कोई एेसी व्यवस्था नहीं सोच सका जिसमें प्रत्येक पंक्ति में 4 कंचे अथवा 5 कंचे हों। इसलिए अब केवल एक व्यवस्था बची, जिसमें एक पंक्ति में सभी 6 कंचों को रख दिया जाए।

पंक्तियों की संख्या = 1
कंचों की कुल संख्या = 6 × 1 = 6
इन परिकलनों में रमेश यह देखता है कि 6 को विभिन्न प्रकार (विधियों) से दो संख्याओं के गुणनफलों के रूप में लिखा जा सकता है, जैसा कि नीचे दिखाया गया है :
6 = 1 × 6; 6 = 2 × 3; 6 = 3 × 2; 6 = 6 × 1
6 = 2 × 3 से यह कहा जा सकता है कि 2 और 3, संख्या 6 को पूरी-पूरी (exactly) विभाजित करती हैं। अर्थात् 2 और 3, संख्या 6 के पूरे-पूरे विभाजक (या भाजक) (divisors) हैं। अन्य गुणनफल 6 = 1 × 6 से 6 के अन्य विभाजक 1 और 6 प्राप्त होते हैं।
इस प्रकार, 1, 2, 3 और 6 संख्या 6 के विभाजक हैं। ये 6 के गुणनखंड (factors) कहलाते हैं।
18 कंचों को पंक्तियों में व्यवस्थित करने का प्रयत्न कीजिए और 18 के गुणनखंड ज्ञात कीजिए।
3.2 गुणनखंड और गुणज
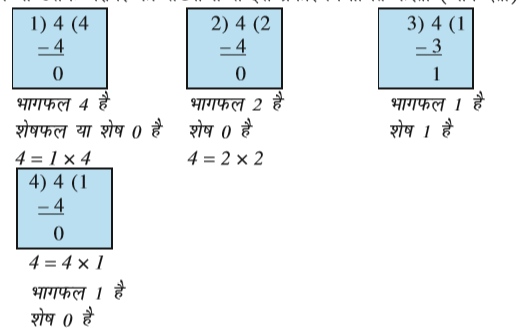
मैरी वे संख्याएँ ज्ञात करना चाहती है जो 4 को पूरी-पूरी विभाजित करती हैं। वह 4 को 4 से कम या उसके बराबर की संख्याओं से इस प्रकार विभाजित करती (भाग देती) है;
वह पाती है कि संख्या 4 को निम्न रूप में लिखा जा सकता है :
4 = 1 × 4; 4 = 2 × 2; 4 = 4 × 1
वह ज्ञात करती है कि 1, 2 और 4 संख्या 4 के पूरे-पूरे विभाजक हैं।
ये संख्याएँ 4 के गुणनखंड कहलाती हैं।
किसी संख्या का गुणनखंड उसका एक पूरा-पूरा (exact) विभाजक (divisor) होता है।
ध्यान दीजिए कि 4 का प्रत्येक गुणनखंड 4 से कम या उसके बराबर है।
 खेल 1 : यह खेल दो व्यक्तियों, मान लीजिए A और B द्वारा खेला जा सकता है। यह खेल गुणनखंड ज्ञात करने के बारे में है।
खेल 1 : यह खेल दो व्यक्तियों, मान लीजिए A और B द्वारा खेला जा सकता है। यह खेल गुणनखंड ज्ञात करने के बारे में है।
इसके लिए 50 कार्डों की आवश्यकता है, जिन पर 1 से 50 तक की संख्याएँ अंकित हैं।
एक मेज़ पर इन कार्डों को नीचे दर्शाए अनुसार व्यवस्थित कीजिए :
चरण :
(a) निर्णय लीजिए कि पहले कौन खेलेगा : A या B।
(b) मान लीजिए A पहले खेलता है। वह मेज़ से एक कार्ड उठाता है और अपने निकट रख लेता है। मान लीजिए इस कार्ड पर 28 लिखा है।
(c) खिलाड़ी B अब वे सभी कार्ड उठाता है जिन पर A के कार्ड पर लिखी संख्या (अर्थात् 28) के गुणनखंड लिखे हैं और उन्हें अपने निकट एक ढेर में रख देता है।
(d) फिर खिलाड़ी B मेज़ पर रखे कार्डों में से एक कार्ड उठाता है। अब मेज़ पर बचे कार्डों से A वे सभी कार्ड उठाता है जिन पर B के कार्ड की संख्या के गुणनखंड लिखे हैं।
(e) यह खेल तब तक जारी रहता है, जब तक कि सभी कार्ड न उठा लिए जाएँ।
(f) A अपने पास रखे कार्डों पर लिखी संख्याओं को जोड़ता है और B भी अपने पास रखे कार्डों पर लिखी संख्याओं को जोड़ता है। जिस खिलाड़ी का योग अधिक होगा उसे ही जीता हुआ माना जाएगा।
कार्डों की संख्या को बढ़ाकर इस खेल को और अधिक रोचक बनाया जा सकता है।
इस खेल को अपने मित्र के साथ खेलिए। क्या आप इस खेल को जीतने की कोई विधि ज्ञात कर सकते हैं?
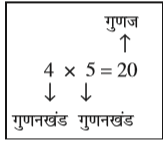
जब हम 20 = 4 × 5 लिखते हैं, तो हम कहते हैं कि 4 और 5, संख्या 20 के गुणनखंड (factor) हैं। हम यह भी कहते हैं कि 20, संख्या 4 और 5 का गुणज (multiple) है।
निरूपण 24 = 2 × 12 यह दर्शाता है कि 2 और 12, संख्या 24 के गुणनखंड हैं तथा 24 संख्या 2 और 12 का एक गुणज है।
हम कह सकते हैं कि एक संख्या अपने प्रत्येक गुणनखंड का एक गुणज होती है।

45, 30 और 36 के संभावित गुणनखंड ज्ञात कीजिए।
आइए, अब गुणनखंडों और गुणजों के बारे में कुछ रोचक तथ्यों को देखें :
(a) लकड़ी या कागज़ की कुछ पट्टियाँ एकत्रित कीजिए, जिनमें से प्रत्येक की लंबाई 3 मात्रक हो।
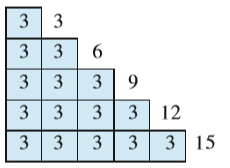
(b) सिरे से सिरा मिला कर इन्हें नीचे दी आकृति के अनुसार जोड़िए :
ऊपरी पट्टी की लंबाई 3 = 1 × 3 मात्रक है।
इसके नीचे वाली पट्टी की लंबाई 3 + 3 = 6 मात्रक (units) है। साथ ही, 6 = 2 × 3 है।
अगली पट्टी की लंबाई 3 + 3 + 3 = 9 मात्रक है। साथ ही, 9 = 3 × 3 है। इस प्रक्रिया को जारी रखते हुए, हम अन्य लंबाइयों को निम्न प्रकार से व्यक्त कर सकते हैं :
हम कहते हैं कि संख्याएँ 3, 6, 9, 12, 15 संख्या 3 के गुणज हैं।
3 के गुणजों की सूची को 18, 21, 24, ... के रूप में आगे बढ़ाया जा सकता है। इनमें से प्रत्येक गुणज 3 से बड़ा या उसके बराबर है।
संख्या 4 के गुणज 4, 8, 12, 16, 20, 24, ...हैं। यह सूची समाप्त नहीं होती है। इनमें से प्रत्येक गुणज 4 से बड़ा या उसके बराबर है।
आइए देखें कि गुणनखंडों और गुणजों के बारे में हम क्या निष्कर्ष निकाल सकते हैं :
1. क्या कोई एेसी संख्या है, जो प्रत्येक संख्या के गुणनखंड के रूप में आती है? हाँ, यह संख्या 1 है। उदाहरणार्थ, 6 = 1 × 6, 18 = 1 × 18 इत्यादि। इसकी जाँच कुछ और संख्याएँ लेकर कीजिए।
अत: हम कहते हैं कि 1 प्रत्येक संख्या का एक गुणनखंड होता है।
2. क्या 7 स्वयं का एक गुणनखंड हो सकता है? हाँ। आप 7 को 7 × 1 के रूप में लिख सकते हैं। 10 के बारे में आप क्या कह सकते हैं? 15 के बारे में आप क्या सोचते हैं? आप देख सकते हैं कि प्रत्येक संख्या को आप इस रूप में लिख सकते हैं।
हम कहते हैं कि प्रत्येक संख्या स्वयं अपना एक गुणनखंड होती है।
3. 16 के गुणनखंड क्या हैं? ये 1, 2, 4, 8 और 16 हैं। इन गुणनखंडों में क्या आप कोई एेसा गुणनखंड ज्ञात कर सकते हैं, जो 16 को विभाजित न करता हो? 20 और 36 के लिए भी उपरोक्त कथन की जाँच करिए।
आप पाएँगे कि एक संख्या का प्रत्येक गुणनखंड उस संख्या का एक पूर्ण विभाजक होता है।
4. 34 के गुणनखंड क्या हैं? ये 1, 2, 17 और स्वयं 34 हैं। इनमें सबसे बड़ा गुणनखंड कौन सा है? यह 34 है। अन्य गुणनखंड 1, 2 और 17 संख्या 34 से छोटे हैं। 64, 81 और 56 के लिए भी इस कथन की जाँच कीजिए। हम कहते हैं कि एक दी हुई संख्या का प्रत्येक गुणनखंड उस संख्या से छोटा या उसके बराबर होता है।
5. 76 के गुणनखंडों की संख्या 5 है। 136 के कितने गुणनखंड हैं? 96 के कितने गुणनखंड हैं? आप पाएँगे कि आप इनमें से प्रत्येक संख्या के गुणनखंडों की संख्याओं को गिन सकते हैं। संख्याएँ 10576, 25642 इत्यादि जैसी बड़ी होने पर भी आप इन संख्याओं के गुणनखंडों को गिन सकते हैं, यद्यपि आपको इन संख्याओं को गुणनखंडित करने में कुछ कठिनाई अवश्य होगी।
हम कह सकते हैं कि एक दी हुई संख्या के गुणनखंडों की संख्या परिमित (finite) होती है।
6. 7 के गुणज क्या हैं? स्पष्टत: ये 7, 14, 21, 28,... हैं। आप पाएँगे कि इनमें से प्रत्येक 7 से बड़ा या उसके बराबर है। क्या यह प्रत्येक संख्या के गुणजों के लिए सत्य होगा? इसकी जाँच 6, 9 और 10 के गुणजों को लेकर कीजिए।
हम पाते हैं कि एक संख्या का प्रत्येक गुणज उस संख्या से बड़ा या उसके बराबर होता है।
7. 5 के गुणज लिखिए। ये 5, 10, 15, 20, ... हैं। क्या आप सोचते हैं कि यह सूची कहीं समाप्त होगी? नहीं, यह सूची समाप्त न होने वाली है। इसकी जाँच 6, 7 इत्यादि के गुणजों को लेकर भी कीजिए।
हम प्राप्त करते हैं कि एक दी हुई संख्या के गुणजों की संख्या अपरिमित (infinite) है।
8. क्या 7 स्वयं का एक गुणज है। हाँ, क्योंकि 7 = 7×1 है। क्या यह अन्य संख्याओं के लिए भी सत्य है? 3, 12 और 16 के लिए इसकी जाँच कीजिए।
आप पाएँगे कि प्रत्येक संख्या स्वयं का एक गुणज है।
6 के सभी गुणनखंड 1, 2, 3 और 6 हैं। साथ ही, 1 + 2 + 3 + 6 = 12 = 2 × 6 है। हम प्राप्त करते हैं कि 6 के सभी गुणनखंडों का योग 6 का दोगुना है। 28 के सभी गुणनखंड 1, 2, 4, 7, 14 और 28 हैं। इन्हें जोड़ने पर हम प्राप्त करते हैं कि
1 + 2 + 4 + 7 + 14 + 28 = 56 = 2 × 28 है।
अर्थात् 28 के सभी गुणनखंडों का योग संख्या 28 का दोगुना है।
वह संख्या जिसके सभी गुणनखंडों का योग उस संख्या का दोगुना हो, एक संपूर्ण संख्या (perfect number) कहलाती है। 6 और 28 संपूर्ण संख्याएँ हैं।
क्या 10 एक संपूर्ण संख्या है?
उदाहरण 1 : 68 के सभी गुणनखंडों को लिखिए।
हल : हम देखते हैं कि
68 = 1 × 68 68 = 2 × 34 68 = 4 × 17 68 =17 × 4
यहाँ रुक जाइए, क्योंकि 4 और 17 पहले आ चुके हैं।
इस प्रकार, 68 के सभी गुणनखंड 1, 2, 4, 17, 34 और 68 हैं।
उदाहरण 2 : 36 के गुणनखंड ज्ञात कीजिए।
हल : 36 = 1 × 36 36 = 2 × 18
36 = 3 × 12 36 = 4 × 9
36 = 6 × 6
यहाँ रुक जाइए, क्योंकि दोनों गुणनखंड (6) समान हैं।
इस प्रकार, वांछित गुणनखंड 1, 2, 3, 4, 6, 9, 12, 18 और 36 हैं।
उदाहरण 3 : 6 के सभी प्रथम पाँच गुणज लिखिए।
हल : वांछित गुणज :
6×1= 6, 6×2 = 12, 6×3 = 18, 6×4 = 24 और 6×5 = 30
अर्थात् 6, 12, 18, 24 और 30 हैं।
प्रश्नावली 3.1
1. निम्नलिखित संख्याओं के सभी गुणनखंड लिखिए :
(a) 24 (b) 15 (c) 21
(d) 27 (e) 12 (f) 20
(g) 18 (h) 23 (i) 36
2. निम्न संख्याओं के प्रथम पाँच गुणज लिखिए :
(a) 5
(b) 8
(c) 9
3. स्तंभ 1 की संख्याओं का स्तंभ 2 के साथ मिलान कीजिए:
4. 9 के सभी गुणज ज्ञात कीजिए जो 100 से कम हों।
3.3 अभाज्य और भाज्य संख्याएँ
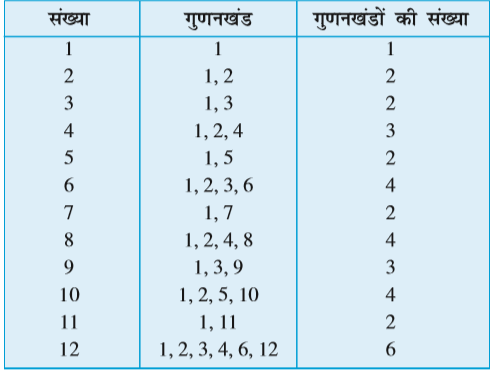
अब हम किसी संख्या के गुणनखंड करने की विधि से परिचित हो चुके हैं। निम्न सारणी में लिखी कुछ संख्याओं के गुणनखंडों की संख्याओं पर ध्यान दीजिए:
हम देखते हैं कि (a) संख्या 1 का एक ही गुणनखंड (स्वयं वही संख्या) है।
(b) कुछ संख्याएँ जैसे 2, 3, 5, 7, 11 इत्यादि एेसी हैं जिनके ठीक दो गुणनखंड (1 और स्वयं वह संख्या) हैं। ये संख्याएँ अभाज्य संख्याएँ (prime numbers) हैं।
ध्यान रखें : 1 न तो अभाज्य संख्या है और न ही भाज्य संख्या
वे संख्याएँ जिनके गुणनखंड 1 और स्वयं वह संख्या ही होते हैं अभाज्य संख्याएँ कहलाती हैं।
इन संख्याओं के अतिरिक्त कुछ अन्य अभाज्य संख्याएँ ज्ञात करने का प्रयत्न कीजिए।
(c) कुछ संख्याएँ जैसे 4, 6, 8, 9, 10 इत्यादि एेसी हैं, जिनके दो से अधिक गुणनखंड हैं, ये संख्याएँ भाज्य संख्याएँ (composite numbers) हैं। वे संख्याएँ जिनके दो से अधिक गुणनखंड होते हैं भाज्य संख्याएँ कहलाती हैं।
क्या 15 एक भाज्य संख्या है? 18 और 25 के बारे में आप क्या सोचते हैं?
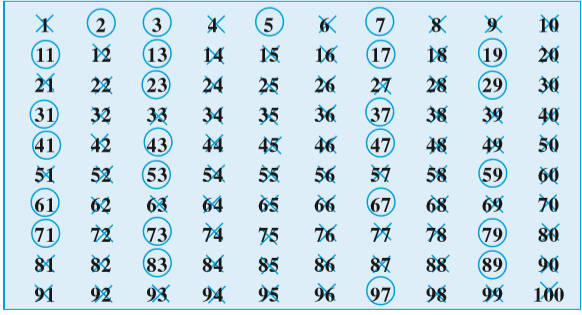
हम एक सरल विधि से 1 से 100 तक के बीच की अभाज्य संख्याएँ बिना उनके गुणनखंड किए ज्ञात करते हैं। यह विधि ई.पूर्व तीसरी शताब्दी में एक यूनानी गणितज्ञ इराटोसथीन्स (Eratosthenes) ने दी थी। आइए, इस विधि को देखें। 1 से 100 तक की संख्याओं को नीचे दर्शाए अनुसार लिखिए :
चरण-1 : 1 को काट दीजिए, क्योंकि यह एक अभाज्य संख्या नहीं है।
चरण-2 : 2 पर घेरा लगाइए और 2 के अतिरिक्त उसके सभी गुणजों, जैसे 4, 6, 8 इत्यादि को काट दीजिए।
चरण-3 : आप पाएँगे कि अगली बिना कटी संख्या 3 है। 3 पर घेरा लगाइए और 3 के अतिरिक्त उसके सभी गुणजों को काट दीजिए।
चरण-4 : अगली बिना कटी संख्या 5 है। 5 पर घेरा लगाइए और 5 के अतिरिक्त उसके सभी गुणजों को काट दीजिए।
चरण-5 : इस प्रक्रिया को तब तक जारी रखिए जब तक कि उपरोक्त सूची में दी हुई संख्याओं पर या तो घेरा न लग जाए या वे काट न दी जाएँ। घेरा लगी हुई सभी संख्याएँ अभाज्य संख्याएँ हैं। 1 के अतिरिक्त सभी काटी गई संख्याएँ भाज्य संख्याएँ हैं। यह विधि इराटोसथीन्स की छलनी (Sieve of Eratosthenes) विधि कहलाती है।

ध्यान दीजिए कि 2 × 3 + 1 = 7 एक अभाज्य संख्या है। यहाँ 2 के एक गुणज में 1 जोड़ कर एक अभाज्य संख्या प्राप्त की गई है। क्या आप इस प्रकार से कुछ और अभाज्य संख्याएँ ज्ञात कर सकते हैं?
उदाहरण 4 : 15 से छोटी सभी अभाज्य संख्याएँ लिखिए।
हल : छलनी विधि से प्राप्त उपरोक्त सारणी को देखकर, हम सरलता से वांछित अभाज्य संख्याएँ लिख सकते हैं। ये हैं : 2, 3, 5, 7, 11 और 13
सम और विषम संख्याएँ
क्या आप संख्याओं 2, 4, 6, 8, 10, 12, 14, ... में कोई प्रतिरूप (pattern) देखते हैं? आप पाएँगे कि इनमें से प्रत्येक 2 का एक गुणज है।
ये संख्याएँ सम संख्याएँ (even numbers) कहलाती हैं। शेष बची सभी प्राकृत संख्याएँ 1, 3, 5, 7, 9, 11,... विषम संख्याएँ (odd numbers) कहलाती हैं।
आप आसानी से जाँच कर सकते हैं कि एक 2 या 3 अंकों वाली संख्या सम संख्या है या नहीं। आप यह कैसे ज्ञात करेंगे कि 756482 जैसी बड़ी संख्या एक सम संख्या है या नहीं? क्या 2 से भाग देकर? क्या यह प्रक्रिया जटिल नहीं होगी?
हम कहते हैं कि वह संख्या जिसके इकाई के स्थान पर 0, 2, 4, 6 या 8 अंक हों एक सम संख्या होगी। इसलिए संख्याएँ 350, 4862 और 59246 सम संख्याएँ हैं। संख्याएँ 457, 2359 और 8231 विषम संख्याएँ हैं। आइए, अब कुछ रोचक तथ्यों को ज्ञात करने का प्रयत्न करें :
(a) सबसे छोटी सम संख्या कौन-सी है? यह 2 है। सबसे छोटी अभाज्य संख्या कौन-सी है? पुन: यह संख्या 2 है।
इस प्रकार, 2 सबसे छोटी अभाज्य संख्या है जो एक सम संख्या भी है।
(b) 2 के अतिरिक्त अभाज्य संख्याएँ 3, 5, 7, 11, .... हैं। क्या आप इस सूची में कोई सम संख्या देख रहे हैं? नहीं, सभी संख्याएँ विषम हैं। कुछ और अभाज्य संख्याएँ देखने का प्रयत्न करें।
इस प्रकार, हम कह सकते हैं कि 2 के अतिरिक्त सभी अभाज्य संख्याएँ विषम हैं।
प्रश्नावली 3.2
1. बताइए कि किन्हीं दो संख्याओं का योग सम होता है या विषम होता है, यदि वे दोनों
(a) विषम संख्याएँ हों (b) सम संख्याएँ हों
2. बताइए कि निम्नलिखित में कौन सा कथन सत्य है और कौन सा असत्य :
(a) तीन विषम संख्याओं का योग सम होता है।
(b) दो विषम संख्याओं और एक सम संख्या का योग सम होता है।
(c) तीन विषम संख्याओं का गुणनफल विषम होता है।
(d) यदि किसी सम संख्या को 2 से भाग दिया जाए, तो भागफल सदैव विषम होता है।
(e) सभी अभाज्य संख्याएँ विषम हैं।
(f) अभाज्य संख्याओं के कोई गुणनखंड नहीं होते।
(g) दो अभाज्य संख्याओं का योग सदैव सम होता है।
(h) केवल 2 ही एक सम अभाज्य संख्या है।
(i) सभी सम संख्याएँ भाज्य संख्याएँ हैं।
(j) दो सम संख्याओं का गुणनफल सदैव सम होता है।
3. संख्या 13 और 31 अभाज्य संख्याएँ हैं। इन दोनों संख्याओं में दो अंक 1 और 3 हैं। 100 तक की संख्याओं में एेसे अन्य सभी युग्म ज्ञात कीजिए।
4. 20 से छोटी सभी अभाज्य और भाज्य संख्याएँ अलग-अलग लिखिए।
5. 1 और 10 के बीच में सबसे बड़ी अभाज्य संख्या लिखिए।
6. निम्नलिखित को दो विषम अभाज्य संख्याओं के योग के रूप में व्यक्त कीजिए :
(a) 44 (b) 36 (c) 24 (d) 18
7. अभाज्य संख्याओं के एेसे तीन युग्म लिखिए जिनका अंतर 2 हो।
[टिप्पणी : दो अभाज्य संख्याएँ जिनका अंतर 2 हो अभाज्य युग्म (twin primes) कहलाती हैं।]
8. निम्नलिखित में से कौन-सी संख्याएँ अभाज्य संख्याएँ हैं?
(a) 23 (b) 51 (c) 37 (d) 26
9. 100 से छोटी सात क्रमागत भाज्य संख्याएँ लिखिए जिनके बीच में कोई अभाज्य संख्या नहीं हो।
10. निम्नलिखित संख्याओं में से प्रत्येक को तीन अभाज्य संख्याओं के योग के रूप में व्यक्त कीजिए :
(a) 21 (b) 31 (c) 53 (d) 61
11. 20 से छोटी अभाज्य संख्याओं के एेसे पाँच युग्म लिखिए जिनका योग 5 से विभाज्य (divisible) हो। (संकेत : 3 + 7 = 10)
12. निम्न में रिक्त स्थानों को भरिए :
(a) वह संख्या जिसके केवल दो गुणनखंड हों एक ______ कहलाती है।
(b) वह संख्या जिसके दो से अधिक गुणनखंड हों एक ______ कहलाती है।
(c) 1 न तो ______ है और न ही ______ ।
(d) सबसे छोटी अभाज्य संख्या ______ है।
(e) सबसे छोटी भाज्य संख्या _____ है।
(f) सबसे छोटी सम संख्या ______है।
3.4 संख्याओं की विभाज्यता की जाँच
क्या संख्या 38 संख्या 2 से विभाज्य है? क्या यह 4 से विभाज्य है? क्या यह 5 से विभाज्य है?
38 को वास्तविक रूप में इन संख्याओं से भाग देने पर हम प्राप्त करते हैं कि यह 2 से विभाज्य है, परंतु 4 और 5 से विभाज्य नहीं है।
आइए देखें कि क्या हम कोई प्रतिरूप (पैटर्न) ज्ञात कर सकते हैं जिससे हम बता सकें कि कोई संख्या 2, 3, 4, 5, 6, 8, 9, 10 या 11 से विभाज्य है या नहीं। क्या आप सोचते हैं कि एेसे प्रतिरूप हम आसानी से देख सकते हैं?
10 से विभाज्यता : चारू 10 के गुणजों 10, 20, 30, 40, 50, 60, ... . को देख रही थी। उसने इन संख्याओं में एक सर्वनिष्ठ (common) गुण देखा। क्या आप बता सकते हैं कि वह गुण क्या है? इनमें प्रत्येक के इकाई के स्थान पर अंक 0 है।
उसने इकाई के स्थान 0 वाली कुछ और संख्याओं के बारे में भी सोचा, जैसे कि 100, 1000, 3200, 7010 । उसने यह भी ज्ञात किया कि ये सभी संख्याएँ 10 से विभाज्य हैं।
इस प्रकार, वह ज्ञात करती है कि यदि किसी संख्या के इकाई के स्थान पर अंक 0 हो, तो वह 10 से विभाज्य होती है।
क्या आप 100 से विभाज्यता का कोई नियम ज्ञात कर सकते हैं?
5 से विभाज्यता : मनि ने संख्याओं 5, 10, 15, 20, 25, 30, 35, ... में एक रोचक प्रतिरूप प्राप्त किया। क्या आप यह प्रतिरूप बता सकते हैं? इन सभी संख्याओं में, इकाई के स्थान पर या तो अंक 0 है या अंक 5 है। उसने ज्ञात किया कि ये सभी संख्याएँ 5 से विभाज्य हैं।
उसने 5 से विभाज्य कुछ और संख्याएँ लीं, जैसे कि 105, 215, 6205, 3500 इत्यादि। इन संख्याओं में भी इकाई के स्थान पर 0 या 5 ही आते हैं।
उसने 23, 56 और 97 को 5 से भाग देने का प्रयत्न किया। क्या वह एेसा करने में समर्थ हो जाएगा? इसकी जाँच कीजिए। वह देखता है कि यदि किसी संख्या का इकाई का अंक 0 हो या 5 हो, तो वह संख्या 5 से विभाज्य होती है।
क्या 1750125 संख्या 5 से विभाज्य है?
2 से विभाज्यता : चारू 2 के कुछ गुणजों 10, 12, 14, 16, ... और कुछ अन्य गुणजों जैसे 2410, 4356, 1358, 2972, 5974 को देखती है। उसे इनमें एक प्रतिरूप दिखाई देता है। क्या आप इस प्रतिरूप को बता सकते हैं? इन संख्याओं के इकाई के स्थान पर 0, 2, 4, 6 और 8 में से ही कोई अंक आता है।
वह इन संख्याओं को 2 से भाग देती है और शेष 0 प्राप्त करती है।
वह यह भी ज्ञात करती है कि संख्याएँ 2467 और 4829 संख्या 2 से विभाज्य नहीं है। इन संख्याओं के इकाई के स्थान पर 0, 2, 4, 6 या 8 में से कोई भी अंक नहीं है।
इन प्रेक्षणों से वह यह निष्कर्ष निकालती है कि यदि किसी संख्या के इकाई के स्थान पर 0, 2, 4, 6 या 8 में से कोई अंक हो, तो वह संख्या 2 से विभाज्य होती है।
3 से विभाज्यता : क्या संख्या 21, 27, 36, 54 और 219 संख्या 3 से विभाज्य हैं?
हाँ, ये हैं।
3 से विभाज्यता के लिए क्या आप कोई प्रतिरूप इकाई स्थान में देख सकते हैं हम नहीं देख सकते, क्योंकि इकाई के स्थान पर समान अंक होने पर वह 3 से विभाजित हो भी सकता है और नहीं भी।
जैसे संख्या 27, 3 से विभाजित है, पर संख्याएँ 17, 37, 3 से विभाजित नहीं है।
अब आप 21, 36, 54 और 219 के अंकों को जोड़िए। क्या आप इनमें कोई विशेष बात देखते हैं? 2 + 1=3, 3 + 6 = 9, 5 + 4 = 9, 2 + 1+ 9 = 12। ये सभी योग 3 से विभाज्य हैं।
25, 37, 260 के अंकों को जोड़िए। हमें 2 + 5 = 7, 3 + 7 = 10, 2 + 6 + 0 = 8 प्राप्त होता है। इनमें से कोई भी योग 3 से विभाज्य नहीं है।
हम कहते हैं कि यदि किसी संख्या के अंकों का योग 3 का एक गुणज हो, तो वह संख्या 3 से विभाज्य होती है।
क्या 7221 संख्या 3 से विभाज्य है?
6 से विभाज्यता : क्या आप कोई एेसी संख्या बता सकते हैं जो 2 और 3 दोनों से विभाज्य है? एेसी एक संख्या 18 है। क्या संख्या 18, 2×3 के गुणनफल 6 से विभाज्य होगी? हाँ, एेसा ही है।
18 जैसी कुछ और संख्याएँ ज्ञात कीजिए और जाँचिए कि क्या वे 6 से भी विभाज्य हैं।
क्या आप कोई एेसी संख्या बता सकते हैं जो 2 से विभाज्य हो, परंतु 3 से विभाज्य न हो?
अब एक एेसी संख्या लिखिए जो 3 से विभाज्य हो, परंतु 2 से विभाज्य न हो। एेसी एक संख्या 27 है।
क्या 27 संख्या 6 से विभाज्य है? नहीं। एेसी कुछ और संख्याएँ ज्ञात करने का प्रयत्न कीजिए।
इन प्रेक्षणों से हम यह निष्कर्ष निकालते हैं कि यदि कोई संख्या 2 और 3 दोनों से विभाज्य हो, तो वह संख्या 6 से भी विभाज्य होती है।
4 से विभाज्यता : क्या आप तीन अंकों की कोई एेसी संख्या बता सकते हैं, जो 4 से विभाज्य है? हाँ, एेसी एक संख्या 212 है। अब कोई चार अंकों की संख्या बताओ जो 4 से विभाज्य हो। एेसी एक संख्या 1936 है।
212 के इकाई और दहाई के स्थानों के अंकों से बनी संख्या को देखिए। यह संख्या 12 है, जो 4 से विभाज्य है। 1936 के लिए यह संख्या 36 है। पुन: यह संख्या भी 4 से विभाज्य है। इसी प्रक्रिया को संख्या 4612; 3516; 9532 पर करने का प्रयत्न कीजिए।
क्या 286 संख्या 4 से विभाज्य है? नहीं। क्या 86 संख्या 4 से विभाज्य है? नहीं।
अत:, हम कहते हैं कि 3 या अधिक अंकों की एक संख्या 4 से विभाज्य होती है, यदि उसके अंतिम दो अंकों (इकाई और दहाई के स्थान के अंकों) से बनी संख्या 4 से विभाज्य हो। इस नियम की जाँच 10 और उदाहरण लेकर कीजिए।
1 या 2 अंकों की संख्या की 4 से विभाज्यता की जाँच वास्तविक रूप में 4 से भाग देकर की जानी चाहिए।
8 से विभाज्यता : क्या संख्याएँ 1000, 2104 और 1416 संख्या 8 से विभाज्य हैं? हाँ, ये 8 से विभाज्य हैं।
इन संख्याओं के इकाई, दहाई और सैकड़े के अंकों से बनी संख्याएँ क्रमश: 000, 104 और 416 हैं। ये तीनों संख्याएँ भी 8 से विभाज्य हैं। एेसी कुछ और संख्याएँ ज्ञात कीजिए जिनके इकाई, दहाई और सैकड़े के स्थानों के अंकों (अंतिम तीन अंक) से बनी संख्याएँ 8 से विभाज्य हों। उदाहरणार्थ 9216, 8216, 7216, 10216, 9995216 इत्यादि। इन संख्याओं में आप पाएँगे कि ये संख्याएँ स्वयं भी 8 से विभाज्य हैं।
हम ज्ञात करते हैं कि 4 या उससे अधिक अंकों की कोई संख्या 8 से विभाज्य होती है, यदि अंतिम तीन अंकों से बनी संख्या 8 से विभाज्य हो।
क्या 73512 संख्या 8 से विभाज्य है?
1, 2 या 3 अंकों वाली संख्याओं की 8 से विभाज्यता की जाँच वास्तविक रूप से भाग देकर की जा सकती है।
9 से विभाज्यता : 9 के गुणज 9, 18, 27, 36, 45, 54,... हैं अर्थात् ये संख्याएँ 9 से विभाज्य हैं। कुछ अन्य संख्याएँ 4608 और 5283 भी हैं जो 9 से विभाज्य हैं।
क्या आप इन संख्याओं के अंकों के योग में कोई प्रतिरूप देखते हैं? हाँ।
1 + 8 = 9, 2 + 7 = 9, 3 + 6 = 9, 4 + 5 = 9,
4 + 6 + 0 + 8 = 18, 5 + 2 + 8 + 3 = 18
इनमें सभी योग 9 से विभाज्य हैं।
क्या 758 संख्या 9 से विभाज्य है? नहीं।
इस संख्या के अंकों का योग 7 + 5 + 8 = 20 भी 9 से विभाज्य नहीं है।
इन प्रेक्षणों के आधार पर, हम कह सकते हैं कि यदि किसी संख्या के अंकों का योग 9 से विभाज्य हो, तो वह संख्या भी 9 से विभाज्य होती है।
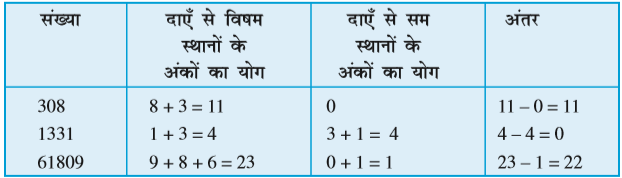
11 से विभाज्यता : संख्याओं 308, 1331 और 61809 में से प्रत्येक संख्या 11 से विभाज्य है।
हम एक सारणी बनाते हैं और देखते हैं कि क्या इन संख्याओं के अंकों से हमें कोई प्रतिरूप प्राप्त होता है।
हम देखते हैं कि प्रत्येक स्थिति में, अंतर या तो 0 है या 11 से विभाज्य है। साथ ही, ये सभी संख्याएँ 11 से विभाज्य हैं।
संख्या 5081 के लिए, एेसे अंकों का अंतर (8 + 5) – (1 + 0) = 12 है, जो 11 से विभाज्य नहीं है। संख्या 5081 भी 11 से विभाज्य नहीं है। इसकी जाँच 11 से 5081 को भाग देकर की जा सकती है।
इस प्रकार, किसी संख्या की 11 से विभाज्यता की जाँच के लिए, दाएँ से विषम स्थानों के अंकों का योग और सम स्थानों के अंकों के योग का अंतर ज्ञात किया जाए। यदि यह अंतर 0 है या 11 से विभाज्य है, तो वह संख्या 11 से विभाज्य होती है।
प्रश्नावली 3.3
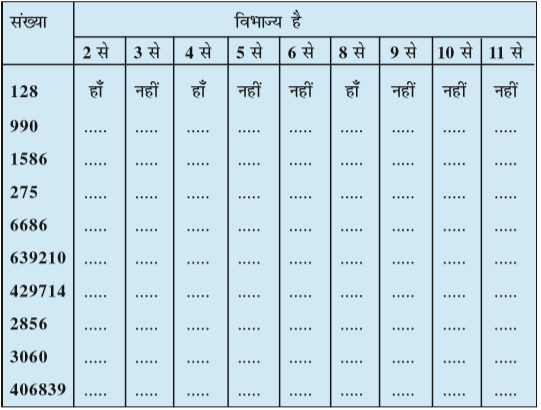
1. विभाज्यता की जाँच के नियमों का प्रयोग करते हुए, पता कीजिए कि निम्नलिखित संख्याओं में से कौन सी संख्याएँ 2 से विभाज्य हैं; 3 से विभाज्य हैं; 4 से विभाज्य हैं; 5 से विभाज्य हैं, 6 से विभाज्य हैं, 8 से विभाज्य हैं, 9 से विभाज्य हैं, 10 से विभाज्य हैं या 11 से विभाज्य हैं (हाँ या नहीं कहिए) :
2. विभाज्यता की जाँच के नियमों द्वारा ज्ञात कीजिए कि निम्नलिखित में से कौन सी संख्याएँ 4 से विभाज्य हैं और कौन सी 8 से विभाज्य हैं :
(a) 572
(b) 726352
(c) 5500
(d) 6000
(e) 12159
(f) 14560
(g) 21084
(h) 31795072
(i) 1700
(j) 2150
3. विभाज्यता की जाँच के नियमों द्वारा ज्ञात कीजिए कि निम्नलिखित में से कौन सी संख्याएँ 6 से विभाज्य हैं :
(a) 297144 (b) 1258 (c) 4335 (d) 61233
(e) 901352 (f) 438750 (g) 1790184 (h) 12583
(i) 639210 (j) 17852
4. विभाज्यता की जाँच के नियमों द्वारा ज्ञात कीजिए कि निम्नलिखित में से कौन सी संख्याएँ 11 से विभाज्य हैं :
(a) 5445 (b) 10824 (c) 7138965
(d) 70169308 (e) 10000001 (f) 901153
5. निम्नलिखित में रिक्त स्थानों में सबसे छोटा अंक तथा सबसे बड़ा अंक लिखिए, जिससे संख्या 3 से विभाज्य हो;
(a) ____ 6724 (b) 4765 _____ 2
6. निम्नलिखित में रिक्त स्थानों में एेसा अंक लिखिए ताकि संख्या 11 से विभाज्य हो :
(a) 92 _____ 389 (b) 8 _____ 9484
3.5 सार्व गुणनखंड और सार्व गुणज
कुछ संख्या के युग्मों के गुणनखंडों को देखिए।
(a) 4 और 18 के गुणनखंड क्या हैं?
4 के गुणनखंड हैं : 1, 2 और 4
18 के गुणनखंड हैं : 1, 2, 3, 6, 9 और 18
दोनों संख्याओं 4 और 18 के गुणनखंड 1 और 2 हैं।
अथवा ये 4 और 18 के उभयनिष्ठ या सार्व गुणनखंड (Common factors) हैं।

निम्न युग्मों के उभयनिष्ठ या सार्व गुणनखंड क्या हैं?
(a) 8, 20 (b) 9, 15
(b) 4 और 15 के सार्व गुणनखंड क्या हैं?
इन दोनों संख्याओं में केवल 1 ही सार्व गुणनखंड हैं।
7 और 16 के सार्व गुणनखंड क्या हैं?
दो संख्याएँ जिनमें केवल 1 ही सार्व गुणनखंड होता है सह-अभाज्य संख्याएँ (co-prime numbers) कहलाती हैं। 4 और 15 सह-अभाज्य संख्याएँ हैं।
क्या 7 और 15, 12 और 49, 18 और 23 सह-अभाज्य संख्याएँ हैं?
(c) क्या हम 4, 12 और 16 के सार्व गुणनखंड ज्ञात कर सकते हैं?
4 के गुणनखंड 1, 2 और 4 हैं।
12 के गुणनखंड 1, 2, 3, 4, 6 और 12 हैं।
16 के गुणनखंड 1, 2, 4, 8 और 16 हैं।
स्पष्टत: 4, 12 और 16 के सार्व गुणनखंड 1, 2 और 4 हैं।
निम्न के सार्व गुणनखंड ज्ञात कीजिए :
(a) 8, 12, 20 (b) 9, 15, 21
आइए, अब एक से अधिक संख्याओं के गुणजों को एक साथ लेकर देखें।
(a) 4 और 6 के गुणज क्या हैं?
4 के गुणज हैं : 4, 8, 12, 16, 20, 24, ... (कुछ और गुणज लिखिए)
6 के गुणज हैं : 6, 12, 18, 24, 30, 36, ... (कुछ और गुणज लिखिए)
इनमें से, क्या कुछ और एेसी संख्याएँ हैं जो दोनों सूचियों में आ रही हैं? हम देखते हैं कि 12, 24, 36, ... 4 और 6 दोनों के गुणज हैं।
क्या आप एेसे कुछ और गुणज लिख सकते हैं?
ये 4 और 6 के उभयनिष्ठ या सार्व गुणज (Common multiples) कहलाते हैं?
(b) 3, 5 और 6 के सार्व गुणज ज्ञात कीजिए।
3 के गुणज 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, ... हैं।
5 के गुणज 5, 10, 15, 20, 25, 30, 35, ... हैं।
6 के गुणज 6, 12, 18, 24, 30, ... है।
3, 5 और 6 के, सार्व गुणज 30, 60, 90, .... हैं।
3, 5 और 6 के कुछ और सार्व गुणज लिखिए।
उदाहरण 5 : 75, 60 और 210 के सार्व गुणनखंड ज्ञात कीजिए।
हल : 75 के गुणनखंड 1, 3, 5, 15, 25 और 75 हैं।
60 के गुणनखंड 1, 2, 3, 4, 5, 6, 10, 12, 15, 30 और 60 हैं।
210 के गुणनखंड 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105 और 210 हैं।
इस प्रकार 75, 60 और 210 के सार्व गुणनखंड 1, 3, 5 और 15 हैं।
उदाहरण 6 : 3, 4 और 9 के सार्व गुणज ज्ञात कीजिए।
हल : 3 के गुणज 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, ... हैं।
4 के गुणज 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48,... हैं।
9 के गुणज 9, 18, 27, 36, 45, 54, 63, 72, 81, ... हैं।
स्पष्टत: 3, 4 और 9 के सार्व गुणज 36, 72, 108,... हैं।
प्रश्नावली 3.4
1. निम्न के सार्व गुणनखंड ज्ञात कीजिए :
(a) 20 और 28 (b) 15 और 25
(c) 35 और 50 (d) 56 और 120
2. निम्न के सार्व गुणनखंड ज्ञात कीजिए :
(a) 4, 8 और 12 (b) 5, 15 और 25
3. निम्न के प्रथम तीन सार्व गुणज ज्ञात कीजिए :
(a) 6 और 8 (b) 12 और 18
4. 100 से छोटी एेसी सभी संख्याएँ लिखिए जो 3 और 4 के सार्व गुणज हैं।
5. निम्नलिखित में से कौन-सी संख्याएँ सह-अभाज्य हैं?
(a) 18 और 35 (b) 15 और 37 (c) 30 और 415
(d) 17 और 68 (e) 216 और 215 (f) 81 और 16
6. एक संख्या 5 और 12 दोनों से विभाज्य है। किस अन्य संख्या से यह संख्या सदैव विभाजित होगी?
7. एक संख्या 12 से विभाज्य है। और कौन सी संख्याएँ हैं जिनसे यह संख्या विभाज्य होगी?
3.6 विभाज्यता के कुछ और नियम
आइए, संख्याओं की विभाज्यता के कुछ और नियमों को देखें।
(i) क्या आप 18 का एक गुणनखंड बता सकते हैं? यह 9 है। 9 के एक गुणनखंड को लिखिए। यह 3 है। क्या संख्या 18 का एक गुणनखंड 3 है। हाँ, यह है। 18 का कोई अन्य गुणनखंड बताइए। यह 6 है। 6 का एक गुणनखंड बताइए। यह 2 है। यह 18 का भी एक गुणनखंड है, अर्थात् 18 को विभाजित करता है। इसकी जाँच 18 के अन्य गुणनखंडों के लिए भी कीजिए।
यही प्रक्रिया 24 के लिए भी कीजिए। यह 8 से विभाज्य है। साथ ही, 24 संख्या 8 के सभी गुणनखंडों 1,2,4 और 8 से भी विभाज्य है।
इसलिए, हम कह सकते हैं कि यदि कोई संख्या एक संख्या से विभाज्य है, तो वह संख्या इस संख्या के प्रत्येक गुणनखंड से भी विभाज्य होगी।
(ii) संख्या 80 संख्याओं 4 और 5 दोनों से विभाज्य है। यह 4 × 5 = 20 से भी विभाज्य है तथा 4 और 5 सह-अभाज्य संख्याएँ हैं।
इसी प्रकार, 60 सह-अभाज्य संख्याओं 3 और 5 से विभाज्य है। 60, गुणनफल 3 × 5 = 15 से भी विभाज्य है।
इसलिए, हम कह सकते हैं कि यदि कोई संख्या दो सह-अभाज्य संख्याओं से विभाज्य हो, तो वह उनके गुणनफल से भी विभाज्य होती है।
(iii) दोनों संख्याएँ 16 और 20 संख्या 4 से विभाज्य हैं। संख्या 16 + 20 = 36 भी 4 से विभाज्य है। इसकी जाँच संख्याओं के कुछ और युग्म लेकर कीजिए।
16 और 20 के अन्य उभयनिष्ठ गुणनखंडों के लिए भी इसकी जाँच कीजिए। इस प्रकार, यदि दी हुई दो संख्याएँ किसी संख्या से विभाज्य हों, तो इन संख्याओं का योग भी उस संख्या से विभाज्य होगा।
(iv) दोनों संख्याएँ 35 और 20 संख्या 5 से विभाज्य हैं। क्या इनका अंतर 35-20 = 15 भी 5 से विभाज्य है? इसकी जाँच संख्याओं के एेसे कुछ अन्य युग्म लेकर भी कीजिए। इस प्रकार, यदि दी हुई दो संख्याएँ किसी संख्या से विभाज्य हाें, तो इन संख्याओं का अंतर भी उस संख्या से विभाज्य होगा। दो संख्याओं के अन्य युग्म लेकर उपर्युक्त दिए गए चारों नियमों की जाँच कीजिए।
3.7 अभाज्य गुणनखंडन
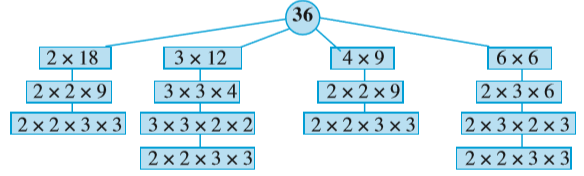
यदि किसी संख्या को उसके गुणनखंडों के गुणनफल के रूप में व्यक्त किया जाए, तो हम कहते हैं कि हमने उस संख्या को गुणनखंडित (factorised) कर लिया है अथवा उसके गुणनखंड कर लिए हैं। इस प्रकार, जब हम 24 = 3 × 8 लिखते हैं, तो हम कहते हैं कि हमने 24 के गुणनखंड कर लिए हैं। यह 24 के गुणनखंडनों में से एक गुणनखंडन है। इसके अन्य गुणनखंडन निम्न हैं :
24 के उपरोक्त सभी गुणनखंडनों में, अंत में हम एक ही गुणनखंडन 2 × 2 × 2 × 3 पर पहुँचते हैं। इस गुणनखंडन में केवल 2 और 3 ही गुणनखंड हैं और ये अभाज्य संख्याएँ हैं। किसी संख्या का इस प्रकार का गुणनखंडन अभाज्य गुणनखंडन (prime factorisation) कहलाता है।
आइए, इसकी जाँच संख्या 36 से करें।
36 का अभाज्य गुणनखंडन 2 × 2 × 3 × 3 है। यह 36 का केवल एक ही अभाज्य गुणनखंडन है।

16, 28 और 38 के अभाज्य गुणनखंडन लिखिए।

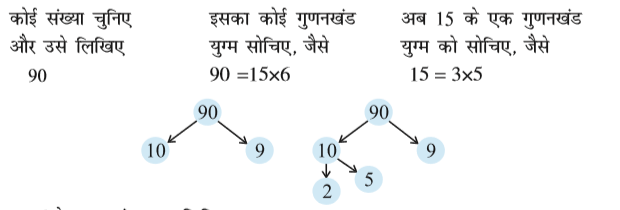
गुणनखंड वृक्ष (Factor Tree)
6 के गुणनखंड युग्म लिखिए
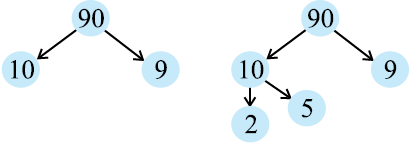
एेसा ही निम्न संख्याएँ लेकर कीजिए।
(a) 8 (b) 12
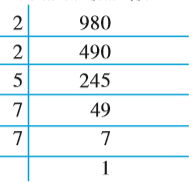
उदाहरण 7 : 980 का अभाज्य गुणनखंडन ज्ञात कीजिए।
हल : हम एेसा निम्न प्रकार करते हैं :
हम संख्या 980 को 2, 3, 5, 7 इत्यादि से इसी क्रम में बार-बार भाग देते हैं। यह प्रक्रिया हम तब तक जारी रखते हैं, जब तक कि भागफल इनसे विभाजित होता रहे।
इस प्रकार 980 का अभाज्य गुणनखंडन है : 980 = 2 × 2 × 5 × 7 × 7
प्रश्नावली 3.5
1. निम्नलिखित में से कौन-से कथन सत्य हैं?
(a) यदि कोई संख्या 3 से विभाज्य है, तो वह 9 से भी विभाज्य होती है।
(b) यदि एक संख्या 9 से विभाज्य है, तो वह 3 से भी अवश्य विभाज्य होगी।
(c) एक संख्या 18 से भी विभाज्य होती है, यदि वह 3 और 6 दोनों से विभाज्य हो।
(d) यदि एक संख्या 9 और 10 दोनों से विभाज्य हो, तो वह 90 से भी विभाज्य होगी।
(e) यदि दो संख्याएँ सह-अभाज्य हों, तो इनमें से कम से कम एक अवश्य ही अभाज्य संख्या होगी।
(f) 4 से विभाज्य सभी संख्याएँ 8 से भी अवश्य विभाज्य होनी चाहिए।
(g) 8 से विभाज्य सभी संख्याएँ 4 से विभाज्य होनी चाहिए।
(h) यदि कोई संख्या दो संख्याओं को अलग-अलग पूरा-पूरा विभाजित करती है, तो वह उनके योग को भी पूरा-पूरा विभाजित करेगी।
(i) यदि कोई संख्या दो संख्याओं के योग को पूरी तरह विभाजित करती है, तो वह उन दोनों संख्याओं को अलग-अलग भी विभाजित करेगी।
2. यहाँ 60 के लिए दो भिन्न-भिन्न गुणनखंड वृक्ष दिए हैं। इनमें अज्ञात संख्याएँ लिखिए।
(a)
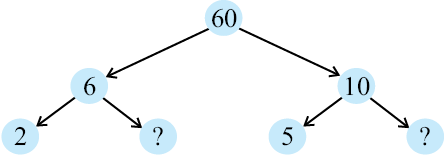
(b)
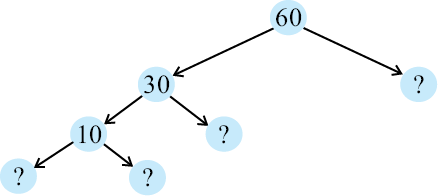
3. एक भाज्य संख्या के अभाज्य गुणनखंडन में किन गुणनखंडों को सम्मिलित नहीं किया जाता है?
4. चार अंकों की सबसे बड़ी संख्या लिखिए और उसे अभाज्य गुणनखंडन के रूप में व्यक्त कीजिए।
5. पाँच अंकों की सबसे छोटी संख्या लिखिए और उसे अभाज्य गुणनखंडन के रूप में व्यक्त कीजिए।
6. 1729 के सभी अभाज्य गुणनखंड ज्ञात कीजिए और उन्हें आरोही क्रम में व्यवस्थित कीजिए। अब दो क्रमागत अभाज्य गुणनखंडों में यदि कोई संबंध है तो लिखिए।
7. तीन क्रमागत संख्याओं का गुणनफल सदैव 6 से विभाज्य होता है। इस कथन को कुछ उदाहरणों की सहायता से स्पष्ट कीजिए।
8. दो क्रमागत विषय संख्याओं का योग 4 से विभाज्य होता है। कुछ उदाहरण लेकर इस कथन का सत्यापन कीजिए।
9. निम्न में से किन व्यंजकों में अभाज्य गुणनखंडन किए गए हैं :
(a) 24 = 2 × 3 × 4 (b) 56 = 1 × 7 × 2 × 2 × 2
(c) 70 = 2 × 5 × 7 (d) 54 = 2 × 3 × 9
10. बिना भाग किए ज्ञात कीजिए कि क्या 25110 संख्या 45 से विभाज्य है।
[संकेत : 5 और 9 सह-अभाज्य संख्याएँ हैं। दी हुई संख्या की 5 और 9 से विभाज्यता की जाँच कीजिए।]
11. संख्या 18, 2 और 3 दोनों से विभाज्य है। यह 2 × 3 = 6 से भी विभाज्य है। इसी प्रकार, एक संख्या 4 और 6 दोनों से विभाज्य है। क्या हम कह सकते हैं कि वह संख्या 4 × 6 = 24 से भी विभाज्य होगी। यदि नहीं, तो अपने उत्तर की पुष्टि के लिए एक उदाहरण दीजिए।
12. मैं चार भिन्न-भिन्न अभाज्य गुणनखंडों वाली सबसे छोटी संख्या हूँ। क्या आप मुझे ज्ञात कर सकते हैं?
3.8 महत्तम समापवर्तक
हम दो संख्याओं के सार्व गुणनखंड ज्ञात करना सीख चुके हैं। अब हम इन सार्व गुणनखंडों में सबसे बड़ा गुणनखंड ज्ञात करने का प्रयत्न करेंगे।
12 और 16 के सार्व गुणनखंड क्या हैं? ये 1, 2 और 4 हैं।
इन सार्व गुणनखंडों में सबसे बड़ा कौन-सा है? यह 4 है। 20, 28 और 36 के सार्व गुणनखंड क्या हैं। ये 1, 2 और 4 हैं तथा इनमें पुन: सबसे बड़ा गुणनखंड 4 है।
दो या दो से अधिक दी हुई संख्याओं के सार्व गुणनखंडों में सबसे बड़ा सार्व गुणनखंड इन दी हुई संख्याओं का महत्तम समापवर्तक (highest common factor) कहलाता है। महत्तम समापवर्तक को संक्षेप में म.स. (या HCF) भी लिखते हैं। इसे महत्तम (सबसे बड़ा) सार्व भाजक (greatest common divisor) या (GCD) भी कहा जाता है।

निम्न का म.स. ज्ञात कीजिए :
(i) 24 और 36 (ii) 15, 25 और 30
(iii) 8 और 12 (iv) 12, 16 और 28
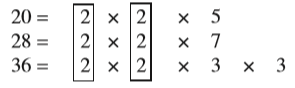
संख्याओं 20, 28 और 36 का म.स. इन संख्याओं के अभाज्य गुणनखंडन द्वारा इस प्रकार ज्ञात किया जा सकता है :
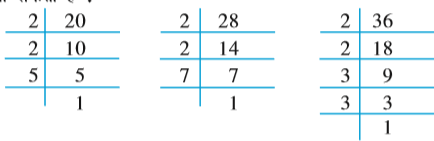
इस प्रकार,
20, 28 और 36 में सार्व गुणनखंड 2 (दो बार आ रहा है) है।
अत:, 20, 28 और 36 का म.स. 2 × 2 = 4 है।
प्रश्नावली 3.6
1. निम्नलिखित संख्याओं के म.स. ज्ञात कीजिए :
(a) 18, 48 (b) 30, 42 (c) 18, 60 (d) 27, 63
(e) 36, 84 (f) 34, 102 (g) 70, 105, 175 (h) 91, 112, 49
(i) 18,54, 81 (j) 12, 45, 75
2. निम्न का म.स. क्या है?
(a) दो क्रमागत संख्याएँ (b) दो क्रमागत सम संख्याएँ
(c) दो क्रमागत विषम संख्याएँ
3. अभाज्य गुणनखंडन द्वारा दो सह-अभाज्य संख्याओं 4 और 15 का म.स. इस प्रकार ज्ञात किया गया :
4 = 2 × 2 और 15 = 3 × 5
चूँकि इन गुणनखंडों में कोई अभाज्य सार्व गुणनखंड नहीं है, इसलिए 4 और 15 का म.स. शून्य है। क्या यह उत्तर सही है? यदि नहीं तो सही म.स. क्या है?
3.9 लघुतम समापवर्त्य
4 और 6 के सार्व गुणज क्या हैं? ये 12, 24, 36, ... हैं। इनमें सबसे छोटा गुणज कौन-सा है? यह 12 है। हम कहते हैं कि 4 और 6 का सबसे छोटा (लघुतम) गुणज या लघुतम समापवर्त्य (lowest common multiple) 12 है। यह वह छोटी से छोटी संख्या है जो दोनों का गुणज है। दो या दो से अधिक दी हुई संख्याओं का लघुतम समापवर्त्य इन संख्याओं के सार्व गुणजों में से सबसे छोटा (लघुतम या निम्नतम) गुणज होता है। संक्षेप में, इसे ल.स. (LCM) भी लिखा जाता है। 8 और 12 का ल.स. क्या है? 4 और 9 का ल.स. क्या है? 6 और 9 का ल.स. क्या है?
उदाहरण 8 : 12 और 18 का ल.स. ज्ञात कीजिए।
हल हम जानते हैं कि 12 और 18 के सार्व गुणज 36, 72, 108 इत्यादि हैं। इनमें सबसे छोटा 36 है। आइए, एक और विधि से इसे निकालें:
12 और 18 के अभाज्य गुणनखंडन इस प्रकार हैं :
12 = 2 × 2 × 3 18 = 2 × 3 × 3
इन अभाज्य गुणनखंडनों में, अभाज्य गुणनखंड 2 अधिकतम दो बार आता है (यह 12 के गुणनखंडों में है)। इसी प्रकार अभाज्य गुणनखंड 3 अधिकतम दो बार आता है (यह 18 के गुणनखंडों में है)। दो संख्याओं का ल.स. उन अभाज्य गुणनखंडों का गुणनफल है जो उन संख्याओं में अधिकतम बार आते हैं। अत: इनका ल.स. = 2 × 2 × 3 × 3 = 36 है।
उदाहरण 9 : 24 और 90 का ल.स. ज्ञात कीजिए।
हल : 24 और 90 के अभाज्य गुणनखंडन इस प्रकार हैं:
24 = 2 × 2 × 2 × 3 90 = 2 × 3 × 3 × 5
इन अभाज्य गुणनखंडनों में, अभाज्य गुणनखंड 2 अधिकतम तीन बार आता है (यह 24 में है); अभाज्य गुणनखंड 3 दो बार आता है (यह 90 में है) और अभाज्य गुणनखंड 5 केवल एक बार 90 में आता है।
इसलिए, वांछित ल.स. = (2 × 2 × 2) × (3 × 3) × 5 = 360
उदाहरण 10 : 40, 48 और 45 का ल.स. ज्ञात कीजिए।
हल : 40, 48 और 45 के अभाज्य गुणनखंडन इस प्रकार हैं :
40 = 2 × 2 × 2 × 5
48 = 2 × 2 × 2 × 2 × 3
45 = 3 × 3 × 5
अभाज्य गुणनखंड 2 अधिकतम चार बार (यह 48 में है), अभाज्य गुणनखंड 3 अधिकतम दो बार (यह 45 में है) और अभाज्य गुणनखंड 5 केवल एक बार (यह 40 और 45 दोनों में है) आता है।
अत: वांछित ल.स. = (2 × 2 × 2 × 2) × (3 × 3) × 5 = 720
लघुतम समापवर्त्य (ल.स.) को एक अन्य विधि से भी ज्ञात किया जा सकता है, जो अगले उदाहरण में दर्शाई गई है :
उदाहरण 11 : 20, 25 और 30 का ल.स. ज्ञात कीजिए।
हल : हम संख्याओं को एक पंक्ति में नीचे दर्शाए अनुसार लिखते हैं :
अत:, ल.स. = 2 × 2 × 3 × 5 × 5 = 300
a. (सबसे छोटी अभाज्य संख्या 2 से भाग दीजिए। 25 जैसी संख्या 2 से विभाज्य नहीं है। इसलिए इन्हें अगली पंक्ति में वैसा का वैसा ही रख दिया जाता है)।
b. (पुन: 2 से भाग दीजिए। इसे तब तक जारी रखिए जब तक 2 के गुणज मिलते रहें)।
c. (अगली अभाज्य संख्या 3 से भाग दीजिए)।
d. (अगली अभाज्य संख्या 5 से भाग दीजिए)।
e. (पुन: 5 से भाग दीजिए)।
3.10 म.स. और ल.स. पर कुछ और उदाहरण
हमें अनेक स्थितियों का सामना करना पड़ता है, जहाँ हम म.स. और ल.स. की संकल्पनाओं का प्रयोग करते हैं। हम इन्हें कुछ उदाहरणों की सहायता से समझाएँगे।
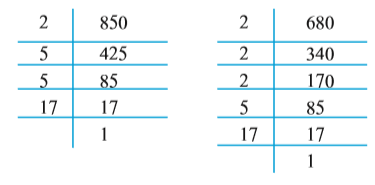
उदाहरण 12 : दो टैंकरों (tankers) में क्रमश: 850 लीटर और 680 लीटर मिट्टी का तेल आता है। उस बर्तन की अधिकतम धारिता (capacity) ज्ञात कीजिए, जो इन दोनों टैंकरों के तेल को पूरा-पूरा माप देगा।
हल : वांछित बर्तन को दोनों टैंकरों के तेल को पूरा-पूरा मापना है। अत: इसकी
धारिता दोनों टैंकरों की धारिताओं का एक पूरा-पूरा विभाजक होगा। साथ ही, इसकी धारिता अधिकतम भी होनी चाहिए। अत: एेसे बर्तन की अधिकतम धारिता 850 और 680 का म.स. होगी। इसे निम्नलिखित प्रकार से ज्ञात किया जाता है :
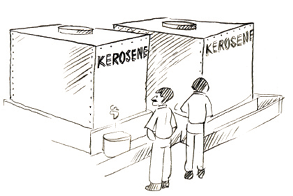
अत:,
850 और 680 के सार्व गुणनखंड 2, 5 और 17 है।
अत:, 850 और 680 का म.स. 2 × 5 × 17 = 170 है।
अत: वांछित बर्तन की अधिकतम धारिता 170 लीटर है। यह पहले बर्तन को 5 बार में और दूसरे को 4 बार में पूरा-पूरा माप देगा।
उदाहरण 13 : प्रात:कालीन सैर में, तीन व्यक्ति एक साथ कदम उठाकर चलना प्रारंभ करते हैं। उनके कदमों की लंबाइयाँ क्रमश: 80 सेमी, 85 सेमी और 90 सेमी हैं। इनमें से प्रत्येक न्यूनतम कितनी दूरी चले कि वे उसे पूरे-पूरे कदमों में
तय करें?
हल : प्रत्येक व्यक्ति द्वारा चली गई दूरी को समान और न्यूनतम रहना है। यह वांछित न्यूनतम दूरी, जो प्रत्येक व्यक्ति को चलनी है, उनके कदमों की मापों का लघुतम समापवर्त्य (ल.स.) होगी। क्या आप बता सकते हैं क्यों?
इसलिए, हम 80, 85 और 90 का ल.स. ज्ञात करते हैं। 80, 85 और 90 का ल.स. 12240 है।
अत: वांछित न्यूनतम दूरी 12240 सेमी है।
उदाहरण 14 : वह सबसे छोटी संख्या ज्ञात कीजिए जिसे 12, 16, 24 और 36 से भाग देने पर प्रत्येक दशा में 7 शेष रहता है।
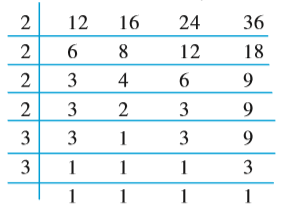
हल : हम 12, 16, 24 और 36 का ल.स. निम्न प्रकार ज्ञात करते हैं :
इस प्रकार, ल.स. = 2 × 2 × 2 × 2 × 3 × 3 = 144
144 वह सबसे छोटी संख्या है जिसे 12, 16, 24 और 36 से भाग देने पर प्रत्येक दशा में 0 शेष रहेगा।
परंतु हमें एेसी सबसे छोटी संख्या चाहिए जिसमें प्रत्येक दशा में 7 शेष रहे। अत: वांछित संख्या 144 से 7 अधिक होगी।
इस प्रकार, वांछित सबसे छोटी संख्या = 144 + 7 = 151 है।
प्रश्नावली 3.7
1. रेणु 75 किग्रा और 69 किग्रा भारों वाली दो खाद की बोरियाँ खरीदती हैं। भार के उस बट्टे का अधिकतम मान ज्ञात कीजिए जो दोनों बोरियों के भारों को पूरा-पूरा माप ले।
2. तीन लड़के एक ही स्थान से एक साथ कदम उठाकर चलना प्रारंभ करते हैं। उनके कदमों की माप क्रमश: 63 सेमी, 70 सेमी और 77 सेमी हैं। इनमें से प्रत्येक कितनी न्यूनतम दूरी तय करे कि वह दूरी पूरे-पूरे कदमों में तय हो जाए?
3. किसी कमरे की लंबाई, चौड़ाई और ऊँचाई क्रमश: 825 सेमी, 675 सेमी और 450 सेमी हैं। एेसा सबसे लंबा फीता (tape) ज्ञात कीजिए जो कमरे की तीनों विमाओं (dimensions) को पूरा-पूरा माप ले।
4. 6,8 और 12 से विभाज्य तीन अंकों की सबसे छोटी संख्या ज्ञात कीजिए।
5. 8,10 और 12 से विभाज्य तीन अंकों की सबसे बड़ी संख्या ज्ञात कीजिए।
6. तीन विभिन्न चौराहों की ट्रैफिक लाइट (traffic lights) क्रमश: प्रत्येक 48 सैकंड, 72 सैकंड और 108 सैकंड बाद बदलती हैं। यदि वे एक साथ प्रात: 7 बजे बदलें, तो वे पुन: एक साथ कब बदलेंगी?
7. तीन टैंकरों में क्रमश: 403 लीटर, 434 लीटर और 465 लीटर डीज़ल है। उस बर्तन की अधिकतम धारिता ज्ञात कीजिए जो इन तीनों टैंकरों के डीज़ल को पूरा-पूरा माप देगा।
8. वह सबसे छोटी संख्या ज्ञात कीजिए जिसे 6, 15 और 18 से भाग देने पर प्रत्येक दशा में 5 शेष रहे।
9. चार अंकों की वह सबसे छोटी संख्या ज्ञात कीजिए जो 18, 24 और 32 से विभाज्य है।
10. निम्नलिखित संख्याओं का ल.स. ज्ञात कीजिए जिनमें एक संख्या सदैव 3 का एक गुणज है।
(a) 9 और 4 (b) 12 और 5
(c) 6 और 5 (d) 15 और 4
प्राप्त ल.स. में एक सामान्य गुण का अवलोकन कीजिए। क्या ल.स. प्रत्येक स्थिति में दोनों संख्याओं का गुणनफल है? क्या हम यह निष्कर्ष निकाल सकते हैं कि दो संख्याओं का ल.स. सदैव 3 का एक गुणज है?
11. निम्नलिखित संख्याओं का ल.स. ज्ञात कीजिए जिनमें एक संख्या दूसरी संख्या का एक गुणनखंड है :
(a) 5, 20 (b) 6, 18
(c) 12, 48 (d) 9, 45
प्राप्त परिणामों में आप क्या देखते हैं?
हमने क्या चर्चा की?
1. गुणजों और गुणनखंडों की पहचान कैसे कर सकते हैं।
2. हमने अब तक चर्चा की और निम्न को खोजा –
(a) एक संख्या का गुणनखंड उस संख्या का पूर्ण विभाजक होता है।
(b) प्रत्येक संख्या स्वयं का एक गुणनखंड होती है। प्रत्येक संख्या का एक गुणनखंड होता है।
(c) दी हुई संख्या का प्रत्येक गुणनखंड उस संख्या से छोटा या उसके बराबर होता है।
(d) प्रत्येक संख्या अपने प्रत्येक गुणनखंडों का एक गुणज होती है।
(e) दी हुई संख्या का प्रत्येक गुणज उस संख्या से बड़ा या उसके बराबर होता है।
(f) प्रत्येक संख्या स्वयं का एक गुणज है।
3. हमने सीखा है –
(a) वह संख्या जिसके दो ही गुणनखंड होते हैं, संख्या स्वयं और 1, अभाज्य संख्या कहलाती है। जिन संख्याओं के दो से अधिक गुणनखंड होते हैं वे संख्याएँ भाज्य संख्याएँ कहलाती हैं।
(b) संख्या 2 सबसे छोटी अभाज्य संख्या है जो एक सम संख्या भी है। अन्य सभी अभाज्य संख्याएँ विषम होती हैं।
(c) दो संख्याएँ जिनका सार्व गुणनखंड केवल 1 हो, सह-अभाज्य संख्याएँ कहलाती हैं।
(d) यदि एक संख्या दूसरी संख्या से विभाज्य है, तो वह दूसरी संख्या के प्रत्येक गुणनखंड से भी विभाजित होगी।
(e) वह संख्या जो दो सह-अभाज्य संख्याओं से विभाज्य होती है, उनके गुणनफल से भी विभाज्य होगी।
4. संख्याओं को बिना भाग की क्रिया किए उनकी छोटी 2, 3, 4, 5, 8, 9 और 11 से विभाज्यता की जाँच कर सकते हैं। हमने संख्या के अंकों का, विभिन्न संख्याओं से विभाज्यता के संबंधों का अन्वेषण किया है।
(a) 2, 5 और 10 से विभाज्यता केवल इकाई अंक को देखकर बताई जा सकती है।
(b) 3 और 9 से विभाज्यता संख्या के अंकों के योग द्वारा की जा सकती है।
(c) 4 से विभाज्यता इकाई और दहाई तथा 8 से विभाज्यता इकाई, दहाई व सैकड़े से बनने वाली संख्या द्वारा जाँची जा सकती है।
(d) 11 से विभाज्यता दाईं ओर से सम स्थानों के अंकों के योग और विषम स्थानों के अंकों के योग के अंतर द्वारा जाँची जा सकती है।
5. यदि दो संख्याएँ एक संख्या से विभाजित होती हैं, तो उन दोनों का योग तथा अंतर भी उस संख्या से विभाजित होता है।
6. (a) दो या अधिक संख्याओं का म.स. (HCF) उसके सार्व गुणनखंडों में से सबसे बड़ा होगा।
(b) दो या अधिक संख्याओं का ल.स. (LCM) उसके सार्व गुणजों में से सबसे छोटा होगा।