Table of Contents
आधारभूत ज्यामिति अवधारणाएँ
4.1 भूमिका
ज्यामिति का एक लंबा और शानदार (बहुमूल्य) इतिहास है। शब्द ‘ज्यामिति’ (Geometry) यूनानी शब्द जिओमीट्रोन (Geometron) का अंग्रेजी तुल्य है। जिया (Geo) का अर्थ है ‘भूमि’ और ‘मीट्रोन (Metron) का अर्थ है ‘मापना’। इतिहासकारों के अनुसार, प्राचीन समय में ज्यामितीय अवधारणाएँ संभवत: कला, वास्तु-कला या शिल्प-कला (Architecture) और भूमि मापन की आवश्यकताओं के कारण विकसित हुईं। इनमें वे अवसर भी सम्मिलित हैं जब खेतिहर की भूमि की परिसीमाओं (boundaries) को बिना किसी शिकायत की संभावना रखते हुए, अंकित किया जाता था। वैभवपूर्ण राजभवनों, मंदिरों, झीलों, बाँधों और नगरों के निर्माणों, कला और वास्तुकला (या शिल्प) ने इन अवधारणाओं को और उजागर किया। आजकल भी कला, मापन, वास्तुकला, इंजीनियरिंग (engineering), कपड़ों के डिज़ाइन इत्यादि के सभी रूपों में ज्यामितीय अवधारणाओं का प्रभाव देखा जा सकता है। आप विभिन्न प्रकार की वस्तुओं, जैसे–बक्स (पेटी), मेज़, पुस्तक, अपने स्कूल में लंच ले जाने के लिए खाने के डिब्बे, गेंद जिससे आप खेलते हैं, आदि को देखते हैं और उनका प्रयोग भी करते हैं। इन सभी वस्तुओं के भिन्न-भिन्न आकार (shapes) होते हैं। जो रूलर (ruler) आप प्रयोग करते हैं और पेंसिल जिससे आप लिखते हैं वे सीधी (straight) हैं। एक चूड़ी, एक रुपये का सिक्का या एक गेंद के चित्र गोल (round) प्रतीत होते हैं।

यहाँ आप कुछ रोचक तथ्यों के बारे में पढ़ेंगे, जो आपके चारों ओर उपस्थित आकारों के बारे में अधिक जानकारी प्राप्त करने में आपकी सहायता करेंगे।
4.2 बिंदु
कागज़ पर एक पेंसिल के नुकीले सिरे से एक चिह्न (dot) अंकित कीजिए। सिरा जितना नुकीला होगा, चिह्न उतना ही सूक्ष्म (छोटा) होगा। लगभग एक बिना दिखाई देने वाला सूक्ष्म चिह्न आपको एक बिंदु की अवधारणा का आभास कराएगा। बिंदु (point) एक स्थिति (या अवस्थिति) (location) निर्धारित करता है।
बिंदु के लिए कुछ उदाहरण इस प्रकार हैं :
यदि आप किसी कागज़ पर, मान लीजिए, तीन बिंदु अंकित करें, तो आपको इनमें भेद बताने की आवश्यकता पड़ेगी। इसके लिए, इन्हें अंग्रेज़ी के बड़े अक्षर A, B, C इत्यादि से व्यक्त किया जाता है।
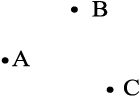 इन बिंदुओं को बिंदु A, बिंदु B और बिंदु C पढ़ा जाता है।
इन बिंदुओं को बिंदु A, बिंदु B और बिंदु C पढ़ा जाता है।
बिंदु नि:संदेह बहुत छोटे होने चाहिए।

1. अपनी पेंसिल के नुकीले सिरे से, एक कागज़ पर चार बिंदु अंकित कीजिए तथा उन्हें नाम A,C,P और H दीजिए। इन बिंदुओं को विभिन्न प्रकारों से नाम दीजिए। नाम देने का एक प्रकार संलग्न आकृति के अनुसार हो सकता है।
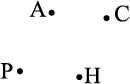
2. आसमान में एक तारा हमें एक बिंदु की अवधारणा का आभास कराता है। अपने दैनिक जीवन से इसी प्रकार की पाँच स्थितियाँ चुनकर दीजिए।
4.3 रेखाखंड
एक कागज़ को मोड़िए और फिर उसे खोल लीजिए। क्या आपको कोई मोड़ का निशान दिखाई देता है? इससे एक रेखाखंड (line segment) की अवधारणा का आभास होता है। इसके दो अंत बिंदु (end points) A और B हैं। एक पतला धागा (या डोरी) लीजिए। इसके दोनों सिरों को कसकर पकड़िए ताकि धागे में कोई ढील न रहे। यह एक रेखाखंड निरूपित करता है। हाथों से पकड़े हुए सिरे इस रेखाखंड के अंत बिंदु हैं।

रेखाखंड के कुछ उदाहरण निम्नलिखित हैं :
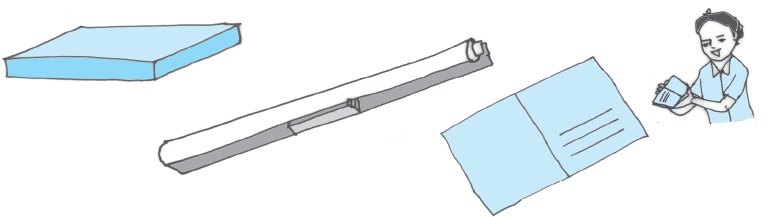
एक बक्स का किनारा एक ट्यूबलाइट एक पोस्टकार्ड का किनारा अपने आस-पास से रेखाखंडों के कुछ और उदाहरण देने का प्रयत्न कीजिए।
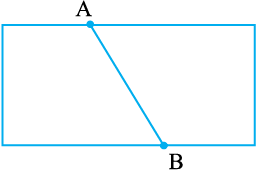
एक कागज़ पर दो बिंदु A और B अंकित कीजिए। इन दोनों बिंदुओं को सभी संभव रास्तों से जोड़ने का प्रयत्न कीजिए (आकृति 4.1)।

आकृति 4.1
A से B तक का सबसे छोटा रास्ता क्या है?
A और B को जोड़ने वाला यह सबसे छोटा रास्ता (इसमें बिंदु A और B भी सम्मिलित हैं), जो संलग्न आकृति 4.1 में दर्शाया गया है, एक रेखाखंड है। इसे 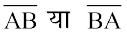 से व्यक्त किया जाता है। बिंदु A और B इस रेखाखंड के अंत बिंदु हैं।
से व्यक्त किया जाता है। बिंदु A और B इस रेखाखंड के अंत बिंदु हैं।

1. संलग्न आकृति में दिए रेखाखंडों के नाम दीजिए (आकृति 4.2)। क्या A प्रत्येक रेखाखंड का एक अंत बिंदु है?
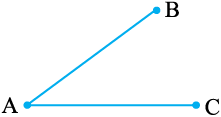
आकृति 4.2
4.4 एक रेखा
कल्पना कीजिए कि A से B तक के रेखाखंड (अर्थात् 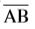
क्या आप सोचते हैं कि आप कागज़ पर पूरी रेखा खींच सकते हैं? नहीं।(क्यों?)

दो बिंदुओं A और B से होकर जाने वाली रेखा को 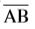
रेखा को निश्चित करने के लिए, दो बिंदु पर्याप्त हैं। हम कहते हैं कि दो बिंदु एक रेखा निर्धारित (determine) करते हैं।
संलग्न आकृति (आकृति 4.3) रेखा 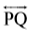

आकृति 4.3
4.5 प्रतिच्छेदी रेखाएँ
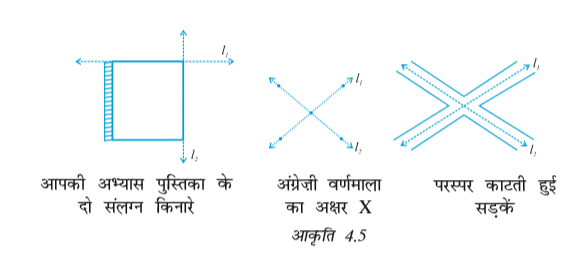
संलग्न आकृति 4.4 को देखिए। इसमें दो रेखाएँ l1 और l2 दर्शाई गई हैं। ये दोनों रेखाएँ बिंदु P से होकर जाती हैं। हम कहते हैं कि रेखाएँ l1 और l2 बिंदु P पर प्रतिच्छेद (intersect) करती हैं। यदि दो रेखाओं में एक उभयनिष्ट बिंदु हो, तो वे प्रतिच्छेदी रेखाएँ (intersecting lines) कहलाती हैं।

आकृति 4.4
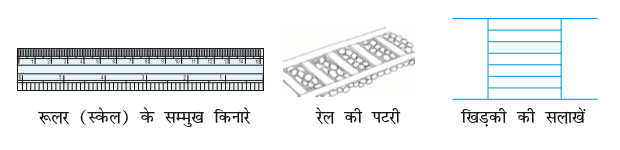
प्रतिच्छेदी रेखाओं के कुछ उदाहरण निम्न हैं :
प्रतिच्छेदी रेखाओं के युग्मों के कुछ और उदाहरण ज्ञात करने का प्रयत्न कीजिए।

एक कागज़ लीजिए। इसे दो बार मोड़िए (और मोड़ के निशान बनाइए) ताकि दो प्रतिच्छेदी रेखाएँ प्राप्त हो जाएँ और चर्चा कीजिए :
(a) क्या दो रेखाएँ एक से अधिक बिंदुओं पर प्रतिच्छेद कर सकती हैं?
(b) क्या दो से अधिक रेखाएँ एक ही बिंदु पर प्रतिच्छेद कर सकती हैं?
4.6 समांतर रेखाएँ
आइए, आकृति 4.6 में दर्शाई गई मेज़ को देखें। इसका ऊपरी सिरा ABCD सपाट (Flat) है। क्या आप कुछ रेखाखंड और बिंदु देख पा रहे हैं? क्या यहाँ प्रतिच्छेदी रेखाएँ हैं?
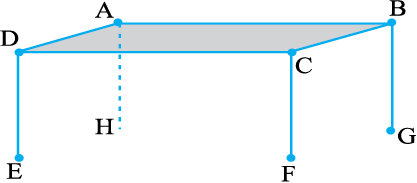
आकृति 4.6
हाँ, 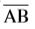
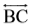
क्या रेखाएँ AD और CD परस्पर प्रतिच्छेद करती हैं?
क्या रेखाएँ AD और BC परस्पर प्रतिच्छेद करती हैं?
आपने देखा कि मेेज़ के ऊपरी पृष्ट पर कुछ रेखाएँ हैं जो परस्पर प्रतिच्छेद नहीं करतीं (उन्हें कितना भी बढ़ाया जाए)। 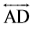
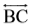
एेसी रेखाएँ (जैसी मेेज़ में ऊपरी सिरे पर हैं) जो प्रतिच्छेद नहीं करतीं समांतर रेखाएँ (parallel lines) कहलाती हैं।
सोचिए, चर्चा कीजिए और लिखिए :
आप समांतर रेखाओं को और कहाँ देखते हैं? इनके 10 उदाहरण ज्ञात करने का प्रयत्न कीजिए।
यदि दो रेखाएँ AB और CD समांतर हों, तो हम इन्हें सांकेतिक रूप में 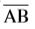
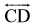
यदि दो रेखाएँ l1 और l2 समांतर हैं, तो हम l1 || l2 लिखते हैं।
क्या आप नीचे दी आकृति में समांतर रेखाएँ बता सकते हैं?
4.7 किरण
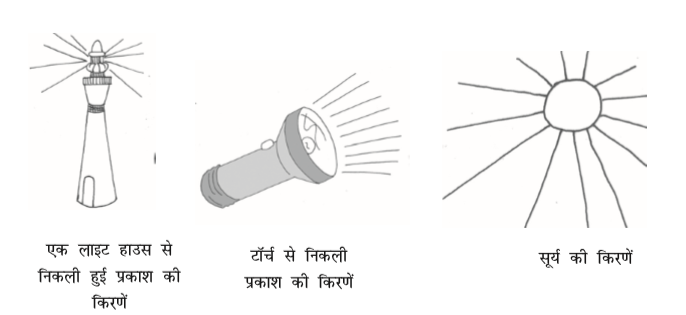
किरण (ray) के लिए कुछ निम्नलिखित मॉडल हैं :
किरण रेखा का एक भाग होता है। यह एक बिंदु से प्रारंभ होती है (जिसे प्रारंभिक बिंदु (initial point) कहते हैं) और एक दिशा में बिना किसी अंत के विस्तृत होती है।
यहाँ दाईं ओर किरण की दी हुई आकृति (आकृति 4.7) को देखिए। इस किरण पर दो बिंदु दर्शाए गए हैं। ये हैं :

आकृति 4.7
(a) A, जो प्रारंभिक बिंदु है।
(b) P, जो किरण पर एक अन्य बिंदु है।
हम इसे 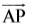
सोचिए, चर्चा कीजिए और लिखिए :
यदि 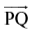
(a) इसका प्रारंभिक बिंदु क्या है?
(b) बिंदु Q किरण पर कहाँ स्थित होता है?
(c) क्या हम कह सकते हैं कि Q इस किरण का प्रारंभिक बिंदु है?

1. सामने दी आकृति (आकृति 4.8) में दर्शाई गई किरणों के नाम लिखिए।
2. क्या T इन सभी किरणों का प्रारंभिक बिंदु है?

संलग्न आकृति 4.9 में, एक किरण OA दी है। यह O से प्रारंभ होती है और A से होकर जाती है। यह किरण बिंदु B से होकर भी जाती है।

आकृति 4.9
क्या आप इसे 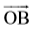
यहाँ 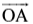
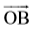
क्या हम किरण 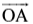
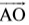
पाँच किरणें खींचिए और उनके उचित नाम लिखिए।
इन किरणों के सिरे पर लगे तीर क्या दर्शाते हैं?
प्रश्नावली 4.1
1. संलग्न आकृति का प्रयोग करके, निम्न के नाम लिखिए :
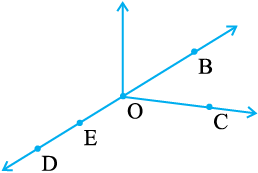
(a) पाँच बिंदु
(b) एक रेखा
(c) चार किरणें
(d) पाँच रेखाखंड
2. संलग्न आकृति में दी हुई रेखा के सभी संभव प्रकारों के नाम लिखिए। आप इन चार बिंदुओं में से किसी भी बिंदु का प्रयोग कर सकते हैं।

3. संलग्न आकृति को देखकर नाम लिखिए :
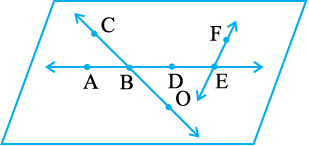
(a) रेखाएँ जिसमें बिंदु E सम्मिलित हैं
(b) A से होकर जाने वाली रेखा
(c) वह रेखा जिस पर O स्थित है
(d) प्रतिच्छेदी रेखाओं के दो युग्म
4. निम्नलिखित से होकर कितनी रेखाएँ खींची जा सकती हैं?
(a) एक बिंदु (b) दो बिंदु
5. निम्नलिखित स्थितियों में से प्रत्येक के लिए एक रफ (Rough) आकृति बनाइए और उचित रूप से उसे नामांकित कीजिए :
(a) बिंदु P रेखाखंड 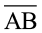 पर स्थित है।
पर स्थित है।
(b) रेखाएँ XY और PQ बिंदु M पर प्रतिच्छेद करती हैं।
(c) रेखा l पर E और F स्थित हैं, परंतु D स्थित नहीं है।
(d) 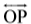
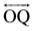
6. रेखा 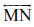

(a) Q, M, O, N और P रेखा 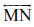
(b) M, O और N रेखाखंड 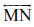
(c) M और N रेखाखंड 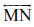
(d) O और N रेखाखंड 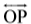
(e) M रेखाखंड 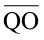 के दोनों अंत बिंदुओं में से एक बिंदु है।
के दोनों अंत बिंदुओं में से एक बिंदु है।
(f) M किरण पर एक बिंदु है।
(g) किरण 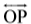
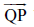
(h) किरण 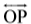
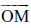
(i) किरण 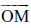
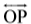
(j) O किरण 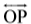
(k) N किरण 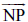
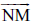
4.8 वक्र
क्या आपने कभी कागज़ पर पेंसिल से टेढ़ी-मेढ़ी रेखाएँ खींची हैं। एेसा करने पर जो आकृतियाँ प्राप्त होती हैं वे वक्र (curves) कहलाते हैं।
इनमें से कुछ आकृतियों (drawing) को आप कागज़ पर बिना पेंसिल उठाए और रूलर का प्रयोग किए बना सकते हैं। ये सभी आकृतियाँ वक्र हैं (आकृति 4.10)।
आम भाज़ा में ‘वक्र’ का अर्थ होता है ‘सीधा नहीं’। गणित में वक्र सीधी भी हो सकती है, जैसा कि ऊपर [(आकृति 4.10 (iv)] में दर्शाया गया है।
ध्यान दीजिए कि आकृति 4.10 में वक्र (iii) और (vii) स्वयं अपने को काट रही हैं, जबकि (i), (ii), (v) और (vi) में वक्र स्वयं को नहीं काटते हैं। यदि कोई वक्र स्वयं को न काटे, तो वह सरल वक्र (Simple Curves) कहलाती हैं।
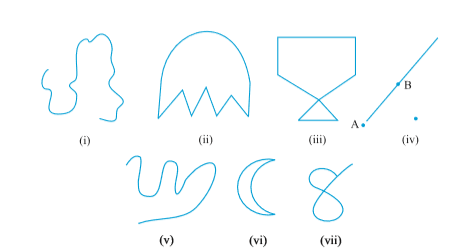
पाँच, सरल वक्र बनाइए और पाँच वक्र बनाइए जो सरल न हों।
अब इन्हें देखें (आकृति 4.11)
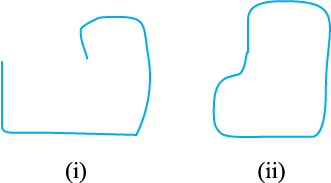
आकृति 4.11
संलग्न आकृति (आकृति 4.11) में दी हुई दोनों वक्रों में क्या अंतर है? पहली, अर्थात् आकृति 4.11 (i) वक्र एक खुली (Open Curve) है, और दूसरी, (अर्थात् आकृति 4.11 (ii) वक्र एक बंद वक्र (Closed Curve) है। क्या आप आकृति 4.10 (i), (ii), (v) और (vi) में, बंद वक्र और खुली वक्र बता सकते हैं?
एक आकृति में स्थितियाँ
एक टेनिस कोर्ट (Tennis Court) में कोर्ट रेखा उसे तीन भागों में बाँटती है। ये भाग हैं : रेखा के एक ओर, रेखा पर और रेखा के दूसरी ओर। आप एक ओर से दूसरी ओर बिना रेखा को पार किए नहीं जा सकते हैं।
आपके घर की परिसीमा (Boundary) घर को सड़क से अलग करती है। आप परिसर के ‘अंदर’, बाड़े की ‘परिसीमा’ और परिसर के ‘बाहर’ की बात करते हैं।
इसी प्रकार, एक बंद वक्र से संबंधित तीन भाग होते हैं, जो एक-दूसरे से पृथक (अलग-अलग) होते हैं।
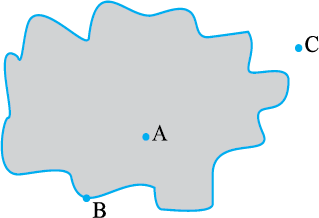
आकृति 4.12
(i) वक्र का अभ्यंतर (interior) (अंदर का भाग)
(ii) वक्र की परिसीमा (boundary) (वक्र पर)
(iii) वक्र का बहिर्भाग (exterior) (बाहर का भाग)
सम्मुख आकृति 4.12 में, A वक्र के अभ्यंतर में है, C उसके बहिर्भाग में है और B स्वयं वक्र की परिसीमा पर स्थित है।
वक्र के अभ्यंतर और उसकी परिसीमा को मिलाकर उस वक्र का क्षेत्र (region) कहा जाता है। जो आपने बंद वक्र खींचा है, उसमें तीन क्षेत्रों को दर्शाया गया है।
4.9 बहुभुज
नीचे दी हुई आकृतियों 4.13 (i), (ii), (iii), (iv) और (v) को देखिए :

आप इनके बारे में क्या कह सकते हैं? क्या ये बंद आकृतियाँ (वक्र) हैं? यह एक दूसरे से किस प्रकार भिन्न हैं? आकृति 4.13 (i), (ii), (iii) और (iv) में कुछ विशेषता हैं। यह केवल रेखाखंडों से ही बनी हैं। एेसी आकृतियाँ बहुभुज (polygons) कहलाती हैं।
अत:, एक आकृति बहुभुज होती है, जब वह एक सरल बंद आकृति हो और केवल रेखाखंडों से ही बनी हो। दस अलग-अलग आकृतियों वाले बहुभुज बनाइए।

निम्न की सहायता से एक बहुभुज बनाने का प्रयत्न कीजिए।
1. माचिस की पाँच तीलियाँ
2. माचिस की चार तीलियाँ
3. माचिस की तीन तीलियाँ
4. माचिस की दो तीलियाँ
उपरोक्त में से किस स्थिति में यह संभव नहीं हुआ? क्यों?
भुजाएँ, शीर्ष और विकर्ण
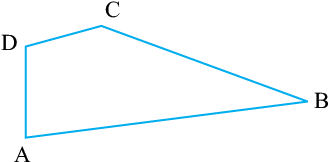
संलग्न आकृति 4.14 को देखिए। इसको बहुभुज कहने के लिए कुछ कारण दीजिए। एक बहुभुज को बनाने वाले रेखाखंड उसकी भुजाएँ (sides) कहलाती हैं।
बहुभुज ABCDE की भुजाओं के नाम क्या हैं?
(ध्यान दीजिए कि कोनों (corners) को किस क्रम में लेकर बहुभुज का नाम लिखा गया है।)
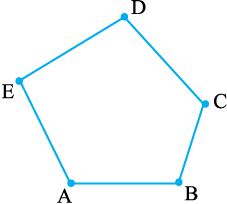
इसकी भुजाएँ 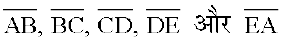 हैं।
हैं।
दो भुजाएँ जहाँ मिलती हैं उस बिंदु को बहुभुज का शीर्ष (vertex) कहते हैं।
भुजाएँ  और
और  बिंदु E पर मिलती हैं, इसलिए E बहुभुज ABCDE का एक शीर्ष है। B और C इसके अन्य दो शीर्ष हैं। क्या आप इन बिंदुओं पर मिलने वाली भुजाओं के नाम लिख सकते हैं?
बिंदु E पर मिलती हैं, इसलिए E बहुभुज ABCDE का एक शीर्ष है। B और C इसके अन्य दो शीर्ष हैं। क्या आप इन बिंदुओं पर मिलने वाली भुजाओं के नाम लिख सकते हैं?
क्या आप उपरोक्त बहुभुज ABCDE के अन्य शीर्षों के नाम लिख सकते हैं?
कोई भी दो भुजाएँ जिनमें एक उभयनिष्ट अंत बिंदु (common end point) हो बहुभुज की आसन्न भुजाएँ (adjacent sides) कहलाती हैं।
क्या AB और BC आसन्न भुजाएँ हैं? AE और DC के बारे में आप क्या कह सकते हैं?
बहुभुज की एक ही भुजा के अंत बिंदु आसन्न शीर्ष (adjacent vertices) कहलाते हैं। शीर्ष E और D आसन्न शीर्ष हैं, जबकि शीर्ष A और D आसन्न शीर्ष नहीं हैं। क्या आप बता सकते हैं कि क्यों?
उन शीर्षों को लीजिए जो आसन्न नहीं हैं। एेसे शीर्षों को मिलाने से बने रेखाखंड बहुभुज के विकर्ण (diagonals) कहलाते हैं।
संलग्न आकृति में, रेखाखंड  ,
,  और
और  बहुभुज के विकर्ण हैं।
बहुभुज के विकर्ण हैं।
क्या रेखाखंड  एक विकर्ण हैं? क्यों या क्यों नहीं?
एक विकर्ण हैं? क्यों या क्यों नहीं?
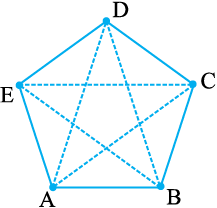
आकृति 4.15
क्या आप आसन्न शीर्षों को जोड़कर विकर्ण प्राप्त कर सकते हैं।
आकृति ABCDE (आकृति 4.15) के सभी भुजाओं, आसन्न भुजाओं और आसन्न शीर्षों के नाम लिखिए।
एक बहुभुज ABCDEFGH बनाइए और उसकी सभी भुजाओं, आसन्न भुजाओं तथा शीर्षों सहित विकर्णों के नाम लिखिए।
प्रश्नावली 4.2
1. नीचे दी हुई वक्रों को (i) खुली या (ii) बंद वक्रों के रूप में वर्गीकृत कीजिए :

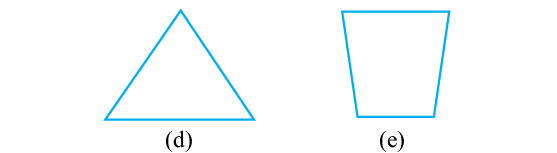
2. निम्न को स्पज़्ट करने के लिए रफ आकृतियाँ बनाइए :
(a) खुला वक्र (b) बंद वक्र
3. कोई भी बहुभुज खींचिए और उसके अभ्यंतर को छायांकित (shade) कीजिए।
4. संलग्न आकृति को देखकर निम्न प्र”नों के उत्तर दीजिए :

(a) क्या यह एक वक्र है?
(b) क्या यह बंद है?
5. रफ आकृतियाँ बनाकर, यदि संभव हो तो निम्न को स्पज़्ट कीजिए:
(a) एक बंद वक्र जो बहुभुज नहीं है।
(b) केवल रेखाखंडों से बनी हुई खुली वक्र
(c) दो भुजाओं वाला एक बहुभुज
4.10 कोण
जब कोने (corner) बनते हैं, तो कोण (angles) भी बनते हैं।
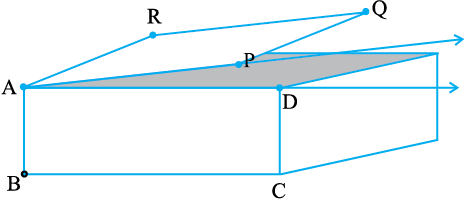
आकृति 4.16
यहाँ एक आकृति 4.16 दी है, जहाँ एक बक्स (Box) का ऊपरी सिरा कब्जा लगे एक दरवाज़े की तरह है। बक्स के किनारे (edge) AD और दरवाज़े के किनारे AP की दो किरणों 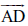
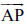
उभयनिष्ट प्रारंभिक बिंदु वाली दो किरणों से एक कोण बनता है।
कोण को बनाने वाली दोनों किरण उसकी भुजाएँ (Arms या sides) कहलाती हैं। उभयनिष्ट प्रारंभिक बिंदु कोण का शीर्ष (vertex) कहलाता है।
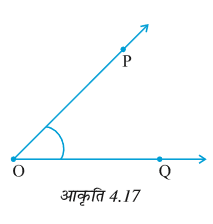
संलग्न आकृति में, किरण 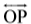
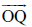
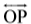
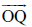
इस कोण को हम किस प्रकार नामांकित कर सकते हैं? इसे हम केवल यह कह सकते हैं कि यह O पर एक कोण है और अधिक विशिज़्टता के लिए, हम कोण की दोनों भुजाओं पर एक-एक बिंदु लेकर और उसके शीर्ष को लेकर कोण का नाम लिख सकते हैं। इस प्रकार, इस कोण को कोण POQ नाम देना एक अच्छा तरीका है। हम इसे ∠POQ से व्यक्त करते हैं।
सोचिए, चर्चा कीजिए और लिखिए :
संलग्न आकृति 4.18 को देखिए। इस कोण का क्या नाम है? क्या हम इसे ∠P कह सकते हैं? परंतु किस कोण को ∠P कहेंगे? ∠P से हमारा क्या तात्पर्य है?
क्या एक कोण को केवल उसके शीर्ष द्वारा नामांकित करना यहाँ सहायक होगा? क्यों नहीं?
∠Pका अर्थ यहाँ ∠APB या ∠ CPB या ∠ APC हो सकता है। इसलिए यहाँ और अधिक सूचना की आवश्यकता है।
ध्यान दीजिए कि कोण को लिखते समय उसके शीर्ष के अक्षर को सदैव बीच में लिखा जाता है।

कोई कोण, मान लीजिए, ∠ABC लीजिए।
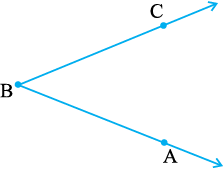
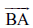
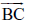

अब 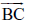
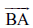

दोनों प्रकार के छायांकित भागों में उभयनिष्ट भाग ∠ABC का अभ्यंतर है (आकृति 4.19)।

आकृति 4.19
(ध्यान दें कि अभ्यंतर एक सीमित क्षेत्र नहीं है। यह अनिश्चित रूप से विस्तृत है, क्योंकि कोणों की दोनाें भुजाएँ अनिश्चित रूप से अपनी-अपनी एक ओर विस्तृत हैं।)
संलग्न आकृति 4.20 में, X कोण के अभ्यंतर में स्थित है। Z कोण के अभ्यंतर में स्थित नहीं है। यह कोण के बहिर्भाग में स्थित है। बिंदु S स्वयं∠ PQR पर स्थित है। अत: कोण से संबंधित भी तीन क्षेत्र होते हैं।
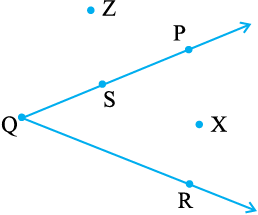
आकृति 4.20
प्रश्नावली 4.3
1. नीचे दी आकृति में, कोणों के नाम लिखिए :
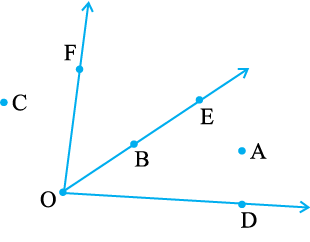
2. संलग्न आकृति में, वे बिंदु लिखिए जो
(a) ∠DOE के अभ्यंतर में स्थित हैं।
(b) ∠EOF के बहिर्भाग में स्थित हैं।
(c) ∠EOF पर स्थित हैं।
3 दो कोणों की रफ आकृतियाँ खींचिए जिससे
(a) उनमें एक बिंदु उभयनिष्ट हो।
(b) उनमें दो बिंदु उभयनिष्ट हों।
(c) उनमें तीन बिंदु उभयनिष्ट हों।
(d) उनमें चार बिंदु उभयनिष्ट हों।
(e) उनमें एक किरण उभयनिष्ट हो।
4.11 त्रिभुज
त्रिभुज (triangle) एक तीन भुजाओं वाला बहुभुज होता है। वास्तव में, यह सबसे कम भुजाओं वाला बहुभुज है।
संलग्न आकृति 4.21 में दिए त्रिभुज को देखिए। हम त्रिभुज ABC के लिए सांकेतिक रूप से ∆ABC लिखते हैं। ∆ABC में कितनी भुजाएँ हैं? इसमें कितने कोण हैं?
आकृति 4.21
इस त्रिभुज की तीन भुजाएँ  ,
,  और
और 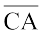 हैं। इसके तीन कोण हैं : ∠ BAC, ∠ BCA और ∠ABC। बिंदु A,B और C इस त्रिभुज के शीर्ष कहलाते हैं।
हैं। इसके तीन कोण हैं : ∠ BAC, ∠ BCA और ∠ABC। बिंदु A,B और C इस त्रिभुज के शीर्ष कहलाते हैं।
एक बहुभुज होने के कारण, एक त्रिभुज का एक बहिर्भाग और एक अभ्यंतर होता है। संलग्न आकृति
4.22 में, P त्रिभुज के अभ्यंतर में स्थित है, R त्रिभुज के बहिर्भाग में स्थित है और Q स्वयं त्रिभुज पर स्थित है।
![]()
आकृति 4.22
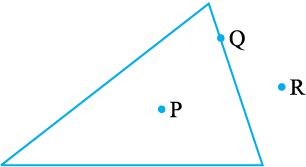
आकृति 4.22
प्रश्नावली 4.4
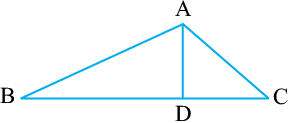
1. त्रिभुज ABC का एक रफ चित्र खींचिए। इस त्रिभुज के अभ्यंतर में एक बिंदु P अंकित कीजिए और उसके बहिर्भाग में एक बिंदु Q अंकित कीजिए। बिंदु A इसके अभ्यंतर में स्थित है या बहिर्भाग में स्थित है?
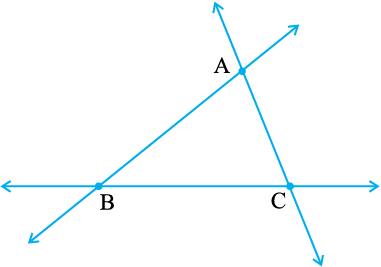
2. (a) संलग्न आकृति में तीन त्रिभुजों की पहचान कीजिए। (b) सात कोणों के नाम लिखिए। (c) इसी आकृति में छ: रेखाखंडों के नाम लिखिए। (d) किन दो त्रिभुजों में ∠B उभयनिष्ट है?
4.12 चतुर्भुज
चार भुजाओं वाला बहुभुज एक चतुर्भुज (Quadrilateral) कहलाता है। इसकी चार भुजाएँ और चार कोण होते हैं। एक त्रिभुज की ही तरह, आप इसके अभ्यंतर को देख सकते हैं।
उस विधि को देखिए जिस क्रम में चतुर्भुज के शीर्षों के नाम लिखे जाते हैं।

चतुर्भुज ABCD (आकृति 4.23) की चार भुजाएँ  ,
,  ,
,  और
और  हैं। इसके चार कोण हैं : ∠A, ∠B, ∠C और ∠D।
हैं। इसके चार कोण हैं : ∠A, ∠B, ∠C और ∠D।
किसी चतुर्भुज ABCD में,  और
और  आसन्न भुजाएँ हैं। क्या आप आसन्न भुजाओं के अन्य युग्म लिख सकते हैं?
आसन्न भुजाएँ हैं। क्या आप आसन्न भुजाओं के अन्य युग्म लिख सकते हैं?
इस चतुर्भुज में,  और
और  सम्मुख भुजाएँ (Opposite sides) हैं। सम्मुख भुजाओं के अन्य युग्म के नाम लिखिए।
सम्मुख भुजाएँ (Opposite sides) हैं। सम्मुख भुजाओं के अन्य युग्म के नाम लिखिए।
∠A और ∠C चतुर्भुज ABCD के सम्मुख कोण (Opposite angles) कहलाते हैं। इसी प्रकार, ∠D और ∠B भी सम्मुख कोण हैं। स्वाभाविक है कि ∠A और ∠B आसन्न कोण (adjacent angles) हैं। अब आप आसन्न कोणों के अन्य युग्म लिख सकते हैं।
प्रश्नावली 4.5
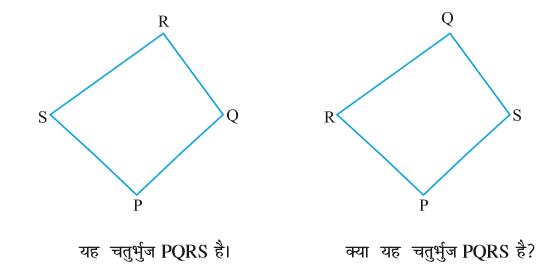
1. चतुर्भुज PQRS का एक रफ चित्र खींचिए। इसके विकर्ण खींचिए। इनके नाम लिखिए। क्या विकर्णों का प्रतिच्छेद बिंदु चतुर्भुज के अभ्यंतर में स्थित है या बहिर्भाग में स्थित है?
2. चतुर्भुज KLMN का एक रफ चित्र खींचिए। बताइए :
(a) सम्मुख भुजाओं के दो युग्म
(b) सम्मुख कोणों के दो युग्म
(c) आसन्न भुजाओं के दो युग्म
(d) आसन्न कोणों के दो युग्म
3. खोज कीजिए :
4.13 वृत्त
आप अपने पर्यावरण में अनेक वस्तुएँ पाएँगे जो गोल होती हैं, जैसे–पहिया, चूड़ी, सिक्का इत्यादि। हम गोल आकृतियों का अनेक प्रकार से प्रयोग करते हैं। एक भारी इस्पात की ट्यूब को खींचने की अपेक्षा लुढ़काना अधिक सरल होता है।
वृत्त (circle) एक सरल बंद वक्र है जो एक बहुभुज नहीं है। इसके कुछ विशिष्ट गुण हैं।

• एक चूड़ी या कोई और गोल वस्तु को कागज़ पर रखिए और उसके चारों ओर पेंसिल घुमाकर एक वृत्ताकार आकृति बनाइए।
• यदि आपको एक वृत्ताकार बाग बनाना हो, तो आप कैसे करेंगे?
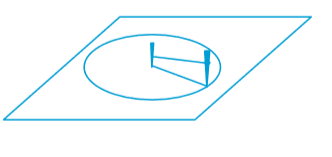
दो डंडी और एक डोरी लीजिए। भूमि पर एक डंडी को गाड़ दीजिए। यह खींचे जाने वाले वृत्त का केन्द्र (centre) है। डोरी के प्रत्येक सिरे पर एक फंदा (loop) बनाकर दो फंदे प्राप्त कीजिए। एक फंदे को केंद्र वाली पहली डंडी में डाल दीजिए और दूसरे फंदे को दूसरी डंडी में डाल दीजिए। इन डंडियों को भूमि के ऊर्ध्वाधर रखिए। डोरी को तनी हुई रखते हुए, भूमि पर दूसरी डंडी को घुमाकर एक पथ बनाइए। आप एक वृत्त (circle) प्राप्त करेंगे।
स्वाभाविक है कि वृत्त पर स्थित प्रत्येक बिंदु केंद्र से बराबर (या समान) दूरी पर है।
वृत्त के भाग
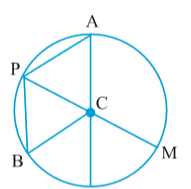
संलग्न आकृति 4.24 में केेंद्र C वाला एक वृत्त है।
A, P, B, M वृत्त पर स्थित कुछ बिंदु हैं। आप
देखेंगे कि CA = CB = CP = CM है।
प्रत्येक रेखाखंड 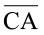 ,
, 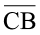 ,
, 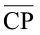 या
या 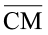 वृत्त की एक त्रिज्या (radius) है। त्रिज्या वह रेखाखंड होता है जो वृत्त पर स्थित बिंदु को उसके केंद्र से जोड़ता है। इसी आकृति में
वृत्त की एक त्रिज्या (radius) है। त्रिज्या वह रेखाखंड होता है जो वृत्त पर स्थित बिंदु को उसके केंद्र से जोड़ता है। इसी आकृति में 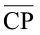 और
और 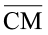 एेसी त्रिज्याएँ हैं कि बिंदु P, C, M एक ही रेखा में हैं। रेखाखंड
एेसी त्रिज्याएँ हैं कि बिंदु P, C, M एक ही रेखा में हैं। रेखाखंड 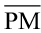 वृत्त का एक व्यास (diameter) कहलाता है। क्या वृत्त का व्यास उसकी त्रिज्या का दोगुना है? हाँ। वृत्त पर स्थित किन्हीं दो बिंदुओं को मिलाने वाला रेखाखंड वृत्त की एक जीवा (chord) कहलाती है।
वृत्त का एक व्यास (diameter) कहलाता है। क्या वृत्त का व्यास उसकी त्रिज्या का दोगुना है? हाँ। वृत्त पर स्थित किन्हीं दो बिंदुओं को मिलाने वाला रेखाखंड वृत्त की एक जीवा (chord) कहलाती है।
चित्र 4.24
इस प्रकार  वृत्त की एक जीवा है। क्या
वृत्त की एक जीवा है। क्या  भी वृत्त की जीवा है?
भी वृत्त की जीवा है?
वृत्त के एक भाग को उसका चाप (arc) कहते हैं।
चित्र 4.25
यदि P और Q वृत्त पर स्थित बिंदु है, तो आपको चाप PQ प्राप्त होगा। हम इसे 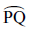
किसी सरल बंद वक्र की ही तरह, आप एक वृत्त के अभ्यंतर और बहिर्भाग के बारे में सोच सकते हैं। वृत्तीय क्षेत्र का वह भाग जो दो त्रिज्याओं और संगत चाप से घिरकर बनता है एक त्रिज्यखंड (sector) कहलाता है। वृत्त की एक जीवा और संगत चाप से घिरा वृत्तीय क्षेत्र का भाग एक वृत्तखंड (segment of a circle) कहलाता है।
कोई भी वृत्ताकार वस्तु लीजिए। एक धागा लीजिए और उसे उस वस्तु के अनुदिश एक बार रखकर धागे की लंबाई को मापिए। धागे की यह लंबाई उस वस्तु के चारों ओर एक चक्कर लगाने में तय की गई दूरी है। यह लंबाई क्या व्यक्त करती है?

चित्र 4.26
वृत्त के अनुदिश चली गई दूरी उसकी परिधि (circumference) कहलाती है।

- एक वृत्ताकार शीट (sheet) लीजिए। इसे मोड़कर दो आधे भाग (halves) बनाइए। दबाकर मोड़ का निशान बनाइए और शीट को खोल लीजिए। क्या आप देखते हैं कि वृत्तीय क्षेत्र उसके व्यास द्वारा दो आधे (बराबर) भागों में विभाजित हो गया है? वृत्त का एक व्यास उसे दो बराबर भागों में विभाजित करता है। प्रत्येक भाग एक अर्धवृत्त (semicircle) कहलाता है।
एक अर्धवृत्त वृत्त का आधा भाग है। जिसमें वृत्त का व्यास (उसके अंत बिंदुओं को छोड़ कर) सम्मिलित नहीं हैं।


प्रश्नावली 4.6
1. संलग्न आकृति देखकर लिखिए :

(a) वृत्त का केंद्र
(b) तीन त्रिज्याएँ
(c) एक व्यास
(d) एक जीवा
(e) अभ्यंतर में दो बिंदु
(f) बहिर्भाग में एक बिंदु
(g) एक त्रिज्यखंड
(h) एक वृत्तखंड
2. (a) क्या वृत्त का प्रत्येक व्यास उसकी एक जीवा भी होता है?
(b) क्या वृत्त की प्रत्येक जीवा उसका एक व्यास भी होती है?
3. कोई वृत्त खींचिए और निम्न को अंकित कीजिए :
(a) उसका केंद्र (b) एक वृत्तखंड
(c) एक त्रिज्या (d) उसके अभ्यंतर में एक बिंदु
(e) एक व्यास (f) उसके बहिर्भाग में एक बिंदु
(g) एक त्रिज्यखंड (h) एक चाप
4. सत्य या असत्य बताइए :
(a) वृत्त के दो व्यास अवश्य ही प्रतिच्छेद करेंगे।
(b) वृत्त का केंद्र सदैव उसके अभ्यंतर में स्थित होता है।
हमने क्या चर्चा की?
1. बिंदु एक स्थिति निर्धारित करता है। इसे सामान्यत: अंग्रेज़ी के बड़े अक्षर से व्यक्त किया जाता है।
2. दो बिंदुओं को जोड़ने वाला सबसे छोटा रास्ता एक रेखाखंड दर्शाता है। बिंदु A और B को मिलाने वाले रेखाखंड को 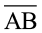 से दर्शाते हैं।
से दर्शाते हैं। 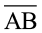 और
और 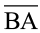 दोनाें एक ही रेखाखंड को दर्शाते हैं।
दोनाें एक ही रेखाखंड को दर्शाते हैं।
3. जब एक रेखाखंड जैसे 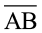 को दोनों तरफ़ बिना किसी अंत के विस्तृत किया जाता है तो हमें एक रेखा प्राप्त होती है। इसे
को दोनों तरफ़ बिना किसी अंत के विस्तृत किया जाता है तो हमें एक रेखा प्राप्त होती है। इसे 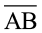 से व्यक्त किया जाता है। इसे कभी-कभी l जैसे अक्षर से भी व्यक्त किया जाता है।
से व्यक्त किया जाता है। इसे कभी-कभी l जैसे अक्षर से भी व्यक्त किया जाता है।
4. दो विभिन्न रेखाएँ जब एक दूसरे को किसी एक बिंदु पर मिलती या काटती हैं तो वे प्रतिच्छेदी रेखाएँ कहलाती हैं।
5. दो रेखाएँ जब एक दूसरे को प्रतिच्छेद नहीं करती अर्थात् नहीं काटती हैं, तो वे समांतर रेखाएँ कहलाती हैं।
6. किरण रेखा का एक भाग होता है जो एक बिंदु से प्रारंभ होकर एक दिशा में बिना किसी अंत के विस्तृत होता है।
7. कागज़ से बिना पेंसिल उठाए कोई भी आकृति (सीधी या टेढ़ी) को एक वक्र कह सकते हैं। इस संदर्भ में एक रेखा भी एक वक्र है।
8. यदि कोई वक्र स्वयं को न काटे तो वह सरल वक्र (Simple Curve) कहलाती है।
9. एक वक्र जिसके सिरे मिले हुए हों, बंद वक्र कहलाती है; अन्यथा उसे खुली वक्र कहते हैं।
10. रेखाखंडों से बनी बंद आकृति एक बहुभुज कहलाती है। यहाँ–
(ii) कोई भी दो भुजाएँ जिनमें एक उभयनिष्ट अंत बिंदु हो, बहुभुज की आसन्न भुजाएँ कहलाती हैं।
(iii) दो भुजाएँ जहाँ मिलती हैं उस बिंदु को बहुभुज का शीर्ष (vertex) कहते हैं।
(iv) बहुभुज की एक ही भुजा के अंत बिंदु आसन्न शीर्ज़ (adjacent verticeे) कहलाते हैं।
(v) एेसे शीर्ष जो आसन्न नहीं हैं को मिलाने से बना रेखाखंड बहुभुज का विकर्ण (diagonal) कहलाता है।
11. उभयनिष्ट प्रारंभिक बिंदु वाली दो किरणों से एक कोण बनता है।
दो किरणें 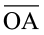 और
और 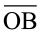 कोण
कोण 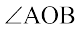 बनाती हैं (इसे
बनाती हैं (इसे 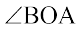 भी लिख सकते हैं)।
भी लिख सकते हैं)।
कोण से संबंधित तीन क्षेत्र हैं :
कोण पर, कोण के अभ्यंतर और कोण के बहिर्भाग।
12. त्रिभुज (Triangle) एक तीन भुजाओं वाला बहुभुज होता है।
13. चार भुजाओं वाला बहुभुज एक चतुर्भुज (Quadrilateral) कहलाता है। इसको शीर्षों के एक क्रम के अनुसार नामांकित करना चाहिए।
किसी चतुर्भुज ABCD में,  और
और  तथा
तथा  और
और  सम्मुख भुजाओं के युग्म हैं। ∠A और ∠C तथा ∠B और ∠D सम्मुख कोणों के युग्म हैं। ∠A और ∠B आसन्न कोण हैं; एेसे ही आसन्न कोणों के तीन अन्य युग्म हैं।
सम्मुख भुजाओं के युग्म हैं। ∠A और ∠C तथा ∠B और ∠D सम्मुख कोणों के युग्म हैं। ∠A और ∠B आसन्न कोण हैं; एेसे ही आसन्न कोणों के तीन अन्य युग्म हैं।
14. एक निश्चित बिंदु से समान दूरी पर चक्कर लगाने से बना बिंदुओं का पथ वृत कहलाता है।
निश्चित बिंदु वृत्त का केंद्र कहलाता है, निश्चित दूरी (समान दूरी) त्रिज्या कहलाती है तथा वृत्त के चारों ओर चली गयी दूरी उसकी परिधि कहलाती है।
वृत्त पर किन्हीं दो बिंदुओं को मिलाने वाला रेखाखंड वृत्त की एक जीवा (chord) कहलाती है।
केंद्र से होकर जाने वाली जीवा वृत का व्यास कहलाती है। वृत्तीय क्षेत्र का वह भाग जो दो त्रिज्याओं और संगत चाप से घिरकर बनता है एक त्रिज्यखंड (sector) कहलाता है। वृत्त की एक जीवा और संगत चाप से घिरा वृत्तीय क्षेत्र का भाग एक वृत्तखंड (segment of a circle) कहलाता है। वृत्त के एक व्यास के दोनों अंत बिंदु उसे दो बराबर भागों में विभाजित करते हैं। प्रत्येक भाग एक अर्धवृत्त (semicircle) कहलाता है।