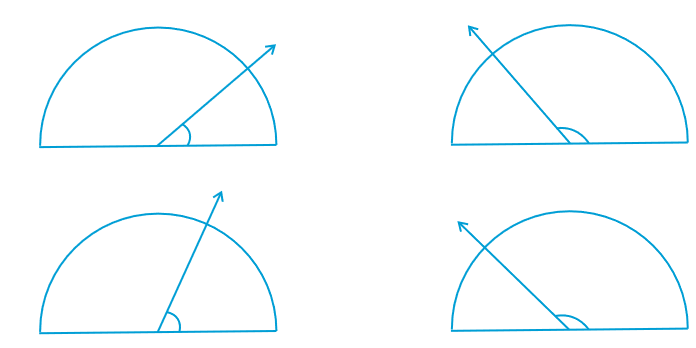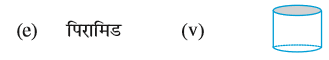Table of Contents
प्रारंभिक आकारों को समझना
5.1 भूमिका
अपने आस-पास हम जो भी आकार (shapes) देखते हैं वे वक्रों या रेखाओं से बने होते हैं। हम अपने परिवेश में कोने, किनारे, तल, खुली वक्र और बंद वक्र देखते हैं। हम इन्हें रेखाखंडों, कोणों, त्रिभुजों, बहुभुजों और वृत्तों में संगठित करते हैं। हम पाते हैं कि ये विभिन्न साइज या मापों के होते हैं। आइए, इनकी मापों की तुलना करने की कुछ
विधियाँ विकसित करें।
5.2 रेखाखंडों का मापना
हमने अनेक बार रेखाखंडों को देखा और खींचा है। एक त्रिभुज तीन रेखाखंडों से बनता है। और एक चतुर्भुज चार रेखाखंडों से बनता है।
एक रेखाखंड (line segment) एक रेखा (line) का एक निश्चित भाग होता है। इससे रेखाखंड को मापना संभव हो जाता है। प्रत्येक रेखाखंड का यह माप (measure) एक अद्वितीय संख्या है, जो उसकी लंबाई (lenghts) कहलाती है। हम इस अवधारणा को रेखाखंडों की तुलना करने में प्रयोग करते हैं।
दो रेखाखंडों की तुलना करने के लिए, हम उनकी लंबाइयों के बीच एक संबंध ज्ञात करते हैं। एेसा अनेक विधियों से किया जा सकता है।
(i) देखकर तुलना

केवल देखकर ही क्या आप बता सकते हैं कि उपरोक्त में से कौन सा रेखाखंड बड़ा है?
आप देख सकते हैं कि रेखाखंड 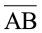 बड़ा है।
बड़ा है।
परंतु आप अपने सामान्य निर्णय के बारे में सदैव निश्चित नहीं हो सकते हैं। उदाहरणार्थ, निम्नलिखित रेखाखंडों को देखिए :

इन दोनों रेखाखंडों की लंबाइयों का अंतर इतना स्पष्ट नहीं है। अत:, हमें तुलना करने की अन्य विधियों की आवश्यकता है।
वास्तव में, संलग्न आकृति में, 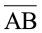 और
और 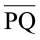 की एक ही लंबाई है। यह इतना स्पष्ट नहीं है।
की एक ही लंबाई है। यह इतना स्पष्ट नहीं है।
इसलिए हमें रेखाखंडों की तुलना करने के लिए और अच्छी विधियों की आवश्यकता है।
(ii) अक्स द्वारा तुलना


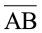 और
और 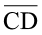 की तुलना करने के लिए, हम एक अक्स कागज़ (tracing paper) का प्रयोग करते हैं। हम अक्स कागज़ पर
की तुलना करने के लिए, हम एक अक्स कागज़ (tracing paper) का प्रयोग करते हैं। हम अक्स कागज़ पर 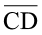 का अक्स खींचते हैं और इस अक्स कागज़ पर बने रेखाखंड को
का अक्स खींचते हैं और इस अक्स कागज़ पर बने रेखाखंड को 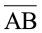 पर रखते हैं।
पर रखते हैं।
क्या अब आप बता सकते हैं कि 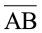 और
और 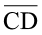 में से कौन बड़ा है?
में से कौन बड़ा है?
यह विधि इस बात पर निर्भर करती है कि हम रेखाखंड का अक्स कितनी शुद्धता से खींचते हैं। इसके अतिरिक्त, यदि आपको किसी और रेखाखंड से तुलना करनी हो, तो उस अन्य रेखाखंड का भी अक्स खींचना पड़ेगा। यह कठिन है, क्योंकि जब रेखाखंडों की तुलना करनी हो, तो आप सदैव रेखाखंड का अक्स ही नहीं खींचते रहेंगे।
(iii) रूलर और डिवाडर द्वारा तुलना
क्या आप अपने ज्यामिति बक्स में रखी वस्तुओं को पहचानते हैं? अन्य वस्तुओं के अतिरिक्त इनमें एक रूलर (ruler) और एक डिवाइडर भी है।

रूलर

डिवाइडर
ध्यान दीजिए कि रूलर पर चिह्न किस प्रकार अंकित हैं। यह 15 बराबर भागों में विभाजित है। प्रत्येक भाग की लंबाई 1 सेमी है।
इनमें से प्रत्येक भाग को आगे और उपविभाजित (sub divide) किया गया है। कैसे? इस प्रकार उपविभाजित प्रत्येक भाग की लंबाई क्या है?
प्रत्येक सेंटीमीटर को दस बराबर भागों मेें उपविभाजित किया गया है। 1 सेमी का प्रत्येक उपविभाजित भाग 1 मिमी है।
कितने मिलीमीटरों से एक सेंटीमीटर बनता है?
1 मिमी 0 .1 सेमी होता है, 2 मिमी 0 .2 सेमी होता है, इत्यादि 2 .3 सेमी का अर्थ होगा 2 सेमी और 3 मिमी
1 सेमी = 10 मिमी होता है तो हम 2 सेमी और 3 मिमी को कैसे लिखेंगे? 7.7 सेमी का क्या अर्थ है?
मान लीजिए रेखाखंड AB की लंबाई मापनी है। रूलर के शून्य चिह्न को A पर रखिए। B के सम्मुख चिह्न को रूलर पर पढ़िए। इससे रेखाखंड 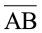 की लंबाई ज्ञात हो जाएगी। मान लीजिए यह लंबाई 5.8 सेमी है। हम इसे लंबाई AB = 5.8 सेमी लिख सकते हैं या केवल AB = 5.8 सेमी लिख सकते हैं।
की लंबाई ज्ञात हो जाएगी। मान लीजिए यह लंबाई 5.8 सेमी है। हम इसे लंबाई AB = 5.8 सेमी लिख सकते हैं या केवल AB = 5.8 सेमी लिख सकते हैं।
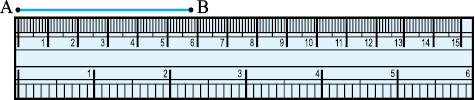
इस प्रक्रिया में भी त्रुटि की संभावना रहती है। रूलर की मोटाई के कारण उस पर अंकित चिह्नों को पढ़ने में कठिनाई हो सकती है।
सोचिए, चर्चा कीजिए और लिखिए
1. अन्य कौन-सी त्रुटियाँ और कठिनाइयाँ हमारे सम्मुख आ सकती हैं?
2. यदि रूलर पर अंकित चिह्नों को ठीक प्रकार से न पढ़ा जाए, तो किस प्रकार की त्रुटियाँ हो सकती हैं? इनसे कैसे बचा जा सकता है?
स्थिति के कारण त्रुटि
सही माप लेने के लिए आँख की स्थिति सही होनी चाहिए। आँख को चिह्न के ठीक ऊपर रखा जाए। अन्यथा तिरछा देखने पर त्रुटि हो सकती है।
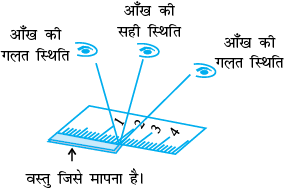
क्या हम इस समस्या से बच सकते हैं? क्या इससे और कोई अच्छी विधि है? आइए, लंबाई मापने के लिए डिवाइडर (divider) का प्रयोग करें।
डिवाइडर को खोलिए। इसकी एक भुजा के अंतबिंदु को A पर रखिए और दूसरी भुजा के अंतबिंदु को B पर रखिए। इस फैलाव में बिना कोई परिवर्तन किए, डिवाइडर को रूलर पर इस प्रकार रखिए कि एक अंतबिंदु रूलर के शून्य चिह्न पर रहे। अब दूसरे अंतबिंदु के सम्मुख चिह्न को पढ़िए। यही रेखाखंड AB की लंबाई है (नीचे दी आकृति देखिए)।
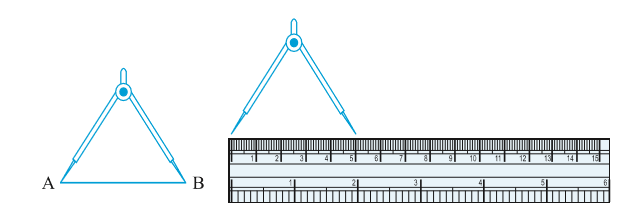

1. एक पोस्टकार्ड लीजिए। उपरोक्त तकनीक का प्रयोग करके, इसकी दो आसन्न भुजाओं को मापिए।
2. कोई तीन वस्तुएँ चुनिए जिनके ऊपरी सिरे सपाट हों। डिवाइडर और रूलर का प्रयोग करते हुए, इन ऊपरी सिरों की सभी भुजाओं को मापिए।
प्रश्नावली 5.1
1. रेखाखंड की तुलना केवल देखकर करने से क्या हानि है?
2. एक रेखाखंड की लंबाई मापने के लिए रूलर की अपेक्षा डिवाइडर का प्रयोग करना क्यों अधिक अच्छा है?
3. कोई रेखाखंड 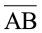 खींचिए। A और B के बीच स्थित कोई बिंदु C लीजिए। AB, BC और CA की लंबाई मापिए। क्या AB = AC + CB है?
खींचिए। A और B के बीच स्थित कोई बिंदु C लीजिए। AB, BC और CA की लंबाई मापिए। क्या AB = AC + CB है?
(टिप्पणी : यदि किसी रेखा पर बिंदु A, B, C इस प्रकार स्थित हों कि AC + CB = AB है, तो निश्चित रूप से बिंदु C बिंदु A और B के बीच स्थित होता है।)
4. एक रेखा पर बिंदु A, B और C इस प्रकार स्थित हैं कि AB = 5 सेमी, BC = 3 सेमी और AC = 8 सेमी है। इनमें से कौन-सा बिंदु अन्य दोनों बिंदुओं के बीच स्थित है?
5. जाँच कीजिए कि संलग्न आकृति में D रेखाखंड 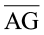 का मध्य-बिंदु है।
का मध्य-बिंदु है।
6. B रेखाखंड 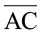 का मध्य-बिंदु है और C रेखाखंड
का मध्य-बिंदु है और C रेखाखंड 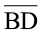 का मध्य बिंदु है, जहाँ A, B, C और D एक ही रेखा पर स्थित हैं। बताइए कि AB = CD क्यों है।
का मध्य बिंदु है, जहाँ A, B, C और D एक ही रेखा पर स्थित हैं। बताइए कि AB = CD क्यों है।
7. पाँच त्रिभुज खींचिए और उनकी भुजाओं को मापिए। प्रत्येक स्थिति में जाँच कीजिए कि किन्हीं दो भुजाओं की लंबाइयों का योग तीसरी भुजा की लंबाई से सदैव बड़ा है।
5.3 कोण–‘समकोण’ और ‘ऋजुकोण’
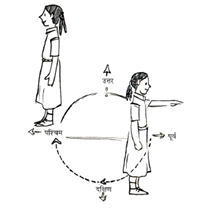
ये हैं : उत्तर (North) (N), दक्षिण (South) (S), पूर्व (East) (E) और पश्चिम (West)(W)।
क्या आप जानते हैं कि उत्तर के विपरीत कौन-सी दिशा है?
पश्चिम के विपरीत कौन-सी दिशा है?

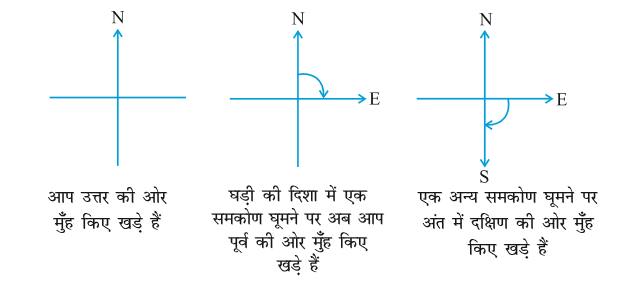
उत्तर की ओर मुँह करके खड़े होइए।
घड़ी की दिशा (दक्षिणावर्त दिशा) (clock-wise) में पूर्व की ओर घूम जाइए।
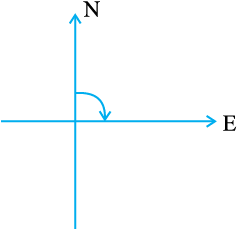
आप एक समकोण (right angle) के बराबर घूम गए हैं। घड़ी की दिशा में एक समकोण और घूमिए। अब आप दक्षिण की ओर मुँह करके खड़े हैं।
यदि आप घड़ी की विपरीत दिशा (वामावर्त दिशा) (anti clock-wise) में एक समकोण घूम जाएँ, तो आपका मुँह किस दिशा में होगा? यह पुन: पूर्व है (क्यों?)
निम्नलिखित स्थितियों को देखिए :
उत्तर की ओर मुँह होने से दक्षिण की ओर मुँह होने तक घूमने में, आप दो समकोण घूम गए हैं। क्या यह दो समकोणों के एक घूर्णन के बराबर नहीं है?
उत्तर से पूर्व तक का घूमना (घूर्णन) एक समकोण के बराबर घूमना है।
उत्तर से दक्षिण तक का घूमना दो समकोणों के बराबर घूमना है।
इसे एक ऋजुकोण (straight angle) कहते हैं। NS एक सीधी रेखा है।
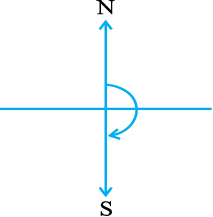
दक्षिण की ओर मुँह करके खड़े होइए।
एक ऋजुकोण के बराबर घूमिए।
अब आप किस दिशा में मुँह किए खड़े हैं?
आप उत्तर दिशा की ओर मुँह किए खड़े हैं।
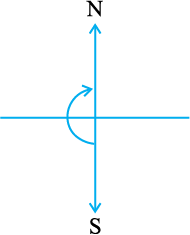
उत्तर से दक्षिण तक घूमने के लिए आप एक ऋजुकोण के बराबर घूमे हैं। पुन: दक्षिण से उत्तर तक आने में आप एक ऋजुकोण के बराबर घूमे हैं। इस प्रकार, दो ऋजुकोणों के बराबर उसी दिशा में घूमने पर आप प्रारंभिक स्थिति में आ जाते हैं।
सोचिए, चर्चा कीजिए और लिखिए :
आप अपनी प्रारंभिक स्थिति तक आने के लिए, एक ही दिशा में कितने समकोण घूमेंगे?
एक ही दिशा में दो ऋजुकोण (या चार समकोण) घूमने पर एक चक्कर पूरा हो जाता है। यह एक पूरा चक्कर एक घूर्णन कहलाता है। एक घूर्णन के लिए कोण एक संपूर्ण कोण (complete angle) कहलाता है।

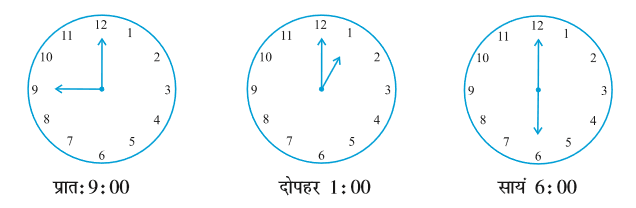
हम इन घूर्णनों (revolutions) को एक घड़ी पर देख सकते हैं। जब घड़ी की एक सुई एक स्थान से अन्य स्थान पर पहुँचती है, तो वह एक कोण (angle) पर घूम जाती है।
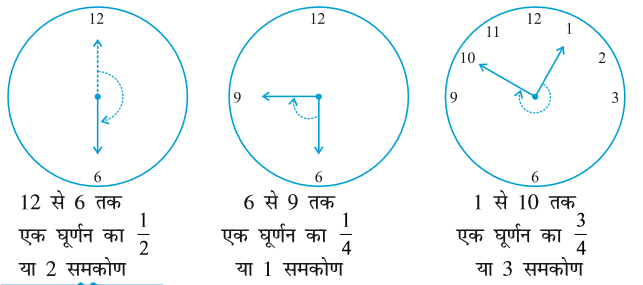
मान लीजिए घड़ी की एक सुई 12 से चलना प्रारंभ करके घूमती हुई 12 पर पुन: पहुँच जाती है। क्या उसने एक घूर्णन पूरा नहीं कर लिया है? अत: उसने कितने समकोण घूम लिए हैं? इन उदाहरणों (आकृतियों) को देखिए :

1. आधे घूर्णन के लिए कोण का नाम क्या है?
2. एक-चौथाई घूर्णन के लिए कोण का नाम क्या है?
3. एक घड़ी पर आधे घूर्णन, एक चौथाई घूर्णन और तीन-चौथाई घूर्णन के लिए पाँच अन्य स्थितियाँ दीजिए।
ध्यान दीजिए कि तीन-चौथाई घूर्णन के लिए कोण का कोई विशेष नाम नहीं है।
प्रश्नावली 5.2
1. घड़ी की घंटे वाली सुई एक घूर्णन के कितनी भिन्न घूम जाती है, जब वह
(a) 3 से 9 तक पहुँचती है? (b) 4 से 7 तक पहुँचती है?
(c) 7 से 10 तक पहुँचती है? (d) 12 से 9 तक पहुँचती है?
(e) 1 से 10 तक पहुँचती है? (f) 6 से 3 तक पहुँचती है?
2. एक घड़ी की सुई कहाँ रुक जाएगी, यदि वह
(a) 12 से प्रारंभ करे और घड़ी की दिशा में 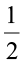 घूर्णन करे?
घूर्णन करे?
(b) 2 से प्रारंभ करे और घड़ी की दिशा में 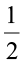 घूर्णन करे?
घूर्णन करे?
(c) 5 से प्रारंभ करे और घड़ी की दिशा में 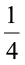 घूर्णन करे?
घूर्णन करे?
(d) 5 से प्रारंभ करे और घड़ी की दिशा में 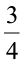 घूर्णन करे?
घूर्णन करे?
3. आप किस दिशा में देख रहे होंगे यदि आप प्रारंभ में
(a) पूर्व की ओर देख रहे हों और घड़ी की दिशा में 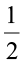 घूर्णन करें?
घूर्णन करें?
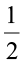 घूर्णन करें?
घूर्णन करें? (c) पश्चिम की ओर देख रहे हों और घड़ी की विपरीत दिशा में 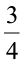 घूर्णन करें?
घूर्णन करें?
(d) दक्षिण की ओर देख रहे हों और एक घूर्णन करें?
(क्या इस अंतिम प्रश्न के लिए, हमें घड़ी की दिशा या घड़ी की विपरीत दिशा की बात करनी चाहिए? क्यों नहीं?
4. आप एक घूर्णन का कितना भाग घूम जाएँगे, यदि आप
(a) पूर्व की ओर मुख किए खड़े हों और घड़ी की दिशा में घूमकर उत्तर की ओर मुख कर लें?
(b) दक्षिण की ओर मुख किए खड़े हों और घड़ी की दिशा में घूमकर पूर्व की ओर मुख कर लें?
(c) पश्चिम की ओर मुख किए खड़े हों और घड़ी की दिशा में घूमकर पूर्व की ओर मुख कर लें?
5. घड़ी की घंटे की सुई द्वारा घूमे गए समकोणों की संख्या ज्ञात कीजिए, जब वह
(a) 3 से 6 तक पहुँचती है। (b) 2 से 8 तक पहुँचती है।
(c) 5 से 11 तक पहुँचती है। (d) 10 से 1 तक पहुँचती है।
(e) 12 से 9 तक पहुँचती है। (f) 12 से 6 तक पहुँचती है।
6. आप कितने समकोण घूम जाएँगे, यदि आप प्रारंभ में
(a) दक्षिण की ओर देख रहे हों और घड़ी की दिशा में पश्चिम की ओर घूम जाएँ?
(b) उत्तर की ओर देख रहे हों और घड़ी की विपरीत (वामावर्त) दिशा में पूर्व की ओर घूम जाएँ?
(c) पश्चिम की ओर देख रहे हों और पश्चिम की ओर घूम जाएँ?
(d) दक्षिण की ओर देख रहे हों और उत्तर की ओर घूम जाएँ?
7. घड़ी की घंटे वाली सुई कहाँ रुकेगी, यदि वह प्रारंभ करे
(a) 6 से और 1 समकोण घूम जाए?
(b) 8 से और 2 समकोण घूम जाए?
(c) 10 से और 3 समकोण घूम जाए?
(d) 7 से और 2 ऋजुकोण घूम जाए?
5.4 कोण–‘न्यून’, ‘अधिक’ और ‘प्रतिवर्ती’
हमने देखा कि एक समकोण और एक ऋजुकोण का क्या अर्थ है। परंतु जो कोण हमें देखने को मिलते हैं वे सदैव इन दोनों प्रकारों के ही नहीं होते हैं। एक सीढ़ी द्वारा दीवार से (या फर्श से) बनाया गया कोण न तो समकोण है और न ही ऋजुकोण है।
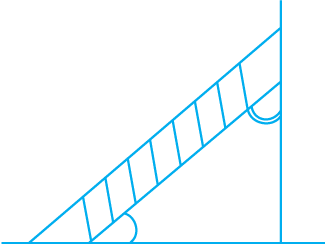
सोचिए, चर्चा कीजिए और लिखिए
क्या कुछ एेसे कोण हैं जो समकोण से छोटे हैं?
क्या कुछ एेसे कोण हैं जो समकोण से बड़े हैं?
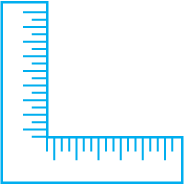
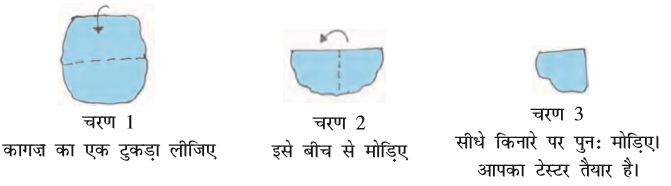
क्या आपने बढ़ई का वर्ग देखा है? यह अंग्रेज़ी वर्णमाला के अक्षर ‘L’ जैसा होता है। वह इससे समकोणों की जाँच करता है। आइए, हम भी समकोणों की जाँच के लिए इसी प्रकार के ‘टेस्टर’ (tester) को बनाएँ।

अपने द्वारा ‘बनाए गए’ समकोण टेस्टर को देखिए (क्या हम इसे RA टेस्टर कहें?) क्या इसका एक किनारा दूसरे पर सीधा खड़ा है?
मान लीजिए कोनों वाला कोई आकार दिया हुआ है। आप इसके कोनों पर बने कोणों की जाँच RA टेस्टर द्वारा कर सकते हैं।
क्या इसके किनारे एक कागज़ के कोणों से दिखाई देते हैं? यदि हाँ, तो यह एक समकोण दर्शाता है।

1. घड़ी की घंटे वाली सुई 12 से 5 तक चलती है। क्या इसका घूर्णन 1 समकोण से अधिक है?

2. घड़ी पर यह कोण कैसा दिखता है? घड़ी की घंटे वाली सुई 5 से 7 तक चलती है। क्या इस सुई द्वारा घूमा गया कोण 1 समकोण से अधिक है?

3. घड़ी पर सुइयों की स्थिति निम्न प्रकार बनाकर कोणों की जाँच RA टेस्टर द्वारा कीजिए।
(a) 12 से 2 तक जाना
(b) 6 से 7 तक जाना
(c) 4 से 8 तक जाना
(d) 2 से 5 तक जाना
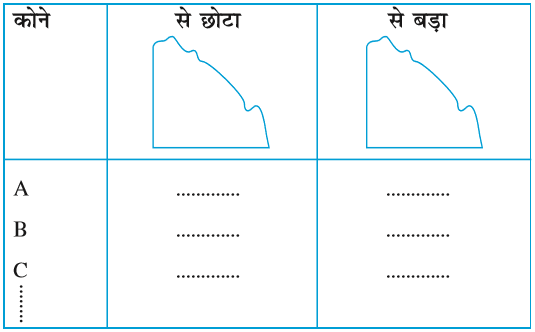
4. कोने वाले पाँच भिन्न-भिन्न आकार लीजिए। कोनों के नाम लिखिए। अपने टेस्टर द्वारा इन कोणों की जाँच कीजिए और प्रत्येक स्थिति के परिणाम को एक सारणी के रूप में निम्न प्रकार लिखिए :
अन्य नाम
- समकोण से छोटा कोण न्यूनकोण (acute augle) कहलाता है। ये कोण न्यून कोण हैं :
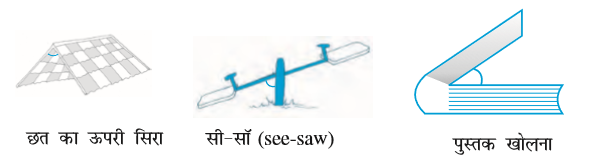
क्या आप देख रहे हैं कि इनमें से प्रत्येक एक घूर्णन के एक-चौथाई से छोटा है? अपने RA टेस्टर से इनकी जाँच कीजिए।
- यदि कोई कोण एक समकोण से बड़ा और एक ऋजुकोण से छोटा है, तो वह एक अधिक कोण (obtuse angle) कहलाता है।
ये कोण अधिक कोण हैं :
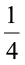 घूर्णन से अधिक है और
घूर्णन से अधिक है और 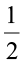 घूर्णन से कम है? इसकी जाँच करने में आपका RA टेस्टर सहायता कर सकता है।
घूर्णन से कम है? इसकी जाँच करने में आपका RA टेस्टर सहायता कर सकता है।पिछले उदाहरणों में भी अधिक कोणों की पहचान कीजिए।
- एक प्रतिवर्ती कोण (reflex angle) एक ऋजुकोण से बड़ा होता है और एक संपूर्ण कोण से छोटा होता है। यह इस आकृति में दर्शाए प्रकार का होता है (घड़ी पर कोण को देखिए)। आपने जो इससे पहले आकृृतियाँ बनाई थीं, क्या उनमें प्रतिवर्ती कोण बने थे? आप इनकी जाँच किस प्रकार करेंगे?
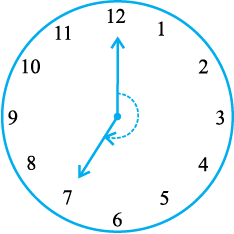

1. आप अपने आस-पास देखिए और कोनों पर मिलने वाले किनारों को पहचानिए, जो कोण बना रहे हों। एेसी दस स्थितियाँ लिखिए।
2. एेसी दस स्थितियाँ लिखिए, जहाँ न्यूनकोण बन रहे हों।
3. एेसी दस स्थितियाँ लिखिए, जहाँ समकोण बन रहे हों।
4. एेसी पाँच स्थितियाँ लिखिए, जहाँ अधिक कोण बन रहे हों।
5. एेसी पाँच स्थितियाँ लिखिए, जहाँ प्रतिवर्ती कोण बन रहे हों।
प्रश्नावली 5.3
1. निम्न को सुमेलित (match) कीजिए :
(i) ऋजुकोण (a) 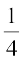 घूर्णन से कम
घूर्णन से कम
(ii) समकोण (b) 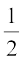 घूर्णन से अधिक
घूर्णन से अधिक
(iii) न्यून कोण (c) 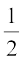 घूर्णन
घूर्णन
(iv) अधिक कोण (d) 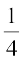 घूर्णन
घूर्णन
(v) प्रतिवर्ती कोण (e) 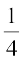 घूर्णन और
घूर्णन और 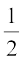 घूर्णन के बीच में
घूर्णन के बीच में
(f) एक पूरा या संपूर्ण घूर्णन
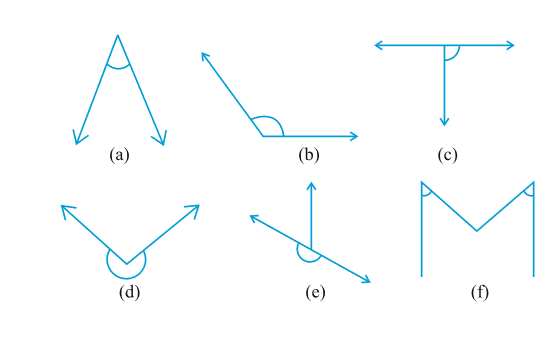
2. निम्न में से प्रत्येक कोण को समकोण, ऋजुकोण, न्यूनकोण, अधिक कोण या प्रतिवर्ती कोण के रूप में वर्गीकृत कीजिए :
5.5 कोणों का मापन
अपने बनाए गए ‘RA टेस्टर’ की सहायता से, हमने कोणों की समकोण से तुलना की। इससे हम कोणों को न्यून कोण, अधिक कोण और प्रतिवर्ती कोणों में वर्गीकृत करने में भी समर्थ हो गए थे।
परंतु इससे कोणों की परिशुद्धता की तुलना नहीं हो पाती है। इससे यह पता नहीं लगता कि दिए हुए दो अधिक कोणों में कौन बड़ा है। इसलिए, कोणों की तुलना अधिक परिशुद्धता से करने के लिए यह आवश्यक है कि उन्हें ‘माप’ लिया जाए। एेसा हम एक चाँदे (protractor) की सहायता से कर सकते हैं।
कोण का माप
हम अपनी इस माप को डिगरी माप (अंश माप) (degree measure) कहते हैं। एक संपूर्ण घूर्णन को 360 बराबर भागों में विभाजित किया जाता है। प्रत्येक भाग एक अंश (degree) कहलाता है। हम तीन सौ साठ अंश कहने के लिए 360o लिखते हैं।
सोचिए, चर्चा कीजिए और लिखिए
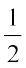 घूर्णन में कितनी डिगरी हैं? 1 समकोण में कितनी डिगरी हैं?
घूर्णन में कितनी डिगरी हैं? 1 समकोण में कितनी डिगरी हैं?
1 ऋजुकोण में कितनी डिगरी (अंश) हैं? कितने समकोणों से 180o बनते हैं? कितने समकोणों से 360o बनते हैं?

1. एक चूड़ी की सहायता से एक वृत्ताकार आकृति बनाइए या इसी मान की एक वृत्ताकार शीट लीजिए।

2. इसे दो बार मोड़िए जिससे दर्शाई गई आकृति प्राप्त हो। इसे एक चतुर्थांश (quadrant) कहते हैं।

3. इसे खोल लीजिए। आपको एक अर्धवृत्त प्राप्त होगा। जिसके बीच में एक मोड़ का निशान है।
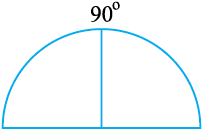
4. इस वृत्त को मोड़कर चतुर्थांश बना लीजिए। इस चतुर्थांश को एक बार पुन: मोड़कर दर्शाई हुई आकृति प्राप्त कीजिए। अब कोण 90º का आधा, अर्थात् 45º है।
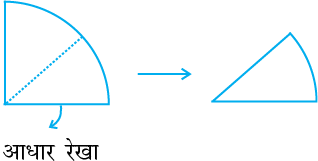
5. अब इसे खोल लीजिए। दोनों ओर एक-एक मोड़ का निशान दिखाई दे रहा है। आधार रेखा की बाईं ओर वाले पहले मोड़ के निशान पर 45º लिखिए।
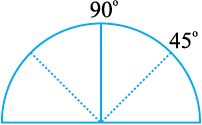
6. दूसरी ओर वाले मोड़ के निशान पर 90º + 45º = 135º लिखा जाएगा।
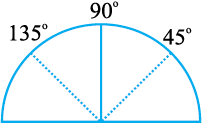
7. कागज़ को अब 45º तक (चतुर्थांश के आधे) मोड़िए। अब इसका आधा कीजिए। आधार रेखा के बाईं ओर वाला पहला मोड़ का निशान 45º का आधा, अर्थात् 22½º दर्शाएगा। 135º के बाईं ओर का कोण 157½º है।
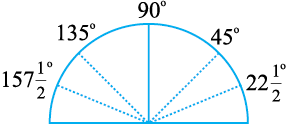
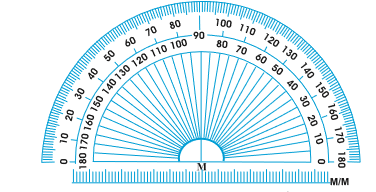
चाँदा
आपके ज्यामिति बक्स में आपको चाँदा बना बनाया मिल जाएगा। इसके वक्रीय किनारे (edge) को 180 बराबर भागों में विभाजित किया गया है। प्रत्येक भाग एक अंश (डिगरी) (degree) कहलाता है। इस पर चिह्न दाईं या बाईं ओर से प्रारंभ करके क्रमश: बाईं या दाईं ओर तक 0º से 180º तक लगे होते हैं।
मान लीजिए आप कोई कोण ABC को मापना चाहते हैं।

2. चाँदे को इस प्रकार समायोजित कीजिए कि किरण BC इस सीधे किनारे के अनुदिश रहे।
3. चाँदे पर दो ‘स्केल’ (scale) हैं : वह स्केल पढ़िए जिससे किरण BC चिह्न 0º से मिल रही है।
4. वक्रीय किनारे पर किरण AB द्वारा दर्शित चिह्न कोण का अंशीय माप (degree measure) ज्ञात कराता है।
आकृति में यह 40º है।
हम इसे m ∠ABC = 40º या केवल ∠ABC = 40º लिखते हैं।
प्रश्नावली 5.4
1. निम्न के क्या माप हैं :
(i) एक समकोण? (ii) एक ऋजुकोण?
2. बताइए सत्य (T) या असत्य (F) :
(a) एक न्यून कोण का माप < 90º है।
(b) एक अधिक कोण का माप < 90º है।
(c) एक प्रतिवर्ती कोण का माप >180º है।
(d) एक संपूर्ण घूर्णन का माप = 360º है।
(e) यदि m∠a = 53º और m < B = 35º है, तो m ∠ A > m ∠ B है।
3. निम्न के माप लिखिए :
(a) कुछ न्यून कोण
(b) कुछ अधिक कोण
(प्रत्येक के दो उदाहरण दीजिए।)
4. निम्न कोणों को चाँदे से मापिए और उनके माप लिखिए :
5. किस कोण का माप बड़ा है?
∠ABC दिया है ∠ABC का मापना
पहले आकलन (estimate) कीजिए और फिर मापिए।
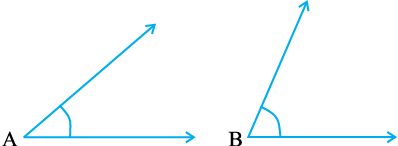
कोण A का माप =
कोण B का माप =
6. निम्न दो कोणों में से किस कोण का माप बड़ा है? पहले आकलन कीजिए और फिर मापन द्वारा पुष्टि कीजिए।
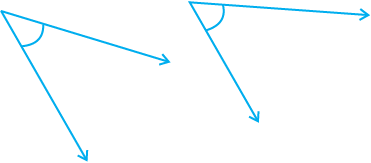
7. न्यून कोण, अधिक कोण, समकोण या ऋजुकोण से रिक्त स्थानों को भरिए :
(a) वह कोण, जिसका माप एक समकोण के माप से कम है, ........................ होता है।
(b) वह कोण, जिसका माप एक समकोण के माप से अधिक हो, ................... होता है।
(c) वह कोण जिसका माप दो समकोणों के योग के बराबर है .................... होता है।
(d) यदि दो कोणों के मापों का योग समकोण के माप के बराबर है, तो प्रत्येक कोण ............. होता है।
(e) यदि दो कोणों के मापों का योग एक ऋजुकोण के माप के बराबर है, और इनमें से एक कोण न्यून कोण है, तो दूसरा कोण .................... होना चाहिए।
8. नीचे दी आकृति में दिए प्रत्येक कोण का माप ज्ञात कीजिए (पहले देखकर आकलन कीजिए और फिर चाँदे से मापिए। ) :
9. नीचे दी प्रत्येक आकृति में घड़ी की सुइयों के बीच के कोण का माप ज्ञात कीजिए :
10. खोज कीजिए :
दी हुई आकृति में चाँदा 30º दर्शा रहा है। इसी आकृति को एक आवर्धन शीशे (magnifying glass) द्वारा देखिए। क्या यह कोण बड़ा हो जाता है?
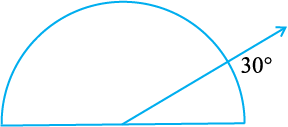
क्या कोण का माप बड़ा हो जाता है?
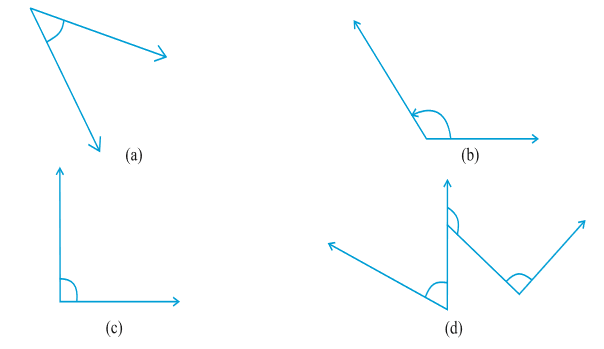
11. मापिए और प्रत्येक कोण को वर्गीकृत कीजिए :
5.6 लंब रेखाएँ
यदि दो रेखाएँ परस्पर प्रतिच्छेद करें और उनके बीच का कोण एक समकोण हो, तो वे रेखाएँ एक दूसरे पर लंब (perpendicular) रेखाएँ कहलाती हैं। यदि एक रेखा AB रेखा CD पर लंब है, तो इसे AB 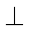 CD लिखते हैं।
CD लिखते हैं।
सोचिए, चर्चा कीजिए और लिखिए
यदि AB 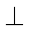 CD है, तो हमें क्या यह भी कहना चाहिए कि CD
CD है, तो हमें क्या यह भी कहना चाहिए कि CD 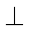 AB है?
AB है?
हमारे आस-पास लंब रेखाएँ!
आप अपने आस-पास की वस्तुओं में से लंब रेखाओं (या रेखाखंडों) के अनेक उदाहरण दे सकते हैं। अंग्रेज़ी वर्णमाला का अक्षर T इनमें से एक है। क्या कोई और अक्षर भी है, जो लंबों का उदाहरण है?
एक पोस्टकार्ड को लीजिए। क्या इसके किनारे परस्पर लंब हैं? मान लीजिए। MN बिंदु M से होकर जाने वाली रेखाखंड AB पर कोई रेखा लंब है। क्या रेखा MN रेखाखंड AB को दो बराबर भागों में विभाजित करती हैं?
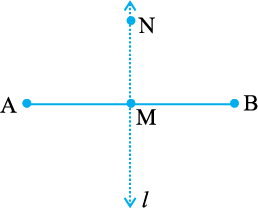
क्या MN रेखाखंड AB पर लंब है?
इस प्रकार, MN रेखाखंड AB को समद्विभाजित करती है (अर्थात् दो बराबर भागों में विभाजित करती है) और उस पर लंब भी है।
इसलिए, हम कहते हैं कि रेखा MN रेखाखंड AB का लंब समद्विभाजक (perpendicular bisector) है।
इसकी रचना करना आप बाद में सीखेंगे।
प्रश्नावली 5.5
1. निम्नलिखित में से कौन लंब रेखाओं के उदाहरण हैं?
(a) मेज़ के ऊपरी सिरे की आसन्न भुजाएँ
(b) रेल पथ की पटरियाँ
(c) अक्षर L बनाने वाले रेखाखंड
(d) अक्षर V बनाने वाले रेखाखंड
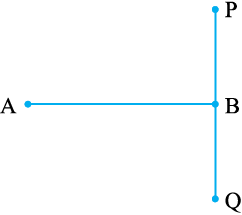
2. मान लीजिए रेखाखंड PQ रेखाखंड XY पर लंब है। मान लीजिए ये परस्पर बिंदु A पर प्रतिच्छेद करते हैं।∠PAY की माप क्या है?
3. आपके ज्यामिति बक्स में दो सेट स्क्वेयर हैं। इनके कोनों पर बने कोणों के माप क्या हैं? क्या इनमें कोई एेसी माप है जो दोनों में उभयनिष्ठ है?
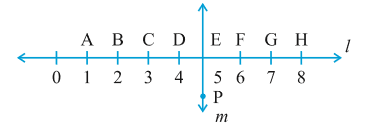
4. इस आकृति को ध्यान से देखिए। रेखा l रेखा m पर लंब है।
(a) क्या CE = EG है?
(b) क्या रेखा PE रेखाखंड CG को समद्विभाजित करती है?
(c) कोई दो रेखाखंडों के नाम लिखिए जिनके लिए PE लंब समद्विभाजक है।
(d) क्या निम्नलिखित सत्य हैं?
(i) AC > FG
(ii) CD = GH
(iii) BC < EH
5.7 त्रिभुजों का वर्गीकरण
क्या आपको सबसे कम भुजाओं वाले बहुभुज के बारे में याद है? यह एक त्रिभुज (triangle) है। आइए, विभिन्न प्रकार के जो त्रिभुज हो सकते हैं, उन्हें देखें।

आइए, नीचे दिए हुए त्रिभुजों के कोणों और भुजाओं को क्रमश: चाँदे और रूलर से मापें। दी हुई सारणी में इनकी मापों को भरिए :
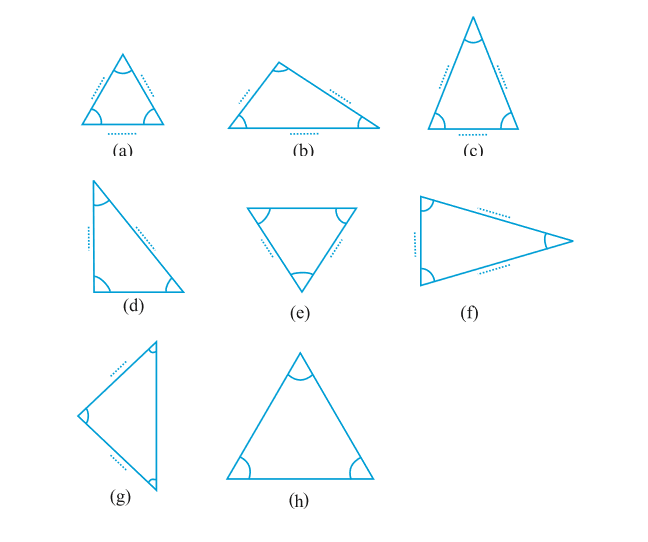
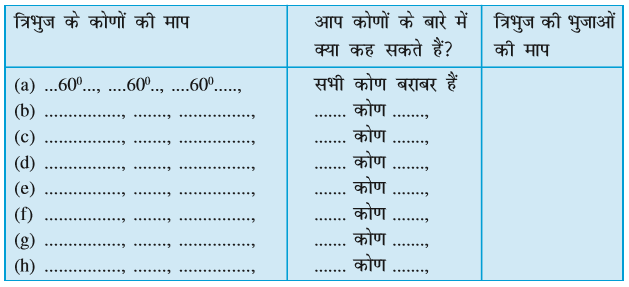
उपरोक्त कोण, त्रिभुज और उनकी भुजाओं की मापों को ध्यानपूर्वक देखिए। क्या इनके बारे में कोई बात कही जा सकती है?
आप क्या प्राप्त करते हैं?
- त्रिभुज जिनके सभी कोण बराबर हैं।
यदि किसी त्रिभुज के सभी कोण बराबर हैं, तो इसकी भुजाएँ भी ............. हैं।
- त्रिभुज जिनमें सभी भुजाएँ बराबर हैं।
यदि एक त्रिभुज की सभी भुजाएँ बराबर हैं, तो उसके कोण भी ............. हैं।
- त्रिभुज जिनमें दो कोण बराबर हैं और दो भुजाएँ बराबर हैं। यदि किसी त्रिभुज की दो भुजाएँ बराबर हैं, तो उसके .............कोण बराबर होते हैं।
- त्रिभुज जिनमें कोई भी दो भुजाएँ बराबर नहीं हैं। यदि किसी त्रिभुज के कोई भी दो कोण बराबर नहीं हैं, तो उसकी कोई भी दो भुजाएँ बराबर नहीं होती हैं। यदि किसी त्रिभुज की तीनों भुजाएँ बराबर नहीं हैं, तो उसके तीनों कोण भी ............. नहीं हैं।
कुछ और त्रिभुज लीजिए और उपरोक्त कथनों की जाँच कीजिए। इसके लिए, हमें त्रिभुजों के कोण और उनकी भुजाओं को पुन: मापना पड़ेगा।
त्रिभुजों को विभिन्न श्रेणियों में वर्गीकृत किया गया है और उन्हें विशेष नाम दिए गए हैं। आइए, देखें कि ये क्या हैं।
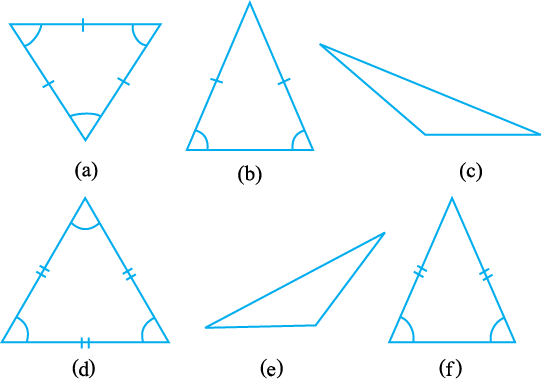
भुजाओं के आधार पर त्रिभुजों का नामकरण
एक त्रिभुज जिसकी तीनों भुजाएँ बराबर नहीं हों, विषमबाहु त्रिभुज (Scalene triangle) कहलाता [(c), (e)] है। एक त्रिभुज जिसकी दो भुजाएँ बराबर हों, एक समद्विबाहु त्रिभुज (Isosceles triangle) कहलाता [(b), (f)] है।
त्रिभुज जिसकी तीनों भुजाएँ बराबर हों, समबाहु त्रिभुज (Equilateral triangle) कहलाता है। [(a), (d)] इन परिभाषाओं का प्रयोग करके उन सभी त्रिभुजों का वर्गीकरण कीजिए, जिनकी भुजाएँ आप पहले माप चुके हैं।
कोणों के आधार पर त्रिभुजों का नामकरण
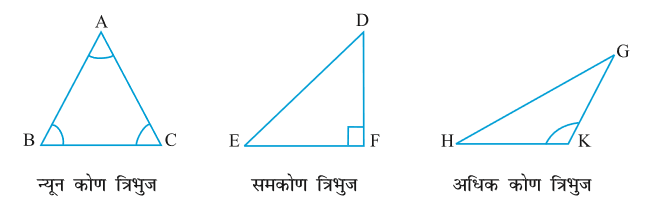
यदि त्रिभुज का प्रत्येक कोण 90o से कम हो, तो वह एक न्यूनकोण त्रिभुज (acute angled triangle) कहलाता है। यदि इसका कोई कोण समकोण हो, तो वह त्रिभुज एक समकोण त्रिभुज (right angled triangle) कहलाता है। यदि इसका कोई कोण 90o से अधिक हो, तो वह त्रिभुज एक अधिक कोण त्रिभुज (obtuse angled triangle) कहलाता है।
उपरोक्त परिभाषाओं के अनुसार, उन त्रिभुजों का वर्गीकरण कीजिए जिनके कोण आप पहले माप चुके हैं। इनमें से कितने समकोण त्रिभुज थे?

निम्न के रफ चित्र खींचने का प्रयत्न कीजिए :
(a) एक विषमबाहु न्यूनकोण त्रिभुज
(b) एक अधिक कोण समद्विबाहु त्रिभुज
(c) एक समकोण समद्विबाहु त्रिभुज
(d) एक विषमबाहु समकोण त्रिभुज
क्या आप सोचते हैं कि निम्न आकृति खींचना संभव है :
(e) एक अधिक कोण समबाहु त्रिभुज?
(f) एक समकोण समबाहु त्रिभुज?
(g) एक त्रिभुज जिसमें दो समकोण हों?
सोचिए, चर्चा कीजिए और फिर अपने निष्कर्षों को लिखिए।
प्रश्नावली 5.6
1. निम्नलिखित त्रिभुजों के प्रकार लिखिए :
(a) त्रिभुज जिसकी भुजाएँ 7 सेमी, 8 सेमी और 9 सेमी हैं।
(b) △ABC जिसमें AB = 8.7 सेमी, AC = 7 सेमी और BC = 6 सेमी है।
(c) △PQR जिसमें PQ = QR = RP = 5 सेमी है।
(d) △DEF जिसमें m ∠D = 90º है।
(e) △XYZ जिसमें m ∠Y = 90o और XY = YZ है।
(f) △LMN जिसमें m ∠ L = 30o, m ∠M = 70º और m ∠N = 80o है।
2. निम्न का सुमेलन कीजिए :
त्रिभुज के माप त्रिभुज का प्रकार
(i) समान लंबाई की तीन भुजाएँ (a) विषमबाहु समकोण त्रिभुज
(ii) समान लंबाई की दो भुजाएँ (b) समद्विबाहु समकोण त्रिभुज
(iii) अलग-अलग लंबाइयों की सभी भुजाएँ (c) अधिक कोण त्रिभुज
(iv) 3 न्यूनकोण (d) समकोण त्रिभुज
(v) 1 समकोण (e) समबाहु त्रिभुज
(vi) 1 अधिक कोण (f) न्यून कोण त्रिभुज
(vii) दो बराबर लंबाइयों की भुजाओं (g) समद्विबाहु त्रिभुज
के साथ 1 समकोण
3. निम्नलिखित त्रिभुजों में से प्रत्येक का दो प्रकार से नामकरण कीजिए (आप कोण का प्रकार केवल देखकर ज्ञात कर सकते हैं।)
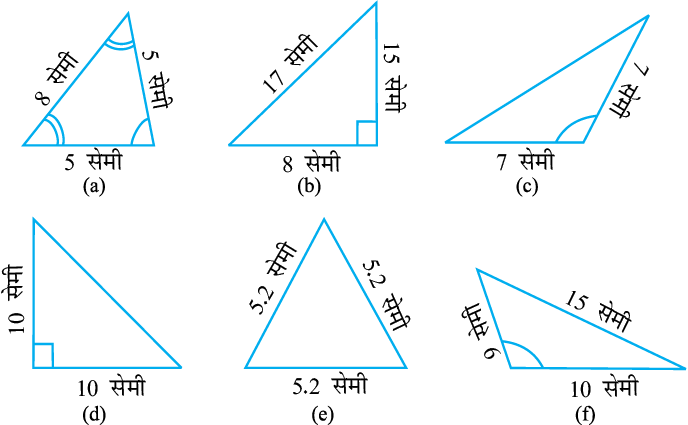
4. माचिस की तीलियों की सहायता से त्रिभुज बनाने का प्रयत्न कीजिए। इनमें से कुछ आकृति में दिखाए गए हैं। क्या आप निम्न से त्रिभुज बना सकते हैं?
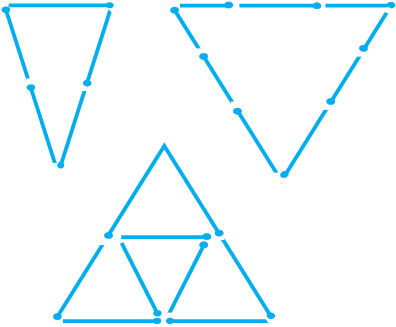
(a) 3 माचिस की तीलियाँ
(b) 4 माचिस की तीलियाँ
(c) 5 माचिस की तीलियाँ
(d) 6 माचिस की तीलियाँ
(ध्यान रखिए कि आपको प्रत्येक स्थिति में सभी उपलब्ध माचिस की तीलियों का उपयोग करना है)।
प्रत्येक स्थिति मेें त्रिभुज के प्रकार का नाम बताइए। यदि आप त्रिभुज नहीं बना पाते हैं, तो उसके कारण के बारे में सोचिए।
5.8 चतुर्भुज
आपको याद होगा कि चार भुजाओं का बहुभुज एक चतुर्भुज (quadrilateral) कहलाता है।

1. दो डंडी लीजिए और उन्हें इस प्रकार रखिए कि उनका एक-एक सिरा एक सिरे पर मिले। अब डंडियों के एक अन्य युग्म को इस प्रकार रखिए कि उनके सिरे डंडियों के पहले युग्म के स्वतंत्र सिरों से जुड़ जाएँ। इस प्रकार हमें क्या आकृति प्राप्त होती है?
यह एक चतुर्भुज है, जो आप सामने देख रहे हैं। इस चतुर्भुज की भुजाएँ 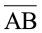 ,
, 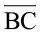 , ___, ___ हैं।
, ___, ___ हैं।
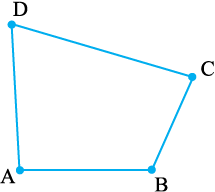
इस चतुर्भुज के चार कोण हैं। ये ∠BAD, ∠ADC, ∠DCB, और _____ हैं।
 इसका एक विकर्ण है। अन्य विकर्ण कौन सा है? सभी भुजाओं और विकर्णों की लंबाइयाँ मापिए। सभी कोणों को भी मापिए।
इसका एक विकर्ण है। अन्य विकर्ण कौन सा है? सभी भुजाओं और विकर्णों की लंबाइयाँ मापिए। सभी कोणों को भी मापिए।
2. जैसा आपने ऊपर क्रियाकलाप किया है, चार डंडियाँ लेकर देखिए कि क्या आप इनसे एेसा चतुर्भुज बना सकते हैं जिसमें
(a) चारों कोण न्यून कोण हैं।
(b) एक कोण अधिक कोण है।
(c) एक कोण समकोण है।
(d) दो कोण अधिक कोण हैं।
(e) दो कोण समकोण हैं।
(f) विकर्ण परस्पर समकोण पर हैं।
आयत

आपके ज्यामिति बक्स में दो सेट स्क्वेयर हैं। एक 30º–60º–90º सेट स्क्वेयर है और दूसरा 45º–45º–90º सेट स्क्वेयर।
आप और आपका मित्र मिलकर इस क्रिया को कर सकते हैं :
(a) आप दोनों के पास एक-एक 30º–60º–90º सेट स्क्वेयर है। इनको आकृति में दर्शाए अनुसार रखिए। क्या आप इस प्रकार बने चतुर्भुज का नाम बता सकते हैं? इसके प्रत्येक कोण का माप क्या है?
यह चतुर्भुज एक आयत (rectangle) है।
आयत का एक और गुण जो आप स्पष्ट रूप से यहाँ देख सकते हैं कि इसकी सम्मुख भुजाएँ बराबर होती हैं।
आप अन्य कौन से गुण ज्ञात कर सकते हैं?

(b) यदि अन्य सेट स्क्वेयर 45º–45º–90º के युग्म का प्रयोग करें, तो आपको एक अन्य चतुर्भुज प्राप्त होगा। यह एक वर्ग (square) है।
क्या आप देख सकते हैं कि सभी भुजाओं की लंबाइयाँ बराबर हैं? आप इसके कोणों और विकर्णों के बारे में क्या कह सकते हैं? वर्ग के कुछ अन्य गुण ज्ञात करने का प्रयत्न कीजिए।

(c) यदि आप 30º–60º–90º सेट स्क्वेयरों को आकृति में दर्शाए अनुसार एक अन्य स्थिति में रखें, तो आपको एक समांतर चतुर्भुज (parallelograms) प्राप्त होता है। क्या आप देख रहे हैं कि इसकी सम्मुख भुजाएँ समांतर हैं? क्या इसकी सम्मुख भुजाएँ बराबर हैं?
क्या इसके विकर्ण बराबर हैं?

(d) यदि आप चार 30o–60o–90o सेट स्क्वेयरों का प्रयोग करें, तो आपको एक समचतुर्भुज (rhombus) प्राप्त होता है।
(e) यदि आप आकृति में दर्शाए अनुसार कई सेट स्क्वेयरों का प्रयोग करें, तो हमें एक एेसा चतुर्भुज प्राप्त होगा जिसकी दो सम्मुख भुजाओं का एक युग्म समांतर है।
यह एक समलंब (trapezium) है।

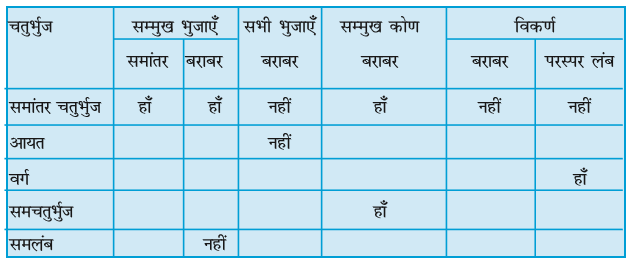
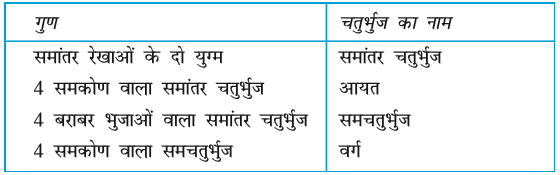
यहाँ आपकी खोजों के सारांश की एक रूपरेखा दी जा रही है। इसे पूरा कीजिए।
प्रश्नावली 5.7
1 . सत्य (T) या असत्य (F) कहिए :
(b) आयत की सम्मुख भुजाओं की लंबाई बराबर होती है।
(c) वर्ग के विकर्ण एक दूसरे पर लंब होते हैं।
(d) समचतुर्भुज की सभी भुजाएँ बराबर लंबाई की होती हैं।
(e) समांतर चतुर्भुज की सभी भुजाएँ बराबर लंबाई की होती हैं।
(f) समलंब की सम्मुख भुजाएँ समांतर होती हैं।
2 . निम्नलिखित के लिए कारण दीजिए :
(a) वर्ग को एक विशेष प्रकार का आयत समझा जा सकता है।
(b) आयत को एक विशेष प्रकार का समांतर चतुर्भुज समझा जा सकता है।
(c) वर्ग को एक विशेष प्रकार का समचतुर्भुज समझा जा सकता है।
(d) वर्ग, आयत, समचतुर्भुज और समांतर चतुर्भुज में से प्रत्येक एक चतुर्भुज भी है।
(e) वर्ग एक समांतर चतुर्भुज भी है।
3 . एक बहुभुज सम (regular) होता है, यदि उसकी सभी भुजाएँ बराबर हों और सभी कोण बराबर हों। क्या आप एक सम चतुर्भुज (regular quadrilateral) की पहचान कर सकते हैं?
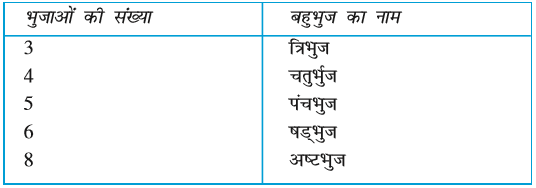
5.9 बहुभुज
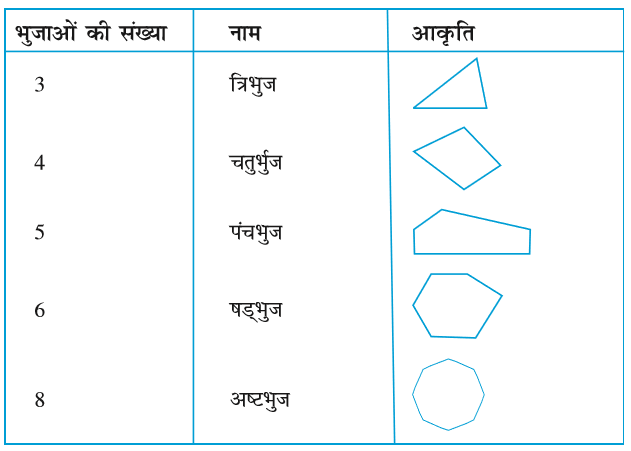
अभी तक आपने 3 और 4 भुजाओं वाले बहुभुजों (polygons) का अध्ययन किया है। जिन्हें क्रमश: त्रिभुज और चतुर्भुज कहते हैं। अब हम बहुभुजों की अवधारणा को एेसी आकृतियों के रूप में विस्तृत करने का प्रयत्न करेंगे, जिनमें चार से अधिक भुजाएँ होंगी। हम बहुभुजों को उनकी भुजाओं की संख्याओें के आधार पर निम्न प्रकार वर्गीकृत कर सकते हैं :
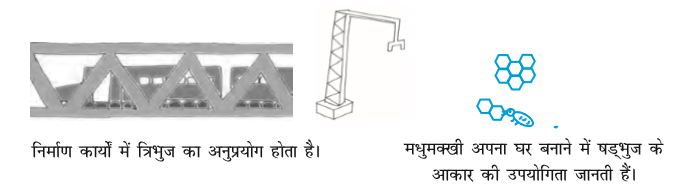
आप इस प्रकार के आकार (shapes) अपने दैनिक जीवन में देखते हैं। खिड़कियाँ, दरवाज़े, दीवार, अलमारियाँ, ब्लैकबोर्ड, अभ्यास-पुस्तिकाएँ आदि सभी आयत के आकार के होते हैं। फर्श की टाइल भी आयताकार होती हैं। त्रिभुज की दृढ़ता वाली प्रकृति के कारण इस आकार का इंजीनियरिंग निर्माणों में लाभप्रद रूप से प्रयोग किया जाता है।
अपने परिवेश में देखिए कि आप इन आकारों को कहाँ-कहाँ पा सकते हैं।
प्रश्नावली 5.8
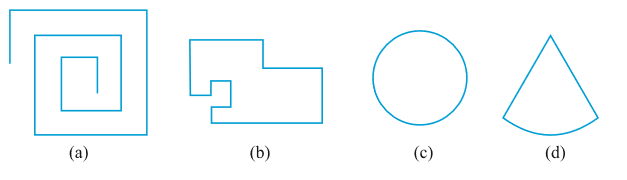
1 . जाँच कीजिए कि निम्न में से कौन-सी आकृतियाँ बहुभुज हैं। यदि इनमें से कोई बहुभुज नहीं है, तो कारण बताइए।
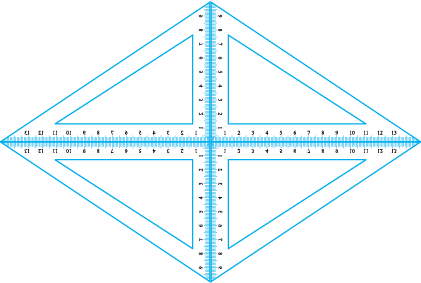
2 . प्रत्येक बहुभुज का नाम लिखिए :
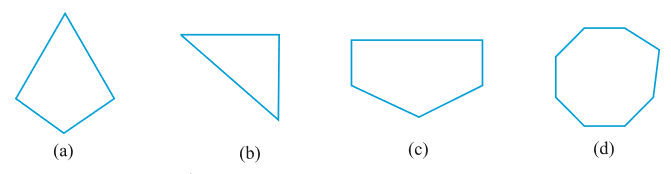
इनमें से प्रत्येक के दो और उदाहरण बनाइए।
3 . एक सम षड्भुज (reguler hexagon) का एक रफ़ चित्र खींचिए। उसके किन्हीं तीन शीर्षों को जोड़कर एक त्रिभुज बनाइए। पहचानिए कि आपने किस प्रकार का त्रिभुज खींच लिया है।
4 . एक सम अष्टभुज (reguler octagon) का रफ़ चित्र खींचिए। [यदि आप चाहें, तो वर्गांकित कागज़ (squared paper) का प्रयोग कर सकते हैं।] इस अष्टभुज के ठीक चार शीर्षों को जोड़कर एक आयत खींचिए।
5 . किसी बहुभुज का विकर्ण उसके किन्हीं दो शीर्षों (आसन्न शीर्षों को छोड़कर) को जोड़ने से प्राप्त होता है (यह इसकी भुजाएँ नहीं होती हैं)। एक पंचभुज का एक रफ़ चित्र खींचिए और उसके विकर्ण खींचिए।
5.10 त्रिविमीय आकार
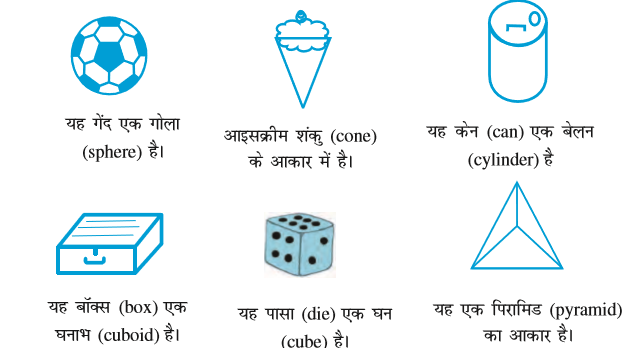
यहाँ कुछ आकार (shapes) दिए जा रहे हैं, जिन्हें आप अपने दैनिक जीवन में देखते हैं। प्रत्येक आकार एक ठोस (solid) है। यह एक ‘सपाट (flat)’ आकार नहीं है।
किन्हीं पाँच वस्तुओं के नाम बताइए जो एक गोले से मिलती-जुलती हों।
किन्हीं एेसी पाँच वस्तुआें के नाम बताइए जो एक शंकु से मिलती-जुलती हों।
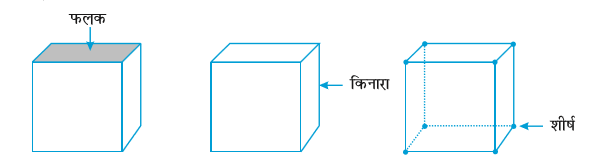
फलक, किनारे और शीर्ष
अनेक त्रिविमीय आकारों (three dimensional shapes) में हम उनके फलकाें, किनारों और शीर्षों की सरलता से पहचान कर सकते हैं। इन तीन पदों, अर्थात् फलक, किनारे और शीर्ष से हमारा क्या तात्पर्य है?
उदाहरण के लिए, एक घन (cube) को लीजिए।
घन का प्रत्येक ऊपरी सपाट (वर्गाकार) पृष्ठ एक फलक है। इसके दो फलक एक रेखाखंड में मिलते हैं, जो घन का एक किनारा कहलाता है। तीन किनारे एक बिंदु पर मिलते हैं, जो घन का शीर्ष कहलाता है।

सामने एक प्रिज़्म (prism) का चित्र दिया है। क्या आपने इसे अपनी प्रयोगशाला में देखा है? इसके दो फलक त्रिभुज के आकार के हैं। इसलिए यह प्रिज्म एक त्रिभुजाकार प्रिज़्म (triangulur prism) कहलाता है।
यह त्रिभुजाकार फलक इसका आधार (base) भी कहलाता है। इस प्रिज़्म के दो सर्वसम (identical) त्रिभुजाकार फलक हैं। एक आधार और दूसरा ऊपरी (top) सिरा कहलाता है। इन दोनाें फलकों के अतिरिक्त अन्य फलक समांतर चतुर्भुज हैं।
यदि प्रिज़्म का आधार आयताकार हो, तो यह प्रिज़्म एक आयताकार (rectangular) प्रिज़्म कहलाता है। आयताकार प्रिज़्म के लिए क्या आपको याद है कि एक अन्य नाम क्या है?
एक पिरामिड वह आकार है जिसमें आधार का फलक किसी भी बहुभुज के आकार का हो सकता है और शेष फलक त्रिभुजाकार होते हैं।
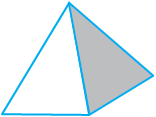

सामने की आकृति में एक वर्ग पिरामिड (square pyramid) का चित्र दिखाया गया है। इसका आधार एक वर्ग है। क्या आप एक त्रिभुजाकार पिरामिड की कल्पना कर सकते हैं? इसका एक रफ़ चित्र बनाने का प्रयत्न कीजिए।
बेलन, शंकु और गोले में कोई सीधा किनारा (straight edge) नहीं होता है। शंकु का आधार क्या है? क्या यह एक वृत्त है? बेलन का आधार भी एक वृत्त है। बेलन का ऊपरी सिरा आधार जैसा एक सर्वसम वृत्त है। नि:संदेह, गोले का कोई फलक नहीं है। इसके बारे में सोचिए !

1. एक घनाभ एक आयताकार बक्स जैसा है। इसके 6 फलक हैं। प्रत्येक फलक के चार किनारे हैं। प्रत्येक फलक के चार कोने हैं (जो इसके शीर्ष कहलाते हैं)।

2. एक घन एेसा घनाभ होता है, जिसके सभी किनारे बराबर लंबाई के होते हैं।

इसके ______ फलक हैं।
प्रत्येक फलक के ______ किनारे हैं।
प्रत्येक फलक के ______ शीर्ष हैं।
3. एक त्रिभुजाकार पिरामिड का आधार एक त्रिभुज होता है। यह चतुष्फलक (tetrahedron) भी कहलाता है।

फलक : ______
किनारे : ______
कोने : ______
4. एक वर्ग पिरामिड का आधार एक वर्ग होता है।
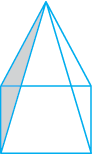
फलक : ______
किनारे : ______
कोने : ______
5. एक त्रिभुजाकार प्रिज़्म प्राय: एक केलाइडोस्कोप (Kaleidoscope) के आकार का होता है। इसका आधार और ऊपरी सिरा त्रिभुज के आकार के होते हैं।
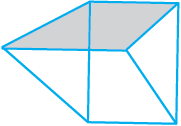
फलक : ______
किनारे : ______
कोने : ______
प्रश्नावली 5.9
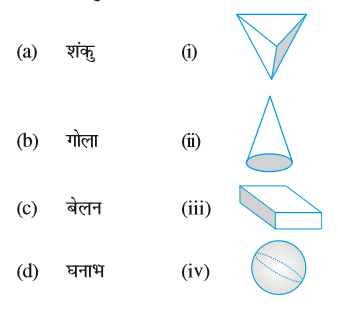
1. निम्न का सुमेलन कीजिए :
इन आकारों में से प्रत्येक के दो और उदाहरण दीजिए।
2. निम्न किस आकार के हैं?
(a) आपका ज्यामिति बक्स
(b) एक ईंट
(c) एक माचिस की डिब्बी
(d) सड़क बनाने वाला रोलर (roller)
(e) एक लड्डू
हमने क्या चर्चा की?
1. एक रेखाखंड के दोनों अंत:बिंदुओं के बीच की दूरी उसकी लंबाई कहलाती है।
2. रेखाखंडों की तुलना करने के लिए एक अंशांकिक रूलर और एक डिवाइडर उपयोगी होते हैं।
3. जब घड़ी की एक सुई एक स्थान से दूसरे स्थान पर जाती है, तो हमें कोण का एक उदाहरण प्राप्त होता है।
सुई का एक पूरा चक्कर 1 घूर्णन कहलाता है।
समकोण 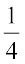 घूर्णन है और ऋजुकोण
घूर्णन है और ऋजुकोण 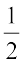 घूर्णन है। कोणों को अंशों (degrees) में मापने के लिए हम चाँदे का प्रयोग करते हैं।
घूर्णन है। कोणों को अंशों (degrees) में मापने के लिए हम चाँदे का प्रयोग करते हैं।
समकोण की माप 90o और ऋजुकोण की माप 180o होती है। एक कोण जिसकी माप समकोण से कम हो, न्यून कोण कहलाता है और जिसकी माप समकोण से अधिक और ऋजुकोण से कम हो अधिक कोण कहलाता है।
एक प्रतिवर्ती कोण ऋजुकोण से बड़ा और संपूर्ण कोण से छोटा होता है।
4. दो प्रतिच्छेदी रेखाएँ परस्पर लंब कहलाती हैं, यदि उनके बीच का कोण 90o हो।
5. एक रेखाखंड का लंब समद्विभाजक उस रेखाखंड पर लंब होता है और उसे दो बराबर भागों में विभाजित करता है।
6. कोणों के आधार पर त्रिभुजों को निम्न प्रकार वर्गीकृत किया जाता है :
7. भुजाओं की लंबाइयों के आधार पर त्रिभुजों का वर्गीकरण निम्न प्रकार होता है :
8. बहुभुजों के नाम उनकी भुजाओं की संख्या के आधार पर निम्न प्रकार हैं :
10. हम अपने परिवेश में (आस-पास) अनेक त्रिविमीय आकार देखते हैं। इनमें से कुछ घन, घनाभ, गोला, बेलन, शंकु और पिरामिड हैं।