सुनीता की माँ के पास 8 केले हैं। सुनीता को अपने मित्रों के साथ एक पिकनिक पर जाना है। वह अपने साथ 10 केले ले जाना चाहती है। क्या उसकी माँ उसे 10 केले दे सकती है? उसके पास पर्याप्त केले नहीं हैं, इसलिए वह अपनी पड़ोसन से 2 केले उधार लेकर उन्हें बाद में लौटाने का आsवासन देती है। सुनीता को 10 केले देने के बाद, उसकी माँ के पास कितने केले बचते हैं? उसके पास कोई भी केला शेष नहीं बचता है, परंतु उसे अपनी पड़ोसन को 2 केले वापस करने हैं। इसलिए जब उसके पास कुछ और केले आ जाएँगे, मान लीजिए 6 केले, तो वह 2 केले वापस कर देगी और उसके पास केवल 4 केले बचेंगे।

रोनाल्ड एक पेन खरीदने बाजार जाता है। उसके पास केवल ₹ 12 हैं, परंतु एक पेन का मूल्य ₹ 15 है। दुकानदार उसकी ओर ₹ 3 की राशि उधार के रूप डायरी में लिख देता है। परंतु वह किस प्रकार याद रखेगा कि उसे ₹ 3 की राशि रोनाल्ड को देनी है या उससे लेनी है? क्या वह इस उधार की राशि को किसी रंग या चिह्न से व्यक्त कर सकता है?

रुचिका और सलमा एक संख्या पट्टी का जिस पर समान अंतराल पर 0 से 25 अंक अंकित हैं एक खेल खेल रही हैं।

प्रारंभ में, वे दोनों शून्य चिह्न पर एक-एक रंगीन टोकन रखती हैं। एक थैले में दो रंगीन पासे (dice) रखे हैं और वे एक के बाद एक निकाले जाते हैं। इन पासों में से एक पासा लाल रंग का है और दूसरा नीले रंग का। यदि पासा लाल रंग का है, तो उसे फेंकने पर जो संख्या प्राप्त होती है टोकन को उतने स्थान आगे बढ़ा दिया जाता है। यदि पासा नीले रंग का है, तो उसे फेंकने पर जो संख्या प्राप्त होती है, टोकन को उतने स्थान पीछे कर दिया जाता है। प्रत्येक चाल के बाद पासों को थैले में वापस रख दिया जाता है, ताकि दोनों व्यक्तियों को दोनों पासों को फेंकने के समान अवसर मिलें। जो 25वें चिह्न पर पहले पहुँचता है, उसे जीता हुआ माना जाता है। वह खेलना प्रारंभ करती हैं। रुचिका लाल पासा प्राप्त करती है और उसे फेंकने पर चार प्राप्त होता है। इस प्रकार, वह टोकन को पट्टी पर चार से अंकित स्थान पर रख देती है। सलमा भी थैले में से लाल पासा निकालती है और उसे फेंकनेे पर संख्या 3 प्राप्त करती है। इस प्रकार, वह अपने टोकन को तीन से अंकित स्थान पर रख देती है।

दूसरे प्रयत्न में, रुचिका लाल पासे से 3 अंक प्राप्त करती है और सलमा नीले पासे से 4 अंक प्राप्त करती है। क्या आप सोच सकते हैं कि दूसरे प्रयत्न के बाद वे अपने-अपने टोकन किन स्थानों पर रखेंगे?

रुचिका आगे बढ़ती है और 4 + 3, अर्थात् 7वें स्थान पर अपना टोकन रखती है।

सलमा अपना टोकन शून्य स्थान पर रखती है। रुचिका ने इस पर आपत्ति जताई और कहा कि उसे शून्य से पीछे होना चाहिए। सलमा उससे सहमत हो जाती है। परंतु शून्य के पीछे कुछ भी नहीं है। वे क्या करें?

तब सलमा और रुचिका ने इस पट्टी को दूसरी ओर बढ़ा दिया। उन्होंने दूसरी ओर एक नीली पट्टी का प्रयोग किया।

अब सलमा ने सुझाव दिया कि चूँकि वह शून्य से एक स्थान पीछे है, इसलिए इस स्थान को नीले एक से अंकित किया जा सकता है। यदि टोकन नीले एक पर है, तो नीले एक के पीछे वाला स्थान ‘नीला दो’ होगा। इसी प्रकार ‘नीले दो’ के पीछे वाला स्थान ‘नीला तीन’ होगा। इस प्रकार से वे पीछे चलने का निर्णय लेती हैं। परंतु उन्हें नीला कागज़ नहीं मिला। तब रुचिका ने कहा कि जब हम विपरीत दिशा में चल रहे हों, तो हमें दूसरी ओर एक चिह्न का प्रयोग कर लेना चाहिए। इस प्रकार, देखिए कि शून्य से छोटी संख्याओं पर जाने के लिए 

हमें एक चिह्न का प्रयोग करने की आवश्यकता होती है। इसके लिए उस संख्या के आगे ऋण (–) चिह्न का प्रयोग किया जाता है। इससे यह प्रदर्शित होता है कि ऋणात्मक (negative) चिह्न लगी हुई संख्याएँ शून्य से छोटी होती हैं। इन्हें ऋणात्मक संख्याएँ कहते हैं।

(कौन कहाँ है)

मान लीजिए डेविड और मोहन ने 0 स्थान से विपरीत दिशाओं में चलना प्रारंभ कर दिया है। मान लीजिए कि 0 के दाईं ओर चले कदमों को ‘+’ चिह्न से निरूपित किया जाता है और 0 से बाईं ओर चले कदमों को ‘–’ चिह्न से निरूपित किया जाता है। यदि मोहन शून्य के दाईं ओर 5 कदम चलता है, तो उसे +5 से निरूपित किया जा सकता है और यदि डेविड शून्य के बाईं ओर 5 कदम चलता है, तो उसे – 5 से निरूपित किया जा सकता है। अब निम्नलिखित स्थानों को + या – चिह्न से निरूपित कीजिए :

(a) शून्य के बाईं ओर 8 कदम

(b) शून्य के दाईं ओर 7 कदम

(c) शून्य के दाईं ओर 11 कदम

(d) शून्य के बाईं ओर 6 कदम

(मेरे पीछे कौन आ रहा है)

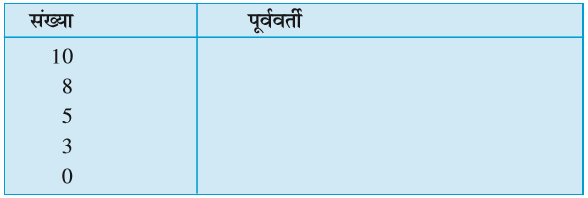
पिछले उदाहरणों में हमने देखा कि यदि एक एेसी संख्या के बराबर चलना है, जो धनात्मक है, तो हम दाईं ओर चलते हैं। यदि इस प्रकार का केवल 1 कदम चला जाता है, तो हमें उस संख्या का परवर्ती (Successor) प्राप्त होता है।

निम्नलिखित संख्याओं के परवर्ती लिखिए :

यदि बाईं ओर केवल 1 कदम चला जाता है, तो हमें उस संख्या का पूर्ववर्ती (Predecessor) प्राप्त होता है।

6.1.1 मेरे साथ एक चिह्न लगाइए

हम देख चुके हैं कि कुछ संख्याओं के आगे ऋण ( – ) चिह्न लगा होता है। उदाहरणार्थ, यदि हम दुकानदार को दी जाने वाली रोनाल्ड की देय राशि को दर्शाना चाहते हैं, तो हम इसे – लिखेंगे।

नीचे एक दुकानदार का खाता दिखाया जा रहा है जो कुछ विशेष वस्तुओं की बिक्री से प्राप्त लाभ और हानि को दर्शाता है :

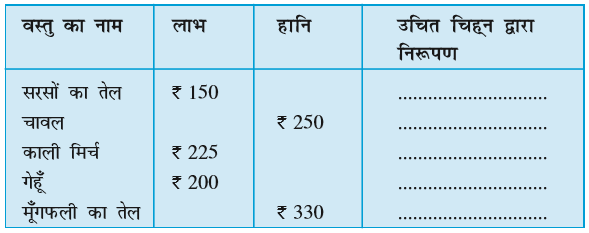
चूँकि लाभ और हानि विपरीत स्थितियाँ हैं, इसलिए यदि लाभ को ‘+’ चिह्न से निरूपित किया जाता है, तो हानि को ‘–’ चिह्न से निरूपित किया जाएगा। उपरोक्त खाते में उचित चिह्न का प्रयोग करते हुए रिक्त स्थानों को भरिए।

इसी प्रकार की अन्य स्थितियाँ, जहाँ हम इन चिह्नों का प्रयोग करते हैं नीचे दी गई हैं।

जैसे-जैसे हम नीचे जाते हैं, ऊँचाई कम होती जाती है। इस प्रकार, समुद्र स्तर (तल) से नीचे की ऊँचाई को हम एक ऋणात्मक संख्या से व्यक्त कर सकते हैं और समुद्र तल से ऊपर की ऊँचाई को एक धनात्मक संख्या से व्यक्त कर सकते हैं।

यदि कमाई गई (अर्जित की गई) राशि को ‘+’ चिह्न से निरूपित किया जाए, तो खर्च (व्यय) की गई राशि को ‘–’ चिह्न से निरूपित किया जा सकता है। इसी प्रकार 0ºC से ऊपर के तापमान को ‘+’ चिह्न और 0ºC से नीचे के तापमान को ‘–’ चिह्न से निरूपित किया जाता है।

उदाहरणार्थ, 0º C से 10º नीचे के तापमान को – 10ºC लिखा जाता है।

6.2 पूर्णांक

सबसे पहले ज्ञात की गईं संख्याएँ प्राकृत संख्याएँ, अर्थात् 1, 2, 3, 4,... हैं। यदि हम प्राकृत संख्याओं के संग्रह में शून्य को सम्मिलित कर लेते हैं, तो हमें संख्याओं का एक नया संग्रह प्राप्त होता है। इन संख्याओं को पूर्ण संख्याएँ कहते हैं। इस प्रकार 0, 1, 2, 3, 4,... पूर्ण संख्याएँ हैं। इन संख्याओं का आप अध्याय 2 में अध्ययन कर चुके हैं। अब हमें ज्ञात हो गया है कि ऋणात्मक संख्याएँ, जैसे –1, – 2, – 3, – 4, – 5, ... भी होती हैं। यदि हम पूर्ण संख्याओं और इन ऋणात्मक संख्याओं को मिला लें, तो हमें संख्याओं का एक नया संग्रह प्राप्त होगा, जो, 1, 2, 3, ..., – 1, – 2, – 3, – 4, .... है। संख्याओं के इस संग्रह को पूर्णांकों (integers) का संग्रह कहते हैं।

इस संग्रह में 1, 2, 3, ... धनात्मक पूर्णांक कहलाते हैं और – 1, – 2, – 3, ... ऋणात्मक पूर्णांक कहलाते हैं।

आइए, इसे निम्न आकृतियों द्वारा समझने का प्रयत्न करें। मान लीजिए ये आकृतियाँ अपने सम्मुख लिखी संख्याओं या उनके संग्रहों को निरूपित करती हैं।

तब पूर्णांकों के संग्रह को निम्नलिखित आरेख से समझा जा सकता है, जिसमें पिछली सभी संख्याएँ और उनके संग्रह सम्मिलित हैं।

6.2.1 संख्या रेखा पर पूर्णांकों का निरूपण

एक रेखा खींचिए और उस पर समान दूरी पर कुछ बिंदु अंकित कीजिए, जैसा कि ऊपर आकृति में दिखाया गया है। इनमें से एक बिंदु को शून्य से अंकित कीजिए। शून्य के दाईं ओर के बिंदु धनात्मक पूर्णांक हैं और इन्हें + 1, + 2, + 3 इत्यादि या केवल 1, 2, 3 इत्यादि से अंकित किया गया है। शून्य के बाईं ओर के बिंदु ऋणात्मक पूर्णांक हैं और इन्हें – 1, – 2, – 3 इत्यादि से अंकित किया गया है।

इस रेखा पर – 6 अंकित करने के लिए, हम शून्य के बाईं ओर 6 बिंदु (कदम) चलते हैं (आकृति 6.1)

इस रेखा पर + 2 अंकित करने के लिए, हम शून्य के दाईं ओर 2 बिंदु चलते हैं (आकृति 6.2)

6.2.2 पूर्णांकों में क्रमबद्धता

रमन और इमरान एक गाँव में रहते हैं, जहाँ सीढ़ियों वाला एक कुआँ है। इस कुएँ में तली तक कुल 25 सीढ़ियाँ हैं।

एक दिन रमन और इमरान कुएँ के अंदर गए और उन्होंने पाया कि उसमें जल स्तर तक 8 सीढ़ियाँ हैं। उन्होंने यह देखने का निर्णय लिया कि वर्ज़ा होने पर उस कुएँ में कितना जल आ जाएगा। उन्होंने इस समय के जल स्तर पर शून्य अंकित किया और उसमें ऊपर की सीढ़ियों को क्रम से 1,2,3,4,... अंकित किया। वर्ज़ा के बाद उन्होंने देखा कि जल स्तर छठी सीढ़ी तक बढ़ गया है। कुछ महीने बाद, उन्होंने देखा कि जल स्तर शून्य के चिह्न से तीन सीढ़ी नीचे पहुँच गया है। अब वे जल स्तर के गिरने को संगत सीढ़ियों से अंकित करके देखना प्रारंभ करने के बारे में सोचने लगे। क्या आप उनकी सहायता कर सकते हैं?

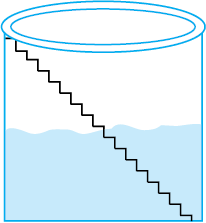
यकायक, रमन को याद आता है कि उसने एक बड़े बाँध पर शून्य से भी नीचे लिखी संख्याओं को देखा था। इमरान इस ओर ध्यान दिलाता है कि शून्य के ऊपर की संख्याओं और शून्य के नीचे की संख्याओं में भेद जानने के लिए कोई न कोई विधि अव”य होनी चाहिए। तब रमन याद करता है कि शून्य चिह्न के नीचे अंकित संख्याओं के आगे ऋण चिह्न लगा हुआ था। इसलिए, उन्होंने शून्य के नीचे की एक सीढ़ी को – 1 से अंकित किया, शून्य के नीचे की दो सीढ़ियों को – 2 से अंकित किया, इत्यादि।

इसलिए, इस समय जल स्तर – 3 है (शून्य से 3 सीढ़ी नीचे)। इसके बाद, जल का प्रयोग होने के कारण, जल स्तर 1 सीढ़ी और नीचे गिर जाता है और – 4 हो जाता है। आप देख सकते हैं कि – 4 < – 3 है।

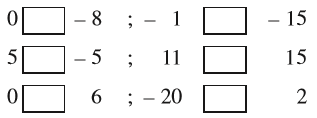
उपरोक्त उदाहरण को ध्यान में रखते हुए, रिक्त खानों को > और < चिह्नों का प्रयोग करते हुए भरिए :

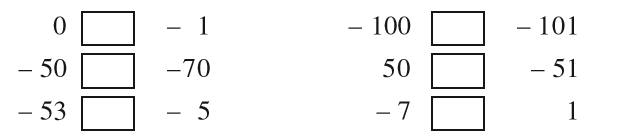
आइए, अब पुन: उन पूर्णांकों को देखें जो एक संख्या रेखा पर निरूपित किए गए हैं।

आकृति 6.3

हम जानते हैं कि 7 > 4 होता है और ऊपर खींची गई संख्या रेखा से हम देखते हैं कि संख्या 7 संख्या 4 के दाईं ओर स्थित है (आकृति 6.3)।

इसी प्रकार, 4 > 0 और संख्या 4 संख्या 0 के दाईं ओर स्थित है। अब चूँकि संख्या 0 संख्या – 3 के दाईं ओर स्थित है इसलिए 0 > – 3 है। पुन: संख्या – 3 संख्या – 8 के दाईं ओर स्थित है। इसलिए – 3 > – 8 है।

इस प्रकार, हम देखते हैं कि संख्या रेखा पर जब हम दाईं ओर चलते हैं, तो संख्या का मान बढ़ता है और जब हम बाईं ओर चलते हैं, तो संख्या का मान घटता है।

अत:, – 3 < – 2, – 2 < – 1, – 1 < 0, 0 < 1, 1 < 2, 2 < 3 इत्यादि।

अत:, पूर्णांकों के संग्रह को..., –5, –4, – 3, – 2, – 1, 0, 1, 2, 3, 4, 5... लिखा जा सकता है।

निम्नलिखित संख्या युग्म > या < का प्रयोग करते हुए तुलना कीजिए :

उदाहरण 1 : संख्या रेखा को देखकर निम्नलिखित प्रश्नों के उत्तर दीजिए :

– 8 और – 2 के बीच में कौन सी पूर्णांक संख्याएँ स्थित हैं? इनमें से कौन-सी संख्या सबसे बड़ी है और कौन-सी संख्या सबसे छोटी है?

हल : – 8 और – 2 के बीच स्थित संख्याएँ – 7, – 6, – 5, – 4 और – 3 है।
इनमें से – 3 सबसे बड़ी संख्या है और – 7 सबसे छोटी संख्या हैं।

यदि मैं शून्य पर नहीं हूँ, तो मेरे चलने पर क्या होता है?

आइए, सलमा और रुचिका द्वारा पहले खेले गए खेल पर विचार करें। मान लीजिए कि रुचिका का टोकन 2 पर है। अगली बार, उसे लाल पासा प्राप्त होता है और उसे फेंकने पर संख्या 3 प्राप्त होती है। इसका अर्थ है कि वह 2 के दाईं ओर 3 स्थान चलेगी।

इस प्रकार, वह 5 पर आ जाती है।

दूसरी ओर, यदि सलमा 1 पर थी और थैले में से नीला पासा निकालती है, जिसे फेंकने पर उसे संख्या 3 प्राप्त होती है, तो इसका अर्थ है कि वह 1 के बाईं ओर 3 स्थान चलेगी। इस प्रकार, वह – 2 पर पहुँच जाएगी।

उदाहरण 2 : (a) – 3 पर एक बटन रखा गया है। – 9 पर पहुँचने के लिए, हम किस दिशा में और कितने कदम चलें?

(b) यदि हम संख्या – 6 के दाईं ओर 4 कदम चलें, तो किस संख्या पर
पहुँच जाएँगे?

हल : (a) हमें – 3 के बाईं ओर 6 कदम चलने पड़ेंगे।

(b) हम संख्या – 2 पर पहुँच जाएँगे।

(c) यदि हम संख्या –6 के दाईं ओर 4 कदम चलें, तो हम संख्या – 2 पर पहुँच जाएँगे।

प्रश्नावली 6.1

1. निम्नलिखित के विपरीत (opposites) लिखिए :

(a) भार में वृद्धि

(b) 30 किमी उत्तर दिशा

(c) 80 मी पूर्व

(d) ₹ 700 की हानि

(e) समुद्र तल से 100 मी ऊपर

2. निम्नलिखित में प्रयुक्त हुई संख्याओं को उचित चिह्न लगाकर पूर्णांकों के रूप में लिखिए :

(a) एक हवाई जहाज़ भूमि से दो हजार मीटर की ऊँचाई पर उड़ रहा है।

(b) एक पनडुब्बी समुद्र तल से 800 मीटर की गहराई पर चल रही है।

(c) खाते में ₹ 200 जमा कराना।

(d) खाते में से ₹ 700 निकालना।

3. निम्नलिखित संख्याओं को संख्या रेखा पर निरूपित कीजिए :

(a) + 5

(b) – 10

(c) + 8

 (d) – 1

 (e) – 6

4. संलग्न आकृति में एक ऊर्ध्वाधर संख्या रेखा को दिखाया गया है, जो पूर्णांकों को निरूपित करती है। इस रेखा को देखिए और निम्नलिखित बिंदुओं के स्थान ज्ञात कीजिए :

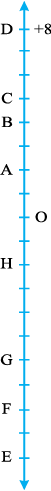
(a) यदि बिंदु D पूर्णांक + 8 है, तो – 8 वाला बिंदु कौन सा है?

(b) क्या G एक ऋणात्मक पूर्णांक है या धनात्मक?

(c) बिंदु B और E के संगत पूर्णांक लिखिए।

(d) इस संख्या रेखा पर अंकित बिंदुओं में से किसका मान सबसे कम है?

(e) सभी बिंदुओं को उनके मानों के घटते हुए क्रम में लिखिए।

5. वर्ज़ के विशेष दिन के लिए भारत के पाँच स्थानों पर रहे तापमानों की सूची नीचे दी गई है :

(a) इन स्थानों के तापमानों को पूर्णांकों के रूप में रिक्त स्तंभ में लिखिए।

(b) निम्नलिखित संख्या रेखा डिग्री सेल्सियस (Degree Celsius) में तापमानों को निरूपित करती है :

उपरोक्त स्थानों के नाम संख्या रेखा पर उनके तापमानों के संगत अंकित कीजिए।

(c) कौन-सा स्थान सबसे ठंडा है?

(d) उन स्थानों के नाम लिखिए जिनका तापमान 10ºC से ऊपर है।

6. निम्नलिखित युग्मों में, कौन-सी संख्या, संख्या रेखा पर दूसरी संख्या के दाईं ओर स्थित है?

(a) 2, 9 

(b) – 3, – 8 

(c) 0, – 1

(d) – 11, 10

(e) – 6, 6

(f) 1, – 100

7. नीचे दिए हुए युग्मों के पूर्णांकों के बीच के सभी पूर्णांक लिखिए (बढ़ते हुए क्रम में लिखिए) :

(a) 0 और – 7

(b) – 4 और 4

(c) – 8 और – 15

(d) – 30 और – 23

8. (a) – 20 से बड़े चार ऋणात्मक पूर्णांक लिखिए।

(b) – 10 से छोटे चार पूर्णांक लिखिए।

9. निम्नलिखित कथनों के लिए सत्य अथवा असत्य लिखिए। यदि कथन असत्य है, तो सत्य बनाइए।

(a) संख्या रेखा पर – 8, – 10 के दाईं ओर स्थित है।

(b) संख्या रेखा पर – 100, – 50 के दाईं ओर स्थित है।

(c) सबसे छोटा ऋणात्मक पूर्णांक – 1 है।

(d) – 26 पूर्णांक – 25 से बड़ा है।

10. एक संख्या रेखा खींचिए और निम्नलिखित प्रश्नों के उत्तर दीजिए :

(a) यदि हम – 2 के दाईं ओर 4 कदम चलें, तो हम किस संख्या पर पहुँच जाएँगे?

(b) यदि हम 1 के बाईं ओर 5 कदम चलें, तो हम किस संख्या पर पहुँच जाएँगे?

(c) यदि हम संख्या रेखा पर – 8 पर हैं, तो – 13 पर पहुँचने के लिए हमें किस दिशा में
चलना चाहिए?

(d) यदि हम संख्या रेखा पर – 6 पर हैं, तो – 1 पर पहुँचने के लिए, हमें किस दिशा में चलना चाहिए?

6.3 पूर्णांकों का योग

(ऊपर और नीचे जाना या चलना)

मोहन के घर में, छत पर जाने के लिए और नीचे गोदाम में जाने के लिए सीढ़ियाँ बनी हुई हैं। आइए, छत पर जाने के लिए सीढ़ियों की संख्या को धनात्मक पूर्णांक मानें और नीचे गोदाम में जाने के लिए सीढ़ियों की संख्या को ऋणात्मक पूर्णांक मानें तथा भूमि तल से निरूपित संख्या को 0 मानें।

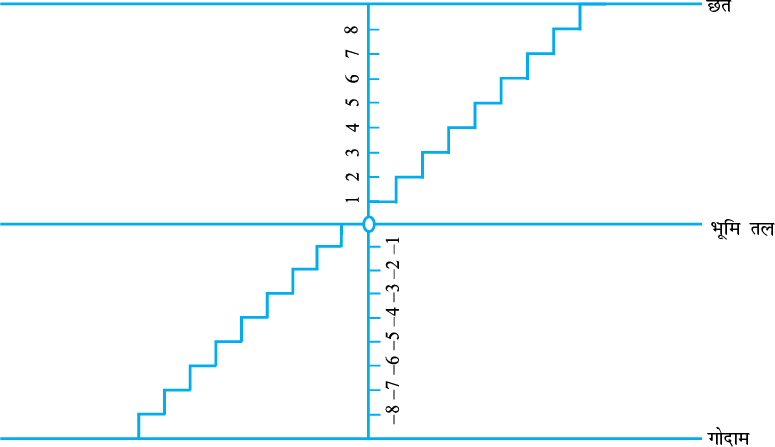
निम्नलिखित प्रश्नों के उत्तर दीजिए और अपने उत्तर को पूर्णांकों के रूप में लिखिए :

(a) भूमि तल से 6 सीढ़ी ऊपर चलिए।

(b) भूमि तल से 4 सीढ़ी नीचे चलिए।

(c) भूमि तल से 5 सीढ़ी ऊपर चलिए और फिर वहाँ से 3 सीढ़ी और ऊपर चलिए।

(d) भूमि तल से 6 सीढ़ी नीचे चलिए और फिर वहाँ से 2 सीढ़ी और नीचे चलिए।

(e) भूमि तल से 5 सीढ़ी नीचे चलिए और फिर वहाँ से 12 सीढ़ी ऊपर चलिए।

(f) भूमि तल से 8 सीढ़ी नीचे चलिए और फिर वहाँ से 5 सीढ़ी ऊपर चलिए।

(g) भूमि तल से 7 सीढ़ी ऊपर चलिए और फिर वहाँ से 10 सीढ़ी नीचे चलिए।

अमीना ने इन्हें नीचे दिखाए अनुसार लिखा :

(a) + 6

(b) – 4

(c) (+ 5) +(+ 3) = + 8

(d) (– 6) + (–2) = – 4

(e) (– 5) + (+ 12) = + 7

(f) (– 8) + (+5) = – 3

(g) (+7) + (–10) = 17

उसने कुछ गलतियाँ की हैं। क्या आप उसके उत्तरों की जाँच कर सकते हैं और गलतियों को सही कर सकते हैं?

एक खेल

एक संख्या पट्टी लीजिए जिस पर + 25 से – 25 तक के पूर्णांक लिखे हों।

दो पासे लीजिए जिनमें से एक पर 1 से 6 तक की संख्याएँ अंकित हाें और दूसरे पर तीन ‘+’ चिह्न और तीन ‘–’ चिह्न अंकित हों।

खिलाड़ी भिन्न-भिन्न रंगों के बटन [(या प्लास्टिक के काउंटर (Counter)] संख्या पट्टी पर 0 स्थान पर रखेंगे। दोनों पासों को प्रत्येक बार फेंकने के बाद, खिलाड़ी देखेगा कि उसने उन पासों पर क्या प्राप्त किया है। यदि पहले पासे पर 3 और दूसरे पासे पर – आता है, तो उसे – 3 प्राप्त हुआ है। यदि पहला पासा 5 दर्शाता है और दूसरा पासा ‘+’ दर्शाता है, तो उसे + 5 प्राप्त हुआ है।

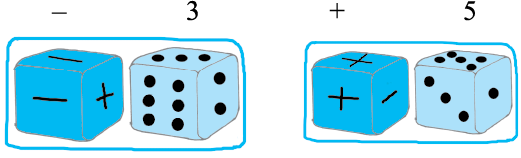
जब किसी खिलाड़ी को + चिह्न प्राप्त होता है, तो वह आगे की दिशा में (+ 25 की ओर) चलता है और जब किसी खिलाड़ी को – चिह्न प्राप्त होता है, तो वह पीछे की ओर ( – 25 की ओर) चलता है।

प्रत्येक खिलाड़ी दोनों पासों को एक साथ फेंकता है। वह खिलाड़ी जिसका बटन (या काउंटर) – 25 को छू लेता है, वह खेल से बाहर हो जाता है और वह खिलाड़ी जिसका बटन (या काउंटर) + 25 को छू लेता है, वह खेल में जीत जाता है।

आप इसी खेल को एेसे 12 कार्ड लेकर जिन पर + 1, + 2, + 3, + 4, + 5 और + 6 तथा – 1, – 2, – 3, – 4, – 5 और – 6 अंकित हो, भी खेल सकते हैं। कार्ड निकालने के प्रत्येक प्रयत्न के बाद उन्हें फेंट लीजिए।

कमला, रे”ामा और मीनू इस खेल को खेल रही हैं :

कमला ने तीन लगातार प्रयत्नों में + 3, + 2, + 6 प्राप्त किया। उसने अपना काउंटर + 1 1 पर रख दिया। रे”ामा ने – 5, + 3 और + 1 प्राप्त किया। उसने अपना काउंटर – 1 पर रख दिया। मीनू ने तीन लगातार प्रयत्नों में + 4, – 3 और – 2 प्राप्त किया। उसका काउंटर किस स्थान पर रखा जाएगा? –1 पर या + 1 पर?

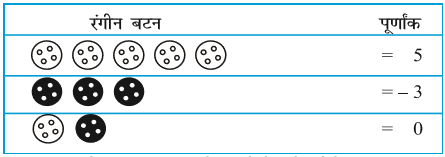
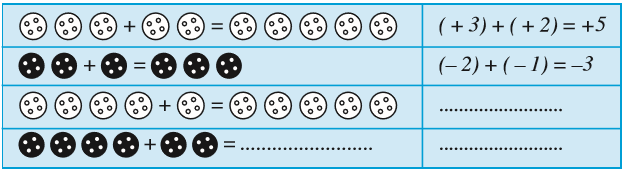
दो भिन्न-भिन्न रंगों के सफ़ेद और काले रंगों के दो बटन लीजिए। आइए, एक सफ़ेद बटन को (+ 1) और एक काले बटन को (– 1) से व्यक्त करें। एक सफ़ेद बटन (+ 1) और एक काले बटन (– 1) का युग्म शून्य व्यक्त करेगा, अर्थात् [1 + (– 1) = 0]

निम्नलिखित सारणी में, पूर्णांकों को रंगीन के बटनों की सहायता से दिखाया गया है :

आइए, इन रंगीन बटनों की सहायता से पूर्णांकों को जोड़ें। निम्नलिखित सारणी को देखिए और उसे पूरा कीजिए :

जब आप दो धनात्मक पूर्णांक प्राप्त करें, तो उन्हें जोड़िए। जैसे (+3) + (+2) = +5 [= 3 + 2] है। जब आप दो ऋणात्मक पूर्णांक प्राप्त करें, तो भी उन्हें जोड़िए, परंतु उत्तर में ऋण चिह्न (–) लगा दें। जैसे (–2) + (–1) = –3 है।

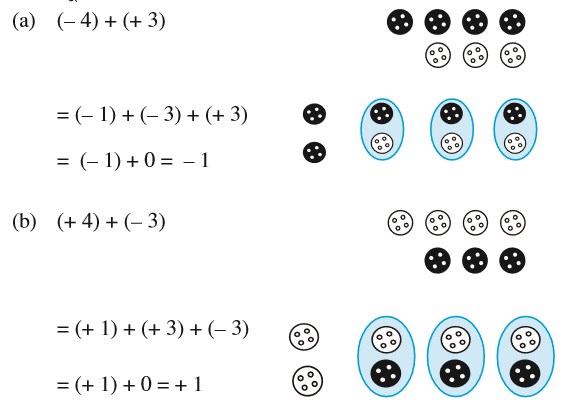
अब इन्हीं बटनों की सहायता से एक धनात्मक पूर्णांक और एक ऋणात्मक पूर्णांक को जोड़िए। बटनों को युग्मों में हटाइए, अर्थात् 1 सफ़ेद बटन और 1 काले बटन को साथ लेकर हटाइए [चूँकि (+ 1) + (– 1) = 0]। शेष बटनों की जाँच कीजिए।

आप देख सकते हैं कि 4 – 3 का उत्तर 1 है और – 4 + 3 = – 1 है।

(c) (+ 5) + (– 8) = (+ 5) + (– 5) + (– 3) = 0 + (– 3) = (– 3)

(d) (+ 6) + (– 4) = (+ 2) + (+ 4) + (– 4) = (+ 2) + 0 = + 2

6.3.1 संख्या रेखा पर पूर्णांकों का जोड़ना (योग)

भिन्न-भिन्न रंगों के बटनों का प्रयोग करके पूर्णांकों को जोड़ना सदैव सरल नहीं होता है। क्या हमें जोड़ने के लिए, संख्या रेखा का प्रयोग करना चाहिए?

(i) आइए, संख्या रेखा पर 3 और 5 को जोड़ें।

संख्या रेखा पर, पहले हम 0 से प्रारंभ करके 0 के दाईं ओर 3 कदम चलते हैं और 3 पर पहुँचते हैं। फिर हम 3 के दाईं ओर 5 कदम चलते हैं और 8 पर पहुँचते हैं (आकृति 6.4)। इस प्रकार, हमें 3 + 5 = 8 प्राप्त होता है।

(ii) आइए, संख्या रेखा पर – 3 और – 5 को जोड़ें

संख्या रेखा पर, पहले हम 0 से प्रारंभ करके 0 के बाईं ओर 3 कदम चलते हैं और – 3 पर पहुँचते हैं। फिर हम – 3 के बाईं ओर 5 कदम चलते हैं और – 8 पर पहुँचते हैं (आकृति 6.5)।

इस प्रकार, हमें (– 3) + (– 5) = – 8 प्राप्त होता है।

हम देखते हैं कि जब हम किन्हीं दो धनात्मक पूर्णांकों को जोड़ते हैं, तो योग एक धनात्मक पूर्णांक होता है। जब हम दो ऋणात्मक पूर्णांकों को जोड़ते हैं, तो योग एक ऋणात्मक पूर्णांक होता है।

(iii) मान लीजिए हम संख्या रेखा पर (+ 5) और (– 3) का योग ज्ञात करना चाहते हैं।

पहले हम, संख्या रेखा पर 0 से प्रारंभ करके 0 के दाईं ओर 5 कदम चलते हैं और 5 पर पहुँचते हैं। फिर हम 5 के बाईं ओर 3 कदम चलते हैं और 2 पर पहुँचते हैं। (आकृति 6.6)

इस प्रकार, (+ 5) + (– 3) = 2 है।

(iv) इसी प्रकार, आइए संख्या रेखा पर (– 5) और (+ 3) का योग ज्ञात करें

पहले हम 0 से प्रारंभ करके, 0 के बाईं ओर 5 कदम चलते हैं और – 5 पर पहुँचते हैं। फिर हम – 5 के दाईं ओर 3 कदम चलते हैं और – 2 पर पहुँचते हैं।

इस प्रकार, (– 5) + (+3) = – 2 है। (आकृति 6.7)

यदि किसी पूर्णांक में एक धनात्मक पूर्णांक जोड़ा जाता है, तो परिणामी पूर्णांक दिए हुए पूर्णांक से बड़ा हो जाता है। यदि किसी पूर्णांक में एक ऋणात्मक पूर्णांक जोड़ा जाता है, तो परिणामी पूर्णांक दिए हुए पूर्णांक से छोटा हो जाता है।

आइए 3 और – 3 को जोड़े। पहले हम 0 से प्रारंभ करके, 0 के दाईं ओर 3 कदम चलकर 3 पर पहुँचते हैं। फिर हम 3 के बाईं ओर 3 कदम चलते हैं। अंत में हम कहाँ पहुँचते हैं?

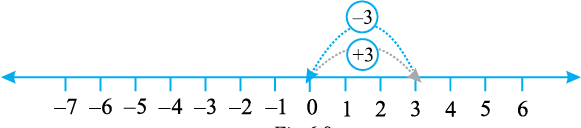
आकृति 6.8 से, हम देख सकते हैं कि हम 0 पर पहुँच गए हैं। अत: 3 + (– 3) = 0 है। इसी प्रकार, यदि हम 2 और – 2 को जोड़े, तो हमें 0 प्राप्त होगा। इस प्रकार, संख्या युग्मों 3 और – 3, 2 और – 2, इत्यादि संख्याओं को जोड़ने पर 0 प्राप्त होता है। एेसी संख्याएँ एक दूसरे के योज्य प्रतिलोम (additive inverse) कहलाती हैं।

6 का योज्य प्रतिलोम क्या है? – 7 का योज्य प्रतिलोम क्या है?

उदाहरण 3 : संख्या रेखा का प्रयोग करते हुए, वह पूर्णांक लिखिए, जो

(a) –1 से 4 अधिक है।

(b) 3 से 5 कम है।

हल : (a) हम वह पूर्णांक ज्ञात करना चाहते हैं जो –1 से 4 अधिक है। इसलिए, हम –1 से प्रारंभ करते हैं और –1 के दाईं ओर 4 कदम चलते हैं। इससे हम 3 पर पहुँच जाते हैं, जैसा कि नीचे आकृति 6.9 में दर्शाया गया है।

अत:, –1 से 4 अधिक पूर्णांक 3 है।

(b) हम वह पूर्णांक ज्ञात करना चाहते हैं, जो 3 से 5 कम है। इसलिए, हम 3 से प्रारंभ करते हैं और 3 के बाईं ओर 5 कदम चलते हैं। इस प्रकार, हम –2 पर पहुँच जाते हैं, जैसा कि आकृति 6.10 में नीचे दिखाया गया है।

अत:, 3 से 5 कम पूर्णांक –2 है।

उदाहरण 4 : योग (– 9) + (+ 4) + (– 6) + (+ 3) ज्ञात कीजिए।

हल : हम संख्याओं को इस प्रकार पुनर्व्यवस्थित कर सकते हैं कि धनात्मक पूर्णांक एक समूह में हों और ऋणात्मक पूर्णांक एक समूह में हों। इस प्रकार

(– 9) + (+ 4) + (– 6) + (+ 3)

= (– 9) + (– 6) + (+ 4) + (+ 3) = (– 15) + (+ 7)

= – 8 + (– 7) + (+ 7) = – 8 + 0 = – 8

उदाहरण 5 : (30) + (– 23) + (– 63) + (+ 55) का मान ज्ञात कीजिए।

हल : (30) + (+ 55) + (– 23) + (– 63)

= 85 + (– 86) = – 1

उदाहरण 6 : (– 10), (92), (84) और (– 15) का योग ज्ञात कीजिए।

हल : (– 10) + (92) + (84) + (– 15)

= (– 10) + (– 15) + 92 + 84

= (– 25) + 176 = 151

प्रश्नावली 6.2

1. संख्या रेखा का प्रयोग करते हुए, वह पूर्णांक ज्ञात कीजिए जो

(a) 5 से 3 अधिक है

(b) –5 से 5 अधिक है

(c) 2 से 6 कम है

(d) –2 से 3 कम है

2. संख्या रेखा का प्रयोग करते हुए निम्नलिखित योग ज्ञात कीजिए :

(a) 9 + (– 6)

(b) 5 + (– 11)

(c) (– 1) + (– 7) 

 (d) (– 5) + 10

(e) (– 1) + (– 2) + (– 3)

(f) (– 2) + 8 + (– 4)

3. संख्या रेखा का प्रयोग किए बिना, निम्नलिखित योग ज्ञात कीजिए :

(a) 11 + (– 7)

(b) (– 13) + (+ 18)

(c) (– 10) + (+ 19)

(d) (– 250) + (+ 150)

(e) (– 380) + (– 270)

(f) (– 217) + (– 100)

4. निम्नलिखित का योग ज्ञात कीजिए :

(a) 137 और – 354

(b) – 52 और 52

(c) – 312, 39 और 192

(d) – 50, – 200 और 300

5. निम्नलिखित के मान ज्ञात कीजिए :

(a) (– 7) + (– 9) + 4 + 16

(b) (37) + (– 2) + (– 65) + (– 8)

6.4 संख्या रेखा की सहायता से पूर्णांकों का व्यवकलन (घटाना)

हम संख्या रेखा पर दो धनात्मक पूर्णांकों को जोड़ चुके हैं। उदाहरणार्थ, 6 + 2 पर विचार कीजिए। हम 6 से प्रारम्भ करते हैं और दाईं ओर 2 कदम चलते हैं। हम 8 पर पहुँचते हैं। अत:, 6 + 2 = 8 है (आकृति 6.11)।

हमने यह भी देखा था कि संख्या रेखा पर 6 और (–2) को जोड़ने के लिए, हम 6 से प्रारंभ कर सकते हैं तथा फिर उसके बाईं ओर 2 कदम चल सकते हैं। हम 4 पर पहुँचते हैं। अत:, हमें 6 + (–2) = 4 प्राप्त होता है (आकृति 6.12)।

इस प्रकार, हम पाते हैं कि एक धनात्मक पूर्णांक जोड़ने के लिए, हम संख्या पर दाईं ओर को चलते हैं तथा एक ऋणात्मक पूर्णांक को जोड़ने के लिए हम संख्या रेखा पर बाईं ओर को चलते हैं।

पूर्ण संख्याओं के लिए, संख्या रेखा का प्रयोग करते समय भी हमने देखा था कि 6 में से 2 घटाने के लिए हम 2 कदम बाईं ओर को चले थे (आकृति 6.13)।

अर्थात् 6 – 2 = 4 है।

हम 6 – (– 2) के लिए क्या करेंगे? क्या हम संख्या रेखा पर बाईं ओर चलेंगे या दाईं ओर चलेंगे?

यदि हम बाईं ओर चलें, तो हम 4 पर पहुँचेेंगे। तब, हमें कहना पड़ेगा कि 6 – (– 2) = 4 है। यह सही नहीं है, क्योंकि हमें ज्ञात है कि 6 – 2 = 4 होता है तथा 6 – 2 ≠ 6 – (– 2) है।

अत:, हमें दाईं ओर चलना होगा (आकृति 6.14)।

इसका अर्थ यह भी है कि जब हम एक ऋणात्मक पूर्णांक घटाते हैं, तो हमें एक बड़ा पूर्णांक प्राप्त होता है। इस पर एक दूसरी प्रकार से विचार कीजिए। हम जानते हैं कि (–2) का योज्य प्रतिलोम 2 है। अत:, इससे एेसा प्रतीत होता है कि 6 में –2 के योज्य प्रतिलोम जोड़ने का अर्थ वही है, जो 6 में से (–2) को घटाने का है।

हम लिखते हैं : 6 – (–2) = 6 + 2

आइए, अब – 5 – (– 4) का मान संख्या रेखा की सहायता से ज्ञात करें। हम कह सकते हैं कि यह –5 + 4 के बराबर है, क्योंकि – 4 का योज्य प्रतिलोम 4 है।

अत:, हम संख्या रेखा पर – 5 से प्रारंभ करके 4 कदम दाईं ओर को चलते हैं (आकृति 6.15)। हम –1 पर पहुँचते हैं।

अर्थात्, – 5 + 4 = – 1 है। इस प्रकार, – 5 – (– 4) = – 1 होगा।

उदाहरण 7 : संख्या रेखा की सहायता से (– 8) – (– 10) का मान ज्ञात कीजिए।

हल : चूँकि – 10 का योज्य प्रतिलोम + 10 है, इसलिए (– 8) – (– 10)
        = – 8 + 10 है।

संख्या रेखा पर, हम – 8 से 10 कदम दाईं ओर को चलेंगे।

हम 2 पर पहुँचते हैं (आकृति 6.16)। अत:, – 8 – (–10) = 2 है।

इस प्रकार, एक पूर्णांक में से एक अन्य पूर्णांक घटाने के लिए, यह पर्याप्त है कि घटाए जाने वाले पूर्णांक के योज्य प्रतिलोम को दूसरे पूर्णांक में जोड़ लिया जाए।

उदाहरण 8 : (– 10) में से (– 4) को घटाइए।

हल : (– 10) – (– 4) = (– 10) + (– 4 का योज्य प्रतिलोम)

           = –10 + 4 = – 6

उदाहरण 9 : (– 3) में से (+ 3) को घटाइए।

हल : (– 3) – (+ 3) = (– 3) + (+ 3 का योज्य प्रतिलोम)

             = (– 3) + (– 3) = – 6

प्रश्नावली 6.3

1. घटाइए :

(a) 35 – (20)

(b) 72 – (90)

(c) (– 15) – (– 18)

(d) (–20) – (13)

(e) 23 – (– 12)

(f) (–32) – (– 40)

2. रिक्त स्थानों को >, < या = से भरिए :

(a) (– 3) + (– 6) ______ (– 3) – (– 6)

(b) (– 21) – (– 10) _____ (– 31) + (– 11)

(c) 45 – (– 11) ______ 57 + (– 4)

(d) (– 25) – (– 42) _____ (– 42) – (– 25)

3. रिक्त स्थानों को भरिए :

(a) (– 8) + _____ = 0 (b) 13 + _____ = 0

(c) 12 + (– 12) = ____ (d) (– 4) + ____ = – 12

(e) ____ – 15 = – 10

4. निम्नलिखित के मान ज्ञात कीजिए :

(a) (– 7) – 8 – (– 25)

(b) (– 13) + 32 – 8 – 1

(c) (– 7) + (– 8) + (– 90)

(d) 50 – (– 40) – (– 2)

हमने क्या चर्चा की?

1. हमने देखा कि कई बार हमें ऋणात्मक चिह्नों वाली संख्याओं की आवश्यकता पड़ती है। यह तब होता है जब हम संख्या रेखा पर शून्य के नीचे जाएँ। ये ऋणात्मक संख्याएँ कहलाती हैं। इनका प्रयोग किए जाने वाले कुछ उदाहरण हैं तापमान, झील या नदी में पानी का स्तर, टैंक में तेल का स्तर इत्यादि। इनका प्रयोग उधार खाते या लेनदारी में भी होता है।

2. ..., – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, ... जैसी संख्याओं के संग्रह को पूर्णांक कहते हैं। अत: – 1, – 2, – 3, – 4, ... ऋणात्मक संख्याएँ हैं जिन्हें ऋणात्मक पूर्णांक कहा जाता है और 1, 2, 3, 4, ... धनात्मक संख्याएँ हैं जिन्हें धनात्मक पूर्णांक कहते हैं।

3. हमने यह भी देखा कि किसी दी हुई संख्या का एक अधिक उसकी परवर्ती संख्या होती है और एक कम लेने पर पूर्ववर्ती संख्या प्राप्त होती है।

4. हमने देखा

(a) जब समान चिह्न हों तो, जोड़िए और वही चिह्न लगाइए।

(i) जब-जब दो धनात्मक पूर्णांकों को जोड़ा जाता है, हमें एक धनात्मक पूर्णांक मिलता है [जैसे, (+ 3) + ( + 2) = + 5]

(ii) जब-जब दो ऋणात्मक पूर्णांकों को जोड़ा जाता है, हमें एक ऋणात्मक पूर्णांक मिलता है [जैसे, (–2) + ( – 1) = – 3]

(b) जब हमारे पास अलग-अलग चिह्न हों तो घटाकर बड़ी संख्या का चिह्न लगा देते हैं।

(c) जब एक धनात्मक और एक ऋणात्मक पूर्णांकों को जोड़ा जाता है तो हम उन्हें पूर्ण संख्याओं की तरह घटाते हैं और बड़े पूर्णांक का चिह्न लगा देते हैं। बड़ी संख्या का अभिप्राय उस संख्या से है जिसका संख्यात्मक मान अधिक हो [जैसे, (+4) + (–3) = + 1 और (–4) + ( + 3) = – 1]

5. हमने दिखाया कि किस प्रकार पूर्णांकों का योग तथा व्यवकलन संख्या-रेखा पर दिखाया जा सकता है।