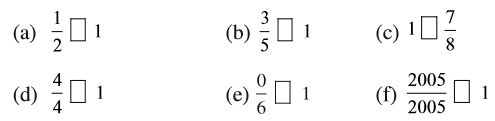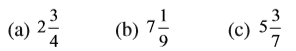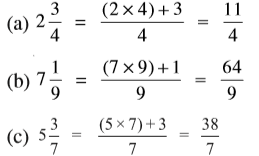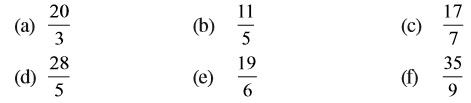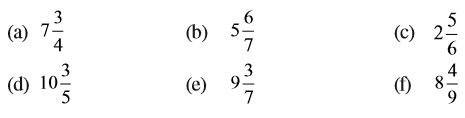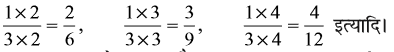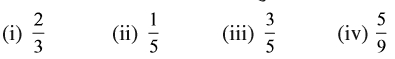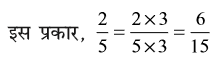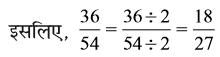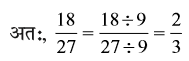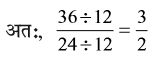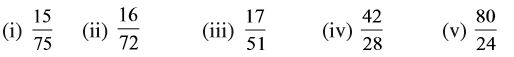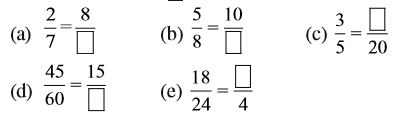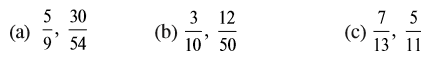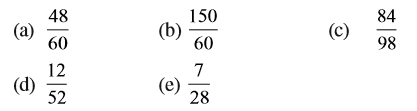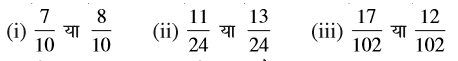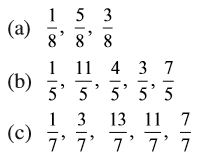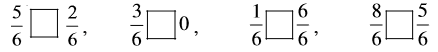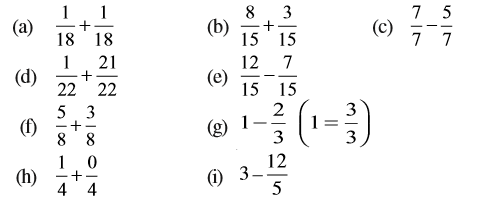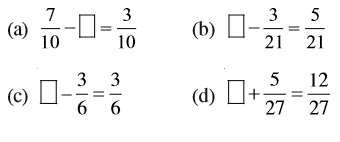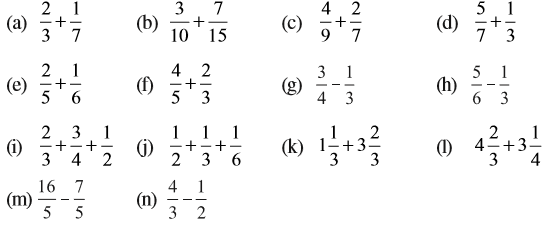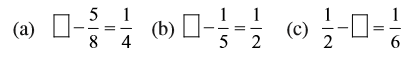Table of Contents
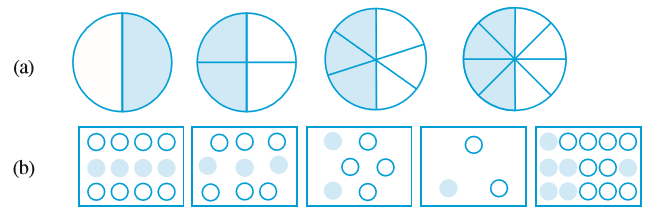
सुभाष ने IV और V कक्षा में भिन्नों (Fractions) के बारे में पढ़ा था। परंतु वह इस बारे में बहुत विश्वस्त नहीं था और इसीलिए जब भी उसे अवसर मिलता वह भिन्नों का प्रयोग करने का प्रयत्न करता था। एक अवसर तब आया जब वह घर से अपना लंच (lunch) लाना भूल गया। उसकी एक मित्र फरीदा ने उसे अपने साथ लंच करने के लिए आमंत्रित किया। उसके लंच बॉक्स में पाँच पूरियाँ थीं। इसलिए, सुभाष और फरीदा दोनों ने दो-दो पूरियाँ ले लीं। फिर फरीदा ने पाँचवीं पूरी के दो बराबर भाग (आधे भाग) किए और उनमें से एक-आधा (one half) भाग सुभाष को दे दिया और दूसरा आधा भाग स्वयं ले लिया। इस प्रकार, सुभाष और फरीदा दोनों ने दो पूर्ण पूरियाँ और एक आधी पूरी ली।
2 पूरियाँ + आधी पूरी-सुभाष 2 पूरियाँ + आधी पूरी-फरीदा
आपको अपने दैनिक जीवन में, किन परिस्थितियों में भिन्नों का सामना करना पड़ता है?
सुभाष जानता था कि एक-आधे (one-half) को 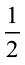 लिखा जाता है। पूरी खाते समय, उसने अपनी आधी पूरी को पुन: दो बराबर भागों में बाँट लिया और फरीदा से पूछा कि यह टुकड़ा पूर्ण पूरी का कौन सा भाग अथवा भिन्न है। (आकृति 7.1)
लिखा जाता है। पूरी खाते समय, उसने अपनी आधी पूरी को पुन: दो बराबर भागों में बाँट लिया और फरीदा से पूछा कि यह टुकड़ा पूर्ण पूरी का कौन सा भाग अथवा भिन्न है। (आकृति 7.1)

बिना कोई उत्तर दिए, फरीदा ने भी अपनी आधी पूरी को दो बराबर भागों में बाँट लिया और सुभाष के भागों के साथ रख दिया। उसने कहा कि इन चारों बराबर भागों से मिलकर एक पूर्ण (whole) बनता है। (आकृति 7.2)

आकृति 7.2
अत:, प्रत्येक बराबर भाग एक पूर्ण पूरी का एक-चौथाई (One-fourth) है और ये चारों भाग मिलकर 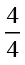 या 1 पूर्ण पूरी होगा।
या 1 पूर्ण पूरी होगा।
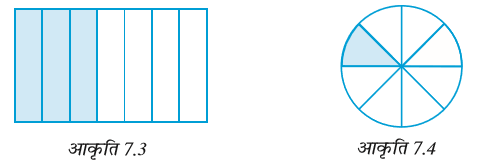
खाते समय उन्होंने यह चर्चा की कि वे भिन्नों के बारे में पहले क्या पढ़ चुके हैं। 4 बराबर भागों में से 3 भाग 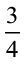 दर्शाते हैं। इसी प्रकार, जब हम एक पूर्ण को 7 बराबर भागों में विभाजित (बाँट) कर उसमें से 3 भाग लें, तो
दर्शाते हैं। इसी प्रकार, जब हम एक पूर्ण को 7 बराबर भागों में विभाजित (बाँट) कर उसमें से 3 भाग लें, तो 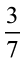 प्राप्त होता है (आकृति 7.3)।
प्राप्त होता है (आकृति 7.3)। 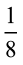 के लिए, हम एक पूर्ण को 8 बराबर भागों में बाँटते हैं और इनमें से एक भाग ले लेते हैं। (आकृति 7.4)
के लिए, हम एक पूर्ण को 8 बराबर भागों में बाँटते हैं और इनमें से एक भाग ले लेते हैं। (आकृति 7.4)
फरीदा ने कहा कि हम पढ़ चुके हैं कि भिन्न वह संख्या है जो एक पूर्ण (whole) का भाग निरूपित करती है। यह पूर्ण एक अकेली वस्तु हो सकती है अथवा वस्तुओं का एक समूह (group) भी हो सकता है। सुभाष ने देखा कि [ये सभी भाग बराबर होने चाहिए।]

7.2 एक भिन्न
आइए, उपरोक्त चर्चा पर पुनर्विचार करें।
एक भिन्न का अर्थ है एक समूह का अथवा एक क्षेत्र (region) का एक भाग।
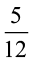 एक भिन्न है। हम इसे ‘पाँच-बारहांश’ (Five-twelveth) पढ़ते हैं।
एक भिन्न है। हम इसे ‘पाँच-बारहांश’ (Five-twelveth) पढ़ते हैं।
"12" क्या दर्शाता है? यह बराबर भागों की वह संख्या है जिनमें एक पूर्ण को बाँटा गया है।
"5" क्या दर्शाता है? यह बराबर भागों की वह संख्या है जो सभी 12 भागों में से लिए गए हैं।
यहाँ 5 अंश (numerator) और 12 हर (denominator) कहलाता है।
भिन्न 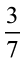 का अंश बताइए।
का अंश बताइए। 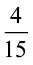 का हर क्या है?
का हर क्या है?
 यह खेल खेलिए :
यह खेल खेलिए :
आप अपने मित्रों के साथ इस खेल को खेल सकते हैं।
यहाँ दर्शाई हुई जाली या ग्रिड (grid) की कई प्रतियाँ लीजिए।

कोई भिन्न, मान लीजिए, 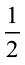 पर विचार कीजिए।
पर विचार कीजिए।
आप में से प्रत्येक विद्यार्थी ग्रिड का 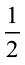 भाग छायांकित करे।
भाग छायांकित करे।
प्रतिबंध यह है कि आप में से किसी का भी छायांकित भाग समान नहीं होना चाहिए।
प्रश्नावली 7.1
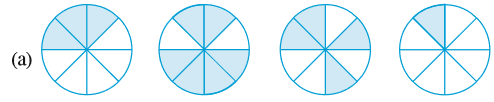
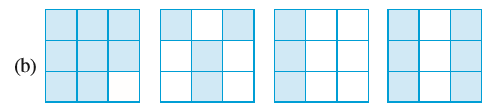
1. छायांकित भाग को निरूपित करने वाली भिन्न लिखिए :
2. दी हुई भिन्न के अनुसार, भागों को छायांकित कीजिए :
3. निम्न में, यदि कोई गलती है, तो पहचानिए :
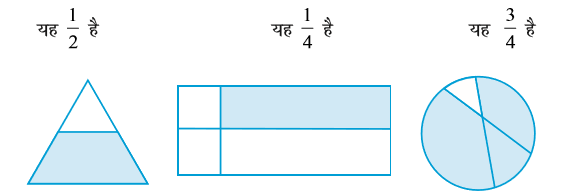
4. 8 घंटे एक दिन की कौन सी भिन्न है?
5. 40 मिनट एक घंटे की कौन सी भिन्न है?
6. आर्या, अभिमन्यु और विवेक एक साथ, बाँटकर खाना खाते हैं। आर्या दो सैंडविच लेकर आता है–एक सब्ज़ी वाला और दूसरा जैम (Jam) वाला। अन्य दो लड़के अपना खाना लाना भूल गए। आर्या अपने सैंडविचों को उन दोनों के साथ बाँटकर खाने को तैयार हो जाता है, ताकि प्रत्येक व्यक्ति को प्रत्येक सैंडविच में से बराबर भाग मिले।
(a) आर्या अपनी सैंडविचों को किस प्रकार बाँटे कि प्रत्येक को बराबर भाग मिले?
(b) प्रत्येक लड़के को एक सैंडविच का कौन-सा भाग मिलेगा?
7. कंचन ड्रेसों (dresses) को रंगती है। उसे 30 ड्रेस रंगनी थीं। उसने अब तक 20 ड्रेस रंग ली हैं। उसने ड्रेसों की कितनी भिन्न रंग ली हैं?
8. 2 से 12 तक की प्राकृत संख्याएँ लिखिए। अभाज्य संख्याएँ इनकी कौन-सी भिन्न हैं?
9. 102 से 113 तक की प्राकृत संख्याएँ लिखिए। अभाज्य संख्याएँ इनकी कौन-सी भिन्न हैं?
10. इन वृत्तों की कौन-सी भिन्नों में X है?

11. क्रिस्तिन अपने जन्म दिन पर एक सीडी प्लेयर (CD Player) प्राप्त करती है। वह तब से सीडी इकट्ठी करना प्रारंभ कर देती है। वह 3 सीडी खरीदती है और 5 सीडी उपहार के रूप में प्राप्त करती है। उसके द्वारा खरीदी गई सीडी की संख्या, कुल सीडी की संख्या की कौन-सी भिन्न है?
7.3 संख्या रेखा पर भिन्न
आप एक संख्या रेखा पर पूर्ण संख्याओं 0,1,2... को दर्शाना सीख चुके हैं। क्या आप भिन्नों को संख्या रेखा पर दर्शा सकते हैं? आइए, एक संख्या रेखा खींचें। क्या हम इस पर 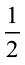 को दर्शा सकते हैं? हम जानते हैं कि
को दर्शा सकते हैं? हम जानते हैं कि 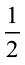 संख्या 0 से बड़ी है और 1 से छोटी है। इसलिए इसे 0 से 1 के बीच में स्थित होना चाहिए।
संख्या 0 से बड़ी है और 1 से छोटी है। इसलिए इसे 0 से 1 के बीच में स्थित होना चाहिए।
चूँकि हमें 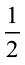 को दर्शाना है, इसलिए हम 0 और 1 के बीच की दूरी को दो बराबर भागों में विभाजित करते हैं और एक भाग को
को दर्शाना है, इसलिए हम 0 और 1 के बीच की दूरी को दो बराबर भागों में विभाजित करते हैं और एक भाग को 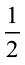 से दर्शाते हैं (जैसा कि आकृति 7.5 में दिखाया गया है)।
से दर्शाते हैं (जैसा कि आकृति 7.5 में दिखाया गया है)।

संख्या रेखा पर 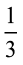 को दर्शाने के लिए, 0 और 1 के बीच की दूरी को कितने बराबर भागों में विभाजित करना चाहिए? हम 0 और 1 के बीच की दूरी को 3 बराबर भागों में विभाजित करते हैं और एक भाग को
को दर्शाने के लिए, 0 और 1 के बीच की दूरी को कितने बराबर भागों में विभाजित करना चाहिए? हम 0 और 1 के बीच की दूरी को 3 बराबर भागों में विभाजित करते हैं और एक भाग को 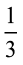 से दर्शाते हैं (जैसा कि आकृति 7.6 में दिखाया गया है।)।
से दर्शाते हैं (जैसा कि आकृति 7.6 में दिखाया गया है।)।

क्या हम इस संख्या रेखा पर 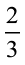 को दर्शा सकते हैं?
को दर्शा सकते हैं? 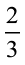 का अर्थ है 3 बराबर भागों में से 2 भाग, जैसा कि आकृति 7.7 में दिखाया गया है।
का अर्थ है 3 बराबर भागों में से 2 भाग, जैसा कि आकृति 7.7 में दिखाया गया है।

इसी प्रकार, आप 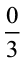 और
और 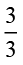 संख्या रेखा पर किस प्रकार दर्शाएँगे?
संख्या रेखा पर किस प्रकार दर्शाएँगे?
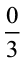 बिंदु शून्य है और चूँकि
बिंदु शून्य है और चूँकि 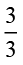 एक पूर्ण है, इसलिए इसे संख्या रेखा पर बिंदु 1 से दर्शाया जा सकता है (जैसा आकृति 7.7 में दिखाया है)।
एक पूर्ण है, इसलिए इसे संख्या रेखा पर बिंदु 1 से दर्शाया जा सकता है (जैसा आकृति 7.7 में दिखाया है)।
अब यदि हमें एक संख्या रेखा पर 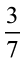 को दर्शाना है, तो हम 0 और 1 के बीच की दूरी को कितने बराबर भागों में विभाजित करेंगे? यदि P भिन्न
को दर्शाना है, तो हम 0 और 1 के बीच की दूरी को कितने बराबर भागों में विभाजित करेंगे? यदि P भिन्न 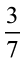 को दर्शाता है, तो शून्य और P के बीच कुल कितने बराबर भाग हैं?
को दर्शाता है, तो शून्य और P के बीच कुल कितने बराबर भाग हैं? 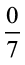 और
और 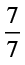 कहाँ स्थित होंगे?
कहाँ स्थित होंगे?

1. संख्या रेखा पर 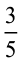 को दर्शाइए।
को दर्शाइए।
2. संख्या रेखा पर 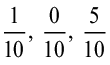 और
और 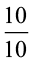 को दर्शाइए।
को दर्शाइए।
3. क्या आप 0 और 1 के बीच कोई अन्य भिन्न को दर्शा सकते हैं? एेसी पाँच भिन्न और लिखिए जिन्हें आप दर्शा सकते हैं और उन्हें संख्या रेखा पर दर्शाइए।
4. 0 और 1 के बीच में कितनी भिन्न स्थित हैं? सोचिए, चर्चा कीजिए और अपने उत्तर को लिखिए।
7.4 उचित भिन्न
अब आप सीख चुके हैं कि भिन्नों को संख्या रेखा पर किस प्रकार दर्शाया जाता है। अलग-अलग संख्या रेखाओं पर भिन्न 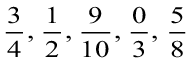 की स्थिति दर्शाइए।
की स्थिति दर्शाइए।
क्या इनमें से कोई भी भिन्न 1 के दाईं ओर है। ये सभी भिन्न 1 के बाईं ओर स्थित हैं, क्योंकि ये 1 से छोटी हैं।
वास्तव में, अभी तक हमारे द्वारा पढ़ी गई भिन्न 1 से छोटी ही हैं। ये उचित भिन्न हैं। जैसाकि फरीदा ने कहा है (अनुच्छेद 7.1), उचित भिन्न वह संख्या है जो एक पूर्ण (Whole) के भाग को निरूपित करती है। इसमें हर यह बताता है कि पूर्ण को कितने बराबर भागों में विभाजित किया गया है तथा अंश यह दर्शाता है कि इसमें से कितने भाग चुने गए हैं। अत:, एक उचित भिन्न में अंश सदैव हर से छोटा होता है।

1. एक उचित भिन्न लिखिए :
(a) जिसका अंश 5 और हर 7 है।
(b) जिसका हर 9 है और अंश 5 है।
(c) जिसके अंश और हर का योग 10 है। आप इस प्रकार की कितनी भिन्न लिख सकते हैं?
(d) जिसका हर उसके अंश से 4 अधिक है।
(कोई पाँच भिन्न बनाइए। आप और कितनी भिन्न बना सकते हैं?)
2. एक भिन्न दी हुई है। इसे देखकर, आप कैसे बता सकते हैं कि यह भिन्न
(a) 1 से छोटी है?
(b) 1 के बराबर है?
3. संकेत ‘>’, ‘<’ या ‘=’ का प्रयोग करके, रिक्त स्थानों को भरिए :
7.5 विषम भिन्न और मिश्रित भिन्न (संख्याएँ)
अनघा, रवि, रेशमा और जॉन ने अपना खाना बाँटकर खाया। अपने साथ वे पाँच सेब भी लाए थे। खाना खाने के बाद चारों मित्र सेब खाना चाहते थे। वे चारों आपस में इन पाँच सेबों को किस प्रकार बाँट सकते हैं?
अनघा ने कहा, आओ हम सभी एक पूरा सेब और पाँचवें का एक-चौथाई ले लें।
रेशमा ने कहा यह ठीक है, परंतु हम प्रत्येक सेब को चार बराबर भागों में बाँट सकते हैं और प्रत्येक सेब का एक-चौथाई ले सकते हैं।
रवि ने कहा, ‘बाँटने की दोनों विधियों से प्रत्येक को बराबर भाग मिलेगा और वह है, 5 चतुर्थांश (quarters)। चूँकि 4 चतुर्थांशों से एक पूर्ण बनता है, इसलिए हम कह सकते हैं कि हममें से प्रत्येक को एक पूर्ण और एक चतुर्थांश (चौथाई) मिलता है। प्रत्येक भाग 5 भाग 4 है। क्या इसे 5 ÷ 4 लिखते हैं? जॉन ने कहा, हाँ इसे 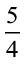 भी लिखा जा सकता है। अनघा ने कहा,
भी लिखा जा सकता है। अनघा ने कहा, 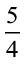 में अंश हर से बड़ा है। वे भिन्न जिनमें अंश हर से बड़ा होता है विषम भिन्न (improper fractions) कहलाती हैं।
में अंश हर से बड़ा है। वे भिन्न जिनमें अंश हर से बड़ा होता है विषम भिन्न (improper fractions) कहलाती हैं।
इस प्रकार, 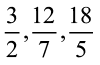 प्रत्येक एक विषम भिन्न हैं।
प्रत्येक एक विषम भिन्न हैं।
1. हर 7 वाली पाँच विषम भिन्न लिखिए।
2. अंश 11 वाली पाँच विषम भिन्न लिखिए।
रवि ने जॉन से पूछा, ‘इस भाग को लिखने की अन्य विधि क्या है? क्या यह 5 सेबों को अनघा द्वारा विभाजित करने की विधि से प्राप्त हो जाता है?’
जॉन ने कहा, ‘हाँ, वास्तव में यह अनघा की विधि से प्राप्त हो जाता है। उसकी विधि में, प्रत्येक का भाग एक पूर्ण और एक चौथाई से मिलकर बना है। यह 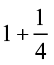 है, जिसे
है, जिसे 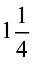 भी लिखा जाता है। याद रखिए
भी लिखा जाता है। याद रखिए 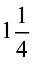 और
और 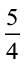 एक ही हैं।’ (आकृति 7.8)
एक ही हैं।’ (आकृति 7.8)
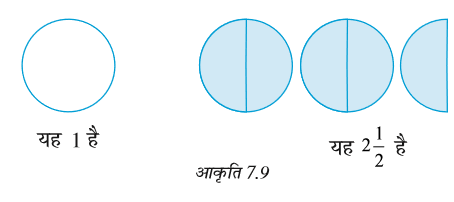
याद कीजिए कि फरीदा ने कितनी पूरियाँ खाई थीं। उसने 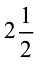 पूरियाँ खाई थीं (आकृति 7.9)।
पूरियाँ खाई थीं (आकृति 7.9)।
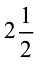 में कितने आधे भाग (halves) छायांकित हैं? इसमें 5 आधे भाग छायांकित हैं।
में कितने आधे भाग (halves) छायांकित हैं? इसमें 5 आधे भाग छायांकित हैं।
इसलिए, यह भिन्न 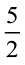 है। स्पष्ट है कि यह
है। स्पष्ट है कि यह 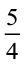 नहीं हैै।
नहीं हैै।
क्या आप जानते हैं?
टेनिस रैकिटों के हत्थे की माप प्राय: मिश्रित संख्याओं में होती हैं। उदाहरणार्थ, एक माप
‘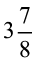 ’ इंच है और अन्य माप ‘
’ इंच है और अन्य माप ‘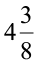 ’ इंच है।
’ इंच है।
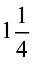 और
और 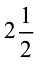 जैसी भिन्न, मिश्रित भिन्न (mixed fractions) कहलाती हैं। एक मिश्रित भिन्न में एक भाग पूर्ण होता है और एक भाग भिन्न होता है।
जैसी भिन्न, मिश्रित भिन्न (mixed fractions) कहलाती हैं। एक मिश्रित भिन्न में एक भाग पूर्ण होता है और एक भाग भिन्न होता है।
आपको मिश्रित संख्याएँ कहाँ-कहाँ मिलती हैं? कुछ उदाहरण दीजिए।
उदाहरण 1 : निम्न को मिश्रित संख्याओं के रूप में व्यक्त कीजिए :
हल :
अर्थात्, 3 पूर्ण और 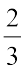 अधिक या
अधिक या 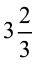
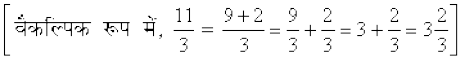
(c) और (d) को उपरोक्त दोनों विधियों द्वारा करने का प्रयत्न कीजिए।
इस प्रकार, हम एक विषम भिन्न को एक मिश्रित संख्या के रूप में व्यक्त कर सकते हैं। इसके लिए हम अंश को हर से भाग देकर भागफल और शेषफल प्राप्त करते हैं। फिर मिश्रित संख्या को  के रूप में लिख लेते हैं।
के रूप में लिख लेते हैं।
उदाहरण 2 : निम्नलिखित मिश्रित भिन्नों को विषम भिन्नों के रूप में व्यक्त कीजिए :
हल :
इस प्रकार, हम एक मिश्रित भिन्न को एक विषम भिन्न के रूप में व्यक्त कर सकते हैं। इसके लिए हम पूर्ण को हर से गुणा करके गुणनफल में अंश को जोड़ते हैं। फिर विषम भिन्न 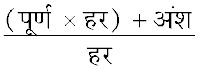 होगा।
होगा।
प्रश्नावली 7.2
1. संख्या रेखाएँ खींचिए और उन पर निम्नलिखित भिन्नों को बिंदु रूप में दर्शाइए :
2. निम्नलिखित को मिश्रित भिन्न के रूप में व्यक्त कीजिए :
3. निम्नलिखित को विषम भिन्नों के रूप में व्यक्त कीजिए :
7.6 तुल्य भिन्न
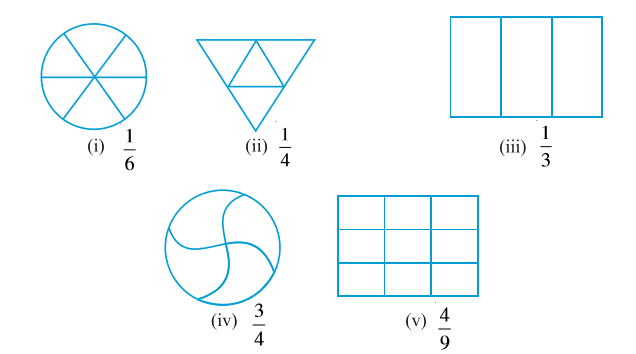
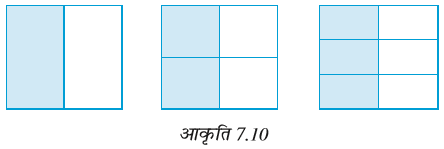
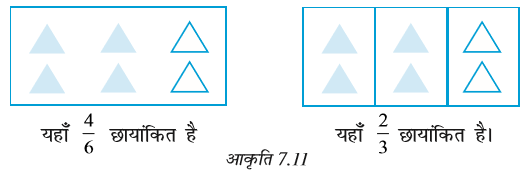
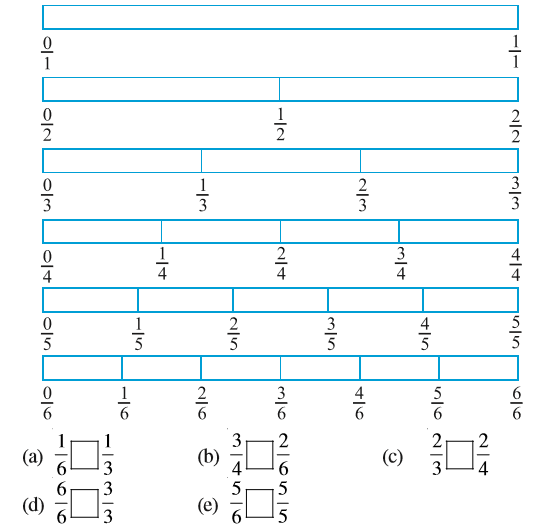
भिन्नों के निम्न निरूपणों को देखिए (आकृति 7.10) :
ये भिन्न 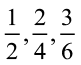 हैं। जो कुल भागों में से लिए गए भागों को दर्शाती हैं। यदि हम इन भिन्नों के चित्रीय निरूपणों को एक दूसरे पर रखें, तो वे बराबर होंगे। क्या आप इससे सहमत हैं?
हैं। जो कुल भागों में से लिए गए भागों को दर्शाती हैं। यदि हम इन भिन्नों के चित्रीय निरूपणों को एक दूसरे पर रखें, तो वे बराबर होंगे। क्या आप इससे सहमत हैं?
एेसी भिन्न तुल्य भिन्न (Equivalent fractions) कहलाती हैं। एेसी ही 3 और भिन्नों को बताइए जो ऊपर ली गई भिन्नों के तुल्य हाें।

1. क्या 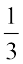 और
और  ;
;  और
और  तथा
तथा 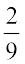 और
और 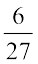 तुल्य भिन्न हैं? कारण दीजिए।
तुल्य भिन्न हैं? कारण दीजिए।
2. चार तुल्य भिन्नों का एक अन्य उदाहरण दीजिए।
3. प्रत्येक भिन्न को पहचानिए। क्या ये भिन्न तुल्य हैं?
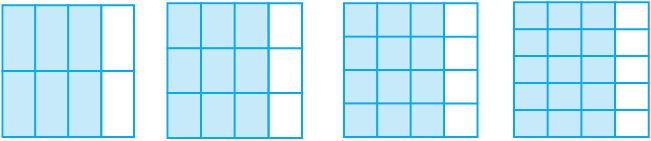
तुल्य भिन्नों को समझना
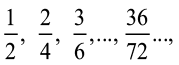 में से सभी तुल्य भिन्न हैं। ये एक पूर्ण का समान भाग निरूपित करती हैं।
में से सभी तुल्य भिन्न हैं। ये एक पूर्ण का समान भाग निरूपित करती हैं।
सोचिए, चर्चा कीजिए और लिखिए :
तुल्य भिन्न एक पूर्ण का समान भाग क्यों निरूपित करती हैं? हम इनमें से एक भिन्न को अन्य भिन्न से किस प्रकार प्राप्त कर सकते हैं?
हम देखते हैं कि 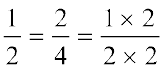 है।
है।
इसी प्रकार, 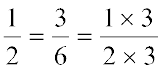 तथा
तथा
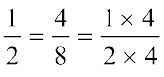 है।
है।
एक दी हुई भिन्न की तुल्य भिन्न ज्ञात करने के लिए, आप उसके अंश और हर को एक समान शून्येतर संख्या से गुणा कर सकते हैं।
रजनी कहती है कि 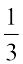 की समतुल्य भिन्न हैं :
की समतुल्य भिन्न हैं :
क्या आप उससे सहमत हैं? कारण सहित स्पष्ट कीजिए।

1. निम्नलिखित में से प्रत्येक की पाँच तुल्य भिन्न ज्ञात कीजिए :
अन्य विधि :
क्या तुल्य भिन्न ज्ञात करने की कोई अन्य विधि भी है? आकृति 7.11 को देखिए:
इनमें छायांकित वस्तुओं की संख्याएँ समान हैं, अर्थात् 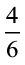 और
और 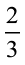 तुल्य भिन्न हैं।
तुल्य भिन्न हैं।
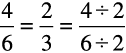
एक दी हुई भिन्न के तुल्य भिन्न ज्ञात करने के लिए हम उस भिन्न के अंश और हर को एक समान शून्येतर संख्या से भाग दे सकते हैं।
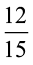 के तुल्य एक भिन्न
के तुल्य एक भिन्न 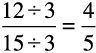 है।
है।
क्या आप  के तुल्य एक एेसी भिन्न ज्ञात कर सकते हैं जिसका हर 5 हो?
के तुल्य एक एेसी भिन्न ज्ञात कर सकते हैं जिसका हर 5 हो?
उदाहरण 3 : 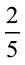 के तुल्य एेसी भिन्न ज्ञात कीजिए जिसका अंश 6 है।
के तुल्य एेसी भिन्न ज्ञात कीजिए जिसका अंश 6 है।
हल : हम जानते हैं कि 2 × 3 = 6 है। इसका अर्थ है कि तुल्य भिन्न प्राप्त करने के लिए, हमें दी हुई भिन्न के अंश और हर को 3 से गुणा करना चाहिए।
अत:, वांछित तुल्य भिन्न 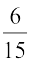 है।
है।
क्या आप इसे चित्रीय रूप से दर्शा सकते हैं?
उदाहरण 4 : 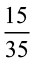 के तुल्य वह भिन्न ज्ञात कीजिए जिसका हर 7 हो।
के तुल्य वह भिन्न ज्ञात कीजिए जिसका हर 7 हो।
हल : हमें प्राप्त है : 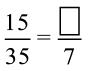
हम हरों को देखें। चूँकि 35 ÷ 5 = 7 है, इसलिए हम 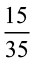 के अंश और हर दोनों को 5 से भाग देंगे।
के अंश और हर दोनों को 5 से भाग देंगे।
हमें प्राप्त होता है 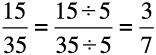
इस प्रकार  को 3 से प्रतिस्थापित कर हम
को 3 से प्रतिस्थापित कर हम 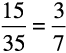 प्राप्त करते हैं।
प्राप्त करते हैं।
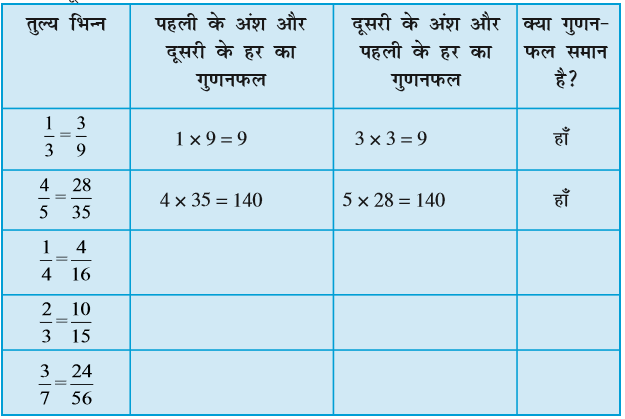
एक रोचक तथ्य :
तुल्य भिन्नों के बारे में एक बात बहुत रोचक है। दी हुर्ह सारणी को पूरा कीजिए। पहली दो पंक्तियाँ पूरी कर दी गई हैं।
उपरोक्त सारणी से हम क्या निष्कर्ष निकालते हैं? इन सभी में, पहली के अंश और दूसरी के हर का गुणनफल दूसरी के अंश और पहली के हर के गुणनफल के बराबर है। ये दोनों गुणनफल कैंची गुणनफल (cross products) कहलाते हैं। तुल्य भिन्नों के अन्य युग्मों के लिए भी कैंची गुणनफल ज्ञात कीजिए। क्या आप तुल्य भिन्नों का एेसा युग्म प्राप्त करते हैं, जिनमें कैंची या क्रास गुणनफल बराबर नहीं हैं? इस नियम से कभी-कभी तुल्य भिन्नों को ज्ञात करने में सहायता मिलती है।
उदाहरण 5 : 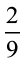 के तुल्य वह भिन्न ज्ञात कीजिए जिसका हर 63 है।
के तुल्य वह भिन्न ज्ञात कीजिए जिसका हर 63 है।
हल : हमें प्राप्त है : 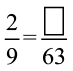
इसके लिए, 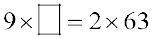 होना चाहिए।
होना चाहिए।
परंतु 63 = 7 × 9 है। इसलिए 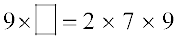 ,
,
= 14 × 9 = 9 × 14
या 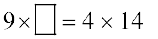
तुलना करने पर 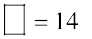 हुआ।
हुआ।
अत:, 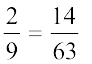 है।
है।
7.7 भिन्न का सरलतम रूप
एक भिन्न 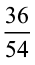 दी हुई है। आइए, इसके तुल्य एक एेसी भिन्न प्राप्त करने का प्रयत्न करें जिसके अंश और हर में 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखंड न हों।
दी हुई है। आइए, इसके तुल्य एक एेसी भिन्न प्राप्त करने का प्रयत्न करें जिसके अंश और हर में 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखंड न हों।
हम एेसा कैसे करते हैं? हम जानते हैं कि 36 और 54 दोनों 2 से विभाज्य हैं।
परंतु 18 और 27 में भी 1 के अतिरिक्त अन्य उभयनिष्ठ गुणनखंड हैं। ये उभयनिष्ठ गुणनखंड 1, 3 और 9 हैं।
चूँकि 2 और 3 में 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखंड नहीं है। इसलिए वांछित भिन्न 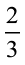 है। इस प्रकार की भिन्न सरलतम रूप (simplest form) की भिन्न कहलाती है। इस प्रकार, एक भिन्न सरलतम रूप (simplest form) या न्यूनतम रूप (lowest form) में तब कही जाती है, जब उसके अंश और हर में 1 के अतिरिक्त कोई अन्य उभयनिष्ठ गुणनखंड न हो।
है। इस प्रकार की भिन्न सरलतम रूप (simplest form) की भिन्न कहलाती है। इस प्रकार, एक भिन्न सरलतम रूप (simplest form) या न्यूनतम रूप (lowest form) में तब कही जाती है, जब उसके अंश और हर में 1 के अतिरिक्त कोई अन्य उभयनिष्ठ गुणनखंड न हो।
एक खेल
यहाँ दी हुई समतुल्य भिन्न बहुत रोचक है। प्रत्येक में 1 से 9 तक के अंक एक बार प्रयोग किए गए हैं।
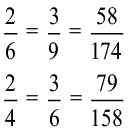
क्या आप एेसी दो और समतुल्य भिन्न ज्ञात कर सकते हैं।
सबसे छोटा रास्ता :
सरलतम रूप में तुल्य भिन्न ज्ञात करने का सबसे छोटा रास्ता यह है कि दी हुई भिन्न के अंश और हर का म.स. निकाला जाए और फिर अंश और हर दोनों को इस म.स. से भाग दे दिया जाए। इस प्रकार, सरलतम रूप में तुल्य भिन्न प्राप्त हो जाएगी।
भिन्न 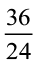 को लीजिए
को लीजिए
36 और 24 का म.स. 12 है।
इस प्रकार, म.स. की अवधारणा एक भिन्न को न्यूनतम (या सरलतम) रूप में बदलने में हमारी सहायता करती है।

1. निम्न को सरलतम में लिखिए :
2. क्या 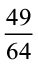 अपने सरलतम रूप में है?
अपने सरलतम रूप में है?
प्रश्नावली 7.3
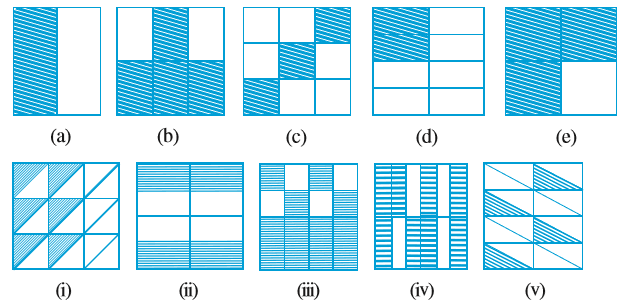
1. प्रत्येक चित्र में छायांकित भागों के लिए भिन्न लिखिए। क्या ये सभी भिन्न तुल्य हैं?
2. छायांकित भागों के लिए भिन्नों को लिखिए और प्रत्येक पंक्ति में से तुल्य भिन्नों को चुनिए।
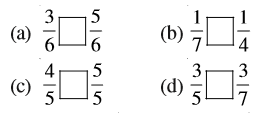
3. निम्न में से प्रत्येक में  को सही संख्या से प्रतिस्थापित कीजिए :
को सही संख्या से प्रतिस्थापित कीजिए :
4. 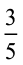 के तुल्य वह भिन्न ज्ञात कीजिए जिसका
के तुल्य वह भिन्न ज्ञात कीजिए जिसका
(a) हर 20 है
b) अंश 9 है
(c) हर 30 है
(d) अंश 27 है
5. 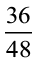 के तुल्य वह भिन्न ज्ञात कीजिए जिसका
के तुल्य वह भिन्न ज्ञात कीजिए जिसका
(a) अंश 9 है
(b) हर 4 है
6. जाँच कीजिए कि निम्न भिन्न तुल्य हैं या नहीं :
7. निम्नलिखित भिन्नों को उनके सरलतम रूप में बदलिए :
8. रमेश के पास 20 पेंसिल थीं। शीलू के पास 50 पेंसिल और जमाल के पास 80 पेंसिल थीं। 4 महीने के बाद रमेश ने 10 पेंसिल तथा शीलू ने 25 पेंसिल प्रयोग कर लीं और जमाल ने 40 पेंसिल प्रयोग कर ली। प्रत्येक ने अपनी पेंसिलों की कौन-सी भिन्न प्रयोग कर ली? जाँच कीजिए कि प्रत्येक ने अपनी पेंसिलों की समान भिन्न प्रयोग की है।
9. तुल्य भिन्नों का मिलान कीजिए और प्रत्येक के लिए दो भिन्न और लिखिए :

7.8 समान भिन्न
इस प्रकार, 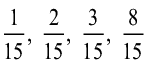 सभी समान भिन्न हैं।
सभी समान भिन्न हैं।
क्या 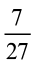 और
और 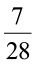 समान भिन्न हैं? इनके हर भिन्न हैं। अत: ये समान भिन्न नहीं हैं। ये असमान भिन्न (unlike fractions) कहलाती हैं।
समान भिन्न हैं? इनके हर भिन्न हैं। अत: ये समान भिन्न नहीं हैं। ये असमान भिन्न (unlike fractions) कहलाती हैं।
समान भिन्नों के पाँच युग्म और असमान भिन्नों के पाँच युग्म लिखिए।
7.9 भिन्नों की तुलना
सोहनी की थाली में 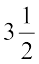 रोटियाँ हैं और रीता की थाली में
रोटियाँ हैं और रीता की थाली में 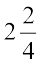 रोटियाँ हैं। किसकी थाली में अधिक रोटियाँ हैं? स्पष्टत:, सोहनी के पास 3 से अधिक रोटियाँ हैं और रीता के पास 3 से कम रोटियाँ हैं। अत:, सोहनी के पास अधिक रोटियाँ हैं।
रोटियाँ हैं। किसकी थाली में अधिक रोटियाँ हैं? स्पष्टत:, सोहनी के पास 3 से अधिक रोटियाँ हैं और रीता के पास 3 से कम रोटियाँ हैं। अत:, सोहनी के पास अधिक रोटियाँ हैं।
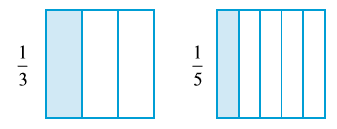
अब आकृति 7.12 में दर्शायी भिन्नों 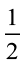 और
और 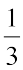 पर विचार कीजिए। पूर्ण के
पर विचार कीजिए। पूर्ण के 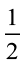 का संगत भाग उसी पूर्ण के
का संगत भाग उसी पूर्ण के 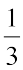 के संगत भाग से स्पष्ट रूप से बड़ा है। अत:,
के संगत भाग से स्पष्ट रूप से बड़ा है। अत:, 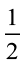 ,
, 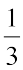 से बड़ी है।
से बड़ी है।
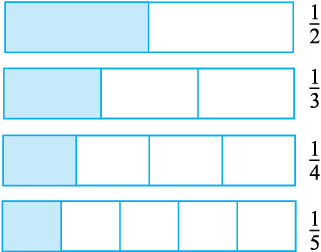
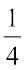 बड़ी है या
बड़ी है या 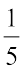 ? इसके लिए, हम भिन्नों को आकृतियों से दर्शाने की सोच सकते हैं (जैसा आकृति 7.12 में है)। परंतु आकृतियाँ बनाना सदैव सरल नहीं होता, विशेषकर जब हर 13 जैसे हों। अत:, हमें भिन्नों की तुलना करने की कोई क्रमबद्ध विधि ज्ञात करनी चाहिए। विशेष रूप से, समान भिन्नों की तुलना करना सरल है। इसलिए हम पहले समान भिन्नों की ही तुलना करते हैं।
? इसके लिए, हम भिन्नों को आकृतियों से दर्शाने की सोच सकते हैं (जैसा आकृति 7.12 में है)। परंतु आकृतियाँ बनाना सदैव सरल नहीं होता, विशेषकर जब हर 13 जैसे हों। अत:, हमें भिन्नों की तुलना करने की कोई क्रमबद्ध विधि ज्ञात करनी चाहिए। विशेष रूप से, समान भिन्नों की तुलना करना सरल है। इसलिए हम पहले समान भिन्नों की ही तुलना करते हैं।
1. आप जूस की बोतल का  वाँ भाग प्राप्त करते हैं और आपकी बहन को उस बोतल का एक-तिहाई भाग मिलता है। किसको अधिक जूस मिलता है?
वाँ भाग प्राप्त करते हैं और आपकी बहन को उस बोतल का एक-तिहाई भाग मिलता है। किसको अधिक जूस मिलता है?
7.9.1 समान भिन्नों की तुलना
समान हर वाली भिन्न, समान भिन्न होती हैं। इनमें से कौन सी भिन्न समान भिन्न हैं?
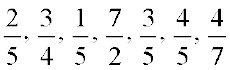
आइए, दो समान भिन्नों 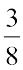 और
और 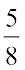 की तुलना करें।
की तुलना करें।

दोनों भिन्नों में पूर्ण को 8 बराबर भागों में विभाजित किया गया है। इन 8 बराबर भागों में से, हम 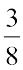 और
और 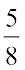 के लिए क्रमश: 3 और 5 भाग लेते हैं। स्पष्ट है कि 5 भागों का संगत भाग 3 भागों के संगत भाग से बड़ा है। अत:,
के लिए क्रमश: 3 और 5 भाग लेते हैं। स्पष्ट है कि 5 भागों का संगत भाग 3 भागों के संगत भाग से बड़ा है। अत:, 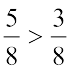 है। ध्यान दीजिए कि लिए गए भाग अंश से प्राप्त होते हैं। अत:, यह स्पष्ट है कि समान हरों वाली दो भिन्नों के लिए, बड़े अंश वाली भिन्न बड़ी होती है।
है। ध्यान दीजिए कि लिए गए भाग अंश से प्राप्त होते हैं। अत:, यह स्पष्ट है कि समान हरों वाली दो भिन्नों के लिए, बड़े अंश वाली भिन्न बड़ी होती है। 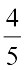 और
और 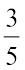 में
में 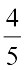 बड़ी भिन्न है।
बड़ी भिन्न है। 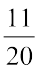 और
और 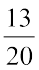 में
में 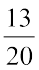 बड़ी है, इत्यादि।
बड़ी है, इत्यादि।

1. कौन-सी भिन्न बड़ी है?
एेसी भिन्नों की तुलना करना क्यों सरल है?
2. निम्न को आरोही क्रम में लिखिए और साथ ही अवरोही क्रम में भी लिखिए :
7.9.2 असमान भिन्नों की तुलना
दो भिन्नें असमान होती हैं, यदि उनके हर भिन्न-भिन्न हों। उदाहरणार्थ 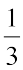 और
और 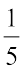 असमान भिन्न हैं।
असमान भिन्न हैं। 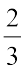 और
और 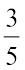 भी असमान भिन्न हैं।
भी असमान भिन्न हैं।
समान अंश वाली असमान भिन्न
असमान भिन्नों 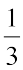 और
और 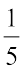 के एक युग्म पर विचार कीजिए, जिसमें अंश समान हैं।
के एक युग्म पर विचार कीजिए, जिसमें अंश समान हैं।
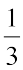 बड़ी है या
बड़ी है या 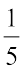 ?
?
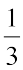 के लिए, हम एक पूर्ण को 3 बराबर भागों में विभाजित करते हैं और उसमें से एक भाग लेते हैं।
के लिए, हम एक पूर्ण को 3 बराबर भागों में विभाजित करते हैं और उसमें से एक भाग लेते हैं। 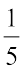 के लिए, हम एक पूर्ण को 5 बराबर भागों में विभाजित करते हैं और उसमें से एक भाग लेते हैं। ध्यान दीजिए कि
के लिए, हम एक पूर्ण को 5 बराबर भागों में विभाजित करते हैं और उसमें से एक भाग लेते हैं। ध्यान दीजिए कि 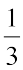 में पूर्ण को
में पूर्ण को 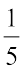 की तुलना में कम भागों में विभाजित किया गया है। अत:,
की तुलना में कम भागों में विभाजित किया गया है। अत:, 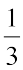 में प्राप्त बराबर भाग
में प्राप्त बराबर भाग 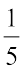 में प्राप्त बराबर भागों से बड़े हैं। चूँकि दोनों स्थितियों में, हम एक ही (1) भाग ले रहे हैं, इसलिए पूर्ण का
में प्राप्त बराबर भागों से बड़े हैं। चूँकि दोनों स्थितियों में, हम एक ही (1) भाग ले रहे हैं, इसलिए पूर्ण का 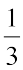 दर्शाने वाला भाग उसके
दर्शाने वाला भाग उसके 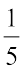 दर्शाने वाले भाग से बड़ा है। अत:,
दर्शाने वाले भाग से बड़ा है। अत:, 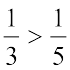 है।
है।
इसी प्रकार, हम कह सकते हैं कि 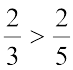 है। इस दशा में, स्थिति पहले जैसी है, केवल यह अंतर है कि अंश 1 न होकर 2 है। पूर्ण
है। इस दशा में, स्थिति पहले जैसी है, केवल यह अंतर है कि अंश 1 न होकर 2 है। पूर्ण 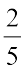 के लिए
के लिए 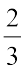 की तुलना में अधिक बराबर भागों में बाँटा गया है। अत:,
की तुलना में अधिक बराबर भागों में बाँटा गया है। अत:, 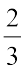 की स्थिति वाला प्रत्येक बराबर भाग
की स्थिति वाला प्रत्येक बराबर भाग 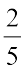 वाली स्थिति के बराबर भाग से बड़ा है। अब हम बराबर भागों की समान संख्या ले रहे हैं (क्योंकि अंश समान हैं)। अत:, पूर्ण का
वाली स्थिति के बराबर भाग से बड़ा है। अब हम बराबर भागों की समान संख्या ले रहे हैं (क्योंकि अंश समान हैं)। अत:, पूर्ण का 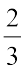 दर्शाने वाला भाग उसके
दर्शाने वाला भाग उसके 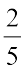 दर्शाने वाले भाग से बड़ा है। इसीलिए,
दर्शाने वाले भाग से बड़ा है। इसीलिए, 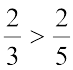 है।
है।
उपरोक्त उदाहरण से, हम देख सकते हैं कि यदि दो भिन्नों में अंश समान हो, तो दोनों भिन्नों में छोटे हर वाली भिन्न बड़ी होती है।
इस प्रकार, 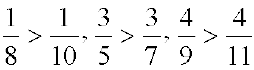 इत्यादि है।
इत्यादि है।
आइए 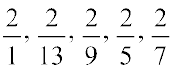 को बढ़ते हुए (आरोही) क्रम में व्यवस्थित करें। ये सभी भिन्न असमान भिन्न हैं, परन्तु इनके अंश समान हैं। अत:, जितना हर बड़ा होगा, भिन्न उतनी ही छोटी होगी। सबसे छोटी भिन्न
को बढ़ते हुए (आरोही) क्रम में व्यवस्थित करें। ये सभी भिन्न असमान भिन्न हैं, परन्तु इनके अंश समान हैं। अत:, जितना हर बड़ा होगा, भिन्न उतनी ही छोटी होगी। सबसे छोटी भिन्न 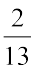 है, क्योंकि इसका हर सबसे बड़ा है। इस क्रम में अगली तीन भिन्न
है, क्योंकि इसका हर सबसे बड़ा है। इस क्रम में अगली तीन भिन्न 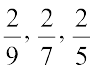 हैं। सबसे बड़ी भिन्न
हैं। सबसे बड़ी भिन्न  है (इसका सबसे छोटा हर है)। अत: आरोही क्रम में भिन्न
है (इसका सबसे छोटा हर है)। अत: आरोही क्रम में भिन्न 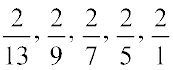 हैं।
हैं।

1. निम्नलिखित भिन्नों को आरोही और अवरोही क्रमों में व्यवस्थित कीजिए :
(c) उपरोक्त प्रकार के तीन और उदाहरण लिखिए तथा उन्हें आरोही और अवरोही क्रमों में व्यवस्थित कीजिए।
मान लीजिए, हम दो असमान भिन्न 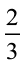 और
और 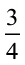 की तुलना करना चाहते हैं। एेसा करना तब संभव होगा, जब हम दोनों भिन्नों के हरों के भाग किसी तरह से बराबर बना लें, अर्थात् उनके हर बराबर बना लें। एक बार एेसा कर लेने पर जो समान भिन्न प्राप्त होगी उसके अंशों के भागों की तुलना करके भिन्नों की तुलना सरलता से की जा सकती है।
की तुलना करना चाहते हैं। एेसा करना तब संभव होगा, जब हम दोनों भिन्नों के हरों के भाग किसी तरह से बराबर बना लें, अर्थात् उनके हर बराबर बना लें। एक बार एेसा कर लेने पर जो समान भिन्न प्राप्त होगी उसके अंशों के भागों की तुलना करके भिन्नों की तुलना सरलता से की जा सकती है।
आइए, पुन: 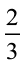 और
और 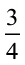 को लें और इनकी तुल्य भिन्न ज्ञात करें।
को लें और इनकी तुल्य भिन्न ज्ञात करें।
अब, 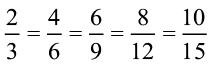 = ....
= ....
इसी प्रकार, 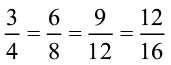 = ....
= ....
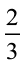 और
और 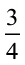 में समान हर 12 वाली तुल्य भिन्न क्रमश:
में समान हर 12 वाली तुल्य भिन्न क्रमश: 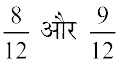 हैं। अर्थात्
हैं। अर्थात्
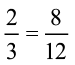 है और
है और 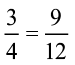 है।
है।
चूँकि, 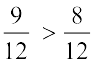 है, इसलिए,
है, इसलिए, 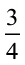 >
>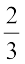 है।
है।
उदाहरण 6 : 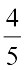 और
और 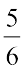 की तुलना कीजिए।
की तुलना कीजिए।
हल : ये असमान भिन्न हैं। इनके अंश भी भिन्न-भिन्न हैं। आइए, इनकी तुल्य भिन्नों को लिखें।
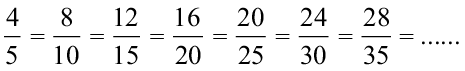
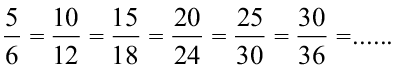
समान हर वाली तुल्य भिन्न हैं :
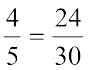 और
और 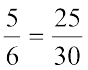
चूँकि 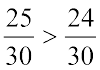 है, इसलिए
है, इसलिए 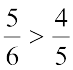 है। ध्यान दीजिए कि तुल्य भिन्नों का समान हर 30 है, जो 5 × 6 के बराबर है। यह 5 और 6 का एक सार्व गुणज है।
है। ध्यान दीजिए कि तुल्य भिन्नों का समान हर 30 है, जो 5 × 6 के बराबर है। यह 5 और 6 का एक सार्व गुणज है।
इसलिए, दो असमान भिन्नों की तुलना करते समय हम पहले इन भिन्नों की एेसी तुल्य भिन्नें ज्ञात करते हैं जिनमें इनके हरों के सार्व गुणज हों।
उदाहरण 7 : 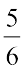 और
और 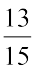 की तुलना कीजिए।
की तुलना कीजिए।
हल : ये असमान भिन्न हैं। पहले हमें 6 और 15 के सार्व गुणज वाली तुल्य भिन्नें ज्ञात करनी चाहिए।
अब, 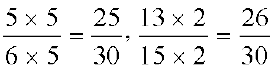 है।
है।
चूँकि 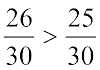 है, इसलिए
है, इसलिए 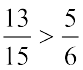 है।
है।
ल.स. क्यों?
6 और 15 का गुणनफल 90 है। स्पष्टत:, 90 भी 6 और 15 का एक सार्व गुणज है। हम 30 के स्थान पर 90 का भी प्रयोग कर सकते हैं। इसमें कोई गलती नहीं होगी। परंतु हम जानते हैं कि छोटी संख्याओं के साथ कार्य करना अधिक सरल और सुविधाजनक होता है। इसलिए हम सार्व गुणज को अधिक से अधिक छोटा लेना चाहेंगे। इसीलिए, समान हर बनाने के लिए हरों के ल.स. को प्राथमिकता दी जाती है।
प्रश्नावली 7.4
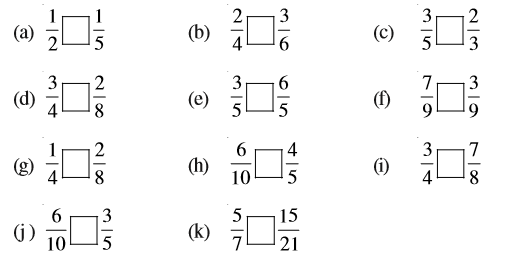
1. प्रत्येक चित्र के लिए भिन्नों को लिखिए। भिन्नों के बीच में सही चिह्न ‘<’, ‘=’, ‘>’ का प्रयोग करते हुए, इन्हें आरोही और अवरोही क्रमों में व्यवस्थित कीजिए :
(c) 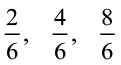 और
और 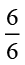 को संख्या रेखा पर दर्शाइए।
को संख्या रेखा पर दर्शाइए।
दी हुई भिन्न के बीच में उचित चिह्न ‘<’ या ‘>’ भरिए :
2. भिन्नों की तुलना कीजिए और उचित चिह्न लगाइए :
3. एेसे ही पाँच और युग्म लीजिए और उचित चिह्न लगाइए।
4. निम्न आकृतियों को देखिए और भिन्नों के बीच में उचित चिह्न ‘>’ = या ‘<’ लिखिए :
एेसे ही पाँच और प्रश्न बनाइए और अपने मित्रों के साथ उन्हें हल कीजिए।
5. देखें कितनी जल्दी आप करते हैं? उचित चिह्न भरिए : ( <, =, >)
6. निम्नलिखित भिन्न तीन अलग-अलग संख्याएँ निरूपित करती हैं इन्हें सरलतम रूप में बदलकर उन तीन तुल्य भिन्नों के समूहों में लिखिए :
7. निम्नलिखित के उत्तर दीजिए। लिखिए और दर्शाइए कि आपने इन्हें कैसे हल किया है?
(a) क्या 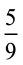 ,
, 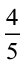 के बराबर है? (b) क्या
के बराबर है? (b) क्या 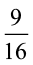 ,
, 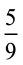 के बराबर है?
के बराबर है?
(c) क्या 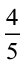 ,
, 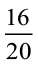 के बराबर है? (d) क्या
के बराबर है? (d) क्या 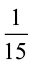 ,
, 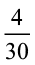 के बराबर है?
के बराबर है?
8. इला 100 पृष्ठों वाली एक पुस्तक के 25 पृष्ठ पढ़ती है। ललिता इसी पुस्तक का 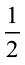 भाग पढ़ती है। किसने कम पढ़ा?
भाग पढ़ती है। किसने कम पढ़ा?
9. रफीक ने एक घंटे के 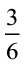 भाग तक व्यायाम किया, जबकि रोहित ने एक घंटे के
भाग तक व्यायाम किया, जबकि रोहित ने एक घंटे के 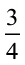 भाग तक व्यायाम किया। किसने लंबे समय तक व्यायाम किया?
भाग तक व्यायाम किया। किसने लंबे समय तक व्यायाम किया?
10. 25 विद्यार्थियों की एक कक्षा A में 20 विद्यार्थी 60% या अधिक अंक लेकर पास हुए और 30 विद्यार्थियों की एक कक्षा B में 24 विद्यार्थी 60% या अधिक अंक लेकर पास हुए। किस कक्षा में विद्यार्थियों का अधिक भाग 60% या अधिक अंक लेकर पास हुआ?
7.10 भिन्नों का योग और व्यवकलन (घटाना)
अभी तक हमने प्राकृत संख्याओं, पूर्ण संख्याओं और पूर्णांकों के बारे में अध्ययन किया है। इस अध्याय में, हम एक नई प्रकार की संख्याओं का अध्ययन कर रहे हैं जिन्हें भिन्न कहते हैं।
जब भी हमें नई संख्याएँ प्राप्त होती हैं, तो हम उन पर संक्रियाएँ करने की सोचते हैं। क्या हम इन्हें जोड़ सकते हैं? यदि हाँ, तो कैसे? क्या हम एक संख्या में से दूसरी संख्या निकाल सकते हैं? अर्थात् क्या हम एक संख्या में से दूसरी संख्या को घटा सकते हैं इत्यादि? संख्याओं के बारे में पहले पढ़े हुए गुण क्या इन नई संख्याओं पर लागू होते हैं। इनके नए गुण क्या हैं? हम यह भी देखते हैं कि ये संख्याएँ हमारे दैनिक जीवन में किस प्रकार उपयोगी हैं।
इस उदाहरण को देखिए : एक चाय की दुकान वाली अपनी दुकान पर सुबह 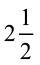 लीटर दूध और शाम को
लीटर दूध और शाम को 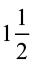 लीटर दूध का प्रयोग चाय बनाने में करती है। अपनी दुकान पर वह एक दिन में कितना दूध प्रयोग करती है?
लीटर दूध का प्रयोग चाय बनाने में करती है। अपनी दुकान पर वह एक दिन में कितना दूध प्रयोग करती है?
अथवा शेखर ने दोपहर के भोजन में 2 चपाती खाई और रात्रि के भोजन में 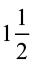 चपाती खाई। उसने कुल कितनी चपातियाँ खाईं?
चपाती खाई। उसने कुल कितनी चपातियाँ खाईं?
स्पष्ट है कि दोनों स्थितियों में भिन्नों को जोड़ने की आवश्यकता है। इनमें से कुछ योग मौखिक रूप से और सरलता से किए जा सकते हैं।

1. मेरी माँ ने एक सेब को चार बराबर भागों में बाँटा। उन्होंने मुझे 2 भाग और मेरे भाई को एक भाग दिया। उन्होंने हम दोनों को कुल सेब का कितना भाग दिया?
2. माँ ने नीलू और उसके भाई से गेहूँ में से कंकड़ बीनने के लिए कहा। नीलू ने कुल कंकड़ों के 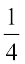 कंकड़ बीने और उसके भाई ने भी कुल कंकड़ों के
कंकड़ बीने और उसके भाई ने भी कुल कंकड़ों के 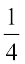 कंकड़ बीने। दोनों ने मिलकर कुल कंकड़ों की कितनी भिन्न बीनी?
कंकड़ बीने। दोनों ने मिलकर कुल कंकड़ों की कितनी भिन्न बीनी?
3. सोहन अपनी अभ्यास पुस्तिका पर कवर चढ़ा रहा था। उसने सोमवार को 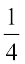 भाग पर कवर चढ़ा लिया। मंगलवार को उसने अन्य
भाग पर कवर चढ़ा लिया। मंगलवार को उसने अन्य 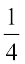 भाग पर कवर चढ़ा लिया और शेष बुधवार को। बुधवार को उसने कवर का कौन सा भाग चढ़ाया?
भाग पर कवर चढ़ा लिया और शेष बुधवार को। बुधवार को उसने कवर का कौन सा भाग चढ़ाया?

अपने मित्रों के साथ एेसे दस प्रश्न बनाइए और उन्हें हल कीजिए।
7.10.1 समान भिन्नों का जोड़ना या घटाना
सभी भिन्नों को मौखिक रूप से जोड़ा नहीं जा सकता। हमें यह जानने की आवश्यकता है कि विभिन्न स्थितियों में इन्हें कैसे जोड़ा जाता है और इस प्रक्रिया को सीखने की आवश्यकता है। हम समान भिन्नों के योग से प्रारंभ करते हैं।
एक 7 × 4 ग्रिड शीट (grid sheet) लीजिए (आकृति 7.13)। इस शीट की प्रत्येक पंक्ति में 7 खाने हैं और प्रत्येक स्तंभ में 4 खाने हैं।

आकृति 7.13
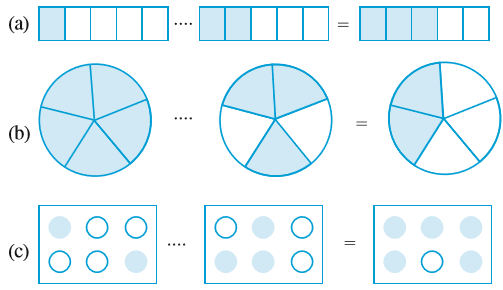
इसमें कुल कितने खाने हैं? इनमें से 5 खानों में हरा रंग भरिए। हरा क्षेत्र एक पूर्ण की कौन सी भिन्न है? अब शीट के 4 खानों में पीला रंग भरिए। पीला क्षेत्र एक पूर्ण की कौन-सी भिन्न है? एक पूर्ण की कुल कितनी भिन्न रंग दी गई है? क्या इससे स्पष्ट होता है कि 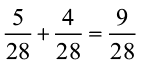 है?
है?
और उदाहरणों को देखिए :
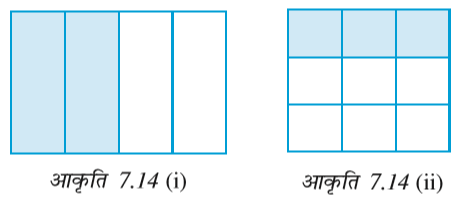
आकृति 7.14 (i) में, आकृति का दो-चौथाई भाग छायांकित है। इसका अर्थ है कि 4 में से 2 भाग, अर्थात् आकृति का 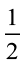 भाग छायांकित है।
भाग छायांकित है।
अर्थात् 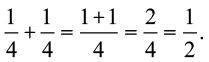 है।
है।
आकृति 7.14 (ii) को देखिए।
आकृति 7.14 (ii) 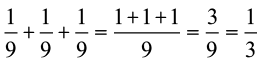 प्रदर्शित करती है।
प्रदर्शित करती है।
आपने इन उदाहरणों से क्या सीखा है? हमने सीखा है कि दो या अधिक समान भिन्नों का योग इस प्रकार प्राप्त किया जा सकता है :
चरण 2 (उभयनिष्ठ या सार्व) हर को वही रखिए।
चरण 3 परिणाम को इस रूप में लिखिए : 

आइए, इस विधि से 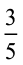 और
और 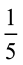 को जोड़ें। हमें प्राप्त होता है :
को जोड़ें। हमें प्राप्त होता है : 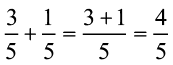
अब बताओ 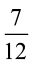 और
और 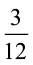 का क्या योग होगा।
का क्या योग होगा।

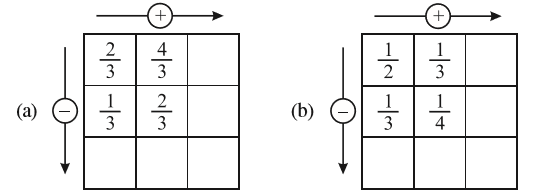
1. आकृतियों की सहायता से जोड़िए :
(i) 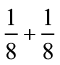 (ii)
(ii) 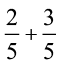 (iii)
(iii) 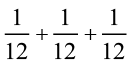
2. 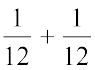 को जोड़ने पर हम क्या प्राप्त करते हैं?
को जोड़ने पर हम क्या प्राप्त करते हैं?
आप चित्र रूप में इसे कैसे दर्शा सकते हो? कागज़ मोड़ने की क्रिया द्वारा कैसे दर्शाया जा सकता है?
3. प्रश्न 1 और 2 जैसे पाँच और प्रश्न बनाइए।
अपने मित्रों के साथ उन्हें हल कीजिए।
शेष ज्ञात करना
शर्मीला के पास एक केक का 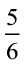 भाग था। उसने केक का
भाग था। उसने केक का 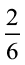 भाग अपने छोटे भाई को दे दिया। उसके पास कितना केक बचा?
भाग अपने छोटे भाई को दे दिया। उसके पास कितना केक बचा?
एक आकृति से इस स्थिति को सरलता से स्पष्ट किया जा सकता है। ध्यान दीजिए कि यहाँ समान भिन्न हैं (आकृति 7.15)।
हम प्राप्त करते हैं 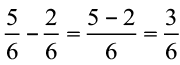 अर्थात्,
अर्थात्, 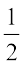 ।
।
(क्या यह समान भिन्नों को जोड़ने जैसी विधि नहीं है?)
इस प्रकार, हम दो समान भिन्नों का अंतर निम्न प्रकार से ज्ञात कर सकते हैं:
चरण 1 बड़े अंश में से छोटे अंश को घटाइए।
चरण 2 (उभयनिष्ठ) हर को वही रखिए।
चरण 3 भिन्न को इस रूप में लिखिए 
क्या अब हम 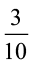 में से
में से 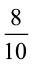 को घटा सकते हैं?
को घटा सकते हैं?

1. 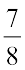 और
और 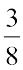 का अंतर ज्ञात कीजिए।
का अंतर ज्ञात कीजिए।
2. माँ ने एक गुड़ की पट्टी गोल आकृति में बनाई। उसने उसे 5 बराबर भागों में विभाजित किया। सीमा ने उसमें से एक टुकड़ा खा लिया। यदि मैं एक अन्य टुकड़ा खा लूँ, तो कितनी गुड़ की पट्टी शेष रहेगी?
3. मेरी बड़ी बहन ने एक तरबूज को 16 बराबर भागों में विभाजित किया। मैंने इसके 7 टुकड़े खा लिए। मेरे मित्र ने 4 टुकड़े खाए। हमने मिलकर कुल कितना तरबूज खाया? मैंने अपने मित्र से कितना अधिक तरबूज खाया? कितना तरबूज शेष रह गया?
4. इसी प्रकार के पाँच प्रश्न और बनाइए और अपने मित्रों के साथ इन्हें कीजिए।
प्रश्नावली 7.5
1. निम्न भिन्नों को योग या घटाने के उचित रूप में लिखिए :
2. हल कीजिए :
3. शुभम ने अपने कमरे की दीवार के 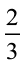 भाग पर पेंट किया। उसकी बहन माधवी ने उसकी सहायता की और उस दीवार के
भाग पर पेंट किया। उसकी बहन माधवी ने उसकी सहायता की और उस दीवार के 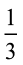 भाग पर पेंट किया। उन दोनों ने मिलकर कुल कितना पेंट किया?
भाग पर पेंट किया। उन दोनों ने मिलकर कुल कितना पेंट किया?
4. रिक्त स्थानों को भरिए :
5. जावेद को संतरों की एक टोकरी का 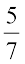 भाग मिला। टोकरी में संतरों का कितना भाग शेष रहा?
भाग मिला। टोकरी में संतरों का कितना भाग शेष रहा?
7.10.2 भिन्नों का जोड़ना और घटाना
हम समान भिन्नों को जोड़ना और घटाना सीख चुके हैं। जिन भिन्नों के हर समान नहीं हैं उन्हें जोड़ना और घटाना भी कठिन नहीं है। जब भिन्नों को जोड़ना और घटाना हो, तो हमें पहले दी हुई भिन्नों को समान हरों वाली भिन्नों में बदलना चाहिए और फिर आगे बढ़ना चाहिए।
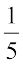 में क्या जोड़ने पर
में क्या जोड़ने पर 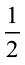 प्राप्त होता है? इसका अर्थ है कि वांछित संख्या प्राप्त करने के लिए,
प्राप्त होता है? इसका अर्थ है कि वांछित संख्या प्राप्त करने के लिए, 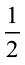 में से
में से 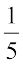 को घटाया जाए।
को घटाया जाए।
चूँकि 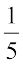 और
और 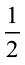 असमान भिन्न हैं, इसलिए घटाने के लिए पहले हम इन्हें समान हरों वाली भिन्नों में बदलते हैं।
असमान भिन्न हैं, इसलिए घटाने के लिए पहले हम इन्हें समान हरों वाली भिन्नों में बदलते हैं। 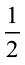 और
और 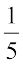 की समान हर वाली तुल्य भिन्न क्रमश:
की समान हर वाली तुल्य भिन्न क्रमश: 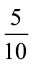 और
और 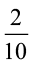 हैं।
हैं।
यह इसलिए है, क्योंकि  है।
है।
अत:, 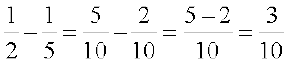
उदाहरण 8 : 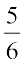 में से
में से 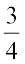 को घटाइए।
को घटाइए।
हल : हमें समान हर वाली 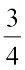 और
और 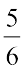 के तुल्य भिन्न बनाने की आवश्यकता है। यह हर 4 और 6 का ल.स. है, जो 12 है।
के तुल्य भिन्न बनाने की आवश्यकता है। यह हर 4 और 6 का ल.स. है, जो 12 है।
अत:, 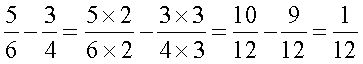
उदाहरण 9 : 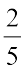 और
और 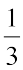 को जोड़िए।
को जोड़िए।
हल : 5 और 3 का ल.स. 15 है।
अत:, 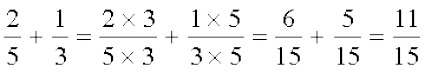
उदाहरण 10 : सरल कीजिए : 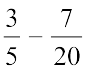
हल : 5 और 20 का ल.स. 20 है।
अत:, 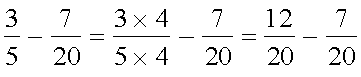
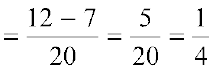

1. 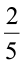 और
और 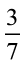 को जोड़िए।
को जोड़िए।
2. 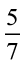 में से
में से 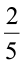 को घटाइए।
को घटाइए।
हम मिश्रित भिन्नों को किस प्रकार जोड़ते या घटाते हैं?
मिश्रित भिन्नों को या तो एक पूर्ण भाग और एक उचित भिन्न के जोड़ के रूप में लिखा जा सकता है या पूर्ण रूप से एक अनुचित भिन्न (विषय भिन्न) के रूप में। मिश्रित भिन्नों को जोड़ने (या घटाने) की एक विधि यह है कि पूर्ण भागों और भिन्नीय भागों पर संक्रियाएँ अलग-अलग की जाएँ तथा दूसरी विधि यह है कि इन्हें पहले अनुचित भिन्नों में बदल लिया जाए और फिर इन्हें सीधे जोड़ा (या घटाया) जाए।
उदाहरण 11 : 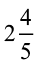 और
और 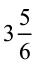 को जोड़िए।
को जोड़िए।
हल : 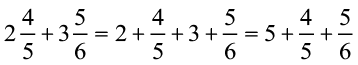 .
.
अब, 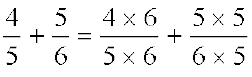 (चूँकि 5 और 6 का ल.स. = 30)।
(चूँकि 5 और 6 का ल.स. = 30)।
= 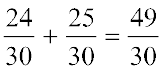 =
= 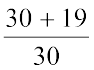
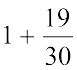
इस प्रकार, 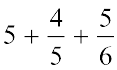 =
= 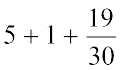
= 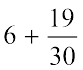 =
= 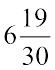
सोचिए, चर्चा कीजिए और लिखिए :
क्या आप इस प्रश्न को हल करने की कोई अन्य प्रक्रिया ज्ञात कर सकते हैं?
उदाहरण 12 : 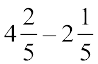 ज्ञात कीजिए।
ज्ञात कीजिए।
हल : पूर्ण संख्या 4 और 2 तथा भिन्नात्मक संख्या 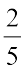 और
और 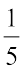 को अलग-अलग घटाया जा सकता है।
को अलग-अलग घटाया जा सकता है।
ध्यान दीजिए कि 4 > 2 है और 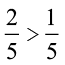 है।
है।
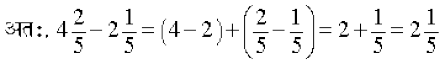
उदाहरण 13 : सरल कीजिए : 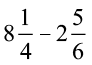
हल : यहाँ 8 > 2 है और  है। इस प्रश्न को निम्न प्रकार हल कर सकते हैं।
है। इस प्रश्न को निम्न प्रकार हल कर सकते हैं।
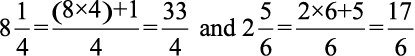
अब,
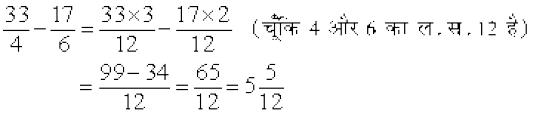
प्रश्नावली 7.6
1. हल कीजिए :
2. सरिता ने 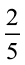 मी. रिबन खरीदा और ललिता ने
मी. रिबन खरीदा और ललिता ने 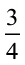 मी. दोनों ने कुल कितना रिबन खरीदा?
मी. दोनों ने कुल कितना रिबन खरीदा?
3. नैना को केक का 1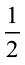 भाग मिला और नजमा को 1
भाग मिला और नजमा को 1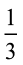 भाग। दोनों को केक का कितना भाग मिला?
भाग। दोनों को केक का कितना भाग मिला?
4. रिक्त स्थान भरिए :
5. योग - व्यवकलन तालिका को पूरा कीजिए :
6. 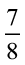 मीटर तार के दो टुकड़े हो जाते हैं। इनमें से एक टुकड़ा
मीटर तार के दो टुकड़े हो जाते हैं। इनमें से एक टुकड़ा 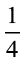 मीटर है। दूसरे टुकड़े की लंबाई क्या है?
मीटर है। दूसरे टुकड़े की लंबाई क्या है?
7. नंदिनी का घर उसके स्कूल से 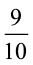 किमी दूर है। वह कुछ दूरी पैदल चलती है और फिर
किमी दूर है। वह कुछ दूरी पैदल चलती है और फिर 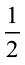 किमी की दूरी बस द्वारा तय करके स्कूल पहुँचती है। वह कितनी दूरी पैदल चलती है?
किमी की दूरी बस द्वारा तय करके स्कूल पहुँचती है। वह कितनी दूरी पैदल चलती है?
8. आशा और सेमुअल के पास एक ही माप की पुस्तक रखने वाली दो अलमारियाँ हैं। आशा की अलमारी पुस्तकों से 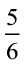 भाग भरी है और सेमुअल की अलमारी पुस्तकों से
भाग भरी है और सेमुअल की अलमारी पुस्तकों से 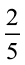 भाग भरी है। किसकी अलमारी अधिक भरी हुई है और कितनी अधिक?
भाग भरी है। किसकी अलमारी अधिक भरी हुई है और कितनी अधिक?
9. जयदेव स्कूल के मैदान का 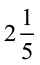 मिनट में चक्कर लगा लेता है। राहुल इसी कार्य को करने में
मिनट में चक्कर लगा लेता है। राहुल इसी कार्य को करने में 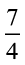 मिनट का समय लेता है। इसमें कौन कम समय लेता है और कितना कम?
मिनट का समय लेता है। इसमें कौन कम समय लेता है और कितना कम?
हमने क्या चर्चा की?
1. (a) एक भिन्न एेसी संख्या है जो एक पूर्ण के एक भाग को निरूपित करती है या संख्या रेखा पर संक्रियाओं को निरूपित करती है। पूर्ण एक अकेली वस्तु भी हो सकती है और वस्तुओं का समूह भी।
(b) किसी स्थिति में गिने हुए भागों को भिन्न में व्यक्त करने के लिए यह आवश्यक है कि उसके सभी भाग बराबर हों।
2. भिन्न 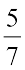 में, 5 अंश तथा 7 भिन्न का हर कहलाता है।
में, 5 अंश तथा 7 भिन्न का हर कहलाता है।
3. भिन्नों को संख्या रेखा पर भी दर्शाया जा सकता है। प्रत्येक भिन्न के लिए संख्या रेखा पर एक निश्चित बिंदु होता है।
4. एक उचित भिन्न में अंश, हर से छोटा होता है और विषम भिन्न में हर हमेशा अंश से बड़ा होता है। विषम भिन्न को एक पूर्ण और एक भाग के रूप में भी लिखा जा सकता है। इस स्थिति में यह भिन्न, मिश्रित कहलाती है।
5. दो भिन्न तुल्य भिन्न कहलाती हैं यदि वे समान मात्रा को निरूपित करती हों। प्रत्येक उचित या विषम भिन्न की अनेक तुल्य भिन्न होती हैं। एक दी हुई भिन्न की तुल्य भिन्न निकालने के लिए हम भिन्न के अंश तथा हर दोनों को समान शून्येतर संख्या से गुणा या भाग कर सकते हैं।
6. एक भिन्न अपने सरलतम रूप (न्यूनतम) में होगी यदि उसके अंश तथा हर में 1 के अलावा कोई दूसरा उभयनिष्ठ गुणनखंड न हो।