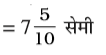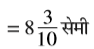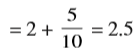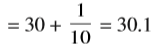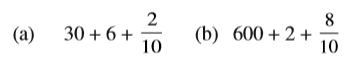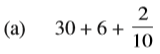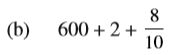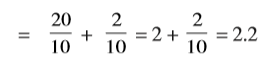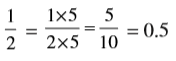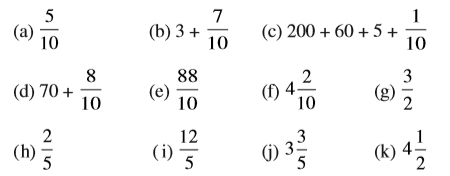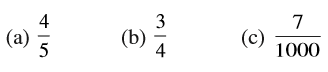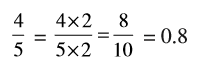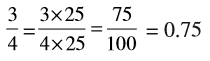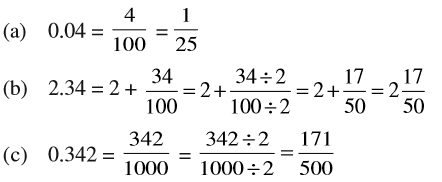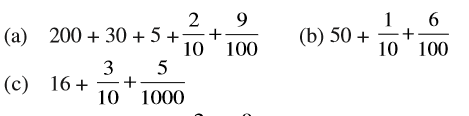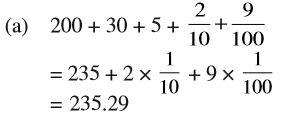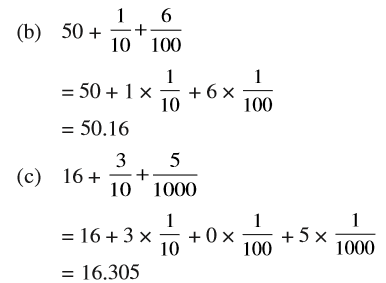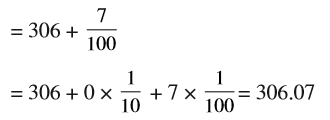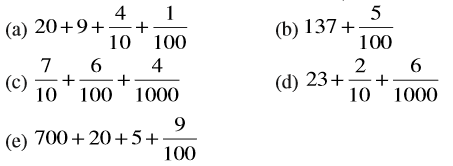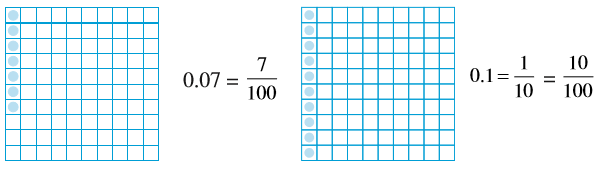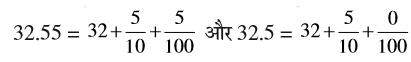Table of Contents
दशमलव
8.1 भूमिका
सविता और शमा स्टेशनरी का कुछ सामान खरीदने बाज़ार जा रही थीं। सविता ने कहा, "मेरे पास ₹ 5. 75 हैं।" शमा ने कहा, ‘‘मेरे पास ₹ 7. 50 हैं।"
वे दोनों रुपयों और पैसों को दशमलव-रूप में लिखना जानती थीं।
इसलिए सविता ने कहा, मेरे पास ₹ 5.75 हैं और शमा ने कहा, मेरे पास ₹ 7.50 हैं। क्या उन दोनों ने सही लिखा था?
हम जानते हैं कि बिंदु एक दशमलव को दर्शाता है। इस अध्याय में, हम दशमलव के विषय में और अधिक सीखेंगे।
8.2 दशांश
रवि तथा राजू ने अपनी-अपनी पेंसिलों की लंबाई मापी। रवि की पेंसिल 7 सेमी 5 मिमी लंबी थी और राजू की 8 सेमी 3 मिमी लंबी थी। क्या आप इन लंबाइयों को सेमी के साथ दशमलव रूप में लिख सकते हो?
हम जानते हैं कि 10 मिमी = 1 सेमी
अत: 1 मिमी = 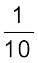 सेमी
सेमी
अब रवि के पेंसिल की लंबाई = 7 सेमी 5 मिमी
अर्थात् 7 सेमी और 1 सेमी का पाँच दशांश भाग
राजू के पेंसिल की लंबाई = 8 सेमी 3 मिमी

अर्थात् 8 सेमी और 1 सेमी का तीन दशांश भाग
आइए, पिछले सीखे हुए को पुन: याद करें :
यदि हम इकाइयों को खंडों द्वारा दर्शाएँ तो एक इकाई एक खंड, दो इकाई दो खंड और इसी नियमानुसार आगे भी।
एक खंड को यदि दस बराबर भागों में बाँटें तो प्रत्येक भाग एक इकाई का 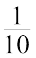 (एक दशांश) है, दो भाग, दो दशांश भाग को दर्शाते हैं और पाँच भाग, पाँच दशांश भाग को आगे और इसी प्रकार दो खंडों और तीन भागों (दशांश) के मेल को इस प्रकार लिखा जाएगा:
(एक दशांश) है, दो भाग, दो दशांश भाग को दर्शाते हैं और पाँच भाग, पाँच दशांश भाग को आगे और इसी प्रकार दो खंडों और तीन भागों (दशांश) के मेल को इस प्रकार लिखा जाएगा:
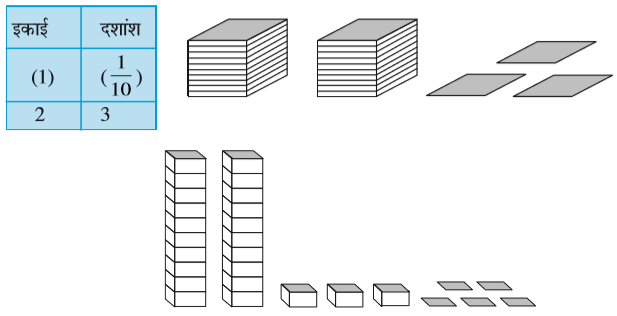
इसे हम 2.3 भी लिख सकते हैं और जो दो दशमलव तीन पढ़ा जाएगा।
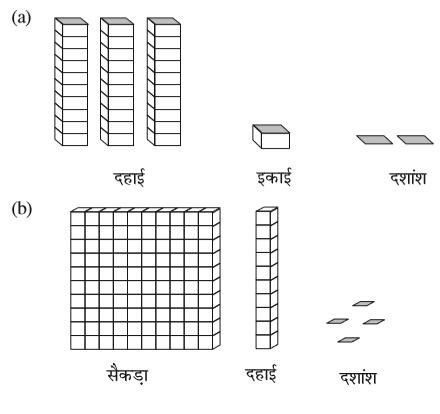
आइए, एक अन्य उदाहरण लें जहाँ एक से अधिक इकाइयाँ हैं। प्रत्येक मीनार 10 इकाइयों को दर्शाती हैं। अत: यहाँ दर्शाई गई संख्या इस प्रकार हैं :
अत: 20 + 3 + 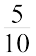 = 23.5
= 23.5
इसे हम तेईस दशमलव पाँच पढ़ेंगे।

1. क्या आप निम्न को दशमलव रूप में लिख सकते हैं?
2. रवि और राजू की पेंसिलों की लंबाइयों को दशमलव का प्रयोग कर सेमी में लिखें।
3. प्रश्न 1 के समरूप तीन अन्य उदाहरण बनाएँ और उन्हें हल करें।
संख्या रेखा पर निरूपण
हमने भिन्नों को संख्या रेखा पर निरूपित किया। आइए, अब दशमलवों को भी संख्या रेखा पर निरूपित करना सीखें। आइए 0.6 को संख्या रेखा पर निरूपित करें।
हम जानते हैं कि 0.6 शून्य से बड़ा है लेकिन एक से कम। इसमें 6-दशांश हैं। संख्या रेखा पर 0 और 1 के बीच की लंबाई को 10 बराबर भागों में विभाजित कीजिए और उनमें से छ: भाग कीजिए जैसा कि नीचे दिखाया गया है।
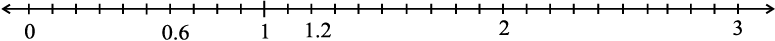
0 और 1 के बीच पाँच संख्याएँ लिखो और उन्हें संख्या रेखा पर दर्शाओ।
क्या अब आप 2.3 को संख्या रेखा पर दर्शा सकते हैं? जाँचिए कि 2.3 में कितनी इकाइयाँ और कितने दशांश हैं। संख्या रेखा पर यह कहाँ स्थित होगी?
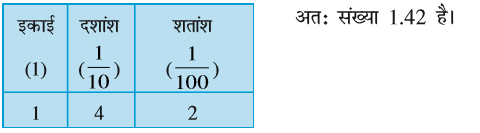
1.4 को संख्या रेखा पर दर्शाओ।
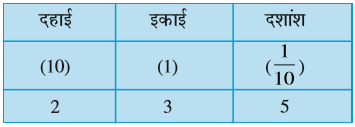
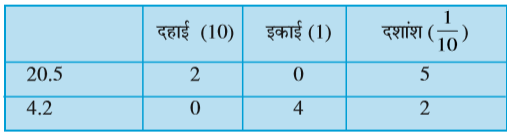
उदाहरण 1 : निम्न संख्याओं को स्थानीय मान सारणी में लिखिए :
(a) 20.5
(b) 4.2
हल : स्थानीय मान सारणी बनाकर संख्या के प्रत्येक अंक को उचित स्थानीय मान देकर उसमें निम्न प्रकार से लिखें :
उदाहरण 2 : निम्न में से प्रत्येक को दशमलव रूप में लिखिए :
(a) दो इकाइयाँ और 5-दशांश
(b) तीस और 1-दशांश
हल : (a) दो इकाइयाँ और 5-दशांश
(b) तीस और 1-दशांश
उदाहरण 3 : प्रत्येक को दशमलव रूप में लिखिए :
हल :
ज्ञात करें कि इस संख्या में कितनी दहाइयाँ, कितनी इकाइयाँ और कितने दशांश हैं।
इसमें 3 दहाइयाँ, 6 इकाइयाँ और 2 दशांश हैं।
अत: दशमलव रूप 36.2 होगा।
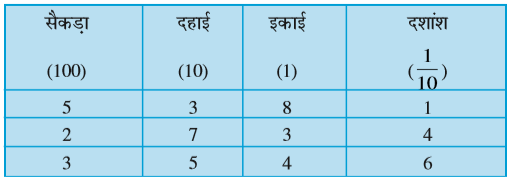
ध्यान से देखने पर पता चलता है कि इस संख्या में 6 सैकड़ा, कोई दहाई अंक नहीं, 2 इकाइयाँ और 8 दशांश हैं।
अत: दशमलव रूप 602.8 होगा।
भिन्न, दशमलव रूप में
हम देख चुके हैं कि एक भिन्न जिसका हर 10 हो, को किस प्रकार दशमलव रूप में लिखा जा सकता है।
आइए, निम्न को दशमलव रूप में लिखने का प्रयास करें (a) 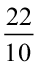 (b)
(b) 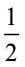
(a) हम जानते हैं, 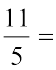
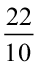 =
= 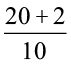
अत:, 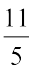 = 2.2 (दशमलव रूप में)
= 2.2 (दशमलव रूप में)
(b) 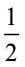 में हर 2 है। दशमलव रूप में लिखने के लिए हर का 10 होना आवश्यक है। तुल्य भिन्न में बदलना हम पहले सीख चुके हैं। अत:,
में हर 2 है। दशमलव रूप में लिखने के लिए हर का 10 होना आवश्यक है। तुल्य भिन्न में बदलना हम पहले सीख चुके हैं। अत:,
इस प्रकार, 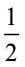 का दशमलव रूप 0.5 है।
का दशमलव रूप 0.5 है।

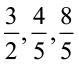 को दशमलव रूप में लिखिए
को दशमलव रूप में लिखिए
दशमलव, भिन्न रूप में
अब तक हमने सीखा है कि किस प्रकार भिन्न जिनका हर 10, 2 या 5 हो, को किस प्रकार दशमलव रूप में लिख सकते हैं।
क्या हम 1.2 को भिन्न संख्या के रूप में लिख सकते हैं।
आइए देखें :
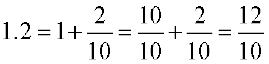
प्रश्नावली 8.1
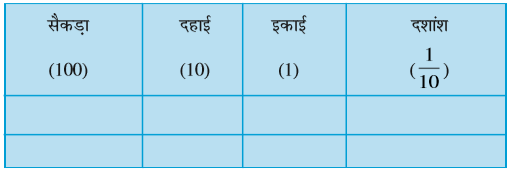
1. निम्न के लिए दी गई सारणी में संख्याएँ लिखिए :
2. निम्न दशमलव संख्याओं को स्थानीय मान सारणी में लिखिए :
(a) 19.4
(b) 0.3
(c) 10.6
(d) 205.9
3. निम्न में से प्रत्येक को दशमलव रूप में लिखिए :
(a) 7 दशांश
(b) 2 दहाई, 9 दशांश
(c) चौदह दशमलव छ:
(d) एक सौ और 2 इकाई
(e) छ: सौ दशमलव आठ
4. निम्न को दशमलव रूप में व्यक्त कीजिए :
5. निम्न दशमलव संख्याओं को भिन्न के रूप में लिखकर न्यूनतम (सरलतम) रूप में बदलिए :
(a) 0.6
(b) 2.5
(c) 1.0
(d) 3.8
(e) 13.7
(f) 21.2
(g) 6.4
6. सेमी का प्रयोग कर निम्न को दशमलव रूप में बदलिए :
(a) 2 मिमी
(b) 30 मिमी
(c) 116 मिमी
(d) 4 सेमी 2 मिमी
(e) 11 सेमी 52 मिमी
(f) 83 मिमी
7. संख्या रेखा पर किन दो पूर्ण संख्याओं के बीच निम्न संख्याएँ स्थित हैं? इनमें से कौन सी पूर्ण संख्या दी हुई दशमलव संख्या के अधिक निकट है?
(a) 0.8 (b) 5.1 (c) 2.6 (d) 6.4 (e) 9.0 (f) 4.9
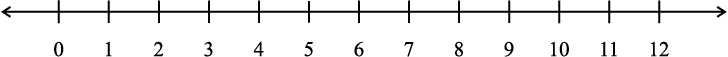
8. निम्न को संख्या रेखा पर दर्शाओ :
(a) 0.2 (b) 1.9 (c) 1.1 (d) 2.5
9. दी हुई संख्या रेखा पर स्थित A, B, C, D बिंदुओं के लिए दशमलव संख्या लिखिए :
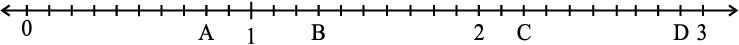
10. (a) रमेश की कॉपी की लंबाई 9 सेमी 5 मिमी है। सेमी में इसकी लंबाई क्या होगी?
(b) चने के एक छोटे पौधे की लंबाई 65 मिमी है। इसकी लंबाई सेमी में व्यक्त कीजिए?
8.3 शतांश
डेविड अपने कमरे की लंबाई माप रहा था। उसने देखा कि उसके कमरे की लंबाई 4 मी और 25 सेमी है।
वह इस लंबाई को मीटर में लिखना चाहता था। क्या आप उसकी मदद कर सकते हैं? एक सेमी एक मीटर का कौन-सा हिस्सा होगा?
1 सेमी = 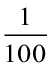 मी या एक मीटर का एक शतांश भाग।
मी या एक मीटर का एक शतांश भाग।

आकृति (i)

इस प्रकार 25 सेमी = 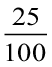 मी
मी 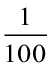 का अर्थ है एक पूरे के 100 हिस्से करने पर उसमें से एक हिस्सा। जैसा हमने
का अर्थ है एक पूरे के 100 हिस्से करने पर उसमें से एक हिस्सा। जैसा हमने 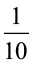 के लिए किया या आइए चित्र द्वारा इसे भी दिखाएँ।
के लिए किया या आइए चित्र द्वारा इसे भी दिखाएँ।
एक वर्ग को दस बराबर भागों में बाँटिए।
छायांकित आयत इस वर्ग का कौन-सा भाग है?
यह 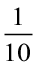 या एक दशांश या 0.1 (आकृति (i) देखिए) अब इसमें से प्रत्येक आयत को दस बराबर भागों में बाँटें।
या एक दशांश या 0.1 (आकृति (i) देखिए) अब इसमें से प्रत्येक आयत को दस बराबर भागों में बाँटें।
इस प्रकार हमें 100 छोटे-छोटे वर्ग प्राप्त होते हैं (आकृति (ii) देखिए) इसमें प्रत्येक छोटा वर्ग बड़े वर्ग का कौन सा भाग है?
प्रत्येक छोटा वर्ग बड़े वर्ग का 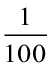 या एक शतांश भाग है।
या एक शतांश भाग है।
दशमलव रूप में हम 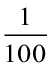 = 0.01 लिखेंगे और इसे ‘शून्य दशमलव शून्य एक’ पढ़ेंगे।
= 0.01 लिखेंगे और इसे ‘शून्य दशमलव शून्य एक’ पढ़ेंगे।
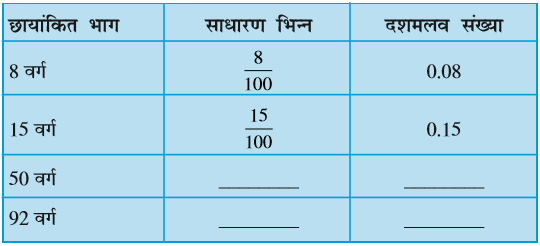
यदि हम बड़े वर्ग के 8 वर्ग छायांकित करें, 15 वर्ग छायांकित करें,
50 वर्ग छायांकित करें, 92 वर्ग छायांकित करें तो वह पूरे वर्ग का कौन-सा भाग होगा?
उपरोक्त को हल करने के लिए निम्न चित्रों की सहायता लें :

आइए, कुछ और स्थानीय मान सारणियों को देखें।
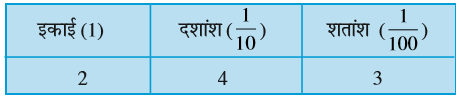
उपरोक्त सारणी में दर्शाई गई संख्या 2 + 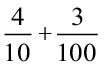 है। दशमलव रूप में इसे 2.43 लिखेंगे जिसे ‘दो दशमलव चार तीन’ पढेंगे।
है। दशमलव रूप में इसे 2.43 लिखेंगे जिसे ‘दो दशमलव चार तीन’ पढेंगे।
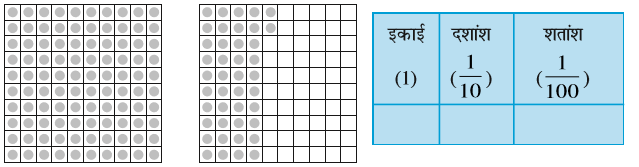
उदाहरण 4: खंडों में दी गई सूचना के आधार पर तालिका में दिए गए खाली स्थानों में दशमलव रूप में संख्याएँ लिखें

हल :
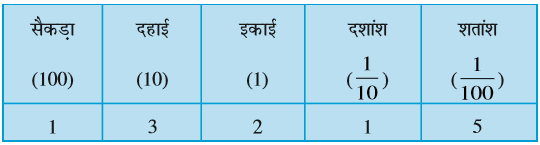
अत: संख्या होगी 100 + 30 + 2 + 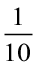 +
+ 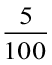 = 132.15
= 132.15
उदाहरण 5 : तालिका के रिक्त स्थानों में दशमलव रूप में संख्या लिखिए :
हल :
उदाहरण 6 : दी गई स्थानीय मान सारणी से संख्या को दशमलव रूप में लिखिए:
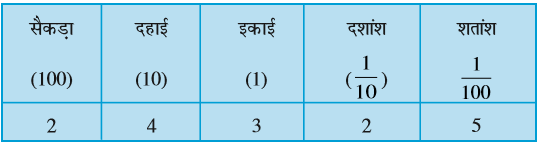
हल : संख्या होगी 2 × 100 + 4 × 10 + 3 × 1 + 2 × 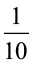 + 5 ×
+ 5 × 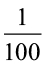
= 200 + 40 + 3 + 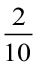 +
+ 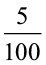 = 243.25
= 243.25
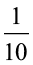 हो जाता है।
हो जाता है। पहले अंक 2 को 100 से गुणा किया, अगले अंक 4 को 10 से (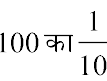 ); अगले अंक 3 को 1 से गुणा किया इसके बाद, अगला गुणनखंड
); अगले अंक 3 को 1 से गुणा किया इसके बाद, अगला गुणनखंड 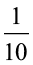 है और फिर
है और फिर 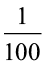 (अर्थात्
(अर्थात् 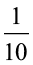 का
का 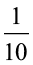 ) है।
) है।
एक दशमलव संख्या में दशमलव बिंदु हमेशा इकाई और दसवें स्थानों के बीच लगाया जाता है।
अत: अब स्वाभाविक रूप से हम स्थानीय मान सारणी को शतांश से (सौवें का 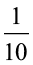 ) हज़ारवें स्थान तक बढ़ा सकते हैं।
) हज़ारवें स्थान तक बढ़ा सकते हैं।
आइए, कुछ उदाहरणों को हल करें।
उदाहरण 7 : दशमलव रूप में लिखिए :
हल : (a) हमें 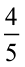 के तुल्य एेसी भिन्न संख्या निकालनी है जिसका हर 10 हो।
के तुल्य एेसी भिन्न संख्या निकालनी है जिसका हर 10 हो।
(b) यहाँ, हमें 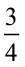 के तुल्य एक एेसी भिन्न संख्या निकालनी है जिसका हर 10 या 100 हो। परंतु एेसी कोई पूर्ण संख्या नहीं जिसे 4 से गुणा करने पर 10 प्राप्त हो। अत: हमें हर को 100 में ही बदलना पड़ेगा।
के तुल्य एक एेसी भिन्न संख्या निकालनी है जिसका हर 10 या 100 हो। परंतु एेसी कोई पूर्ण संख्या नहीं जिसे 4 से गुणा करने पर 10 प्राप्त हो। अत: हमें हर को 100 में ही बदलना पड़ेगा।
(c) 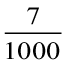 , यहाँ दशांश और शतांश स्थान शून्य है
, यहाँ दशांश और शतांश स्थान शून्य है
अत: हम 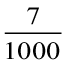 = 0.007 लिखते हैं
= 0.007 लिखते हैं
उदाहरण 8 : भिन्नों को लघुतम रूप में लिखिए :
(a) 0.04 (b) 2.34 (c) 0.342
हल :
उदाहरण 9 : प्रत्येक को दशमलव रूप में लिखिए :
हल :
उदाहरण 10 : निम्न में से प्रत्येक को दशमलव रूप में लिखिए :
(a) तीन सौ छ: और सात शतांश
(b) ग्यारह दशमलव दो तीन पाँच
(c) नौ और पच्चीस हज़ारवें
हल : (a) तीन सौ छ: और सात शतांश
(b) ग्यारह दशमलव दो तीन पाँच = 11.235
(c) नौ और पच्चीस हज़ारवें
प्रश्नावली 8.2
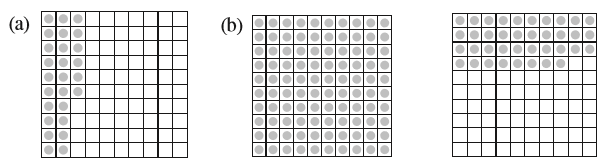
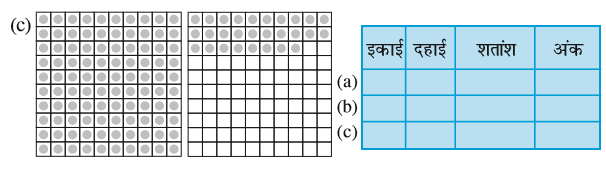
1. इन बक्सों की सहायता से सारणी को पूरा कर दशमलव रूप में लिखिए :
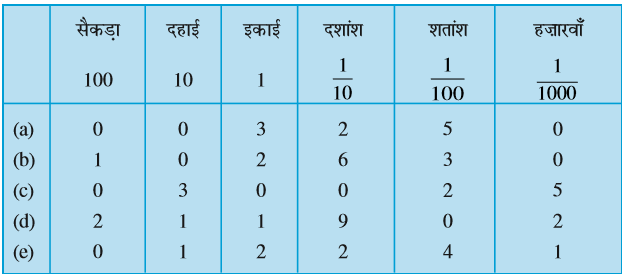
2. स्थानीय मान सारणी को देखकर दशमलव रूप में लिखिए :
3. निम्न दशमलवों को स्थानीय मान सारणी बनाकर लिखिए :
(a) 0.29 (b) 2.08 (c) 19.60 (d) 148.32 (e) 200.812
4. निम्न में से प्रत्येक को दशमलव रूप में लिखिए :
5. निम्न दशमलवों को शब्दों में लिखिए :
(a) 0.03 (b) 1.20 (c) 108.56 (d) 10.07
(e) 0.032 (f) 5.008
6. संख्या रेखा के किन दो बिंदुओं के बीच निम्न संख्याएँ स्थित हैं?
(a) 0.06 (b) 0.45 (c) 0.19 (d) 0.66 (e) 0.92 (f) 0.57
7. न्यूनतम रूप में भिन्न बनाकर लिखिए :
(a) 0.60 (b) 0.05 (c) 0.75 (d) 0.18 (e) 0.25
(f) 0.125 (g) 0.066
8.4 दशमलवों की तुलना
क्या आप बता सकते हैं कि कौन सी संख्या बड़ी है, 0.07 या 0.1?
दो समान आकार के वर्गाकार कागज़ लीजिए। उन्हें 100 बराबर भागों में बाँटिए। 0.07 = 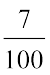 दर्शाने के लिए हमें 100 में से 7 भाग छायांकित करने होंगे।
दर्शाने के लिए हमें 100 में से 7 भाग छायांकित करने होंगे।
अब 0.1 = 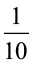 =
= 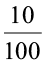 , अत: 0.1 को दर्शाने के लिए 100 में से 10 भाग छायांकित करने होंगे।
, अत: 0.1 को दर्शाने के लिए 100 में से 10 भाग छायांकित करने होंगे।
इस प्रकार 0.1 > 0.07
आइए, अब 32.55 और 32.5 की तुलना करें। इस स्थिति में हम पहले पूर्ण भाग की तुलना करते हैं हम यह देखते हैं कि दोनों संख्याओं का पूर्ण भाग 32 है अर्थात् समान हैं। यद्यपि हम जानते हैं कि ये दो संख्याएँ समान नहीं हैं। इसलिए अब हम इनके दशांश भागों की तुलना करते हैं। हम पाते हैं कि 32.55 और 32.5 के दशांश भाग भी समान हैं। अब हम इनके शतांश भाग की तुलना करते हैं, हम पाते हैं,
इसलिए, 32.55 > 32.5, क्योंकि 32.55 के शतांश स्थान का अंक 32.5 के शतांश स्थान के अंक से बड़ा है।
उदाहरण 11 : कौन सी संख्या बड़ी है?
(a) 1 या 0.99 (b) 1.09 या 1.093
हल :
संख्या 1 का पूर्ण भाग 1, 0.99 के पूर्ण भाग 0 से बड़ा है।
अत: 1 > 0.99
(b)
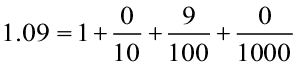
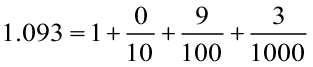
दोनों संख्याओं के शतांश स्थान तक के सभी अंक समान हैं परंतु 1.093 के हज़ारवें स्थान का अंक 1.09 के अंक से बड़ा है।
अत: 1.093 > 1.09
प्रश्नावली 8.3
1. कौन सी बड़ी है? कारण भी लिखिए :
(a) 0.3 या 0.4
(b) 0.07 या 0.02
(c) 3 या 0.8
(d) 0.5 या 0.05
(e) 1.23 या 1.2
(f) 0.099 या 0.19
(g) 1.5 या 1.50
(h) 1.431 या 1.490
(i) 3.3 या 3.300
(j) 5.64 या 5.603
(k) पाँच एेसे ही उदाहरण लिखकर उनमें से बड़ी संख्या ज्ञात कीजिए।
8.5 दशमलवों का प्रयोग
8.5.1 धन
हम जानते हैं कि 100 पैसे = ₹ 1
अत: 1 पैसा = ₹ 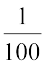 = ₹ 0.01
= ₹ 0.01
इस प्रकार, 65 पैसे = ₹ 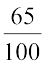 = ₹ 0.65
= ₹ 0.65
और 5 पैसे = ₹ 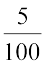 = ₹ 0.05
= ₹ 0.05
105 पैसे कितने होंगे?
यह 1 रुपया 5 पैसा होगा = ₹ 1.05

(i) 2 रुपये 5 पैसे और 2 रुपये 50 पैसों को दशमलव में लिखिए।
(ii) 20 रुपये 7 पैसे और 21 रुपये 75 पैसों को दशमलव में लिखिए।
8.5.2 लंबाई
महेश अपनी मेज़ की ऊपरी सतह को मीटर में मापना चाहता है। उसके पास 50 सेमी वाला फीता है। उसने पाया कि मेज़ की ऊपरी सतह की लंबाई 156 सेमी थी। इसकी लंबाई मीटर में कितनी होगी?
1 सेमी = 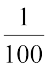 मी या 0.01 मी
मी या 0.01 मी
अत: 56 सेमी = 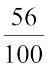 मी = 0.56 मी
मी = 0.56 मी
इस प्रकार मेज़ की ऊपरी सतह की लंबाई
156 सेमी = 100 सेमी + 56 सेमी
= 1 मी + 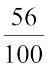 मी = 1.56 मी
मी = 1.56 मी
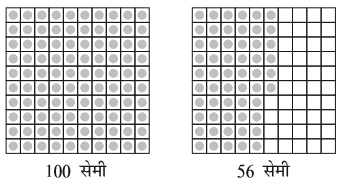
महेश इस लंबाई को चित्र द्वारा दर्शाना चाहता है। उसने समान आकार के वर्गाकार कागज़ों को 100 बराबर भागों में बाँटा और प्रत्येक छोटे वर्ग को एक सेमी माना।

1. क्या 4 मिमी को दशमलव का प्रयोग कर सेमी में लिख सकते हैं?
2. 7 सेमी 5 मिमी को दशमलव का प्रयोग कर सेमी में कैसे लिखेंगे?
3. क्या अब आप 52 मी को दशमलव का प्रयोग करके किमी में लिख सकते हैं? दशमलव का प्रयोग कर 340 मी को किमी में कैसे लिखेंगे? 2008 मी को किमी में कैसे लिखेंगे?
8.5.3 वज़न (या भार)
नंदू ने 500 ग्राम आलू, 250 ग्राम शिमला मिर्च, 700 ग्राम प्याज़, 500 ग्राम टमाटर, 100 ग्राम अदरक और 300 ग्राम मूली खरीदी। सब्ज़ियों का कुल वज़न कितना है? आइए, सभी सब्ज़ियों के वज़न को जोड़ें :
500 ग्रा + 250 ग्रा + 700 ग्रा + 500 ग्रा + 100 ग्रा + 300 ग्रा = 2350 ग्रा
हम जानते हैं कि 1000 ग्रा = 1 किग्रा
अत: 1 ग्रा =  किग्रा = 0.001 किग्रा
किग्रा = 0.001 किग्रा
इस प्रकार 2350 ग्रा = 2000 ग्रा + 350 ग्रा =  किग्रा +
किग्रा + 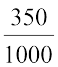 किग्रा
किग्रा
 किग्रा = 0.001 किग्रा)
किग्रा = 0.001 किग्रा)= 2.350 किग्रा
अर्थात् 2350 ग्रा = 2 किग्रा 350 ग्रा = 2.350 किग्रा
अत: थैले में कुल 2.350 किग्रा सब्ज़ी थी।

1. क्या आप 456 ग्रा को दशमलव का प्रयोग कर किग्रा में लिख सकते हैं?
2. किग्रा 9 ग्रा को दशमलव का प्रयोग कर किग्रा में कैसे लिख सकते हैं?
प्रश्नावली 8.4
1. दशमलव का प्रयोग कर ₹ में बदलिए :
(a) 5 पैसे (b) 75 पैसे (c) 20 पैसे
(d) 50 रुपये 90 पैसे (e) 725 पैसे
2. दशमलव का प्रयोग कर मीटर में व्यक्त करिए :
(c) 2 मी 45 सेमी (d) 9 मी 7 सेमी (e) 419 सेमी
3. दशमलव का प्रयोग कर सेमी में करिए :
(a) 5 मिमी (b) 60 मिमी (c) 164 मिमी
(d) 9 सेमी 8 मिमी (e) 93 मिमी
4. दशमलव का प्रयोग कर किमी मेें लिखिए :
(a) 8 मी (b) 88 मी (c) 8888 मी
(d) 70 किमी 5 मी
5. दशमलव का प्रयोग कर किग्रा में लिखिए :
(a) 2 ग्रा (b) 100 ग्रा (c) 3750 ग्रा
(d) 5 किग्रा 8 ग्रा (e) 26 किग्रा 50 ग्रा
8.6 दशमलव संख्याओं का जोड़
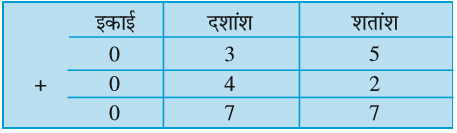
0.35 और 0.42 को जोड़िए।
एक वर्ग लेकर उसे 100 समान भागों में बाँटिए।
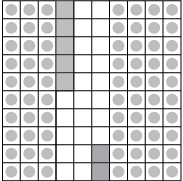
इस वर्ग में 0.35 को दर्शाने के लिए 3 दशांश को छायांकित करें और 5 शतांश में रंग भरें।
इसी वर्ग में 0.42 को दिखाने के लिए 4 दशांश को छायांकित करें और 2 शतांश में रंग भरें।
अब वर्ग में कुल दसवों और कुल सौवों की संख्या निकाल लें।
अत: 0.35 + 0.42
= 0.77
इस प्रकार, जैसे हम पूर्ण संख्याओं को जोड़ते हैं एेसे ही दशमलव संख्याओं को भी जोड़ सकते हैं।
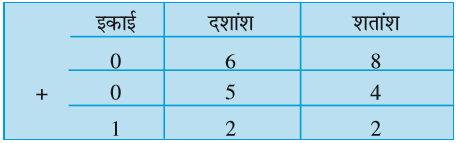
क्या अब आप 0.68 और 0.54 को जोड़ सकते हैं?
अत: 0.68 + 0.54 = 1.22

ज्ञात कीजिए
(i) 0.29 + 0.36 (ii) 0.7 + 0.08
(iii) 1.54 + 1.80 (iv) 2.66 + 1.85
उदाहरण 12 : लता ने ₹ 9.50 का एक पैन खरीदा और ₹ 2.50 की एक पेंसिल खरीदी। उसने कुल कितने रुपये खर्च किये?
हल : पैन पर खर्च किया गया धन = ₹ 9.50
पेंसिल पर खर्च किया गया धन = ₹ 2.50
कुल खर्च किया = ₹ 9.50
+ ₹ 2.50
= ₹ 12.00
उदाहरण 13 : सैमसन ने 5 किमी 52 मी की दूरी बस से, 2 किमी 265 मी कार से और शेष 1 किमी 30 मी पैदल चल कर तय की। उसने कुल कितनी दूरी तय की?
हल : बस द्वारा तय की गई दूरी = 5 किमी 52 मी = 5.052 किमी
कार द्वारा तय की गई दूरी = 2 किमी 265 मी = 2.265 किमी
पैदल तय की गई दूरी = 1 किमी 30 मी = 1.030 किमी
इस प्रकार, तय की गई कुल दूरी है
5.052 किमी
2.265 किमी
+ 1.030 किमी
8.347 किमी
अत: तय की गई कुल दूरी = 8.347 किमी
उदाहरण 14 : राहुल ने 4 किग्रा 9 ग्रा सेब, 2 किग्रा 60 ग्राम अंगूर और 5 किग्रा 300 ग्राम आम खरीदे। खरीदे गए सभी फलों का कुल वज़न कितना था?
हल : सेबों का वज़न = 4 किग्रा 90 ग्रा = 4.090 किग्रा
अंगूरों का वज़न = 2 किग्रा 60 ग्रा = 2.060 किग्रा
आमों का वज़न = 5 किग्रा 300 ग्रा = 5.300 किग्रा
अत: खरीदे गए फलों का कुल वज़न
4.090 किग्रा
2.060 किग्रा
+ 5.300 किग्रा
11.450 किग्रा
खरीदे गए फलों का कुल वज़न = 11.450 किग्रा
प्रश्नावली 8.5
1. निम्न में से प्रत्येक का जोड़ ज्ञात करें :
(a) 0.007 + 8.5 + 30.08 (b) 15 + 0.632 + 13.8
(c) 27.076 + 0.55 + 0.004 (d) 25.65 + 9.005 + 3.7
(e) 0.75 + 10.425 + 2 (f ) 280.69 + 25.2 + 38
2. रशीद ने 35.75 रुपये में गणित की और 32.60 रुपये में विज्ञान की पुस्तक खरीदी। रशीद द्वारा खर्च किया गया कुल धन ज्ञात कीजिए।
3. राधिका की माँ ने उसे 10.50 रुपये दिये और पिता ने 15.80 रुपये दिये। उसके माता-पिता द्वारा दिया गया कुल धन ज्ञात कीजिए।
4. नसरीन ने अपनी कमीज़ के लिए 3 मी 20 सेमी कपड़ा खरीदा और 2 मी 5 सेमी पैंट के लिए खरीदा। उसके द्वारा खरीदे गए कपड़े की कुल लंबाई निकालिए।
5. नरेश प्रात:काल में 2 किमी 35 मी चला और सायंकाल में 1 किमी 7 मी चला। वह कुल कितनी दूरी चला?
6. सुनीता अपने स्कूल पहुँचने के लिए, 15 किमी 268 मी की दूरी बस से, 7 किमी 7 मी की दूरी कार से और 500 मी की दूरी पैदल तय करती है। उसका स्कूल उसके घर से कितनी दूर है?
7. रवि ने 5 किग्रा 400 ग्रा चावल, 2 किग्रा 20 ग्रा चीनी और 100 किग्रा 850 ग्रा आटा खरीदा। उसके द्वारा की गई खरीदारी का कुल भार (या वजन) ज्ञात कीजिए।
8.7 दशमलव संख्याआें का घटाना
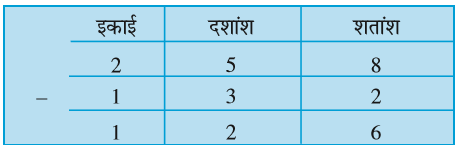
2.58 में से 1.32 घटाइए
इसे हम एक सारणी द्वारा दिखा सकते हैं :
अत: 2.58 – 1.32 = 1.26
इस प्रकार दशमलव संख्याओं को घटाया जा सकता है यदि शतांश में से शतांश स्थान का अंक, दशांश में से दशांश स्थान का अंक और इकाई में से इकाई अंक और आगे इसी प्रकार घटाएँ, जैसे हमने जोड़ में किया।
कभी-कभी, दशमलवों को घटाने के लिए हमें संख्या के अंकों के समूह फिर से बनाने होते हैं जैसा, जोड़ में किया गया।
आइए, 3.5 में से 1.74 घटाएँ
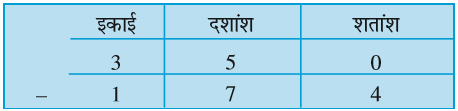
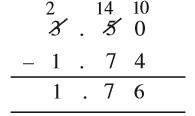
अत: 3.5 – 1.74 = 1.76

5.46 में से 1.85 घटाएँ; 8.28 में से 5.25 घटाएँ;
2.29 में से 0.95 घटाएँ; 5.68 में से 2.25 घटाएँ।
उदाहरण 15 : अभिषेक के पास ₹ 7.45 हैं। वह ₹ 5.30 की टॉफ़ी खरीदता है। अभिषेक के पास अब कितने रुपये शेष बचते हैं?
हल : कुल धन = ₹ 7.45
टॉफ़ी पर किया गया खर्च = ₹ 5.30
शेष धन = ₹ 7.45 – ₹ 5.30
= ₹ 2.15
उदाहरण 16 : उर्मिला का घर उसके स्कूल से 5 किमी 350 मी की दूरी पर है। वह 1 किमी 70 मी पैदल चलती है और शेष दूरी बस से तय करती है। बस द्वारा तय की गई दूरी ज्ञात कीजिए?
हल : स्कूल से घर की कुल दूरी = 5.350 किमी
पैदल तय की गई दूरी = 1.070 किमी
अत: बस द्वारा तय की गई दूरी = 5.350 किमी – 1.070 किमी = 4.280 किमी
इस प्रकार बस द्वारा तय की दूरी = 4.280 किमी
= 4 किमी 280 मी
उदाहरण 17 : कंचन 5 किग्रा 200 ग्रा वज़न का एक तरबूज़ खरीदती है। इसमें से 2 किग्रा 750 ग्रा उसने अपने पड़ोसी को दे दिया। कंचन के पास कितना तरबूज़ बचा?
हल : तरबूज़ का कुल वज़न = 5.200 किग्रा
पड़ोसी को दिए गए तरबूज़ का वज़न= 2.750 किग्रा
अत: बचे हुए तरबूज़ का वज़न = 5.200 किग्रा – 2.750 किग्रा
= 2.450 किग्रा
प्रश्नावली 8.6
1. निम्न को घटाओ :
(a) ₹ 20.75 में से ₹ 18.25 (b) 250 मी में से 202.54 मी
(c) ₹ 8.4 में से ₹ 5.40 (d) 5.206 किमी में से 2.051 किमी
(e) 2.107 किग्रा में से ₹ 0.314
2. मान ज्ञात कीजिए :
(a) 9.756 – 6.28 (b) 21.05 – 15.27
(c) 18.5 – 6.79 (d) 11.6 – 9.847
3. राजू एक पुस्तक ₹ 35.65 की खरीदता है। उसने दुकानदार को ₹ 50 दिये। दुकानदार ने उसे कितने रुपये वापिस दिए?
4. रानी के पास ₹ 18.50 हैं। उसने ₹ 11.75 की एक आइसक्रीम खरीदी। अब उसके पास कितने रुपये बचे?
5. टीना के पास 20 मी 5 सेमी लंबा कपड़ा है। उसमें से उसने एक पर्दा बनाने के लिए 4 मी 50 सेमी कपड़ा काट लिया। टीना के पास अब कितना लंबा कपड़ा बचा?
6. नमिता प्रतिदिन 20 किमी 50 मी की दूरी तय करती है। इसमें से 10 किमी 200 मी दूरी वह बस द्वारा तय करती है और शेष अॉटो-रिक्शा द्वारा। नमिता अॉटो-रिक्शा द्वारा कितनी दूरी तय करती है?

हमने क्या चर्चा की?
1. एक पूरी इकाई के भागों को जानने के लिए हम एक इकाई को खंड से दर्शाएँगे। एक खंड के 10 बराबर भाग करने पर प्रत्येक भाग उस इकाई का 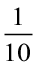 (एक दशांश) होगा। इसे हम 0.1 के रूप में लिख सकते हैं जो कि दशमलव निरूपण है। इस बिंदु को हम दशमलव कहते हैं जो कि इकाई और दशांश स्थान के अंकों के बीच लगाया जाता है।
(एक दशांश) होगा। इसे हम 0.1 के रूप में लिख सकते हैं जो कि दशमलव निरूपण है। इस बिंदु को हम दशमलव कहते हैं जो कि इकाई और दशांश स्थान के अंकों के बीच लगाया जाता है।
2. प्रत्येक भिन्न जिसका हर 10 हो, को दशमलव रूप में लिखा जा सकता है और इसके विपरीत प्रत्येक दशमलव संख्या को भी भिन्न रूप में लिखा जा सकता है।
3. एक खंड को 100 समान भागों में बाँटने पर प्रत्येक भाग उस इकाई का 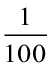 (एक शतांश) भाग है। दशमलव रूप में इसे हम 0.01 लिख सकते हैं।
(एक शतांश) भाग है। दशमलव रूप में इसे हम 0.01 लिख सकते हैं।
4. प्रत्येक भिन्न जिसका हर 100 हो, को दशमलव रूप में लिखा जा सकता है और उसके विपरीत प्रत्येक दशमलव संख्या को भी भिन्न रूप में लिखा जा सकता है।
5. स्थानीय मान सारणी में जैसे-जैसे हम बाएँ से दाएँ की ओर जाते हैं गुणनखंड पिछले गुणक का 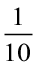 हो जाता है।
हो जाता है।
स्थानीय मान सारणी को हम आगे भी बढ़ा सकते हैं, शतांश स्थान से (शतांश का 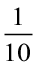 ) हज़ारवें
) हज़ारवें  स्थान तक जिसे हम दशमलव रूप में 0.001 भी लिखते हैं।
स्थान तक जिसे हम दशमलव रूप में 0.001 भी लिखते हैं।
6. दशमलव संख्याओं को संख्या रेखा पर भी दर्शाया जा सकता है।
7. प्रत्येक दशमलव को भिन्न रूप में लिखा जा सकता है।
8. दो दशमलव संख्याओं की आपस में तुलना की जा सकती है। तुलना संख्या के पूर्ण भाग (जो कि दशमलव बिंदु की बाईं ओर के अंक होते हैं) से शुरू की जाती है। यदि पूर्ण भाग समान हैं तो दशांश स्थान के अंकों की तुलना की जाती है और यदि ये भी समान हों तो अगले अंक को देखें यह क्रम आगे बढ़ता रहता है।
9. दशमलवों का प्रयोग धन, लंबाई और भार (वज़न) की इकाइयों को दर्शाने के लिए किया जाता है।