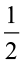Table of Contents
क्षेत्रमिति
10.1 भूमिका
जब हम तल की एेसी आकृतियों के बारे में बात करते हैं, जो नीचे दी हुई हैं, तो हम उन आकृतियों के क्षेत्र तथा परिसीमा के बारे में भी विचार करते हैं। हमें इन आकृतियों की तुलना के लिए कुछ मापों की आवश्यकता होती है। आइए, हम कुछ एेसी ही आकृतियों को देखते हैं।
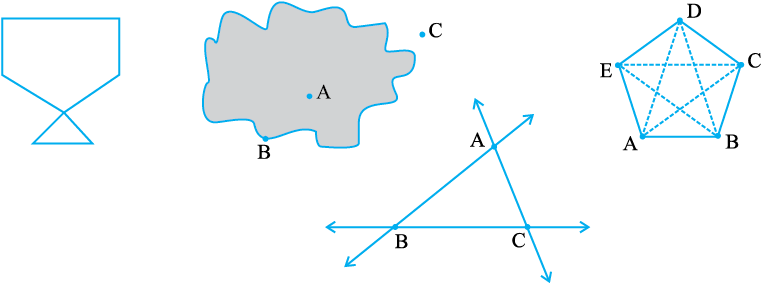
10.2 परिमाप

आइए, नीचे दी गई आकृति 10.1 को देखते हैं। आप इन आकृतियों को एक तार अथवा धागे की सहायता से भी बना सकते हैं।
यदि आप बिंदु S से आरंभ करके रेखाखंडों के साथ-साथ (अनुदिश) चलते हैं तो आप पुन: बिंदु S पर पहुँच जाते हैं। इस प्रकार आपने आकार (आकृति) के चारों तरफ़ अथवा किनारे-किनारे का एक पूरा चक्कर लगाया। यह तय की गई दूरी इन आकृतियों को बनाने में लगे तार की लंबाई के बराबर है।
यह दूरी बंद आकृतियों का परिमाप कहलाती है। दूसरे शब्दों में, हम कह सकते हैं कि इन आकृतियों को बनाने में लगे तार की लंबाई ही परिमाप है।
हमारे दैनिक जीवन में परिमाप की संकल्पना का बहुतायत प्रयोग होता है, जैसे :
- एक किसान जो अपने खेत के चारों तरफ़ बाड़ लगाना चाहता है।
- एक इंजीनियर जो अपने घर के चारों तरफ़ एक चारदीवारी बनाने की योजना तैयार करता है।
- एक व्यक्ति जो खेल कराने के लिए एक पथ तैयार करता है।
ये सभी व्यक्ति ‘परिमाप’ की संकल्पना का प्रयोग करते हैं।
एेसी पाँच स्थितियों का उदाहरण दीजिए जहाँ पर आपको परिमाप को जानने की आवश्यकता होती है।
अत: परिमाप एक एेसी दूरी है जो रेखाखंडों के साथ-साथ (अर्थात् परिसीमा के अनुदिश) चलते हुए एक बंद आकृति बनाती है, जब आप उस आकृति के चारों तरफ़ एक पूरा चक्कर लगाते हैं।

1. अपनी अध्ययन टेबल के ऊपरी चारों सिरों की लंबाइयों को मापिए तथा उन्हें लिखिए।
AB = ____ सेमी
BC = ____ सेमी
CD = ____ सेमी
DA = ____ सेमी
अब चारों भुजाओं की लंबाइयों का योगफल
= AB + BC + CD + DA
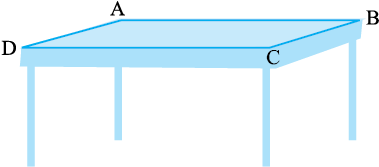
= ___ सेमी +___ सेमी +___ सेमी +___ सेमी
= _____ सेमी
क्या आप बता सकते हैं कि परिमाप कितना है?
2. अपनी नोटबुक के एक पृष्ठ की चारों भुजाओं की लंबाइयों को मापिए और उन्हें लिखिए। चारों भुजाओं की लंबाइयों का योगफल
= AB + BC + CD + DA = ___ सेमी +___ सेमी +___ सेमी +___ सेमी
= _____ सेमी
पृष्ठ का परिमाप कितना है?
3. मीरा 150 मी लंबाई तथा 80 मी चौड़ाई वाले एक पार्क में जाती है। वह इस पार्क का पूरा एक चक्कर लगाती है। उसके द्वारा तय की गई दूरी ज्ञात कीजिए।
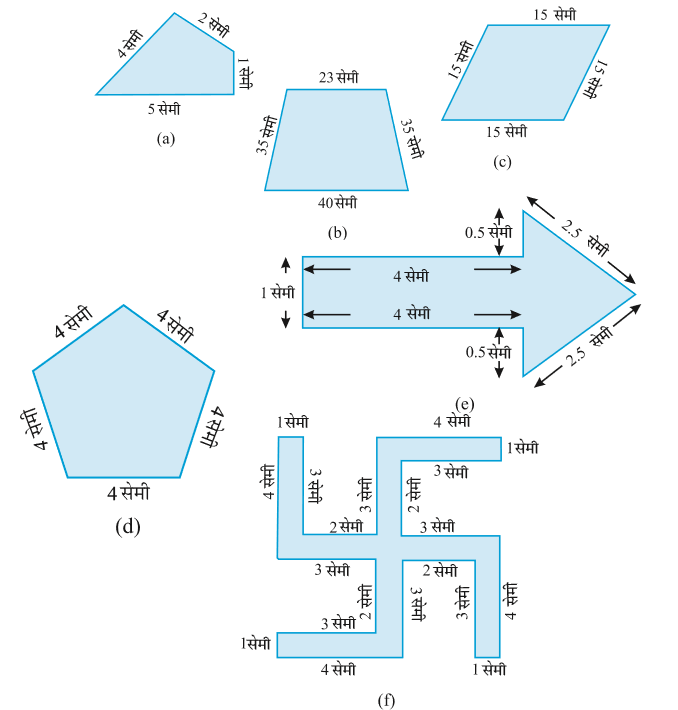
4. निम्न आकृतियों का परिमाप ज्ञात कीजिए :
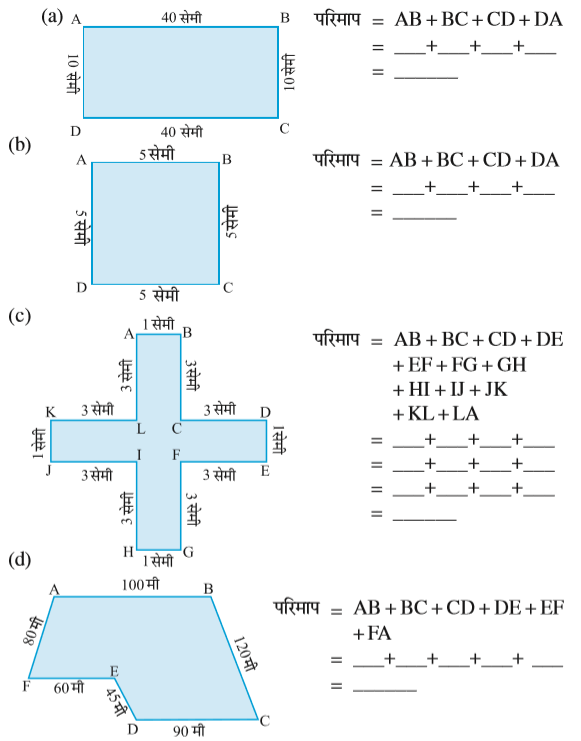
इस प्रकार, आप रेखाख्ांडों के द्वारा निर्मित बंद आकृति का परिमाप कैसे निकालेंगे? साधारणतया, सभी भुजाओं की लंबाइयों का योगफल ज्ञात करके (जो कि रेखाखंड हैं)।
10.2.1 आयत का परिमाप
आइए, अब हम एक आयत ABCD (आकृति 10.2) पर विचार करते हैं जिसकी लंबाई तथा चौड़ाई क्रमश: 15 सेमी तथा 9 सेमी है। आयत का परिमाप कितना होगा?

आयत का परिमाप = चारों भुजाओं की लंबाइयों
का योगफल
= AB + BC + CD + DA
= AB + BC + AB + BC
= 2 × AB + 2 × BC
= 2 × (AB + BC)
= 2 × (15सेमी + 9सेमी)
= 2 × (24सेमी)
= 48 सेमी
AB = CD,
DA = BC
अत: ऊपर दिए हुए उदाहरण में, हमने देखा कि
आयत का परिमाप = लंबाई + चौड़ाई + लंबाई + चौड़ाई
अर्थात् आयत का परिमाप = 2 × (लंबाई + चौड़ाई)

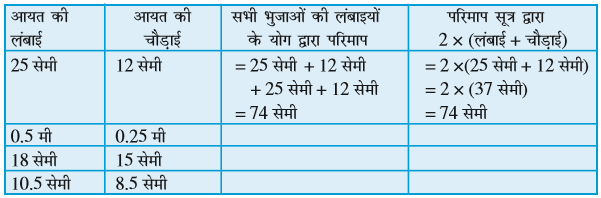
निम्नलिखित आयतों के परिमाप ज्ञात कीजिए :
आइए, अब हम इस विषय या संकल्पना को प्रयोगात्मक रूप में देखते हैं।
उदाहरण 1 : शबाना 3 मी लंबाई और 2 मी चौड़ाई के एक आयताकार टेबल कवर (आकृति 10.3) के चारों ओर एक किनारी (गोटा) लगाना चाहती है। शबाना को कितनी लंबी किनारी की आवश्यकता है।
हल : आयताकार टेबल कवर की लंबाई = 3 मी
आयताकार टेबल कवर की चौड़ाई = 2 मी
शबाना टेबल कवर के चारों ओर किनारी लगाना चाहती है। इसीलिए आवश्यक किनारी की लंबाई, आयताकार टेबल कवर के परिमाप के बराबर होगी।
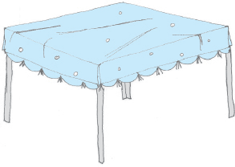
आकृति 10.3
अब आयताकार टेबल कवर का परिमाप
= 2 × (लंबाई + चौड़ाई)
= 2 × (3 मी + 2 मी)
= 2 × 5 मी = 10 मी
अत: आवश्यक किनारी की लंबाई 10 मी है।
उदाहरण 2 : एक धावक 50 मी लंबाई तथा 25 मी चौड़ाई के एक आयताकार पार्क के चारों तरफ़ 10 चक्कर लगाता है। उसके द्वारा तय की गई कुल दूरी ज्ञात कीजिए।
हल : आयताकार पार्क की लंबाई = 50 मी
आयताकार पार्क की चौड़ाई = 25 मी
धावक द्वारा एक चक्कर में तय की गई कुल दूरी, पार्क के परिमाप के बराबर होगी।
अब, आयताकार पार्क का परिमाप
= 2 × (लंबाई + चौड़ाई)
= 2 × (50 मी + 25 मी)
= 2 × 75 मी = 150 मी
धावक द्वारा 1 चक्कर में तय की गई दूरी 150मी है।
इसलिए, 10 चक्कर में तय की गई दूरी = 10 × 150 मी = 1500 मी
अत: धावक द्वारा तय की गई कुल दूरी 1500 मी है।
उदाहरण 3 : एक आयत का परिमाप ज्ञात कीजिए जिसकी लंबाई तथा चौड़ाई क्रमश: 150 सेमी तथा 1 मी है।
हल : आयत की लंबाई = 150 सेमी

आयत की चौड़ाई = 1 मी
= 100 सेमी
आयत का परिमाप
= 2 × (लंबाई + चौड़ाई)
= 2 × (150 सेमी + 100 सेमी)
= 2 × (250 सेमी) = 500 सेमी = 5 मी
उदाहरण 4 : एक किसान के आयताकार खेत की लंबाई तथा चौड़ाई क्रमश: 240 मी तथा 180 मी है। वह खेत के चारों तरफ़ रस्से के द्वारा 3 पूरे चक्कर की बाड़ बनाना चाहता है, जैसा आकृति 10.4 में दिखाया गया है।
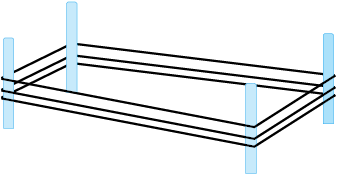
आकृति 10.4
उसके द्वारा प्रयोग किए गए रस्से की कुल लंबाई ज्ञात कीजिए।
हल : किसान को रस्से के द्वारा खेत के परिमाप को 3 गुना पूरा तय करना है। इसलिए, आवश्यक रस्से की लंबाई, खेत के परिमाप की तिगुनी होगी।
खेत का परिमाप = 2 × (लंबाई + चौड़ाई)
= 2 × ( 240 मी + 180 मी )
= 2 × 420 मी = 840 मी
रस्से की कुल लंबाई की आवश्यकता हुई = 3 × 840 मी = 2520 मी
उदाहरण 5 : 250 मी लंबाई और 175 मी चौड़ाई वाले आयताकार बगीचे के चारों ओर बाड़ लगाने का व्यय ₹ 12 प्रति मीटर की दर से ज्ञात कीजिए।
हल : आयताकार बगीचे की लंबाई = 250 मी
आयताकार बगीचे की चौड़ाई = 175 मी
बाड़ लगाने पर व्यय ज्ञात करने के लिए हमें बगीचे के परिमाप की आवश्यकता होती है।
आयताकार बगीचे का परिमाप = 2 × (लंबाई + चौड़ाई)
= 2 × (250 मी + 175 मी)
= 2 × (425 मी) = 850 मी
बगीचे के चारों ओर 1 मी लंबी बाड़ लगाने पर व्यय = ₹ 12
अत: बगीचे के चारों ओर 850 मी लंबी बाड़ लगाने पर कुल व्यय
= ₹ 12 × 850 = ₹ 10200
10.2.2 सम आकृतियों का परिमाप
आइए, इस उदाहरण को देखते हैं :
विश्वामित्र 1 मी भुजा वाले वर्गाकार चित्र के चारों ओर एक रंगीन टेप लगाना चाहता है, जैसा कि आकृति 10.5 में दिखाया गया है। उसे कितनी लंबी रंगीन टेप की आवश्यकता होगी?
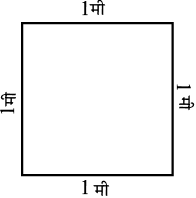
आकृति 10.5
चूँकि विश्वामित्र वर्गाकार चित्र के चारों ओर रंगीन टेप लगाना चाहता है, इसलिए उसे वर्गाकार चित्र के परिमाप को ज्ञात करने की आवश्यकता है।
इसलिए, आवश्यक टेप की लंबाई =
वर्गाकार चित्र का परिमाप = 1 मी + 1 मी + 1 मी + 1 मी= 4 मी
हम जानते हैं कि वर्ग की चारों भुजाओं की लंबाई बराबर होती है। इसलिए, इसे चार बार जोड़ने के स्थान पर, हम वर्ग की एक भुजा की लंबाई को 4 से गुणा कर सकते हैं। इसलिए आवश्यक टेप की लंबाई = 4 × 1 मी = 4 मी
इस उदाहरण से हम देखते हैं कि
वर्ग का परिमाप = 4 × एक भुजा की लंबाई
एेसे ही कुछ और वर्गों को बनाइए और उनका परिमाप ज्ञात कीजिए।
अब हम 4 सेमी भुजा वाले एक समबाहु त्रिभुज (आकृति 10.6) को देखते हैं। क्या हम इसका परिमाप ज्ञात कर सकते हैं?
इस समबाहु त्रिभुज का परिमाप = 4 + 4 + 4 सेमी
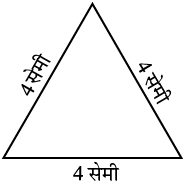
आकृति 10.6
इस समबाहु त्रिभुज का परिमाप = (4 + 4 + 4) सेमी
= 3 × 4 सेमी
= 12 सेमी
इस प्रकार, हम देखते हैं कि
समबाहु त्रिभुज का परिमाप = 3 × एक भुजा की लंबाई
क्या आप बता सकते हैं कि एक वर्ग तथा एक समबाहु त्रिभुज में क्या समानता है? इन आकृतियों में प्रत्येक भुजा की लंबाई बराबर है तथा प्रत्येक कोण की माप बराबर है। एेसी सभी आकृतियाँ, बंद सम आकृतियाँ (regular closed figures) कहलाती हैं।
इसलिए एक वर्ग तथा एक समबाहु त्रिभुज सम बंद आकृतियाँ हैं।
आपने देखा कि
एक वर्ग का परिमाप = 4 × एक भुजा की लंबाई
एक समबाहु त्रिभुज का परिमाप = 3 × एक भुजा की लंबाई
इसी प्रकार, एक सम पंचभुज का परिमाप कितना होगा?
एक सम पंचभुज में 5 बराबर भुजाएँ होती हैं।
इसलिए, एक सम पंचभुज का परिमाप = 5 × एक भुजा की लंबाई और एक सम षट्भुज का परिमाप _______ होगा।
और एक सम अष्टभुज का परिमाप क्या होगा?

अपने चारों ओर एेसी वस्तुओं का पता लगाइए जो सम आकृतियाँ हों और उनका परिमाप भी ज्ञात कीजिए।
उदाहरण 6 : शायना 70 मी भुजा वाले वर्गाकार पार्क के किनारे-किनारे (चारों ओर) 3 चक्कर लगाती है। उनके द्वारा तय की गई दूरी ज्ञात कीजिए।
हल : वर्गाकार पार्क का परिमाप
= 4 × एक भुजा की लंबाई
= 4 × 70 मी = 280 मी
एक चक्कर में तय की गई दूरी = 280 मी
इसलिए, 3 × 280 मी = 840 मी
उदाहरण 7 : पिंकी 75 मी भुजा वाले वर्गाकार मैदान के किनारे-किनारे चक्कर लगाती है। बॉब एक आयताकार मैदान, जिसकी लंबाई तथा चौड़ाई क्रमश: 160 मी और 105 मी है, के किनारे-किनारे चक्कर लगाता है। दोनों में से कौन अधिक और कितनी अधिक दूरी तय करता है।
हल : पिंकी द्वारा एक चक्कर में तय की गई दूरी = वर्ग का परिमाप
= 4 × एक भुजा की लंबाई
= 4 × 75 मी = 300 मी
बॉब द्वारा एक चक्कर में तय की गई दूरी = आयत का परिमाप = 2 × (लंबाई + चौड़ाई)
= 2 × (160 मी + 105 मी )
= 2 × 265 मी = 530 मी
तय की गई दूरियों में अंतर = 530 मी – 300 मी = 230मी
अत: बॉब अधिक दूरी तय करता है और यह दूरी 230 मी अधिक है।
उदाहरण 8 : एक सम पंचभुज का परिमाप ज्ञात कीजिए जिसकी प्रत्येक भुजा की लंबाई 3 सेमी है।
हल : इस सम पंचभुज में 5 भुजाएँ हैं, जिसमें प्रत्येक भुजा की लंबाई 3 सेमी है, सम पंचभुज का परिमाप = 5 × 3 सेमी = 15 सेमी
उदाहरण 9 : एक सम षट्भुज का परिमाप 18 सेमी है। इसकी एक भुजा की लंबाई ज्ञात कीजिए।
हल : परिमाप = 18 सेमी
एक सम षट्भुज में 6 बराबर भुजाएँ होती हैं। इसलिए, एक भुजा की लंबाई ज्ञात करने के लिए, हम परिमाप को 6 से भाग दे सकते हैं।
सम षट्भुज की एक भुजा की लंबाई = 18 सेमी ÷ 6 = 3 सेमी
अत: सम षट्भुज की प्रत्येक भुजा की लंबाई 3 सेमी है।
अब हम कुछ एेसे प्रश्नों को हल करेंगे जो कि अभी तक प्राप्त की गई जानकारी पर आधारित है।
प्रश्नावली 10.1
1. नीचे दी हुई आकृतियों का परिमाप ज्ञात कीजिए :
2. 40 सेमी लंबाई और 10 सेमी चौड़ाई वाले एक आयताकार बॉक्स के ढक्कन को चारों ओर से पूरी तरह एक टेप द्वारा बंद कर दिया जाता है। आवश्यक टेप की लंबाई ज्ञात कीजिए।
4. 32 सेमी लंबाई और 21 सेमी चौड़ाई वाले एक फ़ोटो को लकड़ी की पट्टी से फ्रेम करना है। आवश्यक लकड़ी की पट्टी की लंबाई ज्ञात कीजिए।
5. एक आयताकार भूखंड की लंबाई और चौड़ाई क्रमश: 0.7 किमी और 0.5 किमी है। इसके चारों ओर एक तार से 4 पंक्तियों में बाड़ लगाई जानी है। आवश्यक तार की लंबाई ज्ञात कीजिए।
6. निम्न आकृतियों में प्रत्येक का परिमाप ज्ञात कीजिए :
(a) एक त्रिभुज जिसकी भुजाएँ 3 सेमी, 4 सेमी तथा 5 सेमी हैं।
(b) एक समबाहु त्रिभुज जिसकी एक भुजा की लंबाई 9 सेमी है।
(c) एक समद्विबाहु त्रिभुज जिसकी प्रत्येक समान भुजा 8 सेमी की हो तथा तीसरी भुजा 6 सेमी हो।
7. एक त्रिभुज का परिमाप ज्ञात कीजिए जिसकी भुजाएँ 10 सेमी, 14 सेमी तथा 15 सेमी हैं।
8. एक सम षट्भुज का परिमाप ज्ञात कीजिए, जिसकी प्रत्येक भुजा की माप 8 मी है।
9. एक वर्ग की भुजा ज्ञात कीजिए, जिसका परिमाप 20 मी है।
10. एक सम पंचभुज का परिमाप 100 सेमी है। प्रत्येक भुजा की लंबाई ज्ञात कीजिए।
11. एक धागे का टुकड़ा 30 सेमी लंबाई का है। प्रत्येक भुजा की लंबाई क्या होगी, यदि धागे से बनाया जाता है।
(a) एक वर्ग?
(b) एक समबाहु त्रिभुज?
(c) एक सम षट्भुज?
12. एक त्रिभुज की दो भुजाएँ 12 सेमी तथा 14 सेमी हैं। इस त्रिभुज का परिमाप 36 सेमी है। इसकी तीसरी भुजा की लंबाई क्या होगी?
13. 250 मी भुजा वाले वर्गाकार बगीचे के चारों ओर बाड़ लगाने का व्यय ₹20 प्रति मीटर की दर से ज्ञात कीजिए।
14. एक आयताकार बगीचा जिसकी लंबाई 175 मी तथा चौड़ाई 125 मी है, के चारों ओर ₹12 प्रति मीटर की दर से बाड़ लगाने का व्यय ज्ञात कीजिए।
15. स्वीटी 75 मी भुजा वाले वर्ग के चारों ओर दौड़ती है और बुलबुल 60 मी लंबाई और 45 मी चौड़ाई वाले आयत के चारों ओर दौड़ती है। कौन कम दूरी तय करती है?
16. निम्न प्रत्येक आकृति का परिमाप ज्ञात कीजिए। आप उत्तर से क्या निष्कर्ष निकालते हैं?
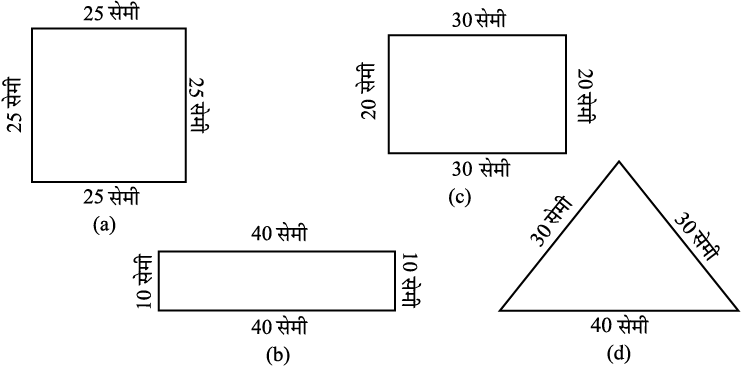
17. अवनीत 9 वर्गाकार टाइल खरीदता है, जिसकी प्रत्येक भुजा 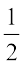 मी है और वह इन टाइलों को एक वर्ग के रूप में रखता है।
मी है और वह इन टाइलों को एक वर्ग के रूप में रखता है।

(a) नए वर्ग का परिमाप क्या है [(आकृति 10.7 (a)]?
(b) शैरी को उसके द्वारा टाइलों को रखने की व्यवस्था पसंद नहीं आती है। वह इन टाइलों को एक क्रॉस के रूप में रखवाती है। इस व्यवस्था का परिमाप कितना होगा [(आकृति 10.7 (b)]?
(c) किसका परिमाप अधिक है?
(d) अवनीत सोचता है, क्या कोई एेसा भी तरीका है जिससे इनसे भी बड़ा परिमाप प्राप्त किया जा सकता हो? क्या आप एेसा करने का कोई सुझाव दे सकते हैं? (टाइलें किनारों से आपस में मिली हुई हों और वे टूटी न हों)।
10.3 क्षेत्रफल
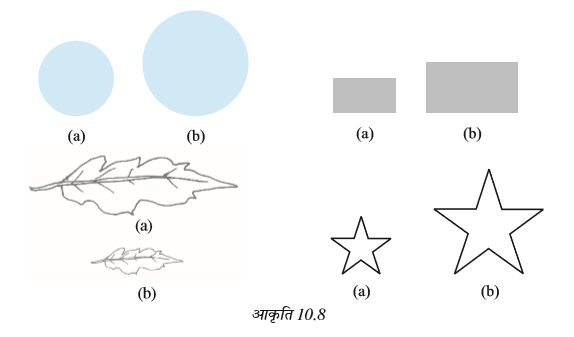
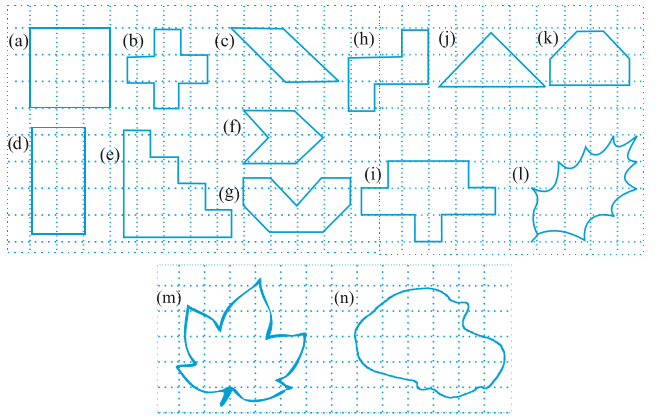
नीचे दी गई बंद आकृतियों को देखिए (आकृति 10.8)। ये सभी आकृतियाँ तल में कुछ क्षेत्र को घेरती हैं। क्या आप बता सकते हैं कि इनमें से कौन सी आकृति ज़्यादा क्षेत्र घेरती है?
बंद आकृतियों द्वारा घेरे गए तल के परिमाण को उसका क्षेत्रफल कहते हैं। इसलिए, क्या आप बता सकते हैं कि ऊपर दी गई आकृतियों में किसका क्षेत्रफल अधिक है?
अब हम नीचे दी गई आकृतियों को देखते हैं (आकृति 10.9)। इनमें से किस आकृति का क्षेत्रफल अधिक है? इन आकृतियों को देखने मात्र से यह बता पाना बहुत ही मुश्किल है। इसलिए, आप क्या करते हैं?
आकृति 10.9
इन्हें एक वर्गांकित पेपर या ग्राफ पेपर पर रखिए जहाँ पर प्रत्येक वर्ग की माप 1 सेमी × 1 सेमी हो।
इन आकृतियों की बाहरी सीमा अर्थात् बाहरी रूपरेखा खींचिए। इस आकृति के द्वारा घेरे गए वर्गों को देखिए। आप देखेंगे कि उनमें कुछ पूरे वर्ग, कुछ आधे वर्ग, कुछ आधे से कम तथा कुछ आधे से अधिक वर्ग घिरे हुए हैं।
आकृति द्वारा घेरे गए आवश्यक सेमी वर्ग की संख्या ही उसका क्षेत्रफल है।
परंतु यहाँ एक समस्या है : आप जिस भी किसी आकृति का क्षेत्रफल मापना या जानना चाहते हैं, वर्ग हमेशा उसे पूर्णतया नहीं ढकते हैं। हम इस समस्या का समाधान एक परिपाटी को अपनाकर कर सकते हैं।
- एक पूरे वर्ग के क्षेत्रफल को हम 1 वर्ग इकाई (मात्रक) लेते हैं। यदि ये वर्ग एक वर्ग सेंटीमीटर के हैं तब एक पूरे वर्ग का क्षेत्रफल 1 वर्ग सेमी होगा।
- जिन वर्गों का आधे से कम भाग आकृति से घिरा है, उन पर ध्यान मत दीजिए अर्थात् उन्हें छोड़ दीजिए।
- यदि किसी वर्ग का आधे से अधिक भाग आकृति से घिरा है, तो एेसे वर्ग को हम एक पूरा वर्ग ही गिनते हैं।
- यदि किसी वर्ग का ठीक-ठीक आधा भाग गिनती में आता है, तो एेसे वर्ग के क्षेत्रफल को
![]() वर्ग इकाई लेते हैं।
वर्ग इकाई लेते हैं।
इस परिपाटी से इच्छित क्षेत्रफल का अनुमान अच्छी तरह लगाया जा सकता है।
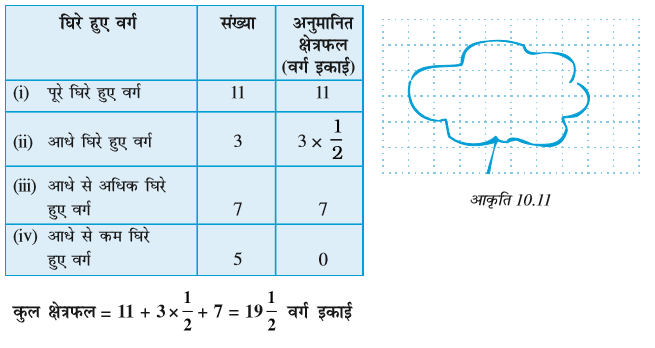
उदाहरण 10 : आकृति 10.10 में दिखाए आकार का क्षेत्रफल ज्ञात कीजिए।
हल : यह आकार (आकृति) रेखाखंडों से मिलकर बना है। यह आकृति केवल पूरे वर्गों तथा आधे से घिरी हुई है। यह हमारे कार्य को और भी आसान बनाता है, कैसे?

आकृति 10.10
(i) पूरे घिरे हुए वर्गों की संख्या = 3
(ii) आधे घिरे हुए वर्गों की संख्या = 3
पूरे वर्गों द्वारा घिरा हुआ क्षेत्रफल = 3 × 1 वर्ग इकाई = 3 वर्ग इकाई
आधे वर्गों द्वारा घिरा (ढका) हुआ क्षेत्रफल
= 3 × 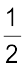 वर्ग इकाई = 1
वर्ग इकाई = 1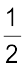 वर्ग इकाई
वर्ग इकाई
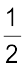 वर्ग इकाई
वर्ग इकाईउदाहरण 11 : वर्गों को गिनकर, आकृति 10.9 (b) का अनुमानित क्षेत्रफल ज्ञात कीजिए।
हल : ग्राफ पेपर पर इस आकृति की बाहरी रूपरेखा खींचिए। वर्ग इस आकृति को कैसे घेरते हैं (आकृति 10.11)?
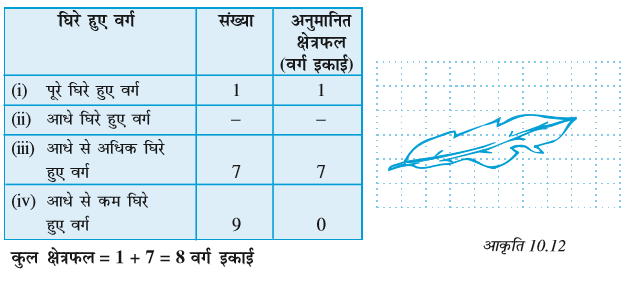
उदाहरण 12 : वर्गों को गिनकर, आकृति 10.9 (a) का अनुमानित क्षेत्रफल ज्ञात कीजिए।
हल : एक ग्राफ पेपर पर इस आकृति की बाहरी रूपरेखा खींचिए। वर्ग इस आकृति को कैसे घेरते हैं। (आकृति 10.12)?

1. ग्राफ पेपर पर कोई एक वृत्त खींचिए। इस वृत्त में उपस्थित वर्गों की संख्या को गिनकर वृत्ताकार क्षेत्र का अनुमानित क्षेत्रफल ज्ञात कीजिए।
2. ग्राफ पेपर पर पत्तियों, फूल की पंखुड़ियों तथा एेसे ही अन्य वस्तुओं को छायांकित कीजिए और उनका क्षेत्रफल ज्ञात कीजिए।
प्रश्नावली 10.2
1. निम्नलिखित आकृतियों के क्षेत्रफल ज्ञात कीजिए :
10.3.1 आयत का क्षेत्रफल
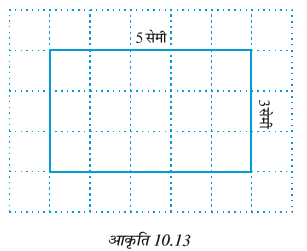
एक वर्गांकित पेपर की सहायता से, क्या हम बता सकते हैं कि एक आयत का क्षेत्रफल कितना होगा, जिसकी लंबाई 5 सेमी तथा चौड़ाई 3 सेमी है?
ग्राफ पेपर पर एक आयत बनाइए जिस पर 1 सेमी × 1 सेमी के वर्ग हों (आकृति 10.13)। यह आयत 15 वर्गों को पूर्णतया ढक लेता है।
आयत का क्षेत्रफल = 15 वर्ग सेमी है, जिसे हम 5 × 3 वर्ग सेमी (लंबाई × चौड़ाई) के रूप में भी लिख सकते हैं।
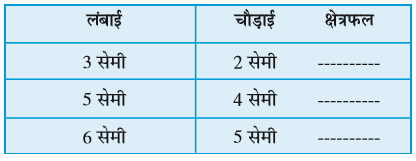
कुछ आयतों की भुजाओं की मापें दी गई हैं। इन्हें ग्राफ पेपर पर रखकर तथा वर्गों की संख्या को गिनकर, इनका क्षेत्रफल ज्ञात कीजिए।
इससे हम क्या निष्कर्ष निकालते हैं?
हमने देखा कि
आयत का क्षेत्रफल = (लंबाई × चौड़ाई)
बिना ग्राफ पेपर की सहायता से, क्या हम एक आयत का क्षेत्रफल ज्ञात कर सकते हैं, जिसकी लंबाई 6 सेमी तथा चौड़ाई 4 सेमी है?
हाँ, यह संभव है।
आयत का क्षेत्रफल
= लंबाई × चौड़ाई
= 6 सेमी × 4 सेमी = 24 वर्ग सेमी

1. अपनी कक्षा के फर्श का क्षेत्रफल ज्ञात कीजिए।
2. अपने घर के किसी एक दरवाज़े का क्षेत्रफल ज्ञात कीजिए।
10.3.2 वर्ग का क्षेत्रफल
आइए, अब हम एक वर्ग पर विचार करते हैं
जिसकी भुजा की लंबाई 4 सेमी है (आकृति 10.14)।

इस वर्ग का क्षेत्रफल कितना होगा?
यदि हम इसे सेंटीमीटर ग्राफ पेपर पर रखते हैं, तब हम क्या देखते हैं?
यह 16 वर्गों को पूर्णतया ढक लेता है।
इसलिए, वर्ग का क्षेत्रफल = 16 वर्ग सेमी
= 4 × 4 वर्ग सेमी
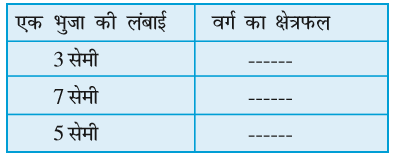
कुछ वर्गों की एक भुजा की लंबाई दी गई है :
ग्राफ पेपर की सहायता से उनके क्षेत्रफलों को ज्ञात कीजिए।
इससे हम क्या निष्कर्ष निकालते हैं? हमने देखा कि प्रत्येक स्थिति में,
वर्ग का क्षेत्रफल = भुजा × भुजा
आप प्रश्नों को हल करते समय इसका प्रयोग एक सूत्र के रूप में कर सकते हैं।
उदाहरण 13 : एक आयत का क्षेत्रफल ज्ञात कीजिए जिसकी लंबाई तथा चौड़ाई क्रमश: 12 सेमी तथा 4 सेमी है।
हल : आयत की लंबाई = 12 सेमी
= 12 सेमी × 4 सेमी = 48 वर्ग सेमी
उदाहरण 14 : एक वर्गाकार भूखंड का क्षेत्रफल ज्ञात कीजिए, जिसकी एक भुजा की लंबाई 8 मी है।
हल : वर्ग की भुजा = 8 मी
वर्ग का क्षेत्रफल = भुजा × भुजा
= 8 मी × 8 मी = 64 वर्ग मी
उदाहरण 15 : एक आयताकार गत्ते का क्षेत्रफल 36 वर्ग सेमी तथा इसकी लंबाई 9 सेमी है। गत्ते की चौड़ाई ज्ञात कीजिए।
हल : आयताकार गत्ते का क्षेत्रफल = 36 वर्ग सेमी
लंबाई = 9 सेमी
चौड़ाई = ?
आयत का क्षेत्रफल = लंबाई × चौड़ाई
इसलिए, चौड़ाई =  =
= 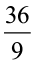 सेमी = 4 सेमी
सेमी = 4 सेमी
अत:, आयताकार गत्ते की चौड़ाई 4 सेमी है।
उदाहरण 16 : बॉब 3 मी चौड़ाई तथा 4 मी लंबाई वाले एक कमरे में वर्गाकार टाइलें लगाना चाहता है। यदि प्रत्येक वर्गाकार टाइल की भुजा 0.5 मी हो, तो कमरे के फर्श को ढकने के लिए कितनी टाइलों की आवश्यकता होगी?
हल : कमरे में लगने वाली सभी टाइलों का कुल क्षेत्रफल, फर्श के क्षेत्रफल के बराबर होगा।
कमरे की लंबाई = 4 मी
कमरे की चौड़ाई = 3 मी
फर्श का क्षेत्रफल = लंबाई × चौड़ाई
= 4 मी × 3 मी
= 12 वर्ग मी
आवश्यक कुल टाइलों की संख्या = 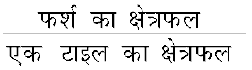
= 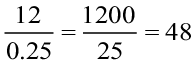 टाइलें
टाइलें
उदाहरण 17 : 1 मी 25 सेमी चौड़ाई तथा 2 मी लंबाई वाले कपड़े के एक टुकड़े का क्षेत्रफल वर्ग मीटर में ज्ञात कीजिए।
हल : कपड़े की लंबाई = 2 मी
कपड़े की चौड़ाई = 1 मी 25 सेमी = 1 मी + 0. 25 मी = 1.25 मी
(चूँकि 25 सेमी = 0.25 मी)
कपड़े का क्षेत्रफल = कपड़े की लंबाई × कपड़े की चौड़ाई
= 2 मी × 1.25 मी = 2.50 वर्ग मी
प्रश्नावली 10.3
1. उन आयतों का क्षेत्रफल ज्ञात कीजिए जिनकी भुजाएँ नीचे दी गई हैं :
(a) 3 सेमी और 4 सेमी
(b) 12 मी और 21 मी
(c) 2 किमी और 3 किमी
(d) 2 मी और 70 सेमी
2. उन वर्गों का क्षेत्रफल ज्ञात कीजिए जिनकी भुजाएँ निम्नलिखित हैं :
(a) 10 सेमी
(b) 14 सेमी
(c) 5 मी
3. तीन आयतों की विमाएँ निम्नलिखित हैं :
(a) 9 मी और 6 मी
(b) 3 मी और 17 मी
(c) 4 मी और 14 मी
इनमें से किसका क्षेत्रफल सबसे अधिक है और किसका सबसे कम?
4. 50 मी लंबाई वाले एक आयताकार बगीचे का क्षेत्रफल 300 वर्ग मीटर है। बगीचे की चौड़ाई ज्ञात कीजिए।
5. 500 मी लंबाई तथा 200 मी चौड़ाई वाले एक आयताकार भूखंड पर ₹ 8 प्रति 100 वर्ग मीटर की दर से टाइल लगाने का व्यय ज्ञात कीजिए।
6. एक मेज़ के ऊपरी पृष्ठ की माप 2 मी × 1 मी 50 सेमी है। मेज़ का क्षेत्रफल वर्ग मीटर में ज्ञात कीजिए।
7. एक कमरे की लंबाई 4 मी तथा चौड़ाई 3 मी 50 सेमी है। कमरे के फर्श को ढकने के लिए कितने वर्ग मीटर गलीचे की आवश्यकता होगी?
8. एक फर्श की लंबाई 5 मी तथा चौड़ाई 4 मी है। 3 मी भुजा वाले एक वर्गाकार गलीचे को फर्श पर बिछाया गया है। फर्श के उस भाग का क्षेत्रफल ज्ञात कीजिए जिस पर गलीचा नहीं बिछा है।
9. 5 मी लंबाई तथा 4 मी चौड़ाई वाले एक आयताकार भूखंड पर 1 मी भुजा वाली वर्गाकार फूलों की 5 क्यारियाँ बनाई जाती हैं। भूखंड के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
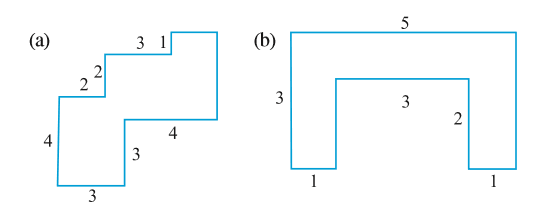
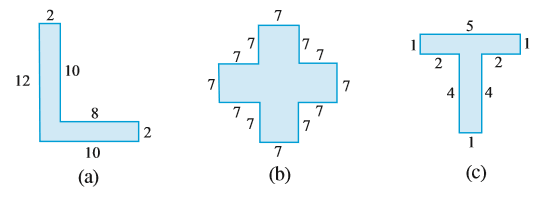
10. निम्नलिखित आकृतियों को आयतों में तोड़िए। इनका क्षेत्रफल ज्ञात कीजिए (भुजाओं की माप सेमी में दी गई है)।
11. निम्नलिखित आकृतियों को आयतों में तोड़िए और प्रत्येक का क्षेत्रफल ज्ञात कीजिए। (भुजाओं की माप सेमी में दी गई है)।
12. एक टाइल की माप 5 सेमी × 12 सेमी है। एक क्षेत्र को पूर्णतया ढकने के लिए, एेसी कितनी टाइलों की आवश्यकता होगी, जिसकी लंबाई और चौड़ाई क्रमश:
(a) 144 सेमी और 100 सेमी है।
(b) 70 सेमी और A36 सेमी है।
एक चुनौती!
एक सेंटीमीटर वर्गांकित पेपर पर आप जितने भी आयत बना सकते हैं बनाइए, जिससे कि आयत का क्षेत्रफल 16 वर्ग सेमी हो जाए (केवल पूर्ण संख्या की लंबाई पर ही विचार करना है)।
(a) किस आयत का क्षेत्रफल सबसे अधिक है?
(b) किस आयत का क्षेत्रफल सबसे कम है?
यदि आप एक एेसा आयत लें जिसका क्षेत्रफल 24 वर्ग सेमी हो, तो आपके उत्तर क्या होंगे? दिए हुए क्षेत्रफल के लिए, क्या अधिकतम परिमाप के आयत के आकार को बताना संभव है? क्या सबसे कम परिमाप के आयत के बारे में बता सकते हैं? उदाहरण दीजिए और कारण बताइए।
हमने क्या चर्चा की?
1. परिमाप एक एेसी दूरी है जो रेखाखंडों के साथ-साथ चलते हुए एक बंद आकृति के चारों ओर एक पूरा चक्कर लगाने में तय करती है।
2. (a) आयत का परिमाप = 2 × (लंबाई + चौड़ाई)
(b) वर्ग का परिमाप = 4 × भुजा की लंबाई
(c) समबाहु त्रिभुज का परिमाप = 3 × भुजा की लंबाई
3. एेसी आकृतियाँ, जिसकी सभी भुजाएँ और कोण बराबर हों, बंद सम आकृतियाँ कहलाती हैं।
4. बंद आकृतियों द्वारा घिरे गए तल के परिमाण को उसका क्षेत्रफल कहते हैं।
5. वर्गांकित पेपर का प्रयोग करके किसी आकृति का क्षेत्रफल ज्ञात करने के लिए निम्नलिखित परिपाटी को अपनाया जाता है :
(a) जिन वर्गों का आधे से कम भाग आकृति से घिरा है, उन्हें छोड़ दीजिए।
(b) यदि किसी वर्ग का आधे से अधिक भाग आकृति से घिरा है, तो एेसे वर्गों को हम एक पूरा वर्ग ही गिनते हैं।
(c) यदि किसी वर्ग का आधा भाग आकृति से घिरा हो तो उसके क्षेत्रफल को 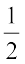 वर्ग इकाई लेते हैं।
वर्ग इकाई लेते हैं।
6. (a) आयत का क्षेत्रफल = लंबाई × चौड़ाई
(b) वर्ग का क्षेत्रफल = भुजा × भुजा