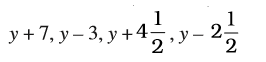Table of Contents
अध्याय 11
बीजगणित
11.1 भूमिका
अभी तक हमारा अध्ययन संख्याओं और आकारों के साथ रहा है। अब तक हम संख्याओं, संख्याओं पर संक्रियाओं और उनके गुणों के बारे में पढ़ चुके हैं। हमने संख्याओं को दैनिक जीवन की विभिन्न समस्याओं को हल करने में उपयोग किया है। गणित की वह शाखा जिसमें हमने संख्याओं का अध्ययन किया, अंकगणित (arithmetic) कहलाती है। हम दो और तीन विमाओं (dimensions) वाली आकृतियाँ तथा उनके गुणों के बारे में भी पढ़ चुके हैं। गणित की वह शाखा जिसमें हम इन आकृतियों अथवा आकारों (shapes) का अध्ययन करते हैं, ज्यामिति (geometry) कहलाती है। अब हम गणित की एक अन्य शाखा का अध्ययन प्रारंभ करने जा रहे हैं, जो बीजगणित (algebra) कहलाती है।
इस नयी शाखा , जिसका अध्ययन हम प्रारंभ करने जा रहे हैं, की मुख्य विशेषता यह है कि इसमें अक्षरों का प्रयोग किया जाता है। अक्षरों के प्रयोग से, हम नियमों और सूत्रों (formulas) को व्यापक रूप में लिख पाने में समर्थ हो जाएँगे। अक्षरों के इस प्रयोग से, हम केवल एक विशेष संख्या की ही बात न करके, किसी भी संख्या की बात कर सकते हैं। दूसरी बात यह है कि अक्षर अज्ञात राशियों के स्थान पर भी प्रयोग किए जा सकते हैं। इन अज्ञात राशियों (unknowns) को निर्धारित करने की विधियों को सीखकर हम पहेलियाँ (puzzles) और दैनिक जीवन से संबंधित अनेक समस्याओं को हल करने के अनेक प्रभावशाली साधन विकसित कर सकते हैं। तीसरी बात यह है कि ये अक्षर संख्याओं के स्थान पर प्रयोग किए जाते हैं, इसलिए इन पर संख्याओं की तरह संक्रियाएँ भी की जा सकती हैं। इससे हम बीजीय व्यंजकों (algebraic expressions) और उनके गुणों के अध्ययन की ओर अग्रसर होते हैं।
आप बीजगणित को रोचक और उपयोगी पाएँगे। यह समस्याओं के हल करने में अति उपयोगी रहता है। आइए, अपने अध्ययन को सरल उदाहरणों द्वारा प्रारंभ करें।
11.2 माचिस की तीलियों से बने प्रतिरूप
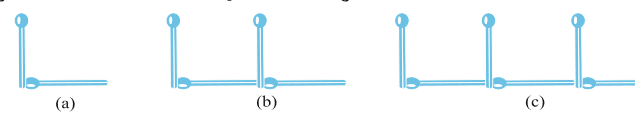
अमीना और सरिता माचिस की तीलियों से प्रतिरूप (Pattern) बना रही हैं। उन्होंने अंग्रेेज़ी वर्णमाला के अक्षरों के सरल प्रतिरूप बनाने का निर्णय किया। अमीना दो तीलियाँ लेकर अक्षर L बनाती है, जैसा कि आकृति 11.1 (a) में दिखाया गया है। फिर सरिता भी दो तीलियाँ लेती है और उनसे एक अन्य L बनाकर अमीना द्वारा बनाए गए L के आगे रख देती है, जैसा कि आकृति 11.1 (b) में दिखाया गया है।
फिर अमीना एक और L बनाकर आगे रख देती है और यह सिलसिला आगे जारी रहता है जैसा कि 11.1 (c) में बिंदुओं से दर्शाया गया है।

आकृति 11.1
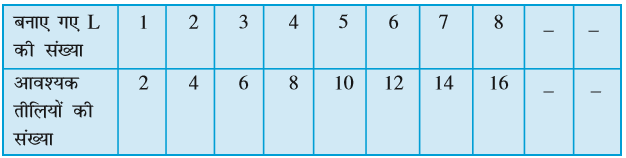
तभी उनका मित्र अप्पू आ जाता है। वह इस प्रतिरूप को देखता है। अप्पू सदैव प्रश्न पूछता रहता है। वह इन लड़कियों से पूछता है, ‘‘सात L बनाने के लिए कितनी तीलियों की आवश्यकता पड़ेगी?’’ अमीना और सरिता सुचारु रूप से कार्य करती हैं। वे 1 L, 2 L, 3 L इत्यादि से प्रतिरूप बनाती रहती हैं और एक सारणी बनाती हैं:
सारणी-1
अप्पू को सारणी-1 से अपना उत्तर प्राप्त हो जाता है। 7 L बनाने के लिए 14 तीलियों की आवश्यकता होगी।
आवश्यक तीलियों की संख्या = 2 × L की संख्या
आइए, सुविधा के लिए, L की संख्या के लिए अक्षर n लिखें।
यदि एक L बनाया जाता है, तो n = 1 है; यदि 2L बनाए जाते हैं तो n = 2 है; इत्यादि। इस प्रकार, n कोई भी प्राकृत संख्या 1, 2, 3, 4, 5, ... हो सकती है। फिर हम लिखते हैं : आवश्यक तीलियों की संख्या = 2 × n है।
2 × n लिखने के स्थान पर, हम इसे 2n लिखते हैं। ध्यान दीजिए 2n वही है जो 2 × n है।

अमीना अपने मित्रों से कहती है कि उसका यह नियम कितनी भी संख्या में L बनाने के लिए आवश्यक तीलियों की संख्या बता सकता है।
इस प्रकार, n = 1 के लिए, आवश्यक तीलियों की संख्या = 2 × 1 = 2;
n = 2 के लिए, आवश्यक तीलियों की संख्या = 2 × 2 = 4;
n = 3 के लिए, आवश्यक तीलियों की संख्या = 2 × 3 = 6 इत्यादि।
ये संख्याएँ सारणी-1 में दी हुई संख्याओं जैसी ही हैं।
सरिता कहती है, ‘‘यह नियम बहुत प्रभावशाली है! इस नियम का प्रयोग करके मैं 100 L बनाने में आवश्यक तीलियों की संख्या भी बता सकती हूँ। एक बार नियम ज्ञात हो जाए, तो मुझे प्रतिरूप खींचने या सारणी बनाने की कोई आवश्यकता नहीं होगी।’’
क्या आप सरिता से सहमत हैं?
11.3 एक चर की अवधारणा
उपरोक्त उदाहरण में, हमने L का एक प्रतिरूप बनाने में आवश्यक तीलियों की संख्या ज्ञात करने के लिए, एक नियम ज्ञात किया था। नियम यह था :
आवश्यक तीलियों की संख्या = 2n
यहाँ n, L के प्रतिरूपों की संख्या है और n के मान 1, 2, 3, 4,... हो सकते हैं। आइए, सारणी-1 को पुन: देखें। सारणी में n का मान बदलता (बढ़ता) जाता है। इसके परिणामस्वरूप, आवश्यक तीलियों की संख्या भी बदलती (बढ़ती) जाती है।
n चर (Variable) का एक उदाहरण है। इसका मान स्थिर (fixed) नहीं है; यह कोई भी मान 1, 2, 3, 4, ... ले सकता है। हमने आवश्यक तीलियों की संख्या के लिए, चर n का प्रयोग करके, नियम लिखा।
शब्द ‘चर’ का अर्थ है वह वस्तु जो विचरण (vary) करती है, अर्थात् बदलती है। चर का मान स्थिर नहीं है। यह विभिन्न मान ले (ग्रहण कर) सकता है।
हम चरों के बारे में और अधिक सीखने के लिए, माचिस की तीलियों से बनाए गए प्रतिरूपों में से एक अन्य उदाहरण को देखेंगे।
11.4 माचिस की तीलियों के और प्रतिरूप
अमीना और सरिता तीलियों के इन प्रतिरूपों में रुचि लेने लगी हैं। अब वे अक्षर C का एक प्रतिरूप बनाने का प्रयत्न करती हैं। एक C बनाने के लिए, वे तीन तीलियों का प्रयोग करती हैं, जैसा कि आकृति 11.2(a) में दर्शाया गया है।
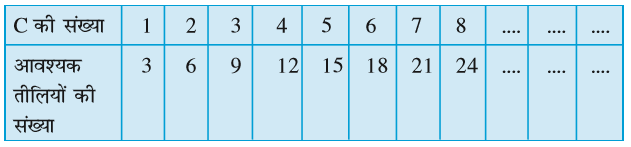
सारणी-2, C का एक प्रतिरूप बनाने के लिए आवश्यक तीलियों की संख्या प्रदान करती है :
सारणी-2
क्या आप उपरोक्त सारणी में, छोड़ी गई रिक्त प्रविष्टियों को पूरा कर सकते हैं?
सरिता ने यह नियम दिया:
आवश्यक तीलियों की संख्या = 3n
उसने C की संख्या के लिए अक्षर n का प्रयोग किया है; n एक चर है जो मान 1, 2, 3, 4, ... इत्यादि ले सकता है।
याद रखिए कि 3n वही है जो 3 × n है।
इसके आगे अब अमीना और सरिता F का एक प्रतिरूप बनाना चाहती हैं। वे चार तीलियों का प्रयोग करके एक F बनाती हैं, जैसा कि आकृति 11.3(a) में दर्शाया गया है।
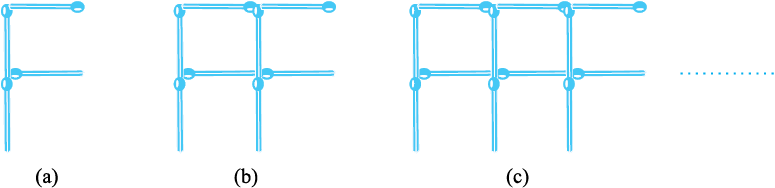
आकृति 11.3
क्या आप F के प्रतिरूप बनाने के लिए अब कोई नियम लिख सकते हैं?
तीलियों से बनाए जाने वाले वर्णमाला के अन्य अक्षरों और आकारों के बारे में सोचिए। उदाहरणार्थ, U ( ), V (
), V ( ), त्रिभुज (
), त्रिभुज ( ), वर्ग (
), वर्ग ( ) इत्यादि। इनमें से कोई पाँच अक्षर या आकार चुनिए और इनके तीलियों के प्रतिरूप बनाने के लिए आवश्यक तीलियों की संख्या के लिए नियम लिखिए।
) इत्यादि। इनमें से कोई पाँच अक्षर या आकार चुनिए और इनके तीलियों के प्रतिरूप बनाने के लिए आवश्यक तीलियों की संख्या के लिए नियम लिखिए।
11.5 चरों के और उदाहरण
हमने एक चर को दर्शाने के लिए अक्षर n का प्रयोग किया है। राजू पूछता है, “ m क्यों नहीं?” n में कोई विशेष बात नहीं है, किसी भी अक्षर का प्रयोग किया जा सकता है।
एक चर को दर्शाने के लिए, किसी भी अक्षर m, l, p, x, y, z इत्यादि का प्रयोग किया जा सकता है। याद रखिए, एक चर वह संख्या है जिसका मान स्थिर नहीं होता। उदाहरणार्थ, संख्या 5 या संख्या 100 या कोई अन्य दी हुई संख्या एक चर नहीं है। इनके मान स्थिर (निश्चित) हैं। इसी प्रकार, त्रिभुज के कोणों की संख्या का मान स्थिर है, जो 3 है। यह एक चर नहीं है। एक चतुर्भुज के कोणों की संख्या (4) स्थिर है। यह भी एक चर नहीं है। परंतु उपरोक्त उदाहरणों, जो हमने देखे हैं, में n एक चर है। यह विभिन्न मान 1, 2, 3, 4, ... ले (ग्रहण कर) सकता है।
आइए, अब एक अधिक परिचित स्थिति में चरों पर विचार करें।
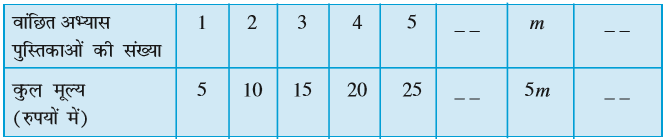
स्कूल के बुक स्टोर से विद्यार्थी अभ्यास-पुस्तिकाएँ खरीदने गए। एक अभ्यास-पुस्तिका का मूल्य 5 रु है। मुन्नू 5, अप्पू 7, सारा 4 अभ्यास-पुस्तिकाएँ खरीदना चाहती हैं। एक विद्यार्थी को बुक स्टोर से अभ्यास-पुस्तिका खरीदने के लिए कितनी धनराशि की आवश्यकता पड़ेगी?

यह इस पर निर्भर रहेगा कि वह विद्यार्थी कितनी अभ्यास-पुस्तिकाएँ खरीदना चाहता है। विद्यार्थी मिलकर एक सारणी बनाते हैं :
सारणी-3
m अभ्यास-पुस्तिकाओं की उस संख्या के लिए प्रयोग किया गया है जो एक विद्यार्थी खरीदना चाहता है। यहाँ m एक चर है, जो कोई भी मान 1, 2, 3, 4, ... ले सकता है। m अभ्यास-पुस्तिकाओं का कुल मूल्य निम्न नियम द्वारा दिया जाता है :
कुल मूल्य (रुपयों में) = 5 × वांछित अभ्यास-पुस्तिकाओं की संख्या
= 5m
यदि मुन्नू 5 अभ्यास-पुस्तिकाएँ खरीदना चाहता है, तो m = 5 लेकर हम कहते हैं कि मुन्नू को ₹ 5 × 5 अर्थात् ₹ 25 अपने साथ ले जाने चाहिए, ताकि वह बुक स्टोर से खरीदारी कर सके।
आइए एक और उदाहरण लें। किसी स्कूल में गणतंत्र दिवस मनाने के अवसर पर, बच्चे मुख्य अतिथि के सम्मुख सामूहिक ड्रिल (Drill) का प्रदर्शन करने जा रहे हैं। वे इस प्रकार खड़े किए जाते हैं कि एक पंक्ति में 10 बच्चे रहें (आकृति 11.4)। इस ड्रिल में कितने बच्चे भाग ले सकते हैं?

आकृति 11.3
बच्चों की संख्या पंक्तियों की संख्या पर निर्भर करेगी। यदि 1 पंक्ति है, तो बच्चों की संख्या 10 होगी। यदि 2 पंक्तियाँ हों, तो बच्चों की संख्या 2 × 10, अर्थात् 20 होगी। यदि r पंक्तियाँ हों, तो बच्चों की संख्या 10r होगी। यहाँ r एक चर है जो पंक्तियों की संख्या प्रदर्शित करता है और यह मान 1, 2, 3, 4, ... ले सकता है।
अभी तक हमने जितने उदाहरण देखे हैं उनमें एक चर को एक संख्या से गुणा किया गया है। परंतु विभिन्न स्थितियाँ एेसी भी हो सकती हैं, जहाँ संख्याओं को चरों में जोड़ा जाता है या चरों में से घटाया जाता है, जैसा कि नीचे देखा जा सकता है।
सरिता का कहना कि उसके कंचों के संग्रह में अमीना के कंचों के संग्रह से 10 अधिक कंचे हैं। यदि अमीना के पास 20 कंचे हैं, तो सरिता के पास 30 कंचे होंगे। यदि अमीना के पास 30 कंचे हैं, तो सरिता के पास 40 कंचे होंगे। हमें यह ज्ञात नहीं है कि अमीना के पास कितने कंचे हैं। उसके पास कंचों की संख्या कुछ भी हो सकती है। परंतु हम जानते हैं कि सरिता के कंचों की संख्या = अमीना के कंचों की संख्या + 10 है।
हम अमीना के कंचों की संख्या को x से दर्शाएँगे। यहाँ x एक चर है, जो मान 1, 2, 3, 4,... ,10,... ,20,... ,30,... ले सकता है। x का प्रयोग करते हुए, हम लिख सकते हैं कि सरिता के कंचे = x + 10 हैं। व्यंजक (x + 10) को, x धन (Plus) 10 पढ़ा जाता है। इसका अर्थ है कि x का मान 20 है, तो (x + 10) का मान 30 होगा। यदि x का मान 30 है, तो (x + 10) का मान 40 होगा इत्यादि।
व्यंजक (x + 10) को और अधिक सरल नहीं किया जा सकता है। x + 10 को 10x से भ्रमित न हों। ये भिन्न-भिन्न हैं। 10x में, x को 10 से गुणा किया गया है। (x + 10) में, 10 को x में जोड़ा गया है। हम इसकी जाँच x के कुछ मान लेकर कर सकते हैं। उदाहरणार्थ,
यदि x = 2, तो 10x = 10 × 2 = 20 है और x + 10 = 2 + 10 = 12 है।
यदि x = 10, तो 10x = 10 × 10 = 100 है और x + 10 = 10 + 10 = 20 है।
राजू और बालू दो भाई हैं। बालू राजू से 3 वर्ज़ छोटा है। अगर राजू 15 वर्ज़ का है, तो बालू 9 वर्ज़ का है। हमें राजू की वर्तमान आयु ज्ञात नहीं है। इसका मान कुछ भी हो सकता है। मान लीजिए, x राजू की वर्ज़ों में आयु व्यक्त करता है। x एक चर है। यदि राजू की आयु वर्ज़ों में x है, तो बालू की आयु वर्ज़ों में (x – 3) है। व्यंजक (x – 3) को x ऋण (minus) 3 पढ़ा जाता है। जैसा कि आप आ”ाा करेंगे, जब x का मान 12 है, तो (x – 3) का मान 9 है और जब x का मान 15 है, तो (x – 3) का मान 12 है।

प्रश्नावली 11.1
1. तीलियों से प्रतिरूप बनाने के लिए आवश्यक तीलियों की संख्या के लिए नियम ज्ञात कीजिए। नियम लिखने के लिए एक चर का प्रयोग कीजिए :
(a) अक्षर T का  के रूप में तीलियों से प्रतिरूप
के रूप में तीलियों से प्रतिरूप
(b) अक्षर Z का  के रूप में तीलियों से प्रतिरूप
के रूप में तीलियों से प्रतिरूप
(c) अक्षर U का  के रूप में तीलियों से प्रतिरूप
के रूप में तीलियों से प्रतिरूप
(d) अक्षर V का  के रूप में तीलियों से प्रतिरूप
के रूप में तीलियों से प्रतिरूप
(e) अक्षर E का  के रूप में तीलियों से प्रतिरूप
के रूप में तीलियों से प्रतिरूप
(f) अक्षर S का 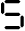 के रूप में तीलियों से प्रतिरूप
के रूप में तीलियों से प्रतिरूप
(g) अक्षर A का  के रूप में तीलियों से प्रतिरूप
के रूप में तीलियों से प्रतिरूप
2. हम अक्षर L, C और F के प्रतिरूपों के लिए नियमों को पहले से जानते हैं। ऊपर प्रश्न 1 में दिए कुछ अक्षरों से वही नियम प्राप्त होता है जो L द्वारा प्राप्त हुआ था। ये अक्षर कौन-कौन से हैं? एेसा क्यों होता है?
3. किसी परेड में कैडेट (Cadets) मार्च (March) कर रहे हैं। एक पंक्ति में 5 कैडेट हैं। यदि पंक्तियों की संख्या ज्ञात हो, तो कैडेटों की संख्या प्राप्त करने के लिए क्या नियम है? (पंक्तियों की संख्या के लिए n का प्रयोग कीजिए)।
4. एक पेटी में 50 आम हैं। आप पेटियों की संख्या के पदों में आमों की कुल संख्या को किस प्रकार लिखेंगे? (पेटियों की संख्या के लिए b का प्रयोग कीजिए)।
5. ε”ाक्षक प्रत्येक विद्यार्थी को 5 पेंसिल देता है। विद्यार्थियों की संख्या ज्ञात होने पर, क्या आप कुल वांछित पेंसिलों की संख्या बता सकते हैं? (विद्यार्थियों की संख्या के लिए s का प्रयोग कीजिए)।
6. एक चिड़िया 1 मिनट में 1 किलोमीटर उड़ती है। क्या आप चिड़िया द्वारा तय की गई दूरी को (मिनटों में) उसके उड़ने के समय के पदों में व्यक्त कर सकते हैं? (मिनटों में उड़ने के समय के लिए t का प्रयोग कीजिए)।
7. राधा बिंदुओं (Dots) से एक रंगोली बना रही है (खड़िया के पाउडर की सहायता से बिंदुओं को जोड़कर रेखाओं का एक सुंदर प्रतिरूप बनाना, जैसे आकृति 11.5 में है)। उसके पास एक पंक्ति में 8 बिंदु हैं। r पंक्तियों की रंगोली में कितने बिंदु होंगे? यदि 8 पंक्तियाँ हों, तो कितने बिंदु होंगे? यदि 10 पंक्तियाँ हों, तो कितने बिंदु होंगे?

आकृति 11.5
8. लीला राधा की छोटी बहन है। लीला राधा से 4 वर्ज़ छोटी है। क्या आप लीला की आयु राधा की आयु के पदों में लिख सकते हैं? राधा की आयु x वर्ज़ है।
9. माँ ने लड्डू बनाए हैं। उन्होंने कुछ लड्डू मेहमानों और परिवार के सदस्यों को दिए। फिर भी 5 लड्डू शेष रह गए हैं। यदि माँ ने l लड्डू दे दिए हों, तो उसने कुल कितने लड्डू बनाए थे?
10. संतरों को बड़ी पेटियों में से छोटी पेटियों में रखा जाना है। जब एक बड़ी पेटी को खाली किया जाता है, तो उसके संतरों से दो छोटी पेटियाँ भर जाती हैं और फिर भी 10 संतरे शेष रह जाते हैं। यदि एक छोटी पेटी में संतरों की संख्या को x लिया जाए, तो बड़ी पेटी में संतरों की संख्या क्या है?
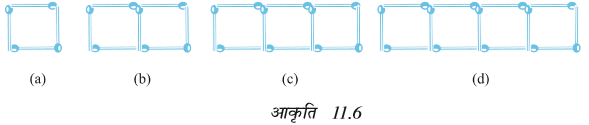
11. (a) तीलियों से बने हुए वर्गों के नीचे दिए प्रतिरूपों को देखिए (आकृति 11.6)। ये वर्ग अलग-अलग नहीं हैं। दो संलग्न वर्गों में एक तीली उभयनिज़्ठ है। इस प्रतिरूप को देखिए और वह नियम ज्ञात कीजिए जो वर्गों की संख्या के पदों में आवश्यक तीलियों की संख्या देता है। (संकेत : यदि आप अंतिम ऊर्ध्वाधर तीली को हटा दें, तो आपको C का प्रतिरूप प्राप्त हो जाएगा)।
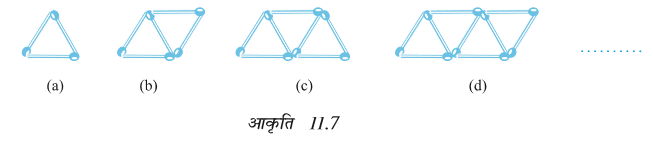
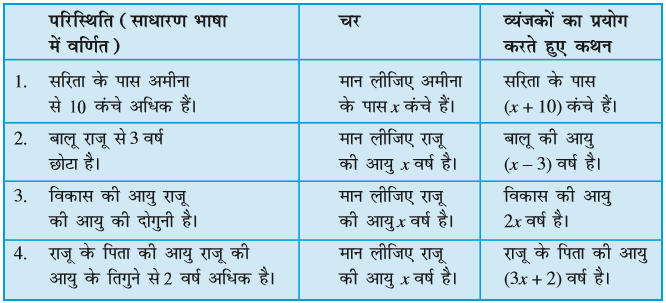
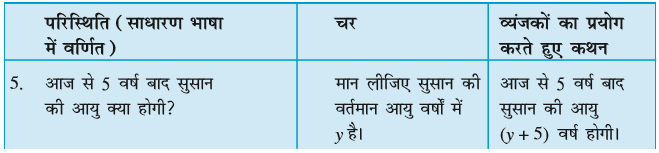
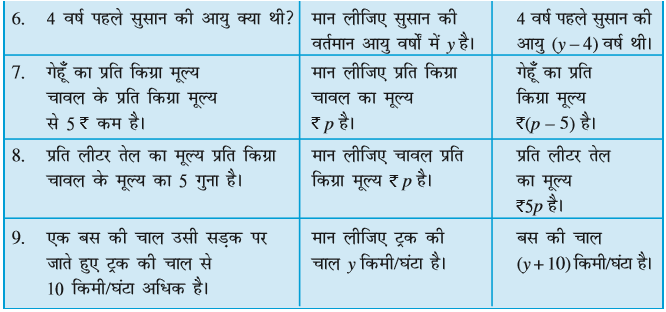
(b) आकृति 11.7 तीलियों से बना त्रिभुजों का एक प्रतिरूप दर्शा रही है। उपरोक्त प्रश्न 11 (a) की तरह, वह व्यापक नियम ज्ञात कीजिए जो त्रिभुजों की संख्या के पदों में आवश्यक तीलियों की संख्या देता है।
11.6 सामान्य नियमों में चरों का प्रयोग
आइए, अब देखें कि गणित के कुछ एेसे सामान्य नियम, जिन्हें हम पहले ही पढ़ चुके हैं, किस प्रकार चरों का प्रयोग करते हुए व्यक्त किए जाते हैं।
ज्यामिति से नियम
हम क्षेत्रमिति (Mensuration) के अध्याय में, वर्ग के परिमाप और आयत के परिमाप के बारे में पहले ही पढ़ चुके हैं। अब हम आपको, उन्हें एक नियम के रूप में लिखने के लिए, वापस लिए चलते हैं।
1. वर्ग का परिमाप : हम जानते हैं कि एक बहुभुज (3 या अधिक रेखाखंडों से बनी बंद आकृति) का परिमाप (perimeter) उसकी भुजाओं की लंबाइयों का योग होता है। वर्ग में चार भुजाएँ होती हैं और प्रत्येक की लंबाई बराबर होती है (आकृति 11.8)।

आकृति 11.8
अत:, वर्ग का परिमाप = वर्ग की भुजाओं की लंबाइयों का योग
= l + l + l + l = 4 × l = 4l
इस प्रकार, हम वर्ग के परिमाप का एक नियम प्राप्त कर लेते हैं। चर l का प्रयोग, हमें एक एेसा व्यापक नियम लिखने में समर्थ बनाता है, जो संक्षिप्त है और जिसे सरलता से याद रखा जा सकता है।
2. आयत का परिमाप : हम जानते हैं कि एक आयत की चार भुजाएँ होती हैं। उदाहरणार्थ, आयत ABCD की चार भुजाएँ AB, BC, CD और DA हैं (आकृति 11.9)। एक आयत की सम्मुख भुजाएँ सदैव बराबर होती हैं। इसलिए, आइए आयत ABCD की भुजाओं AB और CD की लंबाई को l से व्यक्त करें और भुजाओं AD और BC की लंबाई को b से व्यक्त करें।

आकृति 11.9
अत:, आयत का परिमाप = AB की लंबाई + BC की लंबाई + CD की लंबाई + AD की लंबाई
= l + b + l + b
= (l + l) + (b + b)
= 2l + 2b
अत:, नियम यह है :
आयत का परिमाप = 2l + 2b
जहाँ l और b क्रमशः आयत की लंबाई और चौड़ाई हैं।
इसकी चर्चा कीजिए कि l = b होने पर क्या होता है।
यदि हम आयत के परिमाप को चर p से व्यक्त करें, तो आयत के परिमाप का नियम निम्न हो जाता है :
p = 2l + 2b
टिप्पणी : यहाँ l और b दोनों चर हैं। ये एक दूसरे से स्वतंत्र मान ग्रहण करते हैं। अर्थात् एक चर द्वारा ग्रहण किए गए (लिए गए) मान पर दूसरे चर द्वारा ग्रहण किया हुआ मान निर्भर नहीं करता।
ज्यामिति के अपने अध्ययन में, आपके सम्मुख अनेक नियम और सूत्र आएँगे जो समतलीय आकृतियों के परिमापों और क्षेत्रफलों तथा त्रिविमीय आकृतियों के प्रष्ठीय क्षेत्रफलों और आयतनों से संबंधित होंगे। साथ ही, आप एक बहुभुज के अंत:कोणों के योग, एक बहुभुज के विकर्णों की संख्या इत्यादि के सूत्रों को प्राप्त कर सकते हैं। चरों की अवधारणा, जो आपने पढ़ी है, आपको एेसे सभी व्यापक नियमों और सूत्रों के लिखने में अति उपयोगी सिद्ध होगी।
अंकगणित के नियम
3. दो संख्याओं के योग की क्रमविनिमेयता
हम जानते हैं कि
4 + 3 = 7 और 3 + 4 = 7 है।
अर्थात् 4 + 3 = 3 + 4 है।
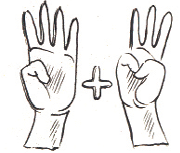
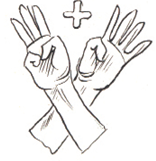
जैसा कि हम पूर्ण संख्याओं के अध्याय में देख चुके हैं, किसी भी दो पूर्ण संख्याओं के लिए यह सत्य है। संख्याओं का यह गुण संख्याओं के योग की क्रमविनिमेयता (commutativity) कहलाता है। ‘क्रमविनिमेय’ का अर्थ है ‘क्रम बदलना’। योग में संख्याओं के क्रम को बदलने से उनके योग में कोई परिवर्तन नहीं आता। चरों का प्रयोग, हमें इस गुण की व्यापकता को एक संक्षिप्त रूप में व्यक्त करने में समर्थ बनाता है। मान लीजिए a और b दो चर हैं जो कोई भी संख्या का मान ले सकते हैं।
तब, a + b = b + a होता है।
एक बार जब हम नियम को इस रूप में लिख लेते हैं, तो इसमें सभी विषिस्ट स्थितियाँ सम्मिलित हो जाती हैं। यदि a = 4 और b = 3 है, तो हमें 4 + 3 = 3 + 4 प्राप्त होता है। यदि a = 37 और b = 73 है, तो हमें 37 + 73 = 73 + 37 प्राप्त होता है, इत्यादि।
4. दो संख्याओं के गुणन की क्रमविनिमेयता
हम पूर्ण संख्याओं के अध्याय में पढ़ चुके हैं कि दो संख्याओं के गुणन के लिए, जिन दो संख्याओं का गुणा किया जाता है तो उनके क्रम से गुणनफल पर कोई प्रभाव नहीं पड़ता है। उदाहणार्थ,
4 × 3 = 12 है और 3 × 4 = 12
अत:, 4 × 3 = 3 × 4 है।
संख्याओं का यह गुण संख्याओं के गुणन की क्रमविनिमेयता कहलाता है। गुणन में संख्याओं के क्रम को बदलने पर गुणनफल में कोई परिवर्तन नहीं आता है। योग की तरह ही, चर a और b का प्रयोग करके, हम दो संख्याओं के गुणन की क्रमविनिमेयता को
a × b = b × a
के रूप में व्यक्त कर सकते हैं। ध्यान दीजिए कि यहाँ a और b कोई भी संख्या मान ले सकते हैं। इस व्यापक नियम से, सभी विषिस्ट स्थितियाँ जैसे 4 × 3 = 3 × 4 या 37 × 73 = 73 × 37; इत्यादि प्राप्त हो जाती हैं।
5. संख्याओं की वितरणता
मान लीजिए हमें 7 × 38 परिकल्पित करने को कहा जाता है। स्पष्टत:, हमें 38 की गुणन सारणी ज्ञात नहीं है। इसलिए, हम निम्न प्रकार से परिकलन करते हैं :
7 × 38 = 7 × (30 + 8)
= 7 × 30 + 7 × 8
= 210 + 56
= 266
7, 30 और 8 जैसी सभी तीन संख्याओं के लिए सत्य है। यह गुण संख्याओं के योग पर गुणन की वितरणता (distributivity of multiplication over addition of numbers) कहलाती है।
चरों का प्रयोग करके, हम संख्याओं के इस गुण को भी एक व्यापक और संक्षिप्त रूप में लिख सकते हैं। मान लीजिए a, b और c कोई तीन चर हैं और इनमें से प्रत्येक कोई भी संख्या का मान ग्रहण कर सकता है। तब,
a × (b + c) = a × b + a × c होता है।
संख्याओं के गुण अति आकर्ज़क होते हैं। आप इनमें कुछ का अध्ययन संख्याओं में इसी वर्ज़ में करेंगे और कुछ का बाद में अपने गणित के अध्ययन के साथ करेंगे। चरों का प्रयोग, हमें इन गुणों को एक अति व्यापक और संक्षिप्त रूप में व्यक्त करने में समर्थ बनाता है। संख्याओं का एक अन्य गुण प्रश्नावली 11.2 के प्रश्न 5 में दिया है। संख्याओं के एेसे ही कुछ और गुणों को ज्ञात कीजिए और उन्हें चरों का प्रयोग करते हुए व्यापक रूप में व्यक्त कीजिए।
प्रश्नावली 11.2
1. एक समबाहु त्रिभुज की भुजा को l से दर्शाया जाता है। इस समबाहु त्रिभुज के परिमाप को l का प्रयोग करते हुए व्यक्त कीजिए।
2. एक सम षड्भुज (Regular hexagon) की एक भुजा को l से व्यक्त किया गया है (आकृति 11.10)। l का प्रयोग करते हुए, इस षड्भुज के परिमाप को व्यक्त कीजिए। (संकेत : एक समज़ड्भुज की सभी 6 भुजाएँ बराबर होती हैं और सभी कोण बराबर होते हैं)।
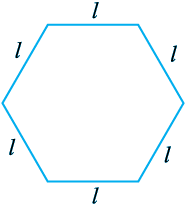
आकृति 11.10
3. घन (Cube) एक त्रिविमीय (three dimensional) आकृति होती है, जैसा कि आकृति 11.11 में दिखाया गया है। इसके 6 फलक होते हैं और ये सभी सर्वसम (identical) वर्ग होते हैं। घन के एक किनारे की लंबाई l से दी जाती है। घन के किनारों की कुल लंबाई के लिए एक सूत्र ज्ञात कीजिए।
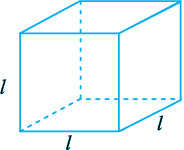
आकृति 11.11
4. वृत्त का एक व्यास वह रेखाखंड है जो वृत्त पर स्थित दो बिंदुओं को जोड़ता है और उसके केंद्र से होकर जाता है। संलग्न आकृति 11.12 में, AB वृत्त का व्यास है और C उसका केंद्र है। वृत्त के व्यास (d) को उसकी त्रिज्या (r) के पदों में व्यक्त कीजिए।

आकृति 11.12
5. तीन संख्याओं 14, 27 और 13 के योग पर विचार कीजिए। हम यह योग दो प्रकार से ज्ञात कर सकते हैं :
(a) हम पहले 14 और 27 को जोड़कर 41 प्राप्त कर सकते हैं और फिर 41 में 13 जोड़कर कुल योग 54 प्राप्त कर सकते हैं। या
(b) हम पहले 27 और 13 को जोड़कर 40 प्राप्त कर सकते हैं और फिर इसे 14 में जोड़कर कुल योग 54 प्राप्त कर सकते हैं। इस प्रकार, (14 + 27) + 13 = 14 + (27 + 13) हुआ।
एेसा किन्हीं भी तीन संख्याओं के लिए किया जा सकता है। यह गुण संख्याओं के योग का साहचर्य (associative) गुण कहलाता है। इस गुण को जिसे हम पूर्ण संख्याओं के अध्याय में पढ़ चुके हैं, चर a, b और c का प्रयोग करते हुए, एक व्यापक रूप में व्यक्त कीजिए।
11.7 चरों वाले व्यंजक
याद कीजिए कि अंकगणित में, हमें 2 × 10 + 3, 3 × 100 + 2 × 10 + 4 इत्यादि जैसे व्यंजक (expressions) प्राप्त हुए थे। ये व्यंजक 2, 3, 4, 10, 100 इत्यादि जैसी संख्याओं से बनते हैं। एेसे व्यंजकों को बनाने के लिए, चारों संक्रियाओं का योग, व्यवकलन, गुणन और विभाजन का प्रयोग किया जा सकता है। उदाहरणार्थ, 2 × 10 + 3 प्राप्त करने के लिए, हमने 2 और 10 का गुणा करके उसके गुणनफल में 3 जोड़ा है। अन्य अंकगणितीय व्यंजकों के उदाहरण निम्न हैं :
3 + (4 × 5), (– 3 × 4) + 5,
8 – (7 × 2), 14 – (5 – 2),
(6 × 2) – 5, (5 × 7) – (3 × 4),
7 + (8 × 2) (5 × 7) – (3 × 4 – 7), इत्यादि।
व्यंजकों को चरों का प्रयोग करके भी प्राप्त किया जा सकता है। वस्तुत:, हम चरों वाले व्यंजकों को पहले ही देख चुके हैं। उदाहरणार्थ, 2n, 5m, x + 10, x – 3 इत्यादि। चरों वाले ये व्यंजक चरों पर योग, व्यवकलन, गुणन और विभाजन की संक्रियाएँ करने के बाद प्राप्त होते हैं। उदाहरणार्थ, व्यंजक 2n चर n को 2 से गुणा करने पर बनता है, व्यंजक (x + 10) चर x में 10 जोड़ने पर बनता है इत्यादि।
हम जानते हैं कि चर विभिन्न मान ले सकते हैं, इनका कोई निश्चित मान नहीं होता है। परंतु ये संख्याएँ हैं। इसी कारण, संख्याओं की ही तरह इन पर योग, व्यवकलन, गुणन और विभाजन की संक्रियाएँ भी की जा सकती हैं।
चरों वाले व्यंजकों के संबंध में एक महत्त्वपूर्ण बात ध्यान देने योग्य है। एक संख्यात्मक व्यंजक जैसे 4 × 3 + 5 का सरलता से मान निकाला जा सकता है। उदाहरणार्थ,
4 × 3 + 5 = 12 + 5 = 17
परंतु (4x + 5) जैसे व्यंजक, जिसमें एक चर x आ रहा है, का मान निकालना संभव नहीं है। यदि चर x का मान दिया हो, केवल तभी व्यंजक का मान निकाला जा सकता है। उदाहरणार्थ, जब x = 3 है, तो
4x + 5 = 4 × 3 + 5 = 17 है, जो ऊपर पहले भी प्राप्त हुआ था।
नीचे आने वाली कुछ पंक्तियों में, हम देखेंगे कि कैसे कुछ व्यंजक बनाए जाते हैं।
इसी प्रकार के दस अन्य सरल व्यंजक लिखिए और बताइए कि वे किस प्रकार बनाए गए हैं।
हमें किसी व्यंजक को उस स्थिति में बनाने में भी समर्थ हो जाना चाहिए, जब यह निर्दे”ा दिए हों कि उसे किस प्रकार बनाना है। निम्नलिखित उदाहरण को देखिए :
निम्न के लिए व्यंजक दीजिए :
सरिता और अमीना ने व्यंजकों का एक खेल खेलने का निर्णय लिया। उन्होंने एक चर x और एक संख्या 3 ली और देखा कि वे कितने व्यंजक बना सकते हैं। इसमें प्रतिबंध यह है कि वे चारों संख्या संक्रियाओं में से केवल एक संक्रिया ही प्रयोग कर सकते हैं और प्रत्येक व्यंजक में x अव”य होना चाहिए। क्या आप इनकी सहायता कर सकते हैं?

क्या (3x + 5) बनाया जा सकता है?
क्या (3x + 3) बनाया जा सकता है?
सरिता (x + 3) सोचती है।
फिर, अमीना (x – 3) बनाती है।
उससे अगला वह 3x कहती है। तब सरिता तुरंत 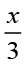 कहती है। दिए हुए प्रतिबंध के अंतर्गत क्या केवल ये चार व्यंजक ही बनाए जा सकते हैं?
कहती है। दिए हुए प्रतिबंध के अंतर्गत क्या केवल ये चार व्यंजक ही बनाए जा सकते हैं?
अब इसके आगे, वे y, 3 और 5 के संयोजनों की सहायता से व्यंजक बनाने का प्रयत्न करती हैं। प्रतिबंध यह है कि वे योग और व्यवकलन में से एक तथा गुणन और विभाजन में से एक संक्रिया चुन सकते हैं। प्रत्येक व्यंजक में y अव”य होना चाहिए। जाँच कीजिए कि क्या उनकेउत्तर जो नीचे दिए गए हैं सही हैं :
y + 5, y + 3, y – 5, y – 3,
3y, 5y, 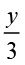 ,
, 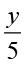 , 3y + 5, 3y – 5, 5y + 3, 5y – 3
, 3y + 5, 3y – 5, 5y + 3, 5y – 3
क्या आप कुछ अन्य व्यंजक बना सकते हैं?
प्रश्नावली 11.3
1. आप तीन संख्या 5, 7 और 8 से संख्याओं वाले (चर नहीं) जितने व्यंजक बना सकते हैं बनाइए। एक संख्या एक से अधिक बार प्रयोग नहीं की जानी चाहिए। केवल योग, व्यवकलन (घटाना) और गुणन का ही प्रयोग करें।
(संकेत : तीन संभावित व्यंजक 5 + (8 – 7), 5 – (8 – 7) और 5 × 8 + 7 हैं। अन्य व्यंजक बनाइए)।
2. निम्नलिखित में से कौन-से व्यंजक केवल संख्याओं वाले व्यंजक ही हैं?
(a) y + 3
(b) 7 × 20 – 8z
(c) 5 (21 – 7) + 7 × 2
(d) 5
(e) 3x
(f) 5 – 5n
(g) 7 × 20 – 5 × 10 – 45 + p
3. निम्न व्यंजकों को बनाने में प्रयुक्त संक्रियाओं (योग, व्यवकलन, गुणन, विभाजन) को पहचानिए (छाँटिए) और बताइए कि ये व्यंजक किस प्रकार बनाए गए हैं :
(a) z +1, z – 1, y + 17, y – 17,
(b) 17y, 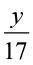 , 5 z,
, 5 z,
(c) 2y + 17, 2 y – 17,
(d) 7 m, – 7 m + 3, – 7 m – 3
4. निम्नलिखित स्थितियों के लिए व्यंजक दीजिए :
(a) p में 7 जोड़ना
(b) p में से 7 घटाना
(c) p को 7 से गुणा करना
(d) p को 7 से भाग देना
(e) – m में से 7 घटाना
(f) – p को 5 से गुणा करना
(g) – p को 5 से भाग देना
(h) p को – 5 से गुणा करना
5. निम्नलिखित स्थितियों के लिए व्यंजक दीजिए:
(a) 2m में 11 जोड़ना
(b) 2m में से 11 घटाना
(c) y के 5 गुने में 3 जोड़ना
(d) y के 5 गुने में से 3 घटाना
(e) y का – 8 से गुणा
(f) y को – 8 से गुणा करके परिणाम में 5 जोड़ना
(g) y को 5 से गुणा करके परिणाम को 16 में से घटाना
(h) y को – 5 से गुणा करके परिणाम को 16 में जोड़ना
6. (a) t और 4 का प्रयोग करके व्यंजक बनाइए। एक से अधिक संख्या संक्रिया का प्रयोग न करें। प्रत्येक व्यंजक में t अव”य होना चाहिए।
(b) y, 2 और 7 का प्रयोग करके व्यंजक बनाइए। प्रत्येक व्यंजक में y अव”य होना चाहिए। केवल दो संख्या संक्रियाओं का प्रयोग करें। ये भिन्न-भिन्न होनी चाहिए।
11.8 व्यावहारिक रूप से व्यंजकों का प्रयोग
हमारे सम्मुख कई व्यावहारिक परिस्थितियाँ आ चुकी हैं, जहाँ व्यंजक उपयोगी होतेे हैं। आइए, कुछ को याद करने का प्रयत्न करें :
आइए, एेसी ही अन्य परिस्थितियों को देखें :
एेसी ही कुछ अन्य परिस्थितियों को ज्ञात करने का प्रयत्न कीजिए। आप यह अनुभव करेंगे कि साधारण भाज़ा में एेसे अनेक कथन हैं, जिन्हें आप चरों वाले व्यंजकों का प्रयोग होने वाले कथनों में बदल सकते हैं। अगले अनुच्छेद में, हम देखेंगे कि किस प्रकार हम इन व्यंजकों द्वारा बने कथनों का अपने कार्यों में प्रयोग करते हैं।
प्रश्नावली 11.4
1. निम्नलिखित प्रश्नों के उत्तर दीजिए :
(a) सरिता की वर्तमान आयु y वर्ज़ लीजिए।
(i) आज से 5 वर्ज़ बाद उसकी आयु क्या होगी?
(ii) 3 वर्ज़ पहले उसकी आयु क्या थी?
(iii) सरिता के दादाजी की आयु उसकी आयु की 6 गुनी है। उसके दादाजी की क्या आयु है?
(iv) उसकी दादीजी दादाजी से 2 वर्ज़ छोटी हैं। दादीजी की आयु क्या है?
(v) सरिता के पिता की आयु सरिता की आयु के तीन गुने से 5 वर्ज़ अधिक है। उसके पिता की आयु क्या है?
(b) एक आयताकार हॉल की लंबाई उसकी चौड़ाई के तिगुने से 4 मीटर कम है। यदि चौड़़़ाई b मीटर है, तो लंबाई क्या है?

(c) एक आयताकार बक्स की ऊँचाई h सेमी है। इसकी लंबाई, ऊँचाई की 5 गुनी है और चौड़ाई, लंबाई से 10 सेमी कम है। बक्स की लंबाई और चौड़ाई को ऊँचाई के पदों में व्यक्त कीजिए।
(d) मीना, बीना और लीना पहाड़ी की चोटी पर पहुँचने के लिए सीढ़ियाँ चढ़ रही हैं। मीना सीढ़ी s पर है। बीना, मीना से 8 सीढ़ियाँ आगे है और लीना मीना से 7 सीढ़ियाँ पीछे है। बीना और लीना कहाँ पर हैं? चोटी पर पहुँचने के लिए कुल सीढ़ियाँ मीना द्वारा चढ़ी गई सीढ़ियों की संख्या के चार गुने से 10 कम है। सीढ़ियों की कुल संख्या को s के पदों में व्यक्त कीजिए।
(e) एक बस v किमी प्रति घंटा की चाल से चल रही है। यह दासपुर से बीसपुर जा रही है। बस के 5 घंटे चलने के बाद भी बीसपुर 20 किमी दूर रह जाता है। दासपुर से बीसपुर की दूरी क्या है? इसे v का प्रयोग करते हुए व्यक्त कीजिए।
2. व्यंजकों के प्रयोग से बने निम्न कथनों को साधारण भाज़ा के कथनों में बदलिए :
(उदाहरणार्थ, एक क्रिकेट मैच में सलीम ने r रन बनाए और नलिन ने (r + 15) रन बनाए। साधारण भाज़ा में, नलिन ने सलीम से 15 रन अधिक बनाए हैं)।
(a) एक अभ्यास-पुस्तिका का मूल्य ₹ p है। एक पुस्तक का मूल्य ₹ 3p है।
(b) टोनी ने मेज़ पर q कंचे रखे। उसके पास डिब्बे में 8 q कंचे हैं।
(c) हमारी कक्षा में n विद्यार्थी हैं। स्कूल में 20 n विद्यार्थी हैं।
(d) जग्गू की आयु z वर्ज़ है। उसके चाचा की आयु 4 z वर्ज़ है और उसकी चाची की आयु (4z – 3) वर्ज़ है।
(e) बिंदुओं (dots) की एक व्यवस्था में r पंक्तियाँ हैं। प्रत्येक पंक्ति में 5 बिंदु हैं।
3. (a) मुन्नू की आयु x वर्ज़ दी हुई है। क्या आप अनुमान लगा सकते हैं कि (x – 2) क्या दर्शाएगा?
(संकेत : मुन्नू के छोटे भाई के बारे में सोचिए)। क्या आप अनुमान लगा सकते हैं कि (x + 4) क्या दर्शाएगा और (3 x + 7) क्या दर्शाएगा?
(b) सारा की वर्तमान आयु y वर्ज़ दी हुई है। उसकी भविज़्य की आयु और पिछली आयु के बारे में सोचिए। निम्नलिखित व्यंजक क्या सूचित करते हैं?
(c) दिया हुआ है कि एक कक्षा के n विद्यार्थी फुटबाल खेलना पंसद करते हैं। 2n क्या दर्शाएगा? 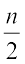 क्या दर्शा सकता है? (संकेत : फुटबाल के अतिरिक्त अन्य खेलों के बारे में सोचिए)।
क्या दर्शा सकता है? (संकेत : फुटबाल के अतिरिक्त अन्य खेलों के बारे में सोचिए)।
11.9 एक समीकरण क्या है?
आइए, आकृति 11.1 में दी हुई तीलियों से बने अक्षर L के प्रतिरूप को याद करें। अपनी सुविधा के लिए, हमने यहाँ आकृति 11.1 को पुन: बनाया है :
विभिन्न संख्याओं के L बनाने के लिए आवश्यक तीलियों की संख्या सारणी-1 में दी गई थी। हम इस सारणी को पुन: यहाँ दे रहे हैं।
सारणी-1
हम जानते हैं कि आवश्यक तीलियों की संख्या निम्न नियम से दी जाती है :
2 n, यदि n बनाए गए L की संख्या है।
अप्पू सदैव अलग तरीके से सोचता है। वह पूछता है, हम जानते हैं कि L की संख्या दी हुई रहने पर आवश्यक तीलियों की संख्या किस प्रकार ज्ञात की जा सकती है। इसकी विपरीत प्रक्रिया के बारे में क्या कहा जा सकता है? माचिस की तीलियों की संख्या दी हुई रहने पर, L की संख्या कैसे ज्ञात की जा सकती है?
हम अपने आपसे एक निश्चित प्रश्न पूछते हैं।
यदि 10 तीलियाँ दी हुई हों, तो कितने L बनेंगे?
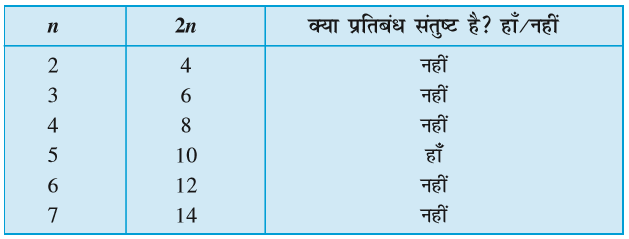
इसका अर्थ है कि हम L की संख्या (अर्थात् n) ज्ञात करना चाहते हैं, यदि तीलियों की संख्या 2n = 10 (1) दी हुई है।
यहाँ हम एक प्रतिबंध प्राप्त करते हैं, जो चर n द्वारा संतुष्ट होना चाहिए। यह प्रतिबंध समीकरण (equation) का एक उदाहरण है।
हमारे प्रश्न का उत्तर सारणी-1 को देखकर प्राप्त किया जा सकता है। n के विभिन्न मानों को देखिए। यदि n = 1 है, तो तीलियों की संख्या 2 है। स्पष्टत:, प्रतिबंध संतुष्ट नहीं हुआ है, क्योंकि संख्या 2 संख्या 10 नहीं है। हम जाँच कर सकते हैं।
हम पाते हैं कि केवल n = 5 के लिए उपरोक्त प्रतिबंध अर्थात् समीकरण 2n = 10 संतुष्ट हो जाती है। 5 के अतिरिक्त n के किसी भी अन्य मान के लिए यह समीकरण संतुष्ट नहीं होती है।
आइए, एक अन्य समीकरण को देखें।
बालू राजू से 3 वर्ज़ छोटा है। राजू की आयु x वर्ज़ लेने पर, बालू की आयु (x – 3) वर्ज़ होगी। मान लीजिए कि बालू की आयु 11 वर्ज़ है। तब, आइए देखें कि हमारी विधि किस प्रकार राजू की आयु ज्ञात करती है।
हमें बालू की आयु, x – 3 = 11 (2)
प्राप्त है।
यह चर x में एक समीकरण है। हम x के विभिन्न मानों के लिए, (x – 3) के मानों की एक सारणी बनाते हैं।
जिन प्रविष्टियों को रिक्त छोड़ा गया है, उन्हें पूरा कीजिए। सारणी से हम ज्ञात करते हैं कि केवल x = 14 के लिए प्रतिबंध x – 3 = 11 संतुष्ट होता है। अन्य मानों जैसे x = 16 या x = 12 के लिए प्रतिबंध संतुष्ट नहीं होता है। अत:, राजू की आयु 14 वर्ज़ है।
उपरोक्त का सार यह है कि एक समीकरण चर पर एक प्रतिबंध होता है। यह चर के केवल एक निश्चित मान के लिए ही संतुष्ट होती है। उदाहरणार्थ, समीकरण 2n = 10 चर n के केवल मान 5 से ही संतुष्ट होती है। इसी प्रकार, समीकरण x – 3 = 11 चर x के केवल मान 14 से ही संतुष्ट होती है।

ध्यान दीजिए कि एक समीकरण के दोनों पक्षों के बीच में समता (समिका) चिह्न (=) होता है। समीकरण बताती है कि बाएँ पक्ष (वाम पक्ष) (LHS) का मान दाएँ पक्ष (दक्षिण पक्ष) (RHS) के मान के बराबर है। यदि बायाँ पक्ष दाएँ पक्ष के बराबर न हो, तो हमें समीकरण प्राप्त नहीं होती।
उदाहरणार्थ, कथन 2n संख्या 10 से बड़ा है, अर्थात् 2n > 10 एक समीकरण नहीं है। इसी प्रकार, कथन 2n संख्या 10 से छोटा है, अर्थात् 2n < 10 भी एक समीकरण नहीं है। साथ ही, कथन (x – 3) > 11 और (x – 3) < 11 समीकरण नहीं हैं।
आइए, अब 8 – 3 = 5 पर विचार करें।
यहाँ भी बाएँ पक्ष और दाएँ पक्ष के बीच में समता का चिह्न ( = ) है। दोनों पक्षों में चर संख्या नहीं है। यहाँ दोनों पक्षों में संख्याएँ हैं। हम इन्हें संख्यात्मक समीकरण कह सकते हैं। सामान्यत: शब्द समीकरण का प्रयोग केवल एक या अधिक चरों के होने पर ही किया जाता है।
आइए, एक प्रश्न हल करें।
बताइए, निम्नलिखित में से कौन-कौन से कथन समीकरण हैं। समीकरण की स्थिति में, समबद्ध चर भी बताइए।
(a) x + 20 = 70 (हाँ, x)
(b) 8 × 3 = 24 (नहीं, यह एक संख्यात्मक समीकरण है)
(c) 2p > 30 (नहीं)
(d) n – 4 = 100 (हाँ, n)
(e) 20b = 80 (हाँ, b)
(f) 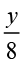 < 50 (नहीं)
< 50 (नहीं)
समीकरणों के कुछ उदाहरण नीचे दिए जा रहे हैं। (कुछ समीकरणों में समबद्ध चर भी दिए गए हैं)।
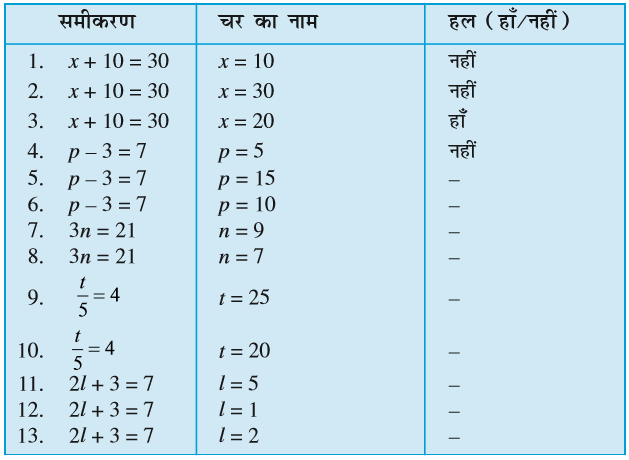
वांछित रिक्त स्थानों को भरिए :
x + 10 = 30 (चर x) (3)
p – 3 = 7 (चर p) (4)
3n = 21 (चर ____ ) (5)
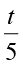 = 4 (चर ____ ) (6)
= 4 (चर ____ ) (6)
2l + 3 = 7 (चर ____ ) (7)
2m – 3 = 5 (चर ____ ) (8)
11.10 एक समीकरण का हल
हम पिछले अनुच्छेद में देख चुके हैं कि समीकरण
2n = 10 (1)
n = 5 से संतुष्ट हो गई थी। n का कोई भी अन्य मान इस समीकरण को संतुष्ट नहीं करता है। समीकरण में चर का वह मान जो समीकरण को संतुष्ट करता है, उस समीकरण का एक हल (solution) कहलाता है। इस प्रकार, n = 5 समीकरण 2 n = 10 का एक हल है।
ध्यान दीजिए कि n = 6 समीकरण 2n = 10 का हल नहीं है, क्योंकि n = 6 के लिए 2n = 2 × 6 = 12 है और यह 10 नहीं है।
साथ ही, n = 4 भी हल नहीं है। बताइए, क्यों नहीं है।
आइए, समीकरण
x – 3 = 11 (2)
को लें। यह समीकरण x = 14 से संतुष्ट हो जाती है, क्योंकि x = 14 के लिए, समीकरण का बायाँ पक्ष = 14 – 3 = 11 = दायाँ पक्ष है। यह समीकरण x = 16 से संतुष्ट नहीं होती है, क्योंकि x = 16 के लिए, समीकरण का बायाँ पक्ष = 16 – 3 = 13 है, जो दाएँ पक्ष के बराबर नहीं है।
इस प्रकार, x = 14 समीकरण x – 3 = 11 का एक हल है, परंतु x = 16 इस समीकरण का हल नहीं है। साथ ही, x = 12 भी इस समीकरण का हल नहीं है।
स्पष्ट कीजिए क्यों नहीं है। अब निम्नलिखित सारणी की प्रविष्टियों को पूरा कीजिए और स्पष्ट कीजिए कि आपके उत्तर हाँ/नहीं क्यों हैं।
समीकरण 2n = 10 का हल ज्ञात करने के लिए, हमने n के विभिन्न मानों की एक सारणी तैयार की थी और फिर इस सारणी से n का वह मान चुन लिया जो समीकरण का हल था (अर्थात् समीकरण को संतुष्ट करता था)। हमने जो किया वह एक प्रयत्न और भूल विधि (a trial and error method) थी। यह हल ज्ञात करने की सीधी (प्रत्यक्ष) या व्यावहारिक विधि नहीं है। अब हम समीकरण को हल करने, अर्थात् उसको ज्ञात करने की एक
सीधी विधि अपनाते हैं। हम केवल अगले वर्ज़ (अर्थात् अगली कक्षा में) ही समीकरण हल करने की एक क्रमबद्ध विधि का अध्ययन करेंगे।
बीजगणित का प्रारंभ
यह कहा जाता है कि गणित की एक शाखा के रूप में बीजगणित का प्रारंभ लगभग 1550 ई. पूर्व में अर्थात् आज से 3500 वर्ज़ पूर्व हुआ, जब मिस्रवासियों ने अज्ञात संख्याओं को व्यक्त करने के लिए संकेतों का प्रयोग करना प्रारंभ किया था।
300 ई. पूर्व के आस-पास भारत में अज्ञातों को अक्षरों से व्यक्त करना और व्यंजक बनाना एक बहुत सामान्य बात थी। अनेक महान भारतीय गणितज्ञों, जैसे आर्यभट्ट (जन्म 476 ई.), ब्रह्मगुप्त (जन्म 598 ई.), महावीर (जो लगभग 850 ई. में रहे) और भास्कर-II (जन्म 1114 ई) तथा कई अन्य ने बीजगणित के अध्ययन में बहुत योगदान दिया। उन्होंने अज्ञात राशियों के लिए बीज, वर्ण इत्यादि जैसे नाम दिए और उन्हें व्यक्त करने के लिए रंगों के नामों के प्रथम अक्षरों के रूप में प्रयोग किया (जैसे काला से ‘का’, नीला से ‘नी’ इत्यादि।) ‘एल्जबरा’ (Algebra) के लिए भारतीय नाम ‘बीजगणित’ इन्हीं प्राचीन भारतीय गणितज्ञों के समय काल का है।
शब्द ‘एल्जबरा’ लगभग 825 ई. में बगदाद के एक अरब गणितज्ञ मुहम्मद इबन अल खोवारिज्मी द्वारा लिखित एक पुस्तक ‘अलजिबार वॉल अलमुगाबालाह’ के शीर्षक से लिया गया है।
प्रश्नावली 11.5
1. बताइए कि निम्नलिखित में से कौन से कथन समीकरण (चर संख्याओं के) हैं? सकारण उत्तर दीजिए। समीकरणों में समबद्ध चर भी लिखिए।
(a) 17 = x + 17
(b) (t – 7) > 5
(c) 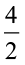 = 2
= 2
(d) 7 × 3 – 13 = 8
(e) 5 × 4 – 8 = 2 x
(f) x – 2 = 0
(g) 2m < 30
(h) 2n + 1 = 11
(i) 7 = 11 × 5 – 12 × 4
(j) 7 = 11 × 2 + p
(k) 20 = 5y
(l) 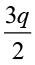 < 5
< 5
(m) z + 12 > 24
(n) 20 – (10 – 5) = 3 × 5
(o) 7 – x = 5
2. सारणी के तीसरे स्तंभ में प्रविष्टियों को पूरा कीजिए :
3. प्रत्येक समीकरण के सम्मुख कोज़्ठकों में दिए मानों में से समीकरण का हल चुनिए। दर्शाइए कि अन्य मान समीकरण को संतुष्ट नहीं करते हैं।
(a) 5m = 60 (10, 5, 12, 15)
(b) n + 12 = 20 (12, 8, 20, 0)
(c) p – 5 = 5 (0, 10, 5, – 5)
(d) 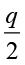 = 7 (7, 2, 10, 14)
= 7 (7, 2, 10, 14)
(e) r – 4 = 0 (4, – 4, 8, 0)
(f) x + 4 = 2 (– 2, 0, 2, 4)
4. (a) नीचे दी हुई सारणी को पूरा कीजिए और इस सारणी को देखकर ही समीकरण m + 10 = 16 का हल ज्ञात कीजिए :
(b) नीचे दी हुई सारणी को पूरा कीजिए और इस सारणी को देखकर ही समीकरण 5t = 35 का हल ज्ञात कीजिए :
(c) सारणी को पूरा कीजिए और समीकरण 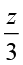 =4 का हल ज्ञात कीजिए :
=4 का हल ज्ञात कीजिए :
(d) सारणी को पूरा कीजिए और समीकरण m – 7 = 3 का हल ज्ञात कीजिए :
5. निम्नलिखित पहेलियों को हल कीजिए। आप एेसी पहेलियाँ स्वयं भी बना सकते हैं।
मैं कौन हूँ?
(i) एक वर्ग के अनुदिशा जाइए।
प्रत्येक कोने को तीन बार
गिनकर और उससे अधिक नहीं,
मुझमें जोड़िए और
ठीक चौंतीस प्राप्त कीजिए।
(ii) सप्ताह के प्रत्येक दिन के लिए,
मेरे से ऊपर गिनिए।
यदि आपने कोई गलती नहीं की है,
तो आप तेईस प्राप्त करेंगे।
(iii) मैं एक विषिस्ट संख्या हूँ।
मुझमें से एक छ: निकालिए।
और क्रिकेट की एक टीम बनाइए।
(iv) बताइए, मैं कौन हूँ।
मैं एक सुंदर संकेत दे रही हूँ
आप मुझे वापिस पाएँगे,
यदि मुझे बाईस में से निकालेंगे।
हमने क्या चर्चा की?
1. हमने तीलियों का प्रयोग करके अक्षरों और अन्य आकार बनाने के प्रतिरूप देखे। हमने किसी आकार को कई बार बनाने के लिए आवश्यक तीलियों की संख्या के लिए व्यापक नियम लिखना सीखा। वह आकार जिसे बनाया जा रहा है, जितनी बार बनाया जाता है वह संख्या बदलती रहती है। इसके मान 1,2,3,... हो सकते हैं। यह एक चर है, जिसे किसी अक्षर जैसे n से व्यक्त किया जाता है।
2. एक चर विभिन्न मान लेता (ग्रहण करता) है। इसका मान स्थिर (निश्चित) नहीं होता। एक वर्ग की लंबाई का कुछ भी मान हो सकता है। यह एक चर है। परंतु किसी त्रिभुज के कोणों की संख्या तीन निश्चित है। यह एक चर नहीं है।
3. हम एक चर को दर्शाने के लिए कोई भी अक्षर n, l, m, p, x, y, z इत्यादि का प्रयोग कर सकते हैं।
4. व्यावहारिक स्थितियों में, हम चरों की सहायता से विभिन्न संबंधों को व्यक्त कर सकते हैं।
5. चर संख्याएँ ही हैं, यद्यपि इनके मान स्थिर या निश्चित नहीं हैं। हम संख्याओं की तरह इन पर योग, व्यवकलन, गुणन और विभाजन की संक्रियाएँ कर सकते हैं। विभिन्न संक्रियाओं का प्रयोग करके, हम चर वाले व्यंजक जैसे x – 3, x + 3, 2n, 5m, 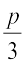 , 2y + 3, 3l – 5 इत्यादि बना सकते हैं।
, 2y + 3, 3l – 5 इत्यादि बना सकते हैं।
6. चर हमें ज्यामिति और अंकगणित दोनों के सामान्य नियमों को व्यापक रूप में व्यक्त करने में समर्थ बनाते हैं। उदाहरणार्थ, यह नियम कि दो संख्याओं को किसी भी क्रम में जोड़ने पर योग वही रहता है, हम a + b = b + a के रूप में लिख सकते हैं। यहाँ चर a और b किसी भी संख्या 1, 32, 1000, – 7, – 20 इत्यादि के मान ले सकते हैं।
7. समीकरण, चर पर एक प्रतिबंध होता है। इसे एक चर वाला व्यंजक बराबर एक स्थिर संख्या के रूप में भी ले सकते हैं, जैसे x – 3 = 10 है।
8. एक समीकरण के दो पक्ष होते हैं–बायाँ पक्ष (LHS) और दायाँ पक्ष (RHS)। इन दोनों के बीच में समता (समिका) का चिह्न (=) होता है।
9. समीकरण का बायाँ पक्ष समीकरण के दाएँ पक्ष के बराबर उस समीकरण में समबद्ध चर के एक निश्चित मान के लिए ही होता है। हम कहते हैं कि चर का वह निश्चित मान समीकरण को संतुष्ट करता है। स्वयं यह मान समीकरण का हल कहलाता है।
10. हल ज्ञात करने की एक विधि प्रयत्न और भूल विधि है। इस विधि में, हम चर को कोई मान देकर यह जाँच करते हैं कि यह मान समीकरण को संतुष्ट करता है या नहीं। चर को हम एेसे विभिन्न मान तब तक देते रहते हैं, जब तक हम चर का वह सही मान न प्राप्त कर लें, जो समीकरण को संतुष्ट करता है।