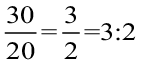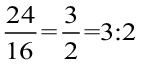Table of Contents
12.1 भूमिका
हमारे दैनिक जीवन में अनेक बार हमें दो-एक जैसी राशियों की तुलना करनी पड़ती है। उदाहरणत: अवनी और शैरी ने अपनी स्क्रैप फ़ाइल के लिए फूल इकट्ठे किए। अवनी ने 30 और शैरी ने 45 फूल इकट्ठे किए।
हम कह सकते हैं कि शैरी ने अवनी से 45 – 30 = 15 फूल अधिक इकट्ठे किए।

यह अंतर द्वारा तुलना की एक विधि है। रहीम का कद 150 सेमी और अवनी का 140 सेमी है। इस प्रकार रहीम का कद अवनी से 150 सेमी –140 सेमी = 10 सेमी अधिक है।
यदि हम एक चींटी और एक टिड्डे की लंबाई की तुलना करना चाहें तो अंतर द्वारा इस तुलना को दिखाना उचित नहीं होगा। टिड्डे की लंबाई 4 सेमी से 5 सेमी होती है जोकि चींटी की लंबाई से बहुत लंबी है क्योंकि चींटी की लंबाई कुछ मिमी ही होती है। तुलना ज्यादा अच्छी होगी यदि हम टिड्डे की लंबाई के बराबर एक के पीछे एक, चींटियों की पंक्ति बना दें। इस प्रकार हम यह कह सकते हैं कि 20 से 30 चींटियों की कुल लंबाई एक टिड्डे की लंबाई के समान है।
अगला उदाहरण लेते हैं, एक कार का मूल्य ₹ 2,50,000 है और एक मोटरसाइकिल का मूल्य ₹ 50,000 है यदि हम उनके मूल्यों का अंतर लें तो यह ₹ 2,00,000 होगा। यदि हम तुलना भाग द्वारा करें तो वह इस प्रकार होगी :
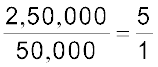
हम कह सकते हैं कि कार का मूल्य मोटरसाइकिल के मूल्य का पाँच गुना है। इस प्रकार कुछ परिस्थितियों में भाग द्वारा तुलना, अंतर द्वारा तुलना से बेहतर सिद्ध होती है। भाग द्वारा तुलना को ही अनुपात कहा जाता है। आगे के खंड में हम अनुपात के विषय में और अधिक सीखेंगे।
12.2 अनुपात
निम्न को देखिए :
ईशा का वज़न 25 किग्रा है और उसके पिता का 75 किग्रा। पिता का वज़न, पुत्री के वज़न का कितना गुना है? यह तीन गुना है।
एक पेन का मूल्य ₹ 10 है और एक पेंसिल का मूल्य ₹ 2 है। पेन का मूल्य पेंसिल के मूल्य का कितने गुना है? स्पष्ट है कि पाँच गुना।
उपरोक्त उदाहरण में हमने दो राशियों की ‘कितने गुना’ के रूप में तुलना की। यह तुलना अनुपात कहलाती है। हम अनुपात को ‘:’ चिह्न द्वारा दर्शाएँगे।
पिछले उदाहरणों को दोबारा लेते हैं। हम कह सकते हैं :
पिता के वजन का पुत्री के वजन के साथ अनुपात = 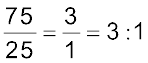
पेन के मूल्य का पेंसिल के मूल्य से अनुपात = 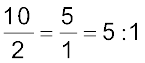

1. एक कक्षा में 20 लड़के और 40 लड़कियाँ हैं लड़कों की संख्या का, लड़कियों की संख्या से क्या अनुपात होगा?
2. रवि एक घंटे में 6 किमी चलता है जबकि रोशन एक घंटे में 4 किमी चलता है। रवि द्वारा तय की गई दूरी सेरोशन द्वारा तय की गई दूरी का अनुपात ज्ञात कीजिए?
इस समस्या की ओर देखिए :
एक कक्षा में 20 लड़के तथा 40 लड़कियाँ हैं। अनुपात ज्ञात कीजिए :
(a) लड़कियों की संख्या का कुल विद्यार्थियों से
(b) लड़कों की संख्या का कुल विद्यार्थियों से
सर्वप्रथम हमें कुल विद्यार्थियों की संख्या की आवश्यकता है जो कि इस प्रकार है :
लड़कियों की संख्या + लड़कों की संख्या = 20 + 40 = 60
तब, लड़कियों की संख्या का कुल विद्यार्थियों की संख्या से अनुपात 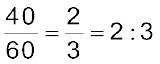
भाग (b) का हल इसी प्रकार निकालिए।
निम्न उदाहरण को लेते हैं :
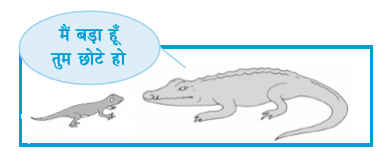
घर में पाई जाने वाली छिपकली की लंबाई 20 सेमी है और मगरमच्छ की लंबाई 4 मीटर।
“मैं तुमसे पाँच गुनी लंबी हूँ” छिपकली ने कहा। जैसा कि हम देख सकते हैं कि यह बिल्कुल गलत है। एक छिपकली की लंबाई मगरमच्छ की लंबाई से पाँच गुना नहीं हो सकती। तो गलती कहाँ है? ध्यान से देखें छिपकली की लंबाई सेमी में है और मगरमच्छ की लंबाई मीटर में दी गई है। अत: हमें उनकी लंबाइयों को एक जैसी इकाइयों में बदलना होगा।
मगरमच्छ की लंबाई = 4 मी = 4 × 100 = 400 सेमी
अत:, मगरमच्छ की लंबाई का छिपकली की लंबाई से अनुपात इस प्रकार होगा
= 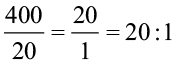 .
.
दो राशियों की तुलना तभी की जा सकती है जब वे दोनों एक ही इकाई में हों।
छिपकली की लंबाई का मगरमच्छ की लंबाई से अनुपात क्या होगा?
यह होगा 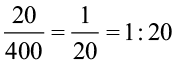
ध्यान दीजिए कि 1 : 20 और 20 : 1 दोनों एक दूसरे से भिन्न हैं। अनुपात 1 : 20 छिपकली की लंबाई का मगरमच्छ की लंबाई से है और 20 : 1 मगरमच्छ की लंबाई का छिपकली की लंबाई के साथ है।
एक और उदाहरण देखते हैं :
पेंसिल की लंबाई 18 सेमी है और इसका व्यास 8 मिमी है। पेंसिल के व्यास का उसकी लंबाई के साथ अनुपात क्या होगा? व्यास तथा लंबाई दोनों की इकाई अलग दी हुई है अत: उन्हें समान इकाई में बदलने की आवश्यकता है।
पेंसिल की लंबाई = 18 सेमी = 18 × 10 मिमी = 180 मिमी
पेंसिल के व्यास का उसकी लंबाई के साथ अनुपात
= 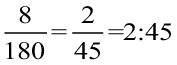

1. सौरभ घर से स्कूल पहुँचने में 15 मिनट लेता है और सचिन एक घंटा लेता है। सौरभ द्वारा लिए गए समय और सचिन द्वारा लिए गए समय का अनुपात ज्ञात करो।
2. एक टॉफी का मूल्य 50 पैसे है और एक चॉकलेट का 10 रुपये। टॉफी के मूल्य का चॉकलेट के मूल्य से अनुपात ज्ञात कीजिए।
3. एक स्कूल में एक वर्ष में 73 छुट्टियाँ बनती हैं। छुट्टियों का वर्ष के कुल दिनों के साथ अनुपात ज्ञात कीजिए।
कुछ और एेसी ही परिस्थितियों के विषय में सोचिए जहाँ आपको दो समान राशियों की तुलना करनी पड़े और दोनों राशियों की इकाइयाँ भिन्न हों।
हम अनुपात की संकल्पना का प्रयोग दैनिक जीवन की बहुत सी परिस्थितियों में बिना जाने ही करते हैं।
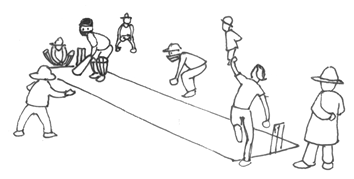
आकृति A तथा B की तुलना करें। आकृति B, आकृति A से ज़्यादा वास्तविक लगती है। क्यों?
आकृति A में टाँगे बाकी शरीर की तुलना में लंबी हैं। ये इसलिए हैं कि हम टाँगों की शरीर के अन्य हिस्सों से तुलना में एक खास अनुपात की आशा रखते हैं।
चित्र में बनी दोनों पेंसिलों की तुलना कीजिए। क्या पहली पेंसिल देखने में पूरी पेंसिल लगती है? नहीं। क्यों नहीं? कारण यह है कि पेंसिल की मोटाई और लंबाई में सही अनुपात नहीं है।
हम अलग-अलग परिस्थितियों में एक जैसा अनुपात देख सकते हैं।
निम्न को देखें :
- एक कमरे की लंबाई 30 मी और इसकी चौड़ाई 20 मी है। अत: कमरे की लंबाई का चौड़ाई से अनुपात =
![]()
- एक पिकनिक में 24 लड़कियाँ और 16 लड़के जा रहे हैं। लड़कियों की संख्या का लड़कों की संख्या से अनुपात =
![]()
दोनों ही उदाहरणों में अनुपात 3 : 2 है।
- न्यूनतम रूप में 30 : 20 और 24 : 16 अनुपात समान हैं, और वे 3 : 2 के बराबर हैं। ये तुल्य अनुपात कहलाते हैं।
क्या आप कुछ और उदाहरण सोच सकते हैं जो न्यूनतम रूप में 3 : 2 के तुल्य हों?
इस प्रकार की परिस्थितियाँ लिखना? जिनसे एक खास अनुपात मिले, रोचक हाेंगी। उदाहरण के लिए एक एेसी परिस्थिति लिखिए जिसमें अनुपात 2 : 3 है।
- मेज़ की चौड़ाई का लंबाई से अनुपात 2 : 3 है।
- शीना के पास 2 कंचे हैं और उसकी मित्र शबनम के पास 3 कंचे हैं, शीना और शबनम के कंचों का अनुपात 2 : 3 है।
क्या आप कुछ और एेसे उदाहरण लिख सकते हैं जिसमें यही अनुपात आए? अपने मित्रों को कुछ अनुपात देकर उनसे उनपर आधारित कुछ उदाहरण बनवाएँ।
रवि और रानी ने एक व्यापार शुरू किया और 2 : 3 में धन निवेश किया, एक वर्ष बाद कुल लाभ ₹ 4,00,000 था।
रवि ने कहा कि हम यह लाभ बराबर बाँट लेते हैं। रानी ने उत्तर दिया, "मुझे ज़्यादा मिलना चाहिए क्योंकि मैंने ज़्यादा निवेश किया है।"
तब यह निर्णय लिया गया कि निवेश के अनुपात में ही लाभ बाँटा जाएगा।
यहाँ 2 : 3 के अनुपात में 2 और 3 दो ही राशियाँ हैं।
इन राशियों का योग = 2 + 3 = 5
इसका क्या अर्थ है?
इसका अर्थ है कि यदि ₹ 5 लाभ है तो रवि को ₹ 2 और रानी को ₹ 3 मिलेंगे।
और हम कह सकते हैं कि 5 हिस्सों में से 2 हिस्से रवि का और 3 हिस्से रानी को मिलेंगे।
इससे अभिप्राय होगा कि रवि को कुल लाभ का 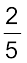 मिलेगा और रानी को
मिलेगा और रानी को 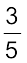 ।
।
यदि कुल लाभ ₹ 500 है
तो रवि को मिलेगा 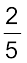 × 500 = ₹ 200
× 500 = ₹ 200
और रानी को 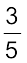 × 500 = ₹ 300
× 500 = ₹ 300
अब, यदि कुल लाभ ₹ 40,000 हो तो प्रत्येक को कितना हिस्सा मिलेगा?
रवि का हिस्सा = 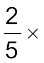 ₹ 400000 = ₹ 1,60,000
₹ 400000 = ₹ 1,60,000
और रानी का हिस्सा = 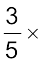 ₹ 400000 = ₹ 2,40,000
₹ 400000 = ₹ 2,40,000
क्या आप कुछ और उदाहरणों के विषय में सोच सकते हैं जहाँ आपको कुछ चीज़ों को एक अनुपात में बाँटना है? तीन एेसी और समस्याओं को बनाइए और अपने मित्रों से हल करवाइए।


1. अपने बैग में रखी कापियों की संख्या का पुस्तकों की संख्या से अनुपात ज्ञात कीजिए।
2. अपनी कक्षा की कुल डैस्कों की संख्या का कुल कुर्सियों की संख्या से अनुपात ज्ञात कीजिए।
3. अपनी कक्षा में उन छात्रों की संख्या ज्ञात कीजिए जिनकी आयु 12 वर्ष से ऊपर है। अब 12 वर्ष से ऊपर आयु वाले छात्रों की संख्या का कक्षा के बाकी छात्रों की संख्या के साथ अनुपात ज्ञात कीजिए।
4. अपनी कक्षा के दरवाज़ों की संख्या का खिड़कियों की संख्या से अनुपात निकालिए।
5. एक आयत बनाइए। उसकी लंबाई का चौड़ाई से अनुपात निकालिए।
अब तक जिस तरह की समस्याओं को हल करना हमने सीखा उन्हें देखें :
उदाहरण 1 : एक आयताकार मैदान की लंबाई और चौड़ाई क्रमश: 50 मी और 15 मी है। मैदान की लंबाई का चौड़ाई से अनुपात ज्ञात कीजिए।
हल : आयताकार मैदान की लंबाई = 50 मी
आयताकार मैदान की चौड़ाई = 15 मी
लंबाई का चौड़ाई से अनुपात = 50 : 15
अनुपात इस प्रकार लिखा जा सकता है 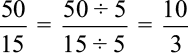 = 10 : 3
= 10 : 3
अत: अनुपात होगा 10 : 3
उदाहरण 2 : 90 सेमी और 1.5 मी का अनुपात ज्ञात कीजिए।
हल : दोनों राशियाँ एक ही इकाई में नहीं हैं। अत: उन्हें समान इकाई में बदलने पर
1.5 मी = 1.5 × 100 सेमी = 150 सेमी
अत: वांछित अनुपात है
90 : 150 = 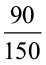 =
= 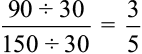
अत: वांछित अनुपात है 3 : 5
उदाहरण 3 : एक दफ्तर में 45 लोग काम करते हैं, जहाँ महिलाओं की संख्या 25 है और शेष पुरुष हैं। निम्न में अनुपात ज्ञात कीजिए :
(a) महिलाओं की संख्या का पुरुषों की संख्या से
(b) पुरुषों की संख्या का महिलाओं की संख्या से
हल : महिलाओं की संख्या = 25
कर्मियों की कुल संख्या = 45
पुरुषों की संख्या = 45 – 25 = 20
अत: महिलाओं की संख्या का पुरुषों की संख्या के साथ अनुपात
= 25 : 20 = 5 : 4
और पुरुषों की संख्या का महिलाओं की संख्या के साथ अनुपात
= 20 : 25 = 4 : 5
(ध्यान दें कि 5 : 4 और 4 : 5 में अंतर है)
उदाहरण 4 : 6 : 4 के दो तुल्य अनुपात लिखिए।
हल : अनुपात 6 : 4 = 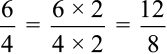
अत:, 12 : 8 और 6 : 4 तुल्य अनुपात हैं।
इसी प्रकार, 6 : 4 = 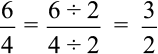
3:2 एक अन्य तुल्य अनुपात है।
इसी प्रकार, हम किसी भी अनुपात का तुल्य अनुपात अंश और हर में एक समान संख्या से गुणा या भाग द्वारा प्राप्त कर सकते हैं।
6 : 4 के दोे और तुल्य अनुपात ज्ञात कीजिए।
उदाहरण 5 : रिक्त स्थानों को भरिए :
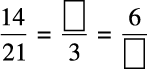
हल : पहला रिक्त स्थान भरने के लिए हम 21 = 3 × 7 तथ्य का प्रयोग करेंगे। अर्थात् 21 को 7 से भाग देने पर 3 प्राप्त होता है। यह दर्शाता है कि दूसरे अनुपात का रिक्त स्थान प्राप्त करने के लिए 14 को 7 से भाग करना पड़ेगा। भाग करने पर, 14 ÷ 7 = 2
अत: दूसरा अनुपात 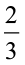 है।
है।
इसी तरह, तीसरे अनुपात के लिए, दूसरे अनुपात की दोनों राशियों को 3 से गुणा करना पड़ेगा।(क्यों?)
अत:, तीसरा अनुपात 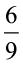 है।
है।
इस प्रकार, 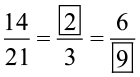 [ये सभी तुल्य अनुपात हैं।]
[ये सभी तुल्य अनुपात हैं।]
उदाहरण 6 : मैरी के घर से स्कूल की दूरी का जॉन के घर से स्कूल की दूरी का अनुपात 2 : 1 है।
(a) स्कूल के अधिक निकट कौन रहता है?
(b) निम्न सारणी को पूरा कीजिए जो कुछ संभव दूरियाँ दर्शाती हैं जहाँ मैरी और जॉन रह सकते हों।
(c) यदि मैरी के घर से स्कूल की दूरी का कलाम के घर से स्कूल की दूरी का अनुपात 1 : 2 हो तो स्कूल के ज़्यादा निकट कौन रहता है।
हल : (a) जॉन स्कूल के ज़्यादा निकट रहता है (क्योंकि अनुपात 2 : 1 है)
(b)
(c) क्योंकि अनुपात 1 : 2 है अत: मैरी स्कूल के ज़्यादा निकट रहती है।
उदाहरण 7 : कृति और किरन के बीच ₹ 60 को 1 : 2 में बाँटिए।
हल : अनुपात के दो हिस्से 1 और 2 हैं।
अत:, दोनों हिस्सों का योग = 1 + 2 = 3
इसका अर्थ है कि यदि ₹ 3 हैं तो कृति को ₹ 1 और किरन को ₹ 2 मिलेंगे। यानी कि 3 में से कृति को एक हिस्सा और किरन को 2 हिस्से मिलेंगे।
अत:, कृति का हिस्सा = 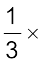 ₹ 60 = ₹ 20
₹ 60 = ₹ 20
और किरन का हिस्सा = 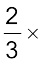 ₹ 60 रु = ₹ 40
₹ 60 रु = ₹ 40
प्रश्नावली 12.1
1. एक कक्षा में 20 लड़कियाँ और 15 लड़के हैं। अनुपात ज्ञात कीजिए :
(a) लड़कियों की संख्या का लड़कों की संख्या से
(b) लड़कियों की संख्या का कुल विद्यार्थियों की संख्या से
2. 30 विद्यार्थियों की कक्षा में 6 फुटबाल, 12 क्रिकेट और बाकी टेनिस पसंद करते हैं। अनुपात ज्ञात कीजिए।
(a) फुटबाल पसंद करने वालों की संख्या का टेनिस पसंद करने वालों की संख्या से
(b) क्रिकेट प्रेमियों का कुल विद्यार्थियों की संख्या से
3. आकृति को देखकर अनुपात निकालिए :

(a) आयत के अंदर के सभी त्रिभुजों की संख्या का वृत्तों की संख्या से।
(b) आयत के अंदर के सभी वर्गों की संख्या का सभी आकृतियों से
(c) आयत के अंदर के सभी वृत्तों का सभी आकृतियों से।
4. हामिद और अख्तर ने एक घंटे में क्रमश: 9 किमी और 12 किमी की दूरी तय की। हामिद और अख्तर की चालों का अनुपात ज्ञात कीजिए।
5. रिक्त स्थानों को भरिए
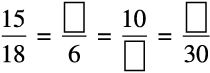 [क्या ये तुल्य अनुपात हैं?]
[क्या ये तुल्य अनुपात हैं?]
6. निम्न में से प्रत्येक का अनुपात ज्ञात कीजिए :
(a) 81 का 108 से
(b) 98 का 63 से
(c) 33 किमी का 121 किमी से
(d) 30 मिनट का 45 मिनट से
7. निम्न में से प्रत्येक का अनुपात ज्ञात कीजिए :
(a) 30 मिनट का 1.5 घंटे
(b) 40 सेमी का 1.5 मी
(c) 55 पैसे का ₹ 1
(d) 500 मिलि का 2 लीटर
8. एक वर्ष में सीमा ₹ 1,50,000 कमाती है और ₹ 50,000 की बचत करती है। प्रत्येक का अनुपात ज्ञात कीजिए।
(a) सीमा द्वारा किया गया व्यय और उसकी बचत का
(b) सीमा द्वारा की गई बचत और उसके द्वारा किए गए व्यय का
9. एक विद्यालय में 3300 विद्यार्थी और 102 शिक्षक हैं। शिक्षकों की संख्या का विद्यार्थियों की संख्या से अनुपात ज्ञात कीजिए।
10. एक कॉलेज में 4320 विद्यार्थियों में से 2300 लड़कियाँ हैं। अनुपात निकालिए :
(a) लड़कियों की संख्या और कुल विद्यार्थियों की संख्या का
(b) लड़कों की संख्या और लड़कियों की संख्या का
(c) लड़कों की संख्या और कुल विद्यार्थियों की संख्या का
11. एक विद्यालय के 1800 विद्यार्थियों में से 750 ने बास्केट बॉल, 800 ने क्रिकेट और शेष ने टेबल टेनिस खेलना पसंद किया है। यदि एक छात्र केवल एक खेल चुने तो अनुपात ज्ञात कीजिए :

(a) बास्केट बॉल खेलने वालोें और टेबल टेनिस खेलने वालों का।
(b) क्रिकेट खेलने वालों और बास्केट बॉल खेलने वालों का।
(c) बास्केट बॉल खेलने वालों और कुल विद्यार्थियों का।
12. एक दर्जन पेन का मूल्य ₹ 180 है और 8 बॉल पेन का मूल्य ₹ 56 है। पेन के मूल्य का बॉल पेन के मूल्य से अनुपात ज्ञात कीजिए।
13. कथन को देखें : एक हॉल की चौड़ाई और लंबाई का अनुपात 2 : 5 है। निम्न सारणी को पूरा कीजिए जो कि हॉल की कुछ संभव चौड़ाई व लंबाई दिखाती है :
14. शीला और संगीता के बीच 20 पेनों को 3 : 2 में बाँटिए।
15. एक माता अपनी बेटी श्रेया और भूमिका में ₹ 36 को उनकी आयु के अनुपात में बाँटना चाहती है। यदि श्रेया की आयु 15 वर्ष और भूमिका की आयु 12 वर्ष हो तो श्रेया और भूमिका को कितना-कितना मिलेगा?

16. पिता की वर्तमान आयु 42 वर्ष और उसके पुत्र की 14 वर्ष है। अनुपात ज्ञात कीजिए :
(a) पिता की वर्तमान आयु का और पुत्र की वर्तमान आयु से
(b) पिता की आयु का पुत्र की आयु से, जब पुत्र 12 वर्ष का था
(c) 10 वर्ष बाद की पिता की आयु का 10 वर्ष बाद की पुत्र की आयु से
(d) पिता की आयु का पुत्र की आयु से जब पिता 30 वर्ष का था
12.3 समानुपात
इस स्थिति को देखिए :
राजू बाज़ार से टमाटर खरीदने जाता है। एक दुकानदार ने कहा कि 5 किग्रा टमाटर का मूल्य 40 रु है। दूसरे दुकानदार ने 6 किग्रा टमाटर का मूल्य 42 रु बताया। अब राजू को क्या करना चाहिए? उसे टमाटर पहले दुकानदार से खरीदने चाहिए या दूसरे दुकानदार से? निर्णय लेने में, क्या अंतर लेकर तुलना करना सहायता करेगा? नहीं। क्यों नहीं?

उसकी सहायता के लिए कोई तरीका सोचिए। अपने मित्रों के साथ विचार-विमर्श कीजिए।
एक और उदाहरण लेते हैं :
भाविका के पास 28 कंचे हैं और विनि के पास 180 फूल हैं। वे दोनों इन्हें आपस में बाँटना चाहती हैं। भाविका ने 14 कंचे विनि को दिए और विनि ने 90 फूल भाविका को। लेकिन विनि संतुष्ट नहीं हुई। उसने सोचा कि उसने भाविका को ज्यादा फूल दिए जबकि भाविका ने उसे कम कंचे दिए।
आप क्या सोचते हैं? क्या विनि सही है? दोनों समस्या के समाधान के लिए विनि की माता पूजा के पास गये।
पूजा ने समझाया कि 28 कंचों में से भाविका ने 14 कंचे विनि को दिए
अत:, अनुपात होगा 14 : 28 = 1 : 2
और 180 फूलों में से 90 फूल विनि ने भाविका को दिए
अत:, अनुपात 90 : 180 = 1 : 2
क्योंकि दोनों अनुपात समान हैं अत: वितरण सही है।
 दो सहेलियाँ आशमा और पंखुरी हेयर क्लिप खरीदने बाजार गईं। उन्होंने ₹ 30 में 20 हेयर क्लिप खरीदे। आशमा ने ₹ 12 दिए और पंखुरी ने ₹ 18 दिए। घर आने पर आशमा ने पंखुरी से 10 हेयर क्लिप देने को कहा। लेकिन पंखुरी ने कहा कि जब मैंने ज्यादा रुपये दिए हैं तो मुझे ज्यादा हेयर क्लिप मिलने चाहिए। उनके अनुसार, आशमा को 8 और उसे 12 हेयर क्लिप मिलने चाहिए।
दो सहेलियाँ आशमा और पंखुरी हेयर क्लिप खरीदने बाजार गईं। उन्होंने ₹ 30 में 20 हेयर क्लिप खरीदे। आशमा ने ₹ 12 दिए और पंखुरी ने ₹ 18 दिए। घर आने पर आशमा ने पंखुरी से 10 हेयर क्लिप देने को कहा। लेकिन पंखुरी ने कहा कि जब मैंने ज्यादा रुपये दिए हैं तो मुझे ज्यादा हेयर क्लिप मिलने चाहिए। उनके अनुसार, आशमा को 8 और उसे 12 हेयर क्लिप मिलने चाहिए।
क्या आप बता सकते हो कि आशमा या पंखुरी में से सही कौन है? क्यों?
आशमा द्वारा दिए गए धन और पंखुरी द्वारा दिए गए धन का अनुपात = 12 : 18 = 2 : 3 है। आशमा के सुझाव के अनुसार,
आशमा के हेयर क्लिपों की संख्या और पंखुरी के हेयर क्लिपों की संख्या का अनुपात = 10 : 10 = 1 : 1
पंखुरी के सुझाव के अनुसार,
आशमा के हेयर क्लिपों की संख्या और पंखुरी के हेयर क्लिपों की संख्या का अनुपात = 8 : 12 = 2 : 3 है।
आशमा द्वारा किए गए वितरण के अनुसार हेयर क्लिप की संख्या का अनुपात, दिए गए धन के अनुपात के समान नहीं है, जो कि होना चाहिए था। जबकि पंखुरी द्वारा किए गए वितरण में दोनों परिस्थितियों में अनुपात समान है।
अत:, पंखुरी ने सही वितरण किया।
एक अनुपात को बाँटने का कुछ अर्थ है!
निम्न उदाहरणों को लेते हैं :
- राज ने 15 रु में 3 पेन खरीदे और अनु ने 50 रु में 10 पेन खरीदे। किसके पेन महँगे थे? राज द्वारा खरीदे गए पेन की संख्या और अनु द्वारा खरीदे गए पेन की संख्या का अनुपात = 3 : 10.
3 : 10 और 15 : 50 समान है। इस प्रकार, दोनों ने समान मूल्य में पेन खरीदे।
- रहीम ने ₹180 में 2 किग्रा सेब बेचे और रोशन ने ₹360 में 4 किग्रा। किसने सेब महंगे बेचे?
सेब के भारों का अनुपात = 2 किग्रा : 4 किग्रा= 1 : 2
मूल्यों का अनुपात = ₹180 : ₹360 = 6 : 12 = 1 : 2
इस प्रकार सेब के भारों का अनुपात = मूल्यों का अनुपात
क्योंकि दोनों अनुपात समान हैं। अत: हम कह सकते हैं कि ये समानुपात में हैं। वे दोनों समान मूल्यों पर सेब बेच रहे हैं।
यदि दो अनुपात एक समान हैं तो वे समानुपात में हैं और इन्हें समान करने के लिए ‘::’ या ‘=’ चिह्न का प्रयोग किया जाता है।
पहले उदाहरण के लिए हम कह सकते हैं कि 3, 10, 15 और 50 समानुपात में हैं जिसे हम 3 : 10 :: 15 : 50 रूप में भी लिख सकते हैं और 3 अनुपात 10 बराबर 15 अनुपात 50 पढ़ेंगे।

दूसरे उदाहरण में 2, 4, 180 और 360 समानुपात में है जिसे हम 2 : 4 :: 180 : 360 लिखेंगे और 2 अनुपात 4 बराबर 180 अनुपात 360 पढ़ेंगे।
आइए, अन्य उदाहरण लें :
एक व्यक्ति 2 घंटे में 35 किमी चलता है। क्या इसी चाल से वह 4 घंटे में 70 किमी चल सकता है?
दोनों द्वारा चली गई दूरियों का अनुपात = 35 : 70 = 1 : 2
दोनों द्वारा लिए गए समय का अनुपात 2 : 4 = 1 : 2 .
इस प्रकार दोनों अनुपात समान हैं। अर्थात् 35 : 70 = 2 : 4
अत: हम कह सकते हैं कि चारों संख्याएँ 35, 70, 2 और 4 समानुपात में हैं।
इस प्रकार हम लिख सकते हैं 35 : 70 :: 2 : 4 और इसे पढ़ सकते हैं 35 अनुपात 70 बराबर 2 अनुपात 4। अत: वह 4 घंटे में 70 किमी उसी चाल से चल सकता है।
अब इस उदाहरण को लें :
2 किग्रा सेब का मूल्य ₹180 है और 5 किग्रा तरबूज का मूल्य ₹45 है।
दोनों के वजनों का अनुपात 2 : 5 है।
दोनों के मूल्यों का अनुपात = 180 : 45 = 4 : 1
यहाँ 2 : 5 और 180 : 45 समान नहीं हैं।
अर्थात् 2 : 5 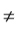
इस प्रकार चारों राशियाँ 2, 5, 180 और 45 समानुपात में नहीं हैं।
यदि दो अनुपात समान नहीं होते हैं तो वे राशियाँ समानुपात में नहीं होती हैं।

जाँच कीजिए कि दिए गए अनुपात समान हैं अर्थात् वे समानुपात में हैं। यदि हाँ, तो उन्हें सही ढंग से लिखिए।
1. 1 : 5 और 3 : 15
2. 2 : 9 और 18 : 81
3. 15 : 45 और 5 : 25
4. 4 : 12 और 9 : 27
5. 10 रु का 15 रु और 4 का 6 से
समानुपात के कथन में, क्रम में ली गई चारों राशियाँ पद कहलाती हैं। पहले और चौथे पद को चरम पद (या सिरों के पद) कहते हैं। दूसरे और तीसरे पद को मध्य पद कहते हैं।
उदाहरण के लिए 35 : 70 : : 2 : 4
35, 70, 2 और 4 चार पद हैं। जिसमें से 35 तथा 4 चरम पद हैं और 70 तथा 2 मध्य पद हैं।
उदाहरण 8 : क्या अनुपात 25 ग्राम : 30 ग्राम और 40 किग्रा : 48 किग्रा समानुपात में हैं?
हल : 25 ग्रा : 30 ग्रा = 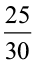 = 5 : 6
= 5 : 6
40 किग्रा : 48 किग्रा = 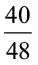 = 5 : 6
= 5 : 6
इसलिए, 25 : 30 = 40 : 48
अत: अनुपात 25 ग्रा : 30 ग्रा और 40 किग्रा : 48 किग्रा समानुपात में हैं अर्थात् 25 : 30 :: 40 : 48
इसमें 25, 48 चरम पद हैं और 30, 40 मध्य पद हैं।
उदाहरण 9 : क्या 30, 40, 45 और 60 समानुपात में हैं?
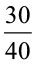 = 3 : 4
= 3 : 4 45 और 60 अनुपात = 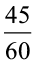 = 3 : 4
= 3 : 4
क्योंकि 30 : 40 = 45 : 60
अत:, 30, 40, 45, 60 समानुपात में हैं।
उदाहरण 10 : क्या 15 सेमी का 2 सेमी से और 10 सेकंड का 3 मिनट से अनुपात, एक समानुपात बनाते हैं?
हल : 15 सेमी का 2 मी से अनुपात
= 15 : 2 × 100 (1 मी = 100 सेमी)
= 3 : 40
10 सेकंड का 3 मिनट से अनुपात
= 10 : 3 × 60 (1 मिनट = 60 सेकंड)
= 1 : 18
क्योंकि 3 : 40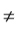
प्रश्नावली 12.2
1. क्या निम्न राशियाँ समानुपात में हैं :
(a) 15, 45, 40, 120
(b) 33, 121, 9,96
(c) 24, 28, 36, 48
(d) 32, 48, 70, 210
(e) 4, 6, 8, 12
(f) 33, 44, 75, 100
2. निम्न में से प्रत्येक कथनों के आगे सत्य या असत्य लिखिए :
(a) 16 : 24 :: 20 : 30
(b) 21: 6 :: 35 : 10
(c) 12 : 18 :: 28 : 12
(d) 8 : 9 :: 24 : 27
(e) 5.2 : 3.9 :: 3 : 4
(f) 0.9 : 0.36 :: 10 : 4
3. क्या निम्न कथन सही हैं?
(a) 40 व्यक्ति : 200 व्यक्ति = 15 रु : 75 रु
(b) 7.5 लि : 15 लि = 5 किग्रा : 10 किग्रा
(c) 99 किग्रा : 45 किग्रा = 44 रु : 20 रु
(d) 32 मी : 64 मी = 6 सेकंड : 12 सेकंड
(e) 45 किमी : 60 किमी = 12 घंटे : 15 घंटे
4. जाँचिए कि क्या निम्न अनुपात, समानुपात बनाते हैं। यदि समानुपात बनता हो, तो मध्य पद और चरम पद भी लिखिए।
(a) 25 सेमी : 1 मी और 40 रु : 160 रु
(b) 39 ली : 65 ली और 6 बोतल : 10 बोतल
(c) 2 किग्रा : 80 किग्रा और 25 ग्रा : 625 ग्रा
(d) 200 मिली : 2.5 ली और 4 रु : 50 रु
12.4 एेकिक विधि
निम्न परिस्थितियों को लें :
- दो सहेलियाँ रेशमा और सीमा बाज़ार से अभ्यास पुस्तिका खरीदने जाती हैं। रेशमा ने ₹ 24 में 2 अभ्यास पुस्तिका खरीदीं। एक अभ्यास पुस्तिका का मूल्य ज्ञात कीजिए।
- 80 किमी की दूरी तय करने में एक स्कूटर में 2 लीटर पेट्रोल लगता है। एक किमी तय करने के लिए कितना पेट्रोल लगेगा?
ये उदाहरण हमारी दैनिक जीवन की समस्याओं पर आधारित हैं। आप इन्हें कैसे हल करेंगे?
पहले उदाहरण को पुन: लें।
2 अभ्यास पुस्तिकाओं का मूल्य = ₹ 24
अत: 1 अभ्यास पुस्तिका का मूल्य = ₹ 24 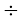 2 = ₹ 12
2 = ₹ 12
यदि आपको 5 एेसी अभ्यास पुस्तिकाओं का मूल्य ज्ञात करने के लिए कहा जाए तो यह इस प्रकार होगा ₹ 12 × 5 = ₹ 60 होगा।
दूसरे उदाहरण को भी पुन: लें :
हम जानना चाहते हैं कि एक किमी जाने में कितना पेट्रोल लगेगा?
80 किमी चलने के लिए पेट्रोल लगता है = 2 लीटर
1 किमी चलने के लिए पेट्रोल लगता है = 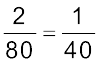 लीटर
लीटर
अब यदि आपसे पूछा जाए कि 120 किमी जाने में कितना पेट्रोल लगेगा,
तब आवश्यक पेट्रोल की मात्रा = 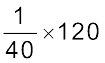 लीटर = 3 लीटर
लीटर = 3 लीटर
वह विधि जिसमें हम पहले एक इकाई का मान निकालते हैं और फिर जितनी इकाइयों का मान निकालने को कहा जाए, निकालते हैं, वह एेकिक विधि कहलाती है।

1. पाँच एेसी ही समस्याएँ बनाएँ और अपने मित्रों से हल करवाएँ।
2. निम्न सारणी को पढ़कर पूरा करें।
करन द्वारा 1 घंटे में तय की गई दूरी = 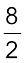 किमी = 4 किमी
किमी = 4 किमी
अत:, करन द्वारा 4 घंटों में तय की गई दूरी = 4 × 4 = 16 किमी
इसी प्रकार कृति द्वारा 4 घंटों में तय की गई दूरी, एक घंटे में तय की गई दूरी निकालकर ज्ञात की जा सकती है।
उदाहरण 11 : यदि 6 जूस की केन का मूल्य ₹ 210 हो तो 4 केन का मूल्य ज्ञात कीजिए?
हल : जूस की 6 केन का मूल्य = ₹ 210
अत:, जूस की 1 केन का मूल्य = 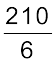 = ₹ 35
= ₹ 35
अत:, जूस की 4 केन का मूल्य = ₹ 35 × 4 = ₹ 140
इस प्रकार जूस की 4 केन का मूल्य ₹ 140 होगा।
उदाहरण 12 : एक मोटरसाइकिल से 220 किमी दूरी तय करने पर 5 लीटर पेट्रोल लगता है तो 1.5 लीटर पेट्रोल में कितनी दूरी तय की जाएगी?
हल : 5 लीटर में मोटरसाइकिल द्वारा तय की गई दूरी = 220 किमी
1 लीटर में मोटरसाइकिल द्वारा तय की गई दूरी = 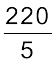 किमी
किमी
1.5 लीटर में मोटरसाइकिल द्वारा तय की गई दूरी 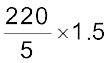 किमी =
किमी = 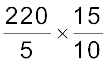 किमी = 66 किमी
किमी = 66 किमी
अत:, 1.5 लीटर पेट्रोल में 66 किमी की दूरी तय की जा सकती है।
उदाहरण 13 : एक दर्जन साबुन की टिक्कियों का मूल्य ₹ 153.60 है। एेसी ही 15 साबुन की टिक्कियों का मूल्य ज्ञात कीजिए।
हल : हम जानते हैं कि 1 दर्जन = 12
क्योंकि 12 साबुन की टिक्कियों का मूल्य = ₹ 153.60
अत:, 1 साबुन की टिक्की का मूल्य = 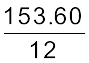 = ₹ 12.80
= ₹ 12.80
अत:, 15 साबुन की टिक्कियों का मूल्य = ₹ 12.80 × 15 = ₹ 192
इस प्रकार, 15 साबुन की टिक्कियों का मूल्य ₹ 192
उदाहरण 14 : 105 लिफ़ाफ़ों का मूल्य ₹ 350 है। ₹ 100 में कितने लिफ़ाफ़े खरीदे जा सकते हैं?
हल : ₹ 350 में खरीदे जा सकने वाले लिफ़ाफ़ों की संख्या = 105
अत:, ₹ 1 में खरीदे जा सकने वाले लिफ़ाफ़ों की संख्या = 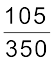
अत:, ₹ 100 में खरीदे जा सकने वाले लिफ़ाफ़ों की संख्या = 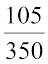 × 100 = 30
× 100 = 30
इस प्रकार ₹ 350 में 30 लिफ़ाफ़े खरीदे जा सकते हैं।
उदाहरण 15 : एक कार 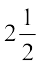 घंटों में 90 किमी चल सकती है।
घंटों में 90 किमी चल सकती है।
(a) उसी चाल से 30 किमी दूरी तय करने में कितना समय लगेगा?
(b) उसी चाल से 2 घंटे में कितनी दूरी तय करेगी?
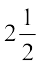 घंटे =
घंटे = 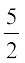 घंटे =
घंटे = 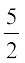 × 60 मिनट = 150 मिनट
× 60 मिनट = 150 मिनट
90 किमी की दूरी तय करने में समय लगा = 150 मिनट
अत:, 1 किमी की दूरी तय करने में समय लगा 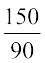 मिनट
मिनट
अत:, 30 किमी की दूरी तय करने में समय लगा 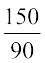 × 30 मिनट
× 30 मिनट
= 50 मिनट
इस प्रकार 30 किमी की दूरी तय करने में 50 मिनट लगेंगे।
(b) इस दूसरी स्थिति में दूरी अज्ञात है और समय ज्ञात है। अत: इस प्रकार आगे बढ़ेंगे :
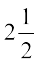 घंटे =
घंटे = 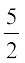 घंटे
घंटे
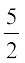 घंटों में तय की गई दूरी = 90 किमी
घंटों में तय की गई दूरी = 90 किमी
अत: 1 घंटे में तय की गई दूरी = 90 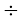
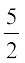 किमी
किमी
= 90 × 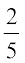 = 36 किमी
= 36 किमी
अत:, 2 घंटों में तय की गई दूरी = 36 × 2 = 72 किमी
इस प्रकार 2 घंटे में 72 किमी की दूरी तय की गई।
प्रश्नावली 12.3
1. यदि 7 मी कपड़े का मूल्य ₹ 1470 हो तो 5 मी कपड़े का मूल्य ज्ञात कीजिए?
2. एकता 10 दिन में ₹ 3000 अर्जित करती है। 30 दिन में वह कितना अर्जित करेगी?
3. यदि पिछले 3 दिन में 276 मिमी वर्षा होती है, तो एक सप्ताह (7 दिन) में कितने सेमी वर्षा होगी? यह मानते हुए कि वर्षा उसी गति से हो रही है।
4. 5 किग्रा गेहूँ का मूल्य ₹ 91.50 हेै
(a) 8 किग्रा गेहूँ का मूल्य क्या होगा?
(b) ₹ 183 में कितना गेहूँ खरीदा जा सकता है?
5. पिछले 30 दिनों में तापमान 15° सेल्सियस गिरता है। यदि तापमान की गिरावट इसी गति से जारी रहे तो, अगले 10 दिनों में तापमान कितने डिग्री गिरेगा?
6. शाइना 3 महीने का किराया ₹ 15000 देती है। उसे पूरे वर्ष का किराया कितना देगा होगा यदि वर्ष भर किराया समान रहे?
7. 4 दर्जन केलों का मूल्य ₹ 180 है। ₹ 90 में कितने केले खरीदे जा सकते हैं?
8. 72 पुस्तकों का भार 9 किग्रा है। एेसी 40 पुस्तकों का भार कितना होगा?
9. एक ट्रक में 594 किमी चलने पर 108 लीटर डीजल लगता है 1650 किमी की दूरी तय करने में कितने लीटर डीजल लगेगा।
10. राजू ने ₹ 150 में 10 पेन और मनीष ने ₹ 84 में 7 पेन खरीदे। ज्ञात कीजिए किसने पेन सस्ते खरीदे?
11. अनीश ने 6 ओवर में 42 रन बनाए और अनूप ने 7 ओवर में 63 रन बनाए। एक ओवर में किसने अधिक रन बनाए?
हमने क्या चर्चा की?
1. एक जैसी राशियों की तुलना करने के लिए हम साधारणत: राशियों के अंतर द्वारा तुलना विधि प्रयोग करते हैं।
2. बहुत सी परिस्थितियों में भाग द्वारा तुलना अधिक अच्छी होती है। अर्थात् एक राशि दूसरी राशि का कितना गुना है। इस विधि को भाग द्वारा तुलना कहते हैं।
उदाहरण के लिए ईशा का भार 25 किग्रा है और उसके पिता का भार 75 किग्रा है। हम कहेंगे कि ईशा के पिता के भार का ईशा के भार के साथ अनुपात 3 : 1 है।
3. अनुपात द्वारा तुलना में, दोनों राशियों की इकाइयाँ समान होनी चाहिए। यदि वे समान नहीं हैं, तो अनुपात लेने से पहले उन्हें समान बना लेना चाहिए।
4. अलग-अलग परिस्थितियों में अनुपात समान हो सकता है।
5. अनुपात 3 : 2 और 2 : 3 एक दूसरे से भिन्न हैं। इस प्रकार जिस क्रम में राशियाँ ली गई हैं वह महत्त्वपूर्ण है।
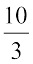 है।
है।7. दो अनुपात तुल्य होंगे, यदि उनकी संगत भिन्न भी तुल्य हों। अत: 3 : 2 तुल्य है 6 : 4 या 12 : 8 के।
8. एक अनुपात को न्यूनतम रूप में बदला जा सकता है। उदाहरण के लिए अनुपात 50 : 15 को 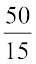 भी लिख सकते हैं और न्यूनतम रूप में
भी लिख सकते हैं और न्यूनतम रूप में 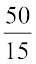 =
= 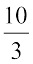 है। इस प्रकार न्यूनतम रूप में 50 : 15 = 10 : 3 है।
है। इस प्रकार न्यूनतम रूप में 50 : 15 = 10 : 3 है।
9. चार राशियाँ समानुपात में कहलाएँगी, यदि पहली और दूसरी राशि का अनुपात, तीसरी और चौथी राशि के अनुपात के बराबर हो। इस प्रकार 3, 10, 15, 50 समानुपात में है क्योंकि 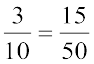 है। हम समानुपात को 3 : 10 :: 15 : 50 के रूप में दर्शाते हैं और 3 अनुपात 10 बराबर 15 अनुपात 50 के रूप में पढ़ते हैं। ऊपर लिखे समानुपात में 3 और 50 चरम पद हैं तथा 10 और 15 मध्य पद हैं।
है। हम समानुपात को 3 : 10 :: 15 : 50 के रूप में दर्शाते हैं और 3 अनुपात 10 बराबर 15 अनुपात 50 के रूप में पढ़ते हैं। ऊपर लिखे समानुपात में 3 और 50 चरम पद हैं तथा 10 और 15 मध्य पद हैं।
10. समानुपात में क्रम महत्त्वपूर्ण है। 3, 10, 15 और 50 समानुपात में हैं लेकिन 3, 10, 50 और 15 नहीं हैं क्योंकि 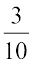 ≠
≠ 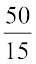 है।
है।
11. वह विधि जिसमें हम पहले एक इकाई का मान निकालते हैं और फिर वांछित इकाइयों का मान निकालते हैं, इकाई विधि कहलाती है। माना कि 6 केन का मूल्य 210 रु है। 4 केन का मूल्य इकाई विधि से ज्ञात करने के लिए, हम पहले 1 केन का मूल्य ज्ञात करेंगे जो कि ₹ 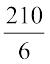 या ₹ 35 होगा। इसी से हम 4 केन का मूल्य ₹ 35 × 4 या ₹ 140 निकालेंगे।
या ₹ 35 होगा। इसी से हम 4 केन का मूल्य ₹ 35 × 4 या ₹ 140 निकालेंगे।