सममिति हमारे दैनिक जीवन में प्रयोग होने वाला एक आम शब्द है। जब हम एेसीे आकृति या आकृतियों को देखते हैं जो बराबर संतुलित अनुपात में हाें तब हम कहते हैं, "ये आकृतियाँ सममित आकृतियाँ हैं।"

अपनी सममित बनावट के कारण इन पुरातत्वीय आकृतियों ने अद्भुत स्थापत्य बना रखा है।

कल्पना कीजिए हम एक आकृति को आधे (अर्ध) से इस तरह मोड़ें कि उसका आधा बायाँ भाग तथा आधा दायाँ भाग एक-दूसरे से पूर्णतया मिलता-जुलता हो तब हम कहेंगे कि आकृति में सममित रेखा उपस्थित है। हम देख सकते हैं कि दोनों आधे भाग एक-दूसरे के (दर्पण) प्रतिबिंब हैं। यदि हम आकृति के मोड़ने वाले स्थान पर एक दर्पण को रख देते हैं, तो आकृति के एक भाग का प्रतिबिंब दूसरे भाग को पूर्णतया ढक लेगा।
एेसा जब भी घटित होता है, तो यह तह या मोड़ (वास्तविक या काल्पनिक), जो दर्पण रेखा है, आकृति की सममिति रेखा (या सममित अक्ष) कहलाती है।

जब आप इन्हें बिंदुकित रेखा की तरफ से मोड़ते हैं तो आकृति का एक आधा भाग, दूसरे आधे भाग को पूर्णतया ढक लेता है। इस आकृति में आप बिंदुु अंकित रेखा को क्या नाम देंगे? आप आकृति में दर्पण को किस जगह पर रखेंगे जिससे कि प्रतिबिंब आकृति के दूसरे भाग को पूर्णतया ढक ले?

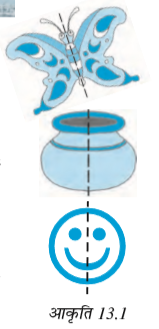
आकृति 13.2 एक सममित आकृति नहीं है।

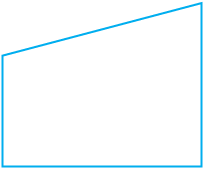
क्या बता सकते हैं, क्यों नहीं?

---

13.2 सममित आकृतियाँ बनाना : इंक-ब्लाट डेविल्स

कागज़ का एक टुकड़ा लीजिए। इसे आधे भाग से मोड़िए। स्याही की कुछ बूँदों को आधे भाग पर डालिए।

अब दोनों आधे भागों को दबाइए।

आप क्या देखते हैं?

क्या प्राप्त आकृति सममित आकृति है? यदि हाँ, तो बताइए सममित रेखा कहाँ है। क्या एेसी कोई अन्य रेखा भी है जहाँ से मोड़ने पर दो समान भाग प्राप्त हो सकते हों? एेसे ही कुछ और प्रतिरूपों का प्रयास कीजिए।

स्याही धागा प्रतिरूप

एक कागज़ को आधे भाग से मोड़िए। उनमें से एक आधे भाग पर कम लंबाई के धागों को अलग-अलग स्याही या पेंट में डुबोकर व्यवस्थित कीजिए। अब दोनों आधे भागों को इकट्ठे दबाइए। प्राप्त आकृति का अध्ययन कीजिए। क्या यह एक सममित आकृति है? इसे और कितने तरीकों से मोड़ा जा सकता है जिससे दो समान भाग प्राप्त हो सकें?

अपनी कक्षा में उपलब्ध कुछ वस्तुओं की सूची बनाइए जैसे श्यामपट्ट (black board), मेज़, दीवार, पाठ्यपुस्तक इत्यादि। इनमें से कौन सी वस्तुएँ सममित हैं और कौन सी सममित नहीं हैं? क्या आप उनमें से सममित वस्तुओं की सममित रेखाएँ पहचान सकते हैं।

प्रश्नावली 13.1

1. अपने घर अथवा विद्यालय की एेसी चार वस्तुओं की सूची बनाइए जो सममित हाें।

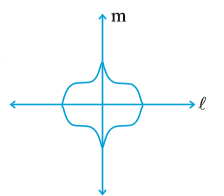
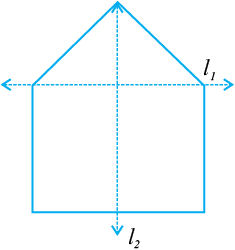
2. दी गई आकृति में कौन सी दर्पण रेखा, अर्थात् सममित रेखा है, l₁ या l₂?

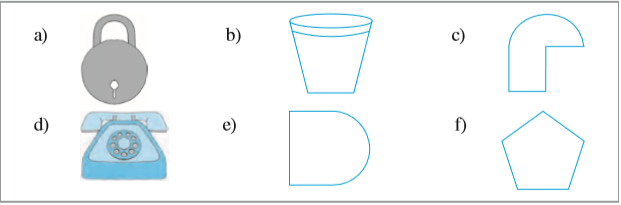
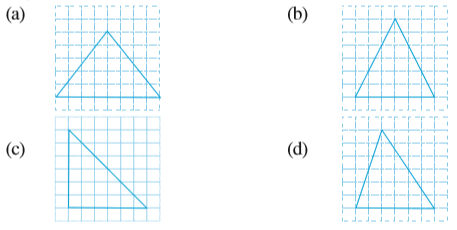
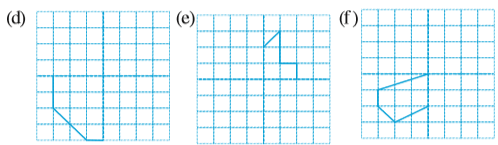
3. नीचे दी गई आकृतियों की पहचान कीजिए। जाँच कीजिए कि क्या ये आकृतियाँ सममित हैं या नहीं। उनकी सममित रेखा भी खींचिए।

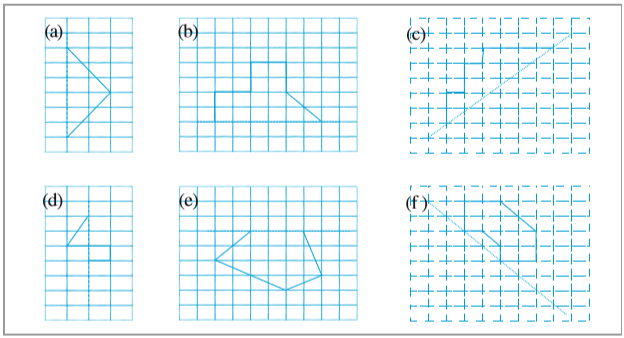
4. नीचे दी गई आकृतियों को वर्गांकित पेपर पर बनाइए। आपने वर्गांकित पेपर का प्रयोग अपनी पिछली कक्षाओं में अंकगणित नोट बुक में किया होगा। इन आकृतियों को इस तरह पूरा कीजिए कि बिंदुकित रेखा ही सममित रेखा हो।

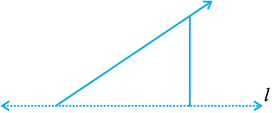
5. नीचे दी गई आकृति में, l सममित रेखा है। इस आकृति को पूरा कीजिए जिससे यह सममित हो जाए।

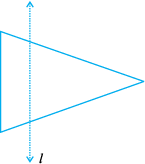
6. आकृति में, l सममित रेखा है। त्रिभुज का प्रतिबिंब खींचिए और इस आकृति को पूरा कीजिए जिससे यह सममित हो जाए।

13.3 आकृतियाँ जिनमें दो सममित रेखाएँ हों

एक पतंग

आपके ज्यामिति बॉक्स में दो सेट स्क्वेयर में से एक के कोणों की माप 30°, 60° और 90° है।

एेसे ही दो समान सेट स्क्वेयर लीजिए। उन्हें आपस में मिलाकर रखिए और एक पतंग बनाइए जैसा आकृति में दिखाया गया है।

इस आकृति में कितनी सममित रेखाएँ हैं? क्या आप सोचते हैं कि कुछ आकृतियों में एक से अधिक सममित रेखाएँ होती हैं।

एक आयत

एक आयताकार कागज़ लीजिए (जैसे डाक-लिफ़ाफ़ा)। इसे एक बार लंबाई की ओर मोड़िए जिससे कि एक आधा भाग दूसरे आधे भाग को पूर्णतया ढक लें। क्या यह मोड़ एक सममित रेखा है। क्यों?

इसे खोलिए और पुन: एक बार चौड़ाई की ओर से समान तरीके से मोड़िए। क्या यह दूसरा मोड़ भी सममित रेखा है? क्यों?

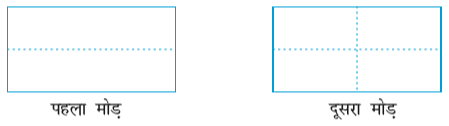
क्या आपको लगता है कि ये दो रेखाएँ, सममित रेखाएँ हैं?

दो तहाें वाले कागज़ से काटी गई आकृति

एक आयताकार कागज़ का टुकड़ा लीजिए। इसे एक बार मोड़िए और पुन: एक बार मोड़िए। कुछ डिज़ाइन बनाइए जैसा कि दिखाया गया है। जो आकृति बनाई गई है उसे काटिए और खोलिए (खोलने से पहले उस आकृति का अनुमान लगाइए जिसे आप प्राप्त करेंगे)।

जिस आकृति को काटा गया है उसमें कितनी सममित रेखाएँ हैं? एेसी कुछ और डिज़ाइनों को बनाइए।

13.4 अनेक सममित रेखाओं (दो से अधिक) वाली आकृतियाँ

एक वर्गाकार कागज़ का टुकड़ा लीजिए। इसे ऊर्ध्वाधर (vertically) में आधे से मोड़िए और पुन: क्षैतिज (horizontally) से आधे भाग से मोड़िए (अर्थात् आपने इसे दो बार मोड़ा)। इसे खोलिए और पुन: वर्ग को आधे भाग से मोड़िए (अर्थात् तीसरी बार), लेकिन इस बार विकर्ण के साथ-साथ जैसा कि आकृति में दिखाया गया है। इसे पुन: खोलिए और आधे भाग से मोड़िए (चौथी बार), लेकिन इस बार दूसरे विकर्ण के साथ-साथ जैसा कि आकृति में दिखाया गया है। इसे खोलिए।

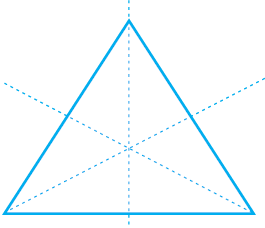
इस आकृति में कितनी सममित रेखाएँ हैं? हम दो सममित रेखाओं वाली आकृतियों की रचना करना उसी प्रकार सीख सकते हैं, जैसी हमने प्रश्नावली 13.1 के प्रश्न 4 में एक सममित रेखा वाली आकृतियों के लिए, एक छोटे भाग को लेकर की थीं।

1. मान लीजिए हमारे पास दाईं ओर जैसी कोई आकृति है।

2. हम इसे इस प्रकार पूरा करना चाहते हैं कि दो सममित रेखाओं वाली आकृति प्राप्त हो जाए। मान लीजिए दोनों सममित रेखाएँ l और m हैं।

3. हम एक भाग आकृति में दर्शाए अनुसार बनाते हैं, जो रेखा l के परित (about) समिमित है, अर्थात् रेखा l समिमित रेखा है।

4. आकृति पूरा करने के लिए, हमें रेखा l के परित सममित भाग भी बनाना होगा। आकृति में दर्शाए अनुसार आकृति का शेष भाग बनाइए।

इस आकृति की दो सममित रेखाएँ l और m हैं।

कुछ आकृतियों में केवल एक ही सममित रेखा होती है, कुछ में दो, और कुछ में तीन या अधिक सममित रेखाएँ होती हैं। क्या आप एक एेसी आकृति को सोच सकते हैं जिसमें 6 सममित रेखाएँ हों?

सममिति, सममिति प्रत्येक स्थान पर

• आप प्रतिदिन एेसे बहुत से मार्गसूचक संकेत या चिह्न देखते हैं जिनमें सममिति की रेखाएँ होती हैं। यहाँ पर एेसे ही कुछ चिह्न (संकेत) दिए गए हैं : एेसे ही कुछ और मार्गसूचक संकेतों को पहचानो और उन्हें बनाओ। सममित रेखाओं को इंगित करना मत भूलिए।
  

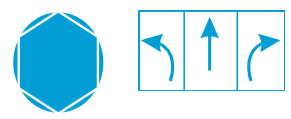
• प्रकृति में बहुत सी वस्तुएँ एेसी हैं जिनकी आकृतियाँ सममित हैं। इन्हें देखिए :
  

• ताश के कुछ पत्तों के डिज़ाइन में सममित रेखाएँ होती हैं। दिए गए ताश के पत्तों में उन्हें पहचानिए।
  

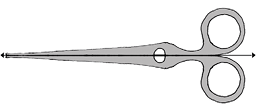
• यहाँ एक कैंची का युग्म है! इसमें कितनी सममित रेखाएँ हैं?

•  इस सुंदर आकृति का निरीक्षण कीजिए।
  

यह एक सममित पैटर्न है जो कि कोच स्नोफलेक (koch's Snowflake) के नाम से जाना जाता है। (यदि आपके पास कंप्यूटर है, तो आप फ्रेक्टल (Fractals) विषय पर ब्राऊस कीजिए और आपको एेसी बहुत सुंदर आकृतियाँ देखने को मिलेंगी।) इन आकृतियों में सममित रेखाएँ ज्ञात कीजिए।

प्रश्नावली 13.2

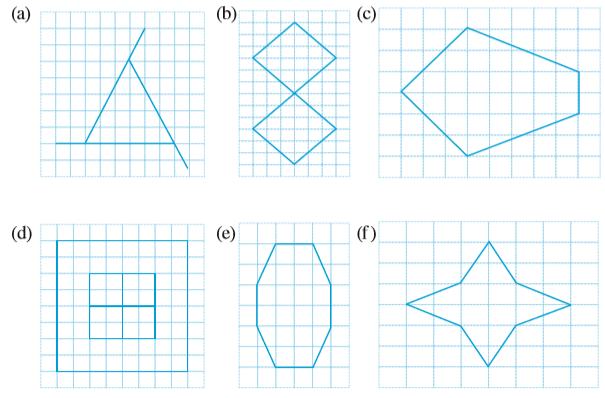
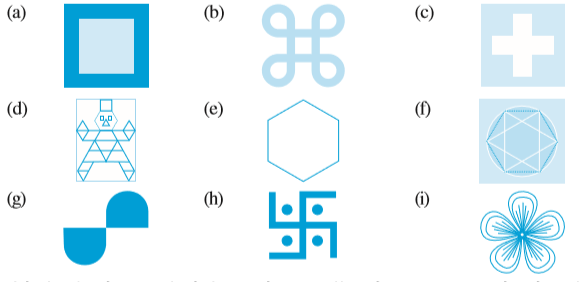
1. नीचे दी गई आकृतियों में प्रत्येक की सममित रेखाओं की संख्या ज्ञात कीजिए।

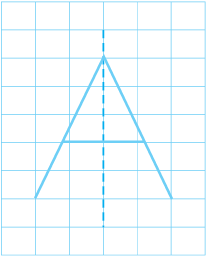
2. नीचे दी गई प्रत्येक आकृति में त्रिभुज को एक वर्गांकित पेपर पर बनाइए। प्रत्येक में सममित रेखा (रेखाओं) को, यदि है तो, उन्हें खींचिए और त्रिभुज के प्रकार को पहचानिए। (आप उनमें से कुछ आकृतियों का अनुरेख (trace) करना पसंद कर सकते हैं। पहले पेपर को मोड़ने वाली विधि द्वारा प्रयास करें)

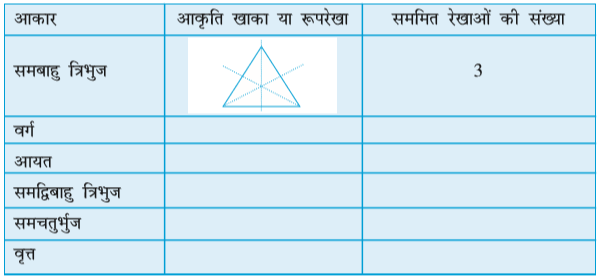
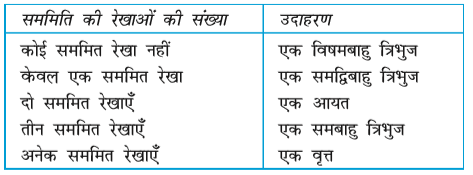
3. निम्न तालिका को पूरा कीजिए :

4. क्या आप एक एेसा त्रिभुज बना सकते हो जिसमें

(a) केवल एक ही सममित रेखा हो?

(b) केवल दो ही सममित रेखाएँ हाें?

(c) केवल तीन ही सममित रेखाएँ हों?

(d) कोई सममित रेखा न हो?

प्रत्येक में आकृति की रूपरेखा (खाका) बनाइए।

5. एक वर्गांकित पेपर पर निम्न की रूपरेखा बनाइए :

(संकेत : आपके लिए सहायक होगा यदि आप पहले सममित रेखा खींचें और उसके बाद आकृति को पूरा करें)

(a) एक त्रिभुज जिसमें क्षैतिज सममित रेखा तो हो परंतु ऊर्ध्वाधर सममित रेखा न हो।

(b) एक चतुर्भुज जिसमें क्षैतिज और ऊर्ध्वाधर दोनों ही सममित रेखाएँ हों।

(c) एक चतुर्भुज जिसमें क्षैतिज सममित रेखा तो हो, परंतु ऊर्ध्वाधर सममित रेखा न हो।

(d) एक षट्भुज जिसमें केवल दो ही सममित रेखाएँ हाें।

(e) एक षट्भुज जिसमें 6 सममित रेखाएँ हाें।

6. प्रत्येक आकृति का अनुरेखण (ट्रेस) कीजिए और सममित रेखाओं को खींचिए।

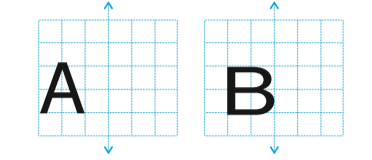
7. अंग्रेज़ी वर्णमाला के A से Z तक के सभी अक्षरों पर विचार कीजिए। इनमें से उन अक्षरों की सूची बनाइए जिनमें

(a) उर्ध्वाधर सममित रेखाएँ हों (जैसा कि A)

(b) क्षैतिज सममित रेखाएँ हाें (जैसा कि B)

(c) सममित रेखाएँ न हों (जैसा कि Q)

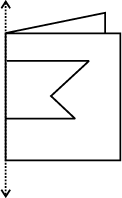
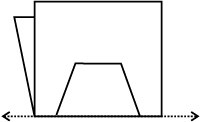
8. यहाँ पर कुछ मुड़ी हुई शीट की आकृतियाँ दी गई हैं जिनकी तह पर आकृतियाँ बनाई गई हैं। प्रत्येक में पूर्ण आकृति की रूपरेखा खींचिए जो डिज़ाइन के काटने के बाद दिखाई देगी।

13.5 प्रतिबिंब और सममिति

सममित रेखा और दर्पण प्रतिबिंब एक दूसरे से प्राकृतिक तौर पर संबंधित हैं।

यहाँ एक आकृति दी गई है जिसमें अंग्रेजी अक्षर M का प्रतिबिंब दिखाया गया है। आप कल्पना कीजिए कि दर्पण अदृश्य है और आप केवल अक्षर M तथा इसकी छाया या प्रतिबिंब को देख सकते हैं।

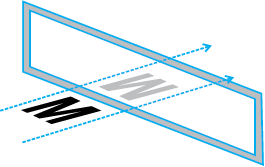
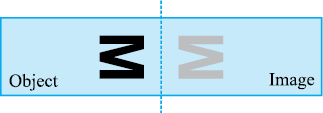
वस्तु और उसका प्रतिबिंब दर्पण रेखा के संदर्भ में सममित है। जब एक पेपर को मोड़ा जाता है तो दर्पण रेखा, सममित रेखा बन जाती है। तब हम कहते हैं कि छाया, दर्पण रेखा में वस्तु का प्रतिबिंब है। आप यह भी देख सकते हैं कि जब वस्तु परावर्तित होती है, तो उसकी लंबाई और कोणों में बिल्कुल भी परिवर्तन नहीं होता है, अर्थात् वस्तु की लंबाई और कोण तथा छाया की संगत लंबाई और कोण समान होते हैं। यद्यपि एक तरह से परिवर्तन भी होता है अर्थात् एक वस्तु तथा उसकी छाया में अंतर होता है। क्या आप कल्पना कर सकते हैं कि यह अंतर क्या है?

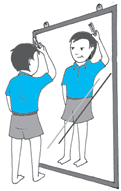
(संकेत : अपने आपको दर्पण में देखिए)

एक वर्गांकित कागज़ पर एक आकृति ABC बनाइए और इसका दर्पण रेखा l में प्रतिबिंब A'B'C' ज्ञात कीजिए।

AB और A'B'; BC और B'C'; AC और A'C'

की लंबाइयों की तुलना कीजिए।

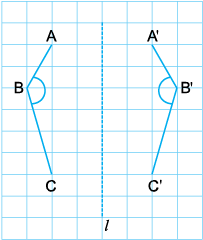
क्या ये अलग हैं?

क्या प्रतिबिंब एक रेखाखंड की लंबाई में परिवर्तन करता है? ABC और A'B'C' कोणों की माप की तुलना कीजिए (कोण मापक की सहायता से मापिए) क्या प्रतिबिंब, कोण के आकार को बदल देता है।

AA', BB' और CC' को मिलाइए। कोण मापक की सहायता से l और AA', l और BB', l और CC' के बीच बने कोणों को मापिए।

दर्पण रेखा l और किसी बिंदुु और इसके प्रतिबिंब को मिलाने से बने रेखाखंड के बीच बने कोण के बारे में आप क्या निष्कर्ष निकालते हैं?

कागज़ों द्वारा सजावट

एक पतला आयताकार रंगीन कागज़ लीजिए। इसे कई बार मोड़िए और कागज़ में कुछ जटिल प्रतिरूप बनाइए जैसा कि आकृति में दिखाया गया है। बार-बार आने वाले डिज़ाइनों में सममित रेखाओं की पहचान कीजिए। एेसे सजावटी कर्तित कागज़ों का प्रयोग त्यौहारों के अवसरों पर कीजिए।

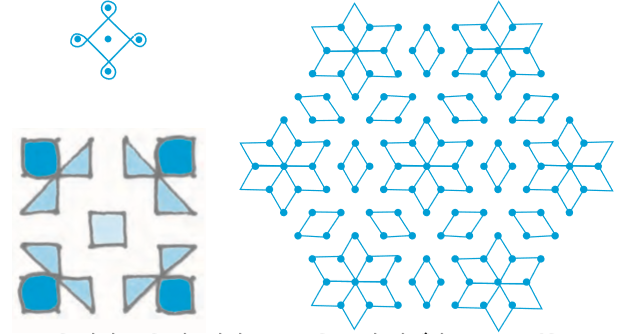
कैलाइडोस्कोप

अनेक दर्पणों वाले एक केलाइडोस्कोप में कई प्रतिबिंब बनते हैं जिनमें अनेक सममिति की रेखाएँ होती हैं (जैसा यहाँ उदाहरण में दिखाया गया है)। प्राय: दो दर्पण पट्टियों को V आकार में रखकर प्रयोग किया जाता है। दर्पणों के बीच बने कोण सममित रेखाओं या सममित रेखाओं की संख्या को बताते हैं।

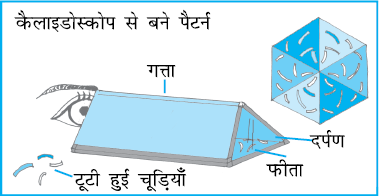
आकृति 13.1

एक केलाइडोस्कोप बनाइए और इसके द्वारा बनाई गई सममित आकृतियों की कुछ और जानकारी प्राप्त करने का प्रयास कीजिए।

एलबम

सममित डिज़ाइनों को एकत्रित करके एक एलबम तैयार कीजिए। यहाँ पर कुछ नमूने दिए गए हैं।

परावर्त्तीय सममिति का उपयोग

एक अखबार बाँटने वाला लड़का अपनी साइकिल को गली में किसी बिंदुु 'P' पर खड़ा करता है और अखबार A और B घरों में बाँटता है। उसे अपनी साइकिल को कहाँ पर खड़ा करना चाहिए, जिससे AP + BP दूरी सबसे कम हो।

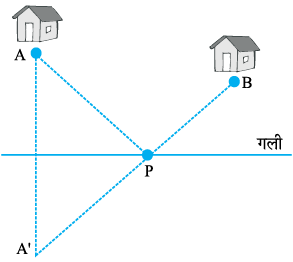
आप यहाँ पर परावर्तीय सममिति का प्रयोग कर सकते हैं। मार्ग को दर्पण रेखा लेने पर, माना A का प्रतिबिंब A' प्राप्त होता है। तब हम कहेंगे कि बिंदुु P साइकिल को खड़ा करने के लिए उपयुक्त स्थान है (जहाँ दर्पण रेखा A'B को काटती है)। क्या आप कह सकते हैं क्यों?

प्रश्नावली 13.3

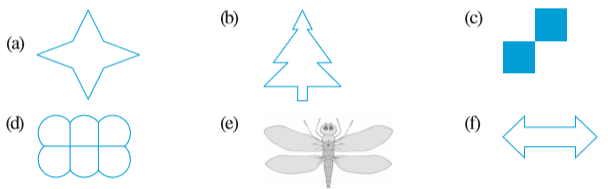
1. नीचे दी गई आकृतियों में सममित रेखाओं की संख्या ज्ञात कीजिए। आप अपने उत्तर की जाँच कैसे करेंगे?

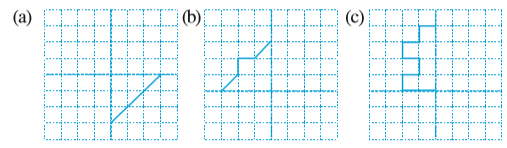
2. नीचे दिए गए आरेखण को वर्गांकित पेपर पर बनाइए। प्रत्येक को पूरा कीजिए जिससे प्राप्त आकृति में दो बिंदुुकित रेखाएँ दो सममित रेखाओं के रूप में हों :

आपने इस आकृति को कैसे पूरा किया?

3. नीचे दी गई प्रत्येक आकृति में, अंग्रेज़ी वर्णमाला के एक अक्षर को ऊर्ध्वाधर रेखा के साथ दिखाया गया है। इस अक्षर का दी हुई दर्पण रेखा में प्रतिबिंब लीजिए। बताइए कौन सा अक्षर परावर्तन के बाद समान रहता है (जैसे कौन सा अक्षर प्रतिबिंब में समान दिखाई देता है) और कौन सा नहीं। क्या आप कल्पना कर सकते हैं क्यों?

रँगोली प्रतिरूप

कोलम और रंगोली हमारे देश में बहुत प्रसिद्ध हैं। कुछ नमूने यहाँ दिए गए हैं। उनमें सममिति के प्रयोग पर ध्यान दीजिए। इन प्रतिरूपों को जितना भी संभव हो सके इकट्ठा कीजिए और एक एलबम तैयार कीजिए।

इन प्रतिरूपों में सममित रेखाओं के साथ सममित भागों को ढूँढ़ने का प्रयास कीजिए।

हमने क्या चर्चा की?

1. एक आकृति में सममित रेखा होती है, यदि एक खींची गई रेखा आकृति को दो बराबर या समान भागों में बाँटती हो। यह रेखा सममित रेखा कहलाती है।

2. एक आकृति में कोई भी सममित रेखा नहीं हो सकती, केवल एक सममित रेखा, दो सममित की रेखाएँ या अनेक सममित की रेखाएँ हो सकती हैं। यहाँ पर कुछ उदाहरण दिए गए हैं।

3. रैखिक सममिति परावर्तन से संबंधित होती है। जब हम परावर्तन के बारे में बात करते हैं, तो हमें बायें↔दायें अभिमुख होने का ध्यान रखना चाहिए।