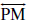Table of Contents
14.1 भूमिका
हम अनेक प्रकार के आकार (Shapes) देखते हैं, जिनसे हम परिचित हैं। हम बहुत से चित्र बनाते हैं। इन चित्रों में विभिन्न आकार निहित होते हैं। हम इन आकारों में से कुछ के बारे में पिछले अध्यायों में पढ़ भी चुके हैं। आप इन आकारों की एक सूची बना लें कि ये किस प्रकार प्रकट होते हैं?
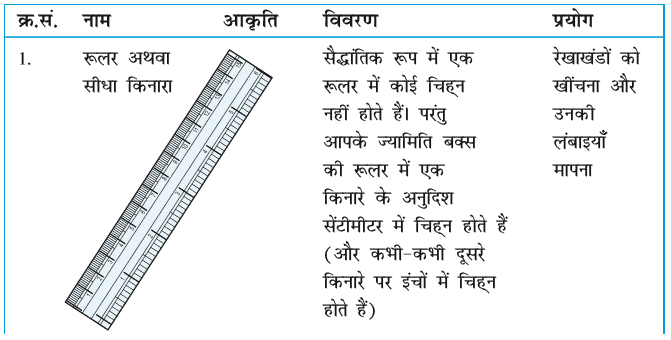
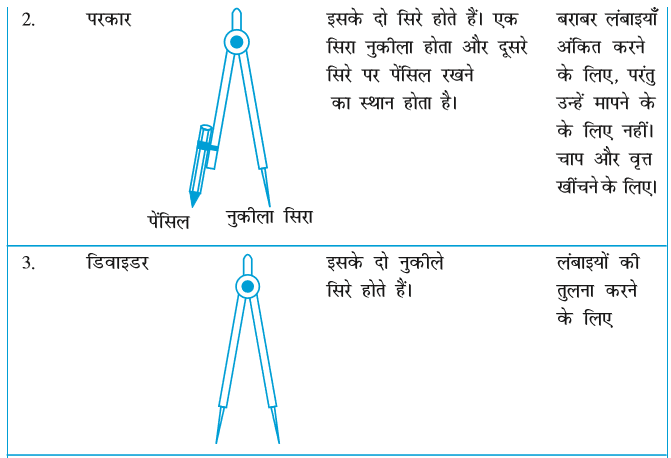
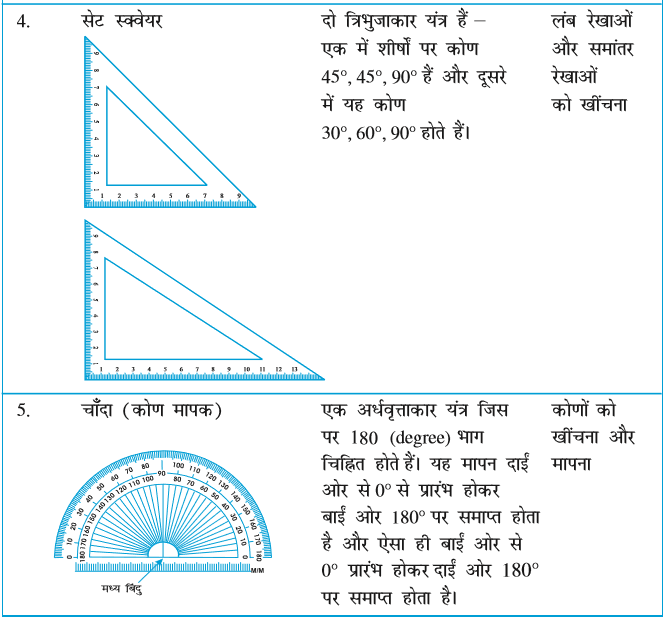
इस अध्याय में, हम इन आकारों को बनाना सीखेंगे। इनको बनाने के लिए, हमें यंत्रों के बारे में जानने की आवश्यकता है। आइए, उन्हें देखें तथा उनके नाम और प्रयोग के बारे में जानकारी प्राप्त करें।
हम ‘रूलर और परकार की रचनाओं’ पर विचार करने जा रहे हैं। इनमें रूलर (ruler) का केवल रेखाएँ खींचने और परकार (compass) का केवल चाप खींचने में प्रयोग किया जाएगा। इन रचनाओं को बनाते समय पूर्ण सावधानी बरतिए। यहाँ आपकी सहायता के लिए कुछ सुझाव दिए जा रहे हैं :
(a) पतली रेखाएँ खींचिए और हल्के बिंदु अंकित कीजिए।
(b) अपने यंत्रों को नुकीले सिरे और पतले किनारे वाला बनाकर रखिए।
(c) अपने बक्स में दो पेंसिल रखिए। एक परकार में रखने के लिए और दूसरी रेखा या वक्र खींचने और बिंदुओं को अंकित करने के लिए।
14.2 वृत्त
सामने दर्शाए गए पहिए को देखिए। इसकी परिसीमा (Boundary) पर स्थित प्रत्येक बिंदु इसके केंद्र से बराबर दूरी पर हैं। क्या आप एेसी कुछ और वस्तुएँ बता सकते हैं और उन्हें खींच सकते हैं? एेसी पाँच वस्तुओं के बारे में सोचिए जो इसी आकार की हों।

14.2.1 एक वृत्त खींचना जब उसकी त्रिज्या ज्ञात हो
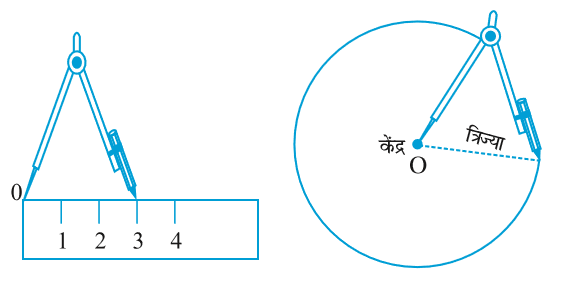
मान लीजिए हम 3 सेमी त्रिज्या का एक वृत्त खींचना चाहते हैं। हमें अपने परकार का प्रयोग करने की आवश्यकता है। यह निम्न चरणों में किया जा सकता है :
चरण 1 परकार को वांछित त्रिज्या 3 सेमी के लिए खोलिए।
चरण 2 एक नुकीली पेंसिल से वह बिंदु अंकित कीजिए जिसे हम वृत्त का केंद्र बनाना चाहते हैं। इसे बिंदु O से नामांकित कीजिए।
चरण 3 परकार के नुकीले सिरे को O पर रखिए।
चरण 4 वृत्त खींचने के लिए, परकार को धीरे-धीरे घुमाइए। ध्यान रखिए कि चक्कर एक ही बार में पूरा हो जाए।
सोचिए, चर्चा कीजिए और लिखिए
क्या आप केंद्र O लेकर एक बिंदु, मान लीजिए P से होकर वृत्त खींच सकते हैं?
प्रश्नावली 14.1
1. 3.2 सेमी त्रिज्या का एक वृत्त खींचिए।
2. एक ही केंद्र O लेकर 4 सेमी और 2.5 सेमी त्रिज्या वाले दो वृत्त खींचिए।
3. एक वृत्त और उसके कोई दो व्यास खींचिए। यदि आप इन व्यासों के सिरों को जोड़ दें, तो कौन सी आकृति प्राप्त होती है? यदि व्यास परस्पर लंब हों, तो कौन सी आकृति प्राप्त होगी? आप अपने उत्तर की जाँच किस प्रकार करेंगे?
4. एक वृत्त खींचिए और बिंदु A, B और C इस प्रकार अंकित कीजिए कि
(a) A वृत्त पर स्थित हो।
(b) B वृत्त के अभ्यंतर में स्थित हो।
(c) C वृत्त के बहिर्भाग में स्थित हो।
5. मान लीजिए A और B समान त्रिज्याओं वाले दो वृत्तों के केंद्र हैं। इन्हें इस प्रकार खींचिए ताकि एक वृत्त दूसरे के केंद्र से होकर जाए। इन्हें C और D पर प्रतिच्छेद करने दीजिए। जाँच कीजिए कि  और
और 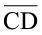 परस्पर समकोण पर हैं।
परस्पर समकोण पर हैं।
14.3 एक रेखाखंड
याद कीजिए कि एक रेखाखंड के दो अंत बिंदु होते हैं। इसी कारण हम इसकी लंबाई रूलर से माप सकते हैं। यदि हमें किसी रेखाखंड की लंबाई ज्ञात हो, तो इसे एक आकृति द्वारा निरूपित करना संभव हो जाता है। आइए, देखें कि हम एेसा कैसे करते हैं।
14.3.1 एक दी हुई लंबाई के रेखाखंड की रचना करना
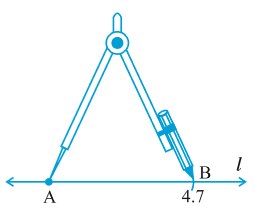
मान लीजिए हम 4.7 सेमी लंबाई के एक रेखाखंड की रचना करना चाहते हैं। हम रूलर का प्रयोग करके 4.7 सेमी की दूरी पर दो बिंदु A और B अंकित करते हैं। A और B को मिलाने पर हमें रेखाखंड  प्राप्त होता है। बिंदु A और B को अंकित करते समय, हमें रूलर पर सीधे नीचे की ओर देखना चाहिए, अन्यथा हमें सही उत्तर प्राप्त नहीं होगा।
प्राप्त होता है। बिंदु A और B को अंकित करते समय, हमें रूलर पर सीधे नीचे की ओर देखना चाहिए, अन्यथा हमें सही उत्तर प्राप्त नहीं होगा।
रूलर और परकार का प्रयोग
एक अच्छी विधि यह होगी कि दी हुई लंबाई के एक रेखाखंड की रचना करने के लिए, परकार का प्रयोग किया जाए
चरण 1 एक रेखा l खींचिए और उस पर एक बिंदु A अंकित कीजिए।

चरण 2 परकार के नुकीले सिरे को रूलर के शून्य पर रखिए। इसे इस प्रकार खोलिए कि पेंसिल वाला सिरा 4.7 सेमी चिह्न पर आ जाए।
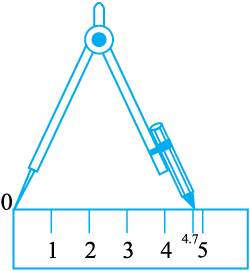
चरण 3 यह सावधानी लेते हुए कि परकार के फैलाव में कोई परिवर्तन न हो, उसके नुकीले सिरे को बिंदु A पर रखें और l को B पर काटता हुआ एक चाप लगा दीजिए।
चरण 4  वांछित लंबाई 4.7 सेमी का एक रेखाखंड है।
वांछित लंबाई 4.7 सेमी का एक रेखाखंड है।

प्रश्नावली 14.2
1. रूलर का प्रयोग करके 7.3 सेमी लंबाई का एक रेखाखंड खींचिए।
2. रूलर और परकार का प्रयोग करते हुए 5.6 सेमी लंबाई का एक रेखाखंड खींचिए।
3. 7.8 सेमी लंबाई का रेखाखंड  खींचिए। इसमें से
खींचिए। इसमें से 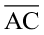 काटिए जिसकी लंबाई 4.7 सेमी हो।
काटिए जिसकी लंबाई 4.7 सेमी हो। 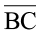 को मापिए।
को मापिए।
4. 3.9 सेमी लंबाई का एक रेखाखंड  दिया है। एक रेखाखंड
दिया है। एक रेखाखंड 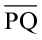 खींचिए जो रेखाखंड का दोगुना हो। मापन से अपनी रचना की जाँच कीजिए।
खींचिए जो रेखाखंड का दोगुना हो। मापन से अपनी रचना की जाँच कीजिए।

(संकेत :  खींचिए ताकि
खींचिए ताकि  लंबाई
लंबाई  की लंबाई के बराबर हो। फिर
की लंबाई के बराबर हो। फिर 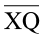 काटिए ताकि
काटिए ताकि 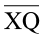 की लंबाई भी
की लंबाई भी  की लंबाई के बराबर हो। इस प्रकार,
की लंबाई के बराबर हो। इस प्रकार,  और
और 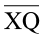 की लंबाइयाँ मिलकर
की लंबाइयाँ मिलकर  की लंबाई का दोगुना हो जाएँगी।)
की लंबाई का दोगुना हो जाएँगी।)
5. 7.3 सेमी लंबाई का रेखाखंड  और 3.4 सेमी लंबाई का रेखाखंड
और 3.4 सेमी लंबाई का रेखाखंड 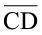 दिया है। एक रेखाखंड
दिया है। एक रेखाखंड 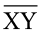 खींचिए ताकि
खींचिए ताकि 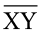 की लंबाई
की लंबाई  और
और 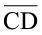 की लंबाइयों के अंतर के बराबर हो।
की लंबाइयों के अंतर के बराबर हो।
14.3.2 एक दिए हुए रेखाखंड के बराबर रेखाखंड की रचना करना
मान लीजिए आप एक एेसे रेखाखंड की रचना करना चाहते हैं, जिसकी लंबाई एक दिए हुए रेखाखंड  की लंबाई के बराबर हो।
की लंबाई के बराबर हो।
एक तुरंत और स्वाभाविक विधि यह होगी कि आप रूलर का प्रयोग करें। (जिस पर सेंटीमीटर और मिलीमीटर के चिह्न अंकित हों) उससे  को माप लिया जाए और फिर उसी लंबाई का प्रयोग करके एक रेखाखंड
को माप लिया जाए और फिर उसी लंबाई का प्रयोग करके एक रेखाखंड 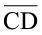 खींच लिया जाए। एक दूसरी विधि यह होगी कि एक पारदर्शक कागज़ का प्रयोग करके
खींच लिया जाए। एक दूसरी विधि यह होगी कि एक पारदर्शक कागज़ का प्रयोग करके  को कागज़ के अन्य भाग पर अक्स (trace) कर लिया जाए। परंतु इन विधियों से सदैव सही परिणाम प्राप्त नहीं हो सकते हैं।
को कागज़ के अन्य भाग पर अक्स (trace) कर लिया जाए। परंतु इन विधियों से सदैव सही परिणाम प्राप्त नहीं हो सकते हैं।
एक और अच्छी विधि होगी कि रचना के लिए, रूलर और परकार का प्रयोग किया जाए। यह रचना  के लिए निम्न प्रकार की जाती है :
के लिए निम्न प्रकार की जाती है :
चरण 1 रेखाखंड  दिया है, जिसकी लंबाई ज्ञात नहीं है।
दिया है, जिसकी लंबाई ज्ञात नहीं है।

चरण 2 परकार के नुकीले सिरे को A पर रखिए और पेंसिल को B पर रखिए। परकार का फैलाव  की लंबाई बताता है।
की लंबाई बताता है।
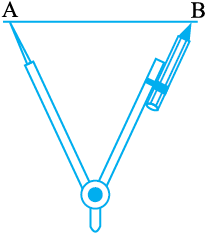
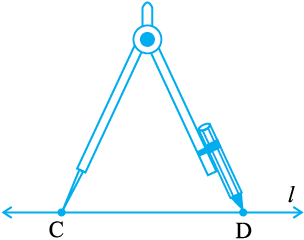
चरण 3 कोई रेखा l खींचिए। l पर कोई बिंदु C लीजिए। परकार के फैलाव में बिना कुछ परिवर्तन किए, उसके नुकीले सिरे को C पर रखिए।
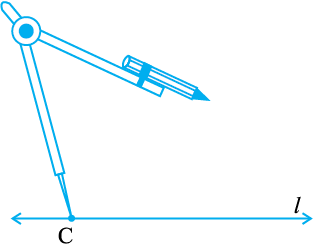
चरण 4 एक चाप लगाइए जो l को D पर (मान लीजिए) काटे। अब 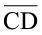 ही
ही  की लंबाई के बराबर का रेखाखंड है।
की लंबाई के बराबर का रेखाखंड है।
प्रश्नावली 14.3
1. कोई रेखाखंड 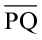 खींचिए। बिना मापे हुए,
खींचिए। बिना मापे हुए, 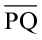 के बराबर एक रेखाखंड की रचना कीजिए।
के बराबर एक रेखाखंड की रचना कीजिए।
2. एक रेखाखंड  दिया हुआ है, जिसकी लंबाई ज्ञात नहीं है। एक रेखाखंड
दिया हुआ है, जिसकी लंबाई ज्ञात नहीं है। एक रेखाखंड 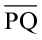 की रचना कीजिए जिसकी लंबाई
की रचना कीजिए जिसकी लंबाई  की लंबाई की दोगुनी हो।
की लंबाई की दोगुनी हो।
14.4 लंब रेखाएँ
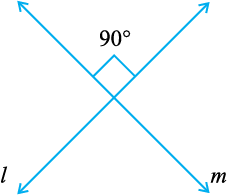
आप जानते हैं कि दो रेखाएँ (या किरणें या रेखाखंड) परस्पर लंब (perpendicular) कही जाती हैं, जब वे इस प्रकार प्रतिच्छेद करती हैं कि उनके बीच के कोण समकोण हों। संलग्न आकृति में l और m परस्पर लंब हैं। एक फुलस्केप (foolscap) कागज़ या आपकी अभ्यास पुस्तिका के कोने दर्शाते हैं कि दो रेखाएँ परस्पर समकोणों पर हैं।


आप अपने आसपास और कहाँ लंब रेखाएँ देखते हैं?
एक कागज़ का पृष्ठ लीजिए और उसे बीच में से मोड़िए तथा मोड़ का निशान (crease) बनाइए। इसी कागज़ को बीच में से अन्य दिशा में मोड़िए। मोड़ का निशान बनाइए और कागज़ को खोल लीजिए। दोनों मोड़ के निशान एक दूसरे पर (परस्पर) लंब हैं।


14.4.1 एक दी हुई रेखा पर स्थित एक बिंदु से होकर लंब खींचना
एक रेखा l कागज़ पर खिंची हुई है और P उस पर स्थित एक बिंदु है। P से होकर गुजरता हुआ l पर लंब खींचना सरल है।
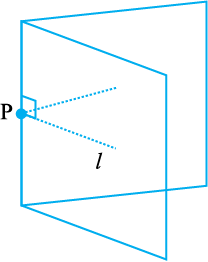
हम कागज़ को केवल इस प्रकार मोड़ सकते हैं कि मोड़ के निशान के दोनों ओर वाले l के भाग एक दूसरे को आच्छादित करें। अक्स कागज़ या कोई पारदर्शक कागज़ क्रियाकलाप के लिए अच्छा रहेगा। आइए, एक कागज़ लें और उस पर कोई रेखा l खींचे। अब l पर कोई बिंदु P अंकित कर लें।
अब कागज़ को इस प्रकार मोड़िए कि l स्वयं पर परावर्तित हो जाए। अर्थात् स्वयं पर गिरे। मोड़ के निशान को इस प्रकार समायोजित कीजिए कि वह P से होकर जाए। कागज़ को खोल लीजिए। मोड़ का निशान P से होकर जाता हुआ रेखा l पर लंब है।
सोचिए, चर्चा कीजिए और लिखिए
आप इसकी जाँच कैसे करेंगे कि यह l पर लंब है? ध्यान दीजिए कि यह P से होकर जाता है।
एक चुनौती : रूलर और सेट स्क्वेयर की सहायता से लंब खींचना (एक एेच्छिक क्रियाकलाप) :
चरण 1 एक रेखा l और एक बिंदु P दिए हुए हैं। ध्यान दीजिए कि P रेखा l पर स्थित है।

चरण 2 रूलर के एक किनारे को रेखा l के अनुदिश रखिए। इसे कस कर पकड़े रहिए।

चरण 3 एक सेट स्क्वेयर को इस प्रकार रेखा l पर रखिए कि उसका समकोण बनाने वाला एक किनारा रूलर के उस किनारे के अनुदिश रहे जो रेखा l के साथ लगा हुआ है तथा सेट स्क्वेयर का समकोण वाला कोना भी रूलर के स्पर्श में रहे।

चरण 4 सेट स्क्वेयर को रूलर के अनुदिश तब तक सरकाइए जब तक कि उसका समकोण वाला कोना बिंदु P पर न आ जाए।

चरण 5 इस स्थिति में, सेट स्क्वेयर को कस कर पकड़े रहिए। सेट सक्वेयर के समकोण के दूसरे किनारे के अनुदिश 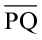 खींचिए
खींचिए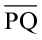 रेखा l पर लंब है (आप इसको दर्शाने के लिए संकेत
रेखा l पर लंब है (आप इसको दर्शाने के लिए संकेत 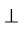
बिंदु P पर बने कोण को माप कर इस रचना की जाँच कीजिए। क्या हम ‘रूलर’ के स्थान पर इस रचना में दूसरे सेट स्क्वेयर का प्रयोग कर सकते हैं? इसके बारे में सोचिए।
रूलर और परकार की विधि
ज्यामिति में लंब डालने की जिस विधि को प्राथमिकता दी जाती है वह ‘रूलर-परकार’ की विधि है। इस रचना को नीचे दिया जा रहा है :
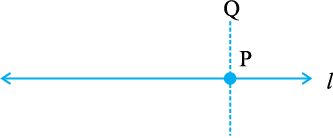
चरण 1 एक रेखा l पर बिंदु P दिया हुआ है।

चरण 2 P को केंद्र मानकर और एक सुविधाजनक त्रिज्या लेकर एक चाप लगाइए जो रेखा l को दो बिंदुओं A और B पर प्रतिच्छेद करें।
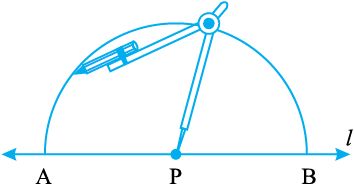
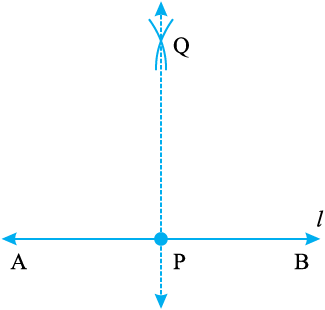
चरण 3 A और B को केंद्र मानकर और AP से अधिक की त्रिज्या लेकर दो चापों की रचना कीजिए जो परस्पर Q पर काटें।
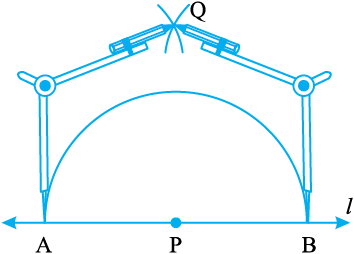
चरण 4 PQ को जोड़िए (या मिलाइए) तब 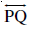
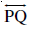
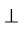
14.4.2 एक रेखा पर उस बिंदु से होकर लंब जो उस पर स्थित नहीं है।

(कागज़ मोड़ना)
यदि हमें एक रेखा l दी हुई है और एक एेसा बिंदु P दिया है, जो रेखा l पर स्थित नहीं है, तो P से होकर जाते हुए रेखा l पर लंब खींचने के लिए हम पहले जैसा कागज़ मोड़ने का सरल क्रियाकलाप पुन: कर सकते हैं।
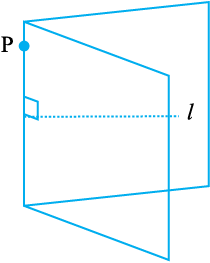
एक कागज़ का पृष्ठ लीजिए (पारदर्शक हो तो अच्छा रहेगा)। उस पर एक रेखा l खींचिए और कोई बिंदु P अंकित कीजिए जो l पर स्थित न हो। कागज़ को इस प्रकार मोड़िए कि मोड़ का निशान P से होकर जाए तथा रेखा l का एक भाग उसके दूसरे भाग पर पड़े। कागज़ को खोल लीजिए। मोड़ का निशान l पर लंब है और P से होकर जाता है।
रूलर और सेट स्क्वेयर की विधि (एक एेच्छिक क्रियाकलाप)

चरण 2 एक सेट स्क्वेयर को l पर इस प्रकार रखिए कि उसके समकोण का एक किनारा l के अनुदिश रहे।
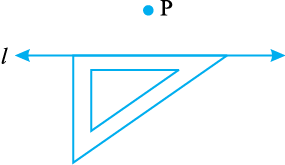
चरण 3 सेट स्क्वेयर के समकोण के सम्मुख किनारे के अनुदिश एक रूलर को रखिए।
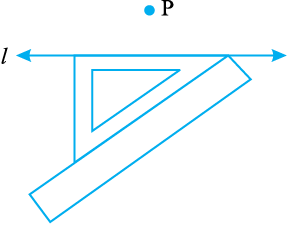
चरण 4 रूलर को कसकर पकड़े रहिए और सेट स्क्वेयर को रूलर के अनुदिश तब तक सरकाइए जब तक कि P समकोण बनाने वाले दूसरे किनारे को स्पर्श न करने लगे।
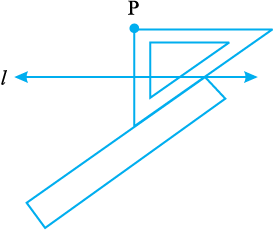
चरण 5 सेट स्क्वेयर के इस किनारे को अनुदिश P से होती हुई रेखा खींचिए जो l को M पर काटती है।
अब रेखा 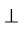
रूलर और परकार की विधि
निस्संदेह, रूलर और परकार प्रयोग करने की विधि ही एक अच्छी विधि है।
चरण 1 रेखा l और एक बिंदु P दिया है जो l पर स्थित नहीं है।

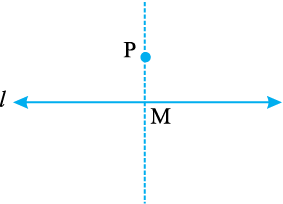
चरण 2 P को केंद्र मान कर और एक सुविधाजनक त्रिज्या लेकर एक चाप लगाइए जो रेखा l को दो बिंदुओं A और B पर प्रतिच्छेद करे।
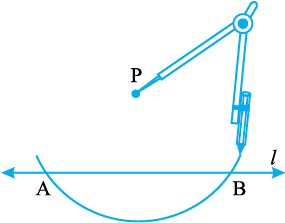
चरण 3 समान त्रिज्या का प्रयोग करके A और B को केंद्र मानकर दो चाप खींचिए जो एक दूसरे को बिंदु P के दूसरी तरफ Q पर प्रतिच्छेद करे।
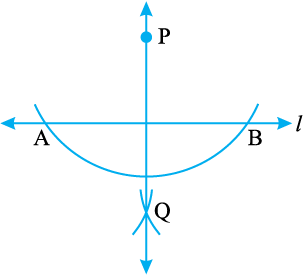
चरण 4 PQ को जोड़िए। तब 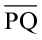 ही रेखा l पर वांछित लंब है।
ही रेखा l पर वांछित लंब है।
प्रश्नावली 14.4
1. एक रेखाखंड  खींचिए। इस पर कोई बिंदु M अंकित कीजिए। M से होकर
खींचिए। इस पर कोई बिंदु M अंकित कीजिए। M से होकर  पर एक लंब, रूलर और परकार द्वारा खींचिए।
पर एक लंब, रूलर और परकार द्वारा खींचिए।
2. एक रेखाखंड 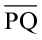 खींचिए। कोई बिंदु R लीजिए जो
खींचिए। कोई बिंदु R लीजिए जो 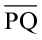 पर न हो। R से होकर
पर न हो। R से होकर 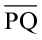 पर एक लंब खींचिए। (रूलर और सेट स्क्वेयर द्वारा)
पर एक लंब खींचिए। (रूलर और सेट स्क्वेयर द्वारा)
3. एक रेखा l खींचिए और उस पर स्थित एक बिंदु X से होकर, रेखा l पर एक लंब रेखाखंड 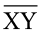 खींचिए।
खींचिए।
अब Y से होकर 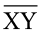 पर एक लंब, रूलर और परकार द्वारा खींचिए।
पर एक लंब, रूलर और परकार द्वारा खींचिए।
14.4.3 एक रेखाखंड का लंब समद्विभाजक
एक कागज़ को मोड़िए। मान लीजिए  मोड़ का निशान है। कहीं पर स्याही से एक बिंदु X अंकित कीजिए।
मोड़ का निशान है। कहीं पर स्याही से एक बिंदु X अंकित कीजिए।  को दर्पण रेखा (mirror line) मानते हुए X का प्रतिबिंब X' ज्ञात कीजिए।
को दर्पण रेखा (mirror line) मानते हुए X का प्रतिबिंब X' ज्ञात कीजिए।

मान लीजिए  और
और 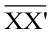 परस्पर O पर प्रतिच्छेद करते हैं। क्या OX = OX'है ? क्यों ?
परस्पर O पर प्रतिच्छेद करते हैं। क्या OX = OX'है ? क्यों ?
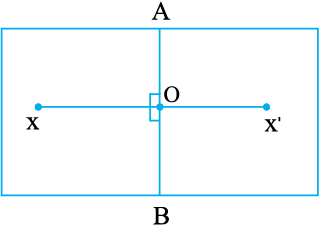
इसका अर्थ है कि  रेखाखंड
रेखाखंड 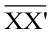 को दो बराबर लंबाइयों के भागों में विभाजित करता है। अर्थात्
को दो बराबर लंबाइयों के भागों में विभाजित करता है। अर्थात्  रेखाखंड
रेखाखंड 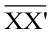 का समद्विभाजक है। यह भी ध्यान दीजिए कि
का समद्विभाजक है। यह भी ध्यान दीजिए कि 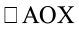 और
और 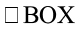 समकोण हैं (क्यों?) अत: रेखा
समकोण हैं (क्यों?) अत: रेखा  रेखाखंड
रेखाखंड 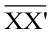 का लंब समद्विभाजक है। आकृति में हम
का लंब समद्विभाजक है। आकृति में हम  का केवल एक हिस्सा ही देखते हैं। दो बिंदुओं को जोड़ने वाले रेखाखंड का लंब समद्विभाजक उनकी सममित अक्ष (line of symmetry) भी है?
का केवल एक हिस्सा ही देखते हैं। दो बिंदुओं को जोड़ने वाले रेखाखंड का लंब समद्विभाजक उनकी सममित अक्ष (line of symmetry) भी है?

(पारदर्शक फीता)
चरण 1 एक रेखाखंड  खींचिए।
खींचिए।

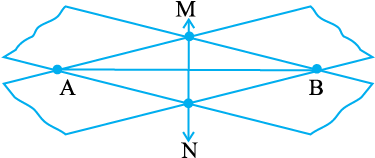
चरण 2 एक आयताकार पारदर्शक फीते की एक पट्टी को  के विकर्णत: इस प्रकार रखें कि इसके किनारे बिंदुओं A और B पर रहें, जैसा कि सामने आकृति में दिखाया गया है।
के विकर्णत: इस प्रकार रखें कि इसके किनारे बिंदुओं A और B पर रहें, जैसा कि सामने आकृति में दिखाया गया है।

चरण 3 इसी प्रक्रिया को एक अन्य पट्टी लेकर इस प्रकार दोहराइए कि दूसरी पट्टी विकर्णत: पहली पट्टी को A और B पर काटे। मान लीजिए ये दोनों पट्टियाँ M और N पर भी काटती हैं।
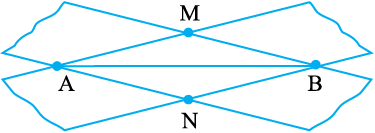
चरण 4 M और N को जोड़िए। क्या 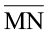 रेखाखंड
रेखाखंड  का समद्विभाजक है? मापकर जाँच कीजिए। क्या यह
का समद्विभाजक है? मापकर जाँच कीजिए। क्या यह  का लंब समद्विभाजक भी है?
का लंब समद्विभाजक भी है?  का मध्य बिंदु कहाँ हैं।
का मध्य बिंदु कहाँ हैं।
रूलर और परकार द्वारा रचना
चरण 1 किसी भी लंबाई का एक रेखाखंड  खींचिए।
खींचिए।

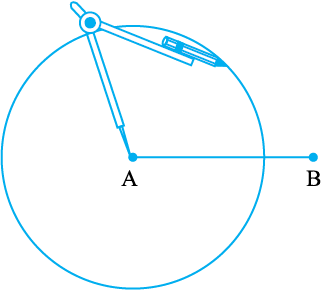
चरण 2 A को केंद्र मानकर, परकार की सहायता से एक वृत्त खींचिए। आपके वृत्त की त्रिज्या  के आधे से अधिक होनी चाहिए।
के आधे से अधिक होनी चाहिए।
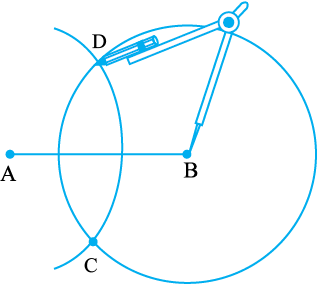
चरण 3 B को केंद्र मानकर और चरण 2 वाली त्रिज्या लेकर एक अन्य वृत्त परकार की सहायता से खींचिए। मान लीजिए वह वृत्त पहले वृत्त को बिंदुओं C और D पर प्रतिच्छेद करता है।
चरण 4 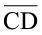 को मिलाइए। यह
को मिलाइए। यह  को O पर प्रतिच्छेद करता है। अपने डिवाइडर का प्रयोग करके जाँच कीजिए कि O रेखाखंड
को O पर प्रतिच्छेद करता है। अपने डिवाइडर का प्रयोग करके जाँच कीजिए कि O रेखाखंड  का मध्य बिंदु है। साथ ही, यह भी जाँच कीजिए कि ∠COA और∠COB समकोण हैं। अत:, रेखाखंड
का मध्य बिंदु है। साथ ही, यह भी जाँच कीजिए कि ∠COA और∠COB समकोण हैं। अत:, रेखाखंड 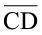 रेखाखंड
रेखाखंड  का लंब समद्विभाजक है।
का लंब समद्विभाजक है।

उपरोक्त रचना में, हमें 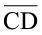 को निर्धारित करने के लिए दो बिंदुओं C और D की आवश्यकता थी। क्या इनको ज्ञात करने के लिए पूरे वृत्तों को खींचने की आवश्यकता है? क्या यह पर्याप्त नहीं है कि इन बिंदुओं को ज्ञात करने के लिए इन वृत्तों के दो छोटे चाप ही खींच लिए जाएँ? वास्तव में, व्यावहारिक रूप में हम यही करते हैं।
को निर्धारित करने के लिए दो बिंदुओं C और D की आवश्यकता थी। क्या इनको ज्ञात करने के लिए पूरे वृत्तों को खींचने की आवश्यकता है? क्या यह पर्याप्त नहीं है कि इन बिंदुओं को ज्ञात करने के लिए इन वृत्तों के दो छोटे चाप ही खींच लिए जाएँ? वास्तव में, व्यावहारिक रूप में हम यही करते हैं।

रूलर और परकार की रचना के चरण 2 में, यदि हम त्रिज्या  के आधे से कम लें, तो क्या होगा?
के आधे से कम लें, तो क्या होगा?
प्रश्नावली 14.5
1. 7.3 सेमी लंबाई का एक रेखाखंड  खींचिए और उसकी सममित अक्ष ज्ञात कीजिए।
खींचिए और उसकी सममित अक्ष ज्ञात कीजिए।
2. 9.5 सेमी लंबा एक रेखाखंड खींचिए और उसका लंब समद्विभाजक खींचिए।
3. एक रेखाखंड 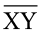 का लंब समद्विभाजक खींचिए जिसकी लंबाई 10.3 सेमी है।
का लंब समद्विभाजक खींचिए जिसकी लंबाई 10.3 सेमी है।
(a) इस लंब समद्विभाजक पर कोई बिंदु P लीजिए। जाँच कीजिए कि PX = PY है।
(b) यदि M रेखाखंड 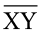 का मध्य बिंदु है, तो MX और XY के विषय में आप क्या कह सकते हैं?
का मध्य बिंदु है, तो MX और XY के विषय में आप क्या कह सकते हैं?
4. लंबाई 12.8 सेमी वाला एक रेखाखंड खींचिए। रूलर और परकार की सहायता से इसके चार बराबर भाग कीजिए। मापन द्वारा अपनी रचना की जाँच कीजिए।
5. 6.1 सेमी लंबाई का एक रेखाखंड 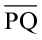 खींचिए और फिर
खींचिए और फिर 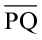 को व्यास मानकर एक वृत्त खींचिए।
को व्यास मानकर एक वृत्त खींचिए।
6. केंद्र C और त्रिज्या 3.4 सेमी लेकर एक वृत्त खींचिए। इसकी कोई जीवा  खींचिए। इस जीवा
खींचिए। इस जीवा  का लंब समद्विभाजक खींचिए। जाँच कीजिए कि क्या यह वृत्त के केंद्र C से होकर जाता है।
का लंब समद्विभाजक खींचिए। जाँच कीजिए कि क्या यह वृत्त के केंद्र C से होकर जाता है।
7. प्रश्न 6 को उस स्थिति के लिए दोबारा कीजिए जब  एक व्यास है।
एक व्यास है।
8. 4 सेमी त्रिज्या का एक वृत्त खींचिए। इसकी कोई दो जीवाएँ खींचिए। इन दोनों जीवाओं के लंब समद्विभाजक खींचिए। ये कहाँ मिलते हैं?
9. शीर्ष O वाला कोई कोण खींचिए। इसकी एक भुजा पर एक बिंदु A और दूसरी भुजा पर एक अन्य बिंदु B इस प्रकार लीजिए कि OA = OB है। 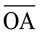 और
और 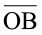 के लंब समद्विभाजक खींचिए। मान लीजिए ये P पर प्रतिच्छेद करते हैं क्या PA = PB है?
के लंब समद्विभाजक खींचिए। मान लीजिए ये P पर प्रतिच्छेद करते हैं क्या PA = PB है?
14.5 कोण
14.5.1 दिए हुए माप का कोण बनाना
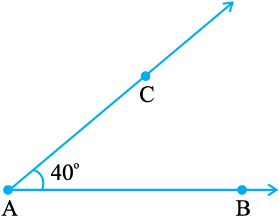
मान लीजिए हम 40º का कोण बनाना चाहते हैं। इसके लिए वांछित चरण निम्न हैं:
चरण 1 एक किरण  खींचिए।
खींचिए।

चरण 2 चाँदे के केंद्र को A पर इस प्रकार रखिए कि इसका शून्य किनारा (0º–0º) किरण  के अनुदिश रहे।
के अनुदिश रहे।

चरण 3 B के पास के शून्य (0) से प्रारंभ करते हुए, 40º के सम्मुख, बिंदु C अंकित कीजिए।

चरण 4 AC मिलाकर किरण AC बनाइए। ∠BAC ही वांछित कोण है।
14.5.2 एक दिए हुए कोण के बराबर कोण बनाना
मान लीजिए हमें एक कोण दिया है जिसका माप हमें ज्ञात नहीं है। हम इस कोण के बराबर एक कोण बनाना चाहते हैं। देखिए कि एेसा किस प्रकार किया जाता है।
∠ A दिया है जिसका माप ज्ञात नहीं है।
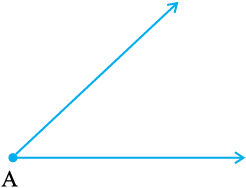
चरण 1 एक रेखा l खींचिए और उस पर एक बिंदु P अंकित कीजिए।

चरण 2 परकार के नुकीले सिरे को A पर रखकर, एक चाप खींचिए जो ∠A की भुजाओं को B और C पर काटता है।
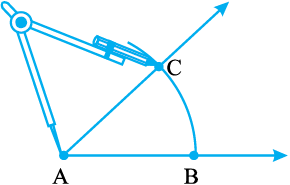
चरण 3 परकार के फैलाव में बिना कोई परिवर्तन किए, उसके नुकीले सिर को P पर रखकर एक चाप लगाइए जो l को Q पर काटता है।
चरण 4 परकार को लंबाई BC के बराबर खोलिए।
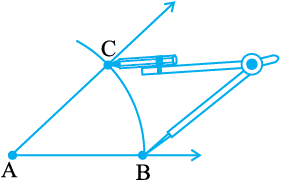
चरण 5 परकार के फैलाव में बिना परिवर्तन किए, उसके नुकीले सिरे को Q पर रखिए और एक चाप लगाइए जो पिछले चाप को R पर काटता है।
चरण 6 PR को मिलाकर किरण PR बनाइए। इससे ∠P प्राप्त होता है। ∠P ही वांछित कोण है जिसका माप ∠A के बराबर है। इसका अर्थ है कि∠QPR और ∠BAC के माप बराबर हैं।
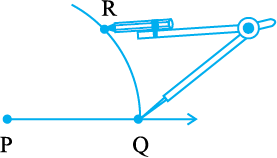
14.5.3 एक कोण का समद्विभाजक

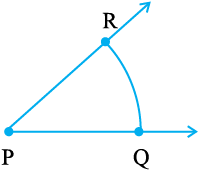
एक कागज़ पर एक बिंदु O अंकित कीजिए। O को प्रारंभिक बिंदु लेकर दो किरणें 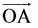
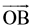
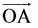
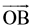
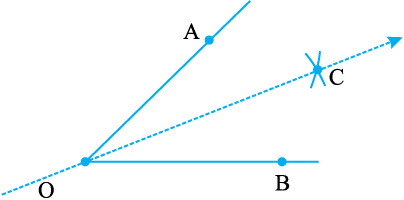
स्पष्टत: किरण OC कोण ∠AOB की सममित अक्ष है।
∠ AOC और ∠COB को मापिए। क्या ये बराबर हैं? अत:, OC कोण ∠AOB की सममित अक्ष है और ∠AOB की समद्विभाजक है।
रूलर और परकार द्वारा रचना
मान लीजिए एक कोण ∠A दिया है।
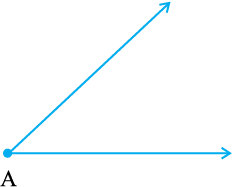
चरण 1 A को केंद्र मानकर परकार की सहायता से एक चाप लगाइए जो ∠A की किरणों (भुजाओं) को B और C पर काटता है।
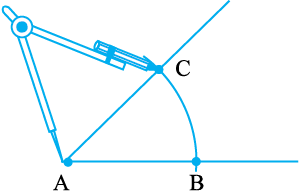
चरण 2 B को केंद्र मानकर और BC के आधे से अधिक की त्रिज्या लेकर एक चाप ∠A के अभ्यंतर में खींचिए।
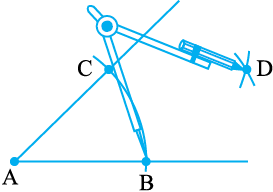
चरण 3 C को केंद्र मानकर एक चरण 2 वाली त्रिज्या लेकर, ∠A के अभ्यंतर में एक और चाप लगाइए। मान लीजिए ये दोनों चाप बिंदु D पर प्रतिच्छेद करते हैं तब 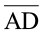 ही ∠A का वांछित समद्विभाजक है।
ही ∠A का वांछित समद्विभाजक है।
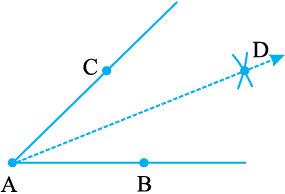

उपरोक्त चरण 2 में, यदि हम त्रिज्या BC के आधे से कम लें, तो क्या कोण होगा?
14.5.4 विशेष मापों के कोण
कुछ विशेष मापों के कोणों की रचना करने की कुछ सुंदर और परिशुद्ध विधियाँ हैं, जिनमें चाँदे का प्रयोग नहीं किया जाता है। इनमें से कुछ की चर्चा हम यहाँ करेंगे।
60º के कोण की रचना
चरण 1 एक रेखा l खींचिए और उस पर एक बिंदु O अंकित कीजिए।

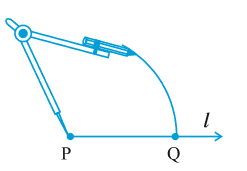
चरण 2 परकार के नुकीले सिरे को O पर रखिए और एक सुविधाजनक त्रिज्या लेकर एक चाप खींचिए, जो रेखा l को, मान लीजिए बिंदु A पर काटता है।
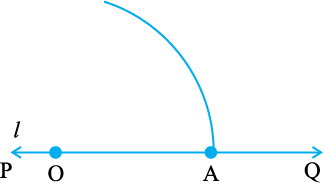
चरण 3 अब A को केंद्र मानकर, O से होकर जाता एक चाप खींचिए।
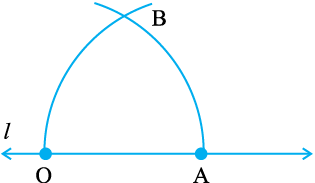
चरण 4 मान लीजिए ये दोनों चाप परस्पर बिंदु B पर काटते हैं। OB को जोड़कर किरण OB बनाइए। तब ∠BOA ही 60º माप का वांछित कोण है।
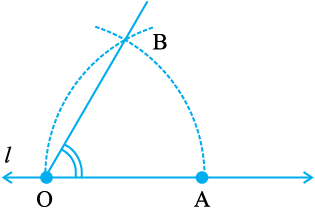
30º माप के कोण की रचना
ऊपर दर्शाए अनुसार 60º के कोण की रचना कीजिए। अब इस कोण को समद्विभाजित कीजिए। प्रत्येक कोण 30º का है। मापन द्वारा अपनी रचना की जाँच कीजिए।

15º के कोण की रचना आप किस प्रकार करेंगे?
120º के कोण की रचना
120º का कोण 60º के कोण के दोगुने के अतिरिक्त कुछ नहीं है। अत:, इसकी रचना निम्न प्रकार की जा सकती है :
चरण 1 एक रेखा l खींचकर उस पर एक बिंदु O अंकित कीजिए।

चरण 2 परकार का नुकीला सिरा O पर रखकर और एक सुविधाजनक त्रिज्या लेकर एक चाप लगाइए जो रेखा l को A पर प्रतिच्छेद करे।

चरण 3 परकार के फैलाव में बिना कोई परिवर्तन किए और A को केंद्र मान कर एक चाप लगाइए जो पिछले चाप को B पर काटता है।

चरण 4 पुन:, परकार के फैलाव में बिना कोई परिवर्तन किए और B को केंद्र मानकर एक चाप लगाइए जो पहले चाप को C पर काटता है।

चरण 5 OC को जोड़कर किरण OC बनाइए। तब, ∠COA ही वह कोण है जिसका माप 120º है।

90º के कोण की रचना
एक रेखा पर उस पर दिए हुए एक बिंदु से होकर एक लंब खींचिए, जो पहले कर चुके हैं। यह वांछित 90º का कोण है।

45º के कोण की रचना आप किस प्रकार करेंगे?
प्रश्नावली 14.6
1. 75º माप वाले कोण ∠POQ की रचना कीजिए और इसकी सममित अक्ष खींचिए।
2. 147º माप वाले एक कोण की रचना कीजिए और उसका समद्विभाजक खींचिए।
3. एक समकोण खींचिए और उसके समद्विभाजक की रचना कीजिए।
4. 153º का एक कोण खींचिए और इसके चार बराबर भाग कीजिए।
5. रूलर और परकार की सहायता से निम्न मापों के कोणों की रचना कीजिए :
(a) 60º (b) 30º (c) 90º (d) 120º (e) 45º (f) 135º
6. 45º का एक कोण खींचिए और उसके समद्विभाजक कीजिए।
7. 135º का एक कोण खींचिए और उसे समद्विभाजित कीजिए।
8. 70o का एक कोण खींचिए। इस कोण के बराबर रूलर और परकार की सहायता से एक कोण बनाइए।
9. 40o का एक कोण खींचिए। इसके संपूरक के बराबर एक कोण बनाइए।
हमने क्या चर्चा की?
इस अध्याय में, ज्यामितीय आकारों को खींचने की विभिन्न विधियाँ बताई गई हैं।
1. आकारों की रचना करने के लिए, हम ज्यामिति बक्स में दिए निम्न यंत्रों का प्रयोग करते हैं:
(i) रूलर (ii) परकार
(iii) डिवाइडर (iv) सेट स्क्वेयर
(v) चाँदा
(i) एक वृत्त जब उसकी त्रिज्या की लंबाई दी हो?
(ii) एक रेखाखंड जब उसकी लंबाई दी हो।
(iii) एक रेखाखंड के बराबर रेखाखंड बनाना।
(iv) एक रेखा पर एक बिंदु से लंब खींचना जब वह बिंदु :
(a) रेखा पर स्थित हो। (b) रेखा पर स्थित न हो।
(v) दी हुई लंबाई के रेखाखंड का लंब समद्विभाजक।
(vi) दिए हुए माप का एक कोण।
(vii) दिए हुए कोण के बराबर कोण बनाना।
(viii) दिए हुए कोण का समद्विभाजक।