Table of Contents
Chapter 5
Lines and Angles
5.1 Introduction
You already know how to identify different lines, line segments and angles in a given shape. Can you identify the different line segments and angles formed in the following figures? (Fig 5.1)
Fig 5.1
Can you also identify whether the angles made are acute or obtuse or right?
Recall that a line segment has two end points. If we extend the two end points in either direction endlessly, we get a line. Thus, we can say that a line has no end points. On the other hand, recall that a ray has one end point (namely its starting point). For example, look at the figures given below:

(i)


Fig 5.2
Here, Fig 5.2 (i) shows a line segment, Fig 5.2 (ii) shows a line and Fig 5.2 (iii) is that of a ray. A line segment PQ is generally denoted by the symbol 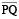 , a line AB is denoted by the symbol
, a line AB is denoted by the symbol 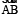 and the ray OP is denoted by
and the ray OP is denoted by 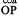 . Give some examples of line segments and rays from your daily life and discuss them with your friends.
. Give some examples of line segments and rays from your daily life and discuss them with your friends.
Again recall that an angle is formed when lines or line segments meet. In Fig 5.1, observe the corners. These corners are formed when two lines or line segments intersect at a point. For example, look at the figures given below:
(i)

(ii)
Fig 5.3
In Fig 5.3 (i) line segments AB and BC intersect at B to form angle ABC, and again line segments BC and AC intersect at C to form angle ACB and so on. Whereas, in
Fig 5.3 (ii) lines PQ and RS intersect at O to form four angles POS, SOQ, QOR and ROP. An angle ABC is represented by the symbol ∠ABC. Thus, in Fig 5.3 (i), the three angles formed are ∠ABC, ∠BCA and ∠BAC, and in Fig 5.3 (ii), the four angles formed are ∠POS, ∠SOQ, ∠QOR and ∠POR. You have already studied how to classify the angles as acute, obtuse or right angle.
Try These
 Listten figures around you and identify the acute, obtuse and right angles found in them.
Listten figures around you and identify the acute, obtuse and right angles found in them.Note: While referring to the measure of an angle ABC, we shall write m∠ABC as simply ∠ABC. The context will make it clear, whether we are referring to the angle or its measure.
5.2 Related Angles
5.2.1 Complementary Angles
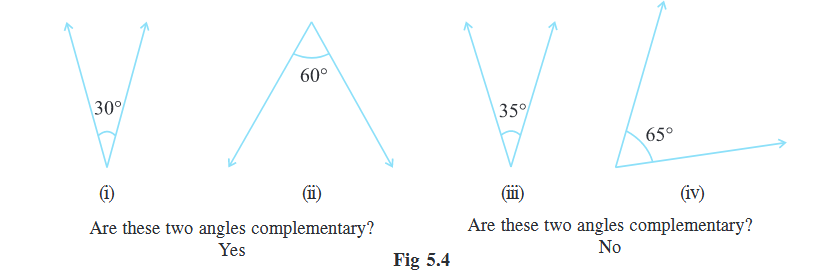
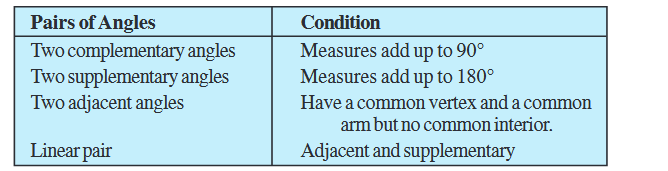
When the sum of the measures of two angles is 90°, the angles are called complementary angles.
Whenever two angles are complementary, each angle is said to be the complement of the other angle. In the above diagram (Fig 5.4), the ‘30° angle’ is the complement of the ‘60° angle’ and vice versa.
Think, Discuss and Write
1. Can two acute angles be complement to each other?

2. Can two obtuse angles be complement to each other?
3. Can two right angles be complement to each other?
Try These
1. Which pairs of following angles are complementary? (Fig 5.5)
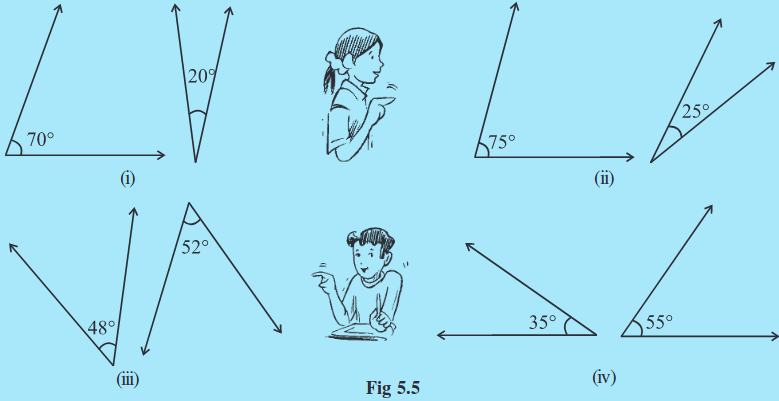
2. What is the measure of the complement of each of the following angles?
(i) 45º (ii) 65º (iii) 41º (iv) 54º
3. The difference in the measures of two complementary angles is 12o. Find the measures of the angles.
5.2.2 Supplementary Angles
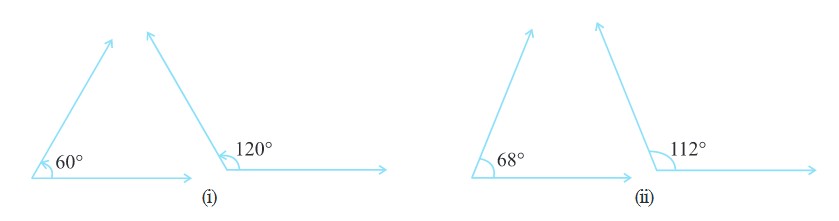
Let us now look at the following pairs of angles (Fig 5.6):
Do you notice that the sum of the measures of the angles in each of the above pairs (Fig 5.6) comes out to be 180º? Such pairs of angles are called supplementary angles. When two angles are supplementary, each angle is said to be the supplement of the other.
Think, Discuss and Write

1. Can two obtuse angles be supplementary?
2. Can two acute angles be supplementary?
3. Can two right angles be supplementary?
Try These
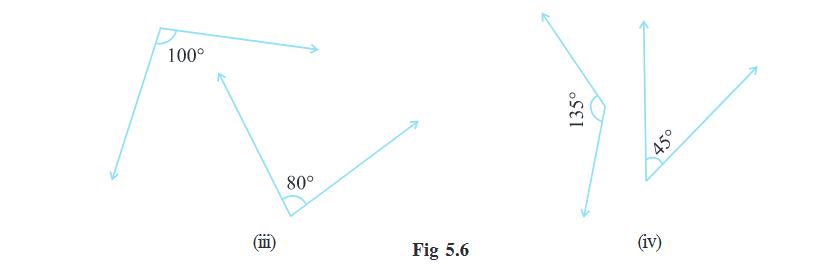
1. Find the pairs of supplementary angles in Fig 5.7:
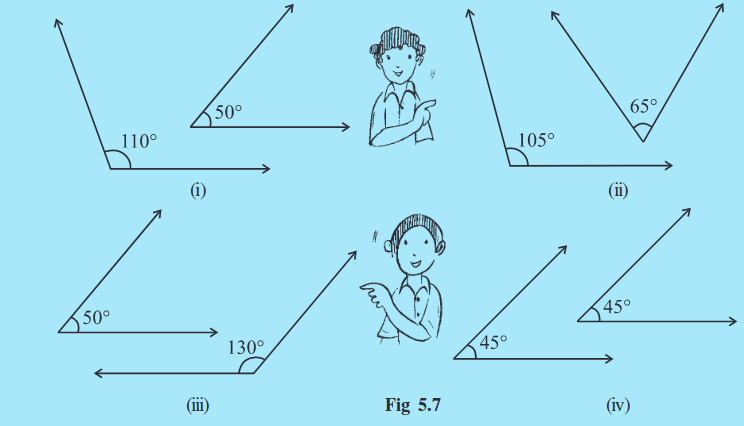
2. What will be the measure of the supplement of each one of the following angles?
(i) 100º (ii) 90º (iii) 55º (iv) 125º
3. Among two supplementary angles the measure of the larger angle is 44o more than the measure of the smaller. Find their measures.
5.2.3. Adjacent Angles
Look at the following figures:
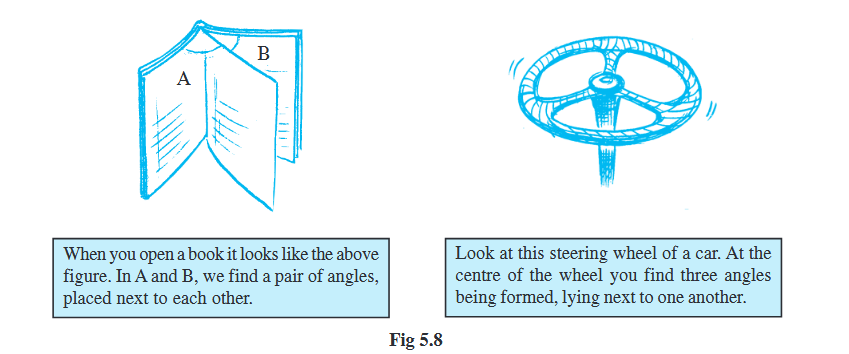
At both the vertices A and B, we find, a pair of angles are placed next to each other.
These angles are such that:
(i) they have a common vertex;
(ii) they have a common arm; and
(iii) the non-common arms are on either side of the common arm.
Such pairs of angles are called adjacent angles. Adjacent angles have a common vertex and a common arm but no common interior points.
Try These
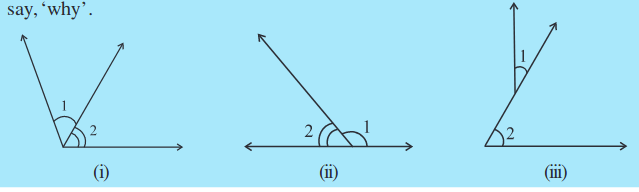

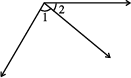
(v)
Fig 5.9
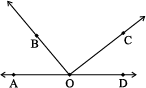
Fig 5.10
2. In the given Fig 5.10, are the following adjacent angles?
(a) ∠AOB and ∠BOC
(b) ∠BOD and ∠BOC
Justify your answer.
Think, Discuss and Write
1. Can two adjacent angles be supplementary?
2. Can two adjacent angles be complementary?
3. Can two obtuse angles be adjacent angles?
4. Can an acute angle be adjacent to an obtuse angle?
5.2.4 Linear Pair
A linear pair is a pair of adjacent angles whose non-common sides are opposite rays.
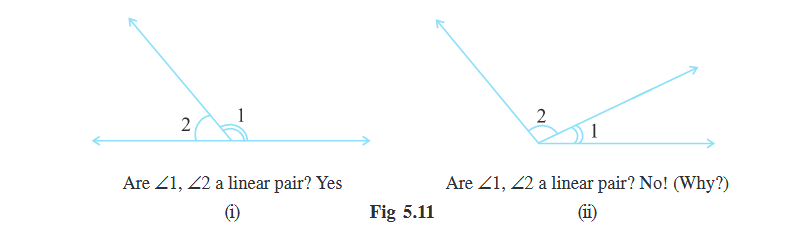
In Fig 5.11 (i) above, observe that the opposite rays (which are the non-common sides of ∠1 and ∠2) form a line. Thus, ∠1 + ∠2 amounts to 180o.
The angles in a linear pair are supplementary.
Have you noticed models of a linear pair in your environment?
Note carefully that a pair of supplementary angles form a linear pair when
placed adjacent to each other. Do you find examples of linear pair in your daily life?
Observe a vegetable chopping board (Fig 5.12).

A pen stand
The pen makes a linear pair of angles with the stand.
Fig 5.12
Think, discuss and write
1. Can two acute angles form a linear pair?
2. Can two obtuse angles form a linear pair?
3. Can two right angles form a linear pair?
Try These
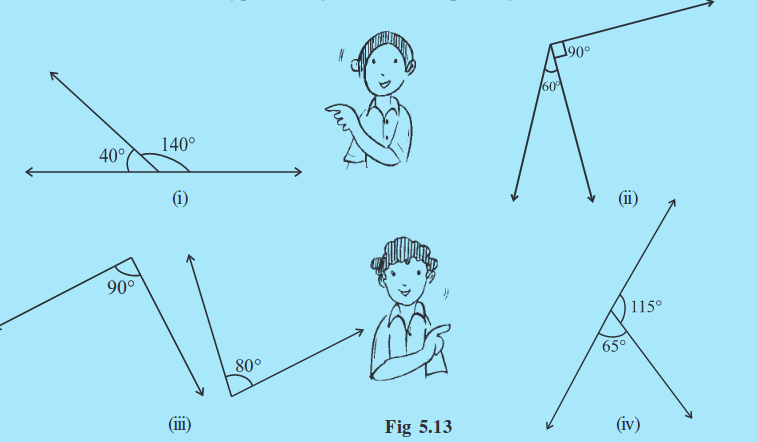
Check which of the following pairs of angles form a linear pair (Fig 5.13):
5.2.5 Vertically Opposite Angles
Next take two pencils and tie them with the help of a rubber band at the middle as shown (Fig 5.14).

Fig 5.14
Look at the four angles formed ∠1, ∠2, ∠3 and ∠4.
∠1 is vertically opposite to ∠3.
and ∠2 is vertically opposite to ∠4.
We call ∠1 and ∠3, a pair of vertically opposite angles.
Can you name the other pair of vertically opposite angles?
Does ∠1 appear to be equal to ∠3? Does ∠2 appear to be equal to ∠4?
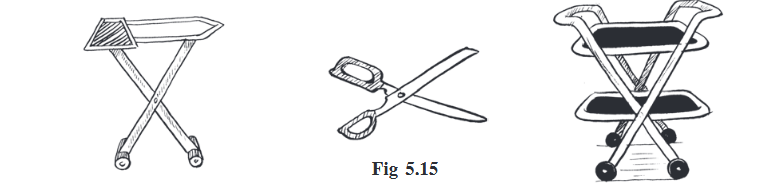
Before checking this, let us see some real life examples for vertically opposite angles (Fig 5.15).
Do This

Draw two lines l and m, intersecting at a point. You can now mark ∠1, ∠2, ∠3 and ∠4 as in the Fig (5.16).
Take a tracecopy of the figure on a transparent sheet.
Place the copy on the original such that ∠1 matches with its copy, ∠2 matches with its copy, ... etc.
Fix a pin at the point of intersection. Rotate the copy by 180o. Do the lines coincide again?
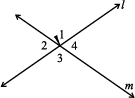 can be rotated to get
can be rotated to get 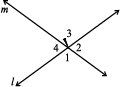
Fig 5.16
You find that ∠1 and ∠3 have interchanged their positions and so have ∠2 and ∠4. This has been done without disturbing the position of the lines.
Thus, ∠1 = ∠3 and ∠2 = ∠4.
We conclude that when two lines intersect, the vertically opposite angles so formed are equal.
Let us try to prove this using Geometrical Idea.
Let us consider two lines l and m. (Fig 5.17)
We can arrive at this result through logical reasoning as follows:
Let l and m be two lines, which intersect at O,
making angles ∠1, ∠2, ∠3 and ∠4.
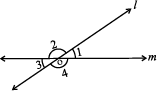
Fig 5.17
We want to prove that ∠1 = ∠3 and ∠2 = ∠4
Now, ∠1 = 180º – ∠2 (Because ∠1, ∠2 form a linear pair, so, ∠1 + ∠2 = 180o) (i)
Similarly, ∠3 = 180º – ∠2 (Since ∠2, ∠3 form a linear pair, so, ∠2 + ∠3 = 180o) (ii)
Therfore, ∠1 = ∠3 [By (i) and (ii)]
Similarly, we can prove that ∠2 = ∠4, (Try it!)
Try These

1. In the given figure, if ∠1 = 30º, find ∠2 and ∠3.
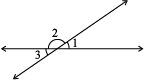
2. Give an example for vertically opposite angles in your surroundings.
Example 1
In Fig (5.18) identify:
(i) Five pairs of adjacent angles. (ii) Three linear pairs.
(iii) Two pairs of vertically opposite angles.
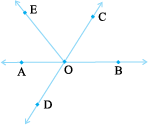
Fig 5.18
Solution
(i) Five pairs of adjacent angles are (∠AOE, ∠EOC), (∠EOC, ∠COB), (∠AOC, ∠COB), (∠COB, ∠BOD), (∠EOB, ∠BOD)
(ii) Linear pairs are (∠AOE, ∠EOB), (∠AOC, ∠COB), (∠COB, ∠BOD)
(iii) Vertically opposite angles are: (∠COB, ∠AOD), and (∠AOC, ∠BOD)
Exercise 5.1
1. Find the complement of each of the following angles:
2. Find the supplement of each of the following angles:
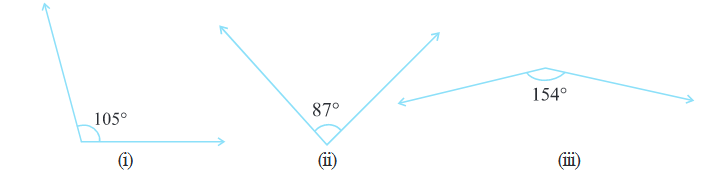
3. Identify which of the following pairs of angles are complementary and which are supplementary.
(i) 65º, 115º (ii) 63º, 27º (iii) 112º, 68º
(iv) 130º, 50º (v) 45º, 45º (vi) 80º, 10º
4. Find the angle which is equal to its complement.
5. Find the angle which is equal to its supplement.
6. In the given figure, ∠1 and ∠2 are supplementary angles.

If ∠1 is decreased, what changes should take place in ∠2 so that both the angles still remain supplementary.
7. Can two angles be supplementary if both of them are:
(i) acute? (ii) obtuse? (iii) right?
8. An angle is greater than 45º. Is its complementary angle greater than 45º or equal to 45º or less than 45º?
9. In the adjoining figure:
(i) Is ∠1 adjacent to ∠2?
(ii) Is ∠AOC adjacent to ∠AOE?
(iii) Do ∠COE and ∠EOD form a linear pair?
(iv) Are ∠BOD and ∠DOA supplementary?
(v) Is ∠1 vertically opposite to ∠4?
(vi) What is the vertically opposite angle of ∠5?
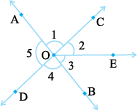
10. Indicate which pairs of angles are:
(i) Vertically opposite angles. (ii) Linear pairs.
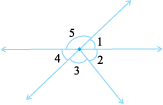
11. In the following figure, is ∠1 adjacent to ∠2? Give reasons.

12. Find the values of the angles x, y, and z in each of the following:
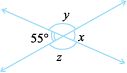
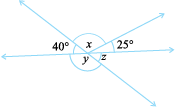
(i) (ii)
13. Fill in the blanks:
(i) If two angles are complementary, then the sum of their measures is _______.
(ii) If two angles are supplementary, then the sum of their measures is ______.
(iii) Two angles forming a linear pair are _______________.
(iv) If two adjacent angles are supplementary, they form a ___________.
(v) If two lines intersect at a point, then the vertically opposite angles are always _____________.
(vi) If two lines intersect at a point, and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are __________.
14. In the adjoining figure, name the following pairs of angles.
(i) Obtuse vertically opposite angles
(ii) Adjacent complementary angles
(iii) Equal supplementary angles
(iv) Unequal supplementary angles
(v) Adjacent angles that do not form a linear pair
5.3 Pairs of Lines
5.3.1 Intersecting Lines
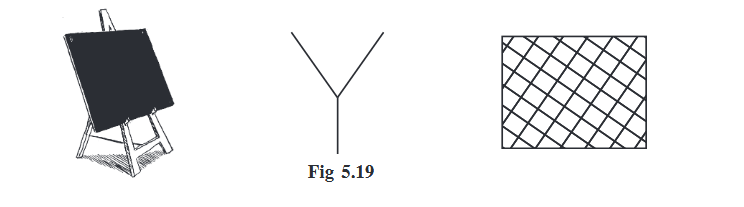
The blackboard on its stand, the letter Y made up of line segments and the grill-door of a window (Fig 5.19), what do all these have in common? They are examples of intersecting lines.
Two lines l and m intersect if they have a point in common. This common point O is their point of intersection.
Think, discuss and write
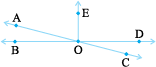
In Fig 5.20, AC and BE intersect at P.

AC and BC intersect at C, AC and EC intersect at C.
Try to find another ten pairs of intersecting line segments.
Should any two lines or line segments necessarily intersect? Can you find two pairs of non-intersecting line segments in the figure?
Can two lines intersect in more than one point? Think about it.
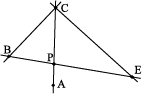
Fig 5.20
Try These

1. Find examples from your surroundings where lines intersect at right angles.
2. Find the measures of the angles made by the intersecting lines at the vertices of an equilateral triangle.
3. Draw any rectangle and find the measures of angles at the four vertices made by the intersecting lines.
4. If two lines intersect, do they always intersect at right angles?
5.3.2 Transversal
You might have seen a road crossing two or more roads or a railway line crossing several other lines (Fig 5.21). These give an idea of a transversal.
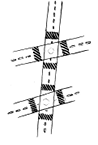
Fig 5.21
A line that intersects two or more lines at distinct points is called a transversal.
In the Fig 5.22, p is a transversal to the lines l and m.
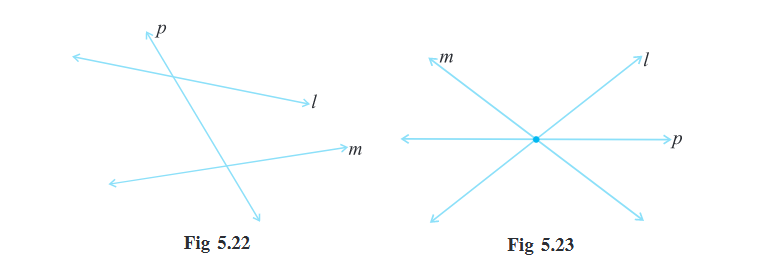
In Fig 5.23 the line p is not a transversal, although it cuts two lines l and m. Can you say, ‘why’?
Try These
1. Suppose two lines are given. How many transversals can you draw for these lines?
2. If a line is a transversal to three lines, how many points of intersections are there?
3. Try to identify a few transversals in your surroundings.
5.3.3. Angles made by a Transversal
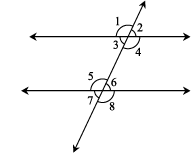
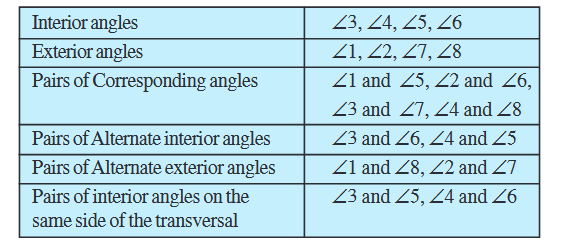
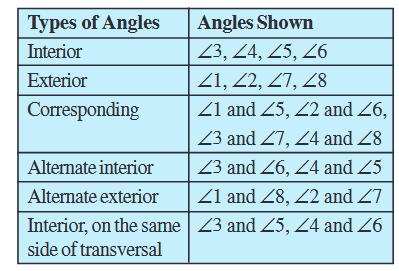
In Fig 5.24, you see lines l and m cut by transversal p. The eight angles marked 1 to 8 have their special names:
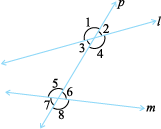
Fig 5.24
Note: Corresponding angles (like ∠1 and ∠5 in Fig 5.25) include
(i) different vertices (ii) are on the same side of the transversal and
(iii) are in ‘corresponding’ positions (above or below, left or right) relative to the two lines.
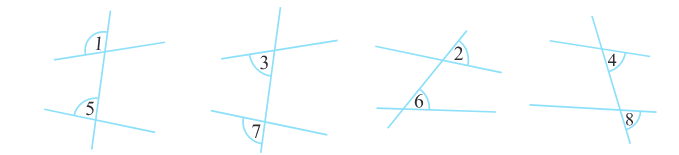
Fig 5.25
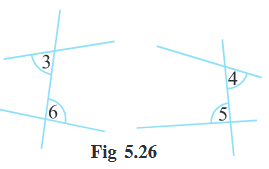
Alternate interior angles (like ∠3 and ∠6 in Fig 5.26)
(i) have different vertices
(ii) are on opposite sides of the transversal and
(iii) lie ‘between’ the two lines.
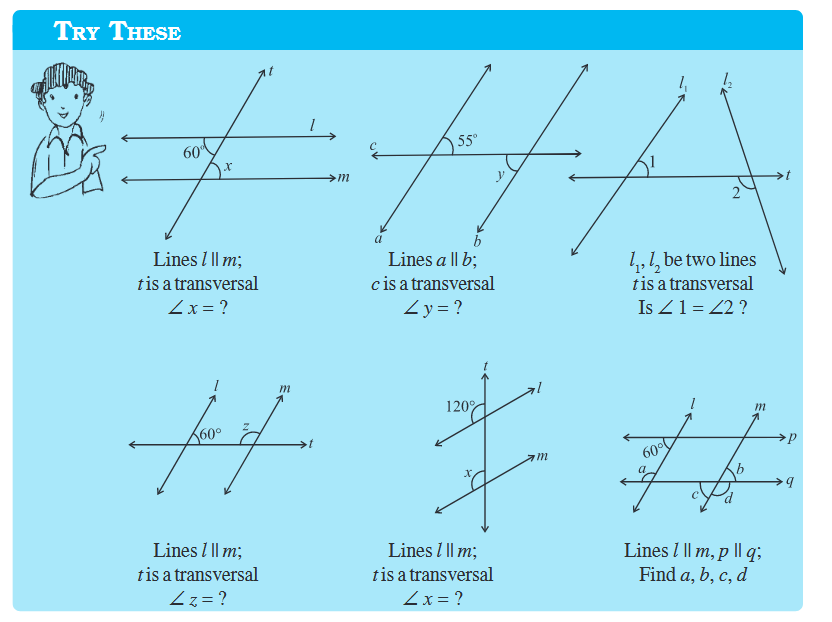
Try These
Name the pairs of angles in each figure:


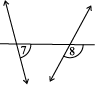
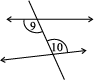
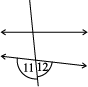
5.3.4 Transversal of Parallel Lines
Do you remember what parallel lines are? They are lines on a plane that do not meet anywhere. Can you identify parallel lines in the following figures? (Fig 5.27)
Transversals of parallel lines give rise to quite interesting results.
Do This
Take a ruled sheet of paper. Draw (in thick colour) two parallel lines l and m.

Draw a transversal t to the lines l and m. Label ∠1 and ∠2 as shown [Fig 5.28(i)].
Place a tracing paper over the figure drawn. Trace the lines l, m and t.
Slide the tracing paper along t, until l coincides with m.
You find that ∠1 on the traced figure coincides with ∠2 of the original figure.
In fact, you can see all the following results by similar tracing and sliding activity.
(i) ∠1 = ∠2 (ii) ∠3 = ∠4 (iii) ∠5 = ∠6 (iv) ∠7 = ∠8
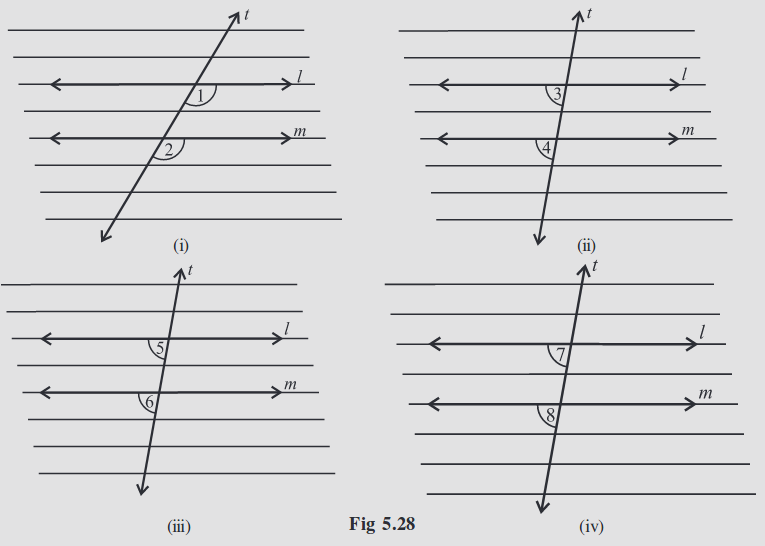
This activity illustrates the following fact:
If two parallel lines are cut by a transversal, each pair of corresponding angles are equal in measure.
We use this result to get another interesting result. Look at Fig 5.29.
When t cuts the parallel lines, l, m, we get, ∠3 = ∠7 (vertically opposite angles).
But ∠7 = ∠8 (corresponding angles). Therefore, ∠3 = ∠8
You can similarly show that ∠1 = ∠6. Thus, we have the following result :
If two parallel lines are cut by a transversal, each pair of alternate interior angles are equal.
This second result leads to another interesting property. Again, from Fig 5.29.
∠3 + ∠1 = 180° (∠3 and ∠1 form a linear pair)
But ∠1 = ∠6 (A pair of alternate interior angles)
Therefore, we can say that ∠3 + ∠6 = 180°.
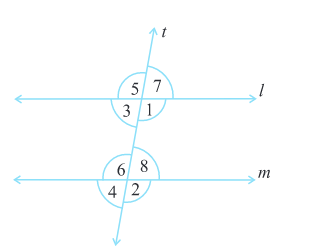
Fig 5.29
Similarly, ∠1 + ∠8 = 180°. Thus, we obtain the following result:
If two parallel lines are cut by a transversal, then each pair of interior angles on the same side of the transversal are supplementary.
You can very easily remember these results if you can look for relevant ‘shapes’.
The F-shape stands for corresponding angles:
Do This
Draw a pair of parallel lines and a transversal. Verify the above three statements by actually measuring the angles.
5.4 Checking for Parallel Lines
If two lines are parallel, then you know that a transversal gives rise to pairs of equal corresponding angles, equal alternate interior angles and interior angles on the same side of the transversal being supplementary.
When two lines are given, is there any method to check if they are parallel or not? You need this skill in many life-oriented situations.
A draftsman uses a carpenter’s square and a straight edge (ruler) to draw these segments (Fig 5.30). He claims they are parallel. How?
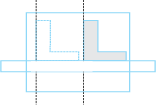
Fig 5.30
Are you able to see that he has kept the corresponding angles to be equal? (What is the transversal here?)
Thus, when a transversal cuts two lines, such that pairs of corresponding angles are equal, then the lines have to be parallel.
Look at the letter Z(Fig 5.31). The horizontal segments here are parallel, because the alternate angles are equal.

Fig 5.31
When a transversal cuts two lines, such that pairs of alternate interior angles are equal, the lines have to be parallel.
Draw a line l (Fig 5.32).
Draw a line m, perpendicular to l. Again draw a line p, such that p is perpendicular to m.
Thus, p is perpendicular to a perpendicular to l.
You find p || l. How? This is because you draw p such that ∠1 + ∠2 = 180o.
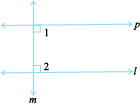
Fig 5.32
Thus, when a transversal cuts two lines, such that pairs of interior angles on the same side of the transversal are supplementary, the lines have to be parallel.
Try These
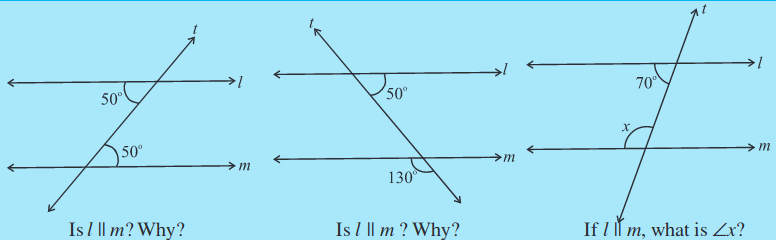
Exercise 5.2
1. State the property that is used in each of the following statements?

(i) If a || b, then ∠1 = ∠5.
(ii) If ∠4 = ∠6, then a || b.
(iii) If ∠4 + ∠5 = 180°, then a || b.
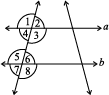
2. In the adjoining figure, identify
(i) the pairs of corresponding angles.
(ii) the pairs of alternate interior angles.
(iii) the pairs of interior angles on the same side of the transversal.
(iv) the vertically opposite angles.
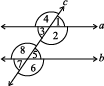
3. In the adjoining figure, p || q. Find the unknown angles.
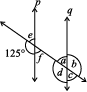
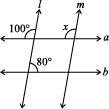
4. Find the value of x in each of the following figures if l || m.
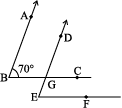
5. In the given figure, the arms of two angles are parallel.
If ∠ABC = 70º, then find
(i) ∠DGC
(ii) ∠DEF
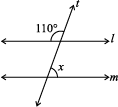
6. In the given figures below, decide whether l is parallel to m.

What have We Discussed?
1. We recall that
(i) A line-segment has two end points.
(ii) A ray has only one end point (its initial point); and
(iii) A line has no end points on either side.
2. An angle is formed when two lines (or rays or line-segments) meet.
3. When two lines l and m meet, we say they intersect; the meeting point is called the point of intersection.
When lines drawn on a sheet of paper do not meet, however far produced, we call them to be parallel lines.
4. (i) When two lines intersect (looking like the letter X) we have two pairs of opposite angles. They are called vertically opposite angles. They are equal in measure.
(ii) A transversal is a line that intersects two or more lines at distinct points.
(iii) A transversal gives rise to several types of angles.
(iv) In the figure, we have
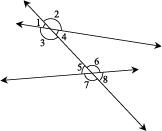
(v) When a transversal cuts two parallel lines, we have the following interesting relationships:
Each pair of corresponding angles are equal.
∠1 = ∠5, ∠3 = ∠7, ∠2 = ∠6, ∠4 = ∠8
Each pair of alternate interior angles are equal.
∠3 = ∠6, ∠4 = ∠5
Each pair of interior angles on the same side of transversal are supplementary.
∠3 + ∠5 = 180°, ∠4 + ∠6 = 180°