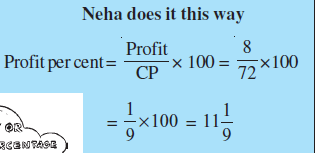Table of Contents

Chapter 8
Comparing Quantities
8.1 Introduction
1. Heena is two times taller than Amir.
Or
2. Amir’s height is 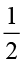 of Heena’s height.
of Heena’s height.
Consider another example, where 20 marbles are divided between Rita and Amit such that Rita has 12 marbles and Amit has 8 marbles. We say,
1. Rita has 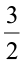 times the marbles that Amit has. Or
times the marbles that Amit has. Or
2. Amit has 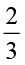 part of what Rita has.
part of what Rita has.
Heena Amir

150 cm 75cm

Yet another example is where we compare speeds of a Cheetah and a man.
The speed of a Cheetah is 6 times the speed of a Man.
Or
The speed of a Man is 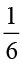 of the speed of the Cheetah.
of the speed of the Cheetah.
Speed of Cheetah 20 km per hour

Do you remember comparisons like this? In Class VI, we have learnt to make comparisons by saying how many times one quantity is of the other. Here, we see that it can also be inverted and written as what part one quantity is of the other.
In the given cases, we write the ratio of the heights as :
Heena’s height : Amir’s height is 150 : 75 or 2 : 1.
Can you now write the ratios for the other comparisons?
These are relative comparisons and could be same for two different situations.
If Heena’s height was 150 cm and Amir’s was 100 cm, then the ratio of their heights would be,
Heena’s height : Amir’s height = 150 : 100 = 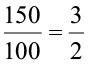 or 3 : 2.
or 3 : 2.
This is same as the ratio for Rita’s to Amit’s share of marbles.
Thus, we see that the ratio for two different comparisons may be the same. Remember that to compare two quantities, the units must be the same.
A ratio has no units.
Example 1 Find the ratio of 3 km to 300 m.
Solution First convert both the distances to the same unit.
So, 3 km = 3 × 1000 m = 3000 m.
Thus, the required ratio, 3 km : 300 m is 3000 : 300 = 10 : 1.
8.2 Equivalent Ratios
Different ratios can also be compared with each other to know whether they are equivalent or not. To do this, we need to write the ratios in the form of fractions and then compare them by converting them to like fractions. If these like fractions are equal, we say the given ratios are equivalent.
Example 2 Are the ratios 1:2 and 2:3 equivalent?
Solution To check this, we need to know whether 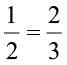 .
.
We have, 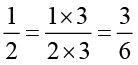 ;
; 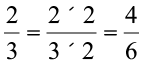
We find that 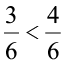 , which means that
, which means that 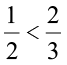 .
.
Therefore, the ratio 1:2 is not equivalent to the ratio 2:3.
Use of such comparisons can be seen by the following example.
Example 3 Following is the performance of a cricket team in the matches it played:
Year Wins Losses
Last year 8 2
This year 4 2
In which year was the record better?
How can you say so?
Solution Last year, Wins: Losses = 8 : 2 = 4 : 1
This year, Wins: Losses = 4 : 2 = 2 : 1
Obviously, 4 : 1 > 2 : 1 (In fractional form, 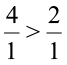 )
)
Hence, we can say that the team performed better last year.
In Class VI, we have also seen the importance of equivalent ratios. The ratios which are equivalent are said to be in proportion. Let us recall the use of proportions.
Keeping things in proportion and getting solutions

Aruna made a sketch of the building she lives in and drew sketch of her mother standing beside the building.
Mona said, “There seems to be something wrong with the drawing”
Can you say what is wrong? How can you say this?
In this case, the ratio of heights in the drawing should be the same as the ratio of actual heights. That is
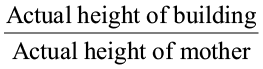 =
=  .
.
Only then would these be in proportion. Often when proportions are maintained, the drawing seems pleasing to the eye.
Another example where proportions are used is in the making of national flags.
Do you know that the flags are always made in a fixed ratio of length to its breadth? These may be different for different countries but are mostly around 1.5 : 1 or 1.7 : 1.
We can take an approximate value of this ratio as 3 : 2. Even the Indian post card is around the same ratio.
Now, can you say whether a card with length 4.5 cm and breadth 3.0 cm is near to this ratio. That is we need to ask, is 4.5 : 3.0 equivalent to 3 : 2?
We note that 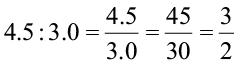
Hence, we see that 4.5 : 3.0 is equivalent to 3 : 2.
We see a wide use of such proportions in real life. Can you think of some more situations?
We have also learnt a method in the earlier classes known as Unitary Method in which we first find the value of one unit and then the value of the required number of units.
Let us see how both the above methods help us to achieve the same thing.
Example 4 A map is given with a scale of 2 cm = 1000 km. What is the actual distance between the two places in kms, if the distance in the map is 2.5 cm?
Solution
Arun has solved it by equating ratios to make proportions and then by solving the equation. Meera has first found the distance that corresponds to 1 cm and then used that to find what 2.5 cm would correspond to. She used the unitary method.
Let us solve some more examples using the unitary method.
Example 5 6 bowls cost 
Solution Cost of 6 bowls is 

Therefore, cost of 1 bowl = 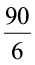
Hence, cost of 10 bowls = 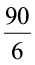 × 10 =
× 10 = 
Example 6 The car that I own can go 150 km with 25 litres of petrol. How far can it go with 30 litres of petrol?
Solution With 25 litres of petrol, the car goes 150 km.
With 1 litre the car will go 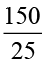 km.
km.
Hence, with 30 litres of petrol it would go 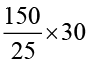 km = 180 km
km = 180 km
In this method, we first found the value for one unit or the unit rate. This is done by the comparison of two different properties. For example, when you compare total cost to number of items, we get cost per item or if you take distance travelled to time taken, we get distance per unit time.
Thus, you can see that we often use per to mean for each.
For example, km per hour, children per teacher etc., denote unit rates.
Think, Discuss and Write

An ant can carry 50 times its weight. If a person can do the same, how much would you be able to carry?
Exercise 8.1

1. Find the ratio of:
(a) ` 5 to 50 paise (b) 15 kg to 210 g
(c) 9 m to 27 cm (d) 30 days to 36 hours
2. In a computer lab, there are 3 computers for every 6 students. How many computers will be needed for 24 students?
3. Population of Rajasthan = 570 lakhs and population of UP = 1660 lakhs.
Area of Rajasthan = 3 lakh km2 and area of UP = 2 lakh km2.
(i) How many people are there per km2 in both these States?
(ii) Which State is less populated?
8.3 Percentage – Another Way of Comparing Quantities
Anita’s Report Rita’s Report
Total 320/400 Total 300/360
Percentage: 80 Percentage: 83.3
Anita said that she has done better as she got 320 marks whereas Rita got only 300. Do you agree with her? Who do you think has done better?
Mansi told them that they cannot decide who has done better by just comparing the total marks obtained because the maximum marks out of which they got the marks are not the same.
She said why don’t you see the Percentages given in your report cards?
Anita’s Percentage was 80 and Rita’s was 83.3. So, this shows Rita has done better.
Do you agree?
Percentages are numerators of fractions with denominator 100 and have been used in comparing results. Let us try to understand in detail about it.
8.3.1 Meaning of Percentage
Per cent is derived from Latin word ‘per centum’ meaning ‘per hundred’.
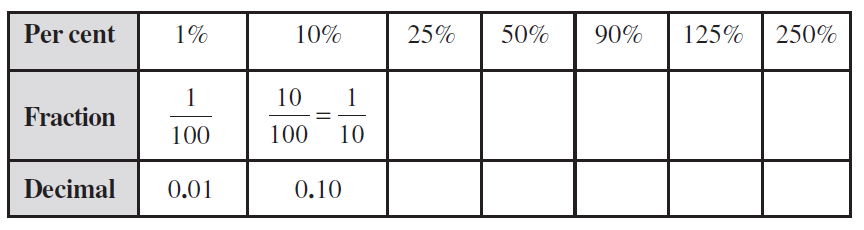
Per cent is represented by the symbol % and means hundredths too. That is 1% means 1 out of hundred or one hundredth. It can be written as: 1% = 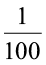 = 0.01
= 0.01
To understand this, let us consider the following example.
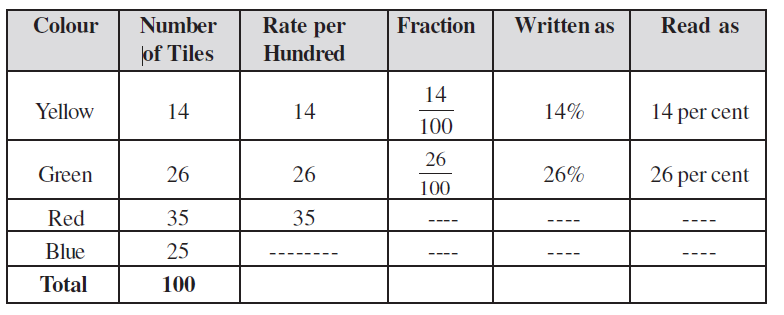
Rina made a table top of 100 different coloured tiles. She counted yellow, green, red and blue tiles separately and filled the table below. Can you help her complete the table?
Try These
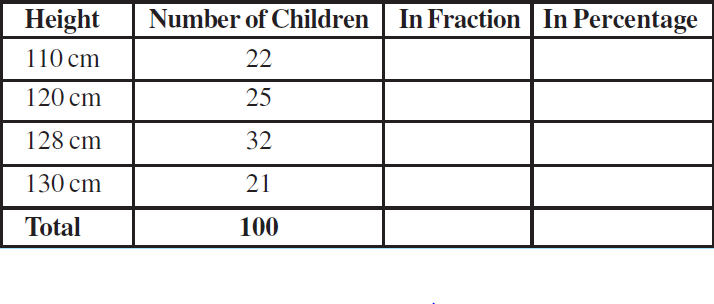
1. Find the Percentage of children of different heights for the following data.
2. A shop has the following number of shoe pairs of different sizes.
Size 2 : 20 Size 3 : 30 Size 4 : 28
Size 5 : 14 Size 6 : 8
Write this information in tabular form as done earlier and find the Percentage of each shoe size available in the shop.
Percentages when total is not hundred
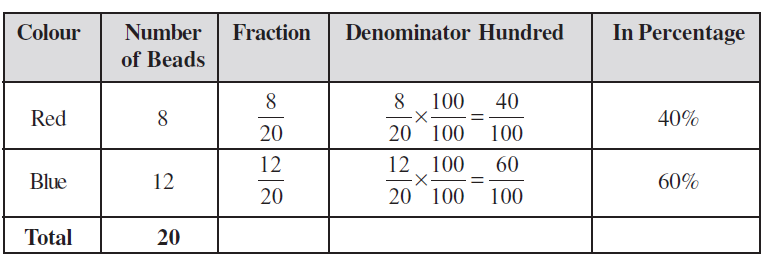
In all these examples, the total number of items add up to 100. For example, Rina had 100 tiles in all, there were 100 children and 100 shoe pairs. How do we calculate Percentage of an item if the total number of items do not add up to 100? In such cases, we need to convert the fraction to an equivalent fraction with denominator 100. Consider the following example. You have a necklace with twenty beads in two colours.
Anwar found the Percentage of red beads like this
Out of 20 beads, the number of red beads is 8.
Hence, out of 100, the number of red beads is
(out of hundred) = 40%
Asha does it like this
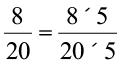
= 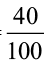 = 40%
= 40%
We see that these three methods can be used to find the Percentage when the total does not add to give 100. In the method shown in the table, we multiply the fraction by 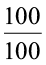 . This does not change the value of the fraction. Subsequently, only 100 remains in the denominator.
. This does not change the value of the fraction. Subsequently, only 100 remains in the denominator.
Anwar has used the unitary method. Asha has multiplied by 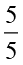 to get 100 in the denominator. You can use whichever method you find suitable. May be, you can make your own method too.
to get 100 in the denominator. You can use whichever method you find suitable. May be, you can make your own method too.
The method used by Anwar can work for all ratios. Can the method used by Asha also work for all ratios? Anwar says Asha’s method can be used only if you can find a natural number which on multiplication with the denominator gives 100. Since denominator was 20, she could multiply it by 5 to get 100. If the denominator was 6, she would not have been able to use this method. Do you agree?
Try These
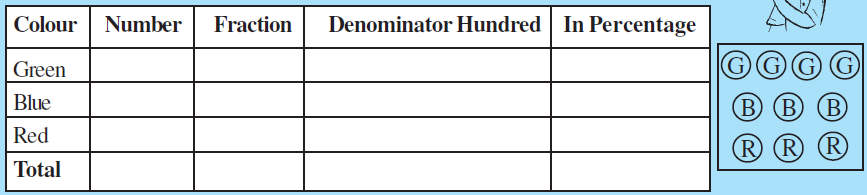
Fill the table and find the percentage of chips of each colour.
2. Mala has a collection of bangles. She has 20 gold bangles and 10 silver bangles. What is the percentage of bangles of each type? Can you put it in the tabular form as done in the above example?
Think, Discuss and Write
1. Look at the examples below and in each of them, discuss which is better for comparison.
In the atmosphere, 1 g of air contains:
.78 g Nitrogen 78% Nitrogen
.21 g Oxygen or 21% Oxygen
.01 g Other gas 1% Other gas
2. A shirt has:
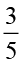 Cotton 60% Cotton
Cotton 60% Cotton
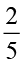 Polyster or 40% Polyster
Polyster or 40% Polyster
8.3.2 Converting Fractional Numbers to Percentage
Fractional numbers can have different denominator. To compare fractional numbers, we need a common denominator and we have seen that it is more convenient to compare if our denominator is 100. That is, we are converting the fractions to Percentages. Let us try converting different fractional numbers to Percentages.
Example 7 Write 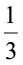 as per cent.
as per cent.
Solution We have, 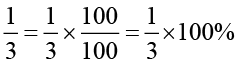
= 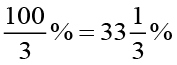
Example 8 Out of 25 children in a class, 15 are girls. What is the percentage of girls?
Solution Out of 25 children, there are 15 girls.
Therefore, percentage of girls = 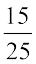 ×100 = 60. There are 60% girls in the class.
×100 = 60. There are 60% girls in the class.
Example 9 Convert 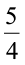 to per cent.
to per cent.
Solution We have, 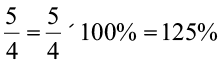
From these examples, we find that the percentages related to proper fractions are less than 100 whereas percentages related to improper fractions are more than 100.
Think, Discuss and Write
Can you eat 150% of a cake?
(ii) Can a price of an item go up by 50%? Can a price of an item go up by 100%?
Can a price of an item go up by 150%?
8.3.3 Converting Decimals to Percentage
We have seen how fractions can be converted to per cents. Let us now find how decimals can be converted to per cents.
Example 10 Convert the given decimals to per cents:
(a) 0.75 (b) 0.09 (c) 0.2
Solution
(a) 0.75 = 0.75 × 100 % (b) 0.09 = 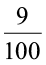 = 9 %
= 9 %
= 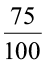 × 100 % = 75%
× 100 % = 75%
(c) 0.2 = 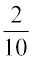 × 100% = 20 %
× 100% = 20 %
1. Convert the following to per cents:
(a) 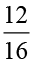 (b) 3.5 (c)
(b) 3.5 (c) 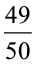 ( d)
( d) 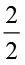 ( e) 0.05
( e) 0.05
2. (i) Out of 32 students, 8 are absent. What per cent of the students are absent?
(ii) There are 25 radios, 16 of them are out of order. What per cent of radios are out of order?
(iii) A shop has 500 items, out of which 5 are defective. What per cent are defective?
(iv) There are 120 voters, 90 of them voted yes. What per cent voted yes?
8.3.4 Converting Percentages to Fractions or Decimals
Make some more such examples and solve them.
We have so far converted fractions and decimals to percentages. We can also do the reverse. That is, given per cents, we can convert them to decimals or fractions. Look at the table, observe and complete it:
Parts always add to give a whole
In the examples for coloured tiles, for the heights of children and for gases in the air, we find that when we add the Percentages we get 100. All the parts that form the whole when added together gives the whole or 100%. So, if we are given one part, we can always find out the other part. Suppose, 30% of a given number of students are boys.
This means that if there were 100 students, 30 out of them would be boys and the remaining would be girls.
Then girls would obviously be (100 – 30)% = 70%.
Try These
1. 35% + _______% = 100%, 64% + 20% +________ % = 100%
45% = 100% – _________ %, 70% = ______% – 30%
2. If 65% of students in a class have a bicycle, what per cent of the student do not have bicycles?
3. We have a basket full of apples, oranges and mangoes. If 50% are apples, 30% are oranges, then what per cent are mangoes?
Think, Discuss and Write
Consider the expenditure made on a dress
20% on embroidery, 50% on cloth, 30% on stitching.
Can you think of more such examples?
8.3.5 Fun with Estimation
Percentages help us to estimate the parts of an area.
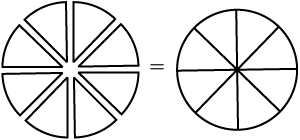
Example 11 What per cent of the adjoining figure is shaded?
Solution We first find the fraction of the figure that is shaded. From this fraction, the percentage of the shaded part can be found.
You will find that half of the figure is shaded. And, 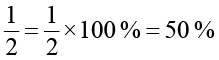
Thus, 50 % of the figure is shaded.

Try These
What per cent of these figures are shaded?
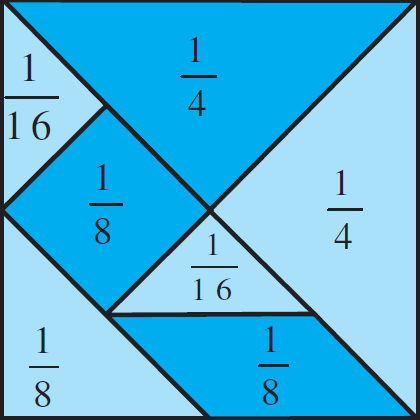
You can make some more figures yourself and ask your friends to estimate the shaded parts.
8.4 Use of Percentages
8.4.1 Interpreting Percentages
We saw how percentages were helpful in comparison. We have also learnt to convert fractional numbers and decimals to percentages. Now, we shall learn how percentages can be used in real life. For this, we start with interpreting the following statements:
— 5% of the income is saved by Ravi. — 20% of Meera’s dresses are blue in colour.
— Rekha gets 10% on every book sold by her.
What can you infer from each of these statements?
By 5% we mean 5 parts out of 100 or we write it as 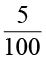 . It means Ravi is saving
. It means Ravi is saving
` 5 out of every ` 100 that he earns. In the same way, interpret the rest of the statements given above.
8.4.2 Converting Percentages to “How Many”
Consider the following examples:
Example 12 A survey of 40 children showed that 25% liked playing football. How many children liked playing football?
Solution Here, the total number of children are 40. Out of these, 25% like playing football. Meena and Arun used the following methods to find the number. You can choose either method.
Arun does it like this
Out of 100, 25 like playing football
So out of 40, number of children who like
playing football = 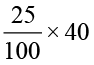 = 10
= 10
Meena does it like this
25% of 40 = 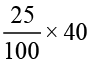
= 10
Hence, 10 children out of 40 like playing football.
Try These
1. Find:
(a) 50% of 164 (b) 75% of 12 (c) 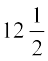 % of 64
% of 64
2. 8% children of a class of 25 like getting wet in the rain. How many children like getting wet in the rain.
Example 13 Rahul bought a sweater and saved 
Solution Rahul has saved 
Mohan’s solution
25% of the original price = 
Let the price (in 
So, 25% of P = 200 or 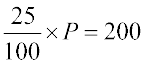
or, 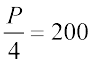 or P = 200 × 4
or P = 200 × 4
Therefore, P = 800
Abdul’s solution


Amount for which 
= 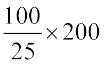 = ` 800
= ` 800
Thus both obtained the original price of sweater as rs800.
Try These
1. 9 is 25% of what number? 2. 75% of what number is 15?
Exercise 8.2
1. Convert the given fractional numbers to per cents.
(a) 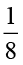 (b)
(b) 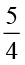 (c)
(c) 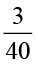 (d)
(d) 
2. Convert the given decimal fractions to per cents.
(a) 0.65 (b) 2.1 (c) 0.02 (d) 12.35
3. Estimate what part of the figures is coloured and hence find the per cent which is coloured.

(i)
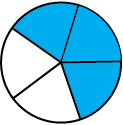
(ii)
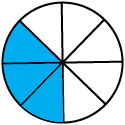
(iii)
4. Find:
(a) 15% of 250 (b) 1% of 1 hour (c) 20% of ` 2500 (d) 75% of 1 kg
5. Find the whole quantity if
(a) 5% of it is 600. (b) 12% of it is ` 1080. (c) 40% of it is 500 km.
(d) 70% of it is 14 minutes. (e) 8% of it is 40 litres.
6. Convert given per cents to decimal fractions and also to fractions in simplest forms:
(a) 25% (b) 150% (c) 20% (d) 5%
7. In a city, 30% are females, 40% are males and remaining are children. What per cent are children?
8. Out of 15,000 voters in a constituency, 60% voted. Find the percentage of voters who did not vote. Can you now find how many actually did not vote?
9. Meeta saves ` 4000 from her salary. If this is 10% of her salary. What is her salary?
10. A local cricket team played 20 matches in one season. It won 25% of them. How many matches did they win?
8.4.3 Ratios to Percents
Sometimes, parts are given to us in the form of ratios and we need to convert those to percentages. Consider the following example:
Example 14 Reena’s mother said, to make idlis, you must take two parts rice and one part urad dal. What percentage of such a mixture would be rice and what percentage would be urad dal?
Solution In terms of ratio we would write this as Rice : Urad dal = 2 : 1.
Now, 2 + 1=3 is the total of all parts. This means 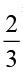 part is rice and
part is rice and 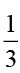 part is urad dal.
part is urad dal.
Then, percentage of rice would be 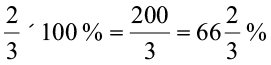 .
.
Percentage of urad dal would be 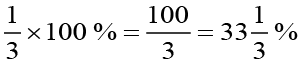 .
.
Example 15 If ` 250 is to be divided amongst Ravi, Raju and Roy, so that Ravi gets two parts, Raju three parts and Roy five parts. How much money will each get? What will it be in percentages?

Solution The parts which the three boys are getting can be written in terms of ratios as 2 : 3 : 5. Total of the parts is 2 + 3 + 5 = 10.
Amounts received by each Percentages of money for each
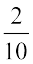 × ` 250 = ` 50 Ravi gets
× ` 250 = ` 50 Ravi gets 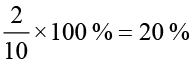
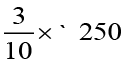 = ` 75 Raju gets
= ` 75 Raju gets 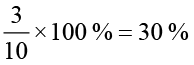
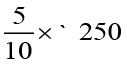 = ` 125 Roy gets
= ` 125 Roy gets 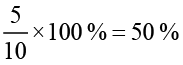
Try These
1. Divide 15 sweets between Manu and Sonu so that they get 20 % and 80 % of them respectively.
2. If angles of a triangle are in the ratio 2 : 3 : 4. Find the value of each angle.
8.4.4 Increase or Decrease as Per cent
There are times when we need to know the increase or decrease in a certain quantity as percentage. For example, if the population of a state increased from 5,50,000 to 6,05,000. Then the increase in population can be understood better if we say, the population increased by 10 %.
How do we convert the increase or decrease in a quantity as a percentage of the initial amount? Consider the following example.
Example 16 A school team won 6 games this year against 4 games won last year. What is the per cent increase?
Solution The increase in the number of wins (or amount of change) = 6 – 4 = 2.
Percentage increase = 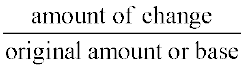 × 100
× 100
= 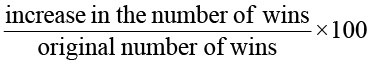 =
=  × 100 = 50
× 100 = 50
Example 17 The number of illiterate persons in a country decreased from 150 lakhs to 100 lakhs in 10 years. What is the percentage of decrease?
Solution Original amount = the number of illiterate persons initially = 150 lakhs.
Amount of change = decrease in the number of illiterate persons = 150 – 100 = 50 lakhs
Therefore, the percentage of decrease
= 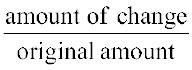 × 100 =
× 100 = 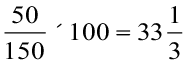
Try Theses
1. Find Percentage of increase or decrease:
– Price of shirt decreased from 

– Marks in a test increased from 20 to 30.
2. My mother says, in her childhood petrol was 

8.5 Prices Related to an Item or Buying and Selling
The buying price of any item is known as its cost price. It is written in short as CP.
The price at which you sell is known as the selling price or in short SP.
What would you say is better, to you sell the item at a lower price, same price or higher price than your buying price? You can decide whether the sale was profitable or not depending on the CP and SP. If CP < SP then you made a profit = SP – CP.
If CP = SP then you are in a no profit no loss situation.
If CP > SP then you have a loss = CP – SP.
Let us try to interpret the statements related to prices of items.



A toy bought for

A T-shirt bought for 

A cycle bought for 

Let us consider the first statement.
The buying price (or CP) is 




Now try interpreting the remaining statements in a similar way.
8.5.1 Profit or Loss as a Percentage
The profit or loss can be converted to a percentage. It is always calculated on the CP.
For the above examples, we can find the profit % or loss %.
Let us consider the example related to the toy. We have CP = 

Profit = 

Thus, the profit is 
profit Per cent is 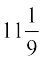 .
.
Similarly you can find the loss per cent in the second situation. Here,
CP = 

Therefore, Loss = 


Try the last case.
Now we see that given any two out of the three quantities related to prices that is, CP, SP, amount of Profit or Loss or their percentage, we can find the rest.
Example 18 The cost of a flower vase is 
Solution We are given that CP = 
Thus, by both methods we get the SP as 
Example 19 Selling price of a toy car is 
Solution We are given that SP =
Thus, by both methods, the cost price is 
Try These
1. A shopkeeper bought a chair for 

2. Cost of an item is 
3. An article was sold for 
4. An item was sold for 
8.6 Charge Given on Borrowed Money or Simple Interest
Sohini said that they were going to buy a new scooter. Mohan asked her whether they had the money to buy it. Sohini said her father was going to take a loan from a bank. The money you borrow is known as sum borrowed or principal.
This money would be used by the borrower for some time before it is returned. For keeping this money for some time the borrower has to pay some extra money to the bank. This is known as Interest.
You can find the amount you have to pay at the end of the year by adding the sum borrowed and the interest. That is, Amount = Principal + Interest.
Interest is generally given in per cent for a period of one year. It is written as say 10% per year or per annum or in short as 10% p.a. (per annum).
10% p.a. means on every 

Example 20
Anita takes a loan of 
Solution
The sum borrowed = 
This means if 


= ` 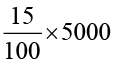 =
= 
So, at the end of the year she has to give an amount of 


We can write a general relation to find interest for one year. Take P as the principal or sum and R % as Rate per cent per annum.
Now on every 

Therefore, on 
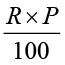 =
= 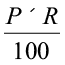 .
.
8.6.1 Interest for Multiple Years
Try These
If the amount is borrowed for more than one year the interest is calculated for the period the money is kept for. For example, if Anita returns the money at the end of two years and the rate of interest is the same then she would have to pay twice the interest i.e., 



We can find the general form for simple interest for more than one year.

We know that on a principal of 
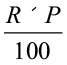 . Therefore, interest I paid for T years would be
. Therefore, interest I paid for T years would be
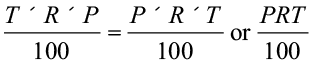
And amount you have to pay at the end of T years is A = P + I
Try These
1. 
2. 
3. 
4. 
Just as in the case of prices related to items, if you are given any two of the three quantities in the relation 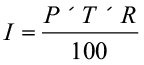 , you could find the remaining quantity.
, you could find the remaining quantity.
Example 21
If Manohar pays an interest of 
` 4,500, find the rate of interest.
Try These
1. You have 

2. On a certain sum the interest paid after 3 years is 
Exercise 8.3
1. Tell what is the profit or loss in the following transactions. Also find profit per cent or loss per cent in each case.
(a) Gardening shears bought for 

(b) A refrigerater bought for 

(c) A cupboard bought for 

(d) A skirt bought for 

2. Convert each part of the ratio to percentage:
(a) 3 : 1 (b) 2 : 3 : 5 (c) 1:4 (d) 1 : 2 : 5
3. The population of a city decreased from 25,000 to 24,500. Find the percentage decrease.
4. Arun bought a car for 

5. I buy a T.V. for ` 10,000 and sell it at a profit of 20%. How much money do I get for it?
6. Juhi sells a washing machine for 
7. (i) Chalk contains calcium, carbon and oxygen in the ratio 10:3:12. Find the percentage of carbon in chalk.
(ii) If in a stick of chalk, carbon is 3g, what is the weight of the chalk stick?
8. Amina buys a book for 
9. Find the amount to be paid at the end of 3 years in each case:
(a) Principal = 

10. What rate gives 

11. If Meena gives an interest of 
What have We Discussed?
1. We are often required to compare two quantities in our daily life. They may be heights, weights, salaries, marks etc.
2. While comparing heights of two persons with heights150 cm and 75 cm, we write it as the ratio 150 : 75 or 2 : 1.
3. Two ratios can be compared by converting them to like fractions. If the two fractions are equal, we say the two given ratios are equivalent.
4. If two ratios are equivalent then the four quantities are said to be in proportion. For example, the ratios 8 : 2 and 16 : 4 are equivalent therefore 8, 2, 16 and 4 are in proportion.
5. A way of comparing quantities is percentage. Percentages are numerators of fractions with denominator 100. Per cent means per hundred.
For example 82% marks means 82 marks out of hundred.
6. Fractions can be converted to percentages and vice-versa.
For example, 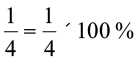 whereas, 75% =
whereas, 75% = 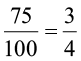
7. Decimals too can be converted to percentages and vice-versa.
For example, 0.25 = 0.25 × 100% = = 25%
8. Percentages are widely used in our daily life,
(a) We have learnt to find exact number when a certain per cent of the total quantity is given.
(b) When parts of a quantity are given to us as ratios, we have seen how to convert them to percentages.
(c) The increase or decrease in a certain quantity can also be expressed as percentage.
(d) The profit or loss incurred in a certain transaction can be expressed in terms of percentages.
(e) While computing interest on an amount borrowed, the rate of interest is given in terms of per cents. For example, ` 800 borrowed for 3 years at 12% per annum.