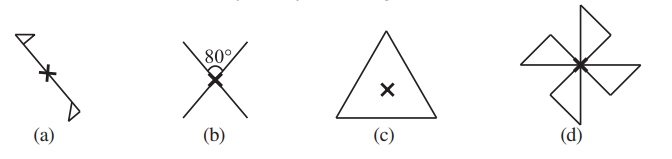Table of Contents

Chapter 14
Symmetry
14.1 Introduction
Symmetry is an important geometrical concept, commonly exhibited in nature and is used almost in every field of activity. Artists, professionals, designers of clothing or jewellery, car manufacturers, architects and many others make use of the idea of symmetry. The beehives, the flowers, the tree-leaves, religious symbols, rugs, and handkerchiefs — everywhere you find symmetrical designs.
You have already had a ‘feel’ of line symmetry in your previous class.
A figure has a line symmetry, if there is a line about which the figure may be folded so that the two parts of the figure will coincide.
You might like to recall these ideas. Here are some activities to help you.
Enjoy identifying lines (also called axes) of symmetry in the designs you collect.
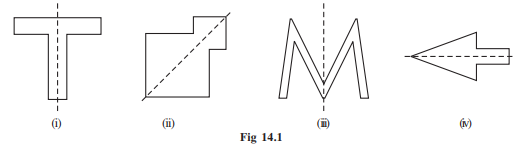
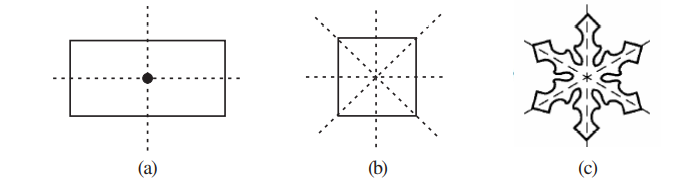
Let us now strengthen our ideas on symmetry further. Study the following figures in which the lines of symmetry are marked with dotted lines. [Fig 14.1 (i) to (iv)]
14.2 Lines of Symmetry for Regular Polygons
You know that a polygon is a closed figure made of several line segments. The polygon made up of the least number of line segments is the triangle. (Can there be a polygon that you can draw with still fewer line segments? Think about it).
A polygon is said to be regular if all its sides are of equal length and all its angles are of equal measure. Thus, an equilateral triangle is a regular polygon of three sides. Can you name the regular polygon of four sides?
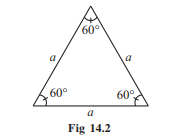
An equilateral triangle is regular because each of its sides has same length and each of its angles measures 60° (Fig 14.2).
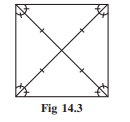
A square is also regular because all its sides are of equal length and each of its angles is a right angle (i.e., 90°). Its diagonals are seen to be perpendicular bisectors of one another (Fig 14.3).
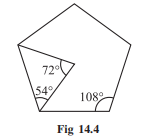
If a pentagon is regular, naturally, its sides should have equal length. You will, later on, learn that the measure of each of its angles is 108° (Fig 14.4).
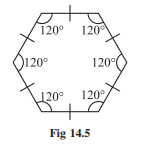
A regular hexagon has all its sides equal and each of its angles measures 120°. You will learn more of these figures later (Fig 14.5).
The regular polygons are symmetrical figures and hence their lines of symmetry are quite interesting,
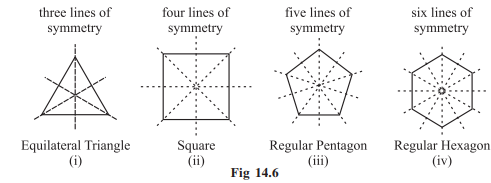
Each regular polygon has as many lines of symmetry as it has sides [Fig 14.6 (i) - (iv)]. We say, they have multiple lines of symmetry.
Perhaps, you might like to investigate this by paper folding. Go ahead!
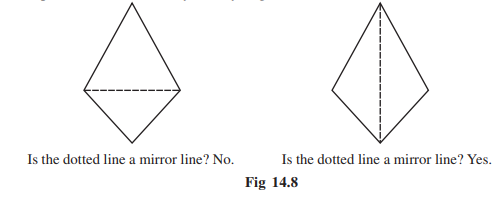
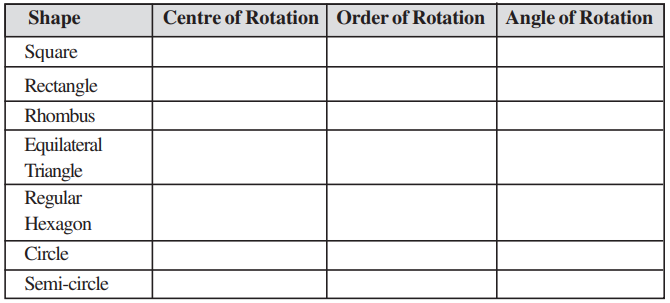
The concept of line symmetry is closely related to mirror reflection. A shape has line symmetry when one half of it is the mirror image of the other half (Fig 14.7). A mirror line, thus, helps to visualise a line of symmetry (Fig 14.8).
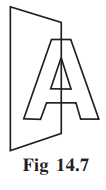
While dealing with mirror reflection, care is needed to note down the left-right changes in the orientation, as seen in the figure here (Fig 14.9).
The shape is same, but the other way round!
Play this punching game!
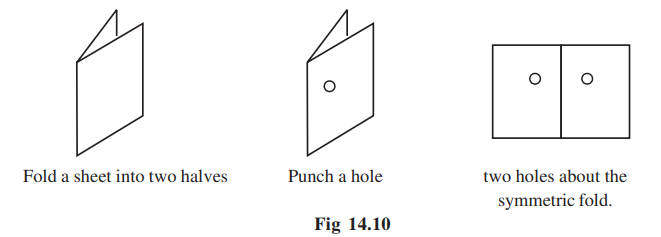
The fold is a line (or axis) of symmetry. Study about punches at different locations on the folded paper and the corresponding lines of symmetry (Fig 14.10).
Exercise 14.1
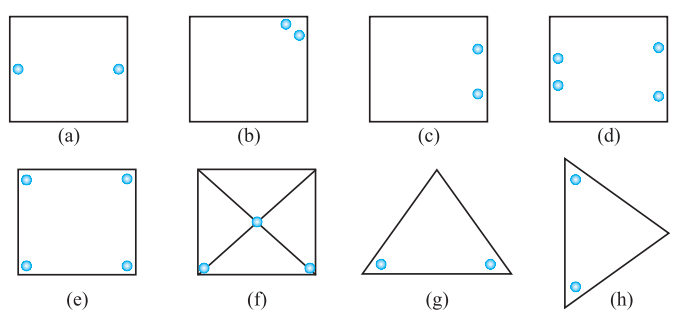
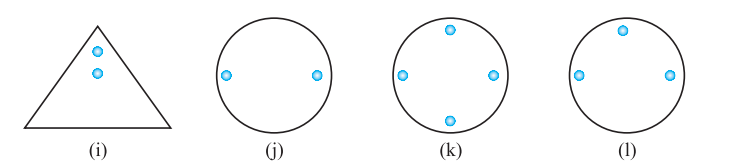
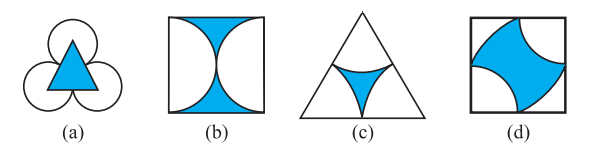
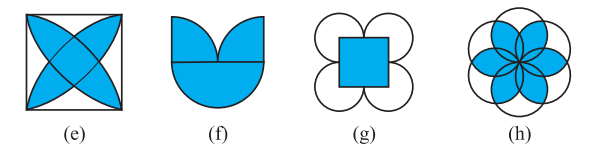
1. Copy the figures with punched holes and find the axes of symmetry for the following:
2. Given the line(s) of symmetry, find the other hole(s):
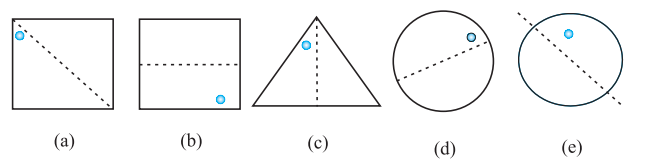
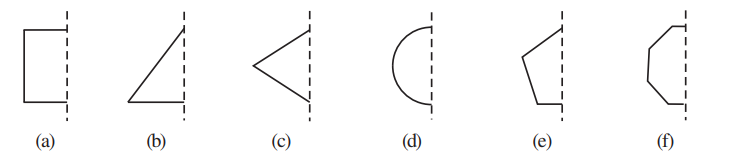
3. In the following figures, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete each figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?
4. The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry.
Identify multiple lines of symmetry, if any, in each of the following figures:
5. Copy the figure given here.

6. Copy the diagram and complete each shape to be symmetric about the mirror line(s):
7. State the number of lines of symmetry for the following figures:
(a) An equilateral triangle (b) An isosceles triangle (c) A scalene triangle
(d) A square (e) A rectangle (f) A rhombus
(g) A parallelogram (h) A quadrilateral (i) A regular hexagon
(j) A circle
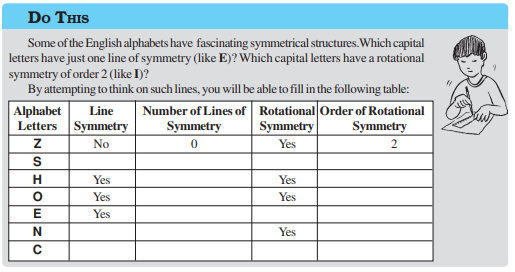
8. What letters of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about.
(a) a vertical mirror (b) a horizontal mirror
(c) both horizontal and vertical mirrors
9. Give three examples of shapes with no line of symmetry.
10. What other name can you give to the line of symmetry of
(a) an isosceles triangle? (b) a circle?
14.3 Rotational Symmetry
What do you say when the hands of a clock go round?
You say that they rotate. The hands of a clock rotate in only one direction, about a fixed point, the centre of the clock-face.
Rotation, like movement of the hands of a clock, is called a clockwise rotation; otherwise it is said to be anticlockwise.
What can you say about the rotation of the blades of a ceiling fan? Do they rotate clockwise or anticlockwise? Or do they rotate both ways?
If you spin the wheel of a bicycle, it rotates. It can rotate in either way: both clockwise and anticlockwise. Give three examples each for (i) a clockwise rotation and (ii) anticlockwise rotation.
When an object rotates, its shape and size do not change. The rotation turns an object about a fixed point. This fixed point is the centre of rotation. What is the centre of rotation of the hands of a clock? Think about it.
The angle of turning during rotation is called the angle of rotation. A full turn, you know, means a rotation of 360°. What is the degree measure of the angle of rotation for (i) a half-turn? (ii) a quarter-turn?
A half-turn means rotation by 180°; a quarter-turn is rotation by 90°.
When it is 12 O’clock, the hands of a clock are together. By 3 O’clock, the minute hand would have made three complete turns; but the hour hand would have made only a quarter-turn. What can you say about their positions at 6 O’clock?
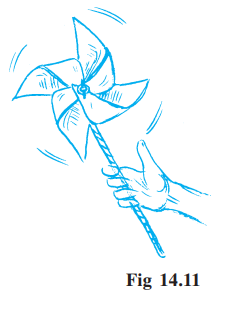
Have you ever made a paper windmill? The Paper windmill in the picture looks symmetrical (Fig 14.11); but you do not find any line of symmetry. No folding can help you to have coincident halves. However if you rotate it by 90° about the fixed point, the windmill will look exactly the same. We say the windmill has a rotational symmetry.
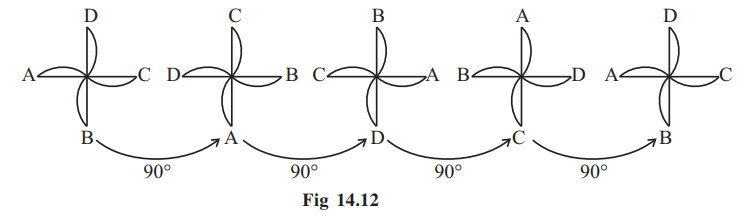
In a full turn, there are precisely four positions (on rotation through the angles 90°, 180°, 270° and 360°) when the windmill looks exactly the same. Because of this, we say it has a rotational symmetry of order 4.
Here is one more example for rotational symmetry.
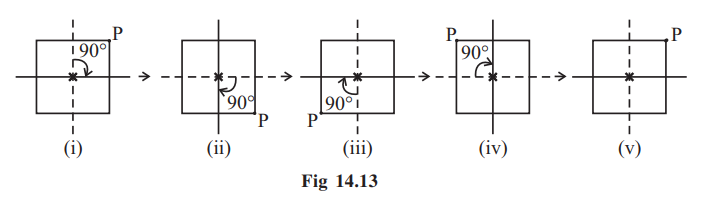
Consider a square with P as one of its corners (Fig 14.13).
Let us perform quarter-turns about the centre of the square marked  .
.
Fig 14.13 (i) is the initial position. Rotation by 90° about the centre leads
to Fig 14.13 (ii). Note the position of P now. Rotate again through 90° and you get
Fig 14.13 (iii). In this way, when you complete four quarter-turns, the square reaches its original position. It now looks the same as Fig14.13 (i). This can be seen with the help of the positions taken by P.
Thus a square has a rotational symmetry of order 4 about its centre. Observe that in this case,
(i) The centre of rotation is the centre of the square.
(ii) The angle of rotation is 90°.
(iii) The direction of rotation is clockwise.
(iv) The order of rotational symmetry is 4.
Do This
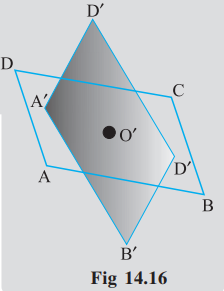
Draw two identical parallelograms, one-ABCD on a piece of paper and the other A’ B’ C’ D’ on a transparent sheet. Mark the points of intersection of their diagonals, O and O’ respectively (Fig 14.16).
Place the parallelograms such that A’ lies on A, B’ lies on B and so on. O’ then falls on O.
Stick a pin into the shapes at the point O.
Now turn the transparent shape in the clockwise direction.
How many times do the shapes coincide in one full round?
What is the order of rotational symmetry?
The point where we have the pin is the centre of rotation. It is the intersecting point of the diagonals in this case.
Every object has a rotational symmetry of order 1, as it occupies same position after a rotation of 360° (i.e., one complete revolution). Such cases have no interest for us.
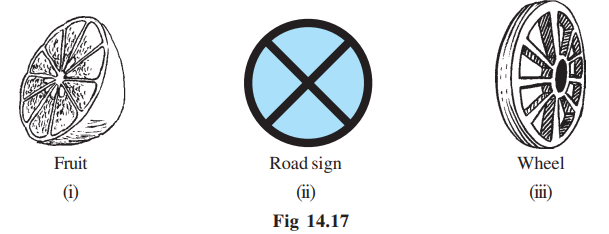
You have around you many shapes, which possess rotational symmetry
(Fig 14.17).
For example, when you slice certain fruits, the cross-sections are shapes with rotational symmetry. This might surprise you when you notice them [Fig 14.17(i)].
Then there are many road signs that exhibit rotational symmetry. Next time when you walk along a busy road, try to identify such road signs and find about the order of rotational symmetry [Fig 14.17(ii)].
Think of some more examples for rotational symmetry. Discuss in each case:
(i) the centre of rotation (ii) the angle of rotation
(iii) the direction in which the rotation is affected and
(iv) the order of the rotational symmetry.
Exercise14.2
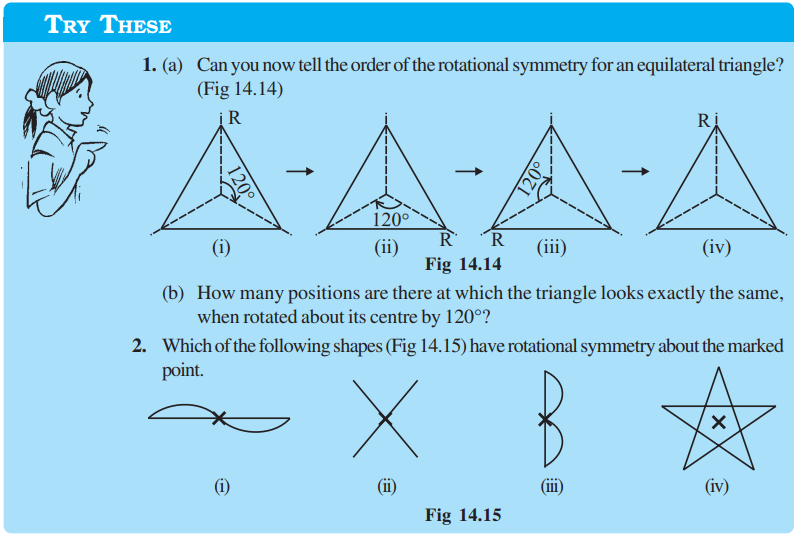
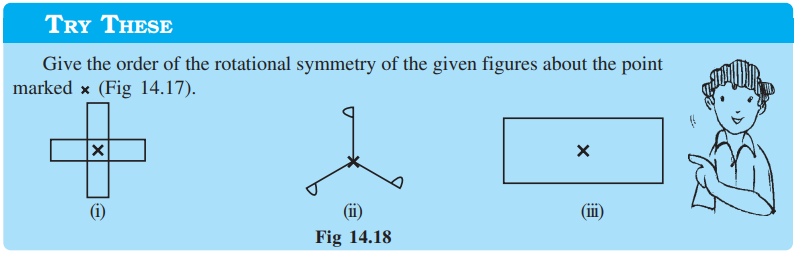
1. Which of the following figures have rotational symmetry of order more than 1:
2. Give the order of rotational symmetry for each figure:
14.4 Line Symmetry and Rotational Symmetry
You have been observing many shapes and their symmetries so far. By now you would have understood that some shapes have only line symmetry, some have only rotational symmetry and some have both line symmetry and rotational symmetry.
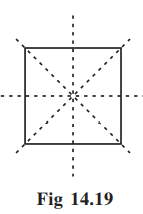
For example, consider the square shape (Fig 14.19).
How many lines of symmetry does it have?
Does it have any rotational symmetry?
If ‘yes’, what is the order of the rotational symmetry?
Think about it.
The circle is the most perfect symmetrical figure, because it can be rotated around its centre through any angle and at the same time it has unlimited number of lines of symmetry. Observe any circle pattern. Every line through the centre (that is every diameter) forms a line of (reflectional) symmetry and it has rotational symmetry around the centre for every angle.
Exercise 14.3
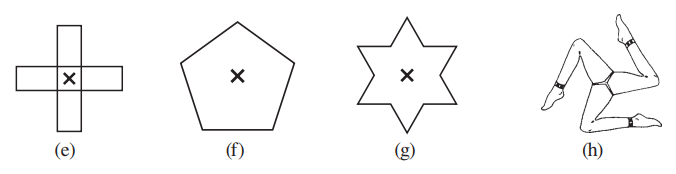
1. Name any two figures that have both line symmetry and rotational symmetry.
2. Draw, wherever possible, a rough sketch of
(i) a triangle with both line and rotational symmetries of order more than 1.
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
(iii) a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
3. If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
4. Fill in the blanks:
5. Name the quadrilaterals which have both line and rotational symmetry of order more than 1.
6. After rotating by 60° about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
7. Can we have a rotational symmetry of order more than 1 whose angle of rotation is
(i) 45°? (ii) 17°?
What have We Discussed?
1. A figure has line symmetry, if there is a line about which the figure may be folded so that the two parts of the figure will coincide.
2. Regular polygons have equal sides and equal angles. They have multiple (i.e., more than one) lines of symmetry.
3. Each regular polygon has as many lines of symmetry as it has sides.
4. Mirror reflection leads to symmetry, under which the left-right orientation have to be taken care of.
5. Rotation turns an object about a fixed point.
This fixed point is the centre of rotation.
The angle by which the object rotates is the angle of rotation.
A half-turn means rotation by 180o; a quarter-turn means rotation by 90o. Rotation may be clockwise or anticlockwise.
6. If, after a rotation, an object looks exactly the same, we say that it has a rotational symmetry.
7. In a complete turn (of 360o), the number of times an object looks exactly the same is called the order of rotational symmetry. The order of symmetry of a square, for example, is 4 while, for an equilateral triangle, it is 3.
8. Some shapes have only one line of symmetry, like the letter E; some have only rotational symmetry, like the letter S; and some have both symmetries like the letter H.
The study of symmetry is important because of its frequent use in day-to-day life and more because of the beautiful designs it can provide us.