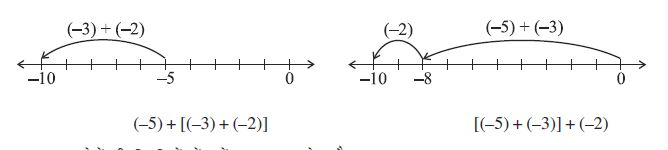Table of Contents
अध्याय 1
पूर्णांक
1.1 भूमिका
हम कक्षा VI में पूर्ण संख्याओं एवं पूर्णांकों के बारे में अध्ययन कर चुके हैं । हम जानते हैं कि पूर्णांक, संख्याओं का एक बड़ा संग्रह होता है, जिसमें पूर्ण संख्याएँ एवं ऋणात्मक संख्याएँ सम्मिलित होती हैं । आपने पूर्णांकों एवं पूर्ण संख्याओ में और क्या अंतर पाया है ? इस अध्याय में, हम पूरणांकों, उनके गुणों एवं संक्रियाओं के बारे में और अधिक अध्ययन करेंगे । सर्वप्रथम हम पिछली कक्षा में पूर्णांको से संबंधित किए गए कार्य की समीक्षा करेंगे एवं उसे दोहराएँगे ।
1.2 पुनरावलोकन
हम जानते हैं कि पूर्णांकों को संख्या रेखा पर कैसे निरूपित किया जाता है । नीचे दी गई संख्या रेखा पर कुछ पूर्णांकों को अंकित किया गया है :


निम्नलिखित संख्या रेखा पर पूर्णांकों के साथ कुछ बिंदु अंकित किए गए हैं । इन पूर्णांकों को अवरोही क्रम में लिखिए ।
प्रयास कीजिये
इन पूर्णांकों का अवरोही क्रम 14, 8, 3, ... है ।
उपर्युक्त संख्या रेखा पर केवल कुछ पूर्णांक लिखे गए हैं । प्रत्येक बिंदु पर उचित संख्या लिखिए ।
1. पूर्णांकों को निरूपित करने वाली एक संख्या रेखा नीचे दी हुई है :
–3 एवं –2 को क्रमशः E और F से अंकित किया गया है । B, D, H, J, M एंव O द्वारा कौन से पूर्णांक अंकित किए जाएँगें ?
2. पूर्णांकों 7, –5, 4, 0 एवं – 4 को आरोही क्रम में क्रमबद्ध कीजिए और अपने उत्तर की जाँच करने के लिए इन्हें एक संख्या रेखा पर अंकित कीजिए ।
हम अपनी पिछली कक्षा में पूर्णांकों के योग एवं व्यवकलन का अध्ययन कर चुके हैं । निम्नलिखित कथनों को पढ़िए :
किसी संख्या रेखा पर जब हम
(i) एक धनात्मक पूर्णांक को जोड़ते हैं, तो दाईं ओर चलते हैं ।
(ii) एक ऋणात्मक पूर्णांक को जोड़ते हैं, तो बाईं ओर चलते हैं ।
(iii) एक धनात्मक पूर्णांक को घटाते हैं, तो बाईं ओर चलते हैं ।
(iv) एक ऋणात्मक पूर्णांक को घटाते हैं, तो दाईं ओर चलते है ।
बताइए कि निम्नलिखित कथन सही हैं अथवा गलत । जो कथन गलत है उनको सही कीजिए।
(i) जब दो धनात्मक पूर्णांकों को जोड़ा जाता है, तो हमें एक धनात्मक पूर्णांक प्राप्त होता है ।
(ii) जब दो ऋणात्मक पूर्णांकों को जोड़ा जाता है, तो हमें एक धनात्मक पूर्णांक प्राप्त होता है ।
(iii) जब एक धनात्मक पूर्णांक और एक ऋणात्मक पूर्णांक को जोड़ा जाता है, तो हमें हमेशा एक ऋणात्मक पूर्णांक प्राप्त होता है ।
(iv) पूर्णांक 8 का योज्य प्रतिलोम (– 8) है एवं पूर्णांक (– 8) का योज्य प्रतिलोम 8 है ।
(v) व्यवकलन के लिए, जिस पूर्णांक को घटाया जाना है उसके योज्य प्रतिलोम को दूसरे पूर्णांक में जोड़ देते हैं ।
(vi) (–10) + 3 = 10 – 3
(vii) 8 + (–7) – (– 4) ≠ 8 + 7 – 4
अपने उत्तरों की तुलना निम्नलिखित उत्तरों के साथ कीजिएः
(i) सही है। उदाहरणतः
(a) 56 + 73 = 129 (b) 113 + 82 = 195 इत्यादि ।
इस कथन के समर्थन में पाँच और उदाहरण दीजिए ।
(ii) गलत, क्योंकि (– 6) + (– 7) = – 13 है, जो कि धनात्मक पूर्णांक नहीं है । सही कथन इस प्रकार है ः
जब दो ऋणात्मक पूर्णांक जोड़े जाते हैं, तो हम एक ऋणात्मक पूर्णांक ही प्राप्त करते हैं । : उदाहरणतः
(a) (– 56) + (– 73) = – 129 (b) (– 113) + (– 82) = – 195, इत्यादि
इस कथन को सत्यापित करने के लिए अपनी तरफ़ से पाँच और उदाहरण दीजिए ।
(iii) गलत, क्योंकि – 9 + 16 = 7, यह एक ऋणात्मक पूर्णांक नहीं है । सही कथन इस प्रकार हैः जब एक धनात्मक पूर्णांक और एक ऋणात्मक पूर्णांक को जोड़ा जाता है, तो हम उनका अंतर लेते हैं और बड़े पूर्णांक का चिह्न उस अंतर के पहले रख दिया जाता है । बड़े पूर्णांक का निर्णय दोनों पूर्णांकों के चिह्नों की अवहेलना करते हुए लिया जाता है । उदाहरणतः
(a) (– 56) + (73) = 17 (b) (– 113) + 82 = – 31
(c) 16 + (– 23) = – 7 (d) 125 + (– 101) = 24
इस कथन का सत्यापन करने के लिए पाँच और उदाहरण बनाइए ।
(iv) सही! योज्य प्रतिलोम के कुछ और उदाहरण निम्नलिखित हैं :
अतः, किसी पूर्णांक a का योज्य प्रतिलोम – a है और (– a) का योज्य प्रतिलोम a है ।
(v) सही! व्यवकलन, योग का विपरीत होता है और इसलिए हम घटाए जाने वाले पूर्णांक के योज्य प्रतिलोम को दूसरे पूर्णांक में जोड़ देते हैं । उदाहरणतः,
(a) 56 – 73 = 56 + 73 का योज्य प्रतिलोम = 56 + (–73) = –17
(b) 56 – (–73) = 56 + (–73) का योज्य प्रतिलोम = 56 + 73 = 129
(c) (–79) – 45 = (–79) + (– 45) = –124
(d) (–100) – (–172) = –100 + 172 = 72 इत्यादि ।
इस कथन का सत्यापन करने के लिए एेसे कम से कम पाँच उदाहरण लिखिए ।
इस प्रकार, हम पाते हैं कि किन्हीं भी दो पूर्णांकों a एवं b के लिए,
a – b = a + b का योज्य प्रतिलोम = a + (– b)
और a – (– b) = a + (– b) का योज्य प्रतिलोम = a + b
(vi) गलत है। क्योंकि (–10) + 3 = –7 और 10 – 3 = 7,
इसलिए (–10) + 3 ≠ 10 – 3 है ।
(vii) गलत । क्योंकि 8 + (–7) – (– 4) = 8 + (–7) + 4 = 1 + 4 = 5
और 8 + 7 – 4 = 15 – 4 = 11 है, इसलिए
8 + (–7) – (– 4) = 8 – 7 + 4 है ।
प्रयास कीजिये
अपनी पिछली कक्षा में हमने संख्याओं के साथ विभिन्न प्रकार के प्रतिरूप (पैटर्न) ज्ञात किए हैं । क्या आप निम्नलिखित में से प्रत्येक के लिए एक पैटर्न ज्ञात कर सकते हैं? यदि हाँ, तो इनको पूरा कीजिए ।
(a) 7, 3, – 1, – 5, _____, _____, _____.
(b) – 2, – 4, – 6, – 8, _____, _____, _____.
(c) 15, 10, 5, 0, _____, _____, _____.
(d) – 11, – 8, – 5, – 2, _____, _____, _____.
एेसे कुछ और पैटर्न बनाइए और उन्हें पूरा करने के लिए अपने मित्रों से कहिए ।
प्रश्नावली 1.1
1. किसी विशिष्ट दिन विभिन्न स्थानों के तापमानों को डिग्री सेल्सियस (°C) में निम्नलिखित संख्या रेखा द्वारा दर्शाया गया है:
(a) इस संख्या रेखा को देखिए और इस पर अंकित स्थानों के तापमान लिखिए ।
(b) उपर्युक्त स्थानों में से सबसे गर्म और सबसे ठंडे स्थानों के तापमानों में क्या अंतर है ?
(c) लाहुलस्पिति एवं श्रीनगर के तापमानों में क्या अंतर है ?
(d) क्या हम कह सकते हैं कि शिमला और श्रीनगर के तापमानों का योग शिमला के तापमान से कम है? क्या इन दोनों स्थानों के तापमानों का योग श्रीनगर के तापमान से भी कम है ?
2. किसी प्रश्नोत्तरी में सही उत्तर के लिए धनात्मक अंक दिए जाते हैं और गलत उत्तर के लिए ऋणात्मक अंक दिए जाते हैं । यदि पाँच उत्तरोतर चक्करों (rounds) में जैक द्वारा प्राप्त किए गए अंक 25, – 5, – 10, 15 और 10 थे, तो बताइए अंत में उसके अंकों का कुल योग कितना था ।
3. सोमवार को श्रीनगर का तापमान – 5°C था और मंगलवार को तापमान 2°C कम हो गया । मंगलवार को श्रीनगर का तापमान क्या था ? बुधवार को तापमान 4°C बढ़ गया । बुधवार को तापमान कितना था ?
4. एक हवाई जहाज़ समुद्र तल से 5000 मीटर की ऊँचाई पर उड़ रहा है। एक विशिष्ट बिंदु पर यह हवाई जहाज़ समुद्र तल से 1200 मीटर नीचे तैरती हुई पनडुब्बी के ठीक ऊपर है । पनडुब्बी और हवाई जहाज़ के बीच की ऊर्ध्वाधर दूरी कितनी है?
5. मोहन अपने बैंक खाते में ₹ 2000 जमा करता है और अगले दिन इसमें से ₹ 1642 निकाल लेता है । यदि खाते में से निकाली गई राशि को ऋणात्मक संख्या से निरूपित किया जाता है, तो खाते में जमा की गई राशि को आप कैसे निरूपित करोगे ? निकासी के पश्चात् मोहन के खाते में शेष राशि ज्ञात कीजिए ।
6. रीता बिंदु A से पूर्व की ओर बिंदु B तक 20 किलोमीटर की दूरी तय करती है । उसी सड़क के अनुदिश बिंदु B से वह 30 किलोमीटर की दूरी पश्चिम की ओर तय करती है । यदि पूर्व की ओर तय की गई दूरी को धनात्मक पूर्णांक से निरूपित किया जाता है, तो पश्चिम की ओर तय की गई दूरी को आप कैसे निरूपित करोगे ? बिंदु A से उसकी अंतिम स्थिति को किस पूर्णांक से निरूपित करोगे ?
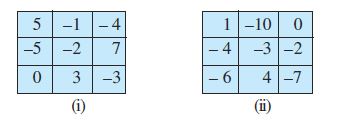
7. किसी मायावी वर्ग में प्रत्येक पंक्ति, प्रत्येक स्तंभ एवं प्रत्येक विकर्ण की संख्याओं का योग समान होता है । बताइए निम्नलिखित में से कौनसा वर्ग एक मायावी वर्ग है ।
8. a और b के निम्नलिखित मानों के लिए a – (– b) = a + b का सत्यापन कीजिए ः
(i) a = 21, b = 18 (ii) a = 118, b = 125
(iii) a = 75, b = 84 (iv) a = 28, b = 11
9. निम्नलिखित कथनों को सत्य बनाने के लिए, बॉक्स में संकेत >, < अथवा = का उपयोग कीजिए ः
(a) (– 8) + (– 4)  (–8) – (– 4)
(–8) – (– 4)
(b) (– 3) + 7 – (19)  15 – 8 + (– 9)
15 – 8 + (– 9)
(c) 23 – 41 + 11  23 – 41 – 11
23 – 41 – 11
(d) 39 + (– 24) – (15)  36 + (– 52) – (– 36)
36 + (– 52) – (– 36)
(e) – 231 + 79 + 51  –399 + 159 + 81
–399 + 159 + 81
10. पानी के एक तालाब में अंदर की ओर सीढ़ियाँ हैं । एक बंदर सबसे ऊपर वाली सीढ़ी (यानी पहली सीढ़ी) पर बैठा हुआ है । पानी नौवीं सीढ़ी पर है ।
(i) वह एक छलाँग में तीन सीढ़ियाँ नीचे की ओर और अगली छलाँग में दो सीढ़ियाँ ऊपर की ओर जाता है । कितनी छलाँगों में वह पानी के स्तर तक पहुँच पाएगा ।
(ii) पानी पीने के पश्चात् वह वापस जाना चाहता है । इस कार्य के लिए वह एक छलाँग में 4 सीढ़ियाँ ऊपर की ओर और अगली छलाँग में 2 सीढ़ियाँ नीचे की ओर जाता है । कितनी छलाँगों मेें वह वापस सबसे ऊपर वाली सीढ़ी पर पहुँच जाएगा ?

(iii) यदि नीचे की ओर पार की गई सीढ़ियों की संख्या को ऋणात्मक पूर्णांक से निरूपित किया जाता है और ऊपर की ओर पार की गई सीढ़ियों की संख्या को धनात्मक पूर्णांक से निरूपित किया जाता है, तो निम्नलिखित को पूरा करते हुए भाग (i) और (ii) में उसकी गति को निरूपित कीजिएः (a) – 3 + 2 + ... = – 8 (b) 4 – 2 + ... = 8.
(a) में योग (– 8) आठ सीढ़ियाँ नीचे जाने को निरूपित करता है, तो (b) में योग 8 किसको निरूपित करेगा ?
1.3 पूर्णांकों के योग एवं व्यवकलन के गुण
1.3.1 योग के अंतर्गत संवृत
हम सीख चुके हैं कि दो पूर्ण संख्याओं का योग पुनः एक पूर्ण संख्या ही होती है । उदाहरणतः 17 + 24 = 41 है, जो कि पुनः एक पूर्ण संख्या है । हम जानते हैं कि यह गुण पूर्ण संख्याओं के योग का संवृत गुण कहलाता है ।
आइए देखें कि क्या यह गुण पूर्णांकों के लिए भी सत्य है अथवा नहीं। पूर्णांकों के कुछ युग्म नीचे दिए जा रहे हैं । नीचे दी हुई सारणी को देखिए और इसे पूरा कीजिए ः
आप क्या देखते हैं ? क्या दो पूर्णांकों का योग हमेशा एक पूर्णांक प्राप्त करता है ?
क्या आपको पूर्णांकों का कोई एेसा युग्म मिला जिसका योग पूर्णांक नहीं है ?
क्योंकि पूर्णांक का योग एक पूर्णांक होता है, इसलिए हम कहते हैं कि पूर्णांक योग के अंतर्गत संवृत (closed) होते हैं ?
व्यापक रूप में, किन्हीं दो पूर्णांकों a तथा b के लिए a + b एक पूर्णांक होता है ।
1.3.2 व्यवकलन के अंतर्गत संवृत
जब हम एक पूर्णांक को दूसरे पूर्णांक में से घटाते हैं, तो क्या होता है ? क्या हम कह सकते हैं कि उनका अंतर भी एक पूर्णांक होता है ?
निम्नलिखित सारणी को देखिए और इसे पूरा कीजिएः
आप क्या देखते हैं? क्या पूर्णांकों का कोई एेसा युग्म है जिसका अंतर पूर्णांक नहीं है ? क्या हम कह सकते हैं कि पूर्णांक व्यवकलन के अंतर्गत संवृत हैं ? हाँ, हम कह सकते हैं कि पूर्णांक व्यवकलन के अंतर्गत संवृत होते हैं ।
अतः, यदि a और b दो पूर्णांक हैं, तो a – b भी एक पूर्णांक होता है । क्या पूर्ण संख्याएँ भी इस गुण को संतुष्ट करती हैं ?
1.3.3 क्रमविनिमेय गुण
हम जानते हैं कि 3 + 5 = 5 + 3 = 8 है, अर्थात् दो पूर्ण संख्याओं को किसी भी क्रम में जोड़ा जा सकता है । दूसरे शब्दों में, पूर्ण संख्याओं के लिए योग क्रमविनिमेय होता है ।
क्या इसी कथन को हम पूर्णांकों के लिए भी कह सकते हैं ?
हम पाते हैं कि 5 + (– 6) = –1 और (– 6) + 5 = –1 है।
इसलिए 5 + (– 6) = (– 6) + 5 है।
क्या निम्नलिखित समान हैं ?
(i) (– 8) + (– 9) और (– 9) + (– 8)
(ii) (– 23) + 32 और 32 + (– 23)
(iii) (– 45) + 0 और 0 + (– 45)
पाँच अन्य पूर्णांकों के युग्मों के लिए एेसा प्रयास कीजिए । क्या आपको पूर्णांकों का कोई एेसा युग्म मिलता है जिसके लिए पूर्णांकों का क्रम बदल देने से उनका योग भी बदल जाता है । निःसन्देह नहीं । योग पूर्णांकों के लिए क्रमविनिमेय होता है ।
व्यापक रूप में, किन्हीं दो पूर्णांकों a और b, के लिए हम कह सकते हैं कि
a + b = b + a
हम जानते हैं कि व्यवकलन पूर्ण संख्याओं के लिए क्रमविनिमेय नहीं है । क्या यह पूर्णांकों के लिए क्रमविनिमेय है ?
पूर्णांक 5 एवं (–3) लीजिए। क्या 5 – (–3) एवं (–3) –5 समान हैं? नहीं, क्योंकि
5 – ( –3) = 5 + 3 = 8 है एवं (–3) – 5 = – 3 – 5 = – 8 है।
पूर्णांकों के कम से कम पाँच विभिन्न युग्म लीजिए और इस कथन की जाँच कीजिए ।
हम यह निष्कर्ष निकालते हैं कि व्यवकलन पूर्णांकों के लिए क्रमविनिमेय नहीं है ।

1.3.4 साहचर्य गुण
निम्नलिखित उदाहरणों को देखिए ः
पूर्णांकों –3, –2 एवं –5 को लीजिए ।
(–5) + [(–3) + (–2)] और [(–5) + (–3)] + (–2) पर ध्यान दीजिए।
प्रथम योग में (–3) और (–2) को मिलाकर एक समूह बनाया गया है और दूसरे योग में (–5) एवं (–3) को मिलाकर एक समूह बनाया गया है । हम इसकी जाँच करेंगे कि क्या हमको विभिन्न परिणाम प्राप्त होते हैं ।
इन दोनों ही स्थितियों में हमें –10 प्राप्त होता है ।
अर्थात्, (–5) + [(–3) + (–2)] = [(–5) + (–2)] + (–3)
इसी प्रकार, –3 , 1 और –7 को लीजिए ।
( –3) + [1 + (–7)] = –3 + __________ = __________
[(–3) + 1] + (–7) = –2 + __________ = __________
क्या (–3) + [1 + (–7)] एवं [(–3) + 1] + (–7) समान हैं ?
इस प्रकार के पाँच और उदाहरण लीजिए । आप एेसा कोई उदाहरण नहीं पाएँगे जिसके लिए इस तरह के योग विभिन्न हैं । यह दर्शाता है कि पूर्णांकों के लिए योग सहचारी (associative) होता है। व्यापक रूप में, पूर्णांकों a, b और c के लिए हम कह सकते हैं कि
a + (b + c) = (a + b) + c
1.3.5 योज्य तत्समक
जब हम किसी पूर्ण संख्या में शून्य को जोड़ते हैं, तो हमें वही पूर्ण संख्या प्राप्त होती है । पूर्ण संख्याओं के लिए शून्य एक योज्य तत्समक (additive identity) है । क्या यह पूर्णांकों के लिए भी एक योज्य तत्समक है ?
निम्नलिखित को देखिए और रिक्त स्थानों की पूर्ति कीजिएः
(i) (– 8) + 0 = – 8 (ii) 0 + (– 8) = – 8
(iii) (–23) + 0 = _____ (iv) 0 + (–37) = –37
(v) 0 + (–59) = _____ (vi) 0 + _____ = – 43
(vii) – 61 + _____ = – 61 (viii) _____ + 0 = _____
उपर्युक्त उदाहरण दर्शाते हैं कि शून्य, पूर्णांकों के लिए भी एक योज्य तत्समक है । आप किन्हीं पाँच अन्य पूर्णांकों में शून्य जोड़कर इसे सत्यापित कर सकते हैं ।
व्यापक रूप में, किसी भी पूर्णांक a के लिए,
a + 0 = a = 0 + a
प्रयास कीजिए
1. एक एेसा पूर्णांक युग्म लिखिए जिसके योग से हमें निम्नलिखित प्राप्त होता है ः
(a) एक ऋणात्मक पूर्णांक (b) शून्य
(c) दोनों पूर्णांकों से छोटा एक पूर्णांक (d) दोनों पूर्णांकों में से केवल किसी
एक से छोटा पूर्णांक
(e) दोनों पूर्णांकों से बड़ा एक पूर्णांक
2. एक एेसा पूर्णांक युग्म लिखिए जिसके अंतर से हमें निम्नलिखित प्राप्त होता है ः
(a) एक ऋणात्मक पूर्णांक (b) शून्य
(c) दोनों पूर्णांकों से छोटा एक पूर्णांक (d) दोनों पूर्णांकों में से केवल किसी
(e) दोनों पूर्णांकों से बड़ा एक पूर्णांक एक से बड़ा पूर्णांक
उदाहरण 1 एेसे पूर्णांक युग्म लिखिए जिनका
(a) योग –3 है (b) अंतर –5 है
(c) अंतर 2 है (d) योग 0 है
हल
क्या आप इन उदाहरणों में और अधिक युग्म लिख सकते हैं ?
प्रश्नावली 1.2
1. एेसा पूर्णांक युग्म लिखिए जिसका
(a) योग –7 है (b) अंतर –10 है (c) योग 0 है
2. (a) एक एेसा ऋणात्मक पूर्णांक युग्म लिखिए जिसका अंतर 8 है ।
(b) एक ऋणात्मक पूर्णांक और एक धनात्मक पूर्णांक लिखिए जिनका योग –5 है ।
(c) एक ऋणात्मक पूर्णांक और एक धनात्मक पूर्णांक लिखिए जिनका अंतर –3 है ।
3. किसी प्रश्नोत्तरी के तीन उत्तरोतर चक्करों (rounds) में टीम A द्वारा प्राप्त किए गए अंक – 40, 10, 0 थे और टीम B द्वारा प्राप्त किए गए अंक 10, 0, – 40 थे । किस टीम ने अधिक अंक प्राप्त किए ? क्या हम कह सकते हैं कि पूर्णांकों को किसी भी क्रम में जोड़ा जा सकता है ?
4. निम्नलिखित कथनों को सत्य बनाने के लिए रिक्त स्थानों की पूर्ति कीजिएः
(i) (–5) + (– 8) = (– 8) + (............)
(ii) –53 + ............ = –53
(iii) 17 + ............ = 0
(iv) [13 + (– 12)] + (............) = 13 + [(–12) + (–7)]
(v) (– 4) + [15 + (–3)] = [– 4 + 15] + ............
1.4 पूर्णांकों का गुणन
हम पूर्णांकों का योग एवं व्यवकलन कर सकते हैं । आईए अब सीखें कि पूर्णांकों को कैसे गुणा किया जाता है।
1.4.1 एक धनात्मक और एक ऋणात्मक पूर्णांक का गुणन
हम जानते हैं कि पूर्ण संख्याओं का गुणन बार-बार योग है ।
उदाहरणतः, 5 + 5 + 5 = 3 × 5 = 15
क्या आप पूर्णांकों के योग को भी इसी प्रकार निरूपित कर सकते हैं ?
निम्नलिखित संख्या रेखा से हम पाते हैं कि (–5) + (–5) + (–5) = –15 है।
परंतु इसे हम निम्नलिखित रूप में भी लिख सकते हैंः
(–5) + (–5) + (–5) = 3 × (–5)
इसलिए, 3 × (–5) = –15
इसी प्रकार, (– 4) + (– 4) + (– 4) + (– 4) + (– 4) = 5 × (– 4) = –20
और (–3) + (–3) + (–3) + (–3) = __________ = __________
साथ ही, (–7) + (–7) + (–7) = __________ = __________
आइए देखें कि संख्या रेखा का उपयोग किए बिना एक धनात्मक पूर्णांक एवं एक ऋणात्मक पूर्णांक का गुणनफल कैसे ज्ञात किया जाए।
आइए एक अन्य प्रकार से 3 × (–5) ज्ञात करें । सर्वप्रथम 3 × 5 ज्ञात कीजिए और प्राप्त गुणनफल से पहले ऋण (–) रखिए । आप –15 प्राप्त करते हैं । अर्थात् –15 प्राप्त करने के लिए हम – (3 × 5) प्राप्त करते हैं ।
इसी प्रकार, 5 × (– 4) = – (5×4) = – 20 है।
इसी प्रकार, निम्नलिखित को ज्ञात कीजिए :
4 × (– 8) = _____ = _____ , 3 × (– 7) = _____ = _____
6 × (– 5) = _____ = _____ , 2 × (– 9) = _____ = _____
इस विधि का उपयोग करते हुए, हम पाते हैं कि
10 × (– 43) = _____ – (10 × 43) = – 430
अभी तक हमने पूर्णांकों को (धनात्मक पूर्णांक) × (ऋणात्मक पूर्णांक) के रूप में गुणा किया है ।
आइए अब इनको (ऋणात्मक पूर्णांक) × (धनात्मक पूर्णांक) के रूप में गुणा करें ।
सर्वप्रथम हम –3 × 5 ज्ञात करते हैं ।
यह ज्ञात करने के लिए निम्नलिखित पैटर्न को देखिएः
हम पाते हैं :
3 × 5 = 15
2 × 5 = 10 = 15 – 5
1 × 5 = 5 = 10 – 5
0 × 5 = 0 = 5 – 5
इसलिए, –1 × 5 = 0 – 5 = –5
–2 × 5 = –5 – 5 = –10
–3 × 5 = –10 – 5 = –15
हम पहले ही प्राप्त कर चुके हैं कि 3 × (–5) = –15
अतः, हम पाते हैं कि (–3) × 5 = –15 = 3 × (–5)
इस प्रकार के पैटर्नों का उपयोग करते हुए, हम (–5) × 4 = –20 = 5 × (– 4) भी प्राप्त करते हैं ।
पैटर्नों का उपयोग करते हुए, (– 4) × 8, (–3) × 7, (– 6) × 5 और (– 2) × 9 ज्ञात कीजिए और जाँच कीजिए कि क्या
(– 4) × 8 = 4 × (– 8), (– 3) × 7 = 3 × (–7), (– 6) × 5 = 6 × (– 5)
और (– 2) × 9 = 2 × (– 9) है?
इसका उपयोग करते हुए, हम (–33) × 5 = 33 × (–5) = –165 प्राप्त करते हैं।
प्रयास कीजिए
1. ज्ञात कीजिएः
(a) 15 × (–16) (b) 21 × (–32)
(c) (– 42) × 12 (d) –55 × 15
2. जाँच कीजिए कि क्या
(a) 25 × (–21) = (–25) × 21 है।
(b) (–23) × 20 = 23 × (–20) है।
इस प्रकार के पाँच और उदाहरण लिखिए ।
व्यापक रूप में, किन्हीं दो धनात्मक पूर्णांकों के लिए, हम कह सकते हैं किः
a × (– b) = (– a) × b = – (a × b)
1.4.2 दो ऋणात्मक पूर्णांकों का गुणन
क्या आप गुणनफल (–3) × (–2) ज्ञात कर सकते हैं ?
निम्नलिखित को देखिए :
–3 × 4 = – 12
–3 × 3 = –9 = –12 – (–3)
–3 × 2 = – 6 = –9 – (–3)
–3 × 1 = –3 = – 6 – (–3)
–3 × 0 = 0 = –3 – (–3)
–3 × (–1) = 0 – (–3) = 0 + 3 = 3
–3 × (–2) = 3 – (–3) = 3 + 3 = 6
क्या आपको कोई पैटर्न दिखाई देता है ? ध्यान दीजिए कि गुणनफल कैसे परिवर्तित हुए हैं ।
इन प्रेक्षणों के आधार पर, निम्नलिखित को पूरा कीजिए :
–3 × –3 = _____, –3 × – 4 = _____
प्रयास कीजिए
(i) (–5) × 4, से शुरू करते हुए, (–5) × (– 6) ज्ञात कीजिए ।
(ii) (– 6) × 3 से शुरू करते हुए, (– 6) × (–7) ज्ञात कीजिए ।
अब इन गुणनफलों को देखिए और रिक्त स्थानों की पूर्ति कीजिएः
– 4 × 4 = –16
– 4 × 3 = –12 = –16 + 4
– 4 × 2 = _____ = –12 + 4
– 4 × 1 = _____
– 4 × 0 = _____
– 4 × (–1) = _____
– 4 × (–2) = _____
– 4 × (–3) = _____
इन पैटर्नों से हम देखते हैं कि
(–3) × (–1) = 3 = 3 × 1
(–3) × (–2) = 6 = 3 × 2
(–3) × (–3) = 9 = 3 × 3
और (– 4) × (–1) = 4 = 4 × 1
इसलिए, (– 4) × (–2) = 4 × 2 = _____
(– 4) × (–3) = _____ = _____
अतः इन गुणनफलों को देखते हुए हम कह सकते हैं कि दो ऋणात्मक पूर्णांकों का गुणनफल एक धनात्मक पूर्णांक होता है। हम दो ऋणात्मक पूर्णांकों को पूर्ण संख्याओं के रूप में गुणा करते हैं और गुणनफल से पहले धनात्मक चिह्न (+) रख देते हैं ।
इस प्रकार, हम पाते हैं कि (–10) × (–12) = +120 = 120 है।
इसी प्रकार, (–15) × (– 6) = +90 = 90 है।
व्यापक रूप में, किन्हीं दो धनात्मक पूर्णांकों a एवं b के लिए,
(– a) × (– b) = a × b
प्रयास कीजिए ज्ञात कीजिए: (–31) × (–100), (–25) × (–72), (–83) × (–28)
खेल 1
(i) एक एेसा बोर्ड लीजिए जिस पर –104 से 104 तक के पूर्णांक अंकित हों, जैसा कि आकृति में दर्शाया गया है ।
(ii) एक थैले में दो नीले पासे और दो लाल पासे लीजिए । नीले पासों पर अंकित बिंदुओं की संख्या धनात्मक पूर्णांकों को दर्शाती हैं और लाल पासों पर अंकित बिंदुओं की संख्या ऋणात्मक पूर्णांकों को दर्शाती हैं ।
(iii) प्रत्येक खिलाड़ी अपने काउंटर को शून्य पर रखेगा ।
(iv) प्रत्येक खिलाड़ी थैले में से एक साथ दो पासे निकालेगा और उनको फेंकेगा ।
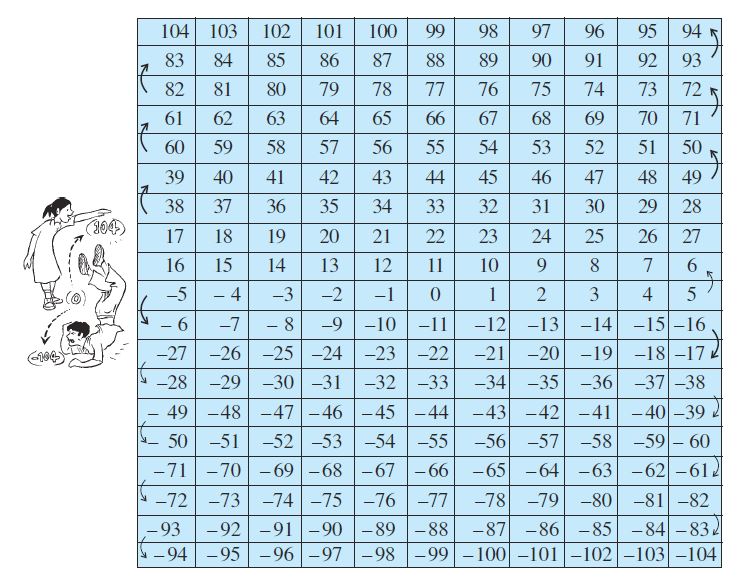
(v) पासों को फेंकने के बाद खिलाड़ी को प्रत्येक बार प्राप्त पासों पर अंकित संख्याओं को गुणा करना है।
(vi) यदि गुणनफल एक धनात्मक पूर्णांक है, तो खिलाड़ी अपने काउंटर को 104 की ओर खिसकाएगा और यदि गुणनफल एक ऋणात्मक पूर्णांक है, तो वह अपने काउंटर को –104 की ओर खिसकाएगा ।
(vii) जो खिलाड़ी पहले –104 या 104 पर पहुँचता है, विजेता कहलाएगा।
1.4.3 तीन अथवा अधिक ऋणात्मक पूर्णांकों का गुणनफल
हमने देखा कि दो ऋणात्मक पूर्णांकों का गुणनफल एक धनात्मक पूर्णांक होता है । तीन ऋणात्मक पूर्णांकों का गुणनफल क्या होगा? चार ऋणात्मक पूर्णांकों का गुणनफल क्या होगा ? आइए निम्नलिखित उदाहरणों को देखते हैं :
(a) (– 4) × (–3) = 12
(b) (– 4) × (–3) × (–2) = [(– 4) × (–3)] × (–2) = 12 × (–2) = – 24
(c) (– 4) × (–3) × (–2) × (–1) = [(– 4) × (–3) × (–2)] × (–1) = (–24) × (–1) = 24
(d) (–5) × [(– 4) × (–3) × (–2) × (–1)] = (–5) × 24 = –120
Euler सबसे पहले गणितज्ञ थे जिन्होंने अपनी पुस्तक Ankitung zur Algebra (1770) में यह सिद्ध करने का प्रयास किया कि
(–1) × (–1) = 1 होता है।
उपर्युक्त उदाहरणों से हम देखते हैं कि
(a) दो ऋणात्मक पूर्णांकों का गुणनफल एक धनात्मक पूर्णांक है ।
(b) तीन ऋणात्मक पूर्णांकों का गुणनफल एक ऋणात्मक पूर्णांक है ।
(c) चार ऋणात्मक पूर्णांकों का गुणनफल एक धनात्मक पूर्णांक है ।
(d) में पाँच ऋणात्मक पूर्णांकों का गुणनफल क्या है ?
6 ऋणात्मक पूर्णांकों का गुणनफल क्या होगा ?
इसके अतिरिक्त हम यह भी देखते हैं कि उपर्युक्त (a) और (c) में गुणा किए गए पूर्णांकों की संख्या सम है (क्रमशः दो और चार) और (a) एवं (c) में प्राप्त गुणनफल धनात्मक पूर्णांक हैं । (b) एवं (d) में गुणा किए गए ऋणात्मक पूर्णांकों की संख्या विषम है । और (b) एवं (d) में प्राप्त गुणनफल ऋणात्मक पूर्णांक हैं ।
एक विशेष स्थिति
निम्नलिखित कथनों एवं परिणामी गुणनफलों पर विचार कीजिए ः
(–1) × (–1) = +1
(–1) × (–1) × (–1) = –1
(–1) × (–1) × (–1) × (–1) = +1
(–1) × (–1) × (–1) × (–1) × (–1) = –1
इसका अर्थ यह हुआ कि यदि पूर्णांक
(–1) को सम संख्या बार गुणा किया जाता है तो गुणनफल +1 है और यदि पूर्णांक (–1) को विषम संख्या बार गुणा किया जाता है तो गुणनफल –1 है । आप ऊपर दिए कथन में (–1) के युग्म बनाकर इसकी जाँच कर सकते हैं । पूर्णांकों का गुणनफल ज्ञात करने में यह बहुत उपयोगी है ।
इस प्रकार, हम पाते हैं कि गुणा किए जाने वाले ऋणात्मक पूर्णांकों की संख्या यदि सम है, तो गुणनफल धनात्मक है और यदि गुणा किए जाने वाले ऋणात्मक पूर्णांकों की संख्या विषम है, तो गुणनफल एक ऋणात्मक पूर्णांक है ।
प्रत्येक प्रकार के पाँच और उदाहरण देकर इस कथन की पुष्टि कीजिए।
सोचिए, चर्चा कीजिए और लिखिए
(i) गुणनफल (–9) × (–5) × (– 6)×(–3) धनात्मक है, जबकि गुणनफल (–9) × ( –5) × 6 × (–3) ऋणात्मक है। क्यों ?
(ii) गुणनफल का चिह्न क्या होगा, यदि हम निम्नलिखित को एक साथ गुणा करते हैं?
(a) आठ ऋणात्मक पूर्णांक एवं तीन धनात्मक पूर्णांक
(b) पाँच ऋणात्मक पूर्णांक और चार धनात्मक पूर्णांक
(c) (–1) को बारह बार
(d) (–1) को 2 m बार, जहाँ m एक प्राकृत संख्या है ।
1.5 पूर्णांको के गुणन के गुण
1.5.1 गुणन के अंतर्गत संवृत
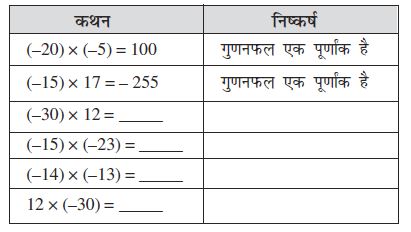
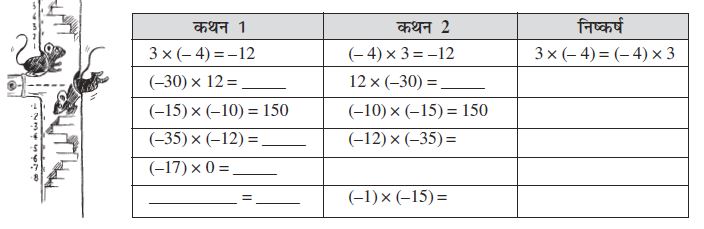
1. निम्नलिखित सारणी को देखिए और इसे पूरा कीजिएः
आप क्या देखते हैं ? क्या आप एक एेसा पूर्णांक युग्म ज्ञात कर सकते हैं जिसका गुणनफल एक पूर्णांक नहीं है ? नहीं, इससे हमें यह ज्ञात होता है कि दो पूर्णांकों का गुणनफल पुनः एक पूर्णांक ही होता है । अतः हम कह सकते हैं कि पूर्णांक गुणन के अंतर्गत संवृत होते हैं ।
व्यापक रूप में,
सभी पूर्णांकों a तथा b के लिए a × b एक पूर्णांक होता है ।
पाँच और पूर्णांक युग्मों के गुणनफल ज्ञात कीजिए और उपर्युक्त कथन को सत्यापित कीजिए ।
1.5.2 गुणन की क्रमविनिमेयता
हम जानते हैं कि पूर्ण संख्याओं के लिए गुणन क्रमविनिमेय होता है । क्या हम कह सकते हैं कि पूर्णांकों के लिए भी गुणन क्रमविनिमेय है ?
निम्नलिखित सारणी को देखिए और इसे पूरा कीजिएः
आप क्या देखते हैं ? उपर्युक्त उदाहरण संकेत करते हैं कि पूर्णांकों के लिए गुणन क्रमविनिमेय है । इस प्रकार के पाँच और उदाहरण लिखिए एवं सत्यापन कीजिए ।
व्यापक रूप में, किन्हीं दो पूर्णांकों a तथा b के लिए,
a × b = b × a
1.5.3 शून्य से गुणन
हम जानते है कि जब किसी पूर्ण संख्या को शून्य से गुणा किया जाता है, तो गुणनफल के रूप में शून्य प्राप्त होता है । ऋणात्मक पूर्णांकों एवं शून्य के निम्नलिखित गुणनफलों को देखिए । पहले किए गए पैटर्नों के आधार पर हम इन्हें प्राप्त करते हैं ।
(–3) × 0 = 0
0 × (– 4) = 0
– 5 × 0 = _____
0 × (– 6) = _____
यह सारणी दर्शाती है कि एक ऋणात्मक पूर्णांक और शून्य का गुणनफल शून्य होता है । व्यापक रूप में, किसी भी पूर्णांक a के लिए,
a × 0 = 0 × a = 0
1.5.4 गुणनात्मक तत्समक
हम जानते है कि पूर्ण संख्याओं के लिए 1 गुणनात्मक तत्समक (multiplicative identity) है ।
जाँच कीजिए कि 1 पूर्णांकों के लिए भी गुणनात्मक तत्समक है । 1 के साथ पूर्णांकों के निम्नलिखित गुणनफलों को देखिए :
(–3) × 1 = –3 1 × 5 = 5
(– 4) × 1 = _____ 1 × 8 = _____
1 × (–5) = _____ 3 × 1 = _____
1 × (– 6) = _____ 7 × 1 = _____
यह दर्शाता है कि 1 पूर्णांकों के लिए भी गुणनात्मक तत्समक है ।
व्यापक रूप में, किसी भी पूर्णांक a के लिए, हम पाते हैं कि
a × 1 = 1 × a = a
यदि किसी भी पूर्णांक को –1से गुणा किया जाए, तो क्या होता है ? निम्नलिखित को पूरा कीजिएः
(–3) × (–1) = 3
3 × (–1) = –3
(– 6) × (–1) = _____
(–1) × 13 = _____
(–1) × (–25) = _____
18 × (–1) = _____
आप क्या देखते हैं ?
क्या हम कह सकते हैं कि –1 पूर्णांकों के लिए गुणनात्मक तत्समक हैे ? नहीं।
पूर्णांकों के लिए शून्य योज्य तत्समक है, जबकि 1 गुणनात्मक तत्समक है । जब किसी पूर्णांक a को (–1) से गुणा किया जाता है, तो हमें उस पूर्णांक का योज्य प्रतिलोम प्राप्त होता है, अर्थात्
a × (–1) = (–1) × a = – a होता है।
1.5.5 गुणन साहचर्य गुण
–3, –2 और 5 को लीजिए ।
[(–3) × (–2)] × 5 और (–3) × [(–2) × 5] पर विचार कीजिए ।
प्रथम स्थिति में, (–3) एवं (–2) को मिलाकर एक समूह बनाया गया है और दूसरी स्थिति में, (–2) एवं 5 को मिलाकर एक समूह बनाया गया है ।
हम पाते हैं कि [(–3) × (–2)] × 5 = 6 × 5 = 30
और (–3) × [(–2) × 5] = (–3) × (–10) = 30
इस प्रकार, दोनों ही स्थितियों में हम एक ही उत्तर प्राप्त करते हैं ।
अतः, [(–3) × (–2)] × 5 = (–3) × [(–2) × 5]
निम्नलिखित पर विचार कीजिए और गुणनफलों को पूरा कीजिएः
[7 × (– 6)] × 4 = __________ × 4 = __________
7 × [(– 6) × 4] = 7 × __________ = __________
क्या [7 × (– 6)] × 4 = 7 × [(– 6) × (4)] है?
क्या पूर्णांकों के विभिन्न प्रकार के समूहों से गुणनफल प्रभावित होता है ?
व्यापक रूप में, किन्हीं तीन पूर्णांकों a, b तथा c के लिए,
(a × b) × c = a × (b × c)
a, b और c मे से प्रत्येक के लिए पाँच मान लीजिए और इस गुण का सत्यापन कीजिए ।
अतः पूर्ण संख्याओं की तरह तीन पूर्णांकों का गुणनफल उनके समूह बनाने पर निर्भर नहीं करता है और यह पूर्णांकों के लिए गुणन का साहचर्य गुण कहलाता है ।
1.5.6 वितरण गुण
हम जानते हैं कि
16 × (10 + 2) = (16 × 10) + (16 × 2) [योग पर गुणन का वितरण नियम]
आइए जाँच करते हैं क्या यह पूर्णांकों के लिए भी सत्य है ? निम्नलिखित को देखिएः
(a) (–2) × (3 + 5) = –2 × 8 = –16
और [(–2) × 3] + [(–2) × 5] = (– 6) + (–10) = –16
अत :, (–2) × (3 + 5) = [(–2) × 3] + [(–2) × 5]
(b) (– 4) × [(–2) + 7] = (– 4) × 5 = –20
और [(– 4) × (–2)] + [(– 4) × 7] = 8 + (–28) = –20
अत ः, (– 4) × [(–2) + 7] = [(– 4) × (–2)] + [(– 4) × 7]
(c) (– 8) × [(–2) + (–1)] = (– 8) × (–3) = 24
और [(– 8) × (–2)] + [(– 8) × (–1)] = 16 + 8 = 24
इसलिए, (– 8) × [(–2) + (–1)] = [(– 8) × (–2)] + [(– 8) × (–1)]
क्या हम कह सकते हैं कि पूर्णांकों के लिए भी योग पर गुणन का वितरण नियम सत्य है ? हाँ
व्यापक रूप में, किन्हीं तीन पूर्णांकों a, b और c के लिए,
a × (b + c) = a × b + a × c
a, b और c में से प्रत्येक के लिए कम से कम पाँच विभिन्न मान लीजिए और उपर्युक्त वितरण गुण को सत्यापित कीजिए ।
प्रयास कीजिये
(i) क्या 10 × [(6 + (–2)] = 10 × 6 + 10 × (–2)?
(ii) क्या (–15) × [(–7) + (–1)] = (–15) × (–7) + (–15) × (–1)?
अब निम्नलिखित पर विचार कीजिए :
क्या हम कह सकते हैं कि 4 × (3 – 8) = 4 × 3 – 4 × 8 है?
आइए इसकी जाँच करें :
4 × (3 – 8) = 4 × (–5) = –20
4 × 3 – 4 × 8 = 12 – 32 = –20
इसलिए, 4 × (3 – 8) = 4 × 3 – 4 × 8 है।
निम्नलिखित पर विचार कीजिए :
( –5) × [( – 4) – ( – 6)] = ( –5) × 2 = –10
[( –5) × ( – 4)] – [ ( –5) × ( – 6)] = 20 – 30 = –10
अत ः, ( –5) × [( – 4) – ( – 6)] = [( –5) × ( – 4)] – [ ( –5) × ( – 6)]
( –9) × [ 10 – ( –3)] और [( –9) × 10 ] – [ ( –9) × ( –3)]
के लिए इस कथन की जाँच कीजिए ।
आप पाएँगे कि ये भी समान हैं ।
व्यापक रूप में किन्हीं भी तीन पूर्णांकों a, b और c के लिए,
a × (b – c) = a × b – a × c
a, b और c में से प्रत्येक के लिए कम से कम पाँच मान लीजिए और इस गुण को सत्यापित कीजिए ।
प्रयास कीजिये
(i) क्या 10 × (6 – (–2)] = 10 × 6 – 10 × (–2) है?
(ii) क्या (–15) × [(–7) – (–1)] = (–15) × (–7) – (–15) × (–1) है?
1.5.7 गुणन को आसान बनाना
निम्नलिखित पर विचार कीजिए :
(i) (–25) × 37 × 4 को हम [(–25) × 37] × 4 = (– 925)× 4 = –3700 के रूप में ज्ञात कर सकते हैं ।
अथवा हम इसे इस प्रकार भी कर सकते हैं :
(–25) × 37 × 4 = (–25) × 4 × 37 = [(–25) × 4] × 37 = (–100) × 37 = –3700
कौन-सी विधि आसान है ?
स्पष्ट रूप से दूसरी विधि आसान है, क्योंकि (–25) को 4 से गुणा करने पर –100 प्राप्त होता है, जिसे 37 से गुणा करना आसान है । ध्यान दीजिए दूसरी विधि में पूर्णांकाें की क्रमविनिमेयता और सहचारिता सम्मिलित हैं ।
इस प्रकार, हम देखते हैं कि पूर्णांकों की क्रमविनिमेयता, सहचारिता और वितरणता, परिकलन को सरल बनाने में हमारी सहायता करती हैं । आइए इससे आगे और देखें कि इन गुणों का उपयोग करते हुए कैसे परिकलनों को आसान बनाया जा सकता है ।
(ii) 16 × 12 ज्ञात कीजिए।
16 × 12 को 16 × (10 + 2) के रूप में लिखा जा सकता है ।
16 × 12 = 16 × (10 + 2) = 16 × 10 + 16 × 2 = 160 + 32 = 192
(iii) (–23) × 48 = (–23) × [50 – 2] = (–23) × 50 – (–23) × 2 = (–1150) – (– 46)
= –1104
(iv) (–35) × (–98) = (–35) × [(–100) + 2] = (–35) × (–100) + (–35) × 2
= 3500 + (–70) = 3430
(v) 52 × (– 8) + (–52) × 2
(–52) × 2 को 52 × (–2) के रूप में भी लिखा जा सकता है।
इसलिए, 52 × (– 8) + (–52) × 2 = 52 × (– 8) + 52 × (–2)
= 52 × [(– 8) + (–2)] = 52 × [(–10)] = –520
प्रयास कीजिये
वितरण गुण का उपयोग करते हुए, (– 49) × 18; (–25) × (–31);
70 × (–19) + (–1) × 70 के मान ज्ञात कीजिए।
उदाहरण 2 निम्नलिखित में से प्रत्येक गुणनफल को ज्ञात कीजिए :
(i) (–18) × (–10) × 9 (ii) (–20) × (–2) × (–5) × 7
(iii) (–1) × (–5) × (– 4) × (– 6)
हल
(i) (–18) × (–10) × 9 = [(–18) × (–10)] × 9 = 180 × 9 = 1620
(ii) (–20) × (–2) × (–5) × 7 = – 20 × (–2 × –5) × 7 = [–20 × 10] × 7 = – 1400
(iii) (–1) × (–5) × (– 4) × (– 6) = [(–1) × (–5)] × [(– 4) × (– 6)] = 5 × 24 = 120
उदाहरण 3
सत्यापित कीजिए
(–30) × [13 + (–3)] = [(–30) × 13] + [(–30) × (–3)]
हल (–30) × [13 + (–3)] = (–30) × 10 = –300
[(–30) × 13] + [(–30) × (–3)] = –390 + 90 = –300
इसलिए, (–30) × [13 + (–3)] = [(–30) × 13] + [(–30) × (–3)]
उदाहरण 4 15 प्रश्नों वाले एक कक्षा टेस्ट में, प्रत्येक सही उत्तर के लिए 4 अंक दिए जाते हैं और प्रत्येक गलत उत्तर के लिए (-2) अंक दिए जाते हैं। (i) गुरुप्रीत सभी प्रश्नों को हल करती है, परंतु उसके उत्तरों में से केवल 9 सही हैं। उसने कुल कितने अंक प्राप्त किए हैं ? (ii) उसके एक मित्र के केवल 5 उत्तर सही हैं । उस मित्र के द्वारा प्राप्त अंक कितने हैं?
हल
(i) एक सही उत्तर के लिए दिए जाने वाले अंक = 4
इसलिए 9 सही उत्तरों के लिए दिए गए अंक = 4 × 9 = 36
एक गलत उत्तर के लिए दिए जाने वाले अंक = –2
इसलिए 6 (= 15 – 9) गलत उत्तरों के लिए दिए जाने वाले अंक = (–2) × 6 = –12
इसलिए, गुरुप्रीत द्वारा प्राप्त किए गए अंक = 36 + ( –12) = 24
(ii) एक सही उत्तर के लिए दिए जाने वाले अंक = 4
इस प्रकार, 5 सही उत्तरों के लिए दिए गए अंक = 4 × 5 = 20
एक गलत उत्तर के लिए दिए जाने वाले अंक = (–2)
अत :, 10 (=15 – 5) गलत उत्तरों के लिए दिए जाने वाले अंक = (–2) × 10 = –20
इसलिए, गुरुप्रीत के मित्र द्वारा प्राप्त किए गए अंक = 20 + ( –20) = 0
उदाहरण 5 मान लीजिए कि हम पृथ्वी से ऊपर की दूरी को धनात्मक पूर्णांक से निरूपित करते हैं और पृथ्वी से नीचे की दूरी को ऋणात्मक पूर्णांक से निरूपित करते हैं, तो निम्नलिखित के उत्तर दीजिए ः
(i) एक उत्थापक (elevator) किसी खान कूपक मे 5 m प्रति मिनट की दर से नीचे जाता है । एक घंटे पश्चात् उसकी स्थिति क्या होगी ?
(ii) यदि वह भूमि से 15 m ऊपर से नीचे जाना शुरू करता है, तो 45 मिनट बाद उसकी स्थिति क्या होगी ?
हल
(i) क्योंकि उत्थापक नीचे की ओर जा रहा है, इसलिए इसके द्वारा तय की गई दूरी को ऋणात्मक पूर्णांक से निरूपित किया जाएगा ।
एक मिनट में उत्थापक की स्थिति में परिवर्तन = –5 m
60 मिनट पश्चात् उत्थापक की स्थिति में परिवर्तन = (–5) × 60 = – 300 m, अर्थात् भूमि की सतह से 300 m नीचे ।
(ii) 45 m में उत्थापक की स्थिति में परिवर्तन = (–5) × 45 = –225 m
इसलिए, उत्थापक की अंतिम स्थिति = –225 + 15 = –210 m, अर्थात् भूमि की सतह से 210 m नीचे ।
प्रश्नावली 1.3
1. निम्नलिखित गुणनफलों को ज्ञात कीजिए :
(a) 3 × (–1) (b) (–1) × 225
(c) (–21) × (–30) (d) (–316) × (–1)
(e) (–15) × 0 × (–18) (f) (–12) × (–11) × (10)
(g) 9 × (–3) × (– 6) (h) (–18) × (–5) × (– 4)
(i) (–1) × (–2) × (–3) × 4 (j) (–3) × (–6) × (–2) × (–1)
2. निम्नलिखित को सत्यापित कीजिए :
(a) 18 × [7 + (–3)] = [18 × 7] + [18 × (–3)]
(b) (–21) × [(– 4) + (– 6)] = [(–21) × (– 4)] + [(–21) × (– 6)]
3. (i) किसी भी पूर्णांक a के लिए, (–1) × a किसके समान है ?
(ii) वह पूर्णांक ज्ञात कीजिए, जिसका (–1) के साथ गुणनफल है :
(a) –22 (b) 37 (c) 0
4. (–1) × 5 से आरंभ करके विभिन्न गुणनफलों द्वारा कोई पैटर्न दर्शाते हुए (–1) × (–1) = 1 को निरूपित कीजिए ।
5. उचित गुणों का उपयोग करते हुए, गुणनफल ज्ञात कीजिए :
(a) 26 × (– 48) + (– 48) × (–36) (b) 8 × 53 × (–125)
(c) 15 × (–25) × (– 4) × (–10) (d) (– 41) × 102
(e) 625 × (–35) + (– 625) × 65 (f) 7 × (50 – 2)
(g) (–17) × (–29) (h) (–57) × (–19) + 57
6. किसी हिमीकरण (ठंडा) प्रक्रिया में, कमरे के तापमान को 40°C से, 5°C प्रति घंटे की दर से कम करने की आवश्यकता है । इस प्रक्रिया के शुरू होने के 10 घंटे बाद, कमरे का तापमान क्या होगा ?
7. दस प्रश्नों वाले एक कक्षा टेस्ट में प्रत्येक सही उत्तर के लिए 5 अंक दिए जाते हैं और प्रत्येक गलत उत्तर के लिए (–2) अंक दिए जाते हैं एवं प्रयत्न नहीं किए गए प्रश्नों के लिए शून्य दिया जाता है ।
(i) मोहन चार प्रश्नों का सही और छः प्रश्नों का गलत उत्तर देता है । उसके द्वारा प्राप्त अंक कितने हैं ?
(ii) रेशमा के पाँच उत्तर सही हैं और पाँच उत्तर गलत है । उसके द्वारा प्राप्त अंक कितने हैं ?
(iii) हीना ने कुल सात प्रश्न किए हैं उनमें से दो का उत्तर सही है और पाँच का उत्तर गलत है । तो उसे कितने अंक प्राप्त होते हैं?
8. एक सीमेंट कंपनी को सफ़ेद सीमेंट बेचने पर ₹ 8 प्रति बोरी की दर से लाभ होता है और स्लेटी (Grey) रंग की सीमेंट बेचने पर ₹ 5 प्रति बोरी की दर से हानि होती है ।
(a) किसी महीने में वह कंपनी 3000 बोरियाँ सफ़ेद सीमेंट की और 5000 बोरियाँ स्लेटी सीमेंट की बेचती है । उसका लाभ अथवा हानि क्या है ?
(b) यदि बेची गई स्लेटी सीमेंट की बोरियों की संख्या 6400 है, तो कंपनी को स्लेटी सीमेंट की कितनी बोरियाँ बेचनी चाहिए, ताकि उसे न तो लाभ हो और ना ही हानि ?
9. निम्नलिखित को सत्य कथन में परिवर्तित करने के लिए, रिक्त स्थान को एक पूर्णांक से प्रतिस्थापित कीजिए ः
(a) (–3) × _____ = 27 (b) 5 × _____ = –35
(c) _____ × (– 8) = –56 (d) _____ × (–12) = 132
1.6 पूर्णांकों का विभाजन
हम जानते हैं कि विभाजन, गुणा की विपरीत संक्रिया है । आइए पूर्ण संख्याओं के लिए एक उदाहरण देखेंः
क्योंकि 3 × 5 = 15 है, इसलिए 15 ÷ 5 = 3 और 15 ÷ 3 = 5 है।
इसी प्रकार, 4 × 3 = 12 से 12 ÷ 4 = 3 एवं 12 ÷ 3 = 4 प्राप्त होता है ।
इस प्रकार, हम कह सकते हैं कि पूर्ण संख्याओं के प्रत्येक गुणन कथन के लिए दो विभाजन या भाग, कथन हैं ।
क्या आप पूर्णांकों के लिए गुणन कथन एवं संगत भाग कथनों को लिख सकते हैं ?
निम्नलिखित सारणी को देखिए और इसे पूरा कीजिए ।
उपर्युक्त से हम देखते हैं कि
(–12) ÷ 2 = (– 6) (–20) ÷ (5) = (– 4)
(–32) ÷ 4 = – 8 (– 45) ÷ 5 = – 9
हम देखते हैं कि जब हम एक ऋणात्मक पूर्णांक को धनात्मक पूर्णांक से भाग देते हैं, तो हम उन्हें पूर्ण संख्याओं के रूप में भाग देते हैं और उसके पश्चात् भागफल से पहले ऋण चिह्न (–) रख देते हैं।
हम यह भी देखते हैं कि
72 ÷ (–8) = –9 और 50 ÷ (–10) = –5
72 ÷ (–9) = – 8 50 ÷ (–5) = –10
इस प्रकार, हम कह सकते हैं कि जब हम एक धनात्मक पूर्णांक को एक ऋणात्मक पूर्णांक से भग देते हैं, तोसर्वप्रथम
हम उन्हें पूर्ण संख्याओं के रूप में भाग देते हैं और उसके पश्चात् भागफल के समने ऋण चिह्न (-) रख देतेहैं।
क्या हम कह सकते हैं कि (– 48) ÷ 8 = 48 ÷ (– 8)? आइए जाँच करते हैं । हम जानते हैं कि (– 48) ÷ 8 = – 6और 48 ÷ (– 8) = – 6। इसलिए (– 48) ÷ 8 = 48 ÷ (– 8)।
निम्नलिखित के लिए इसकी जाँच कीजिए
(i) 90 ÷ (– 45) और (–90) ÷ 45 (ii) (–136) ÷ 4 और 136 ÷ (– 4)
व्यापक रूप में, किन्हीं दो धनात्मक पूर्णांकों a तथा b के लिए,
a ÷ (–b) = (–a) ÷ b, जहाँ b ≠ 0
प्रयास कीजिये
ज्ञात कीजिए : (a) 125 ÷ (–25) (b) 80 ÷ (–5) (c) 64 ÷ (–16)
अंत में, हम देखते हैं कि
(–12) ÷ (– 6) = 2; (–20) ÷ (– 4) = 5; (–32) ÷ (– 8) = 4; (– 45) ÷ (–9) = 5
इस प्रकार, हम कह सकते हैं कि जब हम एक ऋणात्मक पूर्णांक को एक ऋणात्मक पूर्णांक से भाग देते हैं, तो सर्वप्रथम हम उन्हे पूर्ण संख्याओं के रूप में भाग देते हैं और उसके पश्चात् भागफल से पहले धनात्मक चिह्न (+) रख देते हैं।
व्यापक रूप में, किन्हीं दो ऋणात्मक पूर्णांकों a तथा b के लिए,
(– a) ÷ (–b) = a ÷ b, जहाँ b ≠ 0 है।
ज्ञात कीजिए: (a) (–36) ÷ (– 4) (b) (–201) ÷ (–3) (c) (–325) ÷ (–13)
1.7 पूर्णांकों के भाग के गुण
निम्नलिखित सारणी को देखिए और इसे पूरा कीजिए :
आप क्या देखते हैं ? हम देखते हैं कि पूर्णांक भाग के अंतर्गत संवृत नहीं हैं । अपनी ओर से पाँच और उदाहरण लेते हुए, इस कथन की सत्यता के लिए उचित कारण बताइए ।
हम जानते हैं कि पूर्ण संख्याओं के लिए भाग क्रमविनिमेय नहीं है । आइए पूर्णांकों के लिए भी इसकी जाँच करें।
आप सारणी से देख सकते हैं कि (– 8) ÷ (– 4) ≠ (– 4) ÷ (– 8) है।
क्या (– 9) ÷ 3 और 3 ÷ (– 9) एक समान हैं ?
क्या (– 30) ÷ (– 6) और (– 6) ÷ (– 30) एक समान हैं ?
क्या हम कह सकते हैं कि पूर्णांकों के लिए भाग क्रमविनिमेय है ?
नहीं । आप पाँच और पूर्णांक युग्म लेकर इसे सत्यापित कर सकते हैं ।
पूर्ण संख्याओं की तरह, किसी भी पूर्णांक को शून्य से भाग करना अर्थहीन है और शून्येतर पूर्णांक से शून्य को भाग देने पर शून्य प्राप्त होता है, अर्थात् किसी भी पूर्णांक a के लिए a ÷ 0 परिभाषित नहीं है । परंतु 0 ÷ a = 0, a ≠ 0 के लिए है।
जब हम किसी पूर्ण संख्या को 1 से भाग देते हैं, तो हमें वही पूर्ण संख्या प्राप्त होती है । आइए इसकी जाँच करते हैं कि क्या यह ऋणात्मक पूर्णांकों के लिए भी सत्य है ।
निम्नलिखित को देखिए :
(– 8) ÷ 1 = (– 8) (–11) ÷ 1 = –11 (–13) ÷ 1 = –13
(–25) ÷ 1 = ____ (–37) ÷ 1 = ____ (– 48) ÷ 1 = ____
यह दर्शाता है कि ऋणात्मक पूर्णांक को 1 से भाग देने पर वही ऋणात्मक पूर्णाक प्राप्त होता है । अतः किसी भी पूर्णाक को 1 से भाग देने पर वही पूर्णांक प्राप्त होता है । व्यापक रूप में, किसी भी पूर्णांक a के लिए a ÷ 1 = a
किसी पूर्णांक को (-1) से भाग देने पर क्या होता है ? निम्नलिखित सारणी को पूरा कीजिए ः
(– 8) ÷ (–1) = 8 11 ÷ (–1) = –11 13 ÷ (–1) = ____
(–25) ÷ (–1) = ____ (–37) ÷ (–1) = ____ – 48 ÷ (–1) = ____
आप क्या देखतेे हैं ?
हम कह सकते हैं कि किसी भी पूर्णांक को (-1) से भाग देने पर वही पूर्णांक प्राप्त नहीं होता है ।
क्या हम कह सकते हैं कि [(–16) ÷ 4] ÷ (–2) एवं (–16) ÷ [4 ÷ (–2)] समान हैं ?
हम जानते हैं कि [(–16) ÷ 4] ÷ (–2) = (– 4) ÷ (–2) = 2
और (–16) ÷ [4 ÷ (–2)] = (–16) ÷ (–2) = 8
अतः, [(–16) ÷ 4] ÷ (–2) ≠ (–16) ÷ [4 ÷ (–2)]
क्या आप कह सकते हैं कि पूर्णांकों के लिए भाग साहचर्य है नहीं! अपनी ओर से पाँच अन्य उदाहरण लेकर इसे सत्यापित कीजिए ।
उदाहरण 6 किसी टेस्ट में प्रत्येक सही उत्तर के लिए (+5) अंक दिए जाते हैं ओर प्रत्येक गलत उत्तर के लिए (–2) अंक दिए जाते हैं । (i) राधिका ने सभी प्रश्नों के उत्तर दिए और 30 अंक प्राप्त किए, जबकि उसके 10 उत्तर सही पाए गए । (ii) जय ने भी सभी प्रश्नों के उत्तर दिए और उसने (–12) अंक प्राप्त किए, जबकि उसके चार उत्तर सही पा गए गए । उनमें से प्रत्येक ने कितने प्रश्नों के उत्तर गलत दिए ?
हल
(i) एक सही उत्तर के लिए दिए गए अंक = 5
अतः, 10 सही उत्तरों के लिए दिए गए अंक = 5 × 10 = 50
राधिका के द्वारा प्राप्त किए गए अंक = 30
गलत उत्तरों के लिए प्राप्तांक = 30 – 50 = – 20
एक गलत उत्तर के लिए दिए गए अंक = (–2)
इसलिए, गलत उत्तरों की संख्या = (–20) ÷ (–2) = 10
(ii) चार सही उत्तरों के लिए दिए गए अंक = 5 × 4 = 20
जय द्वारा प्राप्त किए गए अंक = –12
गलत उत्तरों के लिए प्राप्तांक = –12 – 20 = – 32
इसलिए, गलत उत्तरों की संख्या = (–32) ÷ (–2) = 16
उदाहरण 7
कोई दुकानदार एक पेन बेचने पर ₹ 1 का लाभ अर्जित करती है और अपने पुराने स्टॉक की पेंसिलों को बेचते हुए 40 पैसे प्रति पेंसिल की हानि उठाती है ।
(i) किसी विशिष्ट महीने में उसने ₹ 5 की हानि उठाई ।
इस अवधि में उसने 45 पेन बेचे । बताइए इस अवधि में उसने कितनी पेंसिलें बेचीं ।
(ii) अगले महीने में उसे न तो लाभ हुआ और न ही हानि हुई। यदि इस महीने में उसने 70 पेन बेचे, तो उसने कितनी पेंसिलें बेचीं ?
हल

(i) एक पेन को बेचने पर अर्जित लाभ = ₹ 1
45 पेनों को बेचने पर अर्जित लाभ = ₹ 45
जिसे हम + ₹ 45 से निर्दिष्ट करते हैं ।
दी हुई कुल हानि = ₹ 5 जिसे – ₹ 5 से निर्दिष्ट करते हैं ।
अर्जित लाभ + उठाई गई हानि = कुल हानि
इसलिए उठाई गई हानि = कुल हानि – अर्जित लाभ
= ₹ (– 5 – 45) = ₹ (–50) = –5000 पैसे
एक पेंसिल को बेचने से उठाई गई हानि = 40 पैसे जिसे हम – 40 पैसे के रूप में लिखते हैं ।
इसलिए बेची गई पेंसिलों की संख्या = (–5000) ÷ (– 40) = 125
(ii) अगले महीने में न तो लाभ हुआ और न ही हानि हुई ।
इसलिए अर्जित लाभ + उठाई गई हानि = 0
अर्थात् अर्जित लाभ = – उठाई गई हानि
अब, 70 पेनों की बेचने से अर्जित लाभ = ₹ 70
इसलिए पेंसिलों को बेचने से उठाई गई हानि = ₹ 70, जिसे हम – ₹ 70 अर्थात् – 7000 पैसे से दर्शाते हैं।
बेची गई पेंसिलों की कुल संख्या = (–7000) ÷ (– 40) = 175 पेंसिलें
प्रश्नावली 1.4
1. निम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए ः
(a) (–30) ÷ 10 (b) 50 ÷ (–5) (c) (–36) ÷ (–9)
(d) (– 49) ÷ (49) (e) 13 ÷ [(–2) + 1] (f) 0 ÷ (–12)
(g) (–31) ÷ [(–30) + (–1)]
(h) [(–36) ÷ 12] ÷ 3 (i) [(– 6) + 5)] ÷ [(–2) + 1]
2. a, b और c के निम्नलिखित मानों में से प्रत्येक के लिए, a ÷ (b + c) ≠ (a ÷ b) + (a ÷ c)
को सत्यापित कीजिए
(a) a = 12, b = – 4, c = 2 (b) a = (–10), b = 1, c = 1
3. रिक्त स्थानों की पूर्ति कीजिए :
(a) 369 ÷ _____ = 369 (b) (–75) ÷ _____ = –1
(c) (–206) ÷ _____ = 1 (d) – 87 ÷ _____ = 87
(e) _____ ÷ 1 = – 87 (f) _____ ÷ 48 = –1
(g) 20 ÷ _____ = –2 (h) _____ ÷ (4) = –3
4. पाँच एेसे पूर्णांक युग्म (a, b) लिखिए, ताकि a ÷ b = –3 हो । एेसा एक युग्म (6, –2) है, क्योंकि 6 ÷ (–2) = (–3) है।
5. दोपहर 12 बजे तापमान शून्य से 10°C ऊपर था । यदि यह आधी रात तक 2°C प्रति घंटे की दर से कम होता है, तो किस समय तापमान शून्य से 8°C नीचे होगा ? आधी रात को तापमान क्या होगा ?
6. एक कक्षा टेस्ट में प्रत्येक सही उत्तर के लिए (+ 3) अंक दिए जाते हैं और प्रत्येक गलत उत्तर के लिए (–2) अंक दिए जाते हैं और किसी प्रश्न को हल करने का प्रयत्न नहीं करने पर कोई अंक नहीं दिया जाता है । (i) राधिका ने 20 अंक प्राप्त किए । यदि उसके 12 उत्तर सही पाए जाते हैं, तो उसने कितने प्रश्नों का उत्तर गलत दिया है ? (ii) मोहिनी टेस्ट में (–5) अंक प्राप्त करती है, जबकि उसके 7 उत्तर सही पाए जाते हैं । उसने कितने प्रश्नों का उत्तर गलत दिया है?
7. एक उत्थापक किसी खान कूपक में 6 m प्रति मिनट की दर से नीचे जाता है। यदि नीचे जाना भूमि तल से 10 m ऊपर से शुरू होता है, तो – 350 m पहुँचने में कितना समय लगेगा ?
हमने क्या चर्चा की ?
1. पूर्णांक, संख्याओं का एक विशाल संग्रह है जिसमें पूर्ण संख्याएँ और उनके ऋणात्मक सम्मिलित हैं । इनका परिचय कक्षा VI मे कराया गया था।
2. आपने पिछली कक्षा में पूर्णांकों को संख्या रेखा पर निरूपित करने के बारे में एवं उनके योग और व्यवकलन के बारे में अध्ययन किया है ।
3. अब हमने योग एवं व्यवकलन द्वारा संतुष्ट होने वाले गुणों का अध्ययन किया है ।
(a) पूर्णांक योग एवं व्यवकलन दोनों के लिए संवृत्त है । अर्थात्, a + b और a – b दोनों पुनः पूर्णाक होते हैं, जहाँ a और b कोई भी पूर्णांक हैं ।
(b) पूर्णांकों के लिए योग क्रमविनिमेय है, अर्थात् सभी पूर्णांकों a तथा b के लिए,
a + b = b + a
(c) पूर्णांकों के लिए योग साहचर्य है, अर्थात् सभी पूर्णांकों a, b तथा c के लिए (a + b) + c = a + (b + c) होता है।
(d) योग के अंतर्गत पूर्णांक शून्य तत्समक है, अर्थात किसी भी पूर्णांक a के लिए, a + 0 = 0 + a = a होता है।
4. हमने यह भी अध्ययन किया है कि पूर्णांकों को कैसे गुणा किया जा सकता है और हमने पाया कि एक धनात्मक एवं एक ऋणात्मक पूर्णांक का गुणनफल एक ऋणात्मक पूर्णांक है, जबकि दो ऋणात्मक पूर्णांकों का गुणनफल एक धनात्मक पूर्णांक है । उदाहरणतः, – 2 × 7 = – 14 और – 3 × (– 8) = 24 है।
5. ऋणात्मक पूर्णांकों की संख्या सम होने पर उनका गुणनफल धनात्मक होता है जबकि यह संख्या विषम होने पर उनका गुणनफल ऋणात्मक होता है ।
6. पूर्णांक गुणन के अंतर्गत कुछ गुणों को दर्शाते हैं।
(a) गुणन के अंतर्गत पूर्णांक संवृत होते हैं, अर्थात् किन्हीं दो पूर्णांकों a तथा b के लिए a × b एक पूर्णांक होता है ।
(b) पूर्णांकों के लिए गुणन क्रमविनिमेय होता है, अर्थात् किन्हीं दो पूर्णांको a तथा b के लिए a × b = b × a होता है।
(c) गुणन के अंतर्गत पूर्णांक 1, तत्समक है, अर्थात् किसी भी पूर्णांक a के लिए 1 × a = a × 1 = a होता है।
(d) पूर्णाकों के लिए गुणन साहचर्य होता है, अर्थात् किन्हीं तीन पूर्णांकों a, b, तथा c के लिए, (a × b) × c = a × (b ×c) होता है।
7. योग एवं गुणन के अंतर्गत पूर्णांक एक गुण को दर्शाते हैं, जिसे वितरण गुण कहा जाता है, अर्थात् किन्हीं तीन पूर्णांकों a, b तथा c के लिए, a × (b + c) = a × b + a × c होता है।
8. योग एवं गुणन के अंतर्गत क्रमविनिमेयता, सहचारिता और वितरणता के गुण हमारे परिकलन को आसान बनाते हैं ।
9. हमने यह भी सीखा है कि पूर्णांकों को कैसे भाग दिया जाता है । हमने पाया कि
(a) जब एक धनात्मक पूर्णांक को एक ऋणात्मक पूर्णांक से भाग दिया जाता है या जब एक ऋणात्मक पूर्णांक को एक धनात्मक पूर्णांक से भाग दिया जाता है, तो प्राप्त भागफल एक ऋणात्मक होता है।
(b) एक ऋणात्मक पूर्णांक को दूसरे ऋणात्मक पूर्णांक से भाग देने पर प्राप्त भागफल एक धनात्मक होता है ।
10. किसी भी पूर्णांक a के लिए, हम पाते हैं कि
(a) a ÷ 0 परिभाषित नहीं है ।
(b) a ÷ 1 = a है।