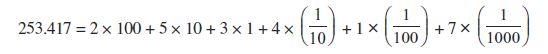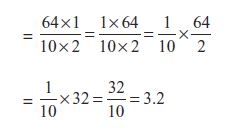Table of Contents
2.1 भूमिका
आपने पिछली कक्षाओं में भिन्न एवं दशमलव के बारे में अध्ययन किया है। भिन्नों के अध्ययन में हम उचित भिन्न, विषम भिन्न, मिश्रित भिन्न और भिन्नों के योग एवं व्यवकलन के बारे में चर्चा कर चुके हैं। हमने, भिन्नों की तुलना, तुल्य भिन्न, भिन्नों को संख्या रेखा पर निरूपित करना और भिन्नों को क्रमबद्ध करना, के बारे में भी अध्ययन किया है।
दशमलवों के अध्ययन में हम, उनकी तुलना, संख्या रेखा पर उनका निरूपण और उनका योग एवं व्यवकलन, के बारे में चर्चा कर चुके हैं।
अब हम भिन्नों एवं दशमलवों के गुणन एवं भाग के बारे में अध्ययन करेंगे।
2.2 भिन्नों के बारे में आपने कितनी अच्छी तरह अध्ययन किया है?
उचित भिन्न वह भिन्न होती है जो संपूर्ण के एक भाग को निरूपित करती है। क्या 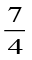 एक उचित भिन्न है? इसके अंश अथवा हर में कौन बड़ा है?
एक उचित भिन्न है? इसके अंश अथवा हर में कौन बड़ा है?
विषम भिन्न, संपूर्ण एवं उचित भिन्न का संयोजन होता है। क्या 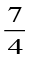 एक विषम भिन्न है? यहाँ अंश अथवा हर में कौन बड़ा है?
एक विषम भिन्न है? यहाँ अंश अथवा हर में कौन बड़ा है?
उदाहरण 1
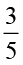 के पाँच तुल्य भिन्न लिखिए।
के पाँच तुल्य भिन्न लिखिए।
हल
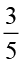 के तुल्य भिन्नों में से एक
के तुल्य भिन्नों में से एक 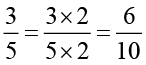 है।
है।
शेष चार तुल्य भिन्न आप स्वयं ज्ञात कीजिए।
उदाहरण 2
रमेश ने एक प्रश्नावली का  भाग हल किया जबकि सीमा ने उस प्रश्नावली का
भाग हल किया जबकि सीमा ने उस प्रश्नावली का 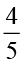 भाग हल किया। ज्ञात कीजिए कि दोनों में से किसने कम भाग हल किया।
भाग हल किया। ज्ञात कीजिए कि दोनों में से किसने कम भाग हल किया।
हल
यह ज्ञात करने के लिए कि किसने प्रश्नावली का कम भाग हल किया, आइए 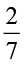 और
और 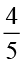 की तुलना करते हैं।
की तुलना करते हैं।
इनको समान भिन्नों मे परिवर्तित करने पर हम पाते हैं :
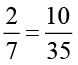 ,
, 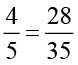

क्योंकि 10 < 28 , इसलिए 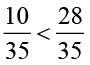 .
.
अतः 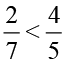 .
.
रमेश ने सीमा की तुलना में कम भाग हल किया।
उदाहरण 3
समीरा ने 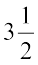 kg सेब और
kg सेब और  kg संतरे खरीदे। समीराद्वारा खरीदे गए फलों का कुल भार कितना है?
kg संतरे खरीदे। समीराद्वारा खरीदे गए फलों का कुल भार कितना है?
हल
फलों का कुल भार 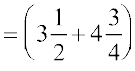 kg
kg 
= 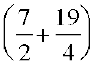 kg
kg 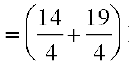 kg
kg
= 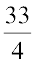 kg
kg 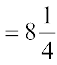 kg है।
kg है।
सुमन प्रतिदिन 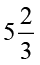 घंटे पढ़ती है। वह अपने इस समय में से
घंटे पढ़ती है। वह अपने इस समय में से 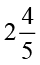 घंटे विज्ञान और गणित में लगा देती है। दूसरे विषयों के लिए वह कितना समय लगाती है?
घंटे विज्ञान और गणित में लगा देती है। दूसरे विषयों के लिए वह कितना समय लगाती है?
हल
सुमन के अध्ययन का कुल समय = 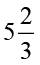 घंटे =
घंटे = 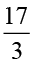 घंटे
घंटे
सुमन द्वारा विज्ञान एवं गणित में लगाया समय = 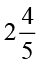 =
= 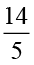 घंटे
घंटे
अतः उसके द्वारा दूसरे विषयों में लगाया गया समय =  घंटे
घंटे
= 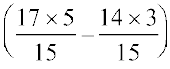 घंटे
घंटे
= 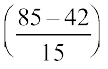 घंटे =
घंटे =  घंटे =
घंटे = 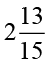 घंटे
घंटे
प्रश्नावली 2.1
1. हल कीजिएः
(i) 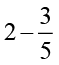 (ii)
(ii) 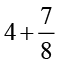 (iii)
(iii) 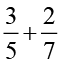 (iv)
(iv) 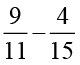
(v) 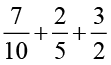 (vi)
(vi)  (vii)
(vii) 
2. निम्नलिखित को अवरोही क्रम में रखिए :
(i) 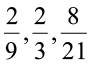 (ii)
(ii) 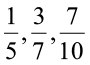 .
.
3. एक ‘‘जादुई वर्ग’’ में प्रत्येक पंक्ति, प्रत्येक स्तंभ एवं प्रत्येक विकर्ण की संख्याओं का योग समान होता है। क्या यह एक जादुई वर्ग है?
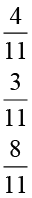
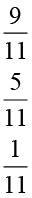
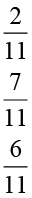 (प्रथम पंक्ति के अनुदिश
(प्रथम पंक्ति के अनुदिश 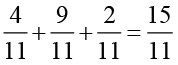 ).
).
4. एक आयताकार कागज़ की लंबाई  cm और चौड़ाई
cm और चौड़ाई 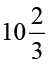 cm है। कागज़ का परिमाप ज्ञात कीजिए।
cm है। कागज़ का परिमाप ज्ञात कीजिए।
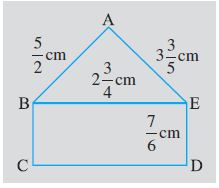
5. दी हुई आकृति में, (i) ∆ ABE (ii) आयत BCDE, का परिमाप ज्ञात कीजिए। किसका परिमाप ज़्यादा है?
6. सलील एक तस्वीर को किसी फ्रेम (चौखट) में जड़ना चाहता है। तस्वीर 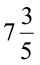 cm चौड़ी है। चौखट में उचित रूप से जड़ने के लिए तस्वीर की चौड़ाई
cm चौड़ी है। चौखट में उचित रूप से जड़ने के लिए तस्वीर की चौड़ाई 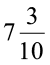 cm से ज़्यादा नहीं हो सकती। तस्वीर की कितनी काट-छाँट की जानी चाहिए।
cm से ज़्यादा नहीं हो सकती। तस्वीर की कितनी काट-छाँट की जानी चाहिए।
7. रीतू ने एक सेब का 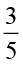 भाग खाया और शेष सेब उसके भाई सोमू ने खाया। सेब का कितना भाग सोमू ने खाया? किसका हिस्स ज़्यादा था? कितना ज़्यादा था?
भाग खाया और शेष सेब उसके भाई सोमू ने खाया। सेब का कितना भाग सोमू ने खाया? किसका हिस्स ज़्यादा था? कितना ज़्यादा था?
8. माइकल ने एक तस्वीर में रंग भरने का कार्य 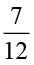 घंटे में समाप्त किया। वैभव ने उसी तस्वीर में रंग भरने का कार्य
घंटे में समाप्त किया। वैभव ने उसी तस्वीर में रंग भरने का कार्य  घंटे में समाप्त किया। किसने ज़्यादा समय कार्य किया? यह समय कितना ज़्यादा था?
घंटे में समाप्त किया। किसने ज़्यादा समय कार्य किया? यह समय कितना ज़्यादा था?
2.3 भिन्नों का गुणन
आप जानते हैं कि एक आयत का क्षेत्रफल कैसे ज्ञात किया जाता है। यह लंबाई × चौड़ाई के बराबर होता है। यदि किसी आयत की लंबाई एवं चौड़ाई क्रमशः 7 cm और 4 cm है तो इसका क्षेत्रफल क्या होगा? इसका क्षेत्रफल 7 × 4 = 28 cm2 होगा।
यदि आयत की लंबाई एवं चौड़ाई क्रमशः  cm एवं
cm एवं 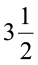 cm है तो इसका क्षेत्रफल क्या होगा? आप कहेंगे कि यह
cm है तो इसका क्षेत्रफल क्या होगा? आप कहेंगे कि यह 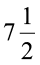 ×
× 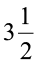 =
=  ×
×  cm2 है। संख्याएँ
cm2 है। संख्याएँ 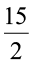 और
और 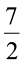 भिन्न हैं। दिए हुए आयत का क्षेत्रफल ज्ञात करने के लिए यह ज्ञात करना आवश्यक है कि भिन्नों को गुणा कैसे किया जाए। हम अब इसे सीखेंगे।
भिन्न हैं। दिए हुए आयत का क्षेत्रफल ज्ञात करने के लिए यह ज्ञात करना आवश्यक है कि भिन्नों को गुणा कैसे किया जाए। हम अब इसे सीखेंगे।
=
2.3.1 एक भिन्न का पूर्ण संख्या से गुणन
 भाग है। दो छायांकित भाग मिलकर वृत्त के कितने भाग को निरूपित करेंगे? ये
भाग है। दो छायांकित भाग मिलकर वृत्त के कितने भाग को निरूपित करेंगे? ये 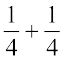 =
= 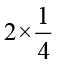 को निरूपित करेंगे।
को निरूपित करेंगे।
दो छायांकित भागों को संयोजित करने पर हम आकृति 2.2 को प्राप्त करते हैं। आकृति 2.2 का छायांकित भाग वृत्त के किस भाग को निरूपित करेगा? यह वृत्त के 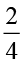 भाग को निरूपित करता है।
भाग को निरूपित करता है।
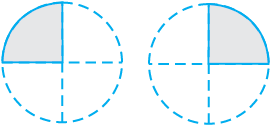
आकृति 2.1

अथवा 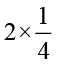 =
= 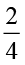
क्या अब आप बता सकते हैं कि आकृति 2.4 किसे निरूपित करेगी?


आइए अब हम  ज्ञात करते हैं।
ज्ञात करते हैं।
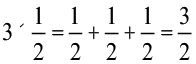
हम यह भी पाते हैं, 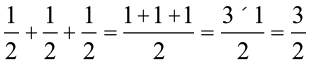
इसलिए 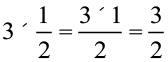
इसी प्रकार 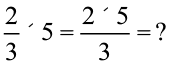
क्या आप बता सकते हैं 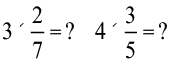
अभी तक हमने जितनी भिन्नों की चर्चा की है अर्थात् 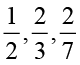 और
और 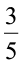 वे सभी उचित भिन्न हैं।
वे सभी उचित भिन्न हैं।
विषम भिन्नों के लिए भी हमारे पास हैः
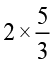 =
= 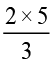 =
= 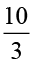
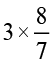 = ?
= ? 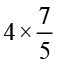 = ?
= ?
प्रयास कीजिए :
अतः किसी पूर्ण संख्या को किसी उचित अथवा विषम भिन्न से गुणा करने के लिए हम पूर्ण संख्या को भिन्न के अंश के साथ गुणा करते हैं और भिन्न के हर को अपरिवर्तित य समान रखा जाता है।
प्रयास कीजिए
1. ज्ञात कीजिएः (a) 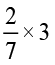 (b)
(b) 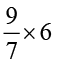 (c)
(c) 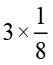 (d)
(d) 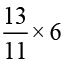
यदि गुणनफल एक विषम भिन्न है तो इसे मिश्रित भिन्न के रूप में व्यक्त कीजिए।
2. 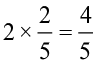 को सचित्र निरूपित कीजिए।
को सचित्र निरूपित कीजिए।
प्रयास कीजिए
ज्ञात कीजिए (i) 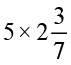
(ii) 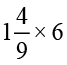
किसी मिश्रित भिन्न को एक पूर्ण संख्या से गुणा करने के लिए सर्वप्रथम मिश्रित भिन्न को विषम भिन्न में परिवर्तित कीजिए और तब गुणा कीजिए।
इसीलिए 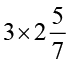 =
=  =
= 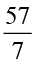 =
= 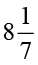
इसी प्रकार,  =
=  = ?
= ?
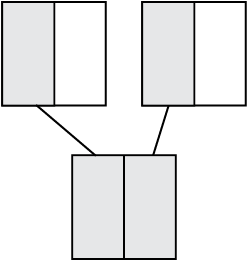
आकृति 2.6
भिन्न, प्रचालक ‘का’ के रूप में
आकृति 2.6 को देखिए। दो वर्ग पूरी तरह से समरूप हैं।
प्रत्येक छायांकित टुकड़ा 1 के 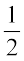 को निरूपित करता है।
को निरूपित करता है।
इसलिए दोनों छायांकित टुकड़े मिलकर 2 के 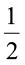 को निरूपित करते हैं।
को निरूपित करते हैं।
2 छायांकित 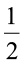 भागों को संयोजित कीजिए। यह 1 को निरूपित करता है।
भागों को संयोजित कीजिए। यह 1 को निरूपित करता है।
इस प्रकार हम कहते हैं कि 2 का 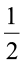 एक भाग है। हम इसे
एक भाग है। हम इसे 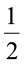 × 2 = 1 के रूप में भी प्राप्त कर सकते हैं।
× 2 = 1 के रूप में भी प्राप्त कर सकते हैं।
अतः 2 का 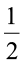 =
= 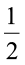 × 2 = 1
× 2 = 1
आकृति 2.7 के समरूप वर्गों को देखिए
प्रत्येक छायांकित टुकड़ा एक के 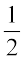 भाग को निरूपित करता है।
भाग को निरूपित करता है।
इसलिए तीन छायांकित टुकड़े मिलकर 3 के 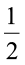 भाग को निरूपित करते हैं।प्रयास कीजिए
भाग को निरूपित करते हैं।प्रयास कीजिए
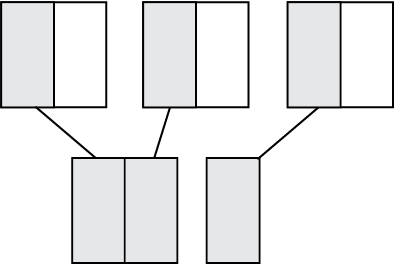
आकृति 2.7
तीन छायांकित भागों को संयोजित कीजिए।
यह 1 अर्थात्
अर्थात् 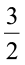 को निरूपित करता है।
को निरूपित करता है।
इसलिए 3 का 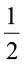 ,
, 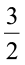 है। और
है। और 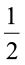 × 3 =
× 3 = 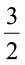
अतः 3 का 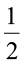 =
= 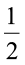 × 3 =
× 3 = 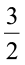
इस प्रकार हम देखते हैं कि ‘का’ गुणन को निरूपित करता है।
फरीदा के पास 20 कँचे हैं। रेशमा के पास फरीदा के कँचों का 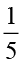 है। रेशमा के पास कितने कँचे हैं? जैसा कि हम जानते हैं, ‘का’ गुणन को दर्शाता हैं। इसलिए रेशमा के पास
है। रेशमा के पास कितने कँचे हैं? जैसा कि हम जानते हैं, ‘का’ गुणन को दर्शाता हैं। इसलिए रेशमा के पास 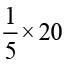 = 4 कँचे हैं।
= 4 कँचे हैं।
इसी प्रकार हम पाते हैं कि 16 का 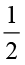 ,
, 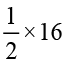 =
= 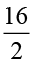 = 8 है।
= 8 है।
प्रयास कीजिए :![Exercise5R.tif]()
क्या आप बता सकते हैं कि (i) 10 का 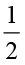 (ii) 16 का
(ii) 16 का 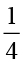 (iii) 25 का
(iii) 25 का 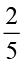 , क्या है?
, क्या है?
उदाहरण 5
40 विद्यार्थियों की एक कक्षा में कुल विद्यार्थियों की संख्या का 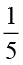 अंग्रेज़ी पढ़ना पसंद करते है, कुल संख्या का
अंग्रेज़ी पढ़ना पसंद करते है, कुल संख्या का 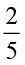 गणित पढ़ना पसंद करते हैं और शेष विद्यार्थी विज्ञान पढ़ना पसंद करते हैं।
गणित पढ़ना पसंद करते हैं और शेष विद्यार्थी विज्ञान पढ़ना पसंद करते हैं।
(i) कितने विद्यार्थी अंग्रेज़ी पढ़ना पसंद करते हैं?
(ii) कितने विद्यार्थी गणित पढ़ना पसंद करते हैं?
(iii) कुल विद्यार्थियों की संख्या का कितना भाग (fraction) विज्ञान पढ़ना पसंद करता है?
हल
कक्षा के कुल विद्यार्थियों की संख्या = 40.
(i) इनमें से कुल संख्या का 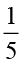 अंग्रेज़ी पढ़ना पसंद करते हैं।
अंग्रेज़ी पढ़ना पसंद करते हैं।
अतः अंग्रेज़ी पढ़ना पसंद करने वाले विद्यार्थियों की संख्या 40 का 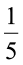 =
= 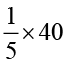 = 8 है।
= 8 है।
(ii) स्वयं प्रयास कीजिए।
(iii) अंग्रेज़ी एवं गणित पसंद करने वाले विद्यार्थियों की संख्या = 8 + 16 = 24 है। अतः विज्ञान पसंद करने वाले विद्यार्थियों की संख्या = 40 – 24 = 16 है।
अतः वांछित भिन्न 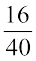 है।
है।
प्रश्नावली 2.2
1. (a) से (d) तक के रेखाचित्रों में निम्नलिखित को कौन दर्शाता है :
(i)  (ii)
(ii) 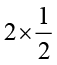 (iii)
(iii)  (iv)
(iv) 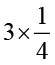
(a)  (b)
(b) 
(c)  (d)
(d) 
2. (a) से (c) तक कुछ चित्र दिए हुए हैं। बताइए उनमें से कौन निम्नलिखित को दर्शाता है ः
(i)  (ii)
(ii) 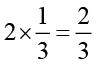 (iii)
(iii) 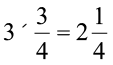



3. गुणा करके न्यूनतम रूप में लिखिए और मिश्रित भिन्न में व्यक्त कीजिए :
(i) 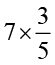 (ii)
(ii) 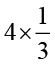 (iii)
(iii) 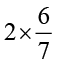 (iv)
(iv) 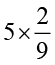 (v)
(v) 
(vi) 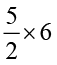 (vii)
(vii) 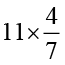 (viii)
(viii) 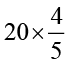 (ix)
(ix)  (x)
(x) 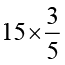
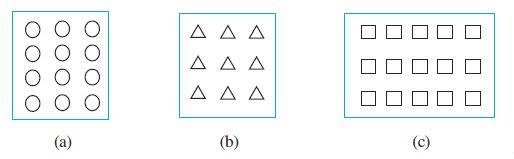
4. छायांकित कीजिए :
(i) बक्सा (a) के वृत्तों का 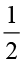 भाग (ii) बक्सा (b) के त्रिभुजों का
भाग (ii) बक्सा (b) के त्रिभुजों का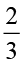 भाग
भाग
(iii) बक्सा (c) के वर्गों का 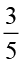 भाग
भाग
5. ज्ञात कीजिए :
(a) (i) 24 का 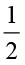 (ii) 46 का
(ii) 46 का 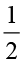 (b) (i) 18 का
(b) (i) 18 का 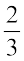 (ii) 27 का
(ii) 27 का 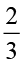
(c) (i) 16 का 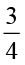 (ii) 36 का
(ii) 36 का  (d) (i) 20 का
(d) (i) 20 का 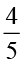 (ii) 35 का
(ii) 35 का 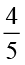
6. गुणा कीजिए और मिश्रित भिन्न के रूप में व्यक्त कीजिए ः
(a)  (b)
(b)  (c)
(c) 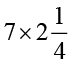
(d)  (e)
(e)  (f)
(f) 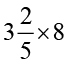
7. ज्ञात कीजिए :
(a) (i) 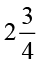 का
का 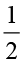 (ii)
(ii) 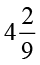 का
का  (b) (i)
(b) (i) 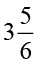 का
का 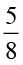 (ii)
(ii)  का
का 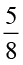
8. विद्या और प्रताप पिकनिक पर गए। उनकी माँ ने उन्हें 5 लीटर पानी वाली एक बोतल दी। विद्या ने कुल पानी का  उपयोग किया। शेष पानी प्रताप ने पिया।
उपयोग किया। शेष पानी प्रताप ने पिया।
(i) विद्या ने कितना पानी पिया?
(ii) पानी की कुल मात्रा का कितना भिन्न (fraction) प्रताप ने पिया?
2.3.2 भिन्न का भिन्न से गुणन
फरीदा के पास 9 cm लंबी एक रिबन की पट्टी थी। उसने इस पट्टी को चार समान भागों में काटा। उसने यह किस प्रकार किया? उसने पट्टी को दो बार मोड़ा। प्रत्येक भाग कुल लंबाई के किस भिन्न को निरूपित करेगा। प्रत्येक भाग, पट्टी का  होगा। उसने इनमें से एक भाग लिया और इस भाग को एक बार मोड़ते हुए इसे दो बराबर भागों में बाँट दिया। इन दो टुकड़ों में से एक टुकड़ा क्या निरूपित करेगा? यह
होगा। उसने इनमें से एक भाग लिया और इस भाग को एक बार मोड़ते हुए इसे दो बराबर भागों में बाँट दिया। इन दो टुकड़ों में से एक टुकड़ा क्या निरूपित करेगा? यह 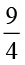 का
का 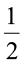 अर्थात्
अर्थात् 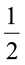 ×
× 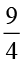 को निरूपित करेगा।
को निरूपित करेगा।
आइए देखते हैं कि दो भिन्नों का गुणनफल जैसे 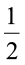 ×
× 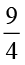 को कैसे ज्ञात किया जाए।
को कैसे ज्ञात किया जाए।
इसे ज्ञात करने के लिए आइए सर्वप्रथम हम 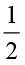 ×
× 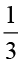 जैसा गुणनफल ज्ञात करना सीखते हैं।
जैसा गुणनफल ज्ञात करना सीखते हैं।
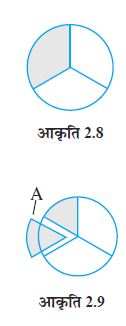
(a) किसी संपूर्ण भाग का  हम कैसे ज्ञात करते हैं? हम संपूर्ण को तीन समान भागों में बाँटते है। तीनों में से प्रत्येक भाग संपूर्ण के
हम कैसे ज्ञात करते हैं? हम संपूर्ण को तीन समान भागों में बाँटते है। तीनों में से प्रत्येक भाग संपूर्ण के 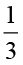 भाग को निरूपित करता है। इन तीनों में से एक हिस्सा लीजिए और इसे छायांकित कर दीजिए जैसा कि आकृति 2.8 में दर्शाया गया है।
भाग को निरूपित करता है। इन तीनों में से एक हिस्सा लीजिए और इसे छायांकित कर दीजिए जैसा कि आकृति 2.8 में दर्शाया गया है।
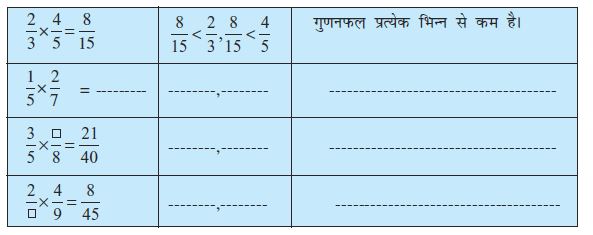
(b) आप इस छायांकित भाग का 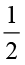 भाग कैसे ज्ञात करोगे? इस छायांकित एक तिहाई (
भाग कैसे ज्ञात करोगे? इस छायांकित एक तिहाई ( ) भाग को 2 समान भागों में बाँटिए। इन दोनों में से प्रत्येक भाग
) भाग को 2 समान भागों में बाँटिए। इन दोनों में से प्रत्येक भाग 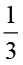 के
के 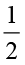 को निरूपित करता है अर्थात्
को निरूपित करता है अर्थात्  ×
× 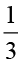 को निरूपित करता है (आकृति 2.9)।
को निरूपित करता है (आकृति 2.9)।
इन दो भागों में से एक को बाहर निकाल लीजिए और इसे ‘A’ नाम दे दीजिए।
‘A’ 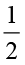 ×
× 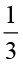 को निरूपित करता है।
को निरूपित करता है।
(c) ‘A’ संपूर्ण का कितना भाग है? यह जानने के लिए शेष  भागों में से प्रत्येक को 2 समान भागों में बाँटिए। अब आपके पास एेसे कितने समान भाग हैं? एेसे 6 समान भाग हैं। ‘A’ इनमें से एक भाग है।
भागों में से प्रत्येक को 2 समान भागों में बाँटिए। अब आपके पास एेसे कितने समान भाग हैं? एेसे 6 समान भाग हैं। ‘A’ इनमें से एक भाग है।
अतः ‘A’ संपूर्ण का  भाग है। इस प्रकार
भाग है। इस प्रकार 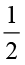 ×
× 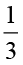 =
= 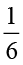
हमने यह कैसे निर्णय लिया कि ‘A’ संपूर्ण का  भाग है? संपूर्ण को 2 × 3 = 6 भागों में बाँटा गया और 1 भाग इसमें से बाहर निकाला गया।
भाग है? संपूर्ण को 2 × 3 = 6 भागों में बाँटा गया और 1 भाग इसमें से बाहर निकाला गया।
अतः 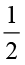 ×
×  =
= 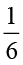 =
= 
अथवा 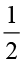 ×
× 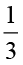 =
= 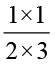
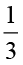 ×
×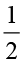 का मान भी इसी प्रकार ज्ञात किया जा सकता है। संपूर्ण को 2 समान भागों में बाँटिए और तब इनमें से किसी एक भाग को 3 समान भागों में बाँटिए। इनमें से एक भाग को लीजिए। यह
का मान भी इसी प्रकार ज्ञात किया जा सकता है। संपूर्ण को 2 समान भागों में बाँटिए और तब इनमें से किसी एक भाग को 3 समान भागों में बाँटिए। इनमें से एक भाग को लीजिए। यह 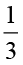 ×
× 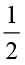 अर्थात्
अर्थात् 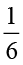 भाग को निरूपित करेगा।
भाग को निरूपित करेगा।
इसलिए जैसा कि पहले चर्चा की जा चुकी है  ×
× 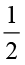 =
= 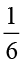 =
= 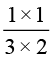
अतः 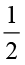 ×
×  =
=  ×
× 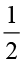 =
= 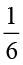
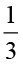 ×
×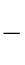 और
और 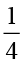 ×
×  ;
; 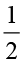 ×
×  और
और 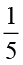 ×
× 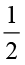 ज्ञात कीजिए और जाँच कीजिए कि क्या आप
ज्ञात कीजिए और जाँच कीजिए कि क्या आप
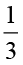 ×
×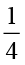 =
= 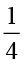 ×
×  ;
; 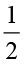 ×
× 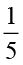 =
= 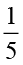 ×
× 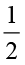 पाते हैं?
पाते हैं?
प्रयास कीजिए
निम्नलिखित बक्सों को भरिए :
(i) 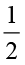 ×
× 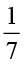 =
= 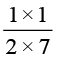 =
=  (ii)
(ii) 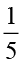 ×
× 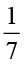 =
=  =
= 
(iii) 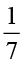 ×
× 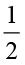 =
=  =
=  (iv)
(iv) 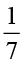 ×
× 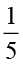 =
=  =
= 
उदाहरण 6
सुशांत एक घंटे में किसी पुस्तक का  भाग पढ़ता है। वह
भाग पढ़ता है। वह 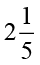 घंटों में पुस्तक का कितना भाग पढ़ेगा?
घंटों में पुस्तक का कितना भाग पढ़ेगा?
हल
सुशांत द्वारा 1 घंटे में पुस्तक का पढ़ा हुआ भाग = 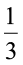 .
.
इसलिए 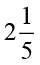 घंटे में उसके द्वारा पुस्तक का पढ़ा हुआ भाग =
घंटे में उसके द्वारा पुस्तक का पढ़ा हुआ भाग = 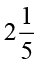 ×
× 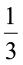
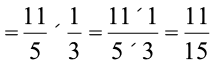
आइए अब हम 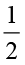 ×
×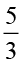 ज्ञात करते हैं। हम जानते हैं कि
ज्ञात करते हैं। हम जानते हैं कि 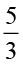 =
= 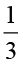 × 5 .
× 5 .
इसलिए, 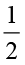 ×
× 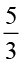 =
= 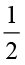 ×
× 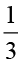 × 5 =
× 5 = 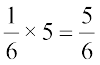
साथ ही,  =
=  । अतः
। अतः 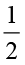 ×
×  =
= 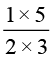 =
=  .
.

इसे नीचे खींची गई आकृतियों में भी दर्शाया गया है। पाँच समान आकारों (आकृति 2.10) में से प्रत्येक पाँच सर्वांगसम वृत्तों के भाग हैं। इस प्रकार का एक आकार लीजिए। इस आकार को प्राप्त करने के लिए सर्वप्रथम हम वृत्त को 3 समान भागों में बाँटते हैं। आगे भी इन तीन भागों में से प्रत्येक को 2 समान भागों में बाँटते हैं। इसका एक भाग वह आकार है जिसकी हमने चर्चा की है। यह क्या निरूपित करेगा? यह 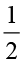 ×
× 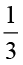 =
=  को निरूपित करेगा। इस प्रकार के भाग मिलाकर कुल 5 ×
को निरूपित करेगा। इस प्रकार के भाग मिलाकर कुल 5 ×  =
= 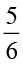 होंगे।
होंगे।
 आकृति 2.10
आकृति 2.10
इसी प्रकार, 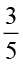 ×
× 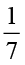 =
= 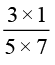 =
= 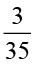 .
.
इस प्रकार हम 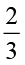 ×
× 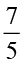 को
को 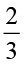 ×
× 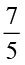 =
=  =
= 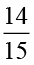 के रूप में ज्ञात कर सकते हैं।
के रूप में ज्ञात कर सकते हैं।

ज्ञात कीजिएः 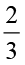 ×
× 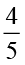 ;
; 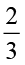 ×
×
प्रयास कीजिए
ज्ञात कीजिएः 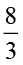 ×
× 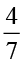 ;
; 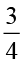 ×
× 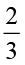
इस प्रकार हम पाते हैं कि हम दो भिन्नों का गुणन के रूप में करते हैं।
गुणनफल का मान
आपने देखा है कि दो पूर्ण संख्याओं का गुणनफल उन दोनों संख्याओं में से प्रत्येक से बड़ा होता है। उदाहरणार्थ 3 × 4 = 12 और 12 > 4, 12 > 3.
जब हम दो भिन्नों को गुणा करते हैं तो गुणनफल के मान को दिए गए भिन्नाें से तुलना कीजिए?
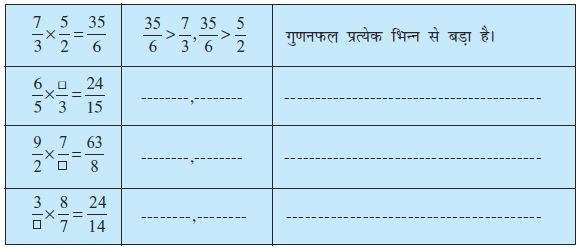
आइए सर्वप्रथम हम दो उचित भिन्नों के गुणनफल की चर्चा करते हैं। हम पाते हैं,
आप पाते हैं कि जब दो उचित भिन्नों को गुणा किया जाता है तो गुणनफल दोनों भिन्नों से कम होता है। अर्थात् दो उचित भिन्नों के गुणनफल का मान दोनों भिन्नों में से प्रत्येक से छोटा होता है। पाँच और उदाहरण बनाकर इसकी जाँच कीजिए।
आइए अब हम दो विषम भिन्नों को गुणा करते हैं।
हम पाते हैं कि दो विषम भिन्नों का गुणनफल उनमें से प्रत्येक भिन्न से बड़ा है। अथवा दो विषम भिन्नों के गुणनफल का मान उनमें से प्रत्येक भिन्न से अधिक है।
एेसे पाँच और उदाहरणों को बनाइए और उपर्युक्त कथन को सत्यापित कीजिए।
आइए अब हम एक उचित और एक विषम भिन्न को गुणा करते हैं।
मान लीजिए 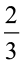 और
और 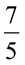 को।
को।
हम पाते हैं ः 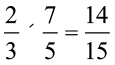 . यहाँ,
. यहाँ, 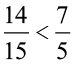 और
और 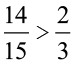
प्राप्त गुणनफल, गुणन में उपयोग किए गए विषम भिन्न से कम है और उचित भिन्न से ज़्यादा है।
 ×
× 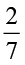 ,
, 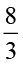 ×
× 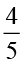 के लिए भी गुणनफल की जाँच कीजिए।
के लिए भी गुणनफल की जाँच कीजिए।
प्रश्नावली 2.3
1. ज्ञात कीजिए :
(i) (a) 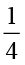 का
का  (b)
(b)  का
का 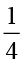 (c)
(c) 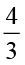 का
का 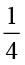
(ii) (a) 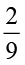 का
का  (b)
(b) 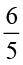 का
का  (c)
(c)  का
का 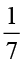
2. गुणा कीजिए और न्यूनतम रूप में बदलिए (यदि संभव है) :
(i) 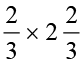 (ii)
(ii) 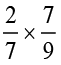 (iii)
(iii) 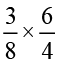 (iv)
(iv) 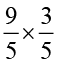
(v) 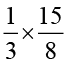 (vi)
(vi) 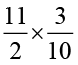 (vii)
(vii) 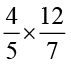
3. निम्नलिखित भिन्नों को गुणा कीजिएः
(i) 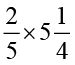 (ii)
(ii) 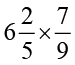 (iii)
(iii) 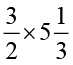 (iv)
(iv) 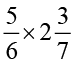
(v) 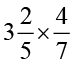 (vi)
(vi) 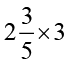 (vii)
(vii) 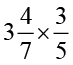
4. कौन बड़ा है :
(i)  का
का 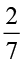 अथवा
अथवा  का
का  (ii)
(ii) 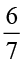 का
का 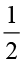 अथवा
अथवा 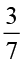 का
का 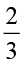
5. सैली अपने बगीचे में चार छोटे पौधे एक पंक्ति में लगाती है। दो क्रमागत छोटे पौधों के बीच की दूरी  m है। प्रथम एवं अंतिम पौधे के बीच की दूरी ज्ञात कीजिए।
m है। प्रथम एवं अंतिम पौधे के बीच की दूरी ज्ञात कीजिए।
6. लिपिका एक पुस्तक को प्रतिदिन 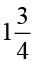 घंटे पढ़ती है। वह संपूर्ण पुस्तक को 6 दिनों में पढ़ती है। उस पुस्तक को पढ़ने में उसने कुल कितने घंटे लगाए?
घंटे पढ़ती है। वह संपूर्ण पुस्तक को 6 दिनों में पढ़ती है। उस पुस्तक को पढ़ने में उसने कुल कितने घंटे लगाए?
7. एक कार 1 लिटर पैट्रोल में 16 किमी दौड़ती है। 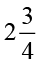 लिटर पैट्रोल में यह कार कुल कितनी दूरी तय करेगी?
लिटर पैट्रोल में यह कार कुल कितनी दूरी तय करेगी?
8. (a) (i) बक्सा 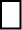 , में संख्या लिखिए, ताकि
, में संख्या लिखिए, ताकि 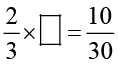 ।
।
(ii) बक्सा  , में प्राप्त संख्या का न्यूनतम रूप _____ है।
, में प्राप्त संख्या का न्यूनतम रूप _____ है।
(b) (i) बक्सा  , में संख्या लिखिए, ताकि
, में संख्या लिखिए, ताकि 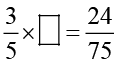 ।
।
(ii) बक्सा  , में प्राप्त संख्या का न्यूनतम रूप _____ है।
, में प्राप्त संख्या का न्यूनतम रूप _____ है।
2.4 भिन्नों की भाग
जॉन के पास 6 cm लंबी कागज़ की एक पट्टी है। वह इस पट्टी को 2 cm लंबी छोटी पट्टियों में काटता है। आप जानते हैं कि वह 6 ÷ 2 =3 पट्टियाँ प्राप्त करेगा। जॉन 6 cm लंबाई वाली एक दूसरी पट्टी को 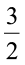 cm लंबाई वाली छोटी पट्टियों में काटता है। अब उसको कितनी छोटी पट्टियाँ प्राप्त होंगी? वह 6 ÷
cm लंबाई वाली छोटी पट्टियों में काटता है। अब उसको कितनी छोटी पट्टियाँ प्राप्त होंगी? वह 6 ÷ 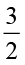 पट्टियाँ प्राप्त करेगा।
पट्टियाँ प्राप्त करेगा।
एक 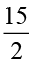 cm लंबाई वाली पट्टी को
cm लंबाई वाली पट्टी को 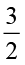 cm लंबाई वाली छोटी पट्टियों में काटा जा सकता है जिससे हमें
cm लंबाई वाली छोटी पट्टियों में काटा जा सकता है जिससे हमें 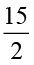 ÷
÷ टुकड़े प्राप्त होंगे।
टुकड़े प्राप्त होंगे।
अतः, हमें एक पूर्ण संख्या को किसी भिन्न से अथवा एक भिन्न को दूसरी भिन्न से भाग देने की आवश्यकता है। आइए हम देखते हैं कि इसे कैसे करना है।
2.4.1 भिन्न से पूर्ण संख्या की भाग
आइए 1÷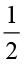 ज्ञात करते हैं।
ज्ञात करते हैं।
हम किसी संपूर्ण को कुछ बराबर भागों में इस प्रकार बाँटते हैं ताकि प्रत्येक भाग संपूर्ण का आधा है। एेसे आधे (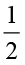 ) भागों की संख्या 1÷
) भागों की संख्या 1÷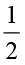 होगी। आकृति 2.11 को देखिए। आपको कितने आधे भाग दिखाई देते हैं? एेसे दो आधे भाग हैं।
होगी। आकृति 2.11 को देखिए। आपको कितने आधे भाग दिखाई देते हैं? एेसे दो आधे भाग हैं।
इसलिए 1 ÷  = 2. साथ ही
= 2. साथ ही 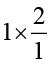 = 1 × 2 = 2 अतः 1 ÷
= 1 × 2 = 2 अतः 1 ÷ 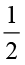 = 1 ×
= 1 × 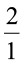
इसी प्रकार, 3 ÷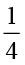 = 3 संपूर्णों में से प्रत्येक को समान
= 3 संपूर्णों में से प्रत्येक को समान 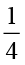 भागों में बाँटने पर,
भागों में बाँटने पर,  भागों की संख्या = 12 (आकृति 2.12 से)
भागों की संख्या = 12 (आकृति 2.12 से)
आकृति 2.12



आकृति 2.11
यह भी देखिए कि 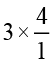 = 3 × 4 = 12. इस प्रकार,
= 3 × 4 = 12. इस प्रकार,  = 12.
= 12.
इसी प्रकार 3 ÷ 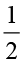 और
और 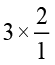 ज्ञात कीजिए।
ज्ञात कीजिए।
भिन्न का व्युत्क्रम
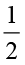 के अंश एवं हर को परस्पर बदलने पर अथवा
के अंश एवं हर को परस्पर बदलने पर अथवा  का प्रतिलोम करने पर संख्या
का प्रतिलोम करने पर संख्या 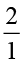 प्राप्त की जा सकती है। इसी प्रकार
प्राप्त की जा सकती है। इसी प्रकार 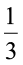 का प्रतिलेाम करने पर
का प्रतिलेाम करने पर  प्राप्त होता है।
प्राप्त होता है।
आइए सर्वप्रथम हम एेसी संख्याओं के प्रतिलोम के बारे में चर्चा करते हैं।
निम्नलिखित गुणनफलों को देखिए और रिक्त स्थानों की पूर्ति कीजिए :

एेसे पाँच और युग्मों को गुणा कीजिए।
एेसी शून्येतर संख्याएँ जिनका परस्पर गुणनफल 1 है, एक दूसरे के व्युत्क्रम कहलाती हैं। इस प्रकार 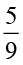 का व्युत्क्रम
का व्युत्क्रम 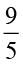 है और
है और 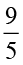 का व्युत्क्रम
का व्युत्क्रम 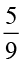 है।
है।  ,
, 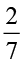 के व्युत्क्रम क्या हैे?
के व्युत्क्रम क्या हैे?
आप देखेंगे कि  का प्रतिलोम करने पर इसका व्युत्क्रम प्राप्त होता है। आप इस प्रकार
का प्रतिलोम करने पर इसका व्युत्क्रम प्राप्त होता है। आप इस प्रकार 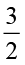 प्राप्त करते हैं।
प्राप्त करते हैं।
सोचिए, चर्चा कीजिए एवं लिखिए

(i) क्या एक उचित भिन्न का व्युत्क्रम भी उचित भिन्न होगी?
(ii) क्या एक विषम भिन्न का व्युत्क्रम भी एक विषम भिन्न होगा?
इसलिए हम कह सकते हैं कि
1 ÷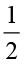 =
=  = 1 × (
= 1 × ( का व्युत्क्रम)
का व्युत्क्रम)
3 ÷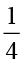 =
= 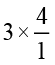 = 3 × (
= 3 × ( का व्युत्क्रम)
का व्युत्क्रम)
3 ÷ = ------ = ----------------------.
= ------ = ----------------------.
अतः, 2 ÷  = 2 × (
= 2 × ( का व्युत्क्रम) =
का व्युत्क्रम) = 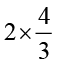 .
.
5 ÷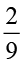 = 5 × ------------------- = 5 × -------------
= 5 × ------------------- = 5 × -------------
इस प्रकार किसी पूर्ण संख्या को एक भिन्न से भाग करने के लिए उस पूर्ण संख्या को उस भिन्न के व्युत्क्रम से गुणा कर दीजिए।
ज्ञात कीजिए : (i) 7 ÷ 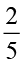 (ii) 6 ÷
(ii) 6 ÷ 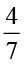 (iii) 2 ÷
(iii) 2 ÷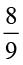
किसी पूर्ण संख्या को एक मिश्रित भिन्न से भाग करते समय, सर्वप्रथम मिश्रित भिन्न को विषम भिन्न में परिवर्तित कीजिए और तब इसको हल कीजिए।
प्रयास कीजिए

इस प्रकार 4 ÷ 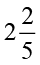 = 4 ÷
= 4 ÷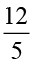 = ? साथ ही 5 ÷ 3
= ? साथ ही 5 ÷ 3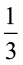 = 5 ÷
= 5 ÷ 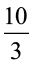 = ?
= ?
2.4.2 पूर्ण संख्या से भिन्न की भाग
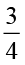 ÷ 3 का मान क्या होगा?
÷ 3 का मान क्या होगा?
पूर्व प्रेक्षणों के आधार पर हम पाते हैं : 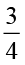 ÷ 3 =
÷ 3 = 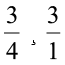 =
= 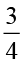 ×
× 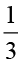 =
=  =
= 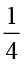
अतः, 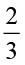 ÷ 7 =
÷ 7 = 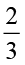 ×
× 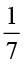 = ?
= ? 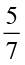 ÷ 6 ,
÷ 6 , 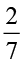 ÷ 8 के मान क्या हैं?
÷ 8 के मान क्या हैं?
मिश्रित भिन्नों को पूर्ण संख्या से भाग करते समय मिश्रित भिन्न को विषम भिन्न में परिवर्तित कीजिए। अर्थात्
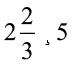 =
=  = ------ ;
= ------ ;  = ------ = ------
= ------ = ------ 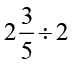 = ------ = ----
= ------ = ----
2.4.3 एक भिन्न की दूसरी भिन्न से भाग
अब हम 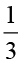 ÷
÷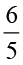 ज्ञात कर सकते हैं।
ज्ञात कर सकते हैं।
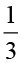 ÷
÷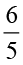 =
= 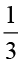 × (
× ( का व्युत्क्रम) =
का व्युत्क्रम) = 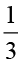 ×
× 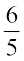 =
= 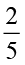
इसी प्रकार, 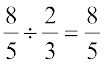 × (
× ( का व्युत्क्रम) = ? और
का व्युत्क्रम) = ? और  ÷
÷ 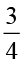 = ?
= ?
प्रयास कीजिए

ज्ञात कीजिएः (i) 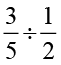 (ii)
(ii) 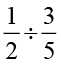 (iii)
(iii) 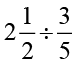 (iv)
(iv) 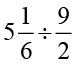
प्रश्नावली 2.4
1. ज्ञात कीजिएः
(i) 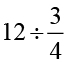 (ii)
(ii) 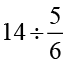 (iii)
(iii) 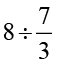 (iv)
(iv) 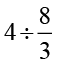
(v) 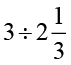 (vi)
(vi) 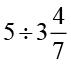
2. निम्नलिखित भिन्नों में से प्रत्येक का व्युत्क्रम ज्ञात कीजिए। व्युत्क्रमों को उचित भिन्न, विषम भिन्न एवं पूर्ण संख्या के रूप में वर्गीकृत कीजिए।
(i) 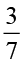 (ii)
(ii) 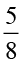 (iii)
(iii) 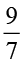 (iv)
(iv) 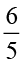
(v) 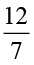 (vi)
(vi) 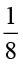 (vii)
(vii) 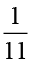
3. ज्ञात कीजिएः
(i)  (ii)
(ii) 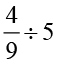 (iii)
(iii) 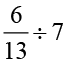 (iv)
(iv) 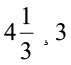
(v)  (vi)
(vi) 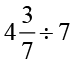
4. ज्ञात कीजिएः
(i) 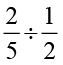 (ii)
(ii) 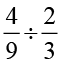 (iii)
(iii) 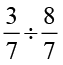 (iv)
(iv) 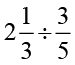 (v)
(v) 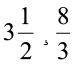
(vi) 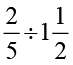 (vii)
(vii) 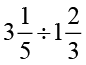 (viii)
(viii) 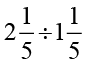
2.5 दशमलव संख्याओं के बारे में आप कितनी अच्छी तरह पढ़ चुके हैं
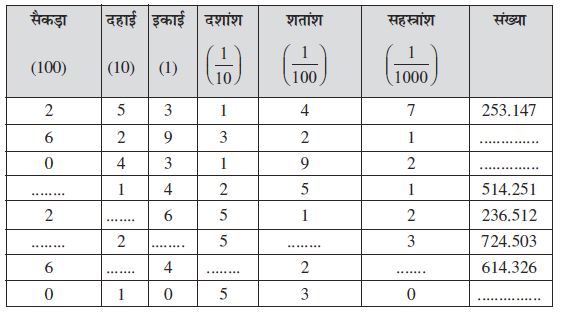
आपने पिछली कक्षाओं में दशमलव संख्याओं के बारे में अध्ययन किया है। आइए यहाँ हम संक्षिप्त में इनका स्मरण करते हैं। निम्नलिखित सारणी को देखिए और रिक्त स्थानों की पूर्ति कीजिए :
उपर्युक्त सारणी में आपने एेसी दशमलव संख्याएँ लिखी हैं जिनका प्रसारित रूप या स्थानीय मान दिया हुआ था। आप विलोम भी कर सकते हैं। अर्थात् यदि आपको संख्या दी हुई है तो आप इसका प्रसारित रूप लिख सकते हैं। उदाहरणतः
जॉन के पास ₹ 15.50 हैं और सलमा के पास ₹ 15.75 हैं। किसके पास अधिक धन है? इसे ज्ञात करने के लिए हमें दशमलव संख्याआें 15.50 एवं 15.75 की तुलना करने की आवश्यकता है। इसके लिए हम सर्वप्रथम दशमलव बिंदु के सबसे बाईं तरफ़ के अंक से शुरू करते हुए बाईं तरफ के अंकों की तुलना करते हैं। यहाँ बिंदु के बाईं तरफ़ के दोनों अंक 1 और 5 दोनों संख्याओं में एक जैसे हैं। इसलिए हम दशांश स्थान से शुरू करते हुए दशमलव बिंदु के दाईं तरफ़ के अंकों की तुलना करते हैं। हम पाते हैं कि 5 < 7, इस प्रकार हम कहते हैं कि 15.50 < 15.75. अतः सलमा के पास जॉन से अधिक धन है।
यदि दशांश स्थान के अंक भी एक जैसे हैं तो शतांश स्थान के अंकों की तुलना कीजिए और इसी प्रकार आगे कीजिए।
अब तुरंत 35.63 और 35.67; 20.1 और 20.01; 19.36 और 29.36 की तुलना कीजिए।
धन, लंबाई और भार की निम्न इकाई को उच्च इकाई में परिवर्तित करते समय हमें दशमलव की आवश्यकता होती है। उदाहरणतः 3 पैसे = ₹  = ₹ 0.03,
= ₹ 0.03,
5 g =  kg = 0.005 kg , 7 cm =
kg = 0.005 kg , 7 cm =  m = 0.07 m
m = 0.07 m
75 पैसे = ₹ ______, 250 g = _____ kg, 85 cm = _____ m, लिखिए
हम यह भी जानते हैं कि दशमलवों को कैसे जोड़ा और घटाया जाता है। इस प्रकार 21.36 + 37.35 है

0.19 + 2.3 का मान क्या है? 29.35 − 4.56 का अंतर है

39.87 − 21.98 का मान बताइए।
प्रश्नावली 2.5
1. कौन बड़ा है?
(i) 0.5 अथवा 0.05 (ii) 0.7 अथवा 0.5 (iii) 7 अथवा 0.7
(iv) 1.37 अथवा 1.49 (v) 2.03 अथवा 2.30 (vi) 0.8 अथवा 0.88.
2. दशमलव का उपयोग करते हुए निम्नलिखित को रुपये के रूप में व्यक्त कीजिए :
(i) 7 पैसे (ii) 7 रुपये 7 पैसे (iii) 77 रुपये 77 पैसे
(iv) 50 पैसे (v) 235 पैसे
3. (i) 5 cm को m एवं km में व्यक्त कीजिए।
(ii) 35 mm को cm, m एवं km में व्यक्त कीजिए।
4. निम्नलिखित को kg में व्यक्त कीजिए :
(i) 200 gm (ii) 3470 gm (iii) 4 kg 8 g
5. निम्नलिखित दशमलव संख्याओं को विस्तारित रूप में लिखिए :
(i) 20.03 (ii) 2.03 (iii) 200.03 (iv) 2.034
6. निम्नलिखित दशमलव संख्याओं में 2 का स्थानीय मान लिखिए :
(i) 2.56 (ii) 21.37 (iii) 10.25 (iv) 9.42 (v) 63.352.
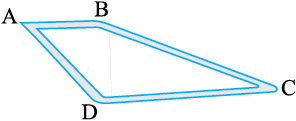
7. दिनेश स्थान A से स्थान B तक गया और वहाँ से स्थान C तक गया। A से B की दूरी 7.5 km है और B से C की दूरी 12.7 km है। अयूब स्थान A से स्थान D तक गया और वहाँ से वह स्थान C को गया। A से D की दूरी 9.3 km है और D से C की दूरी 11.8 km है। किसने ज़्यादा दूरी तय की और वह दूरी कितनी अधिक थी?
8. श्यामा ने 5 kg 300 g सेब और 3 kg 250 g आम खरीदे। सरला ने 4 kg 800 g संतरे और 4 kg 150 g केले खरीदे। किसने अधिक फल खरीदे?
9. 28 km, 42.6 km से कितना कम है?
2.6 दशमलव संख्याओं का गुणन
रेशमा ने ₹ 8.50 प्रति kg की दर से 1.5 kg सब्जी खरीदी। उसे कितने धन का भुगतान करना चाहिए? निश्चित रूप से यह ₹ 8.50 × 1.50 होगा। 8.5 और 1.5 दोनों ही दशमलव संख्याएँ हैं। इस प्रकार हमें एक एेसी परिस्थिति मिलती है जहाँ हमें यह ज्ञात करने की आवश्यकता है कि दो दशमलवों को कैसे गुणा किया जाता है। आइए अब दो 
दशमलव संख्याओं के गुणन को सीखते हैं। सर्वप्रथम हम 0.1 × 0.1 ज्ञात करते हैं।
अब 0.1 = 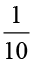 , इसलिए 0.1 × 0.1 =
, इसलिए 0.1 × 0.1 =  =
= 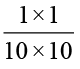 =
= 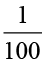 = 0.01.
= 0.01.

आकृति 2.13

आइए इसका सचित्र निरूपण देखते हैं। ( आकृति 2.13)
भिन्न 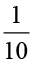 , 10 समान भागों में से एक को निरूपित करती है।
, 10 समान भागों में से एक को निरूपित करती है।
चित्र में छायांकित भाग  को निरूपित करता है।
को निरूपित करता है।
हम जानते हैं कि
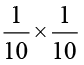 का अर्थ है
का अर्थ है  का
का 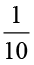 . इसलिए इस
. इसलिए इस 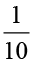 वें भाग को 10 बराबर भागों में बाँटिए और इनमें से एक भाग को लीजिए।
वें भाग को 10 बराबर भागों में बाँटिए और इनमें से एक भाग को लीजिए।
इस प्रकार हम पाते हैं (आकृति 2.14) कि
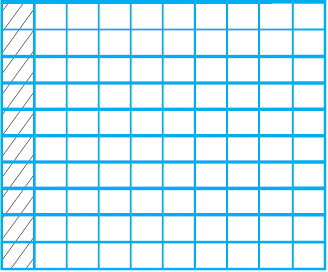
आकृति 2.14
 वें भाग के 10 भागों में एक भाग बिंदु द्वारा चिह्नित वर्ग है। अर्थात् यह
वें भाग के 10 भागों में एक भाग बिंदु द्वारा चिह्नित वर्ग है। अर्थात् यह 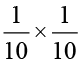 अथवा 0.1 × 0.1 को निरूपित करता है।
अथवा 0.1 × 0.1 को निरूपित करता है।
क्या बिंदु वर्ग को किसी दूसरी विधि से निरूपित किया जा सकता है?
आप आकृति 2.14 में कितने छोटे वर्ग पाते हैं।
इसमें 100 छोटे वर्ग हैं। इस प्रकार बिंदु द्वारा चिह्नित वर्ग 100 में से एक को निरूपित करता है अर्थात् 0.01 को निरूपित करता है। अतः 0.1 × 0.1 = 0.01.
ध्यान दीजिए 0.1 गुणनफल में दो बार सम्मिलित है। 0.1 में दशमलव बिंदु के दाईं तरफ़ एक अंक है। 0.01 में दशमलव बिंदु के दाईं तरफ़ दो (अर्थात् 1 + 1) अंक हैं।

आकृति 2.15
आइए अब हम 0.2 × 0.3 ज्ञात करते हैं।
हम पाते हैं, 0.2 × 0.3 = 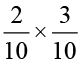
जैसे हमने 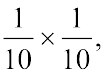 के लिए किया है, वैसे ही आइए हम वर्ग को 10 समान भागों में बाँटते हैं और
के लिए किया है, वैसे ही आइए हम वर्ग को 10 समान भागों में बाँटते हैं और 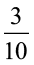 प्राप्त करने के लिए इनमें से 3 भागों को बाहर निकाल लेते हैं। फिर से इन 3 समान भागों में से प्रत्येक भाग को 10 समान भागों में बाँटिए और प्रत्येक में से 2 ले लीजिए। इस प्रकार हम
प्राप्त करने के लिए इनमें से 3 भागों को बाहर निकाल लेते हैं। फिर से इन 3 समान भागों में से प्रत्येक भाग को 10 समान भागों में बाँटिए और प्रत्येक में से 2 ले लीजिए। इस प्रकार हम 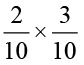 प्राप्त करते हैं।
प्राप्त करते हैं।
बिंदु द्वारा चिह्नित वर्ग, 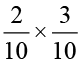 अर्थात् 0.2 × 0.3 को निरूपित करते हैं (आकृति 2.15 देखिए)
अर्थात् 0.2 × 0.3 को निरूपित करते हैं (आकृति 2.15 देखिए)
क्योंकि 100 में से 6 बिंदु द्वारा चिह्नित वर्ग हैं अतः ये 0.06 को भी निरूपित करते हैं।
इस प्रकार 0.2 × 0.3 = 0.06.
ध्यान दीजिए कि 2 × 3 = 6 और 0.06 में दशमलव बिंदु से दाईं तरफ़ अंकों की संख्या 2 (= 1 + 1) हैं।
जाँच कीजिए कि क्या यह 0.1 × 0.1 के लिए भी उचित है।
इन प्रेक्षणों का उपयोग करते हुए 0.2 × 0.4 ज्ञात कीजिए।
0.1 × 0.1 और 0.2 × 0.3 ज्ञात करते समय संभवतः आपने ध्यान दिया होगा कि सर्वप्रथम हमने दशमलव बिंदु की उपेक्षा करते हुए पूर्ण संख्याओं के रूप में गुणा किया था। 0.1 × 0.1 में हमने पाया, 01 × 01 अर्थात् 1 × 1 इसी प्रकार 0.2 × 0.3 में हमने पाया, 02 × 03 = 2 × 3.
तब हमने सबसे दाईं तरफ़ के अंक से शुरू करते हुए और बाईं तरफ़ चलते हुए अंकों की संख्या को गिना। तब हमने वहाँ दशमलव बिंदु रखा। गिने जाने वाले अंकों की संख्या, गुणा की जा रही दशमलव संख्याओं के दशमलव बिंदु के दाईं तरफ़ के अंकों की संख्या का योग करने पर प्राप्त होती है।
आइए अब हम 1.2 × 2.5 ज्ञात करते हैं।
12 एवं 25 को गुणा कीजिए। हम 300 अंक प्राप्त करते हैं। 1.2 और 2.5 दोनों में दशमलव बिंदु के दाईं तरफ एक अंक है। इसलिए 300 में सबसे दाईं तरफ से 1 + 1 = 2 अंक गिन लीजिए (अर्थात् दो 0) और बाईं तरफ़ चलिए। हम 3.00 अर्थात् 3 प्राप्त करते हैं
इसी प्रकार 1.5 × 1.6, 2.4 × 4.2 ज्ञात कीजिए।
2.5 और 1.25 को गुणा करते समय सर्वप्रथम आप 25 एवं 125 को गुणा करेंगे। प्राप्त गुणनफल में दशमलव रखने के लिए आप सबसे दाईं तरफ़ के अंक से शुरू करते हुए 1 + 2 = 3 (क्यों)? अंक गिनेंगे। अतः 2.5 × 1.25 = 3.125। 2.7 × 1.35 ज्ञात कीजिए।

1. ज्ञात कीजिएः (i) 2.7 × 4 (ii) 1.8 × 1.2 (iii) 2.3 × 4.35
2. प्रश्न 1 में प्राप्त गुणनफलों को अवरोही क्रम में क्रमबद्ध कीजिए।
उदाहरण 7
एक समबाहु त्रिभुज की भुजा 3.5 cm है। इसका परिमाप ज्ञात कीजिए।
हल
समबाहु त्रिभुज की सभी भुजाएँ समान होती हैं।
इसलिए, प्रत्येक भुजा की लंबाई = 3.5 cm। अतः परिमाप = 3 × 3.5 cm = 10.5 cm
उदाहरण 8
एक आयत की लंबाई 7.1 cm और इसकी चौड़ाई 2.5 cm है। आयत का क्षेत्रफल क्या है?
हल
आयत की लंबाई = 7.1 cm आयत की चौड़ाई = 2.5 cm
इसलिए आयत का क्षेत्रफल = 7.1 cm × 2.5 cm = 17.75 cm2
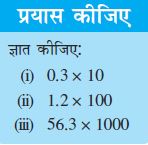
2.6.1 दशमलव संख्याओं का 10,100 और 1000 से गुणन
रेशमा ने देखा कि 2.3 = 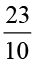 है जबकि 2.35 =
है जबकि 2.35 = 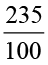 . अतः उसने पाया कि दशमलव बिंदु की स्थिति पर निर्भर करते हुए दशमलव संख्या को 10 अथवा 100 हर वाली भिन्न के रूप में परिवर्तित किया जा सकता है। उसने सोचा कि यदि किसी दशमलव संख्या को 10 अथवा 100 अथवा 1000 से गुणा किया जाए तो क्या होगा?
. अतः उसने पाया कि दशमलव बिंदु की स्थिति पर निर्भर करते हुए दशमलव संख्या को 10 अथवा 100 हर वाली भिन्न के रूप में परिवर्तित किया जा सकता है। उसने सोचा कि यदि किसी दशमलव संख्या को 10 अथवा 100 अथवा 1000 से गुणा किया जाए तो क्या होगा?
आइए देखते हैं क्या हम दशमलव संख्याओं को 10 अथवा 100 अथवा 1000 से गुणा करने का कोई प्रतिरूप (पैटर्न) प्राप्त कर सकते हैं।
नीचे दी हुई सारणी को देखिए और रिक्त स्थानों की पूर्ति कीजिए ः
सारणी में गुणनफल के दशमलव बिंदु के विस्थापन को देखिए। यहाँ संख्याओं को 10,100 एवं 1000 से गुणा किया गया है। 1.76 × 10 = 17.6 में अंक वही हैं अर्थात् दोनों तरफ़ 1, 7 और 6 है। क्या आपने इसे दूसरे गुणनफलों में भी देखा है? 1.76 और 17.6 को भी देखिए। दशमलव बिंदु दाईं अथवा बाईं, किस तरफ़ विस्थापित हुआ है ध्यान दीजिए 10 में 1 के अतिरिक्त एक शून्य है।
1.76×100 = 176.0 में, 1.76 एवं 176.0 को देखिये कि किस तरफ और कितने स्थानों से दशमलव बिंदु का विस्थापन हुआ है। दशमलव बिंदु दाईं तरफ़ दो स्थानों से विस्थापित हुआ है।
ध्यान दीजिए 100 में 1 के अतिरिक्त दो शून्य है।
क्या आप दूसरे गुणनफलों में भी दशमलव बिंदु का इसी प्रकार का विस्थापन देखते हैं?
इस प्रकार हम कहते हैं कि जब किसी दशमलव संख्या को 10, 100 अथवा 1000 से गुणा किया जाता है तो गुणनफल के अंक वही होते हैं जो अंक दशमलव संख्या में होते हैं परंतु गुणनफल में दशमलव बिंदु दाईं तरफ उतने ही स्थानों से विस्थापित होता है जितने 1 के अतिरिक्त शून्य होते हैं। इन प्रेक्षणों के आधार पर अब हम कह सकते हैं किः
0.07 × 10 = 0.7, 0.07 × 100 = 7 और 0.07 × 1000 = 70.
क्या अब आप बता सकते हैं कि 2.97 × 10 = ? 2.97 × 100 = ? 2.97 × 1000 = ?
क्या अब आप रेशमा द्वारा भुगतान किए जाने वाली राशि अर्थात् ₹ 8.50 × 150, ज्ञात करने में उसकी सहायता कर सकते हैं?
प्रश्नावली 2.6
1. ज्ञात कीजिए :
(i) 0.2 × 6 (ii) 8 × 4.6 (iii) 2.71 × 5
(iv) 20.1 × 4 (v) 0.05 × 7 (vi) 211.02 × 4
(vii) 2 × 0.86
2. एक आयत का क्षेत्रफल ज्ञात कीजिए जिसकी लंबाई 5.7 cm और चौड़ाई 3 cm है।
3. ज्ञात कीजिए :
(i) 1.3 × 10 (ii) 36.8 × 10 (iii) 153.7 × 10
(iv) 168.07 × 10 (v) 31.1 × 100 (vi) 156.1 × 100
(vii) 3.62 × 100 (viii) 43.07 × 100 (ix) 0.5 × 10
(x) 0.08 × 10 (xi) 0.9 × 100 (xii) 0.03 × 1000
4. एक दुपहिया वाहन एक लीटर पैट्रोल में 55.3 km की दूरी तय करता है। 10 लीटर पैट्रोल में वह कितनी दूरी तय करेगा?
5. ज्ञात कीजिए :
(i) 2.5 × 0.3 (ii) 0.1 × 51.7 (iii) 0.2 × 316.8
(iv) 1.3 × 3.1 (v) 0.5 × 0.05 (vi) 11.2 × 0.15
(vii) 1.07 × 0.02 (viii) 10.05 × 1.05
(ix) 101.01 × 0.01 (x) 100.01 × 1.1

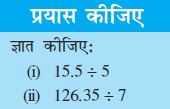
2.7 दशमलव संख्याओं की भाग
सविता अपनी कक्षा की सजावट के लिए एक डिजाईन तैयार कर रही थी। उसे 1.9 cm लंबाई वाली कुछ रंगीन कागज़ की पट्टियों की आवश्यकता थी। उसके पास 9.5 cm लंबाई वाली एक रंगीन कागज़ की पट्टी थी। इस पट्टी में से वह अभीष्ट लंबाई के कितने टुकड़े प्राप्त कर सकेगी। उसने सोचा शायद यह 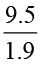 होगा। क्या यह सही है?
होगा। क्या यह सही है?
9.5 और 1.9 दोनों ही दशमलव संख्याएँ हैं। इसलिए हमें दशमलव संख्याओं की भाग भी जानने की आवश्यकता है।
2.7.1 10, 100 और 1000 से भाग
आइए अब हम एक दशमलव संख्या की 10, 100 और 1000 से भाग ज्ञात करते हैं।
आइए हम 31.5 ÷ 10 ज्ञात करते हैं।
31.5 ÷ 10 =  =
= 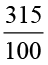 = 3.15
= 3.15
इसी प्रकार 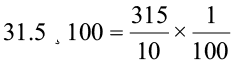

आइए हम यह देखते हैं कि क्या हम संख्याओं को 10, 100 अथवा 1000 से भाग करने का कोई प्रतिरूप ज्ञात कर सकते हैं। यह संख्याओं को 10, 100 अथवा 1000 से, संक्षिप्त विधि से भाग करने में हमारी सहायता कर सकता है।
31.5 ÷ 10 = 3.15 को लीजिए। 31.5 और 3.15 में अंक एक जैसे हैं अर्थात् 3, 1, और 5 परंतु भागफल में दशमलव बिंदु विस्थापित हो गया है। किस तरफ़ और कितने स्थानों से? दशमलव बिंदु बाईं तरफ़ एक स्थान से विस्थापित हो गया है। ध्यान दीजिए 10 में 1 के अतिरिक्त एक शून्य है।
अब 31.5 ÷ 100 = 0.315 की चर्चा करते हैं। 31.5 और 0.315 में अंक एक जैसे हैं परंतु भागफल में दशमलव बिंदु के बारे में क्या कह सकते हैं? यह बाईं तरफ दो स्थानों से विस्थापित हो गया है। ध्यान दीजिए 100 में 1 के अतिरिक्त दो शून्य हैं।
इस प्रकार हम कह सकते हैं कि किसी संख्या को 10, 100 अथवा 1000 से भाग करने पर संख्या एवं भागफल के अंक एक जैसे हैं परंतु भागफल में दशमलव बिंदु बाईं तरफ उतने ही स्थानों से विस्थापित हो जाता है जितने 1 के साथ शून्य होते हैं। इस प्रेक्षण का उपयोग करते हुए अब हम शीघ्रतापूर्वक निम्नलिखित को ज्ञात करते हैं,
2.38 ÷ 10 = 0.238
2.38 ÷ 100 = 0.0238
2.38 ÷ 1000 = 0.00238
2.7.2 पूर्ण संख्या से दशमलव संख्या की भाग
आइए, हम  ज्ञात करते हैं। याद कीजिए हम इसे 6.4 ÷ 2 के रूप में भी लिखते हैं।
ज्ञात करते हैं। याद कीजिए हम इसे 6.4 ÷ 2 के रूप में भी लिखते हैं।
इसलिए, जैसा कि हमने भिन्नों से सीखा हैप्रयास कीजिए
6.4 ÷ 2 =  ÷ 2
÷ 2
= 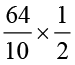
अथवा, आइए सर्वप्रथम हम 64 को 2 से भाग करते है। हम 32 प्राप्त करते हैं। 6.4 में दशमलव बिंदु के दाईं तरफ एक अंक है। 32 में दशमलव इस प्रकार रखिए ताकि दशमलव के दाईं तरफ़ केवल एक ही अंक रह पाए। हम फिर से 3.2 प्राप्त करते हैं।


19.5 ÷ 5 ज्ञात करने के लिए पहले 195 ÷ 5 ज्ञात कीजिए। हम 39 प्राप्त करते हैं। 19.5 में दशमलव बिंदु के दाईं तरफ़ एक अंक है। 39 में दशमलव बिंदु को इस प्रकार रखिए ताकि इसके दाईं तरफ़ केवल एक अंक रह पाए। आप 3.9 प्राप्त करेंगे।
अब 12.96 ÷ 4 = 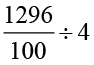
= 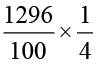
= 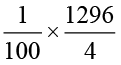
= 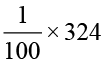 = 3.24
= 3.24
अथवा, 1296 को 4 से भाग दीजिए। आप 324 प्राप्त करते हैं। 12.96 में दशमलव बिंदु के दाईं ओर 2 अंक हैं। 324 में इसी प्रकार दशमलव रखते हुए आप 3.24 प्राप्त करेंगे।
ध्यान दीजिए यहाँ और इससे अगले परिच्छेद में हमने केवल एेसे विभाजनों की चर्चा की है जिनमें, दशमलव को ध्यान में न रखकर, एक संख्या को दूसरी संख्या से पूरी तरह विभाजित किया जा सकेगा अर्थात् शेषफल के रूप में शून्य प्राप्त होगा। जैसा कि 19.5 ÷ 5 में, जब 195 को 5 से विभाजित किया जाता है तो शेषफल शून्य प्राप्त होता है।
यद्यपि एेसी भी स्थितियाँ हैं जिनमें कोई संख्या किसी दूसरी संख्या से पूरी तरह विभाजित नहीं की जा सकती अर्थात् हमें शेषफल के रूप में शून्य की प्राप्ति नहीं होती है। उदाहरणतः 195 ÷ 7 एेसी स्थितियों के बारे में हम अगली कक्षाओं में चर्चा करेंगे।
उदाहरण 9
4.2, 3.8 और 7.6 का औसत ज्ञात कीजिए।
हल
4.2, 3.8 और 7.6 का औसत
=
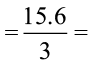 5.2 होगा।
5.2 होगा।
2.7.3 एक दशमलव संख्या का दूसरी दशमलव संख्या से भाग
आइए हम 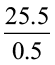 अर्थात् 25.5 ÷ 0.5 ज्ञात करते हैं।
अर्थात् 25.5 ÷ 0.5 ज्ञात करते हैं।
हम पाते हैंः 25.5 ÷ 0.5 = 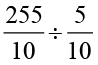 =
= 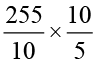 = 51
= 51
अतः 25.5 ÷ 0.5 = 51
आप क्या देखते हैं? 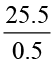 के लिए हम पाते हैं कि 0.5 में दशमलव के दाईं तरफ़ एक अंक है। इसको 10 से भाग करने पर पूर्ण संख्या में परिवर्तित किया जा सकता है। इसी तरह से 25.5 को भी 10 से भाग करके एक भिन्न में परिवर्तित किया गया है।
के लिए हम पाते हैं कि 0.5 में दशमलव के दाईं तरफ़ एक अंक है। इसको 10 से भाग करने पर पूर्ण संख्या में परिवर्तित किया जा सकता है। इसी तरह से 25.5 को भी 10 से भाग करके एक भिन्न में परिवर्तित किया गया है।
अथवा हम कहते हैं कि 0.5 को 5 बनाने के लिए दशमलव बिंदु को दाईं तरफ़ एक स्थान से विस्थापित किया गया है।

इसलिए 25.5 में भी दशमलव बिंदु को दाईं तरफ़ एक स्थान से विस्थापित करके 225 में परिवर्तित किया गया।
अतः 22.5 ÷ 1.5 = 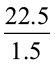 =
= 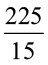 = 15
= 15
इसी प्रकार 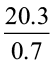 और
और 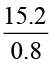 ज्ञात कीजिए।
ज्ञात कीजिए।
आइए अब हम 20.55 ÷ 1.5 ज्ञात करते हैं।
उपर्युक्त चर्चा के अनुसार हम इसे 205.5 ÷ 15 के रूप में लिख सकते हैं। इससे हम 13.7 प्राप्त करते हैं।
 ,
, 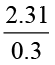 ज्ञात कीजिए।
ज्ञात कीजिए।
अब 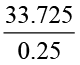 की चर्चा करते हैं। हम इसे
की चर्चा करते हैं। हम इसे 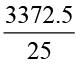 के रूप में लिख सकते हैं (कैसे?) और हम 134.9 के रूप में भागफल प्राप्त करते हैं। आप
के रूप में लिख सकते हैं (कैसे?) और हम 134.9 के रूप में भागफल प्राप्त करते हैं। आप 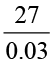 कैसे ज्ञात करेंगे? हम जानते हैं कि 27 को 27.00 के रूप में लिखा जा सकता है।
कैसे ज्ञात करेंगे? हम जानते हैं कि 27 को 27.00 के रूप में लिखा जा सकता है।
इसलिए 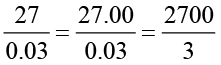 = ?
= ?
उदाहरण 10
एक सम बहुभुज की प्रत्येक भुजा की लंबाई 2.5 cm है। बहुभुज का परिमाप 12.5 cm है। इस बहुभुज की कितनी भुजाएँ हैं?
हल
सम बहुभुज का परिमाप इसकी सभी समान भुजाओं की लंबाई का योग होता है = 12.5 cm
प्रत्येक भुजा की लंबाई = 2.5 cm
अतः भुजाओं की संख्या =  =
= 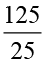 = 5
= 5
बहुभुज की 5 भुजाएँ हैं।
उदाहरण 11
एक कार 2.2 घंटे में 89.1 km की दूरी तय करती है। कार द्वारा 1 घंटे में तय की गई औसत दूरी कितनी है?
हल
कार द्वारा तय की गई दूरी = 89.1 km
इस दूरी को तय करने में लिया गया समय = 2.2 घंटे
इसलिए कार द्वारा 1 घंटे में तय की गई दूरी = 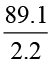
=  = 40.5 km
= 40.5 km
प्रश्नावली 2.7
1. ज्ञात कीजिए :
(i) 0.4 ÷ 2 (ii) 0.35 ÷ 5 (iii) 2.48 ÷ 4
(iv) 65.4 ÷ 6 (v) 651.2 ÷ 4 (vi) 14.49 ÷ 7
(vii) 3.96 ÷ 4 (viii) 0.80 ÷ 5
2. ज्ञात कीजिए :
(i) 4.8 ÷ 10 (ii) 52.5 ÷ 10 (iii) 0.7 ÷ 10
(iv) 33.1 ÷ 10 (v) 272.23 ÷ 10 (vi) 0.56 ÷ 10
(vii) 3.97 ÷10
3. ज्ञात कीजिए :
(i) 2.7 ÷ 100 (ii) 0.3 ÷ 100 (iii) 0.78 ÷ 100
(iv) 432.6 ÷ 100 (v) 23.6 ÷100 (vi) 98.53 ÷ 100
4. ज्ञात कीजिए :
(i) 7.9 ÷ 1000 (ii) 26.3 ÷ 1000
(iii) 38.53 ÷ 1000 (iv) 128.9 ÷ 1000 (v) 0.5 ÷ 1000
5. ज्ञात कीजिए :
(i) 7 ÷ 3.5 (ii) 36 ÷ 0.2 (iii) 3.25 ÷ 0.5
(iv) 30.94 ÷ 0.7 (v) 0.5 ÷ 0.25 (vi) 7.75 ÷ 0.25
(vii) 76.5 ÷ 0.15 (viii) 37.8 ÷ 1.4 (ix) 2.73 ÷ 1.3
6. एक गाड़ी 2.4 लीटर पैट्रोल में 43.2 km की दूरी तय करती है। यह गाड़ी एक लीटर पैट्रोल में कितनी दूरी तय करेगी?
हमने क्या चर्चा की?
1. हमने पिछली कक्षा में भिन्न एवं दशमलव के बारे में, तथा उन पर योग एवं व्यवकलन की संक्रियाओं सहित अध्ययन किया है।
2. अब हमने भिन्नों एवं दशमलवों पर गुणन एवं भाग की संक्रियाओं का अध्ययन किया है।
3. हमने अध्ययन किया है कि भिन्नों को कैसे गुणा किया जाए। दो भिन्नों को गुणा करने के लिए उनके अंशों एवं हरों को पृथक्-पृथक् गुणा किया जाता है और फिर गुणनफल को 
उदाहरणार्थ 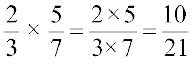
4. भिन्न, प्रचालक ‘का’ के रूप में काम करती है।
उदाहरणतः 2 का 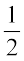 होता है
होता है 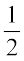 × 2 = 1
× 2 = 1
5. (a) दो उचित भिन्नों का गुणनफल, गुणा किए गए प्रत्येक भिन्न से कम होता है।
(b) एक उचित और एक विषम भिन्न का गुणनफल विषम भिन्न से कम होता है और उचित भिन्न से अधिक होता है।
(c) दो विषम भिन्नों का गुणनफल, गुणा किए गए दोनों भिन्नों में से प्रत्येक से बड़ा होता है।
6. एक भिन्न का व्युत्क्रम इसके अंश और हर को परस्पर बदलने से प्राप्त होता है।
7. हमने देखा है कि दो भिन्नों को कैसे भाग दिया जाता है :
(a) एक पूर्ण संख्या को किसी भिन्न से भाग करते समय हम पूर्ण संख्या को भिन्न के व्युत्क्रम से गुणा करते हैं।
उदाहरणतः 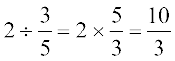
(b) एक भिन्न को पूर्ण संख्या से भाग करने के लिए हम भिन्न को पूर्ण संख्या के व्युत्क्रम से गुणा करते हैं।
उदाहरणतः 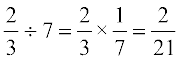
(c) एक भिन्न को दूसरी भिन्न से भाग करने के लिए हम पहली भिन्न को दूसरी भिन्न के व्युत्क्रम से गुणा करते हैं। इसलिए 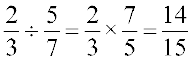 .
.
8. हमने यह भी सीखा है कि दो दशमलव संख्याएँ कैसे गुणा की जाती हैं। दो दशमलव संख्याओं को गुणा करने के लिए सर्वप्रथम हम उन्हें पूर्ण संख्याओं के रूप में गुणा करते हैं। दोनों दशमलव संख्याओं में दशमलव बिंदु के दाईं तरफ़ अंकों की संख्या को गिनते हैं। गिनी हुई अंकों की संख्या का योग ज्ञात करते हैं। सबसे दाएँ स्थान से अंकों को गिनते हुए गुणनफल में दशमलव बिंदु रखा जाता है। यह गिनती पूर्व में प्राप्त योग के समान होनी चाहिए।
उदाहरणतः 0.5 × 0.7 = 0.35
9. एक दशमलव संख्या को 10, 100 अथवा 1000 से गुणा करने के लिए हम उस संख्या में दशमलव बिंदु को दाईं तरफ उतने ही स्थान से विस्थापित करते हैं जितने 1 के अतिरिक्त शून्य होते हैं।
अतः 0.53 × 10 = 5.3, 0.53 × 100 = 53, 0.53 × 1000 = 530
10. हमने देखा है कि दशमलव संख्याएँ कैसे विभाजित की जाती है।
(a) एक दशमलव संख्या को पूर्ण संख्या से भाग करने के लिए सर्वप्रथम हम उन्हें पूर्ण संख्याओं के रूप में भाग देते हैं। तब भागफल में दशमलव बिंदु को वैसे ही रखा जाता है जैसे दशमलव संख्या में।
उदाहरणतः 8.4 ÷ 4 = 2.1
ध्यान दीजिए हम यहाँ पर केवल एेसे विभाजनों की बात कर रहे हैं जिनमें शेषफल शून्य है।
(b) एक दशमलव संख्या को 10, 100 अथवा 1000 से भाग करने के लिए दशमलव संख्या में दशमलव बिंदु को बाईं तरफ़ उतने ही स्थान से विस्थापित करते हैं जितने 1 के अतिरिक्त शून्य होते हैं। इस प्रकार भागफल की प्राप्ति होती है।
इसलिए, 23.9 ÷ 10 = 2.39, 23.9 ÷ 100 = 0 .239, 23.9 ÷ 1000 = 0.0239
(c) दो दशमलव संख्याओं को भाग करते समय सर्वप्रथम हम दोनों संख्याओं में दशमलव बिंदु को दाईं तरफ़ समान स्थानों से विस्थापित करते हैं और तब भाग देते हैं। अतः
2.4 ÷ 0.2 = 24 ÷ 2 = 12.