Table of Contents
4.1 बौद्धिक खेल!

अध्यापिका ने कहा है कि वह गणित का एक नया अध्याय पढ़ाना प्रारंभ करने जा रही हैं और वह है सरल समीकरण। अप्पू, सरिता और अमीना ने कक्षा VI में पढ़े गए बीजगणित वाले अध्याय का पुर्नावलोकन कर लिया है। क्या आपने भी कर लिया है? अप्पू, सरिता और अमीना उत्साहित हैं क्याेंकि उन्होंने एक खेल बनाया है, जिसे वे बौद्धिक खेल (mind reader) कहती हैं तथा वे उसे पूरी कक्षा के सम्मुख प्रस्तुत करना चाहती हैं।
अध्यापिका उनके उत्साह की सराहना करती है और उन्हें अपना खेल प्रस्तुत करने के लिए आमंत्रित करती है। अमीना खेल प्रारंभ करती है। वह सारा से कोई संख्या सोचने को कहती हैै तथा उसे 4 से गुणा करके गुणनफल में 5 जोड़ने को कहती है। इसके बाद वह सारा से इसका परिणाम बताने को भी कहती है। सारा कहती है कि परिणाम 65 है। अमीना तुरंत घोषणा करती है कि सारा द्वारा सोची गई संख्या 15 है। सारा सिर हिलाकर हाँ कहती है। सारा समेत पूरी कक्षा आश्चर्यचकित हो जाती है।
अब अप्पू की बारी है। वह बालू से कोई संख्या सोचने, उसे 10 से गुणा करने और गुणनफल में से 20 घटाने को कहता है। इसके बाद वह बालू से उसका परिणाम बताने को कहता है। बालू कहता है कि यह 50 है। अप्पू तुरंत बालू द्वारा सोची गई संख्या बताता है और कहता है कि वह संख्या 7 है। बालू इसकी पुष्टि करता है।
प्रत्येक व्यक्ति यह जानना चाहता है कि अप्पू, सरिता और अमीना द्वारा प्रस्तुत बौद्धिक खेल किस प्रकार कार्य करता है। क्या आप देख सकते हैं कि यह कैसे कार्य करता है? इस अध्याय और अध्याय 12 को पढ़ने के बाद, आप भली-भाँति यह जान जाएँगे कि यह खेल किस प्रकार कार्य करता है।
4.2 समीकरण बनाना
आइए अमीना का उदाहरण लें। अमीना सारा से कोई संख्या सोचने को कहती है। अमीना संख्या के बारे में कुछ नहीं जानती है। उसके लिए, यह संख्या 1, 2, 3, . . ., 11, . . . , 100, . . . . में से कुछ भी हो सकती है। आइए इस अज्ञात संख्या को एक अक्षर x से व्यक्त करें। आप x के स्थान पर कोई अन्य अक्षर जैसे y, t इत्यादि का प्रयोग कर सकते हैं। इससे कोई प्रभाव नहीं पड़ता कि सारा द्वारा सोची गई अज्ञात संख्या के लिए हम कौन-सा अक्षर प्रयोग करते हैं। सारा जब संख्या को 4 से गुणा करती है, तो उसे 4x प्राप्त होता है। फिर वह इस गुणनफल में 5 जोड़ती है और 4x + 5 प्राप्त करती है। (4x + 5) का मान x के मान पर निर्भर करता है। इस प्रकार, यदि x = 1 है, तो 4x + 5 = 4 ×1 + 5 = 9 है। इसका अर्थ है कि यदि सारा के मस्तिष्क में 1 होता, तो उसके द्वारा प्राप्त परिणाम 9 होता। इसी प्रकार, यदि उसने संख्या 5 सोची होती, तो उसका x = 5 के लिए 4x + 5 = 4 × 5 + 5 = 25 । यानी, सारा ने यदि संख्या 5 सोची होती तो उसका परिणाम 25 होता।
सारा द्वारा सोची संख्या ज्ञात करने के लिए, आइए उसके द्वारा प्राप्त उत्तर 65 से विपरीत की ओर कार्य करना प्रारंभ करें। हमें एेसा x ज्ञात करना है कि
4x + 5 = 65 (4.1)
इस समीकरण (equation) का हल ही हमें सारा के मन की संख्या को बताएगा।
इस प्रकार, आइए अब अप्पू के उदाहरण पर विचार करें। आइए बालू द्वारा चुनी गई संख्या को y मान लें। अप्पू ने बालू से इस संख्या को 10 से गुणा कर और फिर गुणनफल में से 20 घटाने को कहा था। अर्थात् बालू y से, पहले 10y प्राप्त करता है और उसमें से 20 घटा कर (10y – 20) प्राप्त करता है। इसका ज्ञात परिणाम 50 है।
अतः, 10y – 20 = 50 (4.2)
इस समीकरण का हल ही बालू द्वारा सोची गई संख्या बताएगा।
4.3 जो हमें ज्ञात है उसकी समीक्षा
ध्यान दीजिए कि (4.1) और (4.2) समीकरण हैं। आइए याद करें कि कक्षा VI में हमने समीकरणों के बारे में क्या पढ़ा था। समीकरण चर पर एक प्रतिबंध होता है। समीकरण (4.1) में, चर x है तथा समीकरण (4.2) में, चर y है।
शब्द चर (variable) का अर्थ है, एेसी कोई वस्तु जो विचरण कर, अर्थात् बदल सकती हो। एक चर विभिन्न संख्यात्मक मान ले (ग्रहण कर) सकता है, अर्थात् इसका मान निश्चित या स्थिर नहीं होता है। चरों को प्रायः अंग्रेज़ी वर्णमाला के अक्षरों x, y, z, l, m, n, p इत्यादि से व्यक्त किया जाता है। चरों से हम व्यंजकों (expressions) को बनाते हैं। ये व्यंजक चरों पर योग, व्यवकलन, गुणन और विभाजन जैसी संक्रियाएँ करके प्राप्त किए (बनाए) जाते हैं। x से हमने व्यंजक (4x + 5) बनाया था। इसके लिए, हमने पहले x को 4 से गुणा किया और फिर गुणनफल में 5 जोड़ा था। इसी प्रकार, हमने y से व्यंजक (10y – 20) बनाया था। इसके लिए, हमने y को 10 से गुणा किया और फिर गुणनफल में से 20 को घटाया था। ये सभी व्यंजकों के उदाहरण हैं।
उपरोक्त प्रकार के बनाए गए एक व्यंजक का मान, चर के चुने गए मान पर निर्भर करता है। जैसा कि हम पहले ही देख चुके हैं कि जब x = 1 है, तो 4x + 5 = 9 है; जब
x = 5 है, तो 4x + 5 = 25 है इसी प्रकार,
जब x = 15, तो 4 x + 5 = 4×15 + 5 = 65 है;
जब x = 0, तो 4 x + 5 = 4 × 0 + 5 = 5 है, इत्यादि।
समीकरण (4.1) चर x पर एक प्रतिबंध है। यह बताती है कि व्यंजक 4x + 5 का मान 65 है। यह प्रतिबंध x = 15 होने पर संतुष्ट होता है। संख्या 15 समीकरण 4x + 5 = 65 का एक हल (solution) है। जब x = 5 है, तो 4x + 5 = 25 है जो 65 के बराबर नहीं है। इस प्रकार,
x = 5 इस समीकरण का हल नहीं है। इसी प्रकार, x = 0 भी इस समीकरण का हल नहीं है। 15 के अतिरिक्त, x का कोई भी मान प्रतिबंध 4x + 5 = 65 को संतुष्ट नहीं करता है।
प्रयास कीजिये
व्यंजक (10y – 20) का मान y के मान पर निर्भर करता है। y को पाँच भिन्न-भिन्न मान देकर तथा y के प्रत्येक मान के लिए (10 y – 20) का मान ज्ञात करके इसकी पुष्टि कीजिए। (10 y – 20) के प्राप्त किए गए विभिन्न मानों से, क्या आप 10y – 20 = 50 का कोई हल देख रहे हैं? यदि कोई हल प्राप्त नहीं हुआ हे, तो y को कुछ अन्य मान देकर, ज्ञात कीजिए कि प्रतिबंध 10y – 20 = 50 संतुष्ट होता है या नहीं।
4.4 समीकरण क्या है?
एक समीकरण में, समता या समिका (equality) का चिह्न सदैव होता है। समता का चिह्न यह दर्शाता है कि इस चिह्न के बाईं ओर के व्यंजक [बायाँ पक्ष (LHS)] का मान चिह्न के दाईं ओर के व्यंजक [दायाँ पक्ष (RHS)] के मान के बराबर है। समीकरण (4.1) में, L.H.S (4x + 5) है तथा RHS 65 है। समीकरण (4.2) में, LHS (10y – 20) तथा RHS 50 है।
यदि LHS और RHS के बीच में समता चिह्न के अतिरिक्त कोई अन्य चिह्न हो, तो वह एक समीकरण नहीं होती है। इसलिए 4x + 5 > 65 एक समीकरण नहीं है।
यह कथन हमें बताता है कि (4x + 5) का मान 65 से अधिक है।
इसी प्रकार, 4x + 5 < 65 भी एक समीकरण नहीं है। यह कथन हमें बताता है कि (4x + 5) का मान 65 से कम है।
समीकरणों में हम प्रायः यह देखते हैं कि RHS केवल एक संख्या है। समीकरण (4.1) में यह 65 है तथा समीकरण (4.2) में यह 50 है। परंतु एेसा होना सदैव आवश्यक नहीं है। एक समीकरण का दायाँ पक्ष (RHS) चर से संबद्ध एक व्यंजक भी हो सकता है। उदाहरणार्थ, समीकरण
4x + 5 = 6x – 25
में समता चिह्न के बाईं ओर व्यंजक 4x + 5 है तथा उसके दाईं ओर व्यंजक 6x – 25 है।
संक्षिप्त रूप में, एक समीकरण चर पर एक प्रतिबंध होता है। प्रतिबंध यह है कि दोनों व्यंजकों के मान बराबर होने चाहिए। ध्यान दीजिए कि इन दोनों व्यंजकों में से कम से कम एक में चर अवश्य होना चाहिए।
हम समीकरणों का एक सरल और उपयोगी गुण देखते हैं। समीकरण 4x +5 = 65 वही है जो समीकरण 65 = 4x + 5 है। इसी प्रकार, समीकरण 6x – 25 = 4x +5 वही है जो समीकरण 4x + 5 = 6x – 25 है। किसी समीकरण के बाएँ और दाएँ पक्षों के व्यंजकों को आपस में बदलने पर, समीकरण वही रहती है। यह गुण बहुधा समीकरणों को हल करने में उपयोगी रहता है।
उदाहरण 1
निम्नलिखित कथनों को समीकरणों के रूप में लिखिए :
(i) x के तिगुने और 11 का योग 32 है।
(ii) यदि किसी संख्या के 6 गुने में से आप 5 घटाएँ, तो 7 प्राप्त होता है।
(iii) m का एक चौथाई 7 से 3 अधिक है।
(iv) किसी संख्या के एक तिहाई में 5 जोड़ने पर 8 प्राप्त होता है ।
हल
(i) x का तिगुना 3x है।
3x और 11 का योग 3x + 11 है। यह योग 32 है।
अतः, वांछित समीकरण 3x + 11 = 32 है।
(ii) आइए मान लें कि यह संख्या z है। z को 6 से गुणा करने पर 6z प्राप्त होता है।
6z में से 5 घटाने पर 6z – 5 प्राप्त होगा। यह परिणाम 7 है।
अतः, वांछित समीकरण 6z – 5 = 7 है।
(iii) m का एक चौथाई 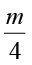 है।
है।
यह 7 से 3 अधिक है। इसका अर्थ है कि अंतर (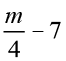 ) बराबर 3 है।
) बराबर 3 है।
अतः, वांछित समीकरण 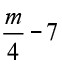 = 3 है।
= 3 है।
(iv) वांछित संख्या को n मान लीजिए। n का एक तिहाई 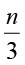 है।
है।
उपरोक्त एक-तिहाई जमा 5, 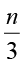 + 5 है। यह 8 के बराबर है ।
+ 5 है। यह 8 के बराबर है ।
अतः, वांछित समीकरण 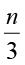 + 5 = 8 है।
+ 5 = 8 है।
उदाहरण 2
निम्नलिखित समीकरणों को सामान्य कथनों के रूप में बदलिए ः
(i) x – 5 = 9 (ii) 5p = 20 (iii) 3n + 7 = 1 (iv) 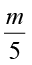 – 2 = 6
– 2 = 6
हल
(i) x में से 5 निकालने पर 9 प्राप्त होता है।
(ii) एक संख्या p का पाँच गुना 20 है।
(iii) 1 प्राप्त करने के लिए n के तीन गुने में 7 जोड़िए।
(iv) किसी संख्या m के 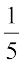 वें भाग में से 2 घटाने पर 6 प्राप्त होता है।
वें भाग में से 2 घटाने पर 6 प्राप्त होता है।
यहाँ ध्यान देने योग्य एक महत्वपूर्ण बात यह है कि एक दिए हुए समीकरण को, केवल एक ही नहीं, बल्कि अनेक सामान्य कथनों के रूप दिए जा सकते हैं। उदाहरणार्थ, उपरोक्त समीकरण (i) के लिए आप कह सकते हैं ः
x में से 5 घटाइए। आपको 9 प्राप्त होता है।
अथवा संख्या x, 9 से 5 अधिक है।
अथवा 9 संख्या x से 5 कम है।
अथवा x और 5 का अंतर 9 है; इत्यादि।
प्रयास कीजिए
उपरोक्त समीकरणों (ii), (iii) और (iv) में से प्रत्येक के लिए, कम से कम एक अन्य कथन के रूप में लिखिए ।
उदाहरण 3
निम्नलिखित स्थिति पर विचार कीजिए :
राजू के पिता की आयु राजू की आयु के तीन गुने से 5 वर्ष अधिक है। राजू के पिता की आयु 44 वर्ष है। राजू की आयु ज्ञात करने के लिए, एक समीकरण बनाइए (स्थापित कीजिए)।
हल
हमें राजू की आयु ज्ञात नहीं है। आइए इसे y वर्ष मान लें। राजू की आयु का तीन गुना 3y वर्ष है। राजू के पिता की आयु 3y वर्ष से 5 वर्ष अधिक है। अर्थात् राजू के पिता की आयु (3y + 5) वर्ष है। यह भी दिया है कि राजू के पिता की आयु 44 वर्ष है।
अतः, 3y + 5 = 44 (4.3)
यह चर y में एक समीकरण है। इसे हल करने पर राजू की आयु ज्ञात हो जाएगी।
उदाहरण 4
एक दुकानदार दो प्रकार की पेटियों में आम बेचता है। ये पेटियाँ छोटी और बड़ी हैं। एक बड़ी पेटी में 8 छोटी पेटियों के बराबर आम और 4 खुले आम आते हैं। प्रत्येक छोटी पेटी में आमों की संख्या बताने वाला एक समीकरण बनाइए। दिया हुआ है कि एक बड़ी पेटी में आमों की संख्या 100 है।
हल
मान लीजिए कि एक छोटी पेटी में m आम हैं। एक बड़ी पेटी में m के 8 गुने से 4 अधिक आम हैं। अर्थात् एक बड़ी पेटी में 8m + 4 आम हैं। परंतु यह संख्या 100 दी हुई है। इस प्रकार,
8m + 4 = 100 (4.4)
इस समीकरण को हल करके, आप एक छोटी पेटी के आमों की संख्या ज्ञात कर सकते हैं।
प्रश्नावली 4.1
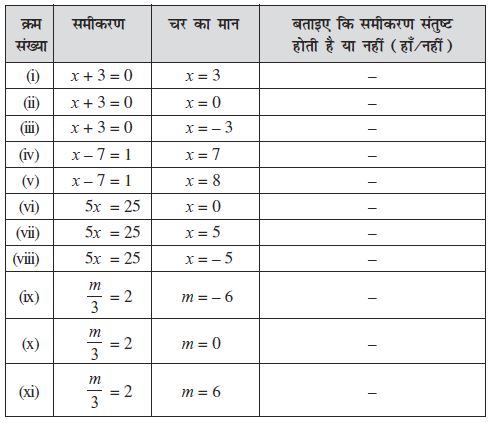
1. निम्नलिखित सारणी के अंतिम स्तंभ को पूरा कीजिए :
2. जाँच कीजिए कि कोष्ठकों में दिये हुए मान, दिए गए संगत समीकरणों के हल हैं या नहीं :
(a) n + 5 = 19 (n = 1) (b) 7n + 5 = 19 (n = – 2) (c) 7n + 5 = 19 (n = 2)
(d) 4p – 3 = 13 (p = 1) (e) 4p – 3 = 13 (p = – 4) (f) 4p – 3 = 13 (p = 0)
3. प्रयत्न और भूल विधि से निम्नलिखित समीकरणों को हल कीजिए :
(i) 5p + 2 = 17 (ii) 3m – 14 = 4
4. निम्नलिखित कथनों के लिए समीकरण दीजिए :
(i) संख्याओं x और 4 का योग 9 है। (ii) y में से 2 घटाने पर 8 प्राप्त होते हैं।
(iii) a का 10 गुना 70 है। (iv) संख्या b को 5 से भाग देने पर 6 प्राप्त होता है।
(v) t का तीन-चौथाई 15 है।
(vi) m का 7 गुना और 7 का योगफल आपको 77 देता है।
(vii) एक संख्या x की चौथाई ऋण 4 आपको 4 देता है।
(viii) यदि आप y के 6 गुने में से 6 घटाएँ, तो आपको 60 प्राप्त होता है।
(ix) यदि आप z के एक-तिहाई में 3 जोड़ें, तो आपको 30 प्राप्त होता है।
5. निम्नलिखित समीकरणों को सामान्य कथनों के रूप में लिखिए :
(i) p + 4 = 15 (ii) m – 7 = 3 (iii) 2m = 7 (iv) 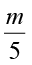 = 3
= 3
(v) 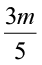 = 6 (vi) 3p + 4 = 25 (vii) 4p – 2 = 18 (viii)
= 6 (vi) 3p + 4 = 25 (vii) 4p – 2 = 18 (viii) 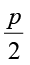 + 2 = 8
+ 2 = 8
6. निम्नलिखित स्थितियों में समीकरण बनाइए :
(i) इरफान कहता है कि उसके पास, परमीत के पास जितने कँचे हैं उनके पाँच गुने से 7 अधिक कँचे हैं। इरफान के पास 37 कँचे हैं। (परमीत के कँचों की संख्या को m लीजिए।)
(ii) लक्ष्मी के पिता की आयु 49 वर्ष है। उनकी आयु, लड़की की आयु के तीन गुने से 4 वर्ष अधिक है। (लक्ष्मी की आयु को y वर्ष लीजिए।)
(iii) अध्यापिका बताती हैं कि उनकी कक्षा में एक विद्यार्थी द्वारा प्राप्त किए गए अधिकतम अंक, प्राप्त किए न्यूनतम अंक का दुगुना धन 7 हैं। प्राप्त किए गए अधिकतम अंक 87 हैं। (न्यूनतम प्राप्त किए गए अंकों को l लीजिए।)
(iv) एक समद्विबाहु त्रिभुज में शीर्ष कोण प्रत्येक आधार कोण का दुगुना है। (मान लीजिए प्रत्येक आधार कोण b डिग्री है। याद रखिए कि त्रिभुज के तीनों कोणों का योग 180 डिग्री होता है।)
4.4.1 एक समीकरण को हल करना
इस समिका पर विचार कीजिए
8 – 3 = 4 + 1 (4.5)
समिका (4.5) सत्य है, क्योंकि इसके दोनों पक्ष बराबर हैं (प्रत्येक 5 के बराबर है)।
आइए दोनों पक्षों में 2 जोड़ें। इसके परिणामस्वरूप, हमें प्राप्त होता हैः
LHS = 8 – 3 + 2 = 5 + 2 = 7, RHS = 4 + 1 + 2 = 5 + 2 = 7.
पुनः, समिका (4.5) सत्य है (अर्थात LHS और RHS समान हैं)।
इस प्रकार, यदि हम एक समिका के दोनों पक्षों में एक ही संख्या जोड़ें, तो भी वह समिका सत्य होती है।
आइए अब दोनों पक्षों में से 2 घटाइए। इसके परिणामस्वरूप, हमें प्राप्त होता है :
LHS = 8 – 3 – 2 = 5 – 2 = 3, RHS = 4 + 1 – 2 = 5 – 2 = 3.
पुनः, वह समिका सत्य है।
इस प्रकार, यदि हम एक समिका के दोनों पक्षों में से एक ही संख्या घटाएँ, तो भी वह समिका सत्य होती है।
इसी प्रकार, यदि हम एक समिका के दोनों पक्षों को एक ही शून्येतर (non-zero) संख्या से गुणा करें या भाग दें, तो भी वह समिका सत्य होती है।
उदाहरणार्थ, आइए उपरोक्त समिका के दोनों पक्षों को 3 से गुणा करें। हमें प्राप्त होता है ः
LHS = 3 × (8 – 3) = 3 × 5 = 15, RHS = 3 × (4 + 1) = 3 × 5 = 15.
समिका सत्य है।
आइए अब हम उपरोक्त समिका के दोनों पक्षों को 2 से भाग करें ।
LHS = 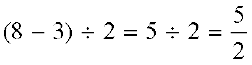
RHS = 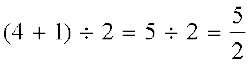 = LHS
= LHS
पुनः, समिका सत्य है।
यदि हम कोई अन्य समिका लें, तो भी हमें यही निष्कर्ष प्राप्त होता है।
मान लीजिए कि हम इस नियम का पालन नहीं करते हैं। विशेष रूप से, मान लीजिए कि हम एक समिका के दोनों पक्षों में भिन्न-भिन्न संख्याएँ जोड़ते हैं। इस स्थिति में, हम देखेंगे कि समिका सत्य नहीं होगी (अर्थात दोनों पक्ष समान नहीं होंगे)। उदाहरणार्थ, आइए समिका (4.5) को पुनः लें ः
8 – 3 = 4 + 1
अब, इसके बाएँ पक्ष में 2 जोड़ें और दाएँ पक्ष में 3 जोड़े। अब नई LHS = 8 – 3 + 2 = 5 + 2 = 7 है तथा नई RHS = 4 + 1 + 3 = 5 + 3 = 8 है। अब, समिका सत्य नहीं है, क्योंकि नई LHS और RHS बराबर नहीं हैं।
इस प्रकार, यदि हम एक समिका के दोनों पक्षों में, कोई गणितीय संक्रिया एक ही संख्या के साथ न करें, तो समिका सत्य नहीं हो सकती है।
समीकरण, एक चरों वाली समिका होती है।

उपरोक्त निष्कर्ष समीकरणों के लिए भी मान्य होते हैं, क्योंकि प्रत्येक समीकरण में चर केवल संख्या ही निरूपित करता है।
प्रायः एक समीकरण को एक तौलने वाली तराजू या तुला (balance) समझा जाता है। एक समीकरण पर एक गणितीय संक्रिया करना इस प्रकार समझना चाहिए, जैसे कि तौलने वाली तराजू के दोनों पलड़ों में बराबर बाँट डालना या उनमें से बराबर बाँट निकाल लेना।
[एक समीकरण एक एेसी तौलने वाली तराजू समझा जा सकता है, जिसके दोनों पलड़ों में बराबर बाँट रखे हों।] इस स्थिति में, तराजू की डंडी ठीक क्षैतिज रहती है। यदि हम दोनों पलड़ों में बराबर बाँट (weights) डालें, तो डंडी अभी भी क्षैतिज ही रहती है। इसी प्रकार, यदि हम दोनों पलड़ों में से बराबर बाँट हटा लें (निकालें), तो भी डंडी क्षैतिज रहती है। इसके विपरीत, यदि हम दोनों पलड़ों में भिन्न बाँट डालें (जोड़ें) या उनमें से भिन्न बाँट निकालें (घटाएँ), तो भी तराजू की डंडी का संतुलन बिगड़ जाता है, अर्थात् डंडी क्षैतिज पर नहीं रहती है।
हम यह सिद्धांत एक समीकरण को हल करने में प्रयोग करते हैं। निस्संदेह, यहाँ तराजू काल्पनिक है तथा संख्याओं को बाँटों की तरह भौतिक रूप से संतुलित करने के लिए प्रयोग नहीं किया जा सकता। इस सिद्धांत को प्रस्तुत करने का यही मुख्य उद्देश्य है। आइए कुछ उदाहरण लें।
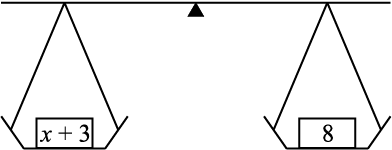
हम 3 को क्यों घटाएँ कोई और संख्या क्यों न घटाएँ? 3 को जोड़ कर देखिए। क्या यह कुछ सहायता करेगा? क्यों नहीं?
निम्नलिखित समीकरण पर विचार कीजिएः
x + 3 = 8 (4.6)
हम इस समीकरण के दोनों पक्षों में से 3 को घटाते हैं।
नई LHS है ः x + 3 – 3 = x तथा नई RHS है ः 8 – 3 = 5
चूँकि इससे संतुलन में कोई परिवर्तन नहीं होता है, इसलिए हमें प्राप्त होता है :
नई LHS = नई RHS या x = 5
यह वही है, जो हम चाहते हैं। अर्थात् यह समीकरण (4.6) का एक हल है।
इसकी पुष्टि करने के लिए कि यह सही है या नहीं, हम प्रारंभिक समीकरण में
x = 5 रखेंगे। हमें LHS = x + 3 = 5 + 3 = 8 प्राप्त होती है, जो RHS के बराबर है। यही हल सही होने के लिए आवश्यक है।
समीकरण के दोनों पक्षों में सही गणितीय संक्रिया करने से (अर्थात् 3 घटाने से), हम समीकरण के हल पर पहुँच गए ।
आइए एक अन्य समीकरण लें :
x – 3 = 10 (4.7)
यहाँ हमें क्या करना चाहिए? हमें दोनों पक्षों में 3 जोड़ना चाहिए। एेसा करने से, समीकरण का संतुलन बना रहेगा तथा L.H.S में केवल x रह जाएगा।
नई LHS = x – 3 + 3 = x , नई RHS = 10 + 3 = 13
अतः x = 13 है, जो वांछित हल है।
प्रारंभिक समीकरण (4.7) में x = 13 रखने पर, हम इसकी पुष्टि करते हैं कि यह हल सही है ः
प्रारंभिक समीकरण की LHS = x – 3 = 13 – 3 = 10 है।
जैसा कि वांछनीय है यह, RHS के बराबर है।
एेसा इसलिए किया है, क्योंकि 3 को घटाने पर L.H.S. में x रह जाता है।
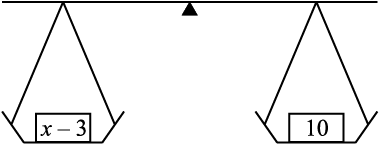
इसी प्रकार, आइए निम्नलिखित समीकरणों को देखें ः
5y = 35 (4.8)
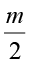 = 5 (4.9)
= 5 (4.9)
पहली स्थिति में, हम दोनों पक्षों को 5 से भाग देंगे। इससे LHS में केवल y रह जाता है।
नई LHS = 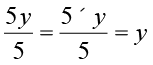 , नई RHS =
, नई RHS = 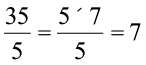
अतः y = 7
यही समीकरण का वांछित हल है। हम समीकरण (4.8) में y = 7 प्रतिस्थापित करके इसकी जाँच कर सकते हैं कि समीकरण संतुष्ट हो जाता है।
दूसरी स्थिति में, हम दोनों पक्षों को 2 से गुणा करते हैं। इससे LHS में केवल m रह जाता है।
नई LHS = 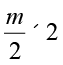 = m. तथा नई RHS = 5 × 2 = 10 है।
= m. तथा नई RHS = 5 × 2 = 10 है।
अतः, m = 10 (यही वांछित हल है। आप इसकी जाँच कर सकते हैं कि यह हल सही है या नहीं)।
उपरोक्त उदाहरणों से यह देखा जा सकता है कि समीकरण के हल करने के लिए, हमें जिस संक्रिया की आवश्यकता पड़ेगी वह समीकरण पर निर्भर करता है। हमारा प्रयास यह होना चाहिए कि समीकरण में चर पृथक् हो जाए। कभी-कभी एेसा करने के लिए, हमें एक से अधिक गणितीय संक्रियाएँ करनी पड़ सकती हैं। इसको मस्तिष्क में रखते हुए, आइए कुछ और समीकरण हल करें।
उदाहरण 5
हल कीजिएः
(a) 3n + 7 = 25 (4.10)
(b) 2p – 1 = 23 (4.11)
हल
(a) हम समीकरण की LHS में चर n को पृथक् करने के लिए, एक चरणबद्ध विधि से कार्य करते हैं। LHS यहाँ 3n + 7 है। पहले हम इसमें से 7 घटाएँगे, जिससे
3n प्राप्त होगा। इससे अगले चरण में, हम इसे 3 से भाग देंगे, जिससे n प्राप्त होगा। याद रखिए कि हमें समीकरण के दोनों पक्षों में एक ही संक्रिया करनी चाहिए। अतः, दोनों पक्षों में से 7 घटाने पर,
3n + 7 – 7 = 25 – 7 (चरण 1)
या, 3n = 18
अब दोनों पक्षों को 3 से भाग दीजिए :
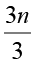 =
= 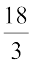 (चरण 2)
(चरण 2)
या, n = 6, जो इसका हल है।
(b) यहाँ हमें क्या करना चाहिए? पहले हम दोनों पक्षों में 1 जोड़ते हैं ः
2p – 1 + 1 = 23 + 1 (चरण 1)
या 2p = 24
अब, दोनों पक्षों को 2 से भाग देते हैं :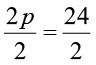 (चरण 2)
(चरण 2)
या p = 12, जो इसका हल है।
आपको एक अच्छी आदत विकसित कर लेनी चाहिए, जो यह है कि प्राप्त किए हल की जाँच अवश्य कर लें। यद्यपि हमने यह (a) के लिए नहीं किया है, परंतु आइए इस उदाहरण (b) के लिए एेसा करें।
आइए इस हल p = 12 को समीकरण में रखें ।
LHS = 2p – 1 = 2 × 12 – 1 = 24 – 1
= 23 = RHS
इस प्रकार, हल की सत्यता की जाँच हो गई।
उपरोक्त (a) के हल की भी अब आप जाँच कर ही लीजिए ।
अब हम इस स्थिति में हैं कि अप्पू, सरिता और अमीना द्वारा प्रस्तुत किए गए बौद्धिक खेल पर वापस जाएँ और समझें कि उन्होंने अपने उत्तर किस प्रकार ज्ञात किए। इस कार्य के लिए, आइए समीकरणों (4.1) और (4.2) को देखें, जो क्रमशः अमीना और अप्पू के उदाहरणों के संगत हैं।
पहले निम्नलिखित समीकरण पर विचार कीजिएः 4x + 5 = 65. (4.1)
दोनों पक्षों में से 5 घटाने पर, 4x + 5 – 5 = 65 – 5.
अर्थात्, 4x = 60
x को पृथक् करने के लिए, दोनों पक्षों को 4 से भाग देने पर, 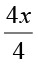 =
= 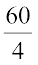
या x = 15, जो वांछित हल है। (जाँच कीजिए कि यह सही है।)
अब निम्नलिखित समीकरण पर विचार कीजिएः
10y – 20 = 50 (4.2)
दोनों पक्षों में, 20 जोड़ने पर, हमें प्राप्त होता हैः
10y – 20 + 20 = 50 + 20 या 10y = 70
दोनों पक्षों को 10 से भाग देने पर, हमें प्राप्त होता है : 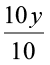 =
= 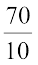
या, y = 7, जो वांछित हल है। (जाँच कीजिए कि यह सही है।)
आप यह अनुभव करेंगे कि ठीक यही उत्तर अप्पू, सरिता और अमीना ने दिए थे। उन्होंने समीकरण बनाना और फिर उन्हें हल करना सीख लिया था। इसी कारण वे अपना बौद्धिक खेल बनाकर संपूर्ण कक्षा पर अपना प्रभाव डाल पाए। हम इस पर अनुच्छेद 4.7 में वापस आएँगे।
प्रश्नवली 4.2
1. पहले चर को पृथक् करने वाला चरण बताइए और फिर समीकरण को हल कीजिए :
(a) x – 1 = 0 (b) x + 1 = 0 (c) x – 1 = 5
(d) x + 6 = 2 (e) y – 4 = – 7 (f) y – 4 = 4
(g) y + 4 = 4 (h) y + 4 = – 4
2. पहले चर को पृथक् करने के लिए प्रयोग किए जाने वाले चरण को बताइए और फिर समीकरण को हल कीजिए :
(a) 3l = 42 (b) 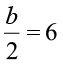 (c)
(c) 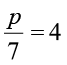 (d) 4x = 25
(d) 4x = 25
(e) 8y = 36 (f) 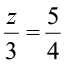 (g)
(g) 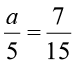 (h) 20t = – 10
(h) 20t = – 10
3. चर को पृथक् करने के लिए, जो आप चरण प्रयोग करेंगे, उसे बताइए और फिर समीकरण को हल कीजिए :
(a) 3n – 2 = 46 (b) 5m + 7 = 17 (c) 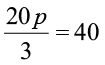 (d)
(d) 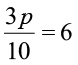
4. निम्नलिखित समीकरणों को हल कीजिए :
(a) 10p = 100 (b) 10p + 10 = 100 (c) 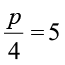 (d)
(d) 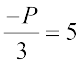
(e) 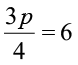 (f) 3s = –9 (g) 3s + 12 = 0 (h) 3s = 0
(f) 3s = –9 (g) 3s + 12 = 0 (h) 3s = 0
(i) 2q = 6 (j) 2q – 6 = 0 (k) 2q + 6 = 0 (l) 2q + 6 = 12
4.5 कुछ और समीकरण
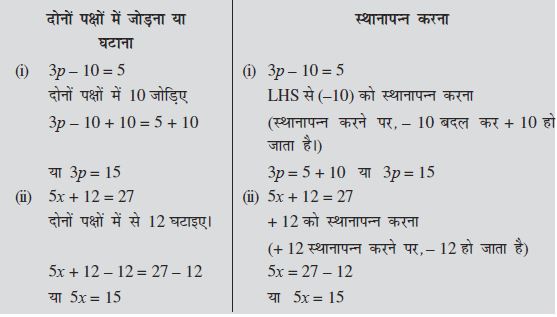
आइए कुछ और समीकरणों को हल करने का अभ्यास करें। इन समीकरणों को हल करते समय, हम एक संख्या (पद) को स्थानापन्न (transpose) करने (अर्थात् एक पक्ष से दूसरे पक्ष में ले जाने) के बारे में पढ़ेंगे (सीखेंगे) हम किसी संख्या को, समीकरण के दोनों पक्षों में जोड़ने या दोनों पक्षों में घटाने के एवज में, स्थानापन्न कर सकते हैं।
उदाहरण 6
हल कीजिए : 12p – 5 = 25 (4.12)
हल
समीकरण के दोनों पक्षों में 5 जोड़ने पर,
12p – 5 + 5 = 25 + 5 या, 12p = 30
दोनों पक्षों को 12 से भाग देने पर,
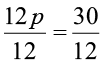 या p =
या p = 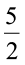
ध्यान दीजिए कि दोनों पक्षों में 5 जोड़ने का वही अर्थ है, जो (– 5) का पक्ष बदलने का है!
12p – 5 = 25
12p = 25 + 5
पक्ष बदलने को स्थानापन्न करना कहते हैं। स्थानापन्न करने में, संख्या का चिह्न बदल जाता है।
जाँच : समीकरण (4.12) की LHS में, p = 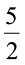 रखने पर
रखने पर
LHS = 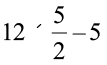
= 6 × 5 – 5
= 30 – 5 = 25 = RHS
जैसा कि हमने किसी समीकरण को हल करते समय देखा है, सामान्यतः हम समीकरण के दोनों पक्षों में एक ही संख्या जोड़ते हैं या उनमें से एक ही संख्या को घटाते हैं। किसी संख्या को स्थानापन्न करना (अर्थात् संख्या के पक्षों में परिवर्तन करना) संख्या को दोनों पक्षों में जोड़ने या दोनों पक्षों में से घटाने जैसा ही है। एेसा करने के लिए, उस संख्या का चिह्न बदलना पड़ता है। जो नियम संख्याओं के लिए प्रयोग किया जाता है, वही नियम व्यंजकों के लिए भी प्रयोग किया जाता है। आइए स्थानापन्न के दो और उदाहरण लें।
अब हम दो और समीकरणों को हल करेंगे। जैसा कि आप देख सकते हैं, इन समीकरणों में कोष्ठक भी हैं, जिन्हें सर्वप्रथम खोलना पड़ेगा।
उदाहरण 7
हल कीजिए :
(a) 4 (m + 3) = 18 (b) – 2(x + 3) = 8
हल
(a) 4(m + 3) = 18
आइए दोनों पक्षों को 4 से विभाजित करें। इससे LHS में से कोष्ठक हट जाएँगे। हमें प्राप्त होता हैः
(b) –2(x + 3) = 8
LHS में से कोष्ठकों को हटाने के लिए, हम दोनाें पक्षों को – 2 से भाग देते हैं। हमें प्राप्त होता है ः
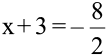 या x + 3 = – 4
या x + 3 = – 4
या, x = – 4 – 3 (3 को RHS में स्थानापन्न करने पर)
या x = –7 (वांछित हल)
जाँच LHS = –2(–7+3)
= –2(–4)
= 8 = RHS जो होना चाहिए।
4.6 हल से समीकरण
अतुल सदैव अलग प्रकार से सोचता है। वह किसी विद्यार्थी द्वारा समीकरण हल करने में लिए गए उत्तरोतर चरणों को देखता है। वह सोचता है कि क्यों न इसके विपरीत (उल्टे) पथ का अनुसरण किया जाए।
समीकरण हल (सामान्य पथ)
हल समीकरण (विपरीत पथ)
वह नीचे दिए पथ का अनुसरण करता है :
प्रारंभ कीजिए x = 5
दोनों पक्षों को 4 से गुणा कीजिए 4x = 20 दोनों पक्षों को 4 से भाग दीजिए
दोनों पक्षों में से 3 घटाइए 4x – 3 = 17 दोनों पक्षों में 3 जोड़िए
इससे एक समीकरण प्राप्त हो जाती है। यदि हम प्रत्येक चरण के लिए, उसके विपरीत पथ का अनुसरण करें। (जैसे दाईं ओर दर्शाया गया है), तो हमें समीकरण का हल प्राप्त हो जाता है।
हेतल इसमें रुचि लेने लगती है। वह उसी पहले चरण से प्रारंभ करती है और एक अन्य समीकरण बना लेती है।
प्रयास कीजिए
x = 5
दोनों पक्षों को 3 से गुणा करने पर, 3x = 15
दोनों पक्षों में 4 जोड़ने पर, 3x + 4 = 19
y = 4 से प्रारंभ कीजिए और इससे दो भिन्न-भिन्न समीकरण बनाइए। अपने तीन मित्रों से भी एेसा करने को कहिए। क्या उनके समीकरण आपसे भिन्न हैं?
क्या यह अच्छा नहीं है कि आप समीकरणों को केवल हल ही नहीं कर सकते, अपितु उनको बना भी सकते हैं। साथ ही, क्या आपने यह देखा कि एक दी हुई समीकरण का आप केवल एक ही हल प्राप्त करते हैं, लेकिन एक दिए हुए हल से आप अनेक समीकरण बना सकते हैं।
अब सारा यह चाहती है कि पूरी कक्षा यह जान जाए कि वह क्या सोच रही है। वह कहती है, ‘‘मैं हेतल की समीकरण को लेकर उसे एक कथन के रूप में बदलूँगी, जिससे एक पहेली बन जाएगी। उदाहरणार्थ,
कोई संख्या सोचिए, उसे 3 से गुणा कीजिए और गुणनफल में 4 जोड़िए। अब बताइए कि आपने क्या संख्या प्राप्त की है।
प्रयास कीजिए
यदि योग 19 है, तो हेतल द्वारा प्राप्त किये गए समीकरण से पहेली हल हो जाएगी। वास्तव में, हम जानते हैं कि यह 5 है, क्योंकि हेतल ने इससे प्रारंभ किया था।’’
वह अप्पू, सरिता और अमीना की ओर मुख करके पूछती है कि क्या उन्होंने एेसे ही अपनी पहेली बनाई थी। वे तीनों कहते है, ‘‘हाँ’’।
अब हम जान गए हैं कि किस प्रकार अनेक संख्या पहेलियों और अन्य समस्याओं को बनाया जा सकता है।
प्रश्नावली 4.3
1. निम्नलिखित समीकरणों को हल कीजिए :

(a) 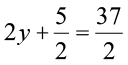 (b) 5t + 28 = 10 (c)
(b) 5t + 28 = 10 (c) 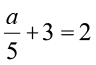 (d)
(d) 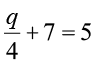
(e) 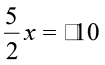 (f)
(f) 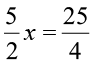 (g)
(g) 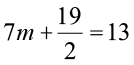 (h) 6z + 10 = –2
(h) 6z + 10 = –2
(i) 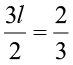 (j)
(j) 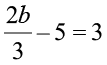
2. निम्नलिखित समीकरणों को हल कीजिए :
(a) 2(x + 4) = 12 (b) 3(n – 5) = 21 (c) 3(n – 5) = – 21
(d) – 4(2 + x) = 8 (e) 4(2 – x) = 8
3. निम्नलिखित समीकरणों को हल कीजिए :
(a) 4 = 5(p – 2) (b) – 4 = 5(p – 2)
(c) 16 = 4 + 3(t + 2) (d) 4+5(p – 1) = 34 (e) 0 = 16 + 4(m – 6)
4. (a) x = 2 से प्रारंभ करते हुए, 3 समीकरण बनाइए।
(b) x = – 2 से प्रारंभ करते हुए, 3 समीकरण बनाइए।
4.7 व्यावहारिक स्थितियों में सरल समीकरणों के अनुप्रयोग
हम एेसे कई उदाहरण देख चुके हैं, जिनमें हमने दैनिक जीवन की भाषा से कथनों को लेकर, उन्हें सरल समीकरणों के रूप में बदला था। हम यह भी सीख चुके हैं कि सरल समीकरणों को किस प्रकार हल किया जाता है। इस प्रकार, अब हम पहेलियों और व्यावहारिक स्थितियों से संबंधित समस्याओं को हल करने के लिए, पूर्णतया समर्थ हो चुके हैं। इसकी विधि यह है कि पहले इन स्थितियों के संगत समीकरणों को बना लिया जाए और फिर इन पहेलियों/समस्याओं के हल प्राप्त करने के लिए प्राप्त समीकरणों को हल कर लिया जाए। हम उसी से प्रारंभ करते हैं, जिसे हम पहले ही देख चुके हैं [उदाहरण 1 (i) और (iii), अनुच्छेद 4.2]
उदाहरण 8
किसी संख्या के तिगुने और 11 का योग 32 है। वह संख्या ज्ञात कीजिए।
हल
यदि अज्ञात संख्या को x मान लिया जाए, तो उसका तिगुना 3x होगा तथा 3x और
11 का योग 32 है। अर्थात् 3x + 11 = 32.
इस समीकरण को हल करने के लिए, हम 11 को RHS में स्थानापन्न करते हैं, जिससे हमें प्राप्त होता है ः
3x = 32 – 11 या, 3x = 21
अब दोनों पक्षों को 3 से भाग देने पर, हमें प्राप्त होता हैः
x = 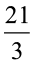 = 7
= 7
अतः वांछनीय संख्या 7 है। (हम इसकी जाँच के लिए 7 के तिगुने में 11 जोड़कर देख सकते हैं कि परिणाम 32 आता है)।
उदाहरण 9
वह संख्या ज्ञात कीजिए जिसका एक-चौथाई, 7 से 3 अधिक है।
हल
आइए अज्ञात संख्या को y लें। इसका एक-चौथाई 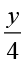 है।
है।
संख्या 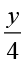 संख्या 7 से 3 अधिक है।
संख्या 7 से 3 अधिक है।
अतः, हमें y में निम्नलिखित समीकरण प्राप्त होता है : 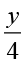 – 7 = 3
– 7 = 3
इस समीकरण को हल करने के लिए पहले – 7 को RHS में स्थानापन्न कीजिए।
इस प्रकार, 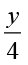 = 3 + 7 = 10.
= 3 + 7 = 10.
फिर हम दोनों पक्षों को 4 से गुणा करके, प्राप्त करते हैं :
प्रयास कीजिए
(i) जब आप एक संख्या को 6 से गुणा करते हैं और फिर गुणनफल में से 5 घटाते हैं, तो आपको 7 प्राप्त होता है। क्या आप बता सकते हैं कि वह संख्या क्या है?
(ii) वह कौन-सी संख्या है, जिसके एक-तिहाई में 5 जोड़ने पर 8 प्राप्त होता है?
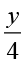 × 4 = 10 × 4 या, y = 40 (वांछित संख्या)
× 4 = 10 × 4 या, y = 40 (वांछित संख्या)
जाँच y का मान रखने पर,
LHS = 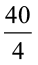 – 7 = 10 – 7 = 3 = RHS, जो होना चाहिए।
– 7 = 10 – 7 = 3 = RHS, जो होना चाहिए।
उदाहरण 10
राजू के पिता की आयु राजू की आयु के तीन गुने से 5 वर्ष अधिक है। राजू की आयु ज्ञात कीजिए, यदि उसके पिता की आयु 44 वर्ष है।
हल
उदाहरण 3 के अनुसार राजू की आयु (y) ज्ञात करने का समीकरण हैः 3y + 5 = 44
इसे हल करने के लिए, पहले हम 5 को स्थानापन्न करते हैं। हमें प्राप्त होता हैः
3y = 44 – 5 = 39
दोनों पक्षों को 3 से भाग देने पर, हमें प्राप्त होता हैः y = 13
अर्थात् राजू की आयु 13 वर्ष है। (आप अपने उत्तर की जाँच कर सकते हैं।)
मापों के अनुसार, दो प्रकार की पेटियाँ हैं, जिनमें आम रखे हुए हैं। प्रत्येक बड़ी पेटी में रखे आमों की संख्या 8 छोटी पेटियों में रखे आमों की संख्या से 4 अधिक हैं। प्रत्येक बड़ी पेटी में 100 आम हैं। प्रत्येक छोटी पेटी में कितने आम हैं?
प्रश्नावली 4.4
1. निम्नलिखित स्थितियों के लिए समीकरण बनाइए और फिर उन्हें हल करके अज्ञात संख्याएँ ज्ञात कीजिए :
(a) एक संख्या के आठ गुने में 4 जोड़िए; आपको 60 प्राप्त होगा।
(b) एक संख्या का 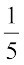 घटा 4, संख्या 3 देता है।
घटा 4, संख्या 3 देता है।
(c) यदि मैं किसी संख्या का तीन-चौथाई लेकर इसमें 3 जोड़ दूँ, तो मुझे 21 प्राप्त होते हैं।
(d) जब मैंने किसी संख्या के दुगुने में से 11 को घटाया, तो परिणाम 15 प्राप्त हुआ।
(e) मुन्ना ने 50 में से अपनी अभ्यास-पुस्तिकाओं की संख्या के तिगुने को घटाया, तो उसे परिणाम 8 प्राप्त होता है।
(f) इबेनहल एक संख्या सोचती है। वह इसमें 19 जोड़कर योग को 5 से भाग देती है, उसे 8 प्राप्त होता है।
(g) अनवर एक संख्या सोचता है। यदि वह इस संख्या के 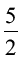 में से 7 निकाल दे, तो परिणाम 23 है।
में से 7 निकाल दे, तो परिणाम 23 है।
2. निम्नलिखित को हल कीजिए :
(a) अध्यापिका बताती है कि उनकी कक्षा में एक विद्यार्थी द्वारा प्राप्त किए गए अधिकतम अंक, प्राप्त किए न्यूनतम अंक का दुगुना जमा 7 है। प्राप्त किए गए अधिकतम अंक 87 हैं। प्राप्त किए गए न्यूनतम अंक क्या हैं?
(b) किसी समद्विबाहु त्रिभुज में आधार कोण बराबर होते हैं। शीर्ष कोण 40° है। इस त्रिभुज के आधार कोण क्या हैं? (याद कीजिए कि त्रिभुज के तीनों कोणों का योग 180° होता है।)
(c) सचिन द्वारा बनाए गए रनों की संख्या राहुल द्वारा बनाए गए रनों की संख्या की दुगुनी है। उन दोनों द्वारा मिलकर बनाए गए कुल रन एक दोहरे शतक से 2 रन कम हैं। प्रत्येक ने कितने रन बनाए थे?
3. निम्नलिखित को हल कीजिए :
(i) इरफान कहता है कि उसके पास परमीत के पास जितने कँचे हैं उनके पाँच गुने से 7 अधिक कँचे हैं। इरफान के पास 37 कँचे हैं। परमीत के पास कितने कँचे हैं?
(ii) लक्ष्मी के पिता की आयु 49 वर्ष है। उनकी आयु लक्ष्मी की आयु के तीन गुने से 4 वर्ष अधिक है। लक्ष्मी की आयु क्या है?
(iii) सुंदरग्राम के निवासियों ने अपने गाँव के एक बाग में कुछ पेड़ लगाए। इनमें से कुछ पेड़ फलों के पेड़ थे। उन पेड़ों की संख्या, जो फलों के नहीं थे, फलों वाले पेड़ों की संख्या के तिगुने से 2 अधिक थी। यदि एेसे पेड़ों की संख्या, जो फलों के नहीं थे, 77 है, तो लगाए गए फलों के पेड़ों की संख्या क्या थी?
4. निम्नलिखित पहेली को हल कीजिए :
मैं एक संख्या हूँ,
मेरी पहचान बताओ!
मुझे सात बार लो,
और एक पचास जोड़ो!
एक तिहरे शतक तक पहुँचने के लिए
आपको अभी भी चालीस चाहिए!
हमने क्या चर्चा की?
1. एक समीकरण, एक चर पर एेसा प्रतिबंध होता है जिसमें दोनों पक्षों में व्यंजकों का मान बराबर होना चाहिए ।
2. चर का वह मान जिसके लिए समीकरण संतुष्ट होता है, समीकरण का हल कहलाता है ।
3. किसी समीकरण के बाएँ और दाएँ पक्षों को परस्पर बदलने पर, समीकरण नहीं बदलता ।
4. एक संतुलित समीकरण की स्थिति में यदि हम
(i) दोनों पक्षों में एक ही संख्या जोड़ें या (ii) दोनों पक्षों में से एक ही संख्या घटाएँ या (iii) दोनों पक्षों को एक ही संख्या से गुणा करें या (iv) दोनों पक्षों को एक ही संख्या से भाग दें तो संतुलन में कोई परिवर्तन नहीं होता है अर्थात् LHS और RHS के मान समान रहते हैं ।
5. उपरोक्त गुणों द्वारा समीकरण को चरणबद्ध विधि से हल किया जा सकता है। हमें दोनों पक्षों में एक से अधिक गणितीय संक्रियाएँ करनी पड़ती हैं, जिससे कि दोनों में से एक पक्ष में हमें केवल चर प्राप्त हो। अंतिम चरण समीकरण का हल है।
6. स्थानापन्न का अर्थ है एक पक्ष से दूसरे पक्ष में जाना । किसी संख्या को स्थानापन्न करना, संख्या को दोनों पक्षाें में जोड़ने या दोनाें पक्षों में से घटाने के समान ही है। जब आप एक संख्या को एक पक्ष से दूसरे पक्ष में स्थानापन्न करते हैं तो आप उसके चिह्न को बदल देते हैं । उदाहरणार्थ, समीकरण x + 3 = 8 में + 3 का स्थानापन्न LHS से RHS करने पर x = 8 – 3 = 5 प्राप्त होता है । हम व्यंजकों का भी स्थानापन्न उसी विधि से करते हैं जैसे एक संख्या का स्थानापन्न करते हैं ।
7. हमने व्यावहारिक स्थितियों को, संगत सरल बीजीय व्यंजक के रूप में लिखना भी सीखा।
8. हमने यह भी सीखा कि हम किसी समीकरण के हल से प्रारंभ कर, दोनों पक्षों पर समान गणितीय संक्रियाओं की विधि का प्रयोग कर (उदाहरण के लिए दोनों पक्षों में समान संख्या जोड़ना या घटाना) एक समीकरण कैसे बना सकते हैं। साथ ही हमने यह भी सीखा कि हम किसी दिए गए समीकरण का व्यावहारिक स्थिति से संबंध बना सकते हैं और उस समीकरण के लिए कोई व्यावहारिक समस्या या पहेली भी बना सकते हैं ।