Table of Contents
5.1 रेखा
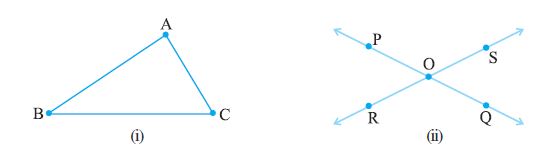
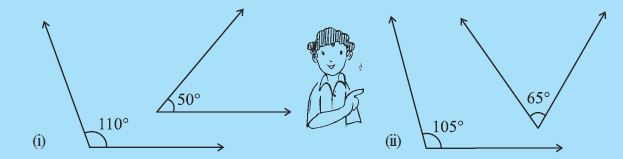
आप पहले से ही जानते हैं कि किसी दिए हुए आकार में विभिन्न रेखाएँ, रेखाखंडों एवं कोणों की पहचान कैसे की जाती है। क्या आप निम्नलिखित आकृतियों में विभिन्न रेखाखंडों एवं कोणों की पहचान कर सकते हैं? (आकृति 5.1)

आकृति 5.1
क्या आप यह भी जान सकते हैं कि निर्मित कोण, न्यून कोण अथवा अधिक कोण अथवा सम कोण हैं?
स्मरण कीजिए कि एक रेखाखंड के दो अंत बिंदु होते हैं। यदि हम इन दो अंत बिंदुओं को अपनी-अपनी दिशाओं में अपरिमित रूप में बढ़ाते हैं तो हमें एक रेखा प्राप्त होती है। इस प्रकार हम कह सकते हैं कि एक रेखा का कोई अंत बिंदु नहीं होता है। दूसरी तरफ़ स्मरण कीजिए कि किरण का एक अंत बिंदु (नामतः प्रारंभिक बिंदु) होता है। उदाहरणतः नीचे दी हुई आकृतियों को देखिएः
आकृति 5.2
यहाँ आकृति 5.2 (i) रेखाखंड, आकृति 5.2 (ii) रेखा एवं आकृति 5.2 (iii) एक किरण, को दर्शाती है। सामान्यतः एक रेखाखंड PQ को संकेत 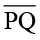 , रेखा AB को संकेत
, रेखा AB को संकेत  एवं किरण OP को संकेत
एवं किरण OP को संकेत 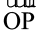 , से निर्दिष्ट किया जाता है। अपने दैनिक जीवन से रेखाखंडों एवं किरणों के कुछ उदाहरण दीजिए और उनके बारे में अपने मित्रों से चर्चा कीजिए।
, से निर्दिष्ट किया जाता है। अपने दैनिक जीवन से रेखाखंडों एवं किरणों के कुछ उदाहरण दीजिए और उनके बारे में अपने मित्रों से चर्चा कीजिए।
पुनः स्मरण कीजिए कि रेखाएँ अथवा रेखाखंडों के मिलने पर कोण निर्मित होता है। उपर्युक्त आकृतियों (आकृति 5.1) में कोनों (corners) को प्रेक्षित कीजिए। जब दो रेखाएँ अथवा रेखाखंड किसी बिंदु पर प्रतिच्छेद करते हैं तो इन कोनों का निर्माण होता है। उदाहरणतः नीचे दी हुई आकृतियों को देखिएः
प्रयास कीजिए
आकृति 5.3
आकृति 5.3 (i) में रेखाखंड AB एवं BC, कोण ABC का निर्माण करने के लिए, एक दूसरे को बिंदु B पर प्रतिच्छेद करते हैं और रेखाखंड BC एवं AC, कोण ACB का निर्माण करने के लिए एक दूसरे को C पर प्रतिच्छेद करते हैं इत्यादि। जबकि आकृति 5.3 (ii) में रेखाएँ PQ एवं RS एक दूसरे को बिंदु O पर प्रतिच्छेद करती हैं जिससे कोण POS, SOQ, QOR और ROP निर्मित होते हैं। कोण ABC को संकेत ∠ABC द्वारा निरूपित किया जाता है। इस प्रकार आकृति 5.3 (i) में निर्मित तीन कोण ∠ABC, ∠BCA एवं ∠BAC हैं और आकृति 5.3 (ii) में निर्मित चार कोण ∠POS, ∠SOQ, ∠QOR एवं ∠POR हैं। आप पहले से ही अध्ययन कर चुके हैं कि न्यून कोण, अधिक कोण अथवा सम कोण के रूप में कोणों का वर्गीकरण कैसे किया जाता है।
टिप्पणी कोण ABC के माप के संदर्भ में, m∠ABC को साधारणतः ∠ABC के रूप में लिखेंगे। प्रकरण से यह बात स्पष्ट हो जाएगी कि हम कोण के संदर्भ में अथवा इसके माप के सदंर्भ में बात कर रहे हैं।
5.2 संबंधित कोण
5.2.1 पूरक कोण
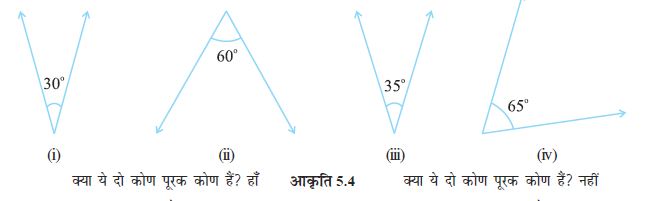
जब दो कोणों के मापों का योग 90° होता है, तो ये कोण पूरक कोण (complementary angles) कहलाते हैं।
जब दो कोण पूरक होते हैं, तो इनमें से प्रत्येक कोण दूसरे कोण का पूरक कहलाता है। उपर्युक्त आरेख (आकृति 5.4) में ‘‘30° का कोण’’, ‘‘60° के कोण’’ का पूरक है और विलोमतः
सोचिए, चर्चा कीजिए एवं लिखिए
1. क्या दो न्यून कोण एक दूसरे के पूरक हो सकते हैं?
2. क्या दो अधिक कोण एक दूसरे के पूरक हो सकते हैं?
3. क्या दो समकोण एक दूसरे के पूरक हो सकते हैं?
5.2.2 संपूरक कोण
आइए कोणों के निम्नलिखित युग्मों को देखते हैं (आकृति 5.6):

आकृति 5.6
क्या आप देखते हैं कि उपर्युक्त प्रत्येक युग्म में (आकृति 5.6) कोणों के मापों का योग 180º पाया जाता है ? कोणों के एेसे युग्म संपूरक कोण (supplementary angles) कहलाते हैं। जब दो कोण संपूरक होते हैं तो उनमें से प्रत्येक कोण दूसरे कोण का संपूरक कहलाता है।
सोचिए, चर्चा कीजिए एवं लिखिए
1. क्या दो अधिक कोण संपूरक हो सकते हैं?
2. क्या दो न्यून कोण संपूरक हो सकते हैं? 3. क्या दो सम कोण संपूरक हो सकते हैं?
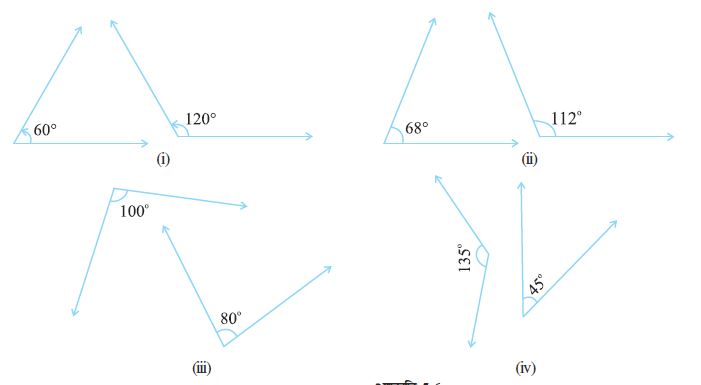
1. आकृति 5.7 में संपूरक कोणों के युग्म ज्ञात कीजिए :
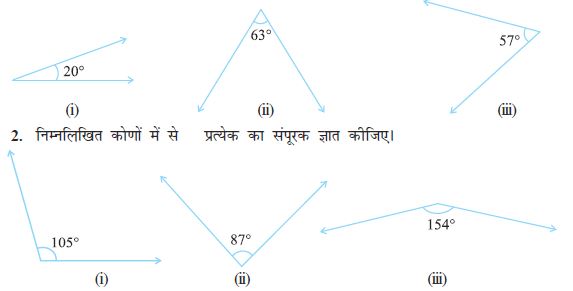
2. निम्नलिखित कोणों में प्रत्येक के संपूरक का माप क्या होगा?
(i) 100º (ii) 90º (iii) 55º (iv) 125º
3. दो संपूरक कोणों में बड़े कोण का माप छोटे कोण के माप से 44º अधिक है। कोणों के माप ज्ञात कीजिए।
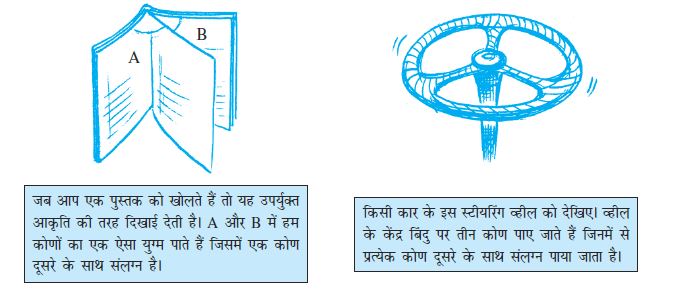
5.2.3. आसन्न कोण
निम्नलिखित आकृतियों को देखिए :
आकृति 5.8
दोनों शीर्षों A और B पर, हम पाते हैं कि कोणों का एक युग्म एक दूसरे से संलग्न रखा गया है।
ये कोण इस प्रकार हैं कि :
(i) उनका एक उभयनिष्ठ शीर्ष है
(ii) उनमें एक उभयनिष्ठ भुजा है और
(iii) जो भुजाएँ उभयनिष्ठ नहीं हैं, वे उभयनिष्ठ भुजा के एक-एक तरफ़ हैं।
कोणों के एेसे युग्म आसन्न कोण (Adjacent angles) कहलाते हैं। आसन्न कोणों में उभयनिष्ठ शीर्ष एवं उभयनिष्ठ भुजा होती है परंतु कोई भी अंतः बिंदु उभयनिष्ठ नहीं होता है।
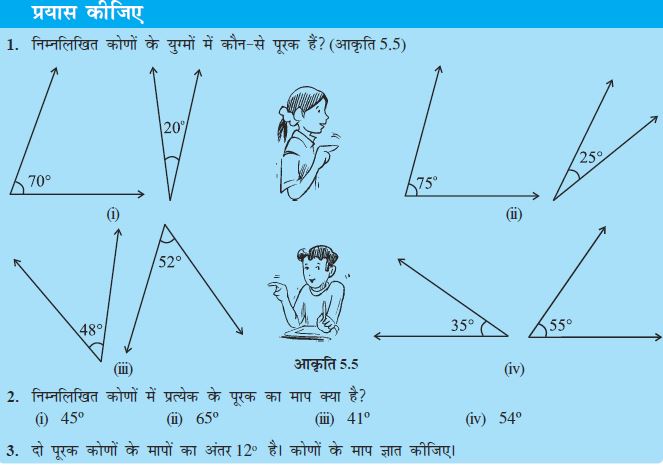
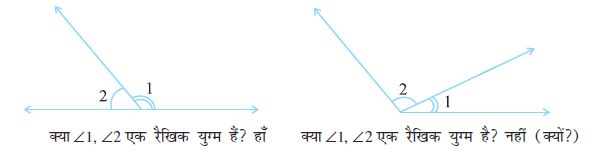
1. क्या 1 और 2 से अंकित कोण आसन्न हैं? [आकृति 5.9 (i)-(v)] यदि ये आसन्न नहीं हैं तो बताइए, ‘क्यों’?
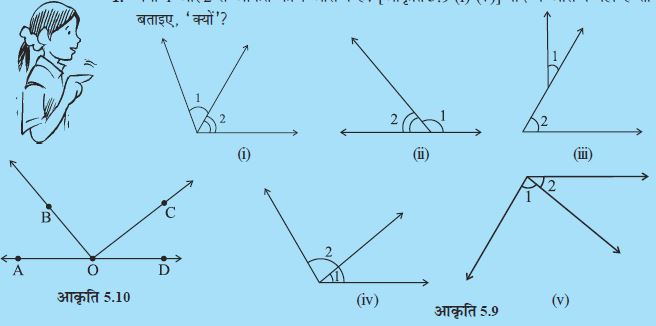
2. आकृति 5.10 में, क्या निम्नलिखित कोण आसन्न हैं?
(a) ∠AOB और ∠BOC (b) ∠BOD और ∠BOC
अपने उत्तर की पुष्टि कीजिए।
सोचिए, चर्चा कीजिए एवं लिखिए
1. क्या दो आसन्न कोण संपूरक हो सकते हैं? 2. क्या दो आसन्न कोण पूरक हो सकते हैं?
3. क्या दो अधिक कोण आसन्न कोण हो सकते हैं?
4. क्या एक न्यून कोण, अधिक कोण का आसन्न हो सकता है?
5.2.4 रैखिक युग्म
एक रैखिक युग्म (linear pair), एेसे आसन्न कोणों का युग्म होता है जिनकी वे भुजाएँ जो उभयनिष्ठ नहीं हैं, विपरीत दिशा में किरणें होती हैं।
(i) आकृति 5.11 (ii)
उपर्युक्त आकृति 5.11 (i) में देखिए कि सम्मुख किरणें (जो ∠1 एवं ∠2 की उभयनिष्ठ भुजाएँ नहीं हैं) एक रेखा का निर्माण करती हैं। इस प्रकार ∠1 + ∠2 का मान 180o हो जाता है।
रैखिक युग्म के कोण संपूरक होते हैं।
क्या आपने अपने आसपास में रैखिक युग्म के मॉडलों पर ध्यान दिया है?
सावधानीपूर्वक नोट कीजिए कि संपूरक कोणों का युग्म, रैखिम युग्म तभी बनाता है, जब प्रत्येक को दूसरे के आसन्न रखा जाए।
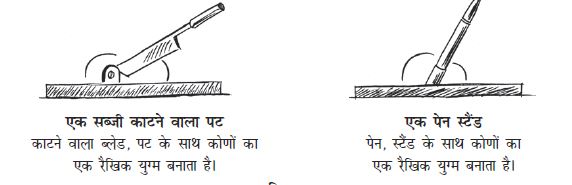
क्या आप अपने दैनिक जीवन में रैखिक युग्म के उदाहरण पाते हैं? सब्जी काटने वाले पट को प्रेक्षित कीजिए (आकृति 5.12)। क्या आप कह सकते हैं कि काटने वाला ब्लेड पट के साथ रैखिक युग्म बनाता है?
एक सब्जी काटने वाला पट एक पेन स्टैंड काटने वाला ब्लेड, पट के साथ कोणों का पेन, स्टैंड के साथ कोणों का
एक रैखिक युग्म बनाता है। एक रैखिक युग्म बनाता है।
आकृति 5.12
फिर से, पेन स्टैंड देखिए (आकृति 5.12)। क्या आप कह सकते हैं कि पेन, स्टैंड के साथ रैखिक युग्म बनाता है ?
सोचिए, चर्चा कीजिए एवं लिखिए
1. क्या दो न्यून कोण एक रैखिक युग्म बना सकते हैं?
2. क्या दो अधिक कोण एक रैखिक युग्म बना सकते हैं?
3. क्या दो समकोण एक रैखिक युग्म बना सकते हैं?
बताइए कोणों के निम्नलिखित युग्मों में से कौन-सा रैखिक युग्म बनाता है? (आकृति 5.13):
5.2.5 शीर्षाभिमुख कोण
दो पेंसिल लीजिए और उन्हें मध्य में रबड़ बैंड की सहायता से एक-दूसरे के साथ बाँध दीजिए, जैसा कि आकृति 5.14 में दर्शाया गया है।
इस प्रकार निर्मित चार कोणों, ∠1, ∠2, ∠3 एवं ∠4 को देखिए
∠1, ∠3 के शीर्षाभिमुख है और ∠4, ∠2 के शीर्षाभिमुख है।
∠1 एवं ∠3 को हम शीर्षाभिमुख कोणों (vertically opposite angles) का एक युग्म कहते हैं।
क्या आप शीर्षाभिमुख कोणों के अन्य युग्म का नाम दे सकते हैं?
क्या ∠1, ∠3 के बराबर दिखाई देता है? क्या ∠2, ∠4 के बराबर दिखाई देता है?
इसको सत्यापित करने से पहले आइए हम शीर्षाभिमुख कोणों के लिए वास्तविक जीवन से कुछ उदाहरण देखते हैं (आकृति 5.15)।
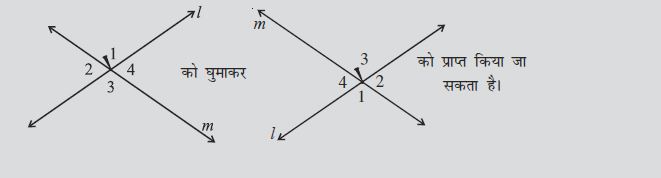

किसी एक बिंदु पर प्रतिच्छेदित करती हुई दो रेखाएँ l और m खींचिए। अब आप ∠1, ∠2, ∠3 एवं ∠4 अंकित कर सकते हैं जैसा कि आकृति 5.16 में दर्शाया गया है।
एक पारदर्शी कागज़ के ऊपर इस आकृति की एक अनुरेख प्रतिलिपि लीजिए।
उसको मूल प्रति के ऊपर इस प्रकार रखिए ताकि ∠1 अपनी प्रतिलिपि को ढक ले, ∠2 अपनी प्रतिलिपि को ढक ले, ... इत्यादि।
प्रतिच्छेदन बिंदु पर एक पिन लगाइए। प्रतिलिपि को 180° से घुमाइए। क्या रेखाएँ फिर से संपाती हो जाती हैं?
आप पाते हैं कि ∠1 एवं ∠3 ने अपनी स्थितियाँ परस्पर बदल ली हैं और इसी प्रकार ∠2 एवं ∠4 ने भी अपनी स्थितियाँ परस्पर बदल ली हैं । यह सब रेखाओं की स्थिति को बदले बिना किया गया है।
इस प्रकार ∠1 = ∠3 एवं ∠2 = ∠4.
हम इस निष्कर्ष पर पहुंँचते हैं कि यदि दो रेखाएँ एक दूसरे को प्रतिच्छेद करती हैं तो इस प्रकार बने शीर्षाभिमुख कोण समान होते हैं।
आइए ज्यामिति का उपयोग करते हुए इसे सिद्ध करने का प्रयास करते हैं।
आइए दो रेखाएँ l और m लेते हैं (आकृति 5.17)।
हम इस परिणाम पर तर्कसंगत युक्ति से निम्नलिखित प्रकार से पहुँच सकते हैं ः
मान लीजिए l एवं m दो रेखाएँ हैं जो एक दूसरे को O पर प्रतिच्छेद करती हैं और
इस प्रकार ∠1, ∠2, ∠3 एवं ∠4 निर्मित करती हैं।
हम सिद्ध करना चाहते हैं कि ∠1 = ∠3 एवं ∠2 = ∠4
अब ∠1 = 180º – ∠2 (∠1 एवं ∠2 रैखिक युग्म बनाते हैं इसलिए ∠1 + ∠2 = 180°) (i)
इसी प्रकार ∠3 = 180º – ∠2 ( ∠2, ∠3 रैखिक युग्म बनाते हैं इसलिए ∠2 + ∠3 = 180°) (ii)
इसलिए ∠1 = ∠3 [(i) और (ii) से]
इसी प्रकार हम सिद्ध कर सकते हैं कि ∠2 = ∠4 (प्रयास कीजिए)।
1. दी हुई आकृति में यदि
∠1 = 30º, तो ∠2 एवं ∠3 ज्ञात कीजिए।
2. अपने आसपास से शीर्षाभिमुख कोणों
का एक उदाहरण दीजिए।
उदाहरण 1 आकृति 5.18 में निम्नलिखित की पहचान कीजिएः
(i) आसन्न कोणों के पाँच युग्म (ii) तीन रैखिक युग्म
(iii) शीर्षाभिमुख कोणों के दो युग्म।
हल
(i) आसन्न कोणों के पाँच युग्म हैं ः (∠AOE, ∠EOC), (∠EOC, ∠COB),
(∠AOC, ∠COB), (∠COB, ∠BOD), (∠EOB, ∠BOD)
(ii) रैखिक युग्म हैं ः (∠AOE, ∠EOB), (∠AOC, ∠COB), (∠COB, ∠BOD)
(iii) शीर्षाभिमुख कोण हैं ः (∠COB, ∠AOD), (∠AOC, ∠BOD)
प्रश्नावली 5.1
1. निम्नलिखित कोणों में से प्रत्येक का पूरक ज्ञात कीजिए :
3. कोणों के निम्नलिखित युग्मों में से पूरक एवं संपूरक युग्मों की पृथक्-पृथक् पहचान कीजिए ः
(i) 65º, 115º (ii) 63º, 27º (iii) 112º, 68º
(iv) 130º, 50º (v) 45º, 45º (vi) 80º, 10º
4. एेसा कोण ज्ञात कीजिए जो अपने पूरक के समान हो।
5. एेसा कोण ज्ञात कीजिए जो अपने संपूरक के समान हो।
6. दी हुई आकृति में ∠1 एवं ∠2 संपूरक कोण हैं। यदि ∠1 में कमी की जाती है, तो ∠2 में क्या परिवर्तन होगा ताकि दोनों कोण फिर भी संपूरक ही रहें।
7. क्या दो एेसे कोण संपूरक हो सकते हैं यदि उनमें से दोनों
(i) न्यून कोण हैं? (ii) अधिक कोण हैं? (iii) समकोण हैं?
8. एक कोण 45º से बड़ा है। क्या इसका पूरक कोण 45º से बड़ा है अथवा 45º के बराबर है अथवा 45º से छोटा है?
9. संलग्न आकृति में ः
(i) क्या ∠1, ∠2 का आसन्न है?
(ii) क्या ∠AOC, ∠AOE का आसन्न है?
(iii) क्या ∠COE एवं ∠EOD रैखिक युग्म बनाते हैं?
(iv) क्या ∠BOD एवं ∠DOA संपूरक है?
(v) क्या ∠1 का शीर्षाभिमुख कोण ∠4 है?
(vi) ∠5 का शीर्षाभिमुख कोण क्या हैं?
10. पहचानिए कि कोणों के कौन से युग्म ः
(i) शीर्षाभिमुख कोण हैं। (ii) रैखिक युग्म हैं।
11. निम्नलिखित आकृति में क्या ∠1, ∠2 का आसन्न है? कारण लिखिए ।
12. निम्नलिखित में से प्रत्येक में कोण x, y एवं z के मान ज्ञात कीजिए।
(i) (ii)
13. रिक्त स्थानों की पूर्ति कीजिए ः
(i) यदि दो कोण पूरक हैं, तो उनके मापों का योग _______ है।
(ii) यदि दो कोण संपूरक हैं तो उनके मापों का योग ______ है।
(iii) रैखिक युग्म बनाने वाले दो कोण _______________ होते हैं।
(iv) यदि दो आसन्न कोण संपूरक हैं, तो वे ___________ बनाते हैं।
(v) यदि दो रेखाएँ एक-दूसरे को एक बिंदु पर प्रतिच्छेद करती हैं तो शीर्षाभिमुख कोण हमेशा _____________ होते हैं।
(vi) यदि दो रेखाएँ एक-दूसरे को एक बिंदु पर प्रतिच्छेद करती है और यदि शीर्षाभिमुख कोणों का एक युग्म न्यून कोण है, तो शीर्षाभिमुख कोणों का दूसरा युग्म ________ है।
14. संलग्न आकृति में निम्नलिखित कोण युग्मों को नाम दीजिए ः
(i) शीर्षाभिमुख अधिक कोण
(ii) आसन्न पूरक कोण
(iii) समान संपूरक कोण
(iv) असमान संपूरक कोण
(v) आसन्न कोण जो रैखिक युग्म नहीं बनाते हैं।
5.3 रेखा युग्म
5.3.1 प्रतिच्छेदी रेखाएँ
स्टैंड पर रखा हुआ श्यामपट्ट, रेखाखंडों द्वारा निर्मित अक्षर Y और एक खिड़की का जालीदार दरवाज़ा, इन सभी में उभयनिष्ठ क्या हैं? ये प्रतिच्छेदी रेखाओं (intersecting lines) के उदाहरण हैं (आकृति 5.19)। दो रेखाएँ l और m प्रतिच्छेद करती हैं यदि उनमें एक बिंदु उभयनिष्ठ है। यह उभयनिष्ठ बिंदु उनका प्रतिच्छेद बिंदु कहलाता है।
सोचिए, चर्चा कीजिए एवं लिखिए
आकृति 5.20 में, AC और BE, P पर प्रतिच्छेद करती हैं।
AC और BC, C पर प्रतिच्छेद करती हैं। AC और EC, C पर प्रतिच्छेद करती हैं।
प्रतिच्छेदी रेखाखंडों के दस अन्य युग्म ज्ञात करने का प्रयास कीजिए।
क्या दो रेखाएँ अथवा रेखाखंड आवश्यक रूप से प्रतिच्छेद करने चाहिए?
क्या आप इस आकृति में दो रेखाखंडों के युग्म ज्ञात कर सकते हैं जो प्रतिच्छेदी नहीं है? क्या दो रेखाएँ एक से ज्यादा बिंदुओं पर प्रतिच्छेद कर सकती हैं। इसके बारे में विचार कीजिए।
1. अपने आसपास के परिवेश से एेसे उदाहरण ज्ञात कीजिए जहाँ रेखाएँ सम कोण पर प्रतिच्छेद करती हैं।
2. एक समबाहु त्रिभुज के शीर्षों पर प्रतिच्छेदी रेखाओं द्वारा निर्मित कोणों के माप ज्ञात कीजिए।
3. एक आयत खींचिए और प्रतिच्छेदी रेखाओं द्वारा निर्मित चार शीर्षों के कोणों के माप ज्ञात कीजिए।
4. यदि दो रेखाएँ एक-दूसरे को प्रतिच्छेद करती हैं, तो क्या वे हमेशा एक-दूसरे को सम कोण पर प्रतिच्छेद करती हैं?
प्रयास कीजिए
1. मान लीजिए दो रेखाएँ दी हुई हैं। इन रेखाओं के लिए आप कितनी तिर्यक छेदी रेखाएँ खींच सकते हैं?
2. यदि एक रेखा तीन रेखाओं की तिर्यक छेदी रेखा है, तो बताइए कितने प्रतिच्छेदन बिंदु हैं।
3. अपने आसपास कुछ तिर्यक छेदी रेखाएँ ढूँढने का प्रयास कीजिए।
5.3.2 तिर्यक छेदी रेखा
शायद, आपने दो अथवा अधिक सड़कों को पार करते हुए एक सड़क देखी होगी अथवा कई अन्य रेल पटरियों को पार करते हुए एक रेल पटरी देखी होगी। इनसे तिर्यक छेदी रेखा या तिर्यक रेखा (transversal) का अनुभव प्राप्त होता है (आकृति 5.21)।
(i) आकृति 5.21 (ii)
एक एेसी रेखा जो दो अथवा अधिक रेखाओं को भिन्न बिंदुओं पर प्रतिच्छेद करती है, तिर्यक छेदी रेखा (transversal) कहलाती है। आकृति 5.22 में, p, रेखाएँ l और m की तिर्यक छेदी रेखा है।
आकृति 5.23 में, p एक तिर्यक छेदी रेखा नहीं है तथापि यह रेखाएँ l और m को काटती है। क्या आप बता सकते हैं ‘क्यों’?
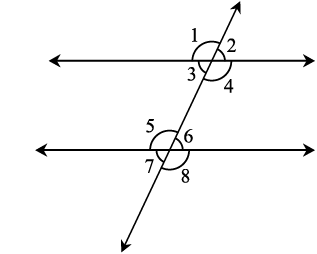
5.3.3 तिर्यक छेदी रेखा द्वारा निर्मित कोण
आकृति 5.24 में, आप देखते हैं कि रेखाएँ l एवं m तिर्यक छेदी रेखा p द्वारा काटी जा रही है। इस प्रकार बनने वाले 1 से 8 तक अंकित कोणों के विशिष्ट नाम हैंः
अंतःकोण ∠3, ∠4, ∠5, ∠6,
बाह्य कोण ∠1, ∠2, ∠7, ∠8
संगत कोणों के युग्म ∠1 और ∠5, ∠2 और ∠6,
∠3 और ∠7, ∠4 और ∠8.
एकांतर अंतः कोणों के युग्म ∠3 और ∠6, ∠4 और ∠5
एकांतर बाह्य कोणों के युग्म ∠1 और ∠8, ∠2 और ∠7
तिर्यक छेदी रेखा के एक ही तरफ़ ∠3 और ∠5, ∠4 और ∠6
बने अंतःकोणों के युग्म
टिप्पणीः आकृति 5.25 में (∠1 एवं ∠5 जैसे) संगत कोणों में निम्नलिखित सम्मिलित होते हैं ः
(i) विभिन्न शीर्ष (ii) तिर्यक छेदी रेखा के एक ही तरफ बने होते हैं।
(iii) दो रेखाओं के सापेक्ष संगत स्थितियों (ऊपर अथवा नीचे, बायाँ अथवा दायाँ) में होते हैं।
आकृति 5.26 में (∠3 एवं ∠6 जैसे) अंतः एकांतर कोण
(i) के विभिन्न शीर्ष होते हैं।
(ii) तिर्यक छेदी रेखा के सम्मुख स्थिति पर बने होते हैं।
(iii) दो रेखाओं के ‘‘मध्य’’ स्थित होते हैं।
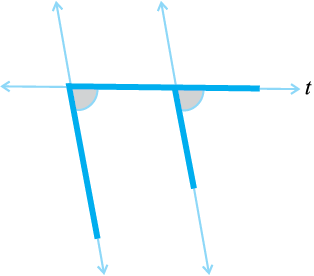
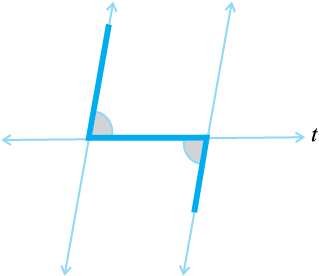
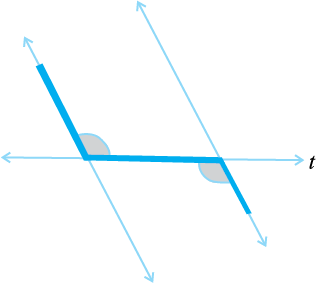
प्रत्येक आकृति में कोण-युग्म को नाम दीजिए ः
5.3.4 समांतर रेखाओं की तिर्यक छेदी रेखा
क्या आपको याद है कि समांतर रेखाएँ क्या हैं । ये किसी तल में एेसी रेखाएँ होती हैं जो एक-दूसरे से कहीं नहीं मिलती। क्या आप निम्नलिखित आकृतियों में समांतर रेखाओं की पहचान कर सकते हैं? (आकृति 5.27)
समांतर रेखाओं की तिर्यक छेदी रेखा या तिर्यक रेखा से बहुत ही रुचिकर परिणाम प्राप्त होते हैं।
एक रेखांकित कागज़ लीजिए। दो मोटी रंगीली समांतर रेखाएँ l और m खींचिए।
रेखाएँ l और m की एक तिर्यक छेदी रेखा t खींचिए। ∠1 और ∠2 को लेबल कीजिए जैसा कि आकृति 5.28(i) में दर्शाया गया है।
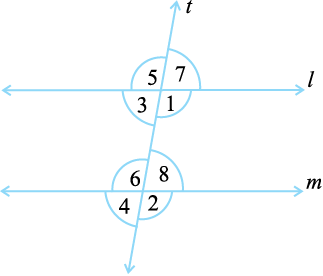
आकृति 5.29
खींची गई आकृति पर एक अनुरेखण कागज़ (ट्रेसिंग पेपर) रखिए। रेखाएँ l, m और t की प्रतिलिपि बनाइए।
ट्रेसिंग पेपर को t के अनु तब तक खिसकाइए जब तक l, m के संपाती न हो जाए।
आप पाते हैं कि प्रतिलिपित आकृति का ∠1, मूल आकृति के ∠2 के संपाती हो जाता है।
वास्तव में आप निम्नलिखित परिणामों को अनुरेखण एवं खिसकाने के क्रियाकलाप से सत्यापित कर सकते हैं।
(i) ∠1 = ∠2 (ii) ∠3 = ∠4 (iii) ∠5 = ∠6 (iv) ∠7 = ∠8
यह क्रियाकलाप निम्नलिखित तथ्य को दृष्टांतित करती है ः
यदि दो समांतर रेखाएँ किसी तिर्यक छेदी रेखा द्वारा काटी जाती है, तो संगत कोणों के प्रत्येक युग्म का माप समान होता है।
इस परिणाम का उपयोग करते हुए हम एक दूसरा रुचिकर परिणाम प्राप्त करते हैं।आकृति 5.29 को देखिए।
जब समांतर रेखाएँ l और m, रेखा t द्वारा काटी जाती हैं, तो ∠3 = ∠7 (शीर्षाभिमुख कोण)
परंतु ∠7 = ∠8 (संगत कोण) इसलिए ∠3 = ∠8
इसी प्रकार आप दर्शा सकते हैं कि ∠1 = ∠6.
अतः हमें निम्नलिखित परिणाम की प्राप्ति होती हैः
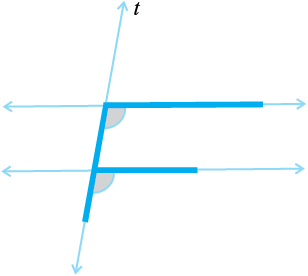
यदि दो समांतर रेखाएँ किसी तिर्यक छेदी रेखा द्वारा काटी जाती हैं, तो अंतः एकांतर कोणों का प्रत्येक युग्म समान होता है।
यह दूसरा परिणाम हमें एक ओर रुचिकर गुणधर्म की ओर अग्रसर करता है। फिर से आकृति 5.29 में दिए हुए आलेख से, ∠3 + ∠1 = 180° (∠3 और ∠1 रैखिक युग्म बनाते हैं)
परंतु ∠1 = ∠6 (अंतः एकांतर कोणों का एक युग्म)

इस प्रकार हम कह सकते हैं कि ∠3 + ∠6 = 180°।
इसी प्रकार ∠1 + ∠8 = 180°. इस प्रकार हमें निम्नलिखित परिणाम की प्राप्ति होती है ः
यदि दो समांतर रेखाएँ किसी एक तिर्यक छेदी रेखा द्वारा काटी जाती हैं तो तिर्यक छेदी रेखा के एक ही तरफ़ को बने अंतः कोणों का प्रत्येक युग्म संपूरक होता है।
5.4 समांतर रेखाओं की जाँच
यदि दो रेखाएँ समांतर हैं, तो आप जानते हैं कि एक तिर्यक छेदी रेखा की सहायता से, समान संगत कोणों का एक युग्म प्राप्त होता है, समान अंतः एकांतर कोणों का युग्म प्राप्त होता है और तिर्यक छेदी रेखा के एक ही तरफ़ बनें अंतः कोण, जो संपूरक होते हैं।
जब दो रेखाएँ दी हुई हैं तो क्या कोई एेसी विधि है जिसकी सहायता से यह जाँच की जा सके कि दी हुई रेखाएँ समांतर हैं अथवा नहीं? जीवन से जुड़ी अनेक परिस्थितियों में आपको इस कौशल की आवश्यकता होती है।
इन खंडों को (आकृति 5.30) खींचने के लिए एक नक्शानवीश, बढ़ई के वर्ग एवं रुलर का प्रयोग करता है। वह दावा करता है कि ये समांतर हैं। कैसे?
क्या आप देख पाते हैं कि उसने संगत कोणों को समान रखा है? (यहाँ तिर्यक छेदी रेखा क्या है?)
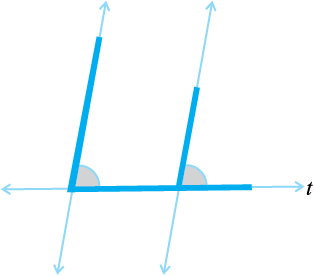
अतः जब एक तिर्यक छेदी रेखा दो रेखाओं को इस प्रकार काटती है कि संगत कोणों के युग्म समान हैं, तो रेखाएँ समांतर होती हैं।
अक्षर Z (आकृति 5.31) को देखिए। यहाँ क्षैतिज खंड समांतर हैं क्योंकि एकांतर कोण समान हैं।
जब एक तिर्यक छेदी रेखा दो रेखाओं को इस प्रकार काटती है कि अंतः एकांतर कोणों का युग्म समान है, तो रेखाएँ समांतर होती हैं।
एक रेखा l खींचिए (आकृति 5.32).
रेखा l के लंबवत् एक रेखा m खींचिए। एक रेखा p इस प्रकार खींचिए ताकि p, m के लंबवत् हो। इस प्रकार p, l लंब पर लंब है। आप पाते हैं p || l कैसे? यह इसलिए है क्योंकि आपने p को इस प्रकार खींचा है कि ∠1 + ∠2 = 180°.
अतः जब एक तिर्यक छेदी रेखा दो रेखाओं को इस प्रकार काटती है कि तिर्यक छेदी रेखा के एक ही तरफ़ बने अंतः कोणों का युग्म संपूरक है, तो रेखाएँ समांतर होती हैं।
प्रश्नावली 5.2
1. निम्नलिखित कथनों में प्रत्येक कथन में उपयोग किए गए गुणधर्म का वर्णन कीजिए (आकृति 5.33)।
(i) यदि a || b, तो ∠1 = ∠5
(ii) यदि ∠4 = ∠6, तो a || b.
(iii) यदि ∠4 + ∠5 = 180°, तो a || b
2. आकृति 5.34 में निम्नलिखित की पहचान कीजिएः
(i) संगत कोणों के युग्म (ii) अंतः एकांतर कोणों के युग्म
(iii) तिर्यक छेदी रेखा के एक तरफ़ बने अंतःकोणों के युग्म
(iv) शीर्षाभिमुख कोण
3. सलंग्न आकृति में p || q। अज्ञात कोण ज्ञात कीजिए।
4. यदि l || m है, तो निम्नलिखित आकृतियों में प्रत्येक में x का मान ज्ञात कीजिए।
(i) (ii)
5. दी हुई आकृति में, दो कोणों की भुजाएँ समांतर हैं।
यदि ∠ABC = 70º, तो
(i) ∠DGC ज्ञात कीजिए।
(ii) ∠DEF ज्ञात कीजिए।
6. नीचे दी हुई आकृतियों में निर्णय लीजिए कि क्या l , m के समांतर है।
हमने क्या चर्चा की?
1. हम स्मरण करते हैं कि
(i) एक रेखाखंड के दो अंत बिंदु होते हैं।
(ii) एक किरण का केवल एक अंत बिंदु (इसका शीर्ष) होता है।
(iii) एक रेखा का किसी भी तरफ़ कोई अंत बिंदु नहीं होता है।
2. एक कोण का निर्माण तब होता है जब दो रेखाएँ (अथवा किरण अथवा रेखाखंड) एक दूसरे को मिलती हैं।
कोण युग्म प्रतिबंध
दो पूरक कोण मापों का योग 90o है।
दो संपूरक कोण मापों का योग 180o है।
दो आसन्न कोण एक उभयनिष्ठ शीर्ष और एक उभयनिष्ठ भुजा होती है। परंतु कोई उभयनिष्ठ अंतस्थ नहीं होता है।
रैखिक युग्म आसन्न एवं संपूरक
3. जब दो रेखाएँ l और m एक दूसरे सेे मिलती हैं तो हम कहते हैं कि ये रेखाएँ प्रतिच्छेद करती हैं। मिलान बिंदु प्रतिच्छेद बिंदु कहलाता है। एेसी रेखाएँ जिन्हें कितना भी बढ़ाया जाए, आपस में नहीं मिलती, समांतर रेखाएँ कहलाती हैं।
4. (i) जब दो रेखाएँ प्रतिच्छेद करती हैं (सामान्यतः, अक्षर X की भाँति दिखाई देती हैं) तो हमें सम्मुख कोणों के दो युग्म प्राप्त होते हैं। इन्हें शीर्षाभिमुख कोण कहा जाता है। इनका माप समान होता है।
(ii) दो अथवा अधिक रेखाओं को विभिन्न बिंदुओं पर प्रतिच्छेद करने वाली रेखा तिर्यक छेदी रेखा कहलाती है।
(iii) एक तिर्यक छेदी रेखा आरेख से विभिन्न प्रकार के कोण प्राप्त होते हैं।
(iv) आकृति में हमें मिलता है
कोणों के प्रकार दर्शाने वाले कोण
अंतः ∠3, ∠4, ∠5, ∠6
बाह्य ∠1, ∠2, ∠7, ∠8
संगत ∠1 तथा ∠5, ∠2 एवं ∠6,
∠3 तथा ∠7, ∠4 एवं ∠8
अंतः एकांतर ∠3 तथा ∠6, ∠4 एवं ∠5,
बाह्य एकांतर ∠1 तथा ∠8, ∠2 एवं ∠7,
तिर्यक छेदी रेखा के ∠3 तथा ∠5, ∠4 एवं ∠6,
एक ही तरफ़ बने
अंतः कोणों के युग्म,
(v) जब एक तिर्यक छेदी रेखा दो समांतर रेखाओं को काटती है, तो हमें निम्नलिखित रुचिकर संबंध प्राप्त होते है। संगत कोणों का प्रत्येक युग्म समान होता हैः ∠1 = ∠5, ∠3 = ∠7, ∠2 = ∠6, ∠4 = ∠8
अंतः एकांतर कोणों के युग्म समान होते हैंः ∠3 = ∠6, ∠4 = ∠5
तिर्यक छेदी रेखा के एक ही तरफ़ बने अंतः कोणों का प्रत्येक युग्म संपूरक होता हैः ∠3 + ∠5 = 180°, ∠4 + ∠6 = 180°