Table of Contents
7.1 भूमिका
अब आप एक बहुत ही महत्त्वपूर्ण ज्यामितीय संकल्पना ‘सर्वांगसमता’ को सीखने जा रहे हैं । विशेषकर, आप त्रिभुजों की सर्वांगसमता के बारे में बहुत कुछ पढ़ेंगे ।
सर्वांगसमता को समझने के लिए, हम कुछ क्रियाकलाप करेंगे ।
एक ही प्रकार (denomination) की दो टिकटे लीजिए (आकृति 7.1)। एक टिकट को दूसरी पर रखिए । आप क्या देखते हैं ?
आकृति 7.1
एक टिकट दूसरे को पूर्णतया ढक लेती है । इसका अर्थ यह है कि दोनों टिकटें एक ही आकार और एक ही माप की हैं । एेसी वस्तुएँ सर्वांगसम कहलाती हैं । आपके द्वारा प्रयोग की गई दोनों टिकटें एक दूसरे के सर्वांगसम हैं । सर्वांगसम वस्तुएँ एक दूसरे की हू-ब-हू प्रतिलिपियाँ होती हैं ।
क्या अब, आप, बता सकते हैं कि निम्न वस्तुएँ सर्वांगसम हैं या नहीं?
1. एक ही कंपनी के शेविंग ब्लेड [आकृति 7.2 (i)]
2. एक ही लेटर पैड की शीटें [आकृति 7.2 (ii)]
3. एक ही पैकट के बिस्कुट [आकृति 7.2 (iii)]
4. एक ही साँचे से बने खिलौने [आकृति 7.2 (iv)]
दो वस्तुओं के सर्वांगसम होने के संबंध को सर्वांगसमता कहते हैं । इस अध्याय में, हम केवल तल में बनी आकृतियों की चर्चा करेंगे यद्यपि सर्वांगसमता एक साधारण विषय है जिसका उपयोग हम त्रिआयामी (3-Dimensional) आकारों के लिए भी करते हैं । अब हम तल में बनी एेसी आकृतियों की सर्वांगसमता का विधिपूर्वक अर्थ जानने की कोशिश करेंगे जिन्हें हम पहल से जानते हैं ।
7.2 तल-आकृतियों की सर्वांगसमता
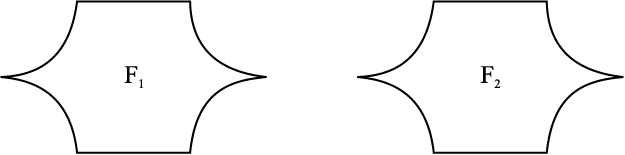
यहाँ दी गई दो आकृतियों को देखिए (आकृति 7.3)। क्या ये आकृतियाँ सर्वांगसम हैं ?




आकृति 7.3
आप अध्यारोपण विधि का प्रयोग कर सकते हैं । इनमें से एक का अक्स (trace-copy) बनाकर दूसरी आकृति पर रखते हैं । यदि ये आकृतियाँ एक दूसरे को पूर्णतया ढक लेती हैं तो वे सर्वांगसम कहलाती हैं । दूसरे ढंग से, आप इनमें से एक आकृति को काट कर उसे दूसरी आकृति पर रख सकते हैं । लेकिन सावधान ! जिस आकृति को आपने काटा है (या अक्स बनाया है) उसे मोड़ने या फैलाने की आपको छूट नहीं है ।
आकृति 7.3 में, यदि आकृति F1, आकृति F2 के सर्वांगसम है तो हम लिखेंगे F1 ≅ F2.
7.3 रेखाखंडों में सर्वांगसमता
दो रेखाखंड कब सर्वांगसम होते हैं ? नीचे दिए गए रेखाखंडों के दो युग्मों को देखिए ।
(i) (ii)
आकृति 7.4
प्रत्येक रेखाखंड युग्म के लिए अक्स प्रतिलिपि बनाकर अध्यारोपण विधि का प्रयोग कीजिए [आकृति 7.4(i)] 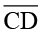 का अक्स बनाकर इसे
का अक्स बनाकर इसे 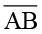 पर रखें । आप देखेंगे कि
पर रखें । आप देखेंगे कि 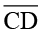
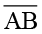 को पूर्णतया ढक लेता है और C, A पर तथा D, B पर स्थित है । अतः हम कह सकते हैं कि दोनों रेखाखंड सर्वांगसम हैं और हम लिखेंगे
को पूर्णतया ढक लेता है और C, A पर तथा D, B पर स्थित है । अतः हम कह सकते हैं कि दोनों रेखाखंड सर्वांगसम हैं और हम लिखेंगे 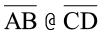 .
.
आकृति 7.4 (ii) के रेखाखंड युग्म के लिए इस क्रियाकलाप को दोहराइए । आप क्या देखते हैं ? ये रेखाखंड सर्वांगसम नहीं हैं । यह आपने कैसे जाना ? क्योंकि जब एक रेखाखंड को दूसरे रेखाखंड पर रखा जाता है तो वे एक दूसरे को पूर्णतया नहीं ढकते हैं ।
आकृति 7.4 (i) में आपने देखा होगा कि रेखाखंडों के युग्म का एक दूसरे के साथ सुमेलन (matching) होता है क्योंकि उनकी लंबाई बराबर है परंतु आकृति 7.4(ii) में एेसी स्थिति नहीं है ।
यदि दो रेखाखंडों की लंबाई समान (यानी बराबर) है तो वे सर्वांगसम होते हैं। यदि दो रेखाखंड सर्वांगसम हैं तो उनकी लंबाइयाँ समान होती हैं ।
ऊपर दिए गए तथ्य को ध्यान में रखते हुए, जब दो रेखाखंड सर्वांगसम होते हैं तो हम कहते हैं कि रेखाखंड बराबर हैं; और हम लिखते हैं AB = CD। (हमारा वास्तव में अर्थ है कि 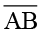 ≅
≅ 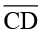 )।
)।
7.4 कोणों की सर्वांगसमता
यहाँ दिए गए चार कोणों को देखिए (आकृति 7.5) ः
(i) (ii) (iii) (iv)
आकृति 7.5
∠PQR का अक्स बनाइए और इससे ∠ABC को ढकने का प्रयास कीजिए । इसके लिए, सबसे पहले Q को B पर और 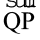 को
को 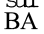 पर रखिए ।
पर रखिए । 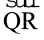 कहाँ पर आएगा ? यह
कहाँ पर आएगा ? यह 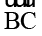 के ऊपर होगा ।
के ऊपर होगा ।
इस प्रकार, ∠PQR का सुमेलन ∠ABC से होता है ।
इस सुमेलन में ∠ABC और ∠PQR सर्वांगसम हैं ।
(ध्यान दीजिए कि इन दोनों सर्वांगसम कोणों की माप समान है)
हम लिखते हैं ∠ABC ≅ ∠PQR (i)
या m∠ABC = m ∠PQR (इस स्थिति में माप 40° है)
अब आप ∠LMN का अक्स बनाइए और इसे ∠ABC पर रखिए । M को B पर तथा 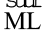 को
को 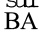 पर रखिए । क्या
पर रखिए । क्या 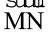 ,
, 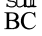 पर आता है ? नहीं, इस स्थिति में एेसा नहीं होता है । आपने देखा कि ∠ABC और ∠LMN एक दूसरे को पूर्णतया नहीं ढकते हैं । इसलिए वे सर्वांगसम नहीं हैं ।
पर आता है ? नहीं, इस स्थिति में एेसा नहीं होता है । आपने देखा कि ∠ABC और ∠LMN एक दूसरे को पूर्णतया नहीं ढकते हैं । इसलिए वे सर्वांगसम नहीं हैं ।
(ध्यान दीजिए, इस स्थिति में ∠ABC और ∠LMN की माप बराबर नहीं है)
∠XYZ और ∠ABC के बारे में आप क्या कहेंगे । आकृति 7.5(iv)में किरण 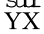 और
और 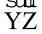 क्रमशः किरण
क्रमशः किरण 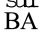 और
और 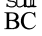 से अधिक लंबी प्रतीत होती है । इसके आधार पर आप सोच सकते हैं कि ∠ABC, ∠XYZ से छोटा है । परंतु याद रखिए कि आकृति में किरण केवल दिशा को ही प्रदर्शित करती है न कि लंबाई को। आप देखेंगे कि ये दोनों कोण भी सर्वांगसम हैं ।
से अधिक लंबी प्रतीत होती है । इसके आधार पर आप सोच सकते हैं कि ∠ABC, ∠XYZ से छोटा है । परंतु याद रखिए कि आकृति में किरण केवल दिशा को ही प्रदर्शित करती है न कि लंबाई को। आप देखेंगे कि ये दोनों कोण भी सर्वांगसम हैं ।
हम लिखते हैं ∠ABC ≅ ∠XYZ (ii)
या m∠ABC = m∠XYZ
(i) और (ii) को ध्यान में रखते हुए, हम यह भी लिख सकते हैं ः
∠ABC ≅ ∠PQR ≅ ∠XYZ
यदि दो कोणों की माप समान हो तो वे सर्वांगसम होते हैं । यदि दो कोण सर्वांगसम हैं तो उनकी माप भी समान होती है।
कोणों की सर्वांगसमता पूर्णतया उनके मापों की समानता के ऊपर निर्भर करती है जैसाकि रेखाखंडों की स्थिति में बताया गया है । इस प्रकार, यह कहना कि दो कोण सर्वांगसम हैं, हम कई बार केवल यही कहते हैं कि कोण बराबर हैं; और हम लिखते हैंः
∠ABC = ∠PQR (अर्थात ∠ABC ≅ ∠PQR).
7.5 त्रिभुजों की सर्वांगसमता
हमने देखा कि दो रेखाखंड सर्वांगसम होते हैं जब उनमें से एक, दूसरे की प्रतिलिपि हो । इसी प्रकार, दो कोण सर्वांगसम होते हैं यदि उनमें से एक, दूसरे की प्रतिलिपि हो । हम इस संकल्पना को अब त्रिभुजों के लिए भी देखते हैं ।
दो त्रिभुज सर्वांगसम होते हैं यदि वे एक दूसरे की प्रतिलिपियाँ हों और एक को दूसरे के ऊपर रखे जाने पर, वे एक दूसरे को आपस में पूर्णतया ढक लें ।
(i) (ii)
आकृति 7.6
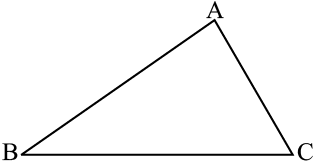
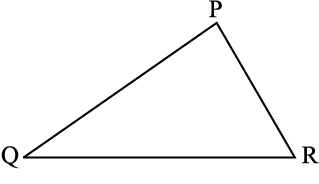
∆ABC और ∆PQR समान आकार एवं समान आमाप के हैं । ये सर्वांगसम हैं । अतः इनको निम्नलिखित प्रकार से दर्शाएँगे ः
∆ABC ≅ ∆PQR.
इसका अर्थ यह है कि यदि आप ∆PQR को ∆ABC पर रखते हैं, तो P, A के ऊपर; Q, B के ऊपर और R, C के ऊपर आता है । इसी प्रकार 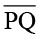 ,
, 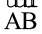 के अनुदिश;
के अनुदिश; 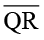 ,
,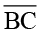 के अनुदिश तथा
के अनुदिश तथा 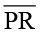 ,
, 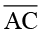 के अनुदिश आते हैं । यदि दिए गए सुमेलन (correspondence) में दो त्रिभुज सर्वांगसम हैं तो उनके संगत भाग (अर्थात् कोण और भुजाएँ) समान होते हैं । अतः इन दोनों सर्वांगसम त्रिभुजों में, हमें प्राप्त होता हैः
के अनुदिश आते हैं । यदि दिए गए सुमेलन (correspondence) में दो त्रिभुज सर्वांगसम हैं तो उनके संगत भाग (अर्थात् कोण और भुजाएँ) समान होते हैं । अतः इन दोनों सर्वांगसम त्रिभुजों में, हमें प्राप्त होता हैः
संगत शीर्ष : A और P, B और Q, C और R.
संगत भुजाएँ : 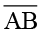 और
और 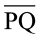 ,
, 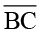 और
और 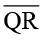 ,
, 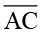 और
और 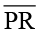 .
.
संगत कोण : ∠A और ∠P, ∠B और ∠Q, ∠C और ∠R.
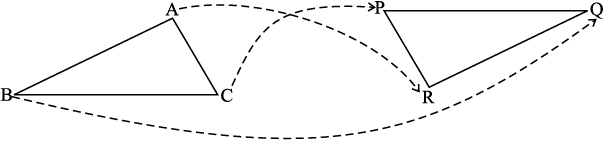
यदि आप ∆PQR को ∆ABC पर इस प्रकार से आरोपित करते हैं कि P, B के ऊपर रखेें तो क्या दूसरे शीर्ष भी यथायोग्य सुमेलित होंगे ? एेसा होना आवश्यक नहीं है ? आप त्रिभुजों की अक्स प्रतिलिपियाँ लीजिए और यह ज्ञात करने का प्रयत्न कीजिए । यह दर्शाता है कि त्रिभुजों की सर्वांगसमता के बारे में चर्चा करते समय न केवल कोणों की माप और भुजाओं की लंबाइयाँ महत्त्व रखती हैं, परंतु शीर्षों का सुमेलन भी उतना ही महत्त्व रखता है । ऊपर दी गई स्थिति में, सुमेलन हैः
A ↔ P, B ↔ Q, C ↔ R
हम इसे, इस प्रकार भी लिख सकते हैं ABC ↔ PQR
उदाहरण 1 यदि ∆ABC और ∆PQR सुमेलन ABC ↔ RQP के अंतर्गत सर्वांगसम हों, तो ∆ABC के वे भाग लिखिए जो निम्न के संगत हों
(i) ∠P (ii) ∠Q (iii) 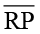
हल इस सर्वांगसमता को अच्छे ढंग से समझने के लिए, आइए हम एक आकृति (आकृति 7.7) का प्रयोग करते हैं ।
यहाँ सुमेलन ABC ↔ RQP है । अर्थात् A ↔ R ; B ↔ Q; C ↔ P.
अतः (i) 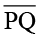 ↔
↔  (ii) ∠Q ↔ ∠B (iii)
(ii) ∠Q ↔ ∠B (iii) 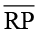 ↔
↔ 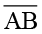
सोचिए, चर्चा कीजिए और लिखिए
जब दो त्रिभुज, मान लीजिए ABC और PQR, दिए हुए हों तो उनमें आपस में कुल छः संभव सुमेलन होते हैं । उनमें से दो सुमेलन ये हैंः
(i) ABC ↔ PQR और (ii) ABC ↔ QRP
दो त्रिभुजों के कट-आउट (cutouts) का प्रयोग करके अन्य चार सुमेलनों को ज्ञात कीजिए । क्या ये सभी सुमेलन सर्वांगसमता दर्शाते हैं ? इसके बारे में विचार कीजिए ।
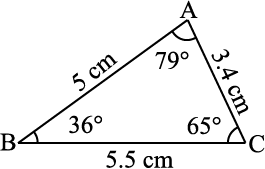
आकृति 7.8
अप्पू द्वारा निर्मित त्रिभुज
प्रश्नावली 7.1
1. निम्न कथनों को पूरा कीजिए ः
(a) दो रेखाखंड सर्वांगसम होते हैं यदि ___________।
(b) दो सर्वांगसम कोणों में से एक की माप 70° है, दूसरे कोण की माप ___________ है।
(c) जब हम ∠A = ∠B लिखते हैं, हमारा वास्तव में अर्थ होता है ___________।
2. वास्तविक जीवन से संबंधित सर्वांगसम आकारों के कोई दो उदाहरण दीजिए ।
3. यदि सुमेलन ABC ↔ FED के अंतर्गत ∆ABC ≅ ∆FED तो त्रिभुजों के सभी संगत सर्वांगसम भागों को लिखिए ।
4. यदि ∆DEF ≅ ∆BCA हो, तो ∆BCA के उन भागों को लिखिए जो निम्न के संगत होः
(i) ∠E (ii) 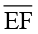 (iii) ∠F (iv)
(iii) ∠F (iv) 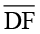
7.6 त्रिभुजों की सर्वांगसमता के लिए प्रतिबंध
हम अपने दैनिक जीवन में त्रिभुजाकार संरचनाओं और नमूनों का प्रायः प्रयोग करते हैं । अतः यह ज्ञात करना लाभकारी होगा कि दो त्रिभुजाकार आकृतियाँ कब सर्वांगसम होंगी । यदि आपकी नोटबुक में दो त्रिभुज बने हैं और आप प्रमाणित करना चाहते हैं कि क्या वे सर्वांगसम हैं तब आप हर बार उनमें से एक को काटकर दूसरे पर रखने (आरोपण) वाली विधि का प्रयोग नहीं कर सकते हैं । इसके बदले यदि हम सर्वांगसमता को सटीक मापों द्वारा निश्चित कर सकें तो यह अधिक उपयोगी होगा। चलिए एेसा करने का प्रयत्न करें।
एक खेल
अप्पू और टिप्पू एक खेल खेलते हैं । अप्पू ने एक त्रिभुज ABC(आकृति 7.8) बनाया । उसने प्रत्येक भुजा की लंबाई और इसके प्रत्येक कोण की माप को ध्यान में रख लिया । टिप्पू ने यह सब ध्यान से नहीं देखा । अप्पू, टिप्पू को चुनौती देता है कि क्या वह कुछ दी सूचनाओं के आधार पर उसके ∆ABC की प्रतिलिपि बना सकता है? अप्पू द्वारा दी गई सूचनाओं का प्रयोग करके टिप्पू ∆ABC के सर्वांगसम एक त्रिभुज बनाने का प्रयास करता है । खेल आरंभ होता है । सावधानी से उनके वार्तालाप और उनके खेल का अवलोकन कीजिए ।
SSS खेल
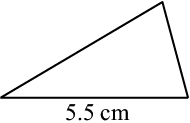
अप्पू ः ∆ABC की एक भुजा 5.5 cm है ।
टिप्पू ः इस सूचना से, मैं अनेक त्रिभुजों को बना सकता हूँ (आकृति 7.9)। लेकिन यह आवश्यक नहीं कि वे ∆ABC की प्रतिलिपि हों। मैं जो त्रिभुज बनाता हूँ वह त्रिभुज अधिक कोण ( obtuse angled) या समकोण ( Right angled) या न्यून कोण ( acute angled) हो सकता है । यहाँ पर कुछ उदाहरण दिए गए हैं ः
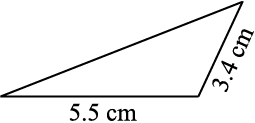
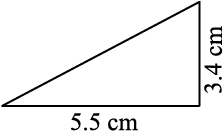
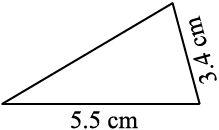
आकृति 7.11
मैंने अन्य भुजाओं के लिए स्वेच्छा से लंबाइयों का प्रयोग किया । इससे मुझे 5.5 cm लंबाई के आधार वाले कई त्रिभुज मिलते हैं ।
अतः दी गई केवल एक ही भुजा की लंबाई से ∆ABC की प्रतिलिपि बनाना, मेरे लिए संभव नहीं।
अप्पू ः अच्छा । मैं तुम्हें एक और भुजा की लंबाई दूँगा । ∆ABC की दो भुजाओं की लंबाइयाँ 5.5 cm और 3.4 cm हैं।
टिप्पू ः यह सूचना भी त्रिभुज बनाने के लिए पर्याप्त नहीं है । मैं इस दी गई सूचना से बहुत से त्रिभुज बना सकता हूँ जो ∆ABC की प्रतिलिपि नहीं होंगे ।
यहाँ पर कुछ त्रिभुज दिए गए हैं जो मेरी बात का समर्थन करते हैं,
आपके त्रिभुज जैसी प्रतिलिपि कोई भी नहीं बना सकता यदि केवल दो भुजाओं की लंबाइयाँ दी गई हों ।
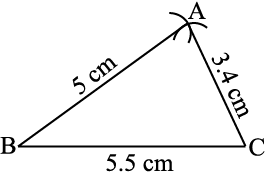
अप्पू ः ठीक है ! मैं तुम्हें त्रिभुज की तीनों भुजाओं की माप देता हूँ । ∆ABC में, मेरे पास AB = 5 cm, BC = 5.5 cm और AC = 3.4 cm है ।
टिप्पू ः मैं सोचता हूँ कि त्रिभुज बनाना अब संभव होना चाहिए । मैं अब कोशिश करता हूँ । सबसे पहले मैं एक खाका (कच्ची) आकृति बनाता हूँ जिससे मैं आसानी से लंबाइयाँ याद रख सकूँ । मैं 5.5 cm 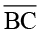 खींचता हूँ ।
खींचता हूँ ।
आकृति 7.12
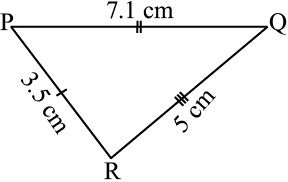
'B' को केंद्र लेकर, मैं 5 cm त्रिज्या वाली एक चाप खींचता हूँ । बिंदु ‘A’ इस चाप पर कहीं स्थित होना चाहिए । 'C' को केंद्र लेकर 3.4 cm त्रिज्या वाली एक चाप खींचता हूँ । बिंदु ‘A’ इस चाप पर भी होना चाहिए । अर्थात्, ‘A’ बिंदु खींची गई दोनों चापों पर स्थित है । अर्थात् ‘A’ दोनों चापों का प्रतिच्छेदी बिंदु है ।
मैं अब बिंदुओं A, B और C की स्थिति जानता हूँ । अहा! मैं इन्हें मिलाकर ∆ABC प्राप्त कर सकता हूँ । (आकृति 7.11)
अप्पू ः बहुत अच्छा ! अतः एक दिए हुए ∆ABC की प्रतिलिपि बनाने के लिए (अर्थात् ∆ABC के सर्वांगसम) हमें तीनों भुजाओं की लंबाइयों की आवश्यकता होती है । क्या हम इस स्थिति को भुजा-भुजा-भुजा (side-side-side) प्रतिबंध कह सकेंगे?
टिप्पू ः क्यों न हम इसे संक्षेप में, SSS प्रतिबंध कहें ।
SSS सर्वांगसमता प्रतिबंध
यदि दिए गए सुमेलन के अंतर्गत, एक त्रिभुज की तीनों भुजाएँ क्रमशः किसी दूसरे त्रिभुज की संगत भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं ।
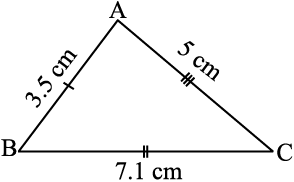
उदाहरण 2 त्रिभुज ABC और PQR में AB = 3.5 cm, BC = 7.1 cm, AC = 5 cm,
PQ = 7.1 cm, QR = 5 cm, और PR = 3.5 cm है (आकृति 7.1)। जाँचिए कि क्या दोनों त्रिभुज सर्वांगसम हैं या नहीं ? यदि हाँ, तो सुमेलन संबंध को सांकेतिक रूप में लिखिए ।
हल यहाँ, AB = RP (= 3.5 cm),
BC = PQ ( = 7.1 cm)
AC = QR (= 5 cm)
आकृति 7.14
2. आकृति 7.15 में AB = AC और D, 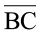 का मध्य बिंदु है ।
का मध्य बिंदु है ।
(i) ∆ADB और ∆ADC में बराबर भागों के तीन युग्म बताइए ।
(ii) क्या ∆ADB ≅ ∆ADC है? कारण दीजिए ।
(iii) क्या ∠B = ∠C है? क्यों?
3. आकृति 7.16 में, AC = BD और AD = BC है । निम्नलिखित कथनों में कौन-सा कथन सत्य है?
(i) ∆ABC ≅ ∆ABD (ii) ∆ABC ≅ ∆BAD
सोचिए, चर्चा कीजिए और लिखिए
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC (आकृति 7.17) है। ∆ABC की एक अक्स प्रतिलिपि लीजिए और इसे भी ∆ABC का नाम दीजिए
(i) ∆ABC और ∆ACB में बराबर भागों के तीन युग्म बताइए ।
(ii) क्या ∆ABC ≅ ∆ACB है ? क्यों अथवा क्यों नहीं ?
(iii) क्या ∠B = ∠C है ? क्यों अथवा क्यों नहीं ?
अप्पू और टिप्पू अब पिछले खेल में कुछ परिवर्तन करके पुनः खेलते हैं ।
ज्ञानवर्धक क्रियाकलाप (Enrichment Activity)
हमने देखा कि अध्यारोपण तल-आकृतियों की सर्वांगसमता को जाँचने की एक उपयोगी विधि है । हमने रेखाखंडों, कोणों और त्रिभुजों की सर्वांगसमता के लिए प्रतिबंधों का वर्णन किया । अब आप इस संकल्पना को बढ़ाकर तल की दूसरी आकृतियों के लिए प्रयत्न कर सकते हैं ।
1. अलग-अलग माप के वर्गों के कट-आउट (cutout) सोचिए । अध्यारोपण विधि का प्रयोग वर्गों की सर्वांगसमता के लिए प्रतिबंध ज्ञात करने के लिए कीजिए । कैसे "सर्वांगसम भागों" की संकल्पना सर्वांगसम के अंतर्गत उपयोग होती है ? क्या यहाँ संगत भुजाएँ हैं ? क्या यहाँ संगत विकर्ण हैं ?
2. यदि आप वृत्त लेते हैं तो क्या होता है ? दो वृत्तों की सर्वांगसमता के लिए प्रतिबंध क्या है ? क्या, आप फिर अध्यारोपण विधि का प्रयोग कर सकते हैं, पता लगाइए ।
3. इस संकल्पना को बढ़ाकर तल की दूसरी आकृतियाँ, जैसे समषट्भुज इत्यादि के लिए प्रयत्न कीजिए ।
4. एक त्रिभुज की दो सर्वांगसम प्रतिलिपियाँ लीजिए । कागज को मोड़कर पता लगाइए कि क्या उनके शीर्षलंब बराबर हैं । क्या उनकी माध्यिकाएँ समान हैं ? आप उनके परिमाप तथा क्षेत्रफलों के बारे में क्या कह सकते हैं ?
हमने क्या चर्चा की?
1. सर्वांगसम वस्तुएँ एक दूसरे की प्रतिलिपियाँ होती हैं ।
2. अध्यारोपण विधि तल-आकृतियों की सर्वांगसमता की जाँच करती है ।
3. दो तल आकृतियाँ, माना, F1 और F2 सर्वांगसम होती हैं यदि F1 की अक्स-प्रतिलिपि F2. को पूर्णतया ढक लेती है । हम इसे F1 ≅ F2 के रूप में लिखते हैं ।
4. दो रेखाखंड, माना,  और
और 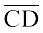 , सर्वांगसम होते हैं यदि उनकी लंबाइयाँ बराबर हों । हम इसे
, सर्वांगसम होते हैं यदि उनकी लंबाइयाँ बराबर हों । हम इसे 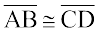 के रूप में लिखते हैं । यद्यपि, साधारणतया इसे
के रूप में लिखते हैं । यद्यपि, साधारणतया इसे  =
= 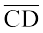 लिखते हैं ।
लिखते हैं ।
5. दो कोण, माना, ∠ABC और ∠PQR, सर्वांगसम होते हैं यदि उनकी माप बराबर हो । हम इसे ∠ABC ≅ ∠PQR याm∠ABC = m∠PQR. के रूप में लिखते हैं । यद्यपि, अभ्यास में इसे साधारणतया ∠ABC = ∠PQR के रूप में लिखते हैं ।
6. दो त्रिभुजों की SSS सर्वांगसमताः
एक दिए हुए सुमेलन के अंतर्गत, दो त्रिभुज सर्वांगसम होते हैं यदि एक त्रिभुज की तीनों भुजाएँ किसी दूसरे त्रिभुज की तीनों संगत भुजाओं के बराबर हो ।
7. दो त्रिभुजों की SAS सर्वांगसमताः
एक दिए हुए सुमेलन के अंतर्गत, दो त्रिभुज सर्वांगसम होते हैं यदि एक त्रिभुज की दो भुजाएँ और उनके अंतर्गत कोण, दूसरे त्रिभुज की दो संगत भुजाओं और उनके अंतर्गत कोण के बराबर हो ।
8. दो त्रिभुजों की ASA सर्वांगसमताः
एक दिए हुए सुमेलन के अंतर्गत, दो त्रिभुज सर्वांगसम होते हैं यदि एक त्रिभुज के दो कोण और उनकी अंतर्गत भुजा किसी दूसरे त्रिभुज के दो संगत कोणों और अंतर्गत भुजा के बराबर हो ।
9. दो त्रिभुजों की RHS सर्वांगसमताः
एक दिए हुए सुमेलन के अंतर्गत, दो समकोण त्रिभुज सर्वांगसम होते हैं यदि किसी समकोण त्रिभुज का कर्ण और एक भुजा किसी दूसरे समकोण त्रिभुज के कर्ण और संगत भुजा के बराबर हो ।
10. दो त्रिभुजों में AAA सर्वांगसमता नहीं होती है।
यह आवश्यक नहीं है कि बराबर संगत कोणों के दो त्रिभुज सर्वांगसम हों । एेसे सुमेलनों में, इनमें से एक, दूसरे की बढ़ी हुई प्रतिलिपि हो सकती है । (वे सर्वांगसम होंगे यदि वे एक दूसरे की एक जैसी प्रतिलिपि हो)।

