Table of Contents
राशियों की तुलना
8.1 भूमिका
हमारे दैनिक जीवन में, अनेक एेसे अवसर आते हैं जब हम दो राशियों की तुलना करते हैं । मान लीजिए हम हीना और आमिर की ऊँचाइयों की तुलना कर रहे हैं । हम पाते हैं कि
1. हीना, आमिर से दो गुनी ऊँची है ।
अथवा
2. आमिर की ऊँचाई हीना की ऊँचाई की आधी है ।
एक और उदाहरण पर विचार कीजिए, जब हम 20 कँचे, रीटा और अमित में इस प्रकार बाँटते हैं कि रीता को 12 कँचे तथा अमित को 8
आदमी की चाल, चीते की चाल का 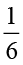 वाँ भाग है ।
वाँ भाग है ।
क्या आपको भी एेसी कुछ अन्य तुलनाएँ याद हैं? कक्षा 6 में हम दो राशियों की तुलना करना सीख चुके हैं, जब हमने बताया कि एक राशि, दूसरी राशि की कितने गुनी है । अब हम यह देखते हैं कि किसी तुलना को भी उल्टा करके यह बताया जा सकता है कि दूसरी राशि पहली राशि का कौन-सा भाग है ।
ऊपर के उदाहरणों में, हम राशियों को, जैसे ऊँचाइयों को, अनुपात के रूप में भी दर्शा सकते हैं ।
जैसे, हीना की ऊँचाई ः आमिर की ऊँचाई = 150ः75 अथवा 2ः1 है।
क्या, अब आप अन्य तुलनाओं को भी अनुपातों के रूप में व्यक्त कर सकते हैं ?
ये परस्पर तुलनाएँ हैं, जो दो विभिन्न स्थितियों में भी समान हो सकती हैं ।
यदि हीना की ऊँचाई 150 cm तथा आमिर की ऊँचाई 100 cm होती, तब उनकी ऊँचाइयों में अनुपात होता :
हीना की ऊँचाई : आमिर की ऊँचाई = 150:100 = 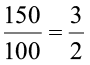 या 3:2 है।
या 3:2 है।
यह वही अनुपात है जो रीता ओर अमित के कंचों में था ।
इस प्रकार, हम देखते हैं कि दो विभिन्न स्थितियों में तुलना करने पर, एक ही अनुपात मिल सकता है ।
ध्यान रखिए कि तुलना करने में दोनों राशियों की इकाइयाँ समान होनी चाहिए। अनुपात की कोई इकाई नहीं होती।
उदाहरण 1 3 km का 300 m के साथ अनुपात ज्ञात कीजिए ।
हल पहले दोनों दूरियों को एक ही इकाई में लिखते हैं ।
अतः, 3 km = 3 × 1000 m = 3000 m
इस प्रकार, अभीष्ट अनुपात 3 kmः300 m, अर्थात्् 3000 mः300 m या 10ः1 है।
8.2 तुल्य अनुपात
विभिन्न अनुपातों की भी आपस में तुलना की जा सकती है, जिससे पता चल सके कि वे तुल्य हैं अथवा नहीं । एेसा करने के लिए, हमें अनुपातों को पहले भिन्नों के रूप में लिखना पड़ता है और फिर उन्हें समान हर वाली भिन्नों में बदलकर उनकी तुलना करते हैं । यदि ये भिन्नें समान हैं तब हम कहते हैं कि दिए हुए अनुपात तुल्य हैं।
उदाहरण 2 क्या अनुपात 1ः2 अनुपात 2ः3 के तुल्य है ?
हल जाँच करने के लिए, हमें देखना होगा कि क्या 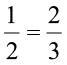 है ?
है ?
हम पाते हैं 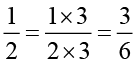 तथा
तथा 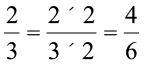
हम देखते हैं कि 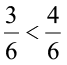 है। अर्थात्
है। अर्थात् 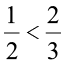 है।
है।
अतः, अनुपात 1 : 2, अनुपात 2 : 3 के तुल्य नहीं है ।
एेसी तुलनाओं का उपयोग निम्न उदाहरण में देखा जा सकता है ः
उदाहरण 3 एक क्रिकेट टीम द्वारा खेले गए कुछ मैचों में प्रदर्शन निम्न प्रकार हैं :
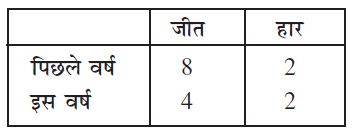
किस वर्ष में प्रदर्शन बेहतर था?
एेसा आप किस आधार पर कह सकते हैं?
हल पिछले वर्ष, जीत : हार = 8 : 2 = 4 : 1
इस वर्ष, जीत : हार = 4 : 2 = 2 : 1
स्पष्ट है कि 4 : 1 > 2 : 1 (भिन्न रूप में 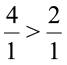 )
)
अतः, हम कह सकते हैं कि पिछले वर्ष टीम का प्रदर्शन बेहतर अर्थात् अधिक अच्छा था ।
कक्षा VI में, हमनें देखा था कि तुल्य अनुपात किस प्रकार महत्वपूर्ण हैं । दो अनुपात यदि तुल्य हों, तो वे एक समानुपात बनाते हैं । आइए समानुपात के बारे में स्मरण करें ।
राशियों को समानुपात में रखना और हल प्राप्त करना
अरुणा ने अपने मकान की रूपरेखा देखकर उसका एक प्रतिरूप कागज़ पर बनाया और मकान के साथ ही अपनी माँ को भी खड़ा दिखाया ।
देखकर मोना बोली "इस चित्रांकन में कुछ गलती नज़र आती है ।"
क्या आप बता सकते हैं कि इसमें क्या गलती है ?
आप एेसा कैसे कह सकते हैं ?
यहाँ चित्र में दर्शाई गई ऊँचाइयों का अनुपात और वास्तव ऊँचाइयों का अनुपात समान होने चाहिए।
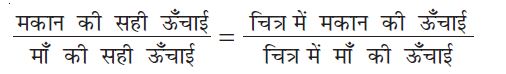
एेसा होने पर ही सही समानुपात बनेगा । प्रायः जब सही समानुपात में कोई चित्र बनाया जाता है, तब ही वह देखने में मोहक एवं आकर्षक लगता है ।
एक अन्य उदाहरण राष्ट्रीय ध्वज का है, जहाँ ध्वज को बनाने में सही समानुपात का ध्यान रखा जाता है ।
क्या आपको पता है कि राष्ट्रीय ध्वज सदैव, लंबाई व चौड़ाई के एक निश्चित अनुपात में ही बनाए जाते हैं, जो विभिन्न देशों के लिए विभिन्न हो सकते हैं? लेकिन प्रायः यह अनुपात 1.5ः1 अथवा 1.7ः1 होता है ।
हम इस अनुपात का मान 3ः2 के लगभग ले सकते हैं । लगभग यही मान भारत में प्रयोग में लाए जाने वाले पोस्ट कार्ड में भी होता है ।
अब, क्या आप कह सकते हैं कि 4.5 cm लंबे तथा 3.0 cm चौड़े कार्ड में यही अनुपात है? इसके लिए आपको अनुपातों 4.5ः3.0 तथा 3ः2 की तुल्यता देखनी होगी ।
हम देखते हैं कि 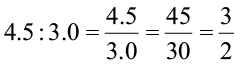
अतः, हम पाते हैं कि 4.5 : 3.0 तथा 3 : 2 तुल्य अनुपात हैं ।
वास्तविक जीवन में समानुपातों के व्यापक उपयोग मिलते हैं । क्या आप एेसी कुछ परिस्थितियों के बारे में सोच सकते हैं ?
हमने पिछली कक्षाओं में एेकिक विधि से भी प्रश्न हल करना सीखा है । इस विधि में पहले हम अनेक से एक और फिर वांछित संख्या के लिए मान ज्ञात करते हैं ।
आइए, अब देखें कि इन दोनों विधियों से एक ही समस्या को कैसे हल किया जाता है।
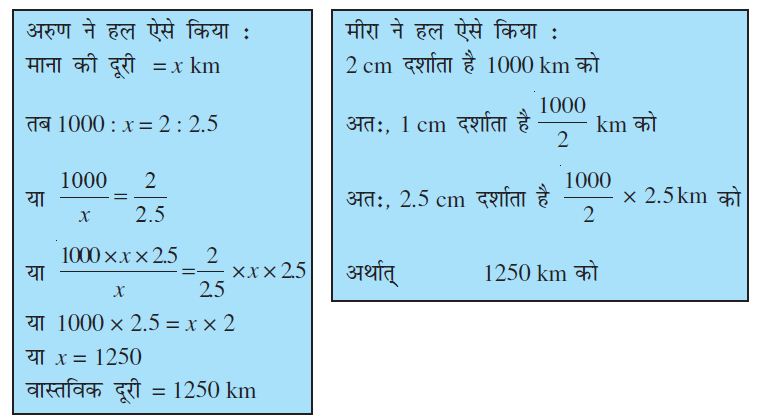
उदाहरण 4 एक मानचित्र 1000 km को 2 cm से दर्शाते हुए बनाया गया है। यदि दो स्थानों के बीच की दूरी मानचित्र में 2.5 cm है, तब उनके बीच की वास्तविक दूरी कितनी होगी ?
हल
अरुण ने पहले समानुपात बनाकर फिर एक समीकरण प्राप्त किया और हल निकाला । मीरा ने पहले 1cm से प्रदर्शित दूरी ज्ञात की और फिर उससे 2.5 km से प्रदर्शित वास्तविक दूरी ज्ञात की । इस प्रकार, उसने एेकिक विधि का प्रयोग किया ।
अब आइए एेकिक विधि को उपयोग में लाते हुए कुछ और समस्याएँ हल करें ।
उदाहरण 5 यदि 6 कटोरियों का मूल्य ₹ 90 है, तब एेसी ही 10 कटोरियों का मूल्य क्या होगा?
हल 6 कटोरियों का मूल्य = ₹ 90
अतः, 1 कटोरी का मूल्य = ₹ 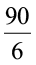
अतः, 10 कटोरियों का मूल्य = ₹ 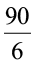 × 10 = ₹ 150
× 10 = ₹ 150
उदाहरण 6 मेरी कार 25 लीटर पैट्रोल में 150 km की दूरी तय कर लेती है । 30 लीटर पैट्रोल में यह कितनी दूरी तय करेगी ?
हल 25 लीटर पैट्रोल में तय की गई दूरी = 150 km
अतः, 1 लीटर पैट्रोल में दूरी चलेगी = 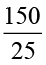 km
km
अतः, 30 लीटर पैट्रोल में दूरी चलेगी = 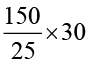 km = 180 km
km = 180 km
इस विधि में, पहले हम एक वस्तु के लिए मान निकालते हैं, अर्थात्् एेकिक दर निकालते हैं । यह दो विभिन्न गुणों की तुलना करके किया जाता है । उदाहरण के लिए, वस्तुओं के मूल्य से तुलना करके एक वस्तु का मूल्य ज्ञात किया जाता है ।
अथवा दूरी तथा समय दिए होने पर इकाई समय में तय होने वाली दूरी ज्ञात कर लेते हैं ।
इस प्रकार आप देख सकते हैं कि प्रत्येक को दर्शाने के लिए हम प्रायः प्रति का प्रयोग करते हैं।
उदाहरण के लिए, किलोमीटर प्रति घंटा (km/h), विद्यार्थी प्रति अध्यापक, आदि, इकाई दर प्रदर्शित करते हैं ।
सोचिए, चर्चा कीजिए और लिखिए
एक चींटी अपने भार से 50 गुना भार ढो सकती है । यदि यही तथ्य मानव पर भी लागू हो, तब ज्ञात कीजिए कि आप कितना भार ढो पाएँगे ?
प्रश्नावली 8.1
1. अनुपात ज्ञात कीजिए :
(a) ₹ 5 का 50 पैसे से (b) 15 kg का 210 g से
(c) 9 m का 27 cm से (d) 30 दिनों का 36 घंटों से
2. एक कंप्यूटर प्रयोगशाला में 6 विद्यार्थियों के लिए 3 कंप्यूटर होने चाहिए । ज्ञात कीजिए कि 24 विद्यार्थियों के लिए कितने कंप्यूटरों की आवश्यकता होगी ?
3. राजस्थान की जनसंख्या = 570 लाख और उत्तर प्रदेश की जनसंख्या = 1660 लाख राजस्थाान का क्षेत्रफल = 3 लाख km2 और उत्तर प्रदेश का क्षेत्रफल = 2 लाख km2, ज्ञात कीजिए
(i) इन दोनों राज्यों में प्रति km2 कितने व्यक्ति हैं ?
(ii) किस राज्य की जनसंख्या कम घनी है ?
8.3 प्रतिशतता-राशियों के तुलना करने की एक और विधि
अनीता की रिपोर्ट रीता की रिपोर्ट
प्राप्तांक : 320/400 प्राप्तांक : 300/360
प्रतिशत : 80 प्रतिशत : 83.3
अनीता कहती है कि उसका परीक्षाफल अधिक अच्छा है, क्योंकि उसने 320 अंक प्राप्त किए है जबकि रीता ने केवल 300 अंक । क्या आप उससे सहमत हैं ? आपके विचार में किसका परीक्षाफल अधिक अच्छा है ?
मानसी कहती है कि केवल प्राप्तांकों की तुलना कर यह नहीं कहा जा सकता है कि किसका परीक्षाफल अधिक अच्छा है क्योंकि अधिकतम अंक जिनमें से दोनों को अंक प्राप्त हुए हैं वे समान नहीं हैं ।
वह कहती है कि रिपोर्ट कार्डों में दिए गए प्रतिशत अंकों पर आप ध्यान क्यों नहीं देती । अनीता के प्रतिशत अंक 80 हैं जबकि रीता के प्रतिशत अंक 83.3 हैं । इससे पता चलता है कि रीता का परीक्षाफल अधिक अच्छा है ।
क्या आप इससे सहमत हैं ?
प्रतिशत उन भिन्नों का अंश होता है जिनका हर 100 होता है, और यहाँ पर परीक्षाफलों की तुलना करने में इसे किया गया है ।
इस प्रकार की भिन्नों को आइए अब विस्तार से समझने का प्रयत्न करें ।
8.3.1 प्रतिशतता के अर्थ
प्रतिशत (percent) शब्द, लेटिन भाषा के एक शब्द 'percentum' से लिया गया है जिसका अर्थ है ‘प्रति एक सौ’।
प्रतिशत को चिह्न % से प्रदर्शित किया जाता है जिसका अर्थ हैं सौवाँ। यानी एक सौवाँ अर्थात्् 1% का अर्थ है सौ में से एक अथवा एक सौवाँ । इसे इस प्रकार लिखते हैंः 1% = 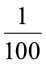 = 0.01। इसे समझने के लिए निम्न उदाहरण पर विचार करते हैं ।
= 0.01। इसे समझने के लिए निम्न उदाहरण पर विचार करते हैं ।
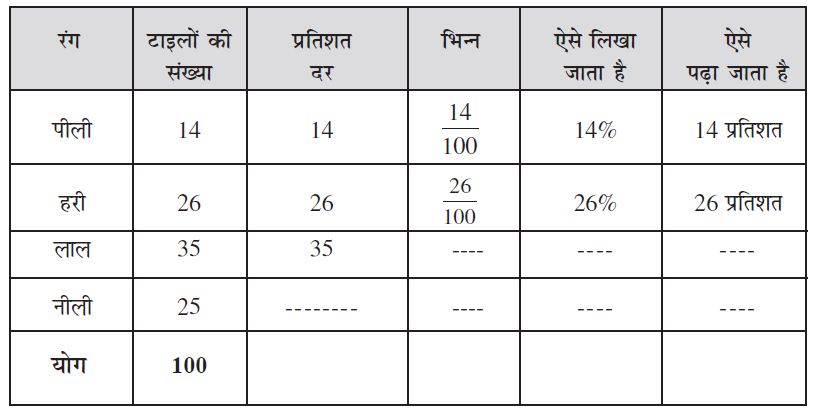
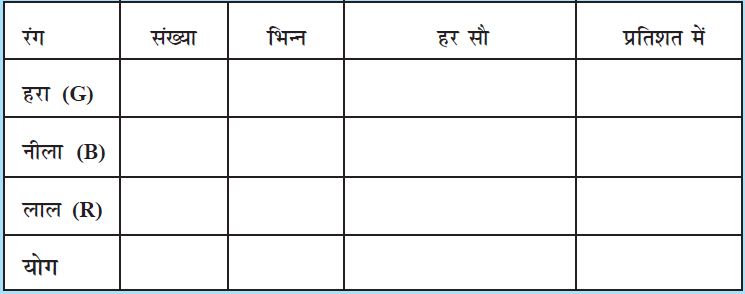
रीना एक मेज़ के ऊपरी भाग (टॉप) को बनाने के लिए 100 भिन्न-भिन्न रंगों वाली टाइलें प्रयोग करती है । उसने पीले, हरे, लाल और नीले रंग वाली टाइलें अलग-अलग गिनी और एक तालिका में निम्न प्रकार लिखा । क्या आप इस तालिका को पूरी करने में उसकी सहायता करेंगे ?
प्रयास कीजिए
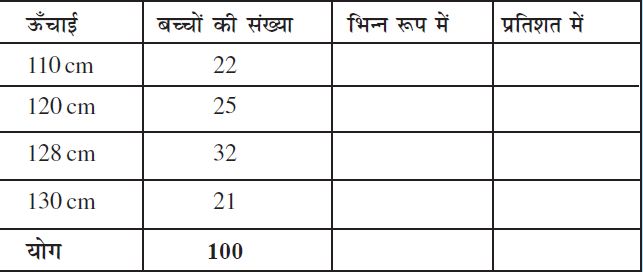
1. निम्न आँकड़ों के लिए विभिन्न ऊँचाई वाले बच्चों का प्रतिशत ज्ञात कीजिए ।
2. एक दुकान में विभिन्न मापों वाले जूतों की जोड़ियों की संख्या निम्न प्रकार है ।
माप 2 : 20; माप 3 : 30; माप 4 : 28; माप 5 : 14; माप 6 : 8
इस सूचना को ऊपर की भाँति एक तालिका के रूप में लिखिए और दुकान में उपलब्ध जूते की हर माप को प्रतिशतता में भी ज्ञात कर लिखिए ।
प्रतिशतता ज्ञात करना जब योग सौ न हो।
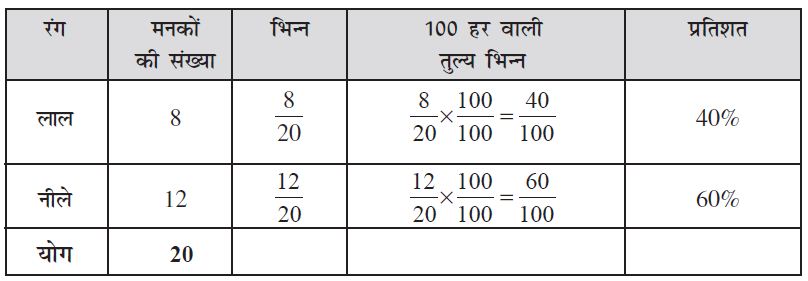
उक्त सभी उदाहरणों में वस्तुओं की संख्याओं का योग 100 हो जाता है । उदाहरण के लिए रीना के पास कुल 100 टाइलें थी; बच्चों की संख्या भी 100 तथा जूतों की संख्या भी 100 ही थी । यदि वस्तुओं की कुल संख्या 100 न हो तो प्रत्येक वस्तु का प्रतिशत रूप में कैसे आकलन किया जाता है ? एेसी स्थिति में हमें प्रत्येक भिन्न को उसकी एेसी तुल्य भिन्न में बदलना पड़ेगा जिसका हर 100 हो । निम्न उदाहरण पर विचार कीजिए । आपके पास गले की एेसी माला है जिसमें दो रंगों के बीस मनके (beads) पिरोए गए हैं।
हम देखते है कि जब वस्तुओं का कुल योग 100 नहीं हो तब प्रतिशत ज्ञात करने के लिए इन तीन विधियों को उपयोग किया जा सकता है । तालिका में दिखाई गई विधि में, हम भिन्न को 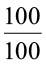 से गुणा करते हैं । इस प्रकार भिन्न का मान भी नहीं बदलता और हमें एेसी भिन्न प्राप्त हो जाती है जिसका हर 100 होता है ।
से गुणा करते हैं । इस प्रकार भिन्न का मान भी नहीं बदलता और हमें एेसी भिन्न प्राप्त हो जाती है जिसका हर 100 होता है ।
अनवर ने एेकिक विधि प्रयोग की है । आशा ने हर में 100 प्राप्त करने के लिए उसे 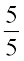 से गुणा किया । आपको जो विधि उपयुक्त लगे, उसे उपयोग में ला सकते हैं। हो सकता है आप अपनी कोई विधि भी सोच सकें ।
से गुणा किया । आपको जो विधि उपयुक्त लगे, उसे उपयोग में ला सकते हैं। हो सकता है आप अपनी कोई विधि भी सोच सकें ।
अनवर ने जिस विधि का उपयोग किया वह सभी अनुपातों के लिए प्रयोग की जा सकती है । क्या, आशा ने जिस विधि का उपयोग किया; वह भी सब अनुपातों के लिए उपयुक्त है ? अनवर का कहना है कि आशा की विधि उन भिन्नों में ही उपयोग में लाई जा सकती है, जिनके हर में एेसी संख्या हो जिसे किसी प्राकृत संख्या से गुणा करने पर 100 प्राप्त हो जाए । क्योंकि उसकी विधि में, हर में संख्या 20 थी जिसे उसने 5 से गुणा कर 100 प्राप्त कर लिया । यदि हर में संख्या 6 होती तब वह इस विधि को उपयोग नहीं कर सकती थी । क्या आप इससे सहमत हैं ?
प्रयास कीजिए
1. विभिन्न रंगों वाली 10 टुकड़ों (chips) का संग्रह इस प्रकार से हैः
तालिका पूर्ण कीजिए तथा प्रत्येक रंग वाले टुकड़ों का प्रतिशत ज्ञात कीजिए ।
2. माला के पास चूड़ियों का एक संग्रह है जिनमें 20 सोने तथा 10 चाँदी की चूड़ियाँ हैं । प्रत्येक प्रकार की चूड़ियों का प्रतिशत क्या है ? क्या आप इसके लिए भी ऊपर की तरह तालिका बना सकते हैं ?
सोचिए, चर्चा कीजिए और लिखिए
निम्न उदाहरणों को ध्यान से देखिए और चर्चा कीजिए कि उनमें प्रत्येक के लिए कौन-सी विधि अधिक उपयुक्त है।
1. वातावरण में, 1 gm वायु में उपस्थित हैंः
.78 ग्राम नाइट्रोजन 78% नाइट्रोजन
.21 ग्राम अॉक्सीजन अथवा 21% अॉक्सीजन
.01 ग्राम अन्य गैस 1% अन्य गैस
2. एक कमीज़ के कपड़े में होते हैंः
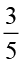 सूती 60% सूती
सूती 60% सूती
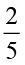 पॉलिस्टर 40% पॉलिस्टर
पॉलिस्टर 40% पॉलिस्टर
8.3.2 भिन्न संख्याओ को प्रतिशत में बदलना
भिन्न संख्याओं में, हर विभिन्न संख्याएँ हो सकती हैं । उनकी तुलना करने के लिए हमें उनके हरों को समान करना पड़ता है और हम देख चुके हैं कि तब उनकी तुलना करना बहुत आसान हो जाता है यदि उनमें प्रत्येक का हर 100 हो । यानी हम भिन्नों को प्रतिशत में बदल रहे हैं । आइए अब कुछ भिन्नों को प्रतिशत में बदलने का प्रयत्न करें ।
उदाहरण 7 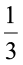 को प्रतिशत रूप में लिखिए ।
को प्रतिशत रूप में लिखिए ।
हल संख्या है, 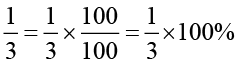
= 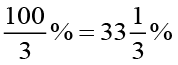
उदाहरण 8 25 बच्चों की कक्षा में 15 लड़कियाँ हैं । लड़कियों का प्रतिशत क्या है ?
हल 25 बच्चों में 15 लड़कियाँ हैं
अतः लड़कियों का प्रतिशत = 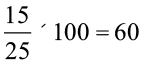 । अर्थात्् कक्षा में 60% लड़कियाँ हैं ।
। अर्थात्् कक्षा में 60% लड़कियाँ हैं ।
उदाहरण 9 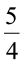 को प्रतिशत में बदलिए ।
को प्रतिशत में बदलिए ।
हल संख्या में, 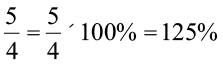
इन उदाहरणों में हम देखते हैं कि एक उचित भिन्न को प्रतिशत में बदलने पर 100 से कम प्रतिशत तथा मिश्र भिन्न को प्रतिशत में बदलने पर 100 से अधिक प्रतिशत प्राप्त होता है ।
सोचिए और चर्चा कीजिए
(i) क्या आप किसी ‘केक’ (cake) का 50% खा सकते हैं ?
क्या आप किसी ‘केक’ (cake) का 100% खा सकते हैं ?
क्या आप किसी ‘केक’ (cake) का 150% खा सकते हैं ?
(ii) क्या किसी वस्तु का मूल्य 50% बढ़ सकता है ?
क्या किसी वस्तु का मूल्य 100% बढ़ सकता है ?
क्या किसी वस्तु का मूल्य 150% बढ़ सकता है ?
8.3.3 दशमलव भिन्न को प्रतिशत में बदलना
हमने देखा कि साधारण भिन्नों को प्रतिशत में किस प्रकार बदला जाता है । अब आइए देखें दशमलव भिन्नों को भी प्रतिशत में कैसे बदला जाता है ।
उदाहरण 10 दिए गए दशमलवों को प्रतिशत में बदलिए ः
(a) 0.75 (b) 0.09 (c) 0.2
हल
(a) 0.75 = 0.75 × 100 % (b) 0.09 = 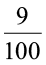 = 9 %
= 9 %
= 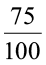 × 100 % = 75%
× 100 % = 75%
(c) 0.2 = 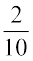 × 100% = 20 %
× 100% = 20 %
प्रयास कीजिए
1. निम्नलिखित भिन्नों को प्रतिशत में बदलिए ।
(a) 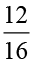 (b) 3.5 (c)
(b) 3.5 (c) 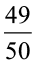
(d) 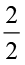 (e) 0.05
(e) 0.05
2. (i) 32 विद्यार्थियों में 8 अनुपस्थित हैं। विद्यार्थियों का क्या प्रतिशत अनुपस्थित है?
(ii) 25 रेडियो सैट में 16 खराब हैं । खराब रेडियो सैटों का प्रतिशत क्या है ?
(iii) एक दुकान में 500 पुर्जे हैं जिनमें 5 बेकार हैं । बेकार पुर्जों का प्रतिशत क्या है ?
(iv) 120 मतदाताओं मेें से 90 ने ‘हाँ’ में मत दिया । कितने प्रतिशत ने ‘हाँ’ में मत दिया?
8.3.4 प्रतिशत को साधारण भिन्न या दशमलव में बदलना
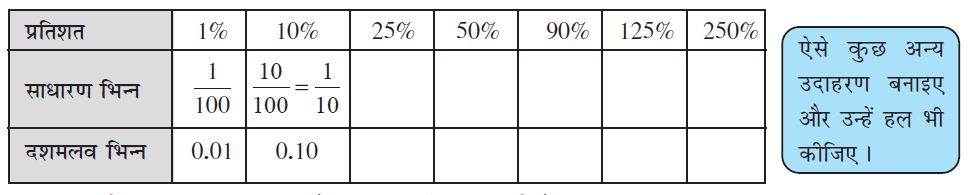
अभी तक हमने साधारण भिन्न या दशमलव भिन्न को प्रतिशत में बदला । हम इसका विपरीत भी कर सकते हैं । यानी, प्रतिशत दिए होने पर उसे साधारण या दशमलव भिन्न मेें भी बदल सकते हैं । निम्न तालिका को ध्यान से देखकर पूरा कीजिएः
किसी वस्तु के सभी भाग मिलकर सदैव एक संपूर्ण वस्तु बनाते हैं ।
रंगीन टाइलों, बच्चों की ऊँचाइयों तथा वातावरण में गैसों के उदाहरणों में हमने देखा कि जब हम उनके प्रतिशतों को जोड़ते हैं तब 100 ही प्राप्त होता है । वे सभी भाग मिलकर जो एक पूर्ण वस्तु बनाते हैं, जोड़ने पर एक या 100% देते हैं । अतः यदि दो भागों में एक भाग दिया हो तब हम दूसरा भाग ज्ञात कर सकते हैं । निम्न उदाहरण पर विचार कीजिएः
विद्यार्थियों की दी गई संख्या में 30% लड़के हैं ।
इसका अर्थ यह हुआ कि यदि 100 विद्यार्थी हैं तो उनमें 30 लड़के हैं तथा शेष लड़कियाँ होंगी ।
स्पष्ट है कि लड़कियाँ होंगी (100-30)% = 70%.
प्रयास कीजिए
1. 35% + _______% = 100%, 64% + 20% +________ % = 100%
45% = 100% – _________ %, 70% = ______% – 30%
2. किसी कक्षा के विद्यार्थियों में 65% के पास साइकिलें हैं । कितने प्रतिशत विद्यार्थियों के पास साइकिलें नहीं हैं?
3. हमारे पास, सेब, संतरों तथा आमों से भरी एक टोकरी है । यदि उसमें 50% सेब तथा 30% संतरे हैं तब आमों का प्रतिशत कितना है ?
सोचिए, चर्चा कीजिए और लिखिए
एक परिधान के बनाने पर हुए व्यय को देखिए । कढ़ाई पर 20%, कपड़े पर 50%, सिलाई पर 30% । क्या आप कुछ अन्य एेसे ही उदाहरण दे सकते हैं ।
8.3.5 अनुमान के साथ मनोरंजन
प्रतिशतता, एक दिए क्षेत्रफल के किसी भाग का अनुमान लगाने में सहायता करती है ।
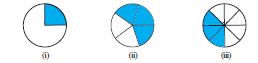
उदाहरण 11 निम्न आकृति में छायांकित भाग पूर्ण का कितने प्रतिशत है ?
हल पहले हम देखते हैं कि पूर्ण आकृति का कितना भाग छायांकित है । इस प्रकार प्राप्त भिन्न से छायांकित भाग की प्रतिशतता ज्ञात की जा सकती है ।
आप देख सकते हैं कि पूर्ण आकृति का आधा भाग छायांकित है ।
तथा 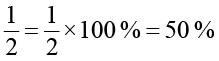
इस प्रकार, 50 % छायांकित है ।
निम्न आकृतियों का कितने प्रतिशत छायांकित है ?
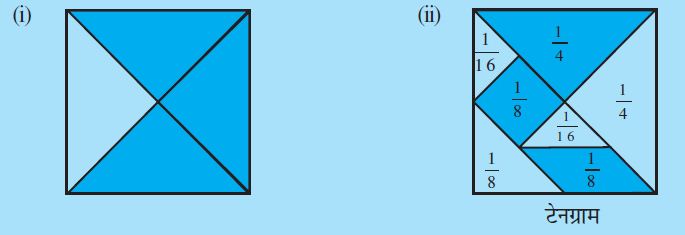
आप इसी प्रकार कुछ अन्य आकृतियाँ बना सकते हैं और अपने साथियों से छायांकित भाग अनुमान करने को कहिए ।
8.4 प्रतिशतता के उपयोग
8.4.1 प्रतिशतता की व्याख्या
आपने देखा कि तुलना करने के लिए प्रतिशतता कितनी उपयोगी है । हमने साधारण व दशमलव भिन्नों को प्रतिशत में बदलना भी सीखा । अब हम देखेंगे कि प्रतिशतता दैनिक जीवन में किस प्रकार प्रयोग में लाई जा सकती है । इसके लिए हम निम्नलिखित कथनों की व्याख्या से आंरभ करते हैं ।
– रवि अपनी आय का 5% बचत करता है ।
– रेखा को प्रत्येक पुस्तक बेचने पर 10% लाभ मिलता हैं ।
– मीरा के 20% वस्त्र नीले रंग के हैं ।
इन कथनों में प्रत्येक से आप क्या निष्कर्ष निकाल सकते हैं ?
5% से हमारा तात्पर्य है 100 में से 5 भाग तथा इसे हम लिखते हैं 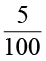 । इसका अर्थ हैं कि रवि, अर्जित किए गए प्रत्येक ₹ 100 मेें से ₹ 5 बचाता है । इस प्रकार आप भी ऊपर दिए गए अन्य कथनों के अर्थ लगाइए।
। इसका अर्थ हैं कि रवि, अर्जित किए गए प्रत्येक ₹ 100 मेें से ₹ 5 बचाता है । इस प्रकार आप भी ऊपर दिए गए अन्य कथनों के अर्थ लगाइए।
8.4.2 प्रतिशतता से संख्या ज्ञात करना
निम्नलिखित उदाहरणों पर ध्यान दीजिए
उदाहरण 12 40 बच्चों के सर्वेक्षण से पता चला कि 25% फुटबॉल खेलना पसंद करते हैं । ज्ञात कीजिए कि इनमें कितने बच्चों को फुटबॉल खेलना पसंद था ।
हल यहाँ पर बच्चों की कुल संख्या 40 है । इनमें से 25% फुटबॉल खेलना पसंद करते हैं । मीना और अरुण ने एेसे बच्चों की संख्या ज्ञात करने के लिए निम्न विधियाँ प्रयुक्त की । आप एेसे प्रश्नों के हल करने के लिए इनमें से कोई भी विधि प्रयोग कर सकते हैं ।
प्रयास कीजिए
1. ज्ञात कीजिए :
दोनों ने ही स्वेटर का वास्तविक मूल्य ₹ 800 ज्ञात किया।
(a) 164 का 50% (b) 12 का 75% (c) 64 का 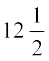 %
%
2. 25 बच्चों की कक्षा में 8% बच्चे वर्षा में भीगना पसंद करते हैं । वर्षा में भीगने वाले बच्चों की संख्या ज्ञात कीजिए ।
उदाहरण 13 जब 25% छूट दी जा रही थी तब राहुल ने एक स्वेटर खरीदा और ₹ 200 बचाए । छूट से पहले स्वेटर का क्या मूल्य था ?
हल राहुल ने ₹ 200 बचाए जब 25% छूट मिली । यानी मूल्य में 25% कम होने के कारण राहुल को ₹ 200 की बचत हुई । आइए देखें कि मोहन और अब्दुल ने स्वेटर का प्रांरभिक मूल्य कैसे ज्ञात किया ?

प्रयास कीजिए
1. 9 किस संख्या का 25% है ? 2. 15 किस संख्या का 75% है ?
प्रश्नमाला 8.2
1. दी गई भिन्न संख्याओं को प्रतिशत में बदलो ।
(a) 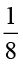 (b)
(b) 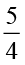 (c)
(c) 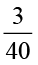 (d)
(d) 
2. दी गई दशमलव भिन्नों को प्रतिशत में बदलो।
(a) 0.65 (b) 2.1 (c) 0.02 (d) 12.35
3. अनुमान लगाइए कि आकृति का कितना भाग रंग दिया गया है और इस प्रकार ज्ञात कीजिए कि कितने प्रतिशत रंगीन है ।
4. ज्ञात कीजिए :
(a) 250 का 15% (b) 1 घंटे का 1%
(c) 2500 का 20% (d) 1 किग्रा का 75%
5. संपूर्ण राशि ज्ञात कीजिए यदि
(a) इसका 5%, 600 है। (b) इसका 12%, 1080 है। (c) इसका 40%, 500 km है ।
(d) इसका 70% 14 मिनट है । (e) इसका 8%, 40 लीटर है ।
6. दिए गए प्रतिशतों को साधारण व दशमलव भिन्नों में बदलो और अपने उत्तर को सरलतम रूप में लिखो ।
(a) 25% (b) 150% (c) 20% (d) 5%
7. एक नगर में 30% महिलाएँ, 40% पुरुष तथा शेष बच्चे हैं । बच्चों का प्रतिशत कितना है ?
8. किसी क्षेत्र के 15,000 मतदाताओं में से 60% ने मतदान में भाग लिया । ज्ञात कीजिए कि कितने प्रतिशत ने मतदान में भाग नहीं लिया । क्या अब ज्ञात कर सकते हैं कि वास्तव में कितने मतदाताओं ने मतदान नहीं किया ?
9. मीता अपने वेतन में से ₹ 4000 बचाती है । यदि यह उसके वेतन का 10% है, तब उसका वेतन कितना है ?
10. एक स्थानीय क्रिकेट टीम ने, एक सत्र (season) में 20 मैच खेले । इनमें से उस टीम ने 25% मैच जीते । जीते गए मैचों की संख्या कितनी थी ?
8.4.3 अनुपातों से प्रतिशत
कभी-कभी किसी वस्तु या राशि के भाग अनुपात के रूप में दिए होते हैं और हमें उन्हें प्रतिशत में बदलना पड़ता है । निम्न उदाहरणों पर ध्यान दीजिए ।
उदाहरण 14 रीना की माता जी ने बताया कि इडली बनाने के लिए 1 भाग उड़द की दाल तथा 2 भाग चावल की आवश्यकता होती है । इडली के एेसे मिश्रण में, उड़द की दाल व चावल का प्रतिशत ज्ञात कीजिए ।
हल मिश्रण को अनुपात रूप में इस प्रकार लिखा जाएगा ।
चावलःउड़द की दाल = 2 : 1
अब, कुल भाग है 2 + 1= 3 । अर्थात्् मिश्रण में 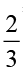 भाग चावल तथा
भाग चावल तथा 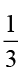 भाग उड़द की दाल है ।
भाग उड़द की दाल है ।
अतः, चावल का प्रतिशत होगा 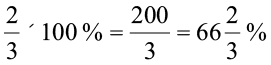
तथा उड़द की दाल का प्रतिशत होगा 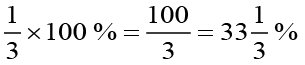
उदाहरण 15 रवि, राजू तथा राय में ₹ 250 इस प्रकार बाँटे गए कि रवि को दो भाग, राजू को तीन भाग तथा राय को पाँच भाग मिले । इस बँटवारे में प्रत्येक को कितना धन मिला तथा उनका प्रतिशत कितना था ?
हल प्रत्येक के भाग को अनुपात रूप में इस प्रकार लिखा जाएगा 2 : 3 : 5 सभी भागों का योग हुआ 2 + 3 + 5 = 10.
क्ल राशि में प्रत्येक का प्रतिशत प्रत्येक को मिली राशि
रवि को मिला 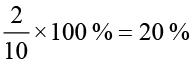
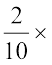 ₹ 250 = ₹50
₹ 250 = ₹50
राजू को मिला 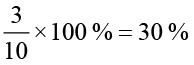
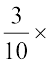 ₹ 250 = ₹75
₹ 250 = ₹75
राय को मिला 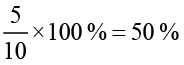
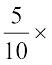 ₹ 250 = ₹125
₹ 250 = ₹125
प्रयास कीजिए
1. 15 मिठाइयों को मनु तथा सोनू में इस प्रकार बाँटिए कि उन्हें कुल का क्रमशः 20 % तथा 80 % मिले।
2. यदि किसी त्रिभुज के कोणों में अनुपात 2 : 3 : 4 है तब उसके प्रत्येक कोण की माप क्या होगी ?
8.4.4 बढ़त या घटत, प्रतिशत रूप में
अनेक अवसरों पर हमें किसी राशि में हुई बढ़त या घटत को प्रतिशत रूप में ज्ञात करने की आवश्यकता होती है । उदाहरण के लिए, यदि किसी प्रदेश की जनसंख्या 5,50,000 से बढ़कर 6,05,000 हो गई तब एेसी स्थिति में जनसंख्या की वृद्धि को प्रतिशत के रूप में समझना अधिक आसान होता है, जैसे कहें कि प्रदेश की जनसंख्या 10 % बढ़ गई ।
हम किसी राशि के बढ़ने या घटने को, कुल राशि के प्रतिशत के रूप में किस प्रकार प्रकट कर सकते हैं? आइए निम्न उदाहरणों पर विचार करें ।
उदाहरण 16 एक विद्यालय की टीम ने इस वर्ष 6 खेलों में जीत प्राप्त की जबकि पिछले वर्ष 4 में ही की थी । पिछले वर्ष की तुलना में जीत कितने प्रतिशत बढ़ी ?
हल जीत की संख्या में वृद्धि = 6 – 4 = 2.
अतः घटने का प्रतिशत 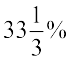 है ।
है ।
प्रयास कीजिए
1. बढ़ने या घटने का प्रतिशत ज्ञात कीजिए ।
– कमीज़ का मूल्य ₹280से घटकर ₹210 हो गया ।
– किसी परीक्षा में प्राप्तांक बढ़कर 20 से 30 हो गए ।
2. मेरी माता जी कहती हैं कि उनके बचपन के समय पैट्रोल की दर ₹ 1 प्रति लीटर थी और आजकल यह ₹ 52 प्रति लीटर है । पैट्रोल की दर में कितने प्रतिशत की वृद्धि हुई ?
8.5 किसी वस्तु से संबंधित मूल्य, अर्थात् क्रय तथा विक्रय
मैंने इसे ₹ 600 में खरीदा
और मैं इसे ₹ 610 में बेचूँगा ।
जिस मूल्य पर कोई वस्तु खरीदी जाती है वह उसका क्रय मूल्य (cost price) कहलाता है इसे संक्षिप्त में क्र.मू. (C.P.) लिखा जाता है । जिस मूल्य पर कोई वस्तु बेची जाती है वह उसका विक्रय मूल्य (selling price) कहलाता है और इसे संक्षिप्त में वि. मू. (S.P.) लिखा जाता है ।
आप किसे अधिक अच्छा कहेंगे, यदि किसी वस्तु को क्रय मूल्य पर ही या उससे कम मूल्य पर या उससे अधिक मूल्य पर बेचा जाए ?
क्रय मूल्य तथा विक्रय मूल्य के आधार पर आप तय कर सकते है कि कोई वस्तु बेचकर आपको लाभ हुआ या नहीं ।
यदि क्रय मूल्य (CP) < विक्रय मूल्य (SP) । तब लाभ = SP – CP.
यदि क्रय मूल्य (CP) = विक्रय मूल्य (SP) । तब ना लाभ तथा ना हानि
यदि क्रय मूल्य (CP) > विक्रय मूल्य (SP)। तब हानि = CP – SP (क्रय मूल्य-विक्रय मूल्य)।
आइए कुछ वस्तुओं के क्रय तथा विक्रय मूल्य देखकर, कथनों को समझने का प्रयत्न करें ।
एक खिलौना ₹ 72 में खरीदा गया और ₹ 80 में बेचा गया ।
एक टी-शर्ट ₹ 120 में खरीदी गई और ₹ 100 में बेची गई ।
एक साइकिल ₹ 800 में खरीदी गई और ₹ 940 में बेची गई ।
अब पहले कथन पर विचार करते हैं । यहाँ क्रय मूल्य ₹ 72 है तथा विक्रय मूल्य ₹ 80 है ।
अतः विक्रय मूल्य अधिक है, क्रय मूल्य से ।
अतः लाभ = SP – CP = ₹ 80 – ₹ 72 = ₹ 8
अब आप अन्य दो कथनों की इसी प्रकार सोचकर व्याख्या करें ।
8.5.1 लाभ या हानि, प्रतिशत में
लाभ या हानि को प्रतिशत रूप में ज्ञात किया जा सकता है। ध्यान में रखिए कि इसे सदैव क्रय मूल्य पर ही परिकलित करते हैं । उपरोक्त उदाहरणों में हम प्रतिशत लाभ या प्रतिशत हानि भी ज्ञात कर सकते हैं ।
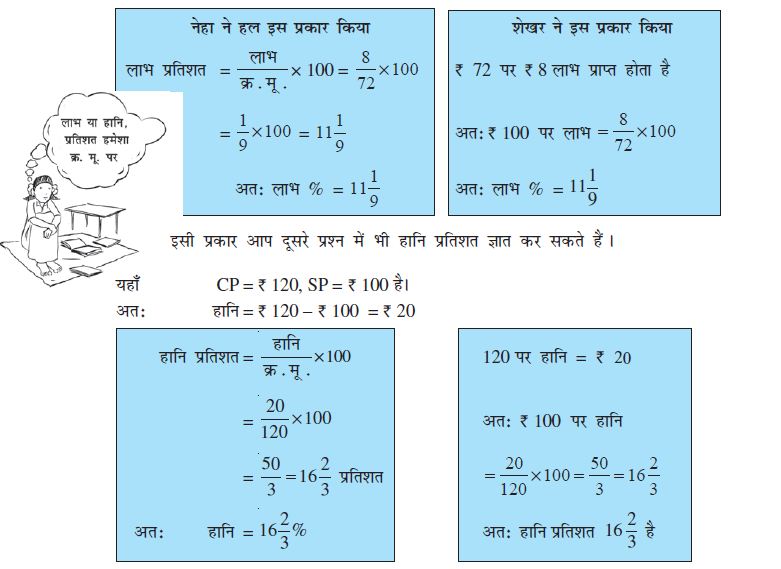
आइए खिलौने वाला उदाहरण ही लेते हैं । यहाँ हैः CP = ₹ 72, SP = ₹ 80, तथा लाभ = ₹ 8। लाभ प्रतिशत ज्ञात करने के लिए नेहा तथा शेखर ने निम्न विधियाँ प्रयुक्त कीं ।
अब आप साईकिल वाला उदाहरण हल करके देखिए ।
हम यहाँ यह भी देखते हैं कि किसी वस्तु से संबंधित क्रय मूल्य, विक्रय मूल्य तथा लाभ या हानि में तीन राशियों में से कोई भी दो राशियाँ ज्ञात हों तो तीसरी राशि ज्ञात की जा सकती है ।
दोनों ही विधियों से विक्रय मूल्य ₹ 108 प्राप्त होता है ।
उदाहरण 18 एक फूलदान का लागत मूल्य ₹ 120है । यदि दुकानदार इसे 10% हानि पर बेचता है तब उसका विक्रय मूल्य ज्ञात कीजिए ।
हल पहले, दी हुई राशियों को पहचानते हैं । दिया है, क्रय मूल्य = ₹ 120 तथा
हानि प्रतिशत = 10, हमें ज्ञात करना है विक्रय मूल्य।
सोहन ने इस प्रकार हल निकाला आनंदी ने इस प्रकार हल किया
10% हानि का अर्थ है यदि क्र.मू. = ₹ 100 हानि = क्रय मूल्य का 10 %
तब हानि = ₹ 10 = ₹ 120 का 10 %
अतः विक्रय मूल्य = ₹ (100 – 10) = ₹ 90 = 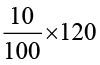 = ₹ 12
= ₹ 12
अतः
जब क्र.मू. = ₹ 100, तब विक्रय मूल्य विक्रय मूल्य = क्रय मूल्य – हानि
= ₹ 90 = ₹ 120 – ₹ 12 = ₹ 108
अतः जब क्र.मू. = ₹ 120 है, तब
विक्रय मूल्य = 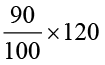 = ₹ 108
= ₹ 108
उदाहरण 19 एक खिलौना कार का विक्रय मूल्य ₹ 540 था । एक दुकानदार ने उसे 20% लाभ पर बेचा । खिलौने का क्रय मूल्य क्या था ?
हल हमें पता है कि विक्रय मूल्य = ₹ 540 तथा लाभ = 20%, हमें ज्ञात करना है क्रय मूल्य
अमीना ने इस प्रकार हल किया :
20% लाभ का अर्थ है कि यदि क्रय मूल्य ₹ 100 हो तो लाभ ₹ 20
तथा विक्रय मूल्य 100 + 20 = ₹ 120 होगा ।
अर्थात् ₹ 120 विक्रय मूल्य होने पर क्रय मूल्य = ₹ 100
अतः ₹ 540 विक्रय मूल्य होने पर क्रय मूल्य 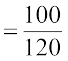 × ₹ 540 = ₹ 450
× ₹ 540 = ₹ 450
अरुण ने प्रश्न इस प्रकार हल कियाः
लाभ = क्रय मूल्य का 20% तथा विक्रय मूल्य = क्रय मूल्य + लाभ
अतः 540 = क्रय मूल्य + क्रय मूल्य का 20%
या 540 = क्रय मूल्य + 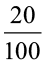 × क्रय मूल्य =
× क्रय मूल्य = 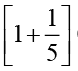 क्रय मूल्य
क्रय मूल्य
= 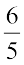 क्रय मूल्य इसलिए,
क्रय मूल्य इसलिए, 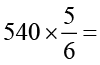 क्रय मूल्य
क्रय मूल्य
या ₹ 450 = क्रय मूल्य ।
इस प्रकार दोनों विधियों से क्रय मूल्य ₹ 450 है।
प्रयास कीजिए
1. एक दुकानदार ने एक कुर्सी 375 में खरीदी तथा ₹ 400 में बेच दी । उसका लाभ प्रतिशत ज्ञात कीजिए ।
2. एक वस्तु ₹ 50 में क्रय की गई तथा 12 प्रतिशत लाभ पर बेच दी गई । उसका विक्रय मूल्य ज्ञात कीजिए ।
3. एक वस्तु ₹ 250 में बेचने पर 5 प्रतिशत लाभ प्राप्त हुआ । उसका क्रय मूल्य क्या था ?
4. एक वस्तु 5 प्रतिशत हानि उठा कर ₹ 540 में बेची गई । उसका क्रय मूल्य क्या था ?
8.6 उधार लिए गए धन पर शुल्क अर्थात् साधारण ब्याज
सोहनी ने बताया कि वे एक नया स्कूटर खरीदने जा रहे हैं । मोहन ने पूछा कि क्या उनके पास इसके लिए पर्याप्त धन है ? सोहनी ने उत्तर दिया कि उसके पिताजी इसके लिए बैंक से
उधार धन (ऋण) लेंगे। उधार लिए गए धन को मूलधन कहते है ।
यह धन, वापस करने से पहले, ऋण प्राप्त करने वाले व्यक्ति द्वारा कुछ समय तक इसका उपयोग किया जाता है; अतः उसे उतने समय का, धन उपयोग में लाने के बदले, कुछ अतिरिक्त धन बैंक को देना होता है । यह अतिरिक्त धन ब्याज कहलाता है ।
एक निश्चित अवधि के बाद आपको मूलधन तथा ब्याज, दोनों को मिलाकर पूरा धन वापस करना होता है जिसे मिश्रधन कहते हैं ।
अर्थात्, मिश्रधन = मूलधन + ब्याज
ब्याज एक निश्चित दर पर परिकलित किया जाता है जो प्रायः प्रत्येक ₹ 100 के लिए एक वर्ष के लिए निर्धारित होता है ।
इसे इस प्रकार लिखा जा सकता है, 10 प्रतिशत प्रति वर्ष या 10 प्रतिशत वार्षिक।
10 प्रतिशत वार्षिक का अर्थ है कि उधार लिए गए प्रत्येक ₹ 100 के लिए, प्रत्येक वर्ष के बाद ₹ 10 ब्याज के रूप में अतिरिक्त देने होंगे ।
एक उदाहरण लेकर देखें कि ब्याज कैसे परिकलित किया जाता है ।
उदाहरण 20 अनीता ₹ 5000 का एक ऋण 15 प्रतिशत वार्षिक की दर से ब्याज पर लेती है । ज्ञात कीजिए कि एक वर्ष के बाद उसे कुल कितना धन वापस करना होगा ।
हल उधार ली गई राशि = ₹ 5000
ब्याज की दर = 15 प्रतिशत प्रति वर्ष
इसका अर्थ है कि यदि वह ₹ 100 उधार लेती है तब उसे एक वर्ष बाद ₹ 15 ब्याज के रूप में भी देने होंगे ।
अतः ₹ 5000 के उधार पर उसे 1 वर्ष बाद देने होंगे ः 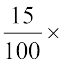 ₹ 5000 = ₹ 750
₹ 5000 = ₹ 750
अर्थात्् एक वर्ष बाद उसे ब्याज मिलाकर मिश्रधन देना होगा ₹ 5000 + ₹ 750 = ₹ 5750
एक वर्ष का ब्याज ज्ञात करने के लिए हम एक संबंध या सूत्र भी प्राप्त कर सकते हैं ।
हम मूलधन को P से तथा दर R % वार्षिक को R से प्रदर्शित करते हैं।
तो हमें प्रत्येक ₹ 100 के लिए एक वर्ष का ₹ R ब्याज देना होगा ।
अतः ₹ P उधार लेने पर एक वर्ष का ब्याज I होगा ।
I = 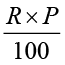 =
= 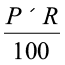
8.6.1 अनेक वर्षों के लिए ब्याज
अगर धन एक वर्ष से अधिक समय के लिए उधार लिया जाता है तब ब्याज भी उस पूरे समय के लिए परिकलित किया जाता है जितने समय के लिए धन रखा गया है । उदाहरण के लिए यदि अनीता वही धन उसी दर पर दो वर्ष बाद वापस करती तब उसे ब्याज भी दुगना देना पड़ता; अर्थात्् ₹ 750 पहले वर्ष के लिए तथा ₹ 750 दूसरे वर्ष के लिए। मूलधन वही रहता है, बदलता नहीं और ब्याज भी प्रत्येक वर्ष के लिए समान ही रहता है । इस प्रकार के ब्याज को साधारण ब्याज कहते हैं। जिस प्रकार वर्षों की संख्या बढ़ती जाती है उसी प्रकार ब्याज की राशि भी । 3 वर्ष के लिए ₹100, 18% वार्षिक दर से उधार लेने पर 3 वर्षों बाद ब्याज देना होगा,
18 + 18 + 18 = 3 × 18 = ₹ 54
हम एक वर्ष से अधिक समय के लिए भी साधारण ब्याज ज्ञात करने के लिए सूत्र प्राप्त कर सकते हैं ।
हम देख चुके हैं कि ₹ P के लिए R % वार्षिक की दर से 1 वर्ष बाद ब्याज देना होता है 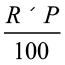 । अतः T वर्षों के लिए दिया गया ब्याज (I) होगाः
। अतः T वर्षों के लिए दिया गया ब्याज (I) होगाः
I = 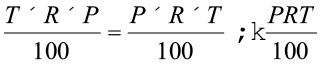
और T वर्षों बाद मिश्रधन A होगा : A = P + I
प्रयास कीजिए
1. ₹ 10,000, 5 प्रतिशत वार्षिक दर से जमा किए जाते हैं । एक वर्ष बाद कितना ब्याज प्राप्त होगा ?
2. ₹ 3500, 7 प्रतिशत वार्षिक दर से उधार दिए जाते हैं । दो वर्ष बाद कितना साधारण ब्याज देय होगा ?
3. ₹ 6050, 6.5 प्रतिशत वार्षिक दर से उधार लिए जाते हैं । 3 वर्ष बाद कितना ब्याज तथा कितना मिश्रधन देय होगा ?
4. ₹ 7000, 3.5 प्रतिशत वार्षिक दर से दो वर्ष के लिए उधार लिए जाते हैं । दो वर्ष बाद कितना मिश्रधन देय होगा ?
जैसा आपने क्रय-विक्रय मूल्यों की समस्याओं में देखा था उसी प्रकार सूत्र 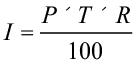 द्वारा, चार राशियों में से कोई भी तीन ज्ञात होने पर चौथी ज्ञात की जा सकती है ।
द्वारा, चार राशियों में से कोई भी तीन ज्ञात होने पर चौथी ज्ञात की जा सकती है ।
उदाहरण 21 ₹ 4500 के ऋण पर 2 वर्ष बाद, मनोहर ₹ 750 साधारण ब्याज देता है । ब्याज की दर प्रतिशत ज्ञात कीजिए ।
हल 1 हल 2
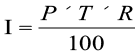 2 वर्ष का ब्याज है = ₹ 750
2 वर्ष का ब्याज है = ₹ 750
अतः 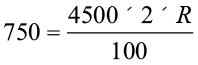 अतः 1वर्ष का ब्याज होगा =
अतः 1वर्ष का ब्याज होगा = 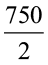 = ₹ 375
= ₹ 375
या 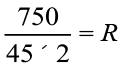 अब ₹ 4500 पर ब्याज = ₹ 375
अब ₹ 4500 पर ब्याज = ₹ 375
अतः ब्याज की दर अतः ₹ 100 पर ब्याज
= 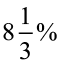 वार्षिक
वार्षिक 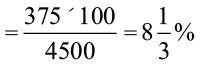
अतः ब्याज की दर = 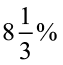 वार्षिक
वार्षिक
प्रयास कीजिए

1. आपके बैंक खाते में ₹ 2400 जमा हैं तथा ब्याज की दर 5 प्रतिशत वार्षिक है । कितने वर्षों बाद ब्याज की राशि ₹ 240 होगी ?
2. किसी धन का 5 प्रतिशत वार्षिक दर से 3 वर्ष का ब्याज ₹ 450 होता है । वह
धन ज्ञात कीजिए ।
प्रश्नवली 8.3
1. क्रय-विक्रय के निम्न सौदों में हानि या लाभ ज्ञात कीजिए । प्रत्येक दशा में प्रतिशत हानि या प्रतिशत लाभ भी ज्ञात कीजिए ।
(a) बग़ीचे में काम आने वाली कैंची ₹ 250 में खरीदी गई तथा ₹ 325 में बेची गई ।
(b) एक रेफ्रीज़रेटर ₹12000 में खरीदा गया और ₹13500 में बेचा गया ।
(c) एक अलमारी ₹2500 में खरीदी गई और ₹3000 में बेची गई ।
(d) एक स्कर्ट ₹250 में खरीद कर ₹150 में बेची गई ।
2. दिए गए प्रत्येक अनुपात के दोनों पदों को प्रतिशत में बदलिए ।
(a) 3:1 (b) 2 : 3 : 5 (c) 1: 4 (d) 1 : 2 : 5
3. एक नगर की जनसंख्या 25000 से घटकर 24500 रह गई । घटने का प्रतिशत ज्ञात कीजिए ।
4. अरुण ने एक कार ₹ 3,50,000 में खरीदी । अगले वर्ष उसका मूल्य बढ़कर ₹ 3,70,000 हो गया । कार के मूल्य की प्रतिशत वृद्धि ज्ञात कीजिए ।
5. मैने एक टी.वी. ₹ 10,000 में खरीद कर 20 प्रतिशत लाभ पर बेच दिया । मुझे बेचने पर कितना धन प्राप्त हुआ ?
6. जूही एक वाशिंग मशीन ₹ 13,500 में बेचने पर 20 प्रतिशत की हानि उठाती है । उसने वह मशीन कितने में खरीदी थी ?
7. (i) चाक-पाउडर में कैल्शियम, कार्बन तथा अॉक्सीजन का अनुपात 10ः3ः12 होता है । इसमे कार्बन की प्रतिशत मात्रा ज्ञात कीजिए ।
(ii) चाक की एक छड़ी में यदि कार्बन की मात्रा 3 gm है तब उसका कुल भार कितना होगा ?
8. अमीना एक पुस्तक ₹ 275 में खरीद कर उसे 15 प्रतिशत हानि पर बेचती है । पुस्तक का विक्रय मूल्य ज्ञात कीजिए ।
9. प्रत्येक दशा में 3 वर्ष बाद कितना मिश्रधन देय होगा ?
(a) मूलधन = ₹ 1200 दर 12% वार्षिक (b) मूलधन = ₹ 7500 दर 5% वार्षिक
10. ₹ 56000 पर, 2 वर्ष पश्चात किस दर से ₹ 280 साधारण ब्याज देय होगा ?
11. मीना ने 9 प्रतिशत वार्षिक दर से, 1 वर्ष पश्चात् ₹ 45 ब्याज के रूप में दिए । उसने कितना धन उधार लिया था ?
हमने क्या चर्चा की?
1. अपने दैनिक जीवन में हमें प्रायः दो राशियों के बीच तुलना करनी पड़ती है । ये राशियाँ ऊँचाई, भार, वेतन, प्राप्तांक आदि हो सकती हैं
2. 150 cm तथा 75 cm ऊँचाई वाले दो व्यक्तियों की तुलना करने पर हम इसे अनुपात रूप में 150ः75 या 2ः1 लिखते हैं ।
3. दो अनुपातों की तुलना, उन्हें समान हर वाली भिन्नों में बदल कर की जा सकती है । यदि दोनों समान हर वाली भिन्ने समान हैं तब हम कहते हैं कि दोनों अनुपात भी तुल्य अनुपात हैं ।
4. यदि दो अनुपात तुल्य हैं तब उनके चारों पद एक समानुपात बनाते हैं । उदाहरण के लिए दो अनुपात 8ः2 तथा 16ः4 तुल्य हैं; अतः 8, 2, 16 तथा 4 समानुपात में हैं ।
5. तुलना करने की एक विधि प्रतिशत भी है । भिन्न, जिनके हर 100 होते हैं, उनके अंश, प्रतिशत प्रकट करते हैं । प्रतिशत का अर्थ होता है प्रत्येक सौ पर ।
6. भिन्नों को प्रतिशत में बदला जा सकता है तथा प्रतिशत को भिन्नों में ।
उदाहरण के लिए 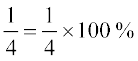 = 25% तथा, 75% =
= 25% तथा, 75% = 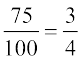
7. दशमलव भिन्न को भी प्रतिशत में बदला जा सकता है तथा प्रतिशत को दशमलव में ।
उदाहरण के लिए, 0.25 = 0.25 × 100% = 25%
8. प्रतिशत के हमारे दैनिक जीवन में व्यापक उपयोग हैंः
(a) जब हमें किसी राशि का प्रतिशत ज्ञात हो तब हम वह संपूर्ण राशि ज्ञात कर सकते हैं ।
(b) यदि हमें किसी राशि के भागों में अनुपात दिया हो तब हम उन्हें प्रतिशत में भी बदल सकते हैं ।
(c) किसी राशि का घटना या बढ़ना भी प्रतिशत में दर्शाया जा सकता है ।
(d) किसी वस्तु के क्रय-विक्रय में हुए लाभ या हानि को भी प्रतिशत में दर्शाया जा सकता है ।
(e) उधार लिए गए धन पर ब्याज परिकलन के लिए उसकी दर प्रतिशत में ही दी जाती है । उदाहरण के लिए ₹ 800, 3 वर्ष के लिए 12 प्रतिशत ब्याज की दर पर उधार लिया गया ।