Table of Contents
अध्याय 10
प्रायोगिक ज्यामिति
10.1 भूमिका
आप अनेक प्रकार के आकारों से परिचित हैं। आप पिछली कक्षाओं में इनमें से कुछ आकारों की रचना करना सीख चुके हैं। उदाहरणतः अब आप एक दी हुई लंबाई का रेखाखंड, एक रेखाखंड पर एक लंब रेखा, एक कोण, कोण का समद्विभाजक, एक वृत्त, इत्यादि की रचना कर सकते हैं।
अब आप समांतर रेखाएँ तथा कुछ प्रकार के त्रिभुजों को खींचना सीखेंगे।
10.2 एक दी हुई रेखा के समांतर उस बिंदु से होकर रेखा खींचना जो उस रेखा पर स्थित नहीं है
आइए एक क्रियाकलाप से प्रारंभ करें। (आकृति 10.1)
(i) एक कागज़ की शीट लीजिए और इसे मोड़कर एक निशान बनाइए। यह मोड़ का निशान एक रेखा l को निरूपित करता है।
(ii) कागज़ को खोल लीजिए। इस कागज़ पर l के बाहर एक बिंदु A अंकित कीजिए।
(iii) इस बिंदु A से होकर जाता हुआ और रेखा l पर लंब एक मोड़ का निशान बनाइए। इस लंब का नाम AN रखिए।
(iv) अब, बिंदु A से होकर इस लंब के लंबवत एक मोड़ का निशान बनाइए। इस नयी लंबवत रेखा का नाम m रखिए। अब, l || m है क्या आप देख सकते हैं कि एेसा क्यों है?
यहाँ समांतर रेखाओं का कौन-सा गुण या कौन-से गुण यह कहने में सहायता कर सकता है या कर सकते हैं कि रेखाएँ l और m समांतर हैं?
आप तिर्यक रेखा और समांतर रेखाओं से संबंधित गुणों में से किसी भी गुण का प्रयोग करके इस रचना को केवल पैमाना (रूलर) और परकार का प्रयोग करके कर सकते है
चरण 5 परकार के नुकीले सिरे को C पर रखिए और इसे खोल कर इस प्रकार समायोजित कीजिए कि पेंसिल की नोक D पर रहे [आकृति 10.2 (v)]।
चरण 6 G को केंद्र मानकर और परकार का खुलाव (opening) चरण 5 वाला ही रखते हुए, एक चाप खींचिए जो चाप EF को H पर काटे [आकृति 10.2 (vi)] ।
चरण 7 अब AH को मिलाकर रेखा m खींचिए [आकृति 10.2 (vii)]।
ध्यान दीजिए कि ∠ABC और ∠BAH एकांतर अंतःकोण हैं, जो परस्पर बराबर हैं। इसलिए m || l है।
सोचिए, चर्चा कीजिए और लिखिए
1. उपरोक्त रचना में, क्या आप A से होकर जाती हुई अन्य रेखा खींच सकते हैं जो l के समांतर हो?
2. क्या आप इस रचना में इस प्रकार का परिवर्तन कर सकते हैं कि बराबर एकांतर अंतःकोण बनाने के स्थान पर बराबर संगत कोण बनें?
प्रश्नावली 10.1
1. एक रेखा, (मान लीजिए AB) खींचिए और इसके बाहर स्थित कोई बिंदु C लीजिए। केवल पैमाना (रूलर) और परकार का प्रयोग करते हुए, C से होकर AB के समांतर एक रेखा खींचिए।
2. एक रेखा l खींचिए और l पर स्थित किसी भी बिंदु पर l पर लंब खींचिए। इस लंब रेखा पर एक बिंदु X लीजिए जो l से 4 cm की दूरी पर हो। X से होकर l के समांतर एक रेखा m खींचिए।
3. मान लीजिए l एक रेखा है और P एक बिंदु है जो l पर स्थित नहीं है। P से होकर l के समांतर एक रेखा m खींचिए। अब P को l के किसी बिंदु Q से जोड़िए। m पर कोई अन्य बिंदु R चुनिए। R से होकर, PQ के समांतर एक रेखा खींचिए। मान लीजिए यह रेखा, रेखा l से बिंदु S पर मिलती है। समांतर रेखाओं के इन दोनों युग्मों से क्या आकृति बनती है?
10.3 त्रिभुजों की रचना
इस अनुच्छेद को पढ़ने से पहले, यह अच्छा होगा कि आप त्रिभुजों की अवधारणाओं, विशेष रूप से त्रिभुजों के गुणों और त्रिभुजों की सर्वांगसमता वाले अध्यायों को याद करें।
a + b > c
आप भुजाओं और कोणों के आधारों पर त्रिभुजों को वर्गीकृत करना तथा त्रिभुजों से संबंधित निम्नलिखित महत्वपूर्ण गुणों के बारे में जानते हैं :
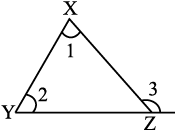
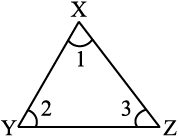
(i) एक त्रिभुज का बाह्यकोण उसके दोनों अभिमुख अंतःकोणों के योगफल के बराबर होता है।
(ii) त्रिभुज के तीनों अन्तः कोणों का योग 180° होता है।
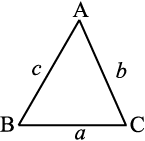
(iii) त्रिभुज की किन्हीं भी दो भुजाओं की लंबाइयों का योग तीसरी भुजा की लंबाई से अधिक होता है।
∠1 + ∠2 + ∠3 = 180°
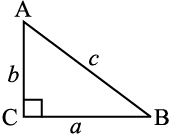
b2+ a2 = c2
(iv) एक समकोण त्रिभुज में कर्ण पर बना वर्ग शेष दो भुजाओं के वर्गों के योगफल के बराबर होता है।
‘त्रिभुजों की सर्वांगसमता’ वाले अध्याय में हमने देखा था कि एक त्रिभुज प्राप्त किया जा सकता है, यदि उसके निम्नलिखित माप समूहों में से कोई एक दिया हुआ हैः
(i) तीन भुजाएँ
(ii) दो भुजाएँ और उनके बीच का कोण
(iii) दो कोण और उनके बीच की भुजा
(iv) समकोण त्रिभुज के लिए, कर्ण और एक पाद (leg)
अब, हम इन अवधारणाओं का त्रिभुजों की रचनाओं में प्रयोग करेंगे।
10.4 एक त्रिभुज की रचना जब उसकी तीनों भुजाओं की लंबाइयाँ दी हों (SSS कसौटी)
इस अनुच्छेद में, हम त्रिभुजों की रचना करेंगे जब उसकी तीनों भुजाएँ ज्ञात हों। पहले हम इसकी एक रफ़ (rough) आकृति खींचते हैं, जिससे उसकी भुजाओं का कुछ अनुमान लग जाए और फिर तीनों भुजाओं में से एक भुजा लेकर रचना प्रारंभ करते हैं। निम्नलिखित उदाहरण को समझिए :
उदाहरण 1 एक त्रिभुज ABC की रचना कीजिए, जबकि AB = 5 cm, BC = 6 cm और AC = 7 cm दिया है।
हल
चरण 1 पहले हम दी हुई मापों की एक रफ आकृति खींचते हैं (इससे हमें आगे बढ़ने में सहायता मिलेगी) [आकृति 10.3(i)]।
चरण 2 6 cm लंबाई का रेखा खंड BC खींचिए
[आकृति 10.3(ii)]।
चरण 3 बिंदु B से, बिंदु A, 5 cm की दूरी पर है। अतः, B को केंद्र मान कर और 5 cm त्रिज्या लेकर एक चाप खींचिए। (अब A इस चाप पर कहीं स्थित एक बिंदु है। यह ज्ञात करना हमारा काम है कि A बिल्कुल ठीक इस चाप पर कहाँ है) [आकृति 10.3(iii)]।
चरण 4 C से, बिंदु A, 7 cm की दूरी पर है। अतः, C को केंद्र मान कर और 7 cm त्रिज्या लेकर एक चाप खींचिए। (A इस चाप पर कहीं स्थित होगा। हमें इसका पता लगाना है) [आकृति 10.3(iv)]।
चरण 5 A को खींचे गए इन दोनों चापों पर स्थित होना चाहिए। अतः, यह इन दोनों चापों का प्रतिच्छेद बिंदु है। इन चापों के प्रतिच्छेद बिंदु को A से अंकित कीजिए। AB और AC को जोड़िए। अब ∆ABC तैयार है [आकृति 10.3(v)]।
इन्हें कीजिए
 आइए अब एक अन्य त्रिभुज DEF की रचना करें, जिसमें DE = 5 cm, EF = 6 cm और DF = 7 cm है। ∆DEF को काट कर उसे ∆ABC पर रखिए।
आइए अब एक अन्य त्रिभुज DEF की रचना करें, जिसमें DE = 5 cm, EF = 6 cm और DF = 7 cm है। ∆DEF को काट कर उसे ∆ABC पर रखिए।हम देखते हैं कि ∆DEF, ∆ABC को पूर्णतया ढक लेता है, अर्थात्् उसके साथ संपाती हो जाता है। (ध्यान दीजिए कि इन दोनों त्रिभुजों की रचना दी हुई तीन भुजाओं से की गई है।) इस प्रकार, यदि एक त्रिभुज की तीन भुजाएँ दूसरे त्रिभुज की संगत तीन भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं। यह SSS सर्वांगसमता नियम (या कसौटी) कहलाता है, जिसे आप पिछले अध्याय में पढ़ चुके हैं।
सोचिए, चर्चा कीजिए और लिखिए
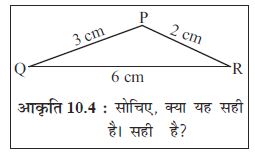
एक विद्यार्थी ने एक एेसा त्रिभुज खींचने का प्रयत्न किया, जिसकी रफ़ आकृति यहाँ दी गई है। पहले उसने QR खींचा। फिर उसने Q को केंद्र मान कर और 3 cm त्रिज्या लेकर एक चाप खींची तथा R को केंद्र मान कर और 2 cm त्रिज्या लेकर एक अन्य चाप खींची। परंतु वह P नहीं प्राप्त कर सका। इसका क्या कारण है? इस प्रश्न से संबंधित त्रिभुज के किस गुण को आप जानते हैं? क्या एेसे त्रिभुज का अस्तित्व है? (त्रिभुजों के इस गुण को याद कीजिएः किसी त्रिभुज की दो भुजाओं का योग सदैव तीसरी भुजा से बड़ा होता है)।
प्रश्नावली 10.2
1. ∆xyz की रचना कीजिए, जिसमें xy = 4.5 cm, yz = 5 cm और zx = 6 cm है।
2. 5.5 cm भुजा वाले एक समबाहु त्रिभुज की रचना कीजिए।
3. ∆PQR की रचना कीजिए, जिसमें PQ = 4 cm, QR = 3.5 cm और PR = 4 cm है। यह किस प्रकार का त्रिभुज है?
4. ABC की रचना कीजिए, ताकि AB = 2.5 cm, BC = 6 cm और AC = 6.5 cm हो।
∠B को मापिए।
10.5 एक त्रिभुज की रचना जब दो भुजाओं की लंबाइयाँ और उनके बीच के कोण की माप दी हो (SAS कसौटी)
यहाँ, हमें दो भुजाएँ और उनके बीच का कोण दिया हुआ है। पहले हम एक रफ़ आकृति खींचते हैं और फिर दिए हुए रेखाखंडों में से एक रेखाखंड खींचते हैं। इसके बाद अन्य चरणों का अनुसरण किया जाता है। उदाहरण 2 देखिए।
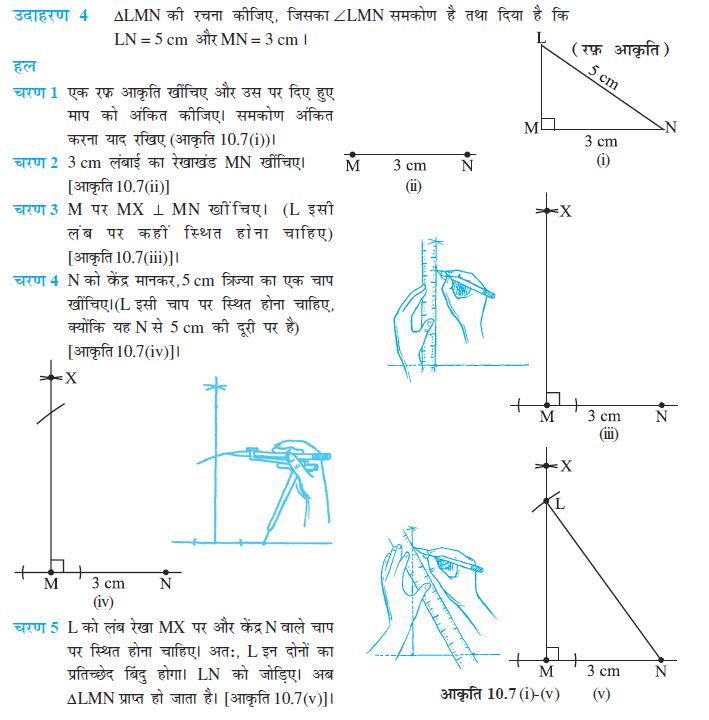
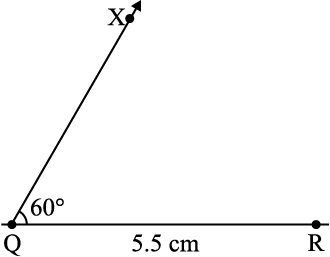
उदाहरण 2 एक त्रिभुज PQR की रचना कीजिए, जब दिया है कि PQ = 3 cm, QR = 5.5 cm और ∠PQR = 60° है।
हल
चरण 1 पहले हम दी हुई मापों के अनुसार, एक रफ़ आकृति खींचते हैं। (इससे हमें रचना की प्रक्रिया निर्धारित करने में सहायता मिलेगी) [आकृति 10.5(i)]।
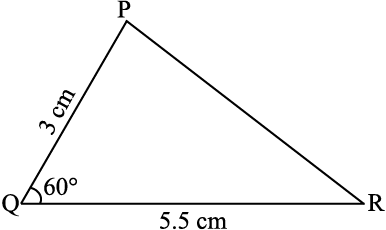
चरण 2 5.5 cm लंबाई का एक रेखाखंड QR खींचिए [आकृति 10.5(ii)]।
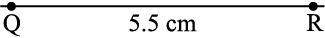
चरण 3 Q पर किरण QX खींचिए, जो QR के साथ 60° का कोण बनाए। (बिंदु P कोण की इसी किरण पर कहीं स्थित होगा) [आकृति 10.5(iii)]।
चरण 4 (P को निश्चित करने के लिए, दूरी QP दी हुई है।) Q को केंद्र मान कर
3 cm त्रिज्या वाली एक चाप खींचिए।
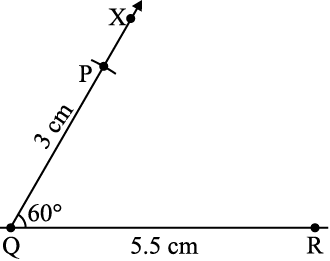
[आकृति 10.5(iv)]।
चरण 5 PR को जोड़िए। इस प्रकार, ∆PQR प्राप्त हो जाता है [आकृति 10.5(v)]।
आकृति 10.5 (i)-(v)
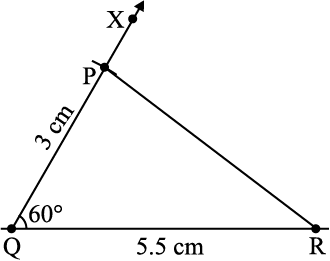
कीजिए
आईए अब एक अन्य त्रिभुज ABC की रचना करें ताकि Ab = 3 cm, BC = 6.5 cm और ∠ABC = 60° हो। इस ∆ABC को काट कर ∆PQR पर रखिए। हम क्या देखते हैं? हम देखते हैं कि ∆ABC पूर्णतया ∆PQR के साथ संपाती हो जाता है, अर्थात्् उसे ढक लेता है। इस प्रकार, यदि एक त्रिभुज की दो भुजाएँ और उनके मध्य स्थित (बीच का) कोण एक अन्य त्रिभुज की संगत भुजाओं और उनके मध्य स्थित कोण के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं। यह SAS सर्वांगसमता नियम या कसौटी है, जिसे हम पिछले अध्याय में पढ़ चुके हैं। (ध्यान दीजिए कि दोनों त्रिभुजों की रचना दी हुई दो भुजाओं और उनके मध्य स्थित (बीच के) कोण द्वारा की गई है।)
सोचिए, चर्चा कीजिए और लिखिए
उपरोक्त रचना में, दो भुजाओं की लंबाइयाँ और एक कोण का माप दिया हुआ था। अब, निम्नलिखित समस्या का अध्ययन कीजिए :
एक ∆ABC में, यदि AB = 3 cm, AC = 5 cm और ∠C = 30° है, तो क्या हम इस त्रिभुज की रचना कर सकते हैं? हम AC = 5 cm खींच कर, ∠C = 30° खींच सकते हैं। ∠C की एक भुजा CA है। बिंदु B को इस कोण C की दूसरी भुजा पर स्थित होना चाहिए। परंतु, ध्यान दीजिए कि बिंदु B को एक अद्वितीय रूप से निर्धारित नहीं किया जा सकता है। अतः, त्रिभुज ABC की रचना करने के लिए, दिए हुए आँकड़े पर्याप्त नहीं हैं।
अब ∆ABC की रचना करने का प्रयत्न कीजिए, जब AB = 3 cm, AC = 5 cm और∠B = 30° है। हम क्या प्रेक्षित करते हैं? पुनः, ∆ABC की रचना अद्वितीय रूप से नहीं की जा सकती है। इस प्रकार, हम निष्कर्ष निकाल सकते हैं कि एक अद्वितीय त्रिभुज की रचना तभी की जा सकती है जब उसकी दो भुजाओं की लंबाइयाँ और उनके मध्य स्थित (बीच के) कोण का माप दिया हुआ हो।
प्रश्नावली 10.3
1. ∆DEF की रचना कीजिए, ताकि DE = 5 cm, DF = 3 cm और m∠EDF = 90° हो।
2. एक समद्विबाहु त्रिभुज की रचना कीजिए, जिसकी प्रत्येक समान भुजा की लंबाई 6.5 cm हो और उनके बीच का कोण 110° का हो।
3. BC = 7.5 cm और AC = 5 cm और m∠C = 60° वाले ∆ABC की रचना कीजिए।
10.6 एक त्रिभुज की रचना जब उसके दो कोणों के माप और इन कोणों के बीच की भुजा की लंबाई दी हो (ASA कसौटी)
जैसा पहले किया था, एक रफ़ आकृति खींεंचए। अब, दिया हुआ रेखाखंड खींचिए। दोनों अंत बिंदुओं पर कोण बनाइए। उदाहरण 3 देखिए।
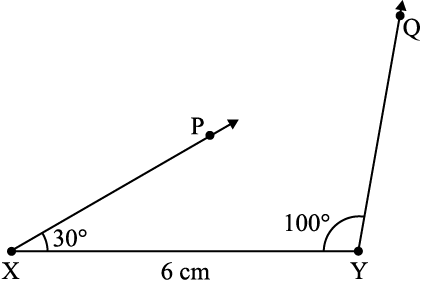
उदाहरण 3 ∆xyz की रचना कीजिए, यदि, XY = 6 cm, m∠ZXY = 30° और m∠XYZ = 100° है।
हल
चरण 1 वास्तविक रचना से पहले, हम इस पर अंकित मापों के अनुसार एक रफ़ आकृति खींचते हैं। (इससे कुछ अनुमान लग जाता है कि कैसे रचना की जाए) [आकृति 10.6(i)]।
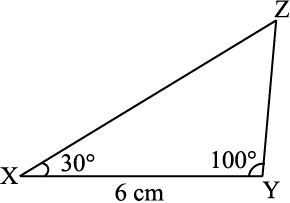
चरण 2 6 cm लंबाई का रेखाखंड xy खींचिए
[आकृति 10.6(ii)]।
चरण 3 x पर एक किरण XP खींचिए जो XY से 30° का कोण बनाए। दिए हुए प्रतिबंध के अनुसार बिंदु Z किरण xP पर कहीं स्थित होना चाहिए [आकृति 10.6(iii)]।
चरण 4 y पर एक किरण yq खींचिए, जो YX से 100° का कोण बनाए। दिए हुए प्रतिबंध के अनुसार z किरण yQ पर भी अवश्य स्थित होना चाहिए
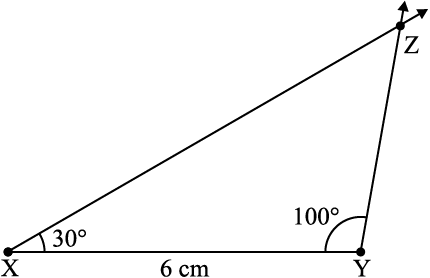
चरण 5 z को दोनों किरणों xp और Yq पर स्थित होना चाहिए। अतः, इन दोनों किरणों का प्रतिच्छेद बिंदु ही z है। अब ∆xyz पूरा बन जाता है [आकृति 10.6(v)]।
इन्हें कीजिए
अब एक अन्य त्रिभुज LMN खींचिए, जिसमें m∠NLM = 30°, LM = 6 cm और m∠NML = 100° हो। इस त्रिभुज LMN को काटकर त्रिभुज xyz पर रखिए। हम देखते हैं कि त्रिभुज LMN त्रिभुज xyz के साथ पूर्णतया संपाती हो जाता है। इस प्रकार, यदि एक त्रिभुज के दो कोण और उनके मध्य स्थित भुजा दूसरे त्रिभुज के संगत दो कोणों और उनके मध्य स्थित भुजा के बराबर हो, तो दोनों त्रिभुज सर्वांगसम होते हैं। यह ASA सर्वांगसमता नियम या कसौटी है, जिसे आप पिछले अध्याय में पढ़ चुके हैं। (ध्यान दीजिए कि यहाँ दो त्रिभुजों की रचना की गई है, जब दो कोण और उनके मध्य स्थित भुजा दी गई है।)
सोचिए, चर्चा कीजिए और लिखिए
उपरोक्त उदाहरण में, एक भुजा की लंबाई और दो कोणों के माप दिए गए थे। अब निम्नलिखित समस्या का अध्ययन कीजिए :
∆ABC, में, यदि AC = 7 cm, m∠A = 60° और m∠B = 50° है, तो क्या आप त्रिभुज की रचना कर सकते हैं? (त्रिभुज का कोण योग गुण आपकी सहायता कर सकता है!)
प्रश्नावली 10.4
1. ∆ABC, की रचना कीजिए, जब m∠A = 60°, m∠B = 30° और AB = 5.8 cm दिया है।
2. ∆PQR की रचना कीजिए, यदि PQ = 5 cm, m∠PQR = 105° और m∠QRP = 40° दिया है।
(संकेत ः त्रिभुज के कोण योग गुण को याद कीजिए)।
3. जाँच कीजिए कि आप ∆DEF की रचना कर सकते हैं या नहीं, यदि EF = 7.2 cm,
m∠E = 110° और m∠F = 80° है। अपने उत्तर की पुष्टि कीजिए।
10.7 एक समकोण त्रिभुज की रचना, जब उसके एक पाद (भुजा) और कर्ण की लंबाईयाँ दी हुई हों। (RHS कसौटी)
यहाँ, रफ़ आकृति बनाना सरल है। अब दी हुई भुजा के अनुसार, एक रेखाखंड खींचिए। इसके एक अंतः बिंदु पर एक समकोण बनाइए। त्रिभुज की दी हुई लंबाइयों की भुजा और कर्ण खींचने के लिए परकार का प्रयोग कीजिए। त्रिभुज को पूरा कीजिए। निम्नलिखित उदाहरण पर विचार कीजिए :
प्रश्नावली 10.5
1. समकोण ∆PQR की रचना कीजिए, जहाँ m∠Q = 90°, QR = 8 cm और PR = 10 cm है।
2. एक समकोण त्रिभुज की रचना कीजिए, जिसका कर्ण 6 cm लंबा है और एक पाद 4 cm लंबा है।
3. एक समद्विबाहु समकोण त्रिभुज ABC की रचना कीजिए, जहाँ m∠ACB = 90° है और AC = 6 cm है।
विविध प्रश्न
नीचे कुछ त्रिभुजों की भुजाओं और कोणों के माप दिए गए हैं। इनमें से उनकी पहचान कीजिए, जिनकी रचना नहीं की जा सकती तथा यह भी बताइए कि आप इनकी रचना क्यों नहीं कर सकते। शेष त्रिभुजों की रचना कीजिए।
त्रिभुज दिए हुए माप
1. ∆ABC m∠A = 85°, m∠B = 115°, AB = 5 cm
2. ∆PQR m∠Q = 30°, m∠R = 60°, QR = 4.7 cm
3. ∆ABC m∠A = 70°, m∠B = 50°, AC = 3 cm
4. ∆LMN m∠L = 60°, m∠N = 120°] LM = 5 cm
5. ∆ABC BC = 2 cm, AB = 4 cm, AC = 2 cm
6. ∆PQR PQ = 3.5 cm, QR = 4 cm, PR = 3.5 cm
7. ∆xyz xy = 3 cm, yz = 4 cm, xz = 5 cm
8. ∆DEF DE = 4.5 cm, EF = 5.5 cm, DF = 4 cm
हमने क्या चर्चा की?
इस अध्याय में हमने पैमाना (रूलर) और परकार की कुछ रचनाओं की विधियों का अध्ययन किया है।
1. एक दी हुई रेखा और एेसे बिंदु के लिए जो इस रेखा पर स्थित नहीं है, हमने तिर्यक छेदी रेखा आकृति में, रेखा के समांतर एक रेखा खींचने के लिए समान एकांतर कोणों की अवधारणा का उपयोग किया है।
इस रचना के लिए हम समान संगत कोणों की अवधारणा का उपयोग भी कर सकते हैं।
2. त्रिभुजों की सर्वांगसमता की संकल्पना का अप्रत्यक्ष रूप से उपयोग करते हुए हमने त्रिभुज की रचना की विधि का अध्ययन किया है।
इस अध्याय में निम्नलिखित उदाहरणों की चर्चा की गई है।
(i) SSS: त्रिभुज की तीन भुजाओं की लंबाई दी हुई है।
(ii) SAS: किन्हीं दो भुजाओं की लंबाई और इन भुजाओं के मध्य स्थित कोण का माप दिया हुआ है।
(iii) ASA: दो कोणों के माप और इनके मध्य स्थित भुजा की लंबाई दी हुई है।
(iv) RHS: समकोण त्रिभुज के कर्ण एवं एक पाद की लंबाई दी हुई है।