Table of Contents


0757CH11.tif


अध्याय 11



परिमाप और क्षेत्रफल



11.1 भूमिका

आप तल में बनी आकृतियों का परिमाप तथा वर्ग और आयत के क्षेत्रफलों के बारे में कक्षा VI में पढ़ चुके हैं। परिमाप एक बंद आकृति के चारों ओर की दूरी है जबकि क्षेत्रफल एक बंद आकृति द्वारा घेरे गए तल के भाग या क्षेत्र को दर्शाता है। इस कक्षा में आप कुछ और तल की आकृतियों के परिमाप और क्षेत्रफल के बारे में सीखेंगे।


11.2 वर्ग और आयत

आयुष और दीक्षा दोनों चित्र बनाते हैं। आयुष ने एक चित्र 60 cm लंबाई तथा 20 cm चौड़ाई वाली एक आयताकार शीट पर बनाया जबकि दीक्षा ने एक चित्र 40 cm लंबाई तथा 35 cm चौड़ाई वाली एक आयताकार शीट पर बनाया। इन दोनों चित्रों को अलग-अलग फ्रेम तथा लेमिनेट कराना है।

यदि फ्रेम कराने का खर्च ₹ 3.00 प्रति cm हो तो कौन-से चित्र को फ्रेम कराने के लिए अधिक रुपये खर्च करने पड़ेंगे?

यदि लेमिनेशन पर खर्च की दर ₹ 2.00 प्रति cm2 हो तो किसके चित्र के लेमिनेशन पर अधिक खर्च करना पड़ेगा?

फ्रेम पर कुल व्यय ज्ञात करने के लिए हमें उनका परिमाप ज्ञात करके, फ्रेम कराने की दर से गुणा करने की आवश्यकता होगी। इसी प्रकार, लेमिनेशन पर कुल व्यय ज्ञात करने के लिए हमें उसका क्षेत्रफल ज्ञात करके उसे लेमिनेशन कराने की दर से गुणा करने की आवश्यकता होगी।


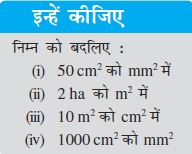
इन्हें कीजिए

नीचे दिए गए प्रश्नों के उत्तर देने के लिए आपको क्षेत्रफल या परिमाप में से किसको ज्ञात करने की आवश्यकता होगी।

1. एक श्यामपट कितनी जगह घेरता है?

2. एक आयताकार फूलों की क्यारी के चारों ओर बाड़ लगाने के लिए आवश्यक तार की लंबाई क्या है?

3. एक तिकोने पार्क के चारों ओर दो बार चक्कर लगाने पर आप कितनी दूरी तय करेंगे?

4. एक आयताकार स्वीमिंग पूल को ढकने के लिए आपको कितनी प्लास्टिक शीट की आवश्यकता होगी?



क्या आप जानते हैं,

समबहुभुज का परिमाप = भुजाओं की संख्या × एक भुजा की लंबाई

वर्ग का परिमाप = 4 × भुजा

आयत का परिमाप = 2 × (l + b)

आयत का क्षेत्रफल = l × b

वर्ग का क्षेत्रफल = भुजा × भुजा

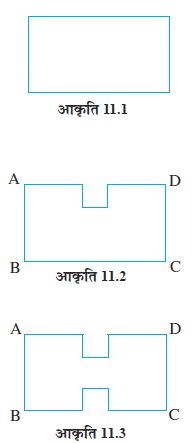
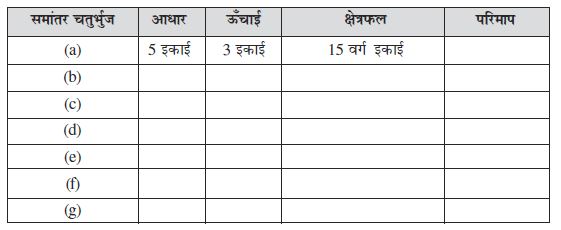
तान्या को एक कोलाज़ (collage) को पूरा करने के लिए एक 4 cm भुजा वाले वर्ग की आवश्यकता थी। उसके पास 28 cm लंबाई तथा 21 cm चौड़ाई वाली एक आयताकार शीट थी (आकृति 11.1)। उसने इस आयताकार शीट में से एक 4 cm भुजा वाले एक वर्ग को काटा। उसकी सहेली ने शीट के शेष भाग को देखा (आकृति 11.2) और तान्या से पूछा, ‘क्या शीट का परिमाप अब बढ़ गया है या कम हो गया है’?

11

क्या भुजा AD की कुल लंबाई, वर्ग काटने के उपरांत बढ़ गई है?

क्या क्षेत्रफल बढ़ गया है या कम हो गया है?

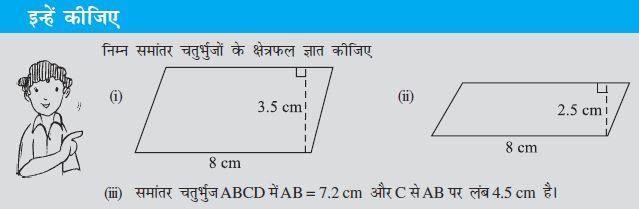
तान्या सम्मुख भुजा में से एक और वर्ग काटती है (आकृति 11.3)।

क्या शीट के शेष भाग का परिमाप पहले से और अधिक हो जाएगा?

क्या क्षेत्रफल पहले से और अधिक बढ़ेगा या कम होगा?

अतः, यहाँ से हम क्या निष्कर्ष निकाल सकते हैं?

इससे यह स्पष्ट है कि परिमाप के बढ़ाए जाने पर क्षेत्रफल का बढ़ना आवश्यक नहीं है।


इन्हे कीजिये 

1. एेसी बहुत सारी आकृतियों और काटी गई आकृतियों पर प्रयोग कीजिए। आप इनका उपयोग इन आकृतियों को वर्गांकित शीटों पर बनाकर क्षेत्रफल और परिमाप ज्ञात करने के लिए कर सकेंगे। आप यह जान चुके हैं कि परिमाप में बढ़त का यह अर्थ नहीं है कि उसका क्षेत्रफल भी बढ़ेगा।

2. दो एेसे उदाहरण दीजिए जहाँ परिमाप के बढ़ने पर उसका क्षेत्रफल भी बढ़ जाए।

3. एेसे दो उदाहरण दीजिए जहाँ परिमाप के बढ़ने पर उसके क्षेत्रफल में बढ़ोतरी न हो।


उदाहरण 1 10 m × 10 m माप वाली एक दीवार में 3 m × 2 m माप वाले एक दरवाज़े का फ्रेम (चौखट) लगाया जाना है। यदि 1 m2 दीवार पर पेंट कराने की मज़दूरी ₹ 2.50 हो तो पूरी दीवार पर पेंट कराने का कुल मज़दूरी खर्च ज्ञात कीजिए।

हल दीवार पर पेंट, दरवाज़े के क्षेत्रफल को छोड़कर होगा।

2686.png

आकृति 11. 4

दरवाज़े का क्षेत्रफल = l × b

= 3 m × 2 m = 6 m2

दरवाज़े सहित, दीवार का क्षेत्रफल = भुजा × भुजा = 10 m × 10 m = 100 m2

दरवाज़े को छोड़कर, दीवार का क्षेत्रफल = (100 − 6) m2 = 94 m2

दीवार पर पेंट कराने की कुल मज़दूरी = 2.50 × 94 = 235 रु


उदाहरण 2 एक आयताकार शीट का क्षेत्रफल 500 cm2 है। यदि शीट की लंबाई 25 cm हो तो इसकी चौड़ाई क्या होगी? आयताकार शीट का परिमाप भी ज्ञात कीजिए।

हल आयताकार शीट का क्षेत्रफल = 500 cm2

लंबाई (l) = 25 cm

आयत का क्षेत्रफल = l × b (जहाँ b = शीट की चौड़ाई)

इसलिए, चौड़ाई b = 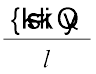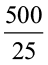4570.png = 4575.png = 20 cm

शीट का परिमाप = 2 × (l + b) = 2 × (25 + 20) cm = 90 cm

इस प्रकार, आयताकार शीट की चौड़ाई 20 cm तथा इसका परिमाप 90 cm है।


उदाहरण 3 अनु अपने घर के सामने वाले बगीचे के तीनों ओर बाड़ लगाना चाहती है (आकृति 11.5)। इनमें से एक बाजू की लंबाई20 m तथा बाकी प्रत्येक बाजू की लंबाई 12 m है। ₹ 150 प्रति मीटर की दर से बाड़ लगाने पर व्यय ज्ञात कीजिए।

हल बाड़ की आवश्यक लंबाई बगीचे का वह परिमाप है जिसमें एक भुजा सम्मिलित नहीं है।
यह 20 m + 12 m + 12 m यानि 44 m के बराबर है।

बाड़ लगाने पर व्यय = ₹ 150 × 44 = ₹ 6600

Pic03.tif

आकृति 11.5


उदाहरण 4 एक तार 10 cm भुजा वाले वर्ग के आकार की है। यदि तार को दुबारा मोड़ कर एक 12 cm लंबाई वाला आयत बनाया जाता है, तो इसकी चौड़ाई ज्ञात कीजिए।

किसका क्षेत्रफल अधिक होगा, वर्ग का या आयत का?

हल वर्ग की भुजा = 10 cm

तार की लंबाई = वर्ग का परिमाप = 4 × भुजा = 4 × 10 cm

= 40 cm

आयत की लंबाई l = 12 cm, b को आयत की चौड़ाई मान लीजिए

आयत का परिमाप = तार की लंबाई = 40 cm

आयत का परिमाप = 2 (l + b)

इस प्रकार 40 = 2 (12 + b)

या 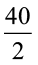4587.png = 12 + b

इसलिए b = 20 − 12 = 8 cm

आयत की चौड़ाई 8 cm है।

वर्ग का क्षेत्रफल = (भुजा)2

= 10 cm × 10 cm = 100 cm2

आयत का क्षेत्रफल = l × b

= 12 cm × 8 cm = 96 cm2

अतः, वर्ग अधिक क्षेत्रफल घेरता है यद्यपि इसका परिमाप आयत के परिमाप के बराबर है।


उदाहरण 5 एक वर्ग और एक आयत क क्षेत्रफल समान है। यदि वर्ग की भुजा 40 cm हो और आयत की चौड़ाई 25 cm हो तो आयत की लंबाई ज्ञात कीजिए। आयत का परिमाप भी ज्ञात कीजिए।

हल वर्ग का क्षेत्रफल = (भुजा)2

= 40 cm × 40 cm = 1600 cm2

यह दिया है कि

आयत का क्षेत्रफल = वर्ग का क्षेत्रफल

आयत का क्षेत्रफल = 1600 cm2

आयत की चौड़ाई = 25 cm

आयत का क्षेत्रफल = l × b

या 1600 = l × 25

या 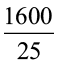4598.png = l

या l = 64 cm

अतः, आयत की लंबाई 64 cm है।

आयत का परिमाप = 2 (l + b) = 2 (64 + 25) cm

= 2 × 89 cm = 178 cm

इस प्रकार, आयत का परिमाप 178 cm है यद्यपि इसका क्षेत्रफल वर्ग के क्षेत्रफल के बराबर है।


प्रश्नावली 11. 1


1. एक आयताकार भूखंड की लंबाई और चौड़ाई क्रमशः 500 m तथा 300 m हैं। ज्ञात कीजिएः

(i) भूखंड का क्षेत्रफल (ii) भूखंड का मूल्य, यदि 1 m2 का मूल्य ₹ 10,000 है।

2. एक वर्गाकार पार्क का क्षेत्रफल ज्ञात कीजिए जिसका परिमाप 320 m है।

3. एक आयताकार भूखंड की चौड़ाई ज्ञात कीजिए यदि इसका क्षेत्रफल 440 m2 और लंबाई 22 m हो। इसका परिमाप भी ज्ञात कीजिए।

4. एक आयताकार शीट का परिमाप 100 cm है। यदि लंबाई 35 cm हो तो इसकी चौड़ाई ज्ञात कीजिए। क्षेत्रफल भी ज्ञात कीजिए।

5. एक वर्गाकार पार्क का क्षेत्रफल एक आयताकार पार्क के बराबर है। यदि वर्गाकार पार्क की एक भुजा 60 m हो और आयताकार पार्क की लंबाई 90 m हो तो आयताकार पार्क की चौड़ाई ज्ञात कीजिए।

6. एक तार आयत के आकार का है। इसकी लंबाई 40 cm और चौड़ाई 22 cm है। यदि उसी तार को दुबारा मोड़कर एक वर्ग बनाया जाता है तो प्रत्येक भुजा की माप क्या होगी? यह भी ज्ञात कीजिए की किस आकार का क्षेत्रफल अधिक होगा?

7. एक आयत का परिमाप 130 cm है। यदि आयत की चौड़ाई 30 cm हो तो आयत की लंबाई ज्ञात कीजिए। आयत का क्षेत्रफल भी ज्ञात कीजिए।

8. 2 m लंबाई और 1 m चौड़ाई वाले दरवाज़े को एक दीवार में लगाया जाता है। दीवार की लंबाई 4.5 m तथा चौड़ाई 3.6 m है(आकृति 11.6). ₹ 20 प्रति m2 की दर से दीवार पर सफ़ेदी (white wash) कराने का व्यय ज्ञात कीजिए।

Pic2.tif

आकृति 11.6


11.2.1 आयत के भाग के रूप में त्रिभुज

8 सेमी और 5 सेमी भुजाओं वाला एक आयत लीजिए। आयत को विकर्ण के अनुदिश एेसा काटिए जिससे दो त्रिभुज प्राप्त हों(आकृति 11.7)।

एक त्रिभुज को दूसरे पर रखिए।

क्या ये दोनों पूर्णतया समान माप के हैं?

क्या आप कह सकते है कि दोनों त्रिभुजों का क्षेत्रफल बराबर है?

क्या ये त्रिभुज सवार्गंसम भी हैं?

इनमें से प्रत्येक त्रिभुज का क्षेत्रफल कितना है?

आप देखेंगे कि दोनों त्रिभुजों के क्षेत्रफलों का योगफल आयत के क्षेत्रफल के बराबर है।

2888.png

आकृति 11.7


2866.png

आकृति 11.8

प्रत्येक त्रिभुज का क्षेत्रफल = 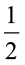4608.png(आयत का क्षेत्रफल)

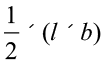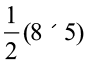
= 4620.png = 4631.png 

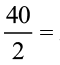= 4642.png20 cm2

अब एक 5 cm भुजा वाला वर्ग लीजिए और इसे 4 त्रिभुजों में बाँटिए जैसा कि आकृति में दिखाया गया है (आकृति 11.8)।

क्या चारों त्रिभुजों का क्षेत्रफल बराबर है?

क्या वे एक दूसरे के सर्वांगसम हैं? (त्रिभुजों को एक-दूसरे पर रख कर जाँचिए)

प्रत्येक त्रिभुज का क्षेत्रफल क्या है?

प्रत्येक त्रिभुज का क्षेत्रफल = 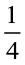4654.png (वर्ग का क्षेत्रफल)

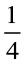= 4664.png (भुजा)2 = 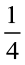4669.png (5)2 cm2 = 6.25 cm2


11.2.2 आयतों के अन्य सर्वांगसम भागों के लिए व्यापीकरण

6 cm लंबाई और 4 cm चौड़ाई वाले एक आयत को दो भागों में बाँटा गया है जैसा आकृति में दिखाया है (आकृति 11.9)। आयत को दूसरे कागज़ पर ट्रेस कीजिए और आयत को EF के अनुदिश काटकर, दो भागों में बाँटिए।

2930.png

आकृति 11.9

एक भाग को दूसरे पर रखिए और देखिए कि क्या वे एक दूसरे को पूर्णतया ढकते हैं। (आपको इन्हें घुमाना भी पड़ सकता है।)

क्या ये सर्वांगसम हैं? दोनों भाग एक-दूसरे से सर्वांगसम हैं। इस प्रकार, एक भाग का क्षेत्रफल दूसरे भाग के क्षेत्रफल के बराबर है।

इसलिए, प्रत्येक सर्वांगसम भाग का क्षेत्रफल = 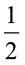4674.png(आयत का क्षेत्रफल)

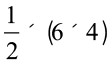= 4678.png cm2 = 12 cm2





इन्हें कीजिए

TryThese3L.tifनीचे दिए गए प्रत्येक आयत जिसकी लंबाई 6 cm और चौड़ाई 4 cm है, सर्वांगसम बहुभुजों से मिलकर बने हैं। प्रत्येक बहुभुज का क्षेत्रफल ज्ञात कीजिए।
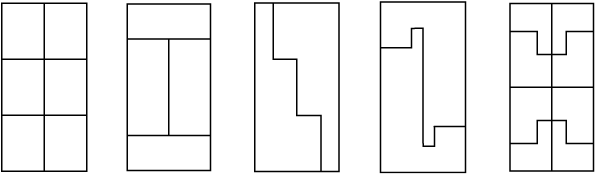
2958.png


11.3 समांतर चतुर्भुज का क्षेत्रफल

हमें वर्ग और आयत के अतिरिक्त बहुत से दूसरे आकार देखने को मिलते हैं।

आप एक भूखंड का क्षेत्रफल कैसे ज्ञात करेंगे जिसका आकार समांतर चतुर्भुज जैसा है?

आइए समांतर चतुर्भुज का क्षेत्रफल प्राप्त करने की एक विधि ज्ञात करें।

क्या एक समांतर चतुर्भुज को एक समान क्षेत्रफल वाले आयत में रूपांतरित किया जा सकता है?

ग्राफ़ पेपर पर एक समांतर चतुर्भुज बनाइए जैसाकि आकृति [11.10(i)] में दिखाया गया है। इस समांतर चतुभुर्ज को काटिए। समांतर चतुर्भुज के एक शीर्ष से इसकी सम्मुख भुजा पर एक लंब खींचिए [आकृति 11.10(ii)]। इस त्रिभुज को काट लीजिए और इस त्रिभुज को समांतर चतुर्भुज की दूसरी भुजा के साथ रखिए [आकृति 11.10(iii)]।


2967.png


आकृति 11.10


आप कैसा आकार प्राप्त करते हैं? आप एक आयत प्राप्त करते हैं।

क्या समांतर चतुर्भुज का क्षेत्रफल बनाए गए आयत के क्षेत्रफल के बराबर है?

हाँ, समांतर चतुर्भुज का क्षेत्रफल = बनाए गए आयत का क्षेत्रफल

आयत की लंबाई और चौड़ाई क्या है?

2997.png

आकृति 11.11

हमने देखा कि बनाए गए आयत की लंबाई, समांतर चतुर्भुज के आधार की लंबाई के बराबर है और आयत की चौड़ाई, समांतर चतुर्भुज की ऊँचाई के बराबर है (आकृति 11.11)।

अब, समांतर चतुर्भुज का क्षेत्रफल = आयत का क्षेत्रफल

= लंबाई × चौड़ाई = l × b

लेकिन आयत की लंबाई l तथा चौड़ाई b क्रमशः समांतर चतुर्भुज का आधार b और ऊँचाई h ही है।

इस प्रकार, समांतर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई = b × h

12


3105.png

आकृति 11.12


निम्न तालिका को पूरा कीजिए :

13

आप दखेंगे कि इन सभी समांतर चतुर्भुजों का क्षेत्रफल तो समान है परंतु परिमाप अलग-अलग हैं। अब, निम्न 7 cm तथा 5 cm भुजाओं वाले समांतर चतुर्भुजों को देखते हैं (आकृति 11.13)।

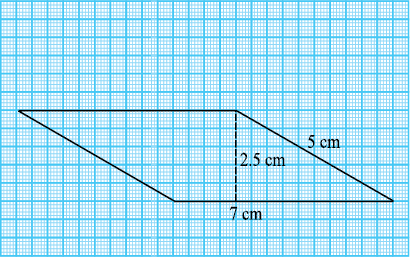
3192.png
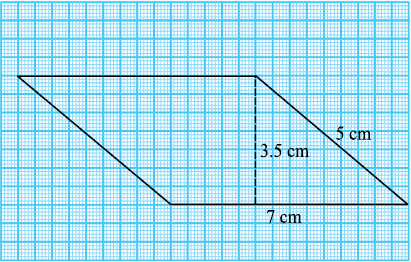
3165.png
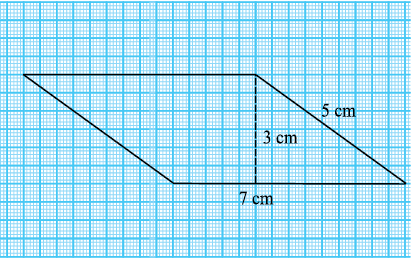
3177.png
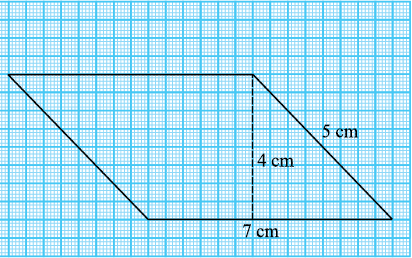
3202.png

आकृति 11.13


प्रत्येक समांतर चतुर्भुज का परिमाप तथा क्षेत्रफल ज्ञात कीजिए। अपने परिणाम का विश्लेषण कीजिए।

आप देखेंगे कि इन समांतर चतुर्भुजों का क्षेत्रफल अलग-अलग हैं लेकिन परिमाप समान हैं।

समांतर चतुर्भुज का क्षेत्रफल ज्ञात करने के लिए आपको समांतर चतुर्भुज का आधार तथा संगत ऊँचाई को ज्ञात करने की आवश्यकता है।

14


11.4 एक त्रिभुज का क्षेत्रफल

एक माली पूरे तिकोने पार्क पर घास लगाने का व्यय जानना चाहता है।

इस स्थिति में हमें त्रिभुजाकार क्षेत्र का क्षेत्रफल ज्ञात करने की आवश्यकता है।

आइए एक त्रिभुज के क्षेत्रफल को प्राप्त करने की विधि ज्ञात करें।

3250.png

कागज़ के एक टुकड़े पर एक विषमबाहु त्रिभुज बनाइए। इस त्रिभुज को काट लीजिए।

इस त्रिभुज को दूसरे कागज़ के टुकड़े पर रखिए और समान माप का एक ओर त्रिभुज काटिए।

इस प्रकार अब आपके पास समान माप के दो विषमबाहु त्रिभुज हैं। क्या दोनों त्रिभुज सर्वांगसम हैं?

एक त्रिभुज को दूसरे पर रखिए जिससे वे एक-दूसरे को पूर्ण रूप से ढक लें। आप दोनों में से एक त्रिभुज को घुमा भी सकते हैं।

अब दोनों त्रिभुजों को इस प्रकार आपस में रखिए जिससे उनकी संगत भुजाओं का एक युग्म आपस में मिल जाएँ (जैसा आकृति 11.14 में दिखाया गया है)।

15

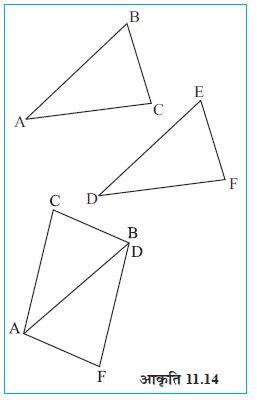
क्या इस प्रकार से बनी आकृति एक समांतर चतुर्भुज है?

प्रत्येक त्रिभुज के क्षेत्रफल की तुलना समांतर चतुर्भुज के क्षेत्रफल से कीजिए।

त्रिभुजों के आधार तथा ऊँचाई की तुलना समांतर चतुर्भुज के आधार तथा ऊँचाई से कीजिए।

आप देखेंगे कि दोनों त्रिभुजों के क्षेत्रफलों का योगफल समांतर चतुर्भुज के क्षेत्रफल के बराबर है। त्रिभुज का आधार और ऊँचाई क्रमशः समांतर चतुर्भुज के आधार और ऊँचाई के बराबर है।

प्रत्येक त्रिभुज का क्षेत्रफल =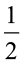4689.png(समांतर चतुर्भुज का क्षेत्रफल)

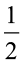= 4693.png(आधार × ऊँचाई) (क्योंकि, समांतर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई)

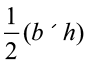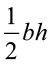= 4697.png (या 4711.png, संक्षेप में)


इन्हें कीजिए

TryThese2L.tif

1. ऊपर दिए गए क्रियाकलापों को अलग-अलग प्रकार के त्रिभुज लेकर कीजिए।

2. अलग-अलग प्रकार के समांतर चतुर्भुज लीजिए। प्रत्येक समांतर चतुर्भुज को दो त्रिभुजों में एक विकर्ण के अनुदिश काटिए। क्या ये त्रिभुज सर्वांगसम हैं।


आकृति (11.15) में सभी त्रिभुज, आधार AB = 6 cm पर स्थित हैं।

आधार AB पर प्रत्येक त्रिभुज की संगत ऊँचाई के बारे में आप क्या कह सकते हैं?

क्या हम कह सकते हैं कि सभी त्रिभुजों का क्षेत्रफल बराबर है? हाँ।

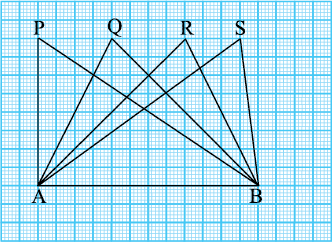
3342.png

आकृति 11 .15

क्या त्रिभुज सर्वांगसम हैं? नहीं।

हम निष्कर्ष निकालते हैं कि सभी सर्वांगसम त्रिभुजों का क्षेत्रफल बराबर होता है लेकिन यह आवश्यक नहीं है कि वे त्रिभुज जिनका क्षेत्रफल बराबर होता है वे सर्वांगसम हैं।

आधार 6 cm वाले एक अधिक कोण (obtuse angled triangle) त्रिभुज ABC पर विचार करते हैं (आकृति 11.16)।

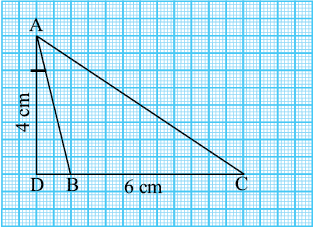
3363.png

आकृति 11 .16

3378.png

आकृति 11.17


इसकी ऊँचाई AD शीर्ष A से DC पर लंब है जो त्रिभुज के बाह्य स्थित है।

क्या आप इस त्रिभुज का क्षेत्रफल ज्ञात कर सकते हैं?


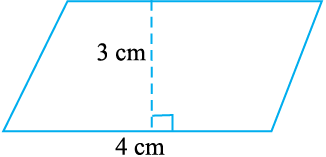
उदाहरण 6 एक समांतर चतुर्भुज की एक भुजा और संगत ऊँचाई क्रमशः 4 cm और 3 cm है। समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए (आकृति 11.17)।

हल आधार की लंबाई दी गई है (b) = 4 cm, ऊँचाई (h) = 3 cm

समांतर चतुर्भुज का क्षेत्रफल = b × h = 4 cm × 3 cm = 12 cm2


उदाहरण 7 यदि एक समांतर चतुर्भुज (आकृति 11.18) का क्षेत्रफल 24 cm2 और आधार 4 cm हो तो ऊँचाई ‘x’ ज्ञात कीजिए।

हल समांतर चतुर्भुज का क्षेत्रफल = b × h

इसलिए, 24 = 4 × x

या 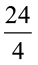4722.png = x

या x = 6 cm

इस प्रकार, समांतर चतुर्भुज की ऊँचाई 6 cm है।

3395.png

आकृति 11.18


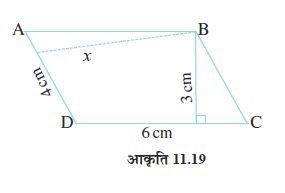
उदाहरण 8 समांतर चतुर्भुज ABCD की दो भुजाओं की लंबाइयाँ 6 cm और 4 cm हैं। आधार CD की संगत ऊँचाई 3 cm है(आकृति 11.19)। ज्ञात कीजिए :

16

(i) समांतर चतुर्भुज का क्षेत्रफल (ii) आधार AD की संगत ऊँचाई

हल

(i) समांतर चतुर्भुज का क्षेत्रफल = b × h

= 6 cm × 3 cm = 18 cm2

(ii) आधार (b) = 4 cm,

ऊँचाई = x (मान लीजिए)

क्षेत्रफल = 18 cm2

समांतर चतुर्भुज का क्षेत्रफल = b × x

18 = 4 × x

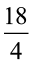4734.png = x

इसलिए, x = 4.5 cm

इस प्रकार, आधार AD की संगत ऊँचाई 4.5 cm है।


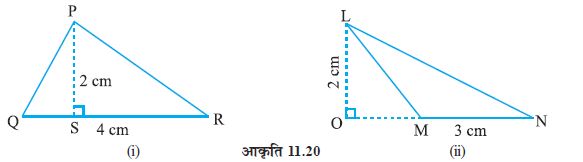
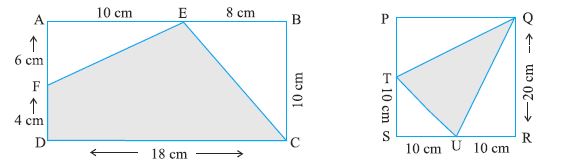
उदाहरण 9 निम्न त्रिभुजों का क्षेत्रफल ज्ञात कीजिए (आकृति 11.20) :

17

(i) आकृति 11.20 (ii)

हल

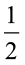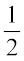(i) त्रिभुज का क्षेत्रफल = 4746.png bh = 4757.png× QR × PS

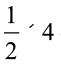= 4762.pngcm × 2 cm = 4 cm2

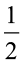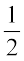(ii) त्रिभुज का क्षेत्रफल = 4773.pngbh = 4778.png× MN × LO

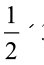= 4783.png3 cm × 2 cm = 3 cm2


उदाहरण 10 BC ज्ञात कीजिए, यदि त्रिभुज ABC का क्षेत्रफल 36 cm2 और ऊँचाई AD 3 cm है। (आकृति 11.21) :

हल ऊँचाई = 3 cm, क्षेत्रफल = 36 cm2

त्रिभुज ABC का क्षेत्रफल = 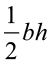4793.png

या 36 = 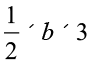4804.png

b = 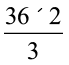4815.png = 24 cm

इसलिए BC = 24 cm

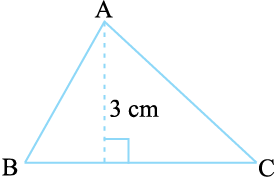
3549.png

आकृति 11.21


उदाहरण 11 ∆PQR में PR = 8 cm, QR = 4 cm और PL = 5 cm (आकृति 11.22)। ज्ञात कीजिएः

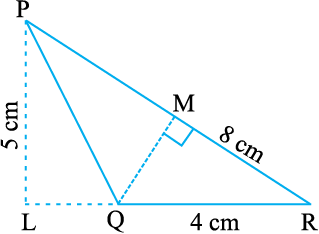
3523.png

आकृति 11.22


(i) ∆PQR का क्षेत्रफल (ii) QM

हल

(i) आधार = 4 cm ऊँचाई = 5 cm

त्रिभुज का क्षेत्रफल = 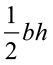4825.png

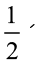= 4831.png 4 cm × 5 cm = 10 cm2

(ii) आधार = 8 cm, ऊँचाई = ? , क्षेत्रफल = 10 cm2

त्रिभुज का क्षेत्रफल = 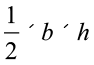4843.png अर्थात्् 10 =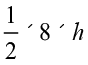 4857.png

h = 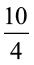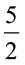4868.png = 4879.png= 2.5 इसलिए, QM = 2.5 cm



प्रश्नावली 11.2

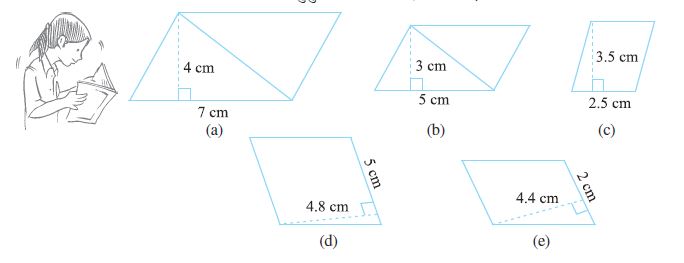
1. निम्न में प्रत्येक समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए :

18


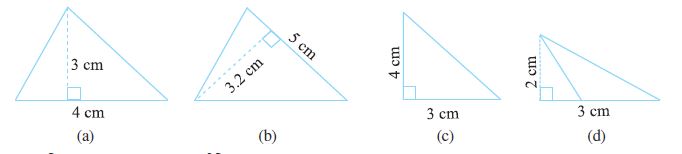
2. निम्न में प्रत्येक त्रिभुज का क्षेत्रफल ज्ञात कीजिए :

19

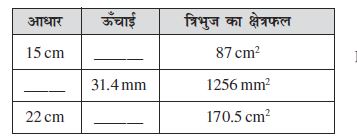
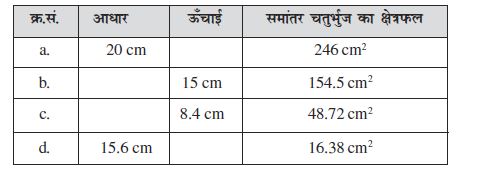
3. रिक्त स्थान का मान ज्ञात कीजिए 

20

4. रिक्त स्थानों का मान ज्ञात कीजिए :

21



5. PQRS एक समांतर चतुर्भुज है (आकृति 11.23)। QM शीर्ष Q से SR तक की ऊँचाई तथा QN शीर्ष Q से PS तक की ऊँचाई है। यदि 
SR = 12 cm और QM = 7.6 cm तो ज्ञात कीजिए :

(a) समांतर चतुर्भुज PQRS का क्षेत्रफल (b) QN, यदि PS = 8 cm

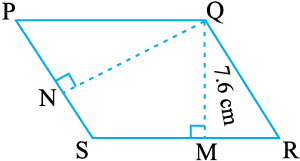
3745.png

आकृति 11.23

6. DL और BM समांतर चतुर्भुज ABCD की क्रमशः भुजाएँ AB और AD पर लंब हैं (आकृति 11.24)। यदि समांतर चतुर्भुज का क्षेत्रफल 1470 cm2 है, AB = 35 cm और AD = 49 cm है, तो BM तथा DL की लंबाई ज्ञात कीजिए।

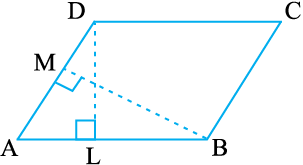
3513.png

आकृति 11.24

7. त्रिभुज ABC, A पर समकोण है (आकृति 11.25), और AD भुजा BC पर लंब है। यदि AB = 5 cm, BC = 13 cm और AC = 12 cm है, तो ∆ABC का क्षेत्रफल ज्ञात कीजिए। AD की लंबाई भी ज्ञात कीजिए।

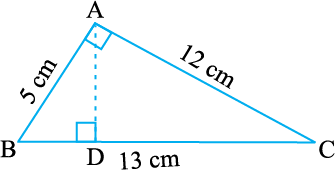
3761.png

आकृति 11.25

8. ∆ABC समद्विबाहु त्रिभुज है जिसमें AB = AC = 7.5 cm और BC = 9 cm है (आकृति 11.26)। A से BC तक की ऊँचाई AD, 6 cm है। ∆ABC का क्षेत्रफल ज्ञात कीजिए। C से AB तक की ऊँचाई, अर्थात्् CE क्या होगी?

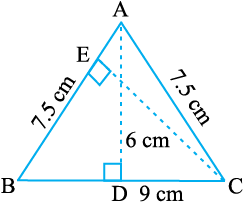
3814.png

आकृति 11.26

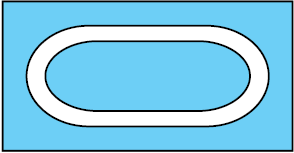
3826.png

आकृति 11.27



11.5 वृत्त

एक दौड़ पथ अपने दोनों किनारों पर अर्धवृत्ताकार है (आकृति 11.27)।

क्या आप एक धावक द्वारा तय की गई दूरी ज्ञात कर सकते हैं यदि वह इस दौड़ पथ के दो पूरे चक्कर लगाता है? जब आकार वृत्ताकार हो तो हमें उसके चारों ओर की दूरी प्राप्त करने की एक विधि ज्ञात करने की आवश्यकता होती है।


11.5.1 वृत्त की परिधि

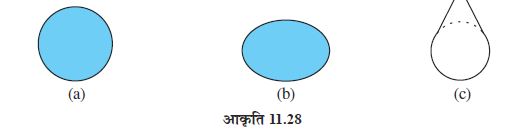
तान्या गत्ते के घुमावदार आकार के अलग-अलग कार्ड काटती है। वह इन कार्डों को सजाने के लिए इनके चारों ओर किनारी लगाना चाहती है। प्रत्येक के लिए उसे कितनी लंबी किनारी की आवश्यकता होगी (आकृति 11.28)?

22


आप एक पैमाने (रूलर) की सहायता से वक्र (curve) को नहीं माप सकते क्योंकि ये आकृतियाँ सीधी नहीं हैं। आप क्या करेंगे?

आकृति 11. 28(a) में दिए गए आकार की आवश्यक किनारी की लंबाई ज्ञात करने के लिए आपको एक तरीका बताया जा रहा है। कार्ड के किनारे पर एक बिंदु अंकित कीजिए और इसे एक टेबल पर रखिए। बिंदु की स्थिति को टेबल पर भी अंकित कीजिए(आकृति 11.29)।

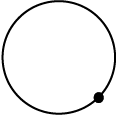
3872.png

आकृति 11.29


अब वृत्ताकार कार्ड को एक सरल रेखा की दिशा में टेबल पर तब तक घुमाइए जब तक अंकित बिंदु टेबल को दुबारा स्पर्श न कर जाए। इस दूरी को रेखा के अनुदिश में मापिए। यह आवश्यक किनारी की लंबाई है। यह कार्ड के अंकित किए गए बिंदु से कार्ड के किनारे-किनारे वापस उसी बिंदु तक की दूरी है।

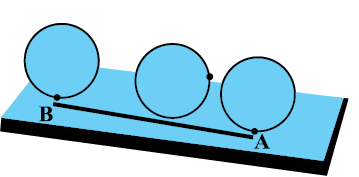
3888.png



आकृति 11.30


आप एक धागे को वृत्ताकार वस्तु के चारों ओर किनारे-किनारे रख कर भी दूरी ज्ञात कर सकते हैं।

एक वृत्ताकार क्षेत्र के चारों ओर की दूरी इसकी परिधि कहलाती है।


इन्हें कीजिए

एक बोतल का ढक्कन, एक चूड़ी या कोई अन्य वृत्ताकार वस्तु लीजिए और इसकी परिधि ज्ञात कीजिए। 

अब, क्या आप इस विधि से एक धावक द्वारा एक पथ पर तय की गई दूरी ज्ञात कर सकते है?

अभी भी, पथ के चारों ओर की दूरी ज्ञात करना या अन्य किसी वृत्ताकार वस्तु को धागे से मापना बहुत ही मुश्किल होगा। तथापि यह माप सही नहीं होगी।

अतः इसके लिए हमें एक सूत्र की आवश्यकता है जैसाकि तल की आकृति या आकारों के लिए हम प्रयोग करते हैं।

आइए हम देखें क्या वृत्तों के व्यास और परिधि के बीच में कोई संबंध है।

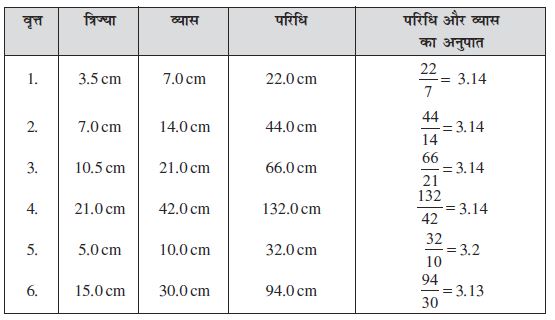
निम्न तालिका पर विचार कीजिए। अलग-अलग त्रिज्याओं के 6 वृत्त खींचिए और धागे की सहायता से उनकी परिधि ज्ञात कीजिए। परिधि और व्यास के अनुपात को भी ज्ञात कीजिए :

23


ऊपर दी गई तालिका से आप क्या निष्कर्ष निकालते हैं? क्या यह अनुपात लगभग समान है? हाँ।

क्या आप कह सकते हैं कि एक वृत्त की परिधि हमेशा इसके व्यास की तीन गुणा है? हाँ।

यह अनुपात स्थिर है और इसे ‘π’ (pi) (पाई) से प्रदर्शित करते हैं। इसका मान लगभग 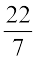4957.png या 3.14 है।

अतः हम कह सकते हैं 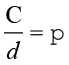4962.png, जहाँ ‘C’ वृत्त की परिधि और ‘d’ इसका व्यास दर्शाता है।

या C = πd

हम जानते हैं कि एक वृत्त का व्यास (d), त्रिज्या (r) का दुगुना होता है; अर्थात्् d = 2r

अतः, C = πd = π × 2r या C = 2πr


आकृति 11.31 में

(a) किस वर्ग का परिमाप अधिक है?

(b) कौन-सा अधिक है, छोटे वर्ग का परिमाप या वृत्त की परिधि?

4038.png

आकृति 11.31


प्रयास कीजिए

एक चौथाई प्लेट तथा एक अर्ध प्लेट लीजिए। प्रत्येक को टेबल की ऊपरी सतह पर एक बार घुमाइए। कौन-सी प्लेट एक पूरे चक्कर में अधिक दूरी तय करती है? कौन-सी प्लेट कम चक्कर में टेबल की ऊपरी सतह की लंबाई को पूरा करेगी?

Pic4.tif

उदाहरण 12 10 cm व्यास वाले एक वृत्त की परिधि ज्ञात कीजिए

(π = 3.14 लीजिए)

हल वृत्त का व्यास (d) = 10 cm

वृत्त की परिधि = πd

= 3.14 × 10 cm = 31.4 cm

अतः, 10 cm व्यास वाले वृत्त की परिधि 31.4 cm है।


उदाहरण 13 एक वृत्ताकार तश्तरी (disc) की परिधि ज्ञात कीजिए जिसकी त्रिज्या 14 cm है।

24


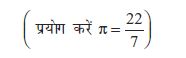
हल वृत्ताकार तश्तरी (disc) की त्रिज्या (r) = 14 cm

तश्तरी की परिधि = 2πr

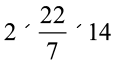= 4986.pngcm = 88 cm

अतः, वृत्ताकार तश्तरी की परिधि 88 cm है।


उदाहरण 14 एक वृत्ताकार पाइप की त्रिज्या 10 cm है। पाइप के चारों ओर एक बार टेप लपेटने की आवश्यक लंबाई ज्ञात कीजिए (प्रयोग करें π = 3.14)।

हल पाइप की त्रिज्या (r) = 10 cm

आवश्यक टेप की लंबाई, पाइप की परिधि के बराबर है।

पाइप की परिधि = 2πr

= 2 × 3.14 × 10 cm = 62.8 cm

इसलिए, पाइप के चारों ओर एक बार टेप लपेटने की आवश्यक लंबाई 62.8 cm है।


उदाहरण 15 दी गई आकृति का परिमाप ज्ञात कीजिए (आकृति 11.32) ।

(π = 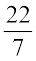4997.png लीजिए)।

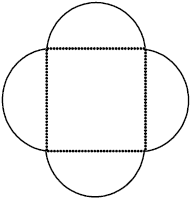
3940.png

आकृति 11.32

हल इस आकृति में हमें वर्ग के प्रत्येक ओर स्थित अर्धवृत्त की परिधि को ज्ञात करने की आवश्यकता है। क्या आपको वर्ग के परिमाप को भी ज्ञात करने की आवश्यकता है? नहीं। इस आकृति की बाह्य परिसीमा अर्धवृत्तों से मिलकर बनी है। प्रत्येक अर्धवृत्त का व्यास 14 cm है।

हम जानते हैं कि, वृत्त की परिधि = πd

अर्धवृत्त की परिधि = 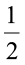5002.pngπd

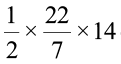= 5013.pngcm = 22 cm

प्रत्येक अर्धवृत्त की परिधि 22 cm है।अतः दी गई आकृति का परिमाप = 4 × 22 cm = 88 cm

उदाहरण 16 सुधांशु 7 cm त्रिज्या वाली एक वृत्ताकार तश्तरी (disc) को दो बराबर भागों में विभाजित करता है। प्रत्येक अर्धवृत्ताकार तश्तरी का परिमाप ज्ञात कीजिए (प्रयोग करें π = 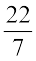5025.png)

हल अर्धवृत्ताकार तश्तरी (disc) के परिमाप को ज्ञात करने के लिए, (आकृति 11.33), हमें ज्ञात करने की आवश्यकता हैः

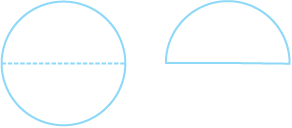
4008.png

आकृति 11.33


(i) अर्धवृत्ताकार आकार की परिधि (ii) व्यास

दी गई त्रिज्या (r) = 7 cm

हम जानते हैं कि वृत्त की परिधि = 2πr

अतः, अर्धवृत्त की परिधि = 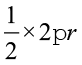5030.png = πr

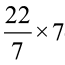= 5041.png cm = 22 cm

इसलिए, वृत्त का व्यास = 2r = 2 × 7 cm = 14 cm

अतः प्रत्येक अर्धवृत्ताकार तश्तरी (disc) का परिमाप = 22 cm + 14 cm = 36 cm



11.5.2 वृत्त का क्षेत्रफल

निम्न पर विचार कीजिए :

एक किसान खेत के केंद्र पर 7 m त्रिज्या वाली एक फूलों की क्यारी खोदता है। उसे खाद को खरीदने की आवश्यकता है। यदि 1 m2 क्षेत्रफल के लिए 1 kg खाद की आवश्यकता हो, तो उसे कितने किलोग्राम खाद खरीदनी चाहिए?

10 रु प्रति m2 की दर से, 2 m त्रिज्या वाले एक वृत्ताकार टेबल के ऊपरी सतह पर पॉलिश कराने का व्यय क्या होगा?

क्या आप बता सकते हैं कि इन स्थितियों में हमें क्या ज्ञात करने की आवश्यकता है, क्षेत्रफल या परिमाप? एेसी स्थितियों में हमें वृत्ताकार क्षेत्र का क्षेत्रफल ज्ञात करने की आवश्यकता होती है। आइए ग्राफ़ पेपर की सहायता से हम एक वृत्त का क्षेत्रफल ज्ञात करते हैं।

4 cm त्रिज्या वाले एक वृत्त को ग्राफ़ पेपर पर बनाइए (आकृति 11.34)। वृत्त के द्वारा घिरे हुए वर्गों को गिनकर इसका क्षेत्रफल ज्ञात कीजिए।

क्योंकि किनारे सीधे नहीं हैं, हमें, इस विधि से, वृत्त के क्षेत्रफल का एक कच्चा (rough) अनुमान ही प्राप्त होता है। एक और विधि से वृत्त का क्षेत्रफल ज्ञात करते हैं।

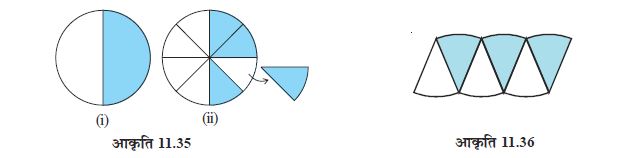
एक वृत्त बनाइए और उसके अर्धभाग को छायांकित कीजिए [आकृति 11.35(i)]अब वृत्त को आठ भागों में मोड़िए और उन्हें मुड़ी हुई तहों के अनुदिश में काटिए (आकृति 11.35(ii))।

25


अलग-अलग टुकड़ों को, जैसा आकृति 11.36 में दिखाया गया है, व्यवस्थित कीजिए, जो एक स्थूल रूप से (roughly) समांतर चतुर्भुज को दर्शाता है।

जितने अधिक त्रिज्याखंड होंगे, उतना ही सही समांतर चतुर्भुज हमें प्राप्त होता है।

जैसा ऊपर किया गया है यदि हम वृत्त को 64 त्रिज्याखंडों में विभाजित करें और उन्हें व्यवस्थित करें, तो हमें लगभग एक आयत प्राप्त होता है (आकृति 11.37)।

इस आयत की चौड़ाई क्या है? इस आयत की चौड़ाई वृत्त की त्रिज्या ही है अर्थात् ‘r’

4106.png
आकृति 11.37

जैसाकि पूरे वृत्त को 64 त्रिज्याखंडों में विभाजित किया गया तथा प्रत्येक ओर 32 त्रिज्यखंड हैं। आयत की लंबाई 32 त्रिज्यखंडों की लंबाइयों के बराबर है जो वृत्त की परिधि की आधी है (आकृति 11.37)।

वृत्त का क्षेत्रफल = बनाए गए आयत का क्षेत्रफल = l × b


26

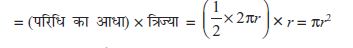
अतः, वृत्त का क्षेत्रफल = πr2


इन्हें कीजिए


ग्राफ़ पेपर पर अलग-अलग त्रिज्याओं के वृत्तों को बनाइए। वर्गों की संख्या को गिनकर क्षेत्रफल ज्ञात कीजिए। सूत्र का प्रयोग करके भी क्षेत्रफल ज्ञात कीजिए। दोनों उत्तरों की तुलना कीजिए।

उदाहरण 17 30 cm त्रिज्या वाले वृत्त का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए)

हल त्रिज्या r = 30 cm

वृत्त का क्षेत्रफल = πr2 = 3.14 × 302 = 2826 cm2


उदाहरण 18 एक वृत्ताकार बगीचे का व्यास 9.8 m है। इसका क्षेत्रफल ज्ञात कीजिए

हल व्यास, d = 9.8 m अतः त्रिज्या r = 9.8 ÷ 2 = 4.9 m

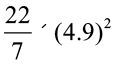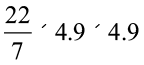वृत्त का क्षेत्रफल = πr2 = 5064.pngm2 = 5074.pngm2 = 75.46 m2


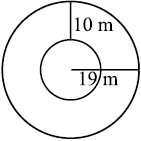
उदाहरण 19 संलग्न आकृति दो वृत्तों को दर्शाती है जिनका केंद्र समान है। बड़े वृत्त की त्रिज्या 10 cm और छोटे वृत्त की त्रिज्या4 cm है।

ज्ञात कीजिए (a) बड़े वृत्त का क्षेत्रफल (b) छोटे वृत्त का क्षेत्रफल (c) दोनों वृत्तों के बीच छायांकित भाग का क्षेत्रफल (π = 3.14)

4129.png

हल

(a) बड़े वृत्त की त्रिज्या = 10 cm

अतः, बड़े वृत्त का क्षेत्रफल = πr2

= 3.14 × 10 × 10 = 314 cm2

(b) छोटे वृत्त की त्रिज्या = 4 cm

छोटे वृत्त का क्षेत्रफल = πr2

= 3.14 × 4 × 4 = 50.24 cm2

(c) छायांकित भाग का क्षेत्रफल = (314 – 50.24) cm2 = 263.76 cm2



प्रश्नावली 11.3

1. निम्न त्रिज्याओं वाले वृत्तों की परिधि ज्ञात कीजिए(π = 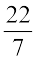5086.png लीजिए)

(a) 14 cm (b) 28 mm (c) 21 cm

2. निम्न वृत्तों का क्षेत्रफल ज्ञात कीजिए। दिया गया है :

(a) त्रिज्या = 14 mm (π = 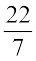5091.png लीजिए) (b) व्यास = 49 m

(c) त्रिज्या = 5 cm

3. यदि एक वृत्ताकार शीट की परिधि 154 m हो तो इसकी त्रिज्या ज्ञात कीजिए। शीट का क्षेत्रफल भी ज्ञात कीजिए। (π = 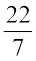5096.png लीजिए)

4. 21 m व्यास वाले एक वृत्ताकार बगीचे के चारों ओर माली बाड़ लगाना चाहता है। खरीदे जाने वाले आवश्यक रस्से की लंबाई ज्ञात कीजिए, यदि वह 2 पूरे चक्कर की बाड़ बनाना चाहता है। 4 रु प्रति मीटर की दर से रस्से पर व्यय ज्ञात कीजिए। (π = 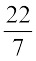5101.png लीजिए)

5. 4 cm त्रिज्या वाली एक वृत्ताकार शीट में से 3 cm त्रिज्या वाले एक वृत्त को निकाल दिया जाता है। शीट के शेष भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए)

6. साइमा 1.5 m व्यास वाले एक वृत्ताकार टेबल कवर के चारों ओर किनारी लगाना चाहती है। आवश्यक किनारी की लंबाई ज्ञात कीजिए और ₹ 15 प्रति मीटर की दर से किनारी लगाने का व्यय ज्ञात कीजिए । (π = 3.14 लीजिए)

7. दी गई आकृति, व्यास के साथ एक अर्धवृत्त है। उसका परिमाप ज्ञात कीजिए।

8. 15 रु प्रति वर्ग मीटर की दर से, 1.6 m व्यास वाले एक वृत्ताकार टेबल के ऊपरी सतह पर पॉलिश कराने का व्यय ज्ञात कीजिए । (π = 3.14 लीजिए)

4206.png

9. शाझली 44 cm लंबाई वाली एक तार लेती है और उसे एक वृत्त के आकार में मोड़ देती है। उस वृत्त की त्रिज्या ज्ञात कीजिए। इसका क्षेत्रफल भी ज्ञात कीजिए। यदि इसी तार को दुबारा एक वर्ग के आकार में मोड़ा जाता है, तो इसकी प्रत्येक भुजा की लंबाई क्या होगी? कौन-सी आकृति अधिक क्षेत्रफल घेरती है वृत्त या वर्ग? (π = 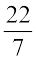5106.png लीजिए)

10. 14 cm त्रिज्या वाली एक वृत्ताकार गत्ते की शीट में से, 3.5 cm त्रिज्या वाले दो वृत्तों को और 3 cm लंबाई तथा 1 cm चौड़ाई वाले एक आयत को निकाल दिया जाता है (जैसाकि आकृति में दिखाया गया है) शीट के शेष भाग का क्षेत्रफल ज्ञात कीजिए (π = 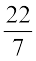5111.png लीजिए)।

11. 6 cm भुजा वाले एक वर्गाकार एल्युमिनियम शीट के टुकड़े में से 2 cm त्रिज्या वाले एक वृत्त को काट दिया जाता है। शीट के शेष भाग का क्षेत्रफल ज्ञात कीजिए? (π = 3.14 लीजिए)

4218.png
4228.png

66m

4244.png

12. एक वृत्त की परिधि 31.4 cm है। वृत्त की त्रिज्या और क्षेत्रफल ज्ञात कीजिए? (π = 3.14 लीजिए)


13. एक वृत्ताकार फूलों की क्यारी के चारों ओर 4 m चौड़ा पथ है तथा फूलों की क्यारी का व्यास 66 m है। इस पथ का क्षेत्रफल ज्ञात कीजिए? (π = 3.14 लीजिए)

14. एक वृत्ताकार फूलों के बगीचे का क्षेत्रफल 314 m2 है। बगीचे के केंद्र में एक घूमने वाला फव्वारा (sprinkler) लगाया जाता है, जो अपने चारों ओर 12 m त्रिज्या के क्षेत्रफल में पानी का छिड़काव करता है। क्या फव्वारा पूरे बगीचे में पानी का छिड़काव कर सकेगा । (π = 3.14)

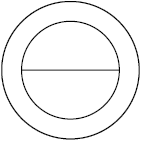
15. आकृति में, अंतः और बाह्य वृत्तों की परिधि ज्ञात कीजिए। (π = 3.14 लीजिए)

16. 28 cm त्रिज्या वाले एक पहिए को 352 m दूरी तय करने के लिए कितनी बार घुमाना पड़ेगा? (π = 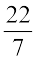5116.png लीजिए)

17. एक वृत्ताकार घड़ी की मिनट की सुई की लंबाई 15 cm है। मिनट की सुई की नोक 1 घंटे में कितनी दूरी तय करती है। (π = 3.14 लीजिए)



11.6 इकाइयों का रूपांतरण

हम जानते हैं कि 1 cm = 10 mm2। क्या आप बता सकते हैं कि 1 cm2 में कितने mm2 होते हैं? आइए हम एेसे ही प्रश्नों को खोजें और ज्ञात करें कि क्षेत्रफलों को मापते हुए इनकी इकाइयों को कैसे रूपांतरित किया जाता है। ग्राफ़ पेपर पर 1 cm भुजा वाला एक वर्ग बनाइए (आकृति 11.38)।

आप देखेंगे कि 1 cm वाले इस वर्ग को 100 वर्गों में विभाजित किया जा सकता है और प्रत्येक वर्ग की भुजा 1 mm है।

1 cm भुजा वाले वर्ग का क्षेत्रफल = 100 वर्गों का क्षेत्रफल, जिसकी प्रत्येक भुजा 1 mm है।

अतः 1 cm2 = 100 × 1 mm2 या 1 cm2 = 100 mm2

इस प्रकार, 1 m2 = 1 m × 1 m = 100 cm × 100 cm (1 m = 100 cm)

= 10000 cm2

अब क्या आप 1 km2 को m2 में बदल सकते हैं?

मिट्रिक प्रणाली में भूखंड के क्षेत्रफल को हेक्टेयर में मापा जाता है [संक्षेप में ha लिखा जाता है]

इस प्रकार, 1 हेक्टेयर = 100 × 100 m2 = 10,000 m2

जब हम क्षेत्रफल की एक इकाई को छोटी इकाई में बदलते हैं तो परिणामस्वरूप इकाइयों की संख्या अधिक होगी।

उदाहरण के लिए 1000 cm2 = 1000 × 100 mm2 = 100000 mm2

परंतु जब हम क्षेत्रफल की एक इकाई को बड़ी इकाई में बदलते हैं तो बड़ी इकाइयों की संख्य कम होगी।

4269.png


4254.png

आकृति 11.38

उदाहरण के लिए, 1000 cm2 = 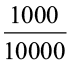5122.png m2 = 0.1 m2

27


11.7 उपयोग

आपने ध्यान दिया होगा कि बहुधा पार्कों या बगीचों में उनके चारों ओर या बीच में चौपड़ की तरह कुछ स्थान पथ के रूप में छोड़ दिया जाता है। एक फ्रेम किए हुए चित्र या पेंटिंग के चारों ओर कुछ स्थान छोड़ दिया जाता है।

हमें एेसे पथों या बार्डरों के क्षेत्रफलों को ज्ञात करने की आवश्यकता होती है, जब हम उनके बनाने का व्यय ज्ञात करना चाहते हैं।


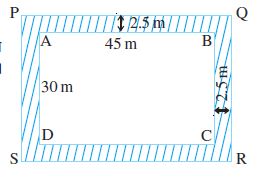
उदाहरण 20 एक आयताकार पार्क 45 m लंबा और 30 m चौड़ा है। पार्क के बाहर चारों ओर एक 2.5 m चौड़ा एक पथ बनाया गया है। पथ का क्षेत्रफल ज्ञात कीजिए।

हल माना ABCD आयताकार पार्क को और छायांकित क्षेत्र 2.5 m चौड़े पथ को दर्शाता है।

पथ के क्षेत्रफल को ज्ञात करने के लिए हमें (आयात PQRS का क्षेत्रफल - आयात ABCD का क्षेत्रफल) ज्ञात करने की आवश्यकता है।

हमें प्राप्त है PQ = (45 + 2.5 + 2.5) m = 50 m

PS = (30 + 2.5 + 2.5) m = 35 m

आयत ABCD का क्षेत्रफल = l × b = 45 × 30 m2 = 1350 m2

आयत PQRS का क्षेत्रफल = l × b = 50 × 35 m2 = 1750 m2

पथ का क्षेत्रफल = आयत PQRS का क्षेत्रफल – आयत ABCD का क्षेत्रफल

= (1750 − 1350) m2 = 400 m2

28

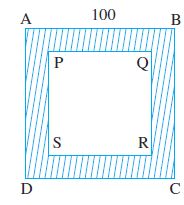
उदाहरण 21 100 m भुजा वाले एक वर्गाकार पार्क की परिसीमा के साथ लगा हुआ भीतर की ओर एक 5 m चौड़ा पथ बना हुआ है। इस पथ का क्षेत्रफल ज्ञात कीजिए। ₹ 250 प्रति 10 m2 की दर से इसे सीमेंट कराने का भी व्यय ज्ञात कीजिए।

हल माना ABCD, 100 m भुजा वाला वर्गाकार पार्क है। छायांकित भाग 5 m चौड़े पथ को दर्शाता है।

PQ = 100 – (5 + 5) = 90 m

वर्ग ABCD का क्षेत्रफल = (भुजा)2 = (100)2 m2 = 10,000 m2

वर्ग PQRS का क्षेत्रफल = (भुजा)2 = (90)2 m2 = 8100 m2

अतः, पथ का क्षेत्रफल = (10000 − 8100) m2 = 1900 m2

10 m2 पर सीमेंट कराने का व्यय = ₹ 250

इसलिए, 1 m2 पर सीमेंट कराने का व्यय = ₹ 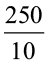5135.png

अतः, 1900 m2 पर सीमेंट कराने का व्यय = 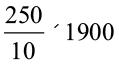5146.png= ₹ 47500


29

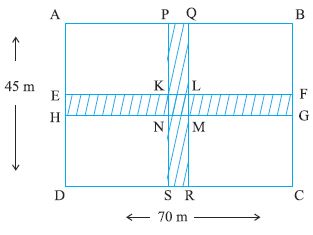
उदाहरण 22 70 m लंबाई और 45 m चौड़ाई वाले एक आयताकार पार्क के मध्य से होकर 5 m चौड़ाई के दो पथ, एक दूसरे पर लंब एेसे बने हुएे हैं जो भुजाओं के समांतर हैं। पथों का क्षेत्रफल ज्ञात कीजिए तथा ₹ 105 प्रति m2 की दर से पथों को बनाने का भी व्यय ज्ञात कीजिए।

हल पथों का क्षेत्रफल, छायांकित भाग का क्षेत्रफल ही है, अर्थात्् आयत PQRS का क्षेत्रफल और आयत EFGH का क्षेत्रफल। परंतु एेसा करते समय, वर्ग KLMN के क्षेत्रफल को दो बार लिया जाता है, जिसे घटाना होगा। अब

PQ = 5 m और PS = 45 m

EH = 5 m और EF = 70 m

KL = 5 m और KN = 5 m

पथों का क्षेत्रफल = आयत PQRS का क्षेत्रफल

+ आयत EFGH का क्षेत्रफल

– वर्ग KLMN का क्षेत्रफल

= PS × PQ + EF × EH – KL × KN

= (45 × 5 + 70 × 5 − 5 × 5) m2

= (225 + 350 − 25) मी2 = 550 m2

पथों को बनाने का व्यय = 105 × 550 = ₹ 5775

30



प्रश्नावली 11.4

1. एक बगीचा 90 m लंबा और 75 m चौड़ा है। इसके बाहर, चारों ओर एक 5 m चौड़ा पथ बनाना है। पथ का क्षेत्रफल ज्ञात कीजिए। बगीचे का क्षेत्रफल हेक्टेयर में भी ज्ञात कीजिए।

2. 125 m लंबाई और 65 m चौड़ाई वाले एक आयताकार पार्क के चारों ओर बाहर एक 3 m चौड़ा एक पथ बना हुआ है। पथ का क्षेत्रफल ज्ञात कीजिए।

3. 8 cm लंबे और 5 cm चौड़े एक गत्ते पर एक चित्र की पेटिंग इस प्रकार बनाई गई है कि इसकी प्रत्येक भुजाओं के अनुदिश 1.5 cm चौड़ा हाशिया (margin) छोड़ा गया है। हाशिये का कुल क्षेत्रफल ज्ञात कीजिए।

4. 5.5 m लंबे और 4 m चौड़े कमरे के चारों ओर बाहर 2.25 m चौड़ा एक बरामदा बनाया गया है। ज्ञात कीजिए ः

(i) बरामदे का क्षेत्रफल

(ii) ₹ 200 प्रति m2 की दर से बरामदे के फर्श पर सीमेंट कराने का व्यय।

5. 30 m भुजा वाले एक वर्गाकार बगीचे की परिसीमा से लगा भीतर की ओर 1 m चौड़ा पथ बना हुआ है। ज्ञात कीजिए ः

(i) पथ का क्षेत्रफल

(ii) ₹ 40 प्रति m2 की दर से बगीचे के शेष भाग पर घास लगवाने का व्यय।

6. 700 m लंबे और 300 m चौड़े एक आयताकार पार्क के मध्य से होकर जाते 10 m चौड़े दो पथ बने हुए हैं जो एक-दूसरे पर परस्पर लंब और चौपड़ के आकार के हैं। इनमें से प्रत्येक पथ का क्षेत्रफल ज्ञात कीजिए तथा पार्क की भुजाओं को छोड़कर पार्क के शेष भाग का भी क्षेत्रफल ज्ञात कीजिए। उत्तर को हेक्टेयर में दीजिए।

7. 90 m लंबाई और 60 m चौड़ाई वाले एक आयताकार मैदान में दो पथ बनाए गए हैं, जो भुजाओं के समांतर हैं, एक-दूसरे को लंबवत् काटते हैं और मैदान के मध्य से होकर निकलते हैं। यदि प्रत्येक पथ की चौड़ाई 3 m हो, तो ज्ञात कीजिए ः

(i) पथों द्वारा आच्छादित क्षेत्रफल

(ii) ₹ 110 प्रति m2 की दर से पथ बनाने का व्यय

8. प्रज्ञा 4 cm त्रिज्या वाले एक वृत्ताकार पाइप के चारों ओर एक रस्सी लपेटती है (जैसा दिखाया गया है) और रस्सी की आवश्यक लंबाई को काट लेती है। इसके बाद वह उसे 4 cm भुजा वाले एक वर्गाकार बॉक्स के चारों ओर लपेटती है (दिखाया गया है)। क्या उसके पास कुछ और रस्सी बचेगी? (π = 3.14)


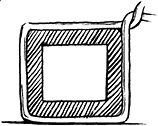
Pic6.tif
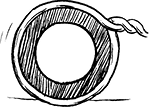
Pic7.tif

9. संलग्न आकृति, एक आयताकार पार्क के मध्य में एक वृत्ताकार फूलों की क्यारी को दर्शाती है। ज्ञात कीजिए ः

(i) पूरे पार्क का क्षेत्रफल

(ii) फूलों की क्यारी का क्षेत्रफल

(iii) फूलों की क्यारी को छोड़कर, पार्क के शेष भाग का क्षेत्रफल

(iv) क्यारी की परिधि

4495.png

10. दी गई आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए :


31


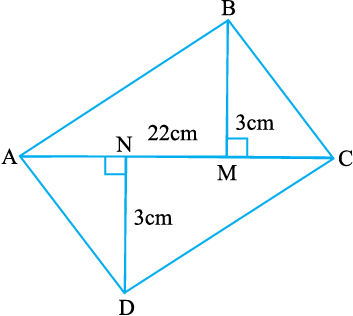
11. चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए। यहाँ
AC = 22 cm, BM = 3 cm, DN = 3 cm और
BM ⊥ AC, DN ⊥ AC

 4523.png

 

हमने क्या चर्चा की?

1. परिमाप एक बंद आकृति के चारों ओर की दूरी है जबकि क्षेत्रफल एक बंद आकृति द्वारा घेरे गए तल के भाग या क्षेत्र को दर्शाता है।

2. हम पिछली कक्षा में जान चुके हैं कि एक वर्ग और आयत का परिमाप तथा क्षेत्रफल कैसे निकालते हैं। जैसे ः

(a) एक वर्ग का परिमाप = 4 × भुजा

(b) एक आयत का परिमाप = 2 × (लंबाई + चौड़ाई)

(c) एक वर्ग का क्षेत्रफल = भुजा × भुजा

(d) एक आयत का क्षेत्रफल = लंबाई × चौड़ाई

3. एक समांतर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई

4. एक त्रिभुज का क्षेत्रफल = 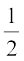5158.png (इससे प्राप्त समांतर चतुर्भुज का क्षेत्रफल)

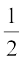= 5163.png × आधार × ऊँचाई

5. एक वृत्ताकार क्षेत्र के चारों ओर की दूरी इसकी परिधि कहलाती है। एक वृत्त की परिधि= πd, जहाँ d वृत्त का व्यास और 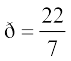5168.png या 3.14 (लगभग) है।

6. एक वृत्त का क्षेत्रफल = πr2, जहाँ r वृत्त की त्रिज्या है।

7. जैसा कि आप जानते हैं कि जिस प्रकार लंबाइयों की इकाइयों का रूपांतरण करते हैं उसी प्रकार क्षेत्रफलों की ईकाइयों को भी रूपांतरित किया जा सकता है।

4560.png