Table of Contents
12.1 भूमिका
हम x + 3, y – 5, 4x + 5, 10y – 5, इत्यादि जैसे सरल बीजीय व्यंजकों से परिचित हो चुके हैं । कक्षा VI में, हमने देखा था कि ये व्यंजक किस प्रकार पहेलियों और समस्याओं को एक सुव्यवस्थित प्रकार से प्रस्तुत करने में सहायक होते हैं । हम सरल समीकरणों वाले अध्याय में भी व्यंजकों के अनेक उदाहरणों को देख चुके हैं ।
बीजगणित में व्यंजकों (expressions) को एक केंद्रीय अवधारणा माना जाता है । यह अध्याय बीजीय व्यंजकों से संबद्ध होगा । जब आप इस अध्याय को पढ़ लेंगे, तो आपको ज्ञात हो जाएगा कि बीजीय व्यंजक किस प्रकार बनते हैं, इन्हें किस प्रकार संयोजित किया (मिलाया) जाता है, इनके मान हम कैसे ज्ञात कर सकते हैं तथा इनका किस प्रकार उपयोग किया जा सकता है ।
12.2 व्यंजक किस प्रकार बनते हैं ?
अब हम भली भाँति जानते हैं कि एक चर (variable) क्या होता है । हम चरों को व्यक्त करने के लिए, अक्षरों x, y, l, m, ... इत्यादि का प्रयोग करते हैं । एक चर के विभिन्न मान हो सकते हैं । इसका मान निश्चित नहीं होता है । इसके दूसरी ओर अचर (constant) का एक निश्चित मान होता है । अचरों के उदाहरण 4,100,-17, इत्यादि हैं ।
हम चरों और अचरों को संयोजित करके बीजीय व्यंजकों को बनाते हैं । इसके लिए
हम योग, व्यवकलन, गुणन और विभाजन की संक्रियाओं का प्रयोग करते हैं । हम,
4x + 5, 10y – 20 जैसे व्यंजकों को पहले ही देख चुके हैं । व्यंजक 4x + 5, ‘x’ चर के प्रयोग से बना है, जिसमें पहले चर x को अचर 4 से गुणा करके और फिर इस गुणनफल में अचर 5 जोड़ कर प्राप्त किया जाता है । इसी प्रकार, 10y – 20 पहले चर y को अचर 10 से गुणा करके और फिर इस गुणनफल में से 20 घटा कर प्राप्त किया जाता है ।
उपरोक्त व्यंजक चरों और अचरों को संयोजित करके प्राप्त किए गए थे । हम व्यंजकों को, चरों को स्वयं उन चरों से अथवा अन्य चरों से संयोजित करके भी प्राप्त कर सकते हैं ।

प्रयास कीजिए
बताइए कि निम्नलिखित व्यंजक किस प्रकार प्राप्त किए जाते हैं :
7xy + 5, x2y, 4x2 – 5x
देखिए कि निम्नलिखित व्यंजक किस प्रकार प्राप्त किए जाते हैं ?
x2, 2y2, 3x2 – 5, xy, 4xy + 7
(i) व्यंजक x2 चर x को स्वयं x से गुणा करके प्राप्त किया जाता है ।
अर्थात् x × x = x2 है ।
जिस प्रकार 4 × 4 = 42 लिखा जाता है, उसी प्रकार हम x × x = x2. लिखते हैं । इसे सामान्यतः x का वर्ग (x squared) पढ़ा जाता है ।
[बाद में, जब आप ‘घातांक और घात’ वाले अध्याय का अध्ययन करेंगे, तब आप अनुभव करेंगे कि x2 को x के ऊपर घात 2 भी पढ़ा जा सकता है]।
इसी प्रकार, हम लिख सकते हैं ः x × x × x = x3
सामान्यतः, x3 को x का घन (x cubed) पढ़ा जाता है । बाद में, आप यह अनुभव करेंगे कि x3 को x के ऊपर घात 3 भी पढ़ा जा सकता है ।
x, x2, x3, ... में से प्रत्येक x से प्राप्त एक बीजीय व्यंजक है ।
(ii) व्यंजक 2y2 को y से इस प्रकार प्राप्त किया जाता हैः 2y2 = 2 × y × y
यहाँ, हम y को y से गुणा करके y2 प्राप्त करते हैं और फिर इस गुणनफल y2 को 2 से गुणा करते हैं ।
(iii) (3x2 – 5) में, हम पहले x2 प्राप्त करते हैं और फिर उसे 3 से गुणा करके 3x2 प्राप्त करते हैं । अंत में, 3x2 – 5 पर पहुँचने के लिए, हम 3x2 में से 5 को घटाते हैं ।
(iv) xy में, हम चर x को एक अन्य चर y से गुणा करते हैं । इस प्रकार, x × y = xy।
(v) 4xy + 7 में, हम पहले xy प्राप्त करते हैं; उसे 4 से गुणा करके 4xy प्राप्त करते हैं और फिर दिया हुआ व्यंजक प्राप्त करने के लिए, 4xy में 7 जोड़ते हैं ।
12.3 एक व्यंजक के पद
अभी तक ऊपर हमने पढ़ा है कि व्यंजक किस प्रकार बनाए जाते हैं, अब हम उसे एक सुव्यवस्थित रूप में रखेंगे । इस कार्य के लिए, हमें यह जानने की आवश्यकता है कि एक व्यंजक के पद (terms) और उनके गुणनखंड (factors) क्या होते हैं, अर्थात् उनके अर्थ क्या हैं ।
व्यंजक (4x + 5) पर विचार कीजिए । इस व्यंजक को बनाने के लिए, पहले हमने अलग से 4 और x का गुणा करके 4x बनाया था और फिर इसमें 5 जोड़ दिया था । इसी प्रकार, व्यंजक (3x2 + 7y) पर विचार कीजिए । यहाँ, हमने पहले अलग से 3, x और x का गुणा करके 3x2 बनाया था। फिर हमने अलग से 7 और y का गुणा करके 7y बनाया था । 3x2 और 7y बनाने के बाद, हमने दिया हुआ व्यंजक प्राप्त करने के लिए, इनको जोड़ दिया था ।
आप पाएँगे कि हम जितने भी व्यंजकों पर कार्य करते हैं वे सभी इसी रूप में देखे जा सकते हैं । इनके भाग होते हैं जो अलग से बनाए जाते हैं और फिर जोड़ दिए जाते हैं। व्यंजकों के इस प्रकार के भाग, जो पहले अलग से बनाए जाते हैं और फिर जोड़ दिए जाते हैं, इस व्यंजक के पद कहलाते हैं । व्यंजक 4x2 – 3xy को देखिए । हम कहते हैं कि इसके दो पद 4x2 और –3xy हैं । पद 4x2 ; 4, x और x का गुणनफल है तथा पद –3xy ; –3, x और y का गुणनफल है ।
व्यंजकों को बनाने के लिए पदों को जोड़ा जाता है । जिस प्रकार व्यंजक (4x + 5) को बनाने के लिए 4x और 5 को जोड़ा जाता है, उसी प्रकार व्यंजक (4x2–3xy) को बनाने के लिए 4x2 और (– 3xy) को जोड़ा जाता है । इसका कारण 4x2 + (–3xy) = 4x2 – 3xy होता है ।
ध्यान दीजिए कि पद में ऋण (minus) चिह्न सम्मिलित होता है । व्यंजक 4x2 –3xy में, हमने पद को 3xy न लेकर (–3xy) लिया था । इसलिए, हमें यह कहने कि आवश्यकता नहीं है कि एक व्यंजक को बनाने के लिए, पदों को जोड़ा या घटाया जाता है । इसके लिए केवल यह कहना ही पर्याप्त है कि पदों को जोड़ा जाता है ।
एक पद के गुणनखंड
हमने ऊपर देखा था कि व्यंजक (4x2 – 3xy) के दो पद 4x2 और –3xy हैं । पद 4x2; 4, x और x का गुणनफल है। हम कहते हैं कि 4, x और x पद 4x2 के गुणनखंड (factors) हैं । एक पद अपने गुणनखंडों का एक गुणनफल होता है । पद –3xy, गुणनखंडों –3, x और y का एक गुणनफल है ।
हम एक व्यंजक के पदों तथा पदों के गुणनखंडों को एक सुविधाजनक और आकर्षक प्रकार से एक व्यंजक पेड़ आरेख (tree diagram) द्वारा निरूपित कर सकते हैं । व्यंजक (4x2 – 3xy) का पेड़ संलग्न आकृति में दर्शाया गया है ।
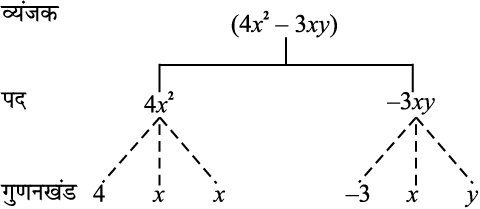
ध्यान दीजिए कि पेड़ आरेख में, हमने गुणनखंड के लिए बिंदुकित रेखाओं का प्रयोग किया तथा पदों के लिए सतत रेखाओं का प्रयोग किया है । यह इनके मिश्रित न होने के लिए किया गया है ।
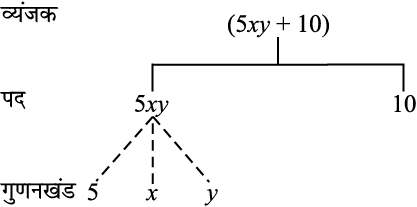
आइए व्यंजक 5xy + 10 का पेड़ आरेख खींचें । गुणनखंड एेसे लिखे जाएँ कि जिनके आगे गुणनखंड न हो सके । इस प्रकार, हम5xy को 5 × xy के रूप में नहीं लिखते हैं, क्योंकि xy के आगे और भी गुणनखंड हो सकते हैं । इसी प्रकार, यदि x3 एक पद होता, तो इसे x × x2 न लिख कर x× x × x लिखा जाए । साथ ही, याद रखिए 1 को अलग से गुणनखंड नहीं लिया जाता है ।
प्रयास कीजिए
1. निम्नलिखित व्यंजकों में कौन-कौन से पद हैं ? दर्शाइए कि ये व्यंजक कैसे बनाए जाते हैं । प्रत्येक व्यंजक के लिए एक पेड़ आरेख भी खींचिए ।
8y + 3x2, 7mn – 4, 2x2 y
2. एेसे तीन व्यंजक लिखिए, जिनमें से प्रत्येक में चार पद हों।
गुणांक
हम एक पद को उसके गुणनखंडों के एक गुणनफल के रूप में लिखना सीख चुके हैं । इनमें से एक गुणनखंड संख्यात्मक (numerical) हो सकता है तथा अन्य बीजीय (algebraic) हो सकते हैं (अर्थात्् इनमें चर होते हैं) । इस संख्यात्मक गुणनखंड को पद का संख्यात्मक गुणांक (numerical coefficient) या केवल गुणांक कहते हैं । इसे शेष पद (जो स्पष्टतः बीजीय गुणनखंडों का गुणनफल है) का गुणांक भी कहते हैं । इस प्रकार, पद 5xy में, xy का गुणांक 5 है । इसी प्रकार, पद 10xyz, में xyz का गुणांक 10 है तथा पद –7x2y2 में x2y2 का गुणांक –7 है ।
जब किसी पद का गुणांक +1 होता है, प्रायः उसे लिखते समय छोड़ दिया जाता है । उदाहरणार्थ, 1x को x लिखा जाता है, 1x2y2 को x2y2 लिखा जाता है, इत्यादि । साथ ही, गुणांक (–1) को केवल ऋण चिह्न (-) से दर्शाया जाता है । इस प्रकार, (-1)x को –x लिखा जाता है, (–1)x2y2 को –x2y2 लिखा जाता है, इत्यादि ।
कभी-कभी शब्द गुणांक का प्रयोग एक अधिक व्यापक रूप में प्रयोग किया जाता है । इस रूप में, हम कहते हैं कि पद 5xy में, xy का गुणांक 5 है, 5y का गुणांक x है तथा 5x का गुणांक y है । 10xy2 में, xy2 का गुणांक 10 है, 10y2 का गुणांक x है तथा 10x का गुणांक y2 है । इस प्रकार, इसे अधिक व्यापक रूप में, गुणांक एक संख्यात्मक गुणनखंड हो सकता है या एक बीजीय गुणनखंड हो सकता है या दो या अधिक गुणनखंडों का गुणनफल भी हो सकता है । इसे शेष गुणनखंडों के गुणनफल का गुणांक कहा जाता है ।
प्रयास कीजिए

निम्नलिखित व्यंजकों के पदों के गुणांकों की पहचान कीजिए :
4x – 3y, a + b + 5,
2y + 5, 2xy
उदाहरण 1 निम्नलिखित व्यंजकों में, वे पद छाँटिए जो अचर नहीं हैं । उनके संख्यात्मक गुणांक भी लिखिए ः
xy + 4, 13 – y2, 13 – y + 5y2, 4p2q – 3pq2 + 5
हल
उदाहरण 2
(a) निम्नलिखित व्यंजकों में x के क्या गुणांक हैं ?
4x – 3y, 8 – x + y, y2x – y, 2z – 5xz
(b) निम्नलिखित व्यंजकों में y के क्या गुणांक हैं ?
4x – 3y, 8 + yz, yz2 + 5, my + m
हल
(a) प्रत्येक व्यंजक में, हम गुणनखंड x वाले पद को देखते हैं । उस पद का शेष भाग x का वांछित गुणांक होगा ।
क्रम संख्या व्यंजक गुणनखंड x वाला पद x का गुणांक
(b) इसकी विधि उपरोक्त (a) की विधि जैसी ही है ।
क्रम संख्या व्यंजक गुणनखंड y वाला पद y का गुणांक
12.4 समान और असमान पद
जब पदों के बीजीय गुणनखंड एक जैसे ही हों, तो वे पद समान पद (like terms) कहलाते हैं। जब पदों के बीजीय गुणनखंड भिन्न-भिन्न हों, तो वे असमान पद (unlike terms) कहलाते हैं । उदाहरणार्थ व्यंजक 2xy – 3x + 5xy – 4, में पदों 2xy और 5xy को देखिए । 2xy के गुणनखंड 2, x और y है । 5xy के गुणनखंड 5, x और y हैं । इस प्रकार, इनके बीजीय (अर्थात् वे जिनमें चर हैं) गुणनखंड एक ही हैं और इसीलिए ये समान पद हैं । इसके विपरीत, पदों 2xy और –3x में भिन्न-भिन्न बीजीय गुणनखंड हैं । ये असमान पद हैं । इसी प्रकार, पद 2xy और 4 असमान पद हैं । साथ ही, –3x और 4 भी असमान पद हैं ।
प्रयास कीजिए
निम्नलिखित में, समान पदों के समूह बनाइए :
12x, 12, – 25x, – 25, – 25y, 1, x, 12y, y
12.5 एकपदी, द्विपद, त्रिपद और बहुपद
वह बीजीय व्यंजक जिसमें केवल एक पद हो, एकपदी (monomial) कहलाता है, जैसे 7xy, – 5m, 3z2, 4 इत्यादि ।
एक व्यंजक जिसमें केवल दो पद हों और वे असमान पद हों वह द्विपद (binomial) कहलाता है, उदाहरणार्थ x + y, m – 5, mn + 4m, a2 – b2 द्विपद हैं । व्यंजक 10pq एक द्विपद नहीं है यह एक एकपदी है । व्यंजक (a + b + 5) एक द्विपद नहीं है । इसमें तीन पद हैं ।
प्रयास कीजिए
निम्नलिखित व्यंजकों को एकपदी, द्विपद और त्रिपद के रूप में वर्गीकृत कीजिए: a, a + b, ab + a + b, ab +
a + b – 5, xy, xy + 5,
5x2 – x + 2, 4pq – 3q + 5p, 7, 4m – 7n + 10, 4mn + 7.
एक व्यंजक जिसमें तीन पद हों, एक त्रिपद (trinomial) कहलाता है,
उदाहरणार्थ x + y + 7, ab + a +b, 3x2 – 5x + 2, m + n + 10 त्रिपद हैं । परंतु व्यंजक ab + a + b + 5 एक त्रिपद नहीं है इसमें तीन पद न होकर चार पद हैं । व्यंजक x + y + 5x एक त्रिपद नहीं है क्योंकि पद x और 5xसमान पद हैं ।
व्यापक रूप में, एक या, अधिक पदों वाला व्यंजक एक बहुपद (Polynomial) कहलाता है । इस प्रकार, एकपदी, द्विपदी और त्रिपदी भी बहुपद हैं ।
उदाहरण 3 कारण सहित बताइए कि पदों के निम्नलिखित युग्मों में कौन-कौन से युग्म समान पदों के हैं तथा कौन-कौन से युग्म असमान पदों के हैं :
(i) 7x, 12y (ii) 15x, –21x (iii) – 4ab, 7ba (iv) 3xy, 3x
(v) 6xy2, 9x2y (vi) pq2, – 4pq2 (vii) mn2, 10mn
हल
निम्नलिखित सरल चरण आपको यह निर्णय लेने में सहायक होंगे कि दिए हुए पद समान पद हैं या असमान पद हैं :
(i) संख्यात्मक गुणांकों पर ध्यान न दीजिए । पदों के बीजीय भाग पर अपना ध्यान केंद्रित कीजिए ।
(ii) पदों में चरों की जाँच कीजिए । ये एक ही होने चाहिए ।
(iii) अब, पदों में प्रत्येक चर की घातों की जाँच कीजिए । ये एक ही होनी चाहिए ।
ध्यान दीजिए कि समान पदों के बारे मे निर्णय लेते समय, इन दो बातों से कोई प्रभाव नहीं पड़ता है : (1) पदों के संख्यात्मक गुणांक तथा (2) पदों में चरों के गुणा करने का क्रम ।
प्रश्नावली 12.1
1. निम्नलिखित स्थितियों में, चरों, अचरों और अंक गणितीय संक्रियाओं का प्रयोग करते हुए, बीजीय व्यंजक प्राप्त कीजिए :
(i) संख्या y में से z को घटाना।
(ii) संख्याओं x और y के योग का आधा ।
(iii) संख्या z को स्वयं उससे गुणा किया जाता है ।
(iv) संख्याओं p और q के गुणनफल का एक-चौथाई ।
(v) दोनों संख्याओं x और y के वर्गों को जोड़ा जाता है ।
(vi) संख्याओं m और n के गुणनफल के तीन गुने में संख्या 5 जोड़ना ।
(vii) 10 में से संख्याओं y और z गुणनफल को घटाना ।
(viii) संख्याओं a और b के गुणनफल में से उनके योग को घटाना ।
2. (i) निम्नलिखित व्यंजकों में पदों ओर उनके गुणनखंडों को छाँटिए । पदों और उनके गुणनखंडों को पेड़ आरेखों द्वारा भी दर्शाइए ।
(a) x – 3 (b) 1 + x + x2 (c) y – y3
(d) 5xy2 + 7x2y (e) – ab + 2b2 – 3a2
(ii) नीचे दिए व्यंजकों में, पदों और उनके गुणनखंडों को छाँटिए ।
(a) – 4x + 5 (b) – 4x + 5y (c) 5y + 3y2
(d) xy + 2x2y2 (e) pq + q (f) 1.2 ab – 2.4 b + 3.6 a
(g)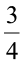 x +
x +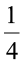 (h) 0.1 p2 + 0.2 q2
(h) 0.1 p2 + 0.2 q2
3. निम्नलिखित व्यंजकों में पदों के संख्यात्मक गुणांकों, जो अचर न हों, की पहचान कीजिए।
(i) 5 – 3t2 (ii) 1 + t + t2 + t3 (iii) x + 2xy + 3y
(iv) 100m + 1000n (v) – p2q2 + 7pq (vi) 1.2 a + 0.8 b
(vii) 3.14 r2 (viii) 2 (l + b) (ix) 0.1 y + 0.01 y2
4. (a) वे पद पहचानिए जिनमें x है और फिर इनमें x का गुणांक लिखिए ।
(i) y2x + y (ii) 13y2 – 8yx (iii) x + y + 2
(iv) 5 + z + zx (v) 1 + x + xy (vi) 12xy2 + 25
(vii) 7 + xy2
(b) वे पद पहचानिए जिनमें y2 है और फिर इनमें y2 का गुणांक लिखिए ।
(i) 8 – xy2 (ii) 5y2 + 7x (iii) 2x2y – 15xy2 + 7y2
5. निम्नलिखित व्यंजकों को एकपदी, द्विपद और त्रिपद के रूप में वर्गीकृत कीजिए ः
(i) 4y – 7z (ii) y2 (iii) x + y – xy (iv) 100
(v) ab – a – b (vi) 5 – 3t (vii) 4p2q – 4pq2 (viii) 7mn
(ix) z2 – 3z + 8 (x) a2 + b2 (xi) z2 + z (xii) 1 + x + x2
6. बताइए कि दिए हुए पदों के युग्म समान पदों के हैं या असमान पदों के हैं ः
(i) 1, 100 (ii) –7x,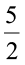 x (iii) – 29x, – 29y
x (iii) – 29x, – 29y
(iv) 14xy, 42yx (v) 4m2p, 4mp2 (vi) 12xz, 12x2z2
7. निम्नलिखित में समान पदों को छाँटिए ः
(a) – xy2, – 4yx2, 8x2, 2xy2, 7y, – 11x2, – 100x, – 11yx, 20x2y,– 6x2, y, 2xy, 3x
(b) 10pq, 7p, 8q, – p2q2, – 7qp, – 100q, – 23, 12q2p2, – 5p2, 41, 2405p, 78qp, 13p2q, qp2, 701p2
12.6 बीजीय व्यंजकों के योग और व्यवकलन
निम्नलिखित समस्याओं पर विचार कीजिए :
1. सरिता के पास कुछ कँचे हैं । अमीना के पास उससे 10 कँचे अधिक हैं । अप्पू कहता है कि उसके पास सरिता और अमीना के पास कुल जितने कँचे हैं उससे 3 अधिक कँचे हैं । आप अप्पू के कँचों की संख्या कैसे ज्ञात करेंगे ?
चूँकि यह नहीं दिया गया है कि सरिता के पास कितने कँचे है, इसलिए हम इन्हें x मान लेते हैं । अमीना के पास इनसे 10 अधिक, अर्थात् x + 10 कँचे हैं । अप्पू कहता है कि उसके पास सरिता और अमीना के कुल कँचों से 3 अधिक कँचे हैं । अतः हम सरिता और अमीना के कँचों का योग ज्ञात करते हैं और उस योग में 3 जोड़ते हैं, अर्थात् हम x, x + 10 और 3 को जोड़ते हैं।
2. रामू के पिता की वर्तमान आयु रामू की आयु की तीन गुनी है । रामू के दादाजी की आयु रामू और रामू के पिता की आयु के योग से 13 वर्ष अधिक है । आप रामू के दादाजी की आयु किस प्रकार ज्ञात करेंगे ?
चूँकि रामू की आयु दी हुई नहीं है, इसलिए आइए इसे y वर्ष मान लें । तब, उसके पिता की आयु 3y वर्ष है । रामू के दादाजी की आयु ज्ञात करने के लिए, हमें रामू की आयु (y) और उसके पिता की आयु (3y) का योग ज्ञात करके इस योग में 13 जोड़ना होगा, अर्थात् हमें y, 3y और 13 का योग ज्ञात करना पड़ेगा ।
3. एक बाग में, गुलाब और गेंदे के पौधे वर्गाकार क्यारियों में लगाए जाते हैं । जिस वर्गाकार क्यारी में गेंदे के फूल लगाए जाते हैं उसकी भुजा की लंबाई उस वर्गाकार क्यारी की भुजा की लंबाई से 3 मीटर अधिक है, जिसमें गुलाब के पौधे लगाए गए हैं । गेंदे की क्यारी गुलाब की क्यारी से क्षेत्रफल में कितनी बड़ी है ?
आइए गुलाब की क्यारी की भुजा को l मीटर मान लेते हैं । तब गेंदे की क्यारी की भुजा (l + 3) मीटर होगी । इनके क्षेत्रफल (वर्ग मीटर में) क्रमशः l2 और (l + 3)2 होंगे । इन दोनों का अंतर ही यह बताएगा कि गेंदे के पौधों वाली क्यारी गुलाबों वाली क्यारी से क्षेत्रफल में कितनी बड़ी है ।
उपरोक्त तीनों स्थितियों में, हमें बीजीय व्यंजकों को जोड़ना या घटाना पड़ा था । दैनिक जीवन में, इसी प्रकार की अनेक एेसी स्थितियाँ हमारे सम्मुख आती हैं, जहाँ हमें बीजीय व्यंजकों का प्रयोग करना पड़ता है तथा उन पर अंकगणितीय संक्रियाएँ करनी पड़ती हैं। इस अनुच्छेद में, हम यह देखेंगे कि बीजीय व्यंजकों को किस प्रकार जोड़ा और घटाया जाता है ।
कम से कम एेसी दो स्थितियों के बारे मे सोचिए जिनमें से प्रत्येक में आपको दो बीजीय व्यंजकों को बनाने की आवश्यकता पड़े और उन्हें जोड़ना या घटाना पड़े ।
समान पदों का जोड़ना और घटाना
सरलतम व्यंजक एकपदी होते हैं । इनमें केवल एक ही पद होता है । प्रारंभ करने के लिए, हम यह सीखेंगे कि समान पदों को किस प्रकार जोड़ा या घटाया जाता है ।
आइए 3x और 4x. को जोड़ें । हम जानते हैं कि x एक संख्या है
तथा इसीलिए 3x और 4x भी संख्याएँ हैं ।.
अब, 3x + 4x = (3 × x) + (4 × x)
= (3 + 4) × x वितरण या बंटन गुण के प्रयोग से
= 7 × x = 7x
या 3x + 4x = 7x
आइए अब आगे 8xy, 4xy और 2xy को जोड़ें ।
8xy + 4xy + 2xy = (8 × xy) + (4 × xy) + (2 × xy)
= (8 + 4 + 2) × xy
= 14 × xy = 14xy
या 8xy + 4xy + 2xy = 14 xy
आइए 7n में से 4n को घटाएँ ।
7n – 4n = (7 × n) – (4 × n)
= (7 – 4) × n = 3 × n = 3n
या 7n – 4n = 3n
इसी प्रकार, 11ab में से 5ab को घटाइए ।
11ab – 5ab = (11 – 5) ab = 6ab
इसी प्रकार, दो या अधिक समान पदों का योग एक समान पद होता है, जिसका संख्यात्मक गुणांक सभी समान पदों के गुणांकों के योग के बराबर होता है ।
चूँकि चर, संख्याएँ ही हैं, इसलिए हम वितरण गुण का प्रयोग कर सकते हैं।
इसी प्रकार, दो समान पदों का अंतर एक समान पद होता है, जिसका संख्यात्मक गुणांक दोनों समान पदों के संख्यात्मक गुणांकों के अंतर के बराबर होता है ।
ध्यान दीजिए कि असमान पदों को उस प्रकार जोड़ा या घटाया नहीं जा सकता, जिस प्रकार कि समान पदों को जोड़ या घटा लिया जाता है । इसके उदाहरण हम पहले ही देख चुके हैं । जब x में 5 को जोड़ा जाता है, तो हम इस परिणाम को (x + 5) लिखते हैं । ध्यान दीजिए कि (x + 5) में 5 और x दोनों ही पद पहले जैसे ही हैं । इसी प्रकार, यदि हम असमान पदों 3xy और 7 को जोड़े, तो योग 3xy + 7 है ।
यदि हम 3xy में से 7 घटाएँ, तो परिणाम 3xy – 7 है ।
व्यापक बीजीय व्यंजकों क जोड़ना और घटाना
आइए कुछ उदाहरण लें
3x + 11 और 7x – 5 को जोड़िए ।
वांछित योग = 3x + 11 + 7x – 5
अब, हम जानते हैं कि पद 3x और 7x समान पद हैं तथा 11 और – 5 भी समान पद हैं ।
साथ ही, 3x + 7x = 10 x और 11 + (– 5) = 6 हैं । अतः, हम उपरोक्त योग को नीचे दिए अनुसार सरल कर सकते हैंः
योग = 3x + 11 + 7x – 5
= 3x + 7x + 11 – 5 (पदों को पुनर्व्यवस्थित करने पर)
= 10x + 6
अतः, 3x + 11 + 7x – 5 = 10x + 6
3x + 11 + 8z और 7x – 5 को जोड़िए ।
योग = 3x + 11 + 8z + 7x – 5
= 3x + 7x + 11 – 5 + 8z (पदों को पुनर्व्यवस्थित करने पर)
ध्यान दीजिए कि हमने समान पदों को एक साथ रखा है तथा अकेला असमान पद 8z उसी प्रकार रहता है ।
अतः, योग = 10x + 6 + 8z
3a – b + 4 में से a – b को घटाइए ।
अंतर = 3a – b + 4 – (a – b)
= 3a – b + 4 – a + b
ध्यान दीजिए कि किस प्रकार हमने a – b को कोष्ठकों में रखा। तथा किस प्रकार कोष्ठकों को खोलते समय चिह्नों का ध्यान रखा है समान पदों को एक साथ रखने के लिए, पदों को पुनर्व्यवस्थित करने पर,
अंतर = 3a – a – b + b + 4
= (3 – 1) a – (1 – 1) b + 4
अंतर = 2a + (0) b + 4 = 2a + 4
या, 3a – b + 4 – (a – b) = 2a + 4
अब, हम अभ्यास के लिए, व्यंजकों के योग और व्यवकलन पर कुछ और उदाहरण हल करेंगे ।
उदाहरण 4 समान पदों को एकत्रित करके, व्यंजक
12m2 – 9m + 5m – 4m2 – 7m + 10 को सरल कीजिए :
ध्यान दीजिएः
जैसे –(5 – 3)= –5 + 3 है, उसी प्रकार – (a – b) = – a + b है। बीजीय पदों के चिह्नों पर उसी प्रकार कार्य किया जाता है, जैसाकि संख्याओं के चिह्नों के साथ किया जाता है।
हल पदों को पुनर्व्यवस्थित करने पर, हमें प्राप्त होता हैः
12m2 – 4m2 + 5m – 9m – 7m + 10
= (12 – 4) m2 + (5 – 9 – 7) m + 10
= 8m2 + (– 4 – 7) m + 10
= 8m2 + (–11) m + 10
= 8m2 – 11m + 10
उदाहरण 5 30ab + 12b + 14a में से 24ab – 10b – 18a को घटाइए ।
हल 30ab + 12b + 14a – (24ab – 10b – 18a)
= 30ab + 12b + 14a – 24ab + 10b + 18a
= 30ab – 24ab + 12b + 10b + 14a + 18a
= 6ab + 22b + 32a
वैकल्पिक रूप से, हम व्यंजकों को एक के नीचे एक करके इस प्रकार रखते हैं कि समान पद एक ही सीध, अर्थात् स्तंभों में रहें, जैसा नीचे दर्शाया गया हैः
प्रयास कीजिए
जोड़िए और घटाइएः
(i) m – n, m + n
(ii) mn + 5 – 2, mn + 3
ध्यान दीजिए कि एक पद घटाने का अर्थ है कि उसके योज्य प्रतिलोम को जोड़ना। अतः,–10b घटाने का अर्थ है कि +10b जोड़ना, –18a घटाने का अर्थ है कि +18a जोड़ना तथा 24ab घटाने का अर्थ है कि – 24ab को जोड़ना। घटाए जाने वाले व्यंजक के नीचे दर्शाए गए चिह्न, घटाने की प्रक्रिया को उचित रूप से करने में सहायक होते हैं।
30ab + 12b + 14a
24ab – 10b – 18a
– + +
6ab + 22b + 32a
उदाहरण 6 2y2 + 3yz, – y2 – yz – z2 और yz + 2z2 के योग में से 3y2 – z2 और –y2 + yz + z2 के योग को घटाइए ।
हल पहले हम 2y2 + 3yz, – y2 – yz – z2 और yz + 2z2 को जोड़ते हैं ।
2y2 + 3yz
– y2 – yz – z2
+ yz + 2z2
y2 + 3yz + z2 (1)
फिर हम, 3y2 – z2 और –y2 + yz + z2 को जोड़ते हैं ।
3y2 – z2
– y2 + yz + z2
2y2 + yz (2)
अब हम योग (1) में से योग (2) को घटाते हैं ।
y2 + 3yz + z2
2y2 + yz
– –
– y2 + 2yz + z2
प्रश्नावली 12.2
1. समान पदों को संयोजित (मिला) करके सरल कीजिए :
(i) 21b – 32 + 7b – 20b
(ii) – z2 + 13z2 – 5z + 7z3 – 15z
(iii) p – (p – q) – q – (q – p)
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
(v) 5x2y – 5x2 + 3yx2 – 3y2 + x2 – y2 + 8xy2 – 3y2
(vi) (3y2 + 5y – 4) – (8y – y2 – 4)
2. जोड़िए :
(i) 3mn, – 5mn, 8mn, – 4mn
(ii) t – 8tz, 3tz – z, z – t
(iii) – 7mn + 5, 12mn + 2, 9mn – 8, – 2mn – 3
(iv) a + b – 3, b – a + 3, a – b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
(vii) 4x2y, – 3xy2, –5xy2, 5x2y
(viii) 3p2q2 – 4pq + 5, – 10 p2q2, 15 + 9pq + 7p2q2
(ix) ab – 4a, 4b – ab, 4a – 4b
(x) x2 – y2 – 1, y2 – 1 – x2, 1 – x2 – y2
3. घटाइए :
(i) y2 में से –5y2
(ii) –12xy में से 6xy
(iii) (a + b) में से (a – b)
(iv) b (5 – a) में से a (b – 5)
(v) 4m2 – 3mn + 8 में से –m2 + 5mn
(vi) 5x – 10 में से – x2 + 10x – 5
(vii) 3ab – 2a2 – 2b2 में से 5a2 – 7ab + 5b2
(viii) 5p2 + 3q2 – pq में से 4pq – 5q2 – 3p2
4. (a) 2x2 + 3xy प्राप्त करने के लिए, x2 + xy + y2 में क्या जोड़ना चाहिए ?
(b) – 3a + 7b + 16 प्राप्त करने के लिए, 2a + 8b + 10 में से क्या घटाना चाहिए ?
5. – x2 – y2 + 6xy + 20 प्राप्त करने के लिए, 3x2 – 4y2 + 5xy + 20 में क्या निकाल लेना चाहिए ?
6. (a) 3x – y + 11 और – y – 11 के योग में से 3x – y – 11 को घटाइए ।
(b) 4 + 3x और 5 – 4x + 2x2 के योग में से 3x2 – 5x और –x2 + 2x + 5 के योग को घटाइए ।
12.7 किसी व्यंजक का मान ज्ञात करना
हम जानते हैं कि एक बीजीय व्यंजक का मान उस व्यंजक को बनाने वाले चरों के मानों पर निर्भर करता है । एेसी अनेक स्थितियाँ हैं, जहाँ हमें व्यंजकों के मान ज्ञात करने होते हैं, जैसे कि हम यह जाँच करना चाहते हैं कि चर का एक विशेष मान एक दिए हुए समीकरण को संतुष्ट करता है या नहीं ।
जब हम ज्यामिति और प्रतिदिन की गणित के सूत्रों का प्रयोग करते हैं, तो भी हम व्यंजकों के मान ज्ञात करते हैं । उदाहरणार्थ, भुजा l वाले वर्ग का क्षेत्रफल l2 होता है । यदि l = 5 cm है, तो क्षेत्रफल 52 cm2 = 25 cm2 है । यदि भुजा = 10 cm है, तो क्षेत्रफल 102 cm2 या 100 cm2 है, इत्यादि । एेसे कुछ और उदाहरणों को हम अगले अनुच्छेद में देखेंगे ।
उदाहरण 7 निम्नलिखित व्यंजकों के मान x = 2 के लिए ज्ञात कीजिए :
(i) x + 4 (ii) 4x – 3 (iii) 19 – 5x2
(iv) 100 – 10x3
हल
(i) x + 4 में, x = 2 रखने पर, हमें x + 4 का निम्नलिखित मान प्राप्त होता हैः
x + 4 = 2 + 4 = 6
(ii) 4x – 3 में, x = 2 रखने पर, हमें प्राप्त होता हैः
4x – 3 = (4 × 2) – 3 = 8 – 3 = 5
(iii) 19 – 5x2 में, x = 2 रखने पर, हमें प्राप्त होता हैः
19 – 5x2 = 19 – (5 × 22) = 19 – (5 × 4) = 19 – 20 = – 1
(v) 100 – 10x3 में, x = 2 रखने पर, हमें प्राप्त होता है ः
100 – 10x3 = 100 – (10 × 23) = 100 – (10 × 8) [ध्यान दीजिए कि 23 = 8 है]
= 100 – 80 = 20
उदाहरण 8 निम्नलिखित व्यंजकों के मान ज्ञात कीजिए, जब n = – 2
(i) 5n – 2 (ii) 5n2 + 5n – 2 (iii) n3 + 5n2 + 5n – 2 है :
हल
(i) 5n – 2 में, n = –2 रखने पर, हमें प्राप्त होता हैः
5(– 2) – 2 = – 10 – 2 = – 12
(ii) 5n2 + 5n – 2 में n = –2 के लिए, 5n – 2 = –12 है,
और, 5n2 = 5 × (– 2)2 = 5 × 4 = 20 [चूँकि (– 2)2 = 4]
दोनों को मिलाने पर, हमें प्राप्त होता है ः
5n2 + 5n – 2 = 20 – 12 = 8
(iii) अब, n = – 2 के लिए
5n2 + 5n – 2 = 8 है तथा
n3 = (–2)3 = (–2) × (–2) × (–2) = – 8 है।
दोनों के मिलाने पर,
n3 + 5n2 + 5n – 2 = – 8 + 8 = 0
अब हम दो चरों के व्यंजकों, जैसे x + y, xy इत्यादि पर विचार करेंगे । दो चरों वाले एक व्यंजक का संख्यात्मक मान ज्ञात करने के लिए, हमें इसमें दोनों चरों के मान रखने की आवश्यकता होती है । उदाहरणार्थ, x = 3 और y = 5 के लिए (x + y) का मान
3 + 5 = 8 है ।
उदाहरण 9 a = 3 और b = 2 के लिए, निम्नलिखित व्यंजकों के मान ज्ञात कीजिएः
(i) a + b (ii) 7a – 4b (iii) a2 + 2ab + b2
(iv) a3 – b3
हल दिए हुए व्यंजकों में, a = 3 और b = 2 रखने पर, हमें प्राप्त होता है ः
(i) a + b = 3 + 2 = 5
(ii) 7a – 4b = 7 × 3 – 4 × 2 = 21 – 8 = 13.
(iii) a2 + 2ab + b2 = 32 + 2 × 3 × 2 + 22 = 9 + 12 + 4 = 25
(iv) a3 – b3 = 33 – 23 = 3 × 3 × 3 – 2 × 2 × 2 = 9 × 3 – 4 × 2 = 27 – 8 = 19
प्रश्नावली 12.3
1. यदि m = 2 है, तो निम्नलिखित के मान ज्ञात कीजिए :
(i) m – 2 (ii) 3m – 5 (iii) 9 – 5m
(iv) 3m2 – 2m – 7 (v)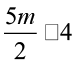
2. यदि p = – 2 है, तो निम्नलिखित के मान ज्ञात कीजिए :
(i) 4p + 7 (ii) – 3p2 + 4p + 7 (iii) – 2p3 – 3p2 + 4p + 7
3. निम्नलिखित व्यंजकों के मान ज्ञात कीजिए, जब x = –1 है :
(i) 2x – 7 (ii) – x + 2 (iii) x2 + 2x + 1
(iv) 2x2 – x – 2
4. यदि a = 2 और b = – 2 है, तो निम्नलिखित के मान ज्ञात कीजिए :
(i) a2 + b2 (ii) a2 + ab + b2 (iii) a2 – b2
5. जब a = 0 और b = – 1 है, तो दिए हुए व्यंजकों के मान ज्ञात कीजिए :
(i) 2a + 2b (ii) 2a2 + b2 + 1 (iii) 2a2b + 2ab2 + ab
(iv) a2 + ab + 2
6. इन व्यंजकों को सरल कीजिए तथा इनके मान ज्ञात कीजिए, जब x का मान 2 है :
(i) x + 7 + 4 (x – 5) (ii) 3 (x + 2) + 5x – 7
(iii) 6x + 5 (x – 2) (iv) 4(2x – 1) + 3x + 11
7. इन व्यंजकों को सरल कीजिए तथा इनके मान ज्ञात कीजिए, जब x = 3, a = – 1और
b = – 2 हैः
(i) 3x – 5 – x + 9 (ii) 2 – 8x + 4x + 4
(iii) 3a + 5 – 8a + 1 (iv) 10 – 3b – 4 – 5b
(v) 2a – 2b – 4 – 5 + a
8. (i) यदि z = 10 है, तो z3 – 3(z – 10) का मान ज्ञात कीजिए :
(ii) यदि p = – 10 है, तो p2 – 2p – 100 का मान ज्ञात कीजिए ।
9. यदि x = 0 पर 2x2 + x – a का मान 5 के बराबर है, तो a का मान क्या होना चाहिए ?
10. व्यंजक 2(a2 + ab) + 3 – ab को सरल कीजिए और इसका मान ज्ञात कीजिए, जब a = 5 और b = – 3 है ।
12.8 बीजीय व्यंजकों के प्रयोग–सूत्र और नियम
हम पहले भी देख चुके हैं कि गणित में सूत्रों (formulas) और नियम (rules) को संक्षिप्त और व्यापक रूप में, बीजीय व्यंजकों का प्रयोग करके लिखा जा सकता है । हम नीचे अनेक उदाहरण देखेंगे ः
परिमाप सूत्र
1. एक समबाहु त्रिभुज का परिमाप = 3 × उसकी भुजा की लंबाई होता है । यदि इस समबाहु त्रिभुज की भुजा की लंबाई को l से व्यक्त करें, तो उसका परिमाप = 3l का होगा ।
2. इसी प्रकार, एक वर्ग का परिमाप = 4l होता है, जहाँ l वर्ग की भुजा की लम्बाई है ।
3. एक सम पंचभुज (regular pentagon) का परिमाप = 5l होता है, जहाँ l उसकी भुजा की लंबाई है, इत्यादि ।
क्षेत्रफल सूत्र
1. यदि हम एक वर्ग की भुजा को l से व्यक्त करें, तो वर्ग का क्षेत्रफल = l2 होता है ।
2. यदि हम एक आयत की लंबाई और चौड़ाई को क्रमशः l और b से व्यक्त करें, तो आयत का क्षेत्रफल = l × b = lb होता है ।
3. इसी प्रकार, यदि एक त्रिभुज का आधार b और ऊचांई h है, तो त्रिभुज का क्षेत्रफल =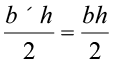 होता है ।
होता है ।
एक बार किसी दी हुई राशि के लिए सूत्र, अर्थात्् बीजीय व्यंजक ज्ञात हो जाए, तो उस राशि का मान वांछित प्रतिबंधों के अंतर्गत परिकलित किया जा सकता है ।
उदाहरणार्थ, लंबाई 3 cm की भुजा वाले एक दिए हुए वर्ग का परिमाप, वर्ग के परिमाप के व्यंजक, अर्थात्् 4l में l= 3 cm रखने पर प्राप्त किया जाता है ।
दिए हुए वर्ग का परिमाप = (4 × 3) cm = 12 cm
इसी प्रकार, इस वर्ग का क्षेत्रफल, वर्ग के क्षेत्रफल के व्यंजक, अर्थात्् l2 में l = 3 cm रख कर प्राप्त किया जाता है ।
दिए हुए वर्ग का क्षेत्रफल = (3)2 cm2 = 9 cm2
संख्या प्रतिरूपों (Patterns) के लिए नियम
निम्नलिखित कथनों का अध्ययन कीजिए :
1. यदि किसी प्राकृत संख्या को n से व्यक्त किया जाए तो उसका परवर्ती (successor) (n + 1) होता है । हम इसकी जाँच किसी भी प्राकृत संख्या के लिए कर सकते हैं । उदाहरणार्थ, यदि प्राकृत संख्या 10 है, तो उसका परिवर्ती 10 + 1 = 11 है, जो सर्वविदित है (ज्ञात है) ।
2. यदि किसी प्राकृत संख्या को n से व्यक्त किया जाए, तो 2n एक सम संख्या होती है तथा (2n + 1) एक विषम संख्या होती है । आइए इसकी जाँच कोई भी प्राकृत संख्या, माना 15 लेकर करें । अब, 2n = 2 ×15 = 30 है, जो वास्तव में एक सम संख्या है तथा 2n + 1 = 2 × 15 + 1 = 30 + 1 = 31 है, जो वास्तव में एक विषम संख्या है ।
माचिस की तीलियों, दाँत साफ़ करने की सीकों या सरकंडों के बराबर लंबाई के टुकड़ों के छोटे रेखाखंडों को लीजिए । उन्हें आकृतियों में दर्शाए अनुसार प्रतिरूपों (patterns) में जोड़िए ः
1. आकृति 12.1 में बने पैटर्न को देखिए ।
इसमें चार रेखाओं से बने आकार की पुनरावृत्ति हो रही हैै । जैसा कि आप देख सकते हैं कि एक आकार को बनाने के लिए चार रेखाखंडों की आवश्यकता होती है, दो आकारों के लिए 7, तीन आकारों के लिए 10, इत्यादि रेखाखंडों की आवश्यकता होती है । यदि आकारों की संख्या n हो, तो उन्हें बनाने के लिए आवश्यक रेखाखंडों की संख्या
की पुनरावृत्ति हो रही हैै । जैसा कि आप देख सकते हैं कि एक आकार को बनाने के लिए चार रेखाखंडों की आवश्यकता होती है, दो आकारों के लिए 7, तीन आकारों के लिए 10, इत्यादि रेखाखंडों की आवश्यकता होती है । यदि आकारों की संख्या n हो, तो उन्हें बनाने के लिए आवश्यक रेखाखंडों की संख्या
(3n + 1) होगी । आप इसकी सत्यता की जाँच n = 1, 2, 3,...,10,... इत्यादि लेकर कर सकते हैं । यदि बनाए गए आकारों की संख्या 3 है, तो आवश्यक रेखाखंडों की संख्या 3 × 3 + 1= 10 होती, जैसाकि आकृति से भी देखा जासकता है ।
2. अब आकृति 12.2 में दिए पैटर्न पर विचार कीजिए । यहाँ आकार  की पुनरावृत्ति हो रही है । आकारों 1,2,3, ... को बनाने के लिए आवश्यक रेखाखंडों की संख्याएँ क्रमशः 3,5,7,9,.... हैं । क्रमशः यदि n बनाए गए आकारों की संख्या को व्यक्त करता है तो आवश्यक रेखाखंडों की संख्या व्यंजक (2n + 1) से प्राप्त होगी । व्यंजक सही है या नहीं, की जाँच आप n के किसी भी मान को लेकर कर सकते हैं । उदाहरणार्थ, n = 4 लेने पर, वांछित रेखाखंडों की संख्या, 2n + 1 = (2 × 4) + 1 = 9, होगी, जो वास्तव में 4
की पुनरावृत्ति हो रही है । आकारों 1,2,3, ... को बनाने के लिए आवश्यक रेखाखंडों की संख्याएँ क्रमशः 3,5,7,9,.... हैं । क्रमशः यदि n बनाए गए आकारों की संख्या को व्यक्त करता है तो आवश्यक रेखाखंडों की संख्या व्यंजक (2n + 1) से प्राप्त होगी । व्यंजक सही है या नहीं, की जाँच आप n के किसी भी मान को लेकर कर सकते हैं । उदाहरणार्थ, n = 4 लेने पर, वांछित रेखाखंडों की संख्या, 2n + 1 = (2 × 4) + 1 = 9, होगी, जो वास्तव में 4 के बनाने के लिए आवश्यक है ।
के बनाने के लिए आवश्यक है ।
आगे बढ़िए और एेसी ही और पैटर्नों की खोज कीजिए ।
आकृति में दर्शाए अनुसार, बिंदुओं (dots) के पैटर्न बनाइए । यदि आप एक आलेख कागज़ या बिंदुकित कागज़ (dot paper) लें, तो पैटर्नों को बनाना सरल रहेगा ।
देखिए कि किस प्रकार बिंदुओं को एक वर्ग के आकार में व्यवस्थित किया गया है । यदि किसी विशिष्ट आकार में एक पंक्ति या एक स्तंभ में बिंदुओं की संख्या चर n लेते हैं, तो आकार में कुल बिंदुओं की संख्या व्यंजक n × n = n2 से प्राप्त होगी । उदाहरणार्थ n = 4 लीजिए । उस आकार के लिए जिसकी प्रत्येक पंक्ति (या प्रत्येक स्तंभ) में 4 बिंदु हैं, तब कुल बिंदुओं की संख्या4 × 4 = 16 होगी, जिसे वास्तव में आकृति से देखा जा सकता है । आप इसी प्रकार की जाँच n के अन्य मान लेकर भी कर सकते हैं । प्राचीन यूनानी गणितज्ञों ने इन संख्याओं 1, 4, 9, 16, ...... को वर्ग संख्याओं (square numbers) से नामांकित किया।
कुछ और संख्या पैटर्न
आइए संख्याओं के एक अन्य पैटर्न पर विचार करें, जिसमें हमारी सहायता के लिए कोई आकृति बनी हुई नहीं है ः 3, 6, 9, 12, ..., 3n, ...
ये संख्याएँ 3 के गुणज (multiples) हैं और इन्हें 3 से प्रारंभ करते हुए आरोही क्रम में व्यवस्थित किया गया है । n वें स्थान पर आने वाले पद को 3n से व्यक्त किया गया है इसकी सहायता से, आप सरलतापूर्वक 10वें स्थान पर आने वाले पद (जो 3 × 10 = 30 है) तथा 100 वें स्थान पर आने वाले पद (जो 3 × 100 = 300 है), इत्यादि ज्ञात कर सकते हैं ।
ज्यामिति में पैटर्न
एक चतुर्भुज के किसी शीर्ष से उसके कितने विकर्ण खींचे जा सकते हैं ? जाँच कीजिए कि इनकी संख्या एक है ।
एक पंचभुज के एक शीर्ष से उसके कितने विकर्ण खींच सकते हैं ? जाँच कीजिए कि इनकी संख्या दो है ।
एक षटभुज के एक शीर्ष से उसके कितने विकर्ण खींचे जा सकते हैं? जाँच कीजिए यह संख्या 3 है ।
n भुजा वाले किसी बहुभुज के एक शीर्ष से हम कुल (n – 3) विकर्ण खींच सकते हैं । एक सप्तभुज (7 भुजाएँ) और अष्टभुज (8 भुजाएँ) के लिए, उनकी आकृतियाँ खींच करके इसकी जाँच कीजिए । यह संख्या एक त्रिभुज (3 भुजाएँ) के लिए क्या है ? ध्यान दीजिए कि किसी बहुभुज के किसी एक शीर्ष से खींचे गए विकर्ण उसे उतने अनानिव्यापी (non-overlapping) (जो एक दूसरे को न ढकते हों) त्रिभुजों में विभाजित करते हैं जितनी विकर्णों की संख्या से अधिक 1 संख्या होती है ।
प्रश्नावली 12.4
1. बराबर लंबाई के रेखाखंडों से बनाए गए अंकों के पैटर्न को देखिए । आप रेखाखंडों से बने हुए इस प्रकार के अंकों को इलैक्ट्रॉनिक घड़ियों या कैलकुलेटरों पर देख सकते हैं ।
यदि बनाए गए अंकों की संख्या n ली जाए, तो उसके लिए आवश्यक रेखाखंडों की (n) संख्या दर्शाने वाला बीजीय व्यंजक प्रत्येक पैटर्न के दाईं ओर लिखा गया है ।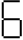 ,
,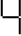 ,
,  के प्रकार के 5,10,100 अंकों को बनाने के लिए कितने रेखाखंडों की आवश्यकता होगी ?
के प्रकार के 5,10,100 अंकों को बनाने के लिए कितने रेखाखंडों की आवश्यकता होगी ?
2. संख्या पैटर्नों की निम्नलिखित सारणी को पूरा करने के लिए, दिए हुए बीजीय व्यंजकों का प्रयोग कीजिए :
क्रम व्यंजक पद
हमने क्या चर्चा की ?
1. चरों और अचरों से बीजीय व्यंजक बनते हैं । व्यंजकों को बनाने के लिए, हम चरों और अचरों पर योग, व्यवकलन, गुणन और विभाजन की संक्रियाएँ करते हैं । उदाहरणार्थ, व्यंजक 4xy + 7 चरों x और y तथा अचरों 4 और 7 से बनाया गया है । अचर 4 तथा चरों x और y को गुणा करके 4xy बनाकर उसमें 7 जोड़ कर 4xy + 7 बनाया जाता है ।
2. व्यंजक पदों से मिलकर बनते हैं । पदों को जोड़ कर व्यंजक बनाया जाता है । उदाहरणार्थ, पदों 4xy और 7 को जोड़ने से व्यंजक 4xy + 7 बन जाता है ।
3. एक पद, गुणनखंडों का एक गुुणनफल होता है । व्यंजक 4xy + 7 में पद 4xy गुणनखंडों x, y और 4 का एक गुणनफल है । चरों वाले गुणनखंड बीजीय गुणनखंड कहलाते हैं ।
4. पद का गुणांक उसका संख्यात्मक गुणनखंड होता है । कभी-कभी पद का कोई भी एक गुणनखंड पद के शेष भाग का गुणांक कहलाता है ।
5. एक या अधिक पदों से बना व्यंजक एक बहुपद कहलाता है । विशिष्ट रूप से, एक पद वाला व्यंजक एकपदी, दो पदों वाला व्यंजक द्विपद तथा तीन पदों वाला व्यंजक त्रिपद कहलाता है ।
6. वे पद जिनमें बीजीय गुणनखंड एक जैसे हों, समान पद कहलाते हैं तथा भिन्न-भिन्न बीजीय गुणनखंडों वाले पद असमान पद कहलाते हैं । इस प्रकार 4xy और –3xy समान पद हैं, परंतु 4xy और –3x समान पद नहीं हैं ।
7. दो समान पदों का योग (या अंतर) एक अन्य समान पद होता है, जिसका गुणांक उन समान पदों के गुणांकों के योग (या अंतर) के बराबर होता है । इस प्रकार,
8xy – 3xy = (8 – 3 )xy, अर्थात्् 5xy।
8. जब हम दो बीजीय व्यंजकों को जोड़ते हैं, तो समान पदों को, ऊपर वर्णित नियम के अनुसार जोड़ा जाता है; जो समान पद नहीं हैं उन्हें वैसे ही छोड़ दिया जाता है। इस प्रकार,
4x2 + 5x और 2x + 3 का योग 4x2 + 7x + 3 है । यहाँ समान पद 5x और 2x जुड़ कर
7x बन जाते हैं तथा असमान पदों 4x2 और 3 को वैसे ही छोड़ दिया जाता है ।
9. एक समीकरण को हल करने और किसी सूत्र का प्रयोग करने जैसी स्थितियों में, हमें एक व्यंजक का मान ज्ञात करने की आवश्यकता होती है । बीजीय व्ंयजक का मान उन चरों के मानों पर निर्भर करता है, जिनसे वह बनाया गया है । इस प्रकार, x = 5 के लिए
7x – 3 का मान 32, है क्योंकि 7 × 5 – 3 = 32 है ।
10. गणित में, बीजीय व्यंजकों का प्रयोग करते हुए, नियमों और सूत्रों को संक्षिप्त और व्यापक रूप में लिखा जाता है ।
इस प्रकार, आयत का क्षेत्रफल = lb, है, जहाँ l आयत की लंबाई तथा b आयत की चौड़ाई है ।
एक संख्या पैटर्न (या अनुक्रम) का व्यापक (nवाँ) पद, n में एक व्यंजक होता है । इस प्रकार, संख्या पैटर्न 11, 21, 31, 41, . . . का n वाँ पद (10n + 1) है ।