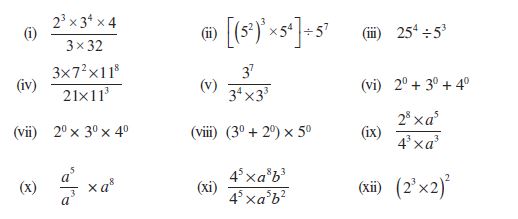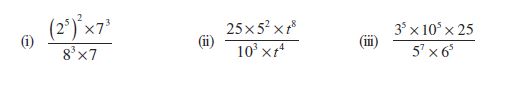Table of Contents
13.1 भूमिका
क्या आप जानते हैं कि पृथ्वी का द्रव्यमान (mass) क्या है? यह
5,970,000,000,000,000,000,000,000 kg है!
क्या आप इस संख्या को पढ़ सकते हैं?
यूरेनस ग्रह (Uranus) का द्रव्यमान 86,800,000,000,000,000,000,000,000 kg है।
किसका द्रव्यमान अधिक है–पृथ्वी या यूरेनस ग्रह?
सूर्य (Sun) और शनि (Saturn) के बीच की दूरी 1,433,500,000,000 m है तथा शनि और यूरेनस ग्रह के बीच की दूरी 1,439,000,000,000 m है। क्या आप इन संख्याओं को पढ़ सकते हैं? इनमें कौन-सी दूरी कम है?
एेसी बहुत बड़ी संख्याओं का पढ़ना, समझना और इनकी तुलना करना कठिन होता है। इन संख्याओं को सरलता से पढ़ने, समझने और इनकी तुलना करने के लिए, हम घातांकों (exponents) का प्रयोग करते हैं। इस अध्याय में, हम घातांकों के बारे में सीखेंगे तथा यह भी सीखेंगे कि इनका प्रयोग किस प्रकार किया जाता है।
13.2 घातांक
हम बड़ी संख्याओं को घातांकों का प्रयोग करके संक्षिप्त रूप में लिख सकते हैं।
निम्नलिखित को देखिएः 10, 000 = 10 × 10 × 10 × 10 = 104
संक्षिप्त संकेतन 104 गुणनफल 10×10×10×10 को व्यक्त करता है। यहाँ, ‘10’ आधार (base) और ‘4’ घातांक कहलाता है। 104 को 10 के ऊपर घात (power) 4 या केवल 10 की चौथी घात पढ़ा जाता है। 104 को 10000 का घातांकीय रूप (exponential form) कहा जाता है।

हम इसी प्रकार 1000 को भी 10 की घात के रूप में व्यक्त कर सकते हैं। ध्यान दीजिए कि
1000 = 10 × 10 × 10 = 103 है।
यहाँ, पुनः 103 संख्या 1000 का घातांकीय रूप है।
इसी प्रकार, 1,00,000 = 10 × 10 × 10 × 10 × 10 = 105 है।
अर्थात्, 105 संख्या 1,00,000 का घातांकीय रूप है।
इन दोनों उदाहरणों में, आधार 10 है। 103 में घातांक 3 है तथा 105 में घातांक 5 है।
हम संख्याओं को विस्तारित या प्रसारित रूप (expanded form) में लिखने के लिए
10, 100, 1000 इत्यादि जैसी संख्याओं का प्रयोग कर चुके हैं।
उदाहरणार्थ, 47561 = 4 × 10000 + 7 × 1000 + 5 × 100 + 6 × 10 + 1 है।
इसे 4 × 104 + 7 ×103 + 5 × 102 + 6 × 10 + 1 के रूप में लिखा जा सकता है।
निम्नलिखित संख्याओं को इसी प्रकार लिखने का प्रयत्न कीजिए :
172, 5642, 6374
उपरोक्त सभी उदाहरणों में, हमने वे संख्याएँ देखी हैं जिनके आधार 10 हैं। परंतु आधार कोई भी संख्या हो सकती है। उदाहरणार्थ,
81 = 3 × 3 × 3 × 3 = 34 के रूप में लिखा जा सकता है। यहाँ आधार 3 है और घातांक 4 है।
कुछ घातों के विशिष्ट नाम हैं। उदाहरणार्थ :
102, जो 10 के ऊपर घात 2 है, इसे 10 का वर्ग (10 squared) भी पढ़ा जाता है।
103, जो 10 के ऊपर घात 3 है, इसे 10 का घन (10 cubed) भी पढ़ा जाता है।
क्या आप बता सकते हैं कि 53 (5 के घन) का क्या अर्थ है?
53 = 5 × 5 × 5 = 125
अतः हम कह सकते हैं कि 125 संख्या 5 की तीसरी घात (third power) है।
53 में आधार तथा घातांक क्या हैं?

प्रयास कीजिए
इसी प्रकार 25 = 2 × 2 × 2 × 2 × 2 = 32 है, जो 2 की पाँचवीं घात है।
25 में, 2 आधार है तथा घातांक 5 है।
इसी विधि के अनुसार, 243 = 3 × 3 × 3 × 3 × 3 = 35,
64 = 2 × 2 × 2 × 2 × 2 × 2 = 26
625 = 5 × 5 × 5 × 5 = 54
आप संक्षिप्त रूप में लिखने की इस विधि को तब भी लागू कर सकते हैं, जब आधार एक ऋणात्मक पूर्णांक हो।
(–2)3 का क्या अर्थ है?
यह (–2)3 = (–2) × (–2) × (–2) = – 8 है।
क्या (–2)4 = 16 है? इसकी जाँच कीजिए।
कोई निश्चित संख्या लेने के स्थान पर, आइए किसी भी संख्या a को आधार लें तथा संख्याओं को निम्नलिखित रूप में लिखें ः
a × a = a2 (इसे ‘a का वर्ग’ या ‘a के ऊपर घात 2’ पढ़ा जाता है)
a × a × a = a3 (इसे ‘a का घन’ या ‘a के ऊपर घात 3’ पढ़ा जाता है)
a × a × a × a = a4 (इसे a के ऊपर घात 4 या ‘a की चौथी घात’ पढ़ा जाता है)
a × a × a × a × a × a × a = a7 (इसे ‘a के ऊपर घात 7’ या ‘a की सातवीं घात’ पढ़ा जाता है) इत्यादि।
a × a × a × b × b को a3b2 के रूप में व्यक्त किया जा सकता है (इसे a का घन गुणा b का वर्ग पढ़ा जाता है)।
a × a × b × b × b × b को a2b4 के रूप में व्यक्त किया जा सकता है (इसे a का वर्ग गुणा b पर 4 घात पढ़ा जाता है)।
प्रयास कीजिए

व्यक्त कीजिए :
(i) 729 को 3 की घात के रूप में
(ii) 128 को 2 की घात के रूप में
(iii) 343 को 7 की घात के रूप में
उदाहरण 1 256 को 2 की घात के रूप में व्यक्त कीजिए।
हल हमें प्राप्त है 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
अतः हम कह सकते हैं कि 256 = 28
उदाहरण 2 23 और 32 में कौन बड़ा है?

हल हमें प्राप्त है कि 23 = 2 × 2 × 2 = 8 है तथा 32 = 3 × 3 = 9 है।
चूँकि 9 > 8 है, इसलिए 32 संख्या 23 से बड़ा है।
उदाहरण 3 82 और 28 में कौन बड़ा है?
हल 82 = 8 × 8 = 64 है।
28 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256 है।
स्पष्टतया, 28 > 82
उदाहरण 4 a3 b2, a2 b3, b2 a3, और b3 a2 को प्रसारित रूप में लिखिए।
क्या ये सभी बराबर हैं?
हल a3 b2 = a3 × b2
= (a × a × a) × (b × b)
= a × a × a × b × b
a2 b3 = a2 × b3
= a × a × b × b × b
b2 a3 = b2 × a3
= b × b × a × a × a
b3 a2 = b3 × a2
= b × b × b × a × a
ध्यान दीजिए कि पद a3 b2 और a2 b3 की स्थिति में, a और b की घातें भिन्न-भिन्न हैं। इस प्रकार, a3 b2 और a2 b3 भिन्न-भिन्न हैं।
इसके विपरीत, a3 b2 और b2 a3 बराबर (एक ही) हैं, चूँकि इनमें a और b की घातें एक ही हैं। गुणनखंडों के क्रम से कोई प्रभाव नहीं पड़ता है।
इस प्रकार, a3 b2 = a3 × b2 = b2 × a3 = b2 a3 है।
इसी प्रकार a2 b3 और b3 a2 भी बराबर हैं।
उदाहरण 5 निम्नलिखित संख्याओं को अभाज्य गुणनखंडों की घातों के गुणनफल के रूप में व्यक्त कीजिए ः
(i) 72 (ii) 432 (iii) 1000 (iv) 16000
हल
(i) 72 = 2 × 36 = 2 × 2 × 18
= 2 × 2 × 2 × 9
= 2 × 2 × 2 × 3 × 3 = 23 × 32
इस प्रकार 72 = 23 × 32 (वांछित अभाज्य गुणनखंडों की घातों के गुणनफल वाला रूप)
(ii) 432 = 2 × 216 = 2 × 2 × 108 = 2 × 2 × 2 × 54
= 2 × 2 × 2 × 2 × 27 = 2 × 2 × 2 × 2 × 3 × 9
= 2 × 2 × 2 × 2 × 3 × 3 × 3
या 432 = 24 × 33 (वांछित रूप)
(iii) 1000 = 2 × 500 = 2 × 2 × 250 = 2 × 2 × 2 × 125
= 2 × 2 × 2 × 5 × 25 = 2 × 2 × 2 × 5 × 5 × 5
या 1000 = 23 × 53
अतुल इस उदाहरण को निम्नलिखित विधि से हल करना चाहता है :
1000 = 10 × 100 = 10 × 10 × 10
= (2 × 5) × (2 × 5) × (2 × 5) (चूँकि 10 = 2 × 5 है)
= 2 × 5 × 2 × 5 × 2 × 5 = 2 × 2 × 2 × 5 × 5 × 5
या 1000 = 23 × 53
क्या अतुल की विधि सही है?
(iv) 16000 = 16 × 1000 = (2 × 2 × 2 × 2) ×1000 (चूँकि 16 = 2 × 2 × 2 × 2 है।)
= (2 × 2 × 2 × 2) × (2 × 2 × 2 × 5 × 5 × 5)
(चूँकि 1000 = 2 × 2 × 2 × 5 × 5 × 5 है।)
= (2 × 2 × 2 × 2 × 2 × 2 × 2 ) × (5 × 5 × 5)
या, 16000 = 27 × 53
उदाहरण 6 निम्नलिखित के मान ज्ञात कीजिए।
(1)5, (–1)3, (–1)4, (–10)3 और (–5)4:
हल
(i) हमें प्राप्त है, (1)5 = 1 × 1 × 1 × 1 × 1 = 1
वास्तव में, 1 की कोई भी घात 1 के बराबर होती है।
(ii) (–1)3 = (–1) × (–1) × (–1) = 1 × (–1) = –1
(iii) (–1)4 = (–1) × (–1) × (–1) × (–1) = 1 × 1 = 1
आप इसकी जाँच कर सकते हैं कि (–1) की कोई भी विषम घात (–1) के बराबर होती है तथा (–1) की कोई भी सम घात (+1) के बराबर होती है।
(iv) (–10)3 = (–10) × (–10) × (–10) = 100 × (–10) = – 1000
(v) (–5)4 = (–5) × (–5) × (–5) × (–5) = 25 × 25 = 625
प्रश्नावली 13.1
1. निम्नलिखित के मान ज्ञात कीजिए :
(i) 26 (ii) 93 (iii) 112 (iv) 54
2. निम्नलिखित को घातांकीय रूप में व्यक्त कीजिए :
(i) 6 × 6 × 6 × 6 (ii) t × t (iii) b × b × b × b
(iv) 5 × 5× 7 × 7 × 7 (v) 2 × 2 × a × a (vi) a × a × a × c × c × c × c × d
3. निम्नलिखित संख्याओं में से प्रत्येक को घातांकीय संकेतन में व्यक्त कीजिए :
(i) 512 (ii) 343 (iii) 729 (iv) 3125
4. निम्नलिखित में से प्रत्येक भाग में, जहाँ भी संभव हो, बड़ी संख्या को पहचानिएः
(i) 43 या 34 (ii) 53 या 35 (iii) 28 या 82
(iv) 1002 या 2100 (v) 210 या 102
5. निम्नलिखित में से प्रत्येक को उनके अभाज्य गुणनखंडों की घातों के गुणनफल के रूप में व्यक्त कीजिए।
(i) 648 (ii) 405 (iii) 540 (iv) 3600
6. सरल कीजिए :
(i) 2 × 103 (ii) 72 × 22 (iii) 23 × 5 (iv) 3 × 44
(v) 0 × 102 (vi) 52 × 33 (vii) 24 × 32 (viii) 32 × 104
7. सरल कीजिए :
(i) (– 4)3 (ii) (–3) × (–2)3 (iii) (–3)2 × (–5)2
(iv) (–2)3 × (–10)3
8. निम्नलिखित संख्याओं की तुलना कीजिए :
(i) 2.7 × 1012 ; 1.5 × 108 (ii) 4 × 1014 ; 3 × 1017
13.3 घातांकों के नियम
13.3.1 एक ही आधार वाली घातों का गुणन
(i) आइए 22 × 23 को परिकलित करें।
22 × 23 = (2 × 2) × (2 × 2 × 2)
= 2 × 2 × 2 × 2 × 2 = 25 = 22+3
ध्यान दीजिए कि 22 और 23 में आधार एक ही (समान) है तथा घातांकों का योग, अर्थात् 2 और 3 का योग 5 है।
(ii) (–3)4 × (–3)3 = [(–3) × (–3) × (–3)× (–3)] × [(–3) × (–3) × (–3)]
= (–3) × (–3) × (–3) × (–3) × (–3) × (–3) × (–3)
= (–3)7
= (–3)4+3
पुनः ध्यान दीजिए कि आधार एक ही है तथा घातांकों का योग 4 + 3 = 7 है।
(iii) a2 × a4 = (a × a) × (a × a × a × a)
= a × a × a × a × a × a = a6
(टिप्पणीः आधार एक ही है तथा घातांकों का योग 2 + 4 = 6 है)
इसी प्रकार, सत्यापित कीजिए कि
42 × 42 = 42+2
तथा 32 × 33 = 32+3 है।
क्या आप बॉक्स में उपयुक्त संख्या लिख सकते हैं?
(–11)2 × (–11)6 = 11
b2 × b3 = b 
(याद रखिए, आधार एक ही है, b कोई भी शून्येतर पूर्णांक है)।
c3 × c4 = c  (c कोई भी शून्येतर पूर्णांक है)।
(c कोई भी शून्येतर पूर्णांक है)।
d10 × d20 = d 
यहाँ से हम व्यापक रूप से यह कह सकते हैं कि एक शून्येतर पूर्णांक a, के लिए, am × an = am + n
होता है, जहाँ m और n पूर्ण संख्याएँ हैं।
प्रयास कीजिए

सरल करके घातांकीय रूप में लिखिए :
(i) 25 × 23
(ii) p3 × p2
(iii) 43 ×42
(iv) a3 × a2 × a7
(v) 53 × 57 × 512 (vi) (–4)100 × (–4)20
सावधानी!
23 × 32 पर विचार कीजिए।
क्या आप घातांकों को जोड़ सकते हैं? नहीं! क्या आप बता सकते हैं ‘क्यों’?
23 का आधार 2 है और 32 का आधार 3 है। आधार एक समान नहीं हैं।
13.3.2 एक ही आधार वाली घातों का विभाजन
आइए 37 ÷ 34 को सरल करें।
37 ÷ 34 = 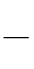 =
= 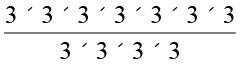
= 3 × 3 × 3 = 33 = 37–4
इस प्रकार, 37 ÷ 34 = 37– 4 है।
[ध्यान दीजिए कि 37 और 34 के आधार एक ही हैं और 37 ÷ 34 = 37–4 हो जाता है।]
इस प्रकार, 56 ÷ 52 = 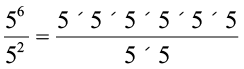
= 5 × 5 × 5 × 5 = 54 = 56 – 2
या, 56 ÷ 52 = 56 – 2 है।
मान लीजिए कि a कोई शून्येतर पूर्णांक है। तब,
a4 ÷ a2 = 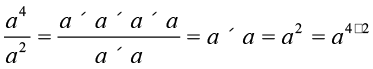
या a4 ÷ a2 = a4 – 2 है।
क्या अब आप तुरंत उत्तर दे सकते हैं?
108 ÷ 103 = 108 – 3 = 105
79 ÷ 76 = 7
a8 ÷ a5 = a
शून्येतर पूर्णांक b और c के लिए
b10 ÷ b5 = b
c100 ÷ c90 = c
व्यापक रूप में, किसी भी शून्येतर पूर्णांक a के लिए,
am ÷ an = am – n
होता है, जहाँ m और n पूर्ण संख्याएँ हैं तथा m > n है।
प्रयास कीजिए
सरल करके घातांकीय रूप में लिखिएः (उदाहरण के लिए, 116 ÷ 112 = 114) (i) 29 ÷ 23 (ii) 108 ÷ 104
(iii) 911 ÷ 97 (iv) 2015 ÷ 2013
(v) 713 ÷ 710
13.3.3 एक घात की घात लेना
निम्नलिखित पर विचार कीजिए :
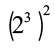 और
और 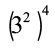 को सरल कीजिए।
को सरल कीजिए।
अब, 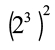 का अर्थ है 23 का स्वयं से दो बार गुणा किया गया है।
का अर्थ है 23 का स्वयं से दो बार गुणा किया गया है।
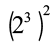 = 23 × 23
= 23 × 23
= 23 + 3 (चूँकि am × an = am + n है।)
= 26 = 23 × 2
अर्थात्् 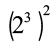 = 23×2
= 23×2
इसी प्रकार, 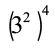 = 32 × 32 × 32 × 32
= 32 × 32 × 32 × 32
= 32 + 2 + 2 + 2
= 38 (देखिए कि 2 और 4 का गुणनफल 8 है।)
= 32 × 4
क्या आप बता सकते हैं कि 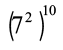 किसके बराबर है?
किसके बराबर है?
प्रयास कीजिए
सरल करके, उत्तर को घातांकीय रूप में व्यक्त कीजिए।
(i) 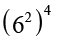 (ii)
(ii) 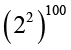
(iii) 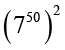 (iv)
(iv) 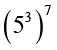
अतः, 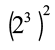 = 23 × 2 = 26
= 23 × 2 = 26
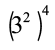 = 32 × 4 = 38
= 32 × 4 = 38
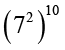 = 72 × 10 = 720
= 72 × 10 = 720
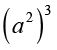 = a 2 × 3 = a6
= a 2 × 3 = a6
(am)3 = am × 3 = a3m
उपरोक्त से, हम व्यापक रूप से कह सकते हैं कि किसी शून्येतर पूर्णांक ‘a’ के लिए,
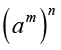 = amn
= amn
होता है, जहाँ m और n पूर्ण संख्याएँ हैं।
उदाहरण 7 क्या आप बता सकते हैं कि (52) × 3 और 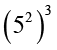 में से कौन बड़ा है?
में से कौन बड़ा है?
हल (52) × 3 का अर्थ है कि 52 को 3 से गुणा किया गया है, अर्थात्् यह
5 × 5 × 3 = 75
परंतु 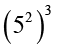 का अर्थ है कि 52 का स्वयं से तीन बार गुणा किया गया है, अर्थात्् यह
का अर्थ है कि 52 का स्वयं से तीन बार गुणा किया गया है, अर्थात्् यह
52 × 52 × 52 = 56 = 15625 है।
अतः, (52)3 > (52) × 3 है।
13.3.4 समान घातांकों वाली घातों का गुणन
क्या आप 23 × 33 को सरल कर सकते हैं? ध्यान दीजिए कि यहाँ दोनों पदों 23 और 33 के आधार भिन्न-भिन्न हैं। परंतु इनके घातांक समान हैं।
अब 23 × 33 = (2 × 2 × 2) × (3 × 3 × 3)
= (2 × 3) × (2 × 3) × (2 × 3)
= 6 × 6 × 6
= 63 (देखिए 6 आधारों 2 और 3 का गुणनफल है)
देखिए 44 × 34 = (4 × 4 × 4 × 4) × (3 × 3 × 3 × 3)
= (4 × 3) × (4 × 3) × (4 × 3) × (4 × 3)
= 12 × 12 × 12 × 12
= 124
साथ ही, देखिए 32 × a2 = (3 × 3) × (a × a)
= (3 × a) × (3 × a)
= (3 × a)2
= (3a)2 (ध्यान दीजिए ः 3×a = 3a )
इसी प्रकार a4 × b4 = (a × a × a × a) × (b × b × b × b)
= (a × b) × (a × b) × (a × b) × (a × b)
= (a × b)4
= (ab)4 (ध्यान दीजिए कि a × b = ab है)
व्यापक रूप में, किसी भी शून्येतर पूर्णांक के लिए,
am × bm = (ab)m होता है जहाँ, m एक पूर्ण संख्या है
उदाहरण 8 निम्नलिखत पदों को घातांकीय रूप में व्यक्त कीजिए ः
(i) (2 × 3)5 (ii) (2a)4 (iii) (– 4m)3
हल
(i) (2 × 3)5 = (2 × 3) × (2 × 3) × (2 × 3) × (2 × 3) × (2 × 3)
= (2 × 2 × 2 × 2 × 2) × (3 × 3× 3 × 3 × 3)
= 25 × 35
(ii) (2a)4 = 2a × 2a × 2a × 2a
= (2 × 2 × 2 × 2) × (a × a × a × a)
= 24 × a4
(iii) (– 4m)3 = (– 4 × m)3
= (– 4 × m) × (– 4 × m) × (– 4 × m)
= (– 4) × (– 4) × (– 4) × (m × m × m) = (– 4)3 × (m)3
प्रयास कीजिए
am × bm = (ab)m का प्रयोग करके, अन्य रूप में बदलिए :
(i) 43 × 23 (ii) 25 × b5
(iii) a2 × t2 (iv) 56 × (–2)6
(v) (–2)4 × (–3)4
13.3.5 समान घातांकों वाल घातों से विभाजन
शून्य घातांक वाली संख्याएँ
क्या आप बता सकते हैं कि 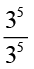 किसके बराबर है?
किसके बराबर है?
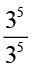 =
= 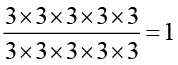 है।
है।
घातांकों के नियमों का प्रयोग करते हुए,
35 ÷ 35 = 35 – 5 = 30 है।
अतः 30 = 1 है।
क्या आप बता सकते हैं कि 70 किसके बराबर है?
73 ÷73 = 73 – 3 = 70
साथ ही, 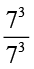 =
= 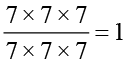 है।
है।
अतः 70 = 1
इसी प्रकार, a3 ÷ a3 = a3–3 = a0 है।
साथ ही a3 ÷ a3 = 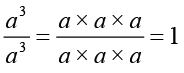 है।
है।
अतः, a0 = 1 (किसी भी शून्येतर पूर्णांक a के लिए)
अतः, हम कह सकते हैं कि किसी भी संख्या (शून्य के अतिरिक्त) पर घात (या घातांक) 0 का मान 1 होता है।
aº क्या है?
निम्नलिखित पैटर्न को देखिए ः
26 = 64
25 = 32
24 = 16
23 = 8
22 = ?
21 = ?
2º = ?
आप केवल पैटर्न देख कर ही 2º के मान का अनुमान लगा सकते हैं।
आप देख सकते हैं कि 2º = 1 है।
यदि 36 = 729, से प्रारंभ करें, तो ऊपर दर्शाई विधि से 35, 34, 33,... इत्यादि ज्ञात करते हुए, क्या आप 3º का मान बता सकते हैं?
13.4 घातांकों के नियमो का विविध उदाहरणों में प्रयोग
आइए ऊपर विकसित किए गए घातांकों के नियमों का प्रयोग करके, कुछ उदाहरण हल करें।
उदाहरण 10 8 × 8 × 8 × 8 के लिए, आधार 2 लेते हुए, इसे घातांकीय रूप में लिखिए।
हल ज्ञात है कि, 8 × 8 × 8 × 8 = 84
परंतु हम जानते हैं कि 8 = 2 × 2 × 2 = 23 है।
अतः, 84 = (23)4 = 23 × 23 × 23 × 23
= 23 × 4 (आप (am)n = amn का भी प्रयोग कर सकते हैं।)
= 212
उदाहरण 11 सरल कीजिए और उत्तर को घातांकीय रूप में लिखिए ः
(i) 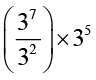 (ii) 23 × 22 × 55 (iii) (62 × 64) ÷ 63
(ii) 23 × 22 × 55 (iii) (62 × 64) ÷ 63
(iv) ((22)3 × 36) × 56 (v) 82 ÷ 23
हल (i) 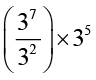 =
= 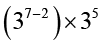
= 35×35 = 35+5 = 310
(ii) 23 × 22 × 55 = 23+2 × 55
= 25× 55 = (2×5)5 = 105
(iii) 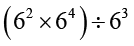 =
= 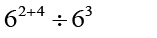
= 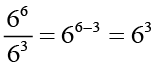
(iv) 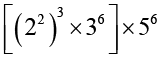 = [26 × 36] × 56
= [26 × 36] × 56
= 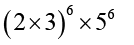
= 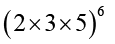 =
= 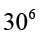
(v) 8 = 2 × 2 × 2 = 23
अतः, 82 ÷ 23 = (23)2 ÷ 23
= 26 ÷ 23 = 26–3 = 
उदाहरण 12 सरल कीजिए :
(i) 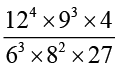 (ii) 23 × a3 × 5a4 (iii)
(ii) 23 × a3 × 5a4 (iii) 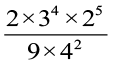
हल (i) यहाँ
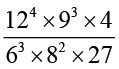 =
= 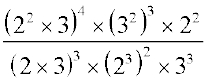
= 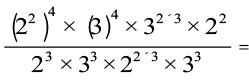
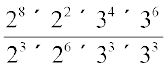
= 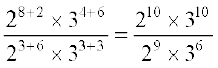
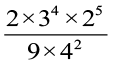
= 210 – 9 × 310 – 6 = 21 × 34
= 2 × 81 = 162
(ii) 23 × a3 × 5a4 = 23× a3 × 5 × a4
= 23 × 5 × a3 × a4 = 8 × 5 × a3 + 4
= 40 a7
(ii) 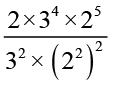 =
= 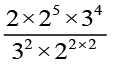 =
= 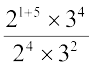
= 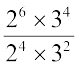 =
= 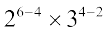 =
= 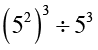
= 22 × 32 = 4 × 9 = 36
टिप्पणीः इस अध्याय में, हमने अधिकांशतः एेसे उदाहरण लिए हैं जिनमें आधार पूर्णांक हैं। परंतु इस अध्याय के सभी परिणाम उन स्थितियों के लिए भी सत्य हैं, जहाँ आधार परिमेय संख्याएँ हैं।
प्रश्नावली 13.2
1. घातांकों के नियमों का प्रयोग करते हुए, सरल कीजिए और उत्तर को घातांकीय रूप में लिखिए :
(i) 32 × 34 × 38 (ii) 615 ÷ 610 (iii) a3 × a2
(iv) 7x ×72 (v) 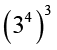 (vi) 25 × 55
(vi) 25 × 55
(vii) a4 × b4 (viii) 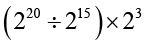 (ix)
(ix) 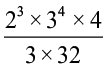
(x) 8t ÷ 82
2. निम्नलिखित में से प्रत्येक को सरल करके घातांकीय रूप में व्यक्त कीजिए :
3. बताइए कि निम्नलिखित कथन सत्य है या असत्य तथा अपने उत्तर का कारण भी दीजिएः
(i) 10 × 1011 = 10011 (ii) 23 > 52 (iii) 23 × 32 = 65
(iv) 30 = (1000)0
4. निम्नलिखित में से प्रत्येक को केवल अभाज्य गुणनखंडों की घातों के गुणनफल के रूप में व्यक्त कीजिए :
(i) 108 × 192 (ii) 270 (iii) 729 × 64
(iv) 768
5. सरल कीजिए :
13.5 दशमलव संख्या पद्धति
आइए 47561 के निम्नलिखित प्रसार को देखें, जिससे हम पहले से ही परिचित हैं ः
47561 = 4 × 10000 + 7 × 1000 + 5 × 100 + 6 × 10 + 1
हम इसे 10 की घातों का प्रयोग करते हुए, घातांकीय रूप में निम्नलिखित प्रकार से व्यक्त कर सकते हैं ः
47561 = 4 × 104 + 7 × 103 + 5 × 102 + 6 × 101 + 1 × 100
[ध्यान दीजिए ः 10000 = 104, 1000 = 103, 100 = 102, 10 = 101 और 1 = 100 है।]
आइए एक और संख्या को प्रसारित रूप में लिखें ः
104278 = 1 × 100,000 + 0 × 10000 + 4 × 1000 + 2 × 100 + 7 × 10 + 8 × 1
= 1 × 105 + 0 × 104 + 4 × 103 + 2 × 102 + 7 × 101 + 8 × 100
= 1 × 105 + 4 × 103 + 2 × 102 + 7 × 101 + 8 × 100
ध्यान दीजिए कि किस प्रकार 10 के घातांक अधिकतम मान 5 से प्रारंभ होते हुए एक-एक करके घटते हुए, 0 तक आ जाते हैं।
13.6 बड़ी संख्याओं को मानक रूप में व्यक्त करना
आइए, इस अध्याय की प्रारंभिक स्थिति पर वापस आ जाएँ। हमने कहा था कि बड़ी संख्याओं को, घातांकों का प्रयोग करके सुविधाजनक रूप से व्यक्त किया जा सकता है। इसे अभी तक हमने दिखाया नहीं है। अब हम एेसा करेंगे।
1. सूर्य हमारी आकाशगंगा (Milky Way Galaxy) के केंद्र से 300,000,000,000,000,000,000 m की दूरी पर स्थित है।
2. हमारी आकाशगंगा में 100,000,000,000 तारे हैं।
3. पृथ्वी का द्रव्यमान 5,976,000,000,000,000,000,000,000 kg है।
ये संख्याएँ पढ़ने और लिखने की दृष्टि से सुविधाजनक नहीं हैं। इनको सुविधाजनक बनाने के लिए, हम घातों (या घातांकों) का प्रयोग करते हैं।
निम्नलिखित को देखिए ः
59 = 5.9 × 10 = 5.9 × 101
590 = 5.9 × 100 = 5.9 × 102
5900 = 5.9 × 1000 = 5.9 × 103
59000 = 5.9 × 10000 = 5.9 × 104 इत्यादि।
हमने इन सभी संख्याओं को मानक रूप (standard form) में व्यक्त कर दिया है। किसी भी संख्या को 1.0 और 10.0 के बीच की एक दशमलव संख्या (जिसमें 1.0 सम्मिलित है) और 10 की किसी घात के गुणनफल के रूप में व्यक्त किया जा सकता है। संख्या के इस रूप को उसका मानक रूप कहते हैं। इस प्रकार,
प्रयास कीजिए
10 की घातों का प्रयोग करते हुए, घातांकीय रूप में प्रसारित कीजिए :
(i) 172
(ii) 5643
(iii) 56439
(iv) 176428
5985 = 5.985 × 1000 = 5.985 × 103 संख्या 5985 का मानक रूप है।
ध्यान दीजिए कि 5985 को 59.85 × 100 या 59.85 × 102 के रूप में भी व्यक्त किया जा सकता है। परंतु यह 5985 का मानक रूप नहीं है। इसी प्रकार
5985 = 0.5985 × 10000 = 0.5985 × 104 भी 5985 का मानक रूप नहीं है।
अब हम इस अध्याय के प्रारंभ में आई हुई संख्याओं को इस मानक रूप में व्यक्त करने में सक्षम हो गए हैं।
हमारी आकाशगंगा के केंद्र से सूर्य की दूरी अर्थात््, 300,000,000,000,000,000,000 m को
3.0 × 100,000,000,000,000,000,000 m = 3.0 × 1020 m
के रूप में लिखा जा सकता है। अब, क्या आप 40,000,000,000 को इसी रूप
में व्यक्त कर सकते हैं? इसमें शून्यों की संख्या को गिनिए। यह 10 है।
अतः 40,000,000,000 = 4.0 × 1010 है।
पृथ्वी का द्रव्यमान = 5,976,000,000,000,000,000,000,000 kg
= 5.976 × 1024 kg है।
क्या आप इस बात से सहमत हैं कि पढ़ने, समझने और तुलना करने की दृष्टि से मानक रूप में लिखी यह संख्या उस 25 अंकों की संख्या की अपेक्षा बहुत अधिक सरल या सुविधाजनक है?
अब, यूरेनस ग्रह का द्रव्यमान = 86,800,000,000,000,000,000,000,000 kg
= 8.68 × 1025 kg है।
अब, उपरोक्त दोनों व्यंजकों में केवल 10 की घातों की तुलना करके ही, आप यह कह सकते हैं कि यूरेनस ग्रह का द्रव्यमान पृथ्वी से अधिक है।
सूर्य और शनि के बीच की दूरी 1,433,500,000,000 m या 1.4335 × 1012 m है। शनि और यूरेनस के बीच की दूरी 1,439,000,000,000 m या 1.439 × 1012 m हैं। सूर्य और पृथ्वी के बीच की दूरी 149, 600,000,000 m या 1.496 × 1011 m है।
क्या आप बता सकते हैं कि इन तीनों दूरियों में कौन-सी दूरी न्यूनतम है?
उदाहरण 13 निम्नलिखित संख्याओं को मानक रूप में व्यक्त कीजिए :
(i) 5985.3 (ii) 65950
(iii) 3,430,000 (iv) 70,040,000,000
हल
(i) 5985.3 = 5.9853 × 1000 = 5.9853 × 103
(ii) 65950 = 6.595 × 10000 = 6.595 × 104
(iii) 3,430,000 = 3.43 × 1000,000 = 3.43 × 106
(iv) 70,040,000,000 = 7.004 × 10,000,000,000 = 7.004 × 1010
यहाँ ध्यान रखने योग्य बात यह है कि दशमलव बिंदु से बाईं ओर के (अंकों की संख्या) गिनकर, उसमें से 1 घटा कर जो प्राप्त होता है, वही 10 का घातांक होता है, जिसे मानक रूप में प्रयोग किया जाता है। हम इस बिंदु की कल्पना, संख्या के (दाएँ) सिरे पर कर लेते हैं। यहाँ से बाईं ओर अंकों की (संख्या) 11 है। इसलिए, मानक रूप में व्यक्त करने के लिए, 10 का घातांक 11 – 1 = 10 है। इसलिए इसके मानक रूप में 10 का घातांक 4 – 1 = 3 है।
प्रश्नावली 13.3
1. निम्नलिखित संख्याओं को प्रसारित रूप में लिखिए :
279404, 3006194, 2806196, 120719, 20068
2. निम्नलिखित प्रसारित रूपों में से प्रत्येक के लिए संख्या ज्ञात कीजिए :
(a) 8 ×104 + 6 ×103 + 0×102 + 4×101 + 5×100
(b) 4 ×105 + 5×103 + 3×102 + 2×100
(c) 3 ×104 + 7×102 + 5×100
(d) 9 ×105 + 2×102 + 3×101
3. निम्नलिखित संख्याओं को मानक रूप में व्यक्त कीजिए :
(i) 5,00,00,000 (ii) 70,00,000 (iii) 3,18,65,00,000
(iv) 3,90,878 (v) 39087.8 (vi) 3908.78
4. निम्नलिखित कथनों में प्रकट होने वाली (आने वाली) संख्याओं को मानक रूप में व्यक्त कीजिए।
(a) पृथ्वी और चंद्रमा के बीच की दूरी 384,000,000 m है।
(b) निर्वात स्थान में प्रकाश की चाल (या वेग) 300,000,000 m/sec. है।
(c) पृथ्वी का व्यास 12756000 m है।
(d) सूर्य का व्यास 1,400,000,000 m है।
(e) एक आकाशगंगा में औसतन 100,000,000,000 तारे हैं।
(f) विश्व मंडल (या सौर मंडल) 12,000,000,000 वर्ष पुराना आकलित किया गया है।
(g) आकाशगंगा के मध्य से सूर्य की दूरी 300,000,000,000,000,000,000 m आकलित की गई है।
(h) 1.8 g भार वाली पानी की एक बूंद में 60,230,000,000,000,000,000,000 अणु (molecules) होते हैं।
(i) पृथ्वी में 1,353,000,000 km3 समुद्र जल है।
(j) मार्च 2001 में भारत की जनसंख्या 1,027,000,000 थी।
हमने क्या चर्चा की?
1. बहुत बड़ी संख्याएँ पढ़ने, समझने, तुलना करने और उन पर संक्रियाएँ करने की दृष्टि से कठिन होती हैं। इनको सरल बनाने के लिए, हम इन अधिकांश बड़ी संख्याओं को घातांकों का प्रयोग करके संक्षिप्त रूप में लिखते हैं।
2. कुछ संख्याओं के घातांकीय रूप निम्नलिखित हैं :
10000 = 104 (इसे 10 के ऊपर घात 4 पढ़ा जाता है)
243 = 35, 128 = 27.
यहाँ, 10, 3 और 2 आधार हैं तथा 4, 5 और 7 क्रमशः इनके घातांक हैं। हम यह भी कहते हैं कि 10 की चौथी घात 10000 है, 3 की पाँचवीं घात 243 है, इत्यादि।
3. घातांकीय रूप में संख्याएँ कुछ नियमों का पालन करती हैं, जो इस प्रकार हैं :
किन्हीं शून्येतर पूर्णांकों a और b तथा पूर्ण संख्याओं m और n के लिए,
(a) am × an = am+n
(b) am ÷ an = am–n, m > n
(c) (am)n = amn
(d) am × bm = (ab)m
(e) am ÷ bm =
(f) a° = 1
(g) (–1)सम संख्या = 1
(–1)विषम संख्या = – 1