Table of Contents
Chapter 1
Rational Numbers
1.1 Introduction
In Mathematics, we frequently come across simple equations to be solved. For example, the equation
x + 2 = 13 .....................(1)
is solved when x = 11, because this value of x satisfies the given equation. The solution 11 is a natural number. On the other hand, for the equation
x + 5 = 5 ...................(2)
the solution gives the whole number 0 (zero). If we consider only natural numbers, equation (2) cannot be solved. To solve equations like (2), we added the number zero to the collection of natural numbers and obtained the whole numbers. Even whole numbers will not be sufficient to solve equations of type
x + 18 = 5 ..................(3)
Do you see ‘why’? We require the number –13 which is not a whole number. This led us to think of integers, (positive and negative). Note that the positive integers correspond to natural numbers. One may think that we have enough numbers to solve all simple equations with the available list of integers. Now consider the equations
2x = 3 ............................(4)
5x + 7 = 0 ........................(5)

for which we cannot find a solution from the integers. (Check this) We need the numbers 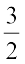 to solve equation (4) and
to solve equation (4) and 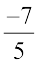 to solve equation (5). This leads us to the collection of rational numbers.
to solve equation (5). This leads us to the collection of rational numbers.
We have already seen basic operations on rational numbers. We now try to explore some properties of operations on the different types of numbers seen so far.
1.2 Properties of Rational Numbers
1.2.1 Closure
(i) Whole numbers
Let us revisit the closure property for all the operations on whole numbers in brief.
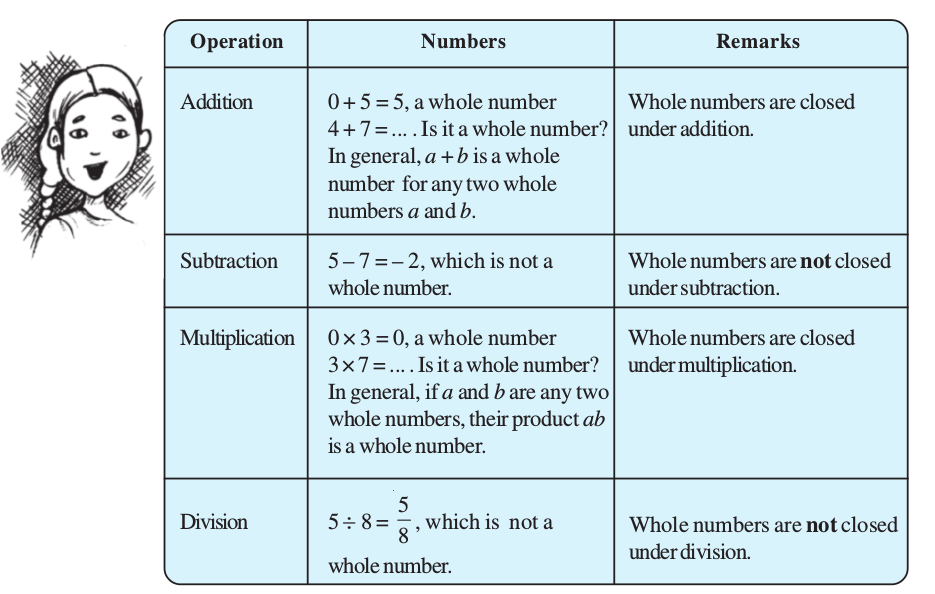
Check for closure property under all the four operations for natural numbers.

(ii) Integers
Let us now recall the operations under which integers are closed.


You have seen that whole numbers are closed under addition and multiplication but not under subtraction and division. However, integers are closed under addition, subtraction and multiplication but not under division.
(iii) Rational numbers
Recall that a number which can be written in the form 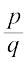 , where p and q are integers and q ≠ 0 is called a rational number. For example,
, where p and q are integers and q ≠ 0 is called a rational number. For example, 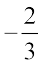 ,
, 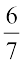 ,
, 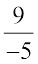 are all rational numbers. Since the numbers 0, –2, 4 can be written in the form
are all rational numbers. Since the numbers 0, –2, 4 can be written in the form 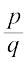 , they are also rational numbers. (Check it!)
, they are also rational numbers. (Check it!)
(a) You know how to add two rational numbers. Let us add a few pairs.
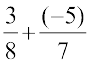 =
= 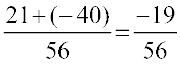 (a rational number)
(a rational number)
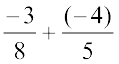 =
= 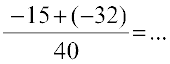 Is it a rational number?
Is it a rational number?
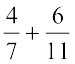 = ... Is it a rational number?
= ... Is it a rational number?
We find that sum of two rational numbers is again a rational number. Check it for a few more pairs of rational numbers.
We say that rational numbers are closed under addition. That is, for any two rational numbers a and b, a + b is also a rational number.
(b) Will the difference of two rational numbers be again a rational number?
We have,
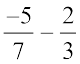 =
= 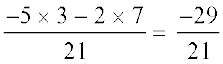 (a rational number)
(a rational number)
 =
= 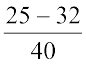 = ... Is it a rational number?
= ... Is it a rational number?
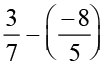 = ... Is it a rational number?
= ... Is it a rational number?
Try this for some more pairs of rational numbers. We find that rational numbers are closed under subtraction. That is, for any two rational numbers a and b, a – b is also a rational number.
(c) Let us now see the product of two rational numbers.
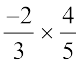 =
= 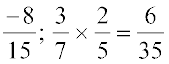 (both the products are rational numbers)
(both the products are rational numbers)
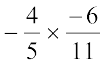 = ... Is it a rational number?
= ... Is it a rational number?
Take some more pairs of rational numbers and check that their product is again a rational number.
We say that rational numbers are closed under multiplication. That is, for any two rational numbers a and b, a × b is also a rational number.
(d) We note that 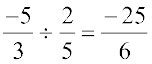 (a rational number)
(a rational number)
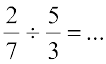 . Is it a rational number?
. Is it a rational number? 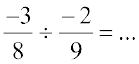 . Is it a rational number?
. Is it a rational number?
Can you say that rational numbers are closed under division?
We find that for any rational number a, a ÷ 0 is not defined.
So rational numbers are not closed under division.
However, if we exclude zero then the collection of, all other rational numbers is closed under division.

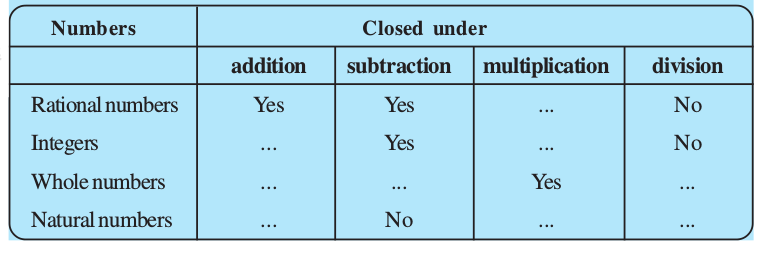
TRY THESE
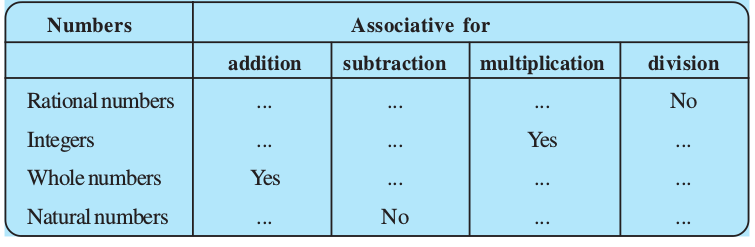
Fill in the blanks in the following table.
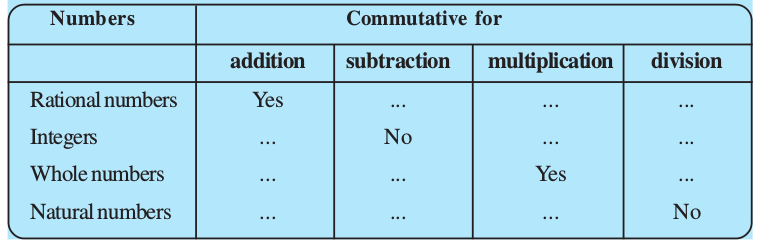
1.2.2 Commutativity


Check whether the commutativity of the operations hold for natural numbers also.
(ii) Integers
Fill in the following table and check the commutativity of different operations for integers:

(iii) Rational numbers
(a) Addition
You know how to add two rational numbers. Let us add a few pairs here.
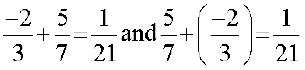
So, 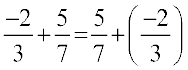
Also, 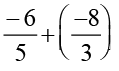 = ... and
= ... and 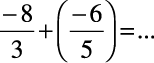
Is  ?
?
Is 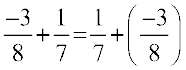 ?
?
You find that two rational numbers can be added in any order. We say that addition is commutative for rational numbers. That is, for any two rational numbers a and b, a + b = b + a.
(b) Subtraction
Is 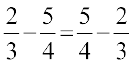 ?
?
Is 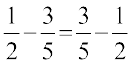 ?
?
You will find that subtraction is not commutative for rational numbers.
Note that subtraction is not commutative for integers and integers are also rational numbers. So, subtraction will not be commutative for rational numbers too.
(c) Multiplication
We have, 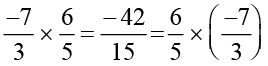
Is 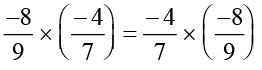 ?
?
Check for some more such products.
You will find that multiplication is commutative for rational numbers.
In general, a × b = b × a for any two rational numbers a and b.
(d) Division
Is 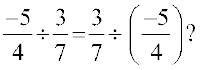
You will find that expressions on both sides are not equal.
So division is not commutative for rational numbers.

TRY THESE

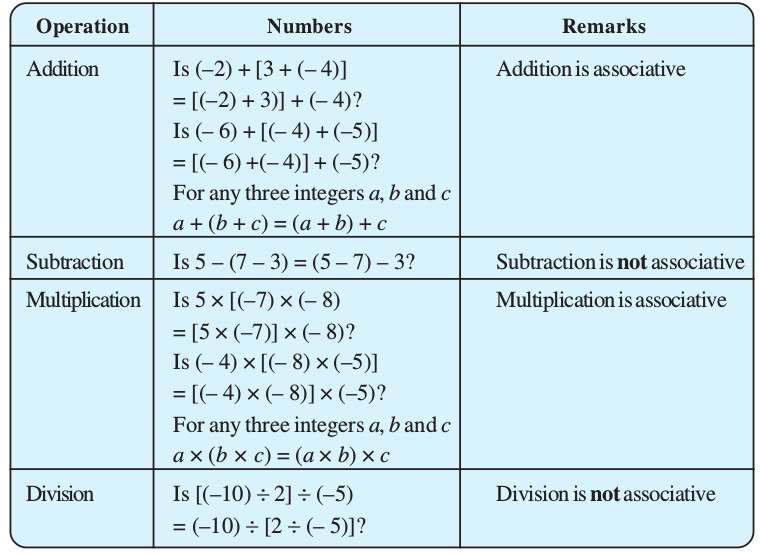
1.2.3 Associativity
(i) Whole numbers
Recall the associativity of the four operations for whole numbers through this table:
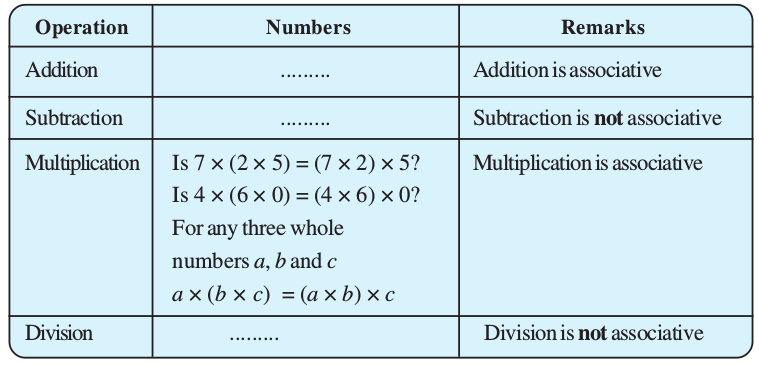
Fill in this table and verify the remarks given in the last column.
Check for yourself the associativity of different operations for natural numbers.

(ii) Integers
Associativity of the four operations for integers can be seen from this table
(iii) Rational numbers
(a) Addition
We have 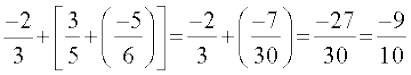
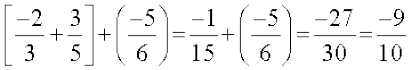
So, 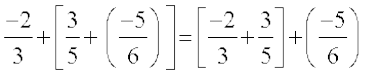
Find 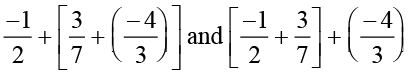 . Are the two sums equal?
. Are the two sums equal?
Take some more rational numbers, add them as above and see if the two sums are equal. We find that addition is associative for rational numbers. That is, for any three rational numbers a, b and c, a + (b + c) = (a + b) + c.

You already know that subtraction is not associative for integers, then what about rational numbers.
Is 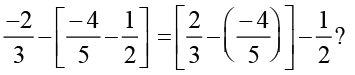
Check for yourself.
Subtraction is not associative for rational numbers.
(c) Multiplication
Let us check the associativity for multiplication.
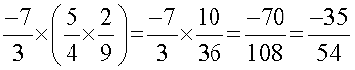
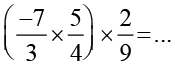
We find that 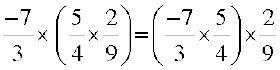
Is 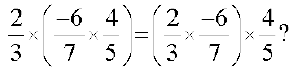
Take some more rational numbers and check for yourself.
We observe that multiplication is associative for rational numbers. That is for any three rational numbers a, b and c, a × (b × c) = (a × b) × c.
(d) Division
Recall that division is not associative for integers, then what about rational numbers?
Let us see if 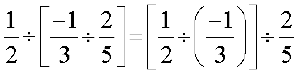
We have, LHS = 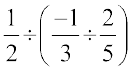 =
=  (reciprocal of
(reciprocal of  is
is 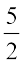 )
)
= 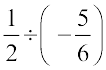 = ...
= ...

RHS = 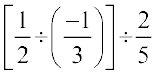
= 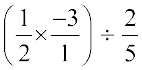 =
= 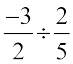 = ...
= ...
Is LHS = RHS? Check for yourself. You will find that division is
not associative for rational numbers.

TRY THESE
Example 1: Find 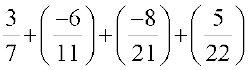
Solution: 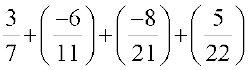
=  (Note that 462 is the LCM of 7, 11, 21 and 22)
(Note that 462 is the LCM of 7, 11, 21 and 22)
= 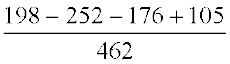 =
= 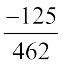
We can also solve it as.
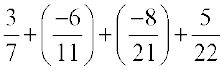
= 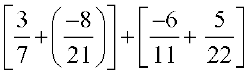 (by using commutativity and associativity)
(by using commutativity and associativity)
= 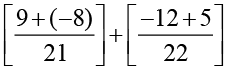 (LCM of 7 and 21 is 21;LCM of 11 and 22 is 22)
(LCM of 7 and 21 is 21;LCM of 11 and 22 is 22)
= 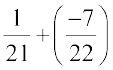 =
= 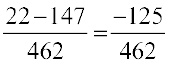
Do you think the properties of commutativity and associativity made the calculations easier?
Example 2: Find 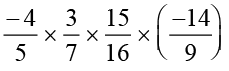
Solution: We have

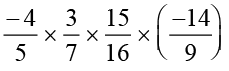
= 
= 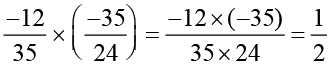
We can also do it as.
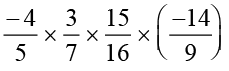
= 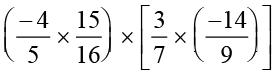 (Using commutativity and associativity)
(Using commutativity and associativity)
= 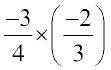 =
= 
1.2.4 The role of zero (0)
Look at the following.
2 + 0 = 0 + 2 = 2 (Addition of 0 to a whole number)
– 5 + 0 = ... + ... = – 5 (Addition of 0 to an integer)
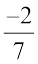 + ... = 0 +
+ ... = 0 + 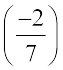 =
= 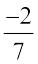 (Addition of 0 to a rational number)
(Addition of 0 to a rational number)
You have done such additions earlier also. Do a few more such additions.
What do you observe? You will find that when you add 0 to a whole number, the sum is again that whole number. This happens for integers and rational numbers also.
In general, a + 0 = 0 + a = a, where a is a whole number
b + 0 = 0 + b = b, where b is an integer
c + 0 = 0 + c = c, where c is a rational number
Zero is called the identity for the addition of rational numbers. It is the additive identity for integers and whole numbers as well.
1.2.5 The role of 1
We have,
5 × 1 = 5 = 1 × 5 (Multiplication of 1 with a whole number)
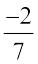 × 1 = ... × ... =
× 1 = ... × ... = 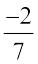
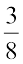 × ... = 1 ×
× ... = 1 × 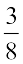 =
= 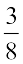
What do you find?
You will find that when you multiply any rational number with 1, you get back the same rational number as the product. Check this for a few more rational numbers. You will find that, a × 1 = 1 × a = a for any rational number a.
We say that 1 is the multiplicative identity for rational numbers.
Is 1 the multiplicative identity for integers? For whole numbers?
THINK, DISCUSS AND WRITE
If a property holds for rational numbers, will it also hold for integers? For whole numbers? Which will? Which will not?

1.2.6 Negative of a number
While studying integers you have come across negatives of integers. What is the negative of 1? It is – 1 because 1 + (– 1) = (–1) + 1 = 0
So, what will be the negative of (–1)? It will be 1.
Also, 2 + (–2) = (–2) + 2 = 0, so we say 2 is the negative or additive inverse of
–2 and vice-versa. In general, for an integer a, we have, a + (– a) = (– a) + a = 0; so, a is the negative of – a and – a is the negative of a.
For the rational number 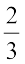 , we have,
, we have,
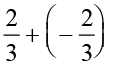 =
= 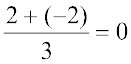
Also,  = 0 (How?)
= 0 (How?)
Similarly, 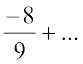 =
= 
 =
= 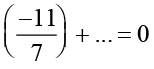
In general, for a rational number 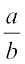 , we have,
, we have,  . We say that
. We say that 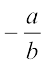 is the additive inverse of
is the additive inverse of 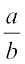 and
and 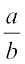 is the additive inverse of
is the additive inverse of 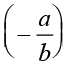 .
.
1.2.7 Reciprocal
By which rational number would you multiply 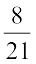 , to get the product 1? Obviously by
, to get the product 1? Obviously by 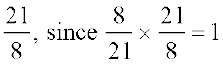 .
.
Similarly, 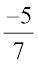 must be multiplied by
must be multiplied by 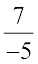 so as to get the product 1.
so as to get the product 1.
We say that 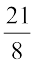 is the reciprocal of
is the reciprocal of 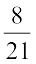 and
and 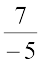 is the reciprocal of
is the reciprocal of 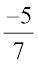 .
.
Can you say what is the reciprocal of 0 (zero)?
Is there a rational number which when multiplied by 0 gives 1? Thus, zero has no reciprocal.
We say that a rational number 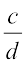 is called the reciprocal or multiplicative inverse of another non-zero rational number
is called the reciprocal or multiplicative inverse of another non-zero rational number 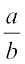 if
if 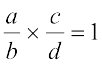 .
.
1.2.8 Distributivity of multiplication over addition for rational numbers
To understand this, consider the rational numbers 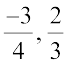 and
and 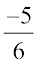 .
.
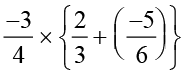 =
= 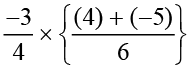
= 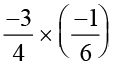 =
= 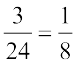
Also 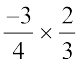 =
= 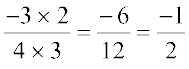
And 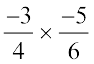 =
= 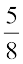
Therefore  =
= 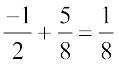
Thus, 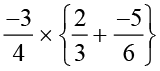 =
= 
TRY THESE
Find using distributivity. (i)  (ii)
(ii) 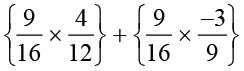
Distributivity of Multi-plication over Addition and Subtraction.
For all rational numbers a, b and c,
a (b + c) = ab + ac
a (b – c) = ab – ac
Example 3: Write the additive inverse of the following:
(i) 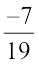 (ii)
(ii) 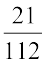

Solution:
(i) 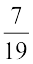 is the additive inverse of
is the additive inverse of 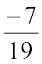 because
because 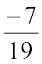 +
+ 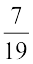 =
= 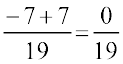 = 0
= 0
(ii) The additive inverse of 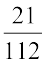 is
is 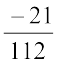 (Check!)
(Check!)
Example 4: Verify that – (– x) is the same as x for
(i) x = 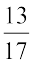 (ii)
(ii) 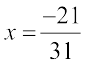
Solution: (i) We have, x = 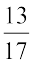
The additive inverse of x = 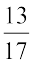 is – x =
is – x = 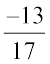 since
since 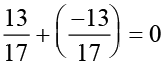 .
.
The same equality 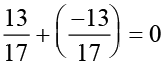 , shows that the additive inverse of
, shows that the additive inverse of 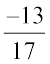 is
is 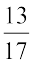
or 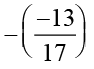 =
= 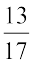 , i.e., – (– x) = x.
, i.e., – (– x) = x.
(ii) Additive inverse of 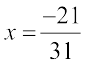 is – x =
is – x = 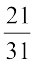 since
since 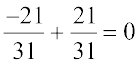 .
.
The same equality 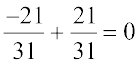 , shows that the additive inverse of
, shows that the additive inverse of 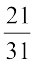 is
is 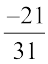 , i.e., – (– x) = x.
, i.e., – (– x) = x.
Example 5: Find 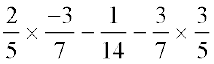
Solution:  =
= 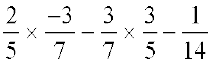 (by commutativity)
(by commutativity)
= 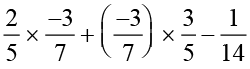
= 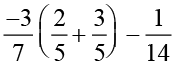 (by distributivity)
(by distributivity)
= 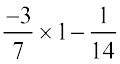 =
= 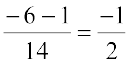

Exercise 1.1
1. Using appropriate properties find.
(i) 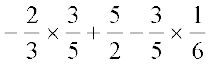 (ii)
(ii) 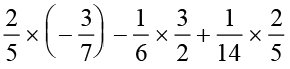
2. Write the additive inverse of each of the following.
(i) 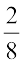 (ii)
(ii) 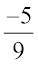 (iii)
(iii) 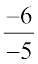 (iv)
(iv) 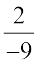 (v)
(v) 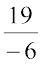
3. Verify that – (– x) = x for.
(i) x = 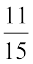 (ii)
(ii) 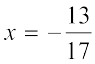
4. Find the multiplicative inverse of the following.
(i) – 13 (ii) 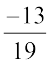 (iii)
(iii) 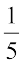 (iv)
(iv) 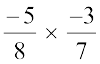
(v) – 1 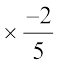 (vi) – 1
(vi) – 1
5. Name the property under multiplication used in each of the following.
(i) 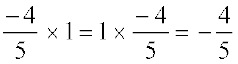 (ii)
(ii) 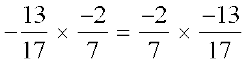
(iii) 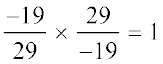
6. Multiply 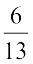 by the reciprocal of
by the reciprocal of 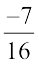 .
.
7. Tell what property allows you to compute  .
.
8. Is 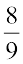 the multiplicative inverse of
the multiplicative inverse of 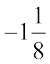 ? Why or why not?
? Why or why not?
9. Is 0.3 the multiplicative inverse of 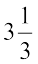 ? Why or why not?
? Why or why not?
10. Write.
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
11. Fill in the blanks.
(i) Zero has ________ reciprocal.
(ii) The numbers ________ and ________ are their own reciprocals
(iii) The reciprocal of – 5 is ________.
(iv) Reciprocal of 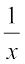 , where x ≠ 0 is ________.
, where x ≠ 0 is ________.
(v) The product of two rational numbers is always a _______.
(vi) The reciprocal of a positive rational number is ________.
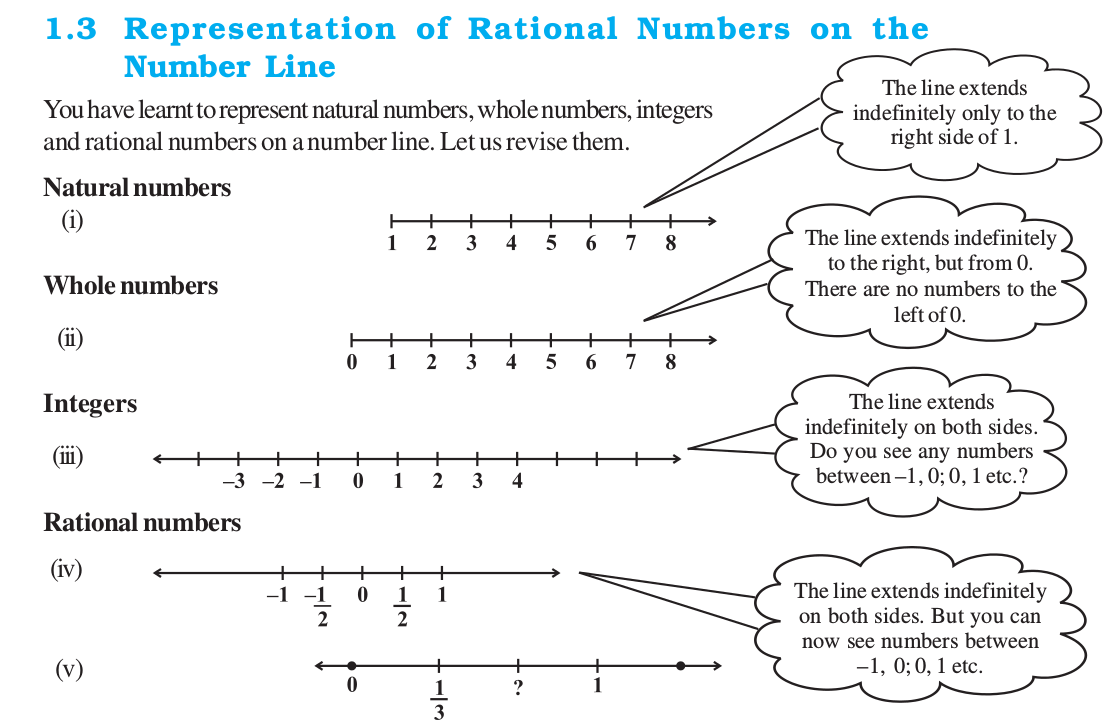
The point on the number line (iv) which is half way between 0 and 1 has been
labelled 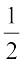 . Also, the first of the equally spaced points that divides the distance between
. Also, the first of the equally spaced points that divides the distance between
0 and 1 into three equal parts can be labelled 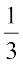 , as on number line (v). How would you label the second of these division points on number line (v)?
, as on number line (v). How would you label the second of these division points on number line (v)?
The point to be labelled is twice as far from and to the right of 0 as the point
labelled 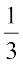 . So it is two times
. So it is two times 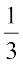 , i.e.,
, i.e., 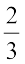 . You can continue to label equally-spaced points on the number line in the same way. In this continuation, the next marking is 1. You can
. You can continue to label equally-spaced points on the number line in the same way. In this continuation, the next marking is 1. You can
see that 1 is the same as 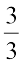 .
.
Then comes 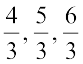 (or 2),
(or 2), 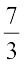 and so on as shown on the number line (vi)
and so on as shown on the number line (vi)
(vi) 
Similarly, to represent 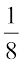 , the number line may be divided into eight equal parts as shown:
, the number line may be divided into eight equal parts as shown: 
We use the number 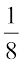 to name the first point of this division. The second point of division will be labelled
to name the first point of this division. The second point of division will be labelled 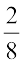 , the third point
, the third point 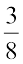 , and so on as shown on number
, and so on as shown on number
line (vii)
(vii) 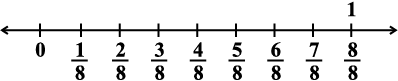
Any rational number can be represented on the number line in this way. In a rational number, the numeral below the bar, i.e., the denominator, tells the number of equal parts into which the first unit has been divided. The numeral above the bar i.e., the numerator, tells ‘how many’ of these parts are considered. So, a rational number such as  means four of nine equal parts on the right of 0 (number line viii) and
means four of nine equal parts on the right of 0 (number line viii) and
for 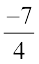 , we make 7 markings of distance
, we make 7 markings of distance 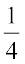 each on the left of zero and starting from 0. The seventh marking is
each on the left of zero and starting from 0. The seventh marking is 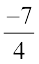 [number line (ix)].
[number line (ix)].
(viii) 
(ix) 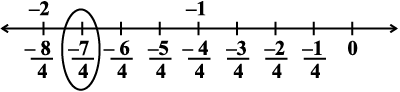

TRY THESE
Write the rational number for each point labelled with a letter.
(i) 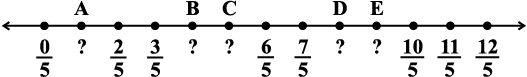
(ii) 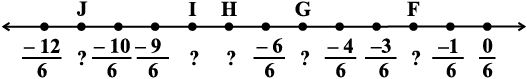
1.4 Rational Numbers between Two Rational Numbers
Can you tell the natural numbers between 1 and 5? They are 2, 3 and 4.
How many natural numbers are there between 7 and 9? There is one and it is 8.
How many natural numbers are there between 10 and 11? Obviously none.
List the integers that lie between –5 and 4. They are – 4, – 3, –2, –1, 0, 1, 2, 3.
How many integers are there between –1 and 1?
How many integers are there between –9 and –10?
You will find a definite number of natural numbers (integers) between two natural numbers (integers).
How many rational numbers are there between 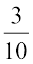 and
and 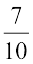 ?
?
You may have thought that they are only 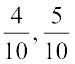 and
and 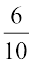 .
.
But you can also write 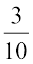 as
as 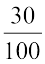 and
and 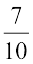 as
as 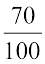 . Now the numbers,
. Now the numbers, 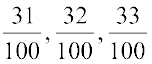
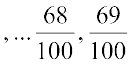 , are all between
, are all between 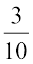 and
and 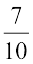 . The number of these rational numbers is 39.
. The number of these rational numbers is 39.
Also 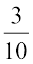 can be expressed as
can be expressed as  and
and 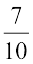 as
as  . Now, we see that the rational numbers
. Now, we see that the rational numbers 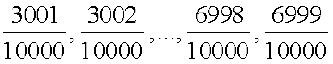 are between
are between 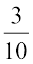 and
and 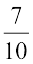 . These are 3999 numbers in all.
. These are 3999 numbers in all.
In this way, we can go on inserting more and more rational numbers between 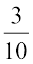
and 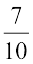 . So unlike natural numbers and integers, the number of rational numbers between two rational numbers is not definite. Here is one more example.
. So unlike natural numbers and integers, the number of rational numbers between two rational numbers is not definite. Here is one more example.
How many rational numbers are there between 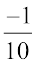 and
and 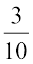 ?
?
Obviously 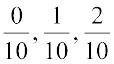 are rational numbers between the given numbers.
are rational numbers between the given numbers.
If we write 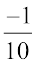 as
as  and
and 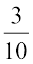 as
as 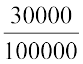 , we get the rational numbers
, we get the rational numbers 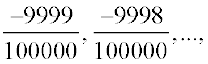
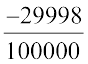 ,
, 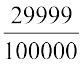 , between
, between 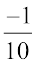 and
and 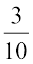 .
.
You will find that you get countless rational numbers between any two given rational numbers.
Example 6: Write any 3 rational numbers between –2 and 0.
Solution: –2 can be written as 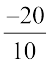 and 0 as
and 0 as 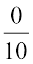 .
.
Thus we have 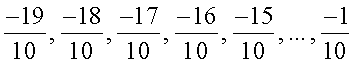 between –2 and 0.
between –2 and 0.
You can take any three of these.
Example 7: Find any ten rational numbers between 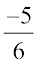 and
and 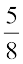 .
.
Solution: We first convert 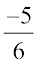 and
and 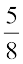 to rational numbers with the same denominators.
to rational numbers with the same denominators.
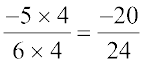 and
and 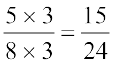
Thus we have 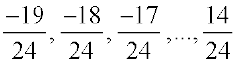 as the rational numbers between
as the rational numbers between 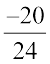 and
and 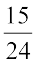 .
.
You can take any ten of these.
Another Method
Let us find rational numbers between 1 and 2. One of them is 1.5 or 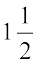 or
or 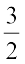 . This is the mean of 1 and 2. You have studied mean in Class VII.
. This is the mean of 1 and 2. You have studied mean in Class VII.
We find that between any two given numbers, we need not necessarily get an integer but there will always lie a rational number.
We can use the idea of mean also to find rational numbers between any two given rational numbers.
Example 8: Find a rational number between 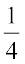 and
and 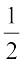 .
.
Solution: We find the mean of the given rational numbers.  =
= 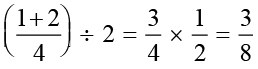
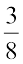 lies between
lies between 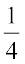 and
and 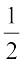 .
.
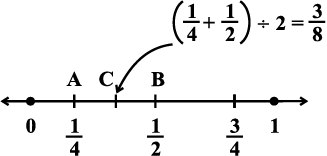
This can be seen on the number line also.
We find the mid point of AB which is C, represented by  =
= 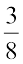 .
.
We find that 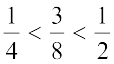 .
.
If a and b are two rational numbers, then 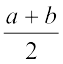 is a rational number between a and b such that a <
is a rational number between a and b such that a < 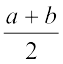 < b.
< b.
This again shows that there are countless number of rational numbers between any two given rational numbers.
Example 9: Find three rational numbers between 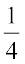 and
and 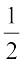 .
.
Solution: We find the mean of the given rational numbers.
As given in the above example, the mean is 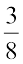 and
and 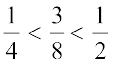 .
.
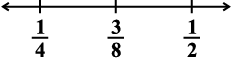
We now find another rational number between 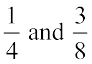 . For this, we again find the mean of
. For this, we again find the mean of 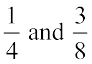 . That is,
. That is, 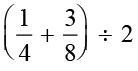 =
= 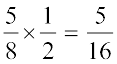
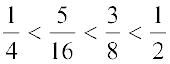
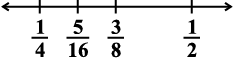
Now find the mean of  . We have,
. We have, 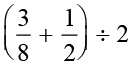 =
= 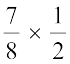 =
= 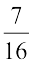
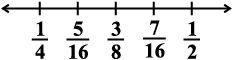
Thus we get 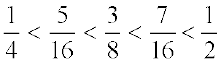 .
.
Thus, 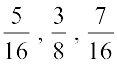 are the three rational numbers between
are the three rational numbers between 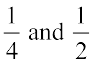 .
.
This can clearly be shown on the number line as follows:
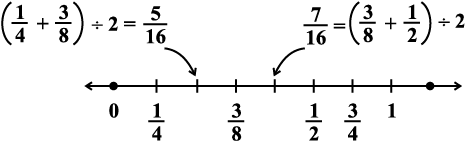
In the same way we can obtain as many rational numbers as we want between two given rational numbers . You have noticed that there are countless rational numbers between any two given rational numbers.

Exercise 1.2
1. Represent these numbers on the number line. (i) 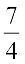 (ii)
(ii) 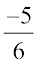
2. Represent 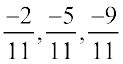 on the number line.
on the number line.
3. Write five rational numbers which are smaller than 2.
4. Find ten rational numbers between 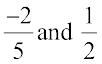 .
.
5. Find five rational numbers between.
(i) 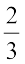 and
and  (ii)
(ii) 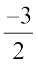 and
and 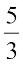 (iii)
(iii) 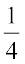 and
and 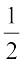
6. Write five rational numbers greater than –2.
7. Find ten rational numbers between 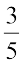 and
and 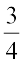 .
.
What have we Discussed?
1. Rational numbers are closed under the operations of addition, subtraction and multiplication.
2. The operations addition and multiplication are
(i) commutative for rational numbers.
(ii) associative for rational numbers.
3. The rational number 0 is the additive identity for rational numbers.
4. The rational number 1 is the multiplicative identity for rational numbers.
5. The additive inverse of the rational number 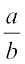 is
is 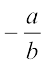 and vice-versa.
and vice-versa.
6. The reciprocal or multiplicative inverse of the rational number 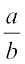 is
is 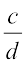 if
if 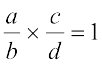 .
.
7. Distributivity of rational numbers: For all rational numbers a, b and c,
a(b + c) = ab + ac and a(b – c) = ab – ac
8. Rational numbers can be represented on a number line.
9. Between any two given rational numbers there are countless rational numbers. The idea of mean helps us to find rational numbers between two rational numbers.
