Table of Contents
Chapter 4
Practical Geometry
4.1 Introduction
You have learnt how to draw triangles in Class VII. We require three measurements (of sides and angles) to draw a unique triangle.
Since three measurements were enough to draw a triangle, a natural question arises whether four measurements would be sufficient to draw a unique four sided closed figure, namely, a quadrilateral.

Do This
Take a pair of sticks of equal lengths, say 10 cm. Take another pair of sticks of equal lengths, say, 8 cm. Hinge them up suitably to get a rectangle of length 10 cm and breadth 8 cm.
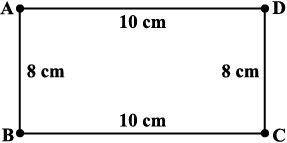
Fig 4.1
This rectangle has been created with the 4 available measurements.
Now just push along the breadth of the rectangle. Is the new shape obtained, still a rectangle (Fig 4.2)? Observe that the rectangle has now become a parallelogram.
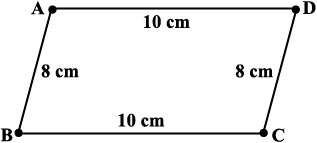
Fig 4.2
Have you altered the lengths of the sticks? No! The measurements of sides remain the same.
Give another push to the newly obtained shape in a different direction; what do you get? You again get a parallelogram, which is altogether different (Fig 4.3), yet the four measurements remain the same.
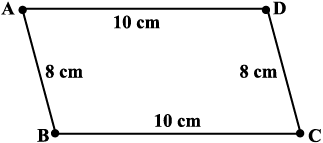
Fig 4.3
This shows that 4 measurements of a quadrilateral cannot determine it uniquely. Can 5 measurements determine a quadrilateral uniquely? Let us go back to the activity!
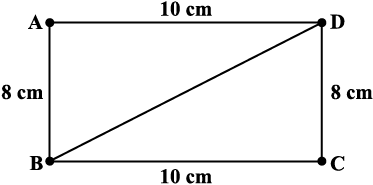
Fig 4.4
You have constructed a rectangle with two sticks each of length 10 cm and other two sticks each of length 8 cm. Now introduce another stick of length equal to BD and tie it along BD (Fig 4.4). If you push the breadth now, does the shape change? No! It cannot, without making the figure open. The introduction of the fifth stick has fixed the rectangle uniquely, i.e., there is no other quadrilateral (with the given lengths of sides) possible now.
Thus, we observe that five measurements can determine a quadrilateral uniquely. But will any five measurements (of sides and angles) be sufficient to draw a unique quadrilateral?

THINK DISCUSS AND WRITE
Arshad has five measurements of a quadrilateral ABCD. These are AB = 5 cm, ∠A = 50°, AC = 4 cm, BD = 5 cm and AD = 6 cm. Can he construct a unique quadrilateral? Give reasons for your answer.
4.2 Constructing a Quadrilateral
We shall learn how to construct a unique quadrilateral given the following measurements:
• When four sides and one diagonal are given.
• When two diagonals and three sides are given.
• When two adjacent sides and three angles are given.
• When three sides and two included angles are given.
• When other special properties are known.
Let us take up these constructions one-by-one.
4.2.1 When the lengths of four sides and a diagonal are given
We shall explain this construction through an example.
Example 1: Construct a quadrilateral PQRS where PQ = 4 cm,QR = 6 cm, RS = 5 cm, PS = 5.5 cm and PR = 7 cm.
Solution: [A rough sketch will help us in visualising the quadrilateral. We draw this first and mark the measurements.] (Fig 4.5)
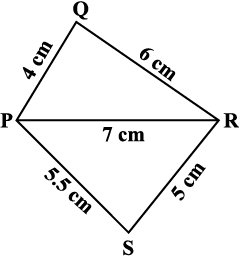
Fig 4.5
Step 1 From the rough sketch, it is easy to see that ∆PQR can be constructed using SSS construction condition. Draw ∆PQR (Fig 4.6).
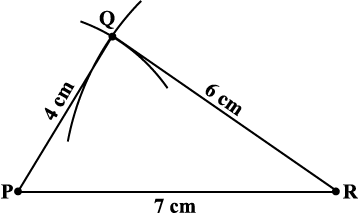
Fig 4.6
Step 2 Now, we have to locate the fourth point S. This ‘S’ would be on the side opposite to Q with reference to PR. For that, we have two measurements.
S is 5.5 cm away from P. So, with P as centre, draw an arc of radius 5.5 cm. (The point S is somewhere on this arc!) (Fig 4.7).
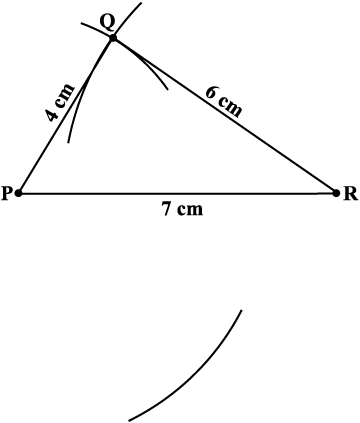
Fig 4.7
Step 3 S is 5 cm away from R. So with R as centre, draw an arc of radius 5 cm (The point S is somewhere on this arc also!) (Fig 4.8).
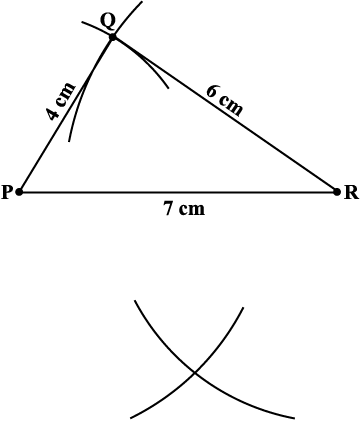
Fig 4.8

Step 4 S should lie on both the arcs drawn. So it is the point of intersection of the two arcs. Mark S and complete PQRS. PQRS is the required quadrilateral
(Fig 4.9).
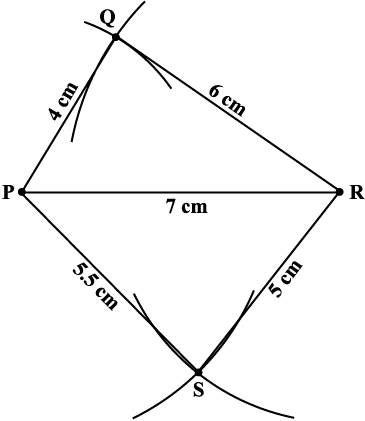
Fig 4.9

THINK, DISCUSS AND WRITE
(i) We saw that 5 measurements of a quadrilateral can determine a quadrilateral uniquely. Do you think any five measurements of the quadrilateral can do this?
AS = 6.5 cm? Why?
(iii) Can you draw a rhombus ZEAL where ZE = 3.5 cm, diagonal EL = 5 cm? Why?
(iv) A student attempted to draw a quadrilateral PLAY where PL = 3 cm, LA = 4 cm, AY = 4.5 cm, PY = 2 cm and LY = 6 cm, but could not draw it. What is the reason?
[Hint: Discuss it using a rough sketch].

Exercise 4.1
1. Construct the following quadrilaterals.
(i) Quadrilateral ABCD.
AB = 4.5 cm
BC = 5.5 cm
CD = 4 cm
AD = 6 cm
AC = 7 cm
(ii) Quadrilateral JUMP
JU = 3.5 cm
UM = 4 cm
MP = 5 cm
PJ = 4.5 cm
PU = 6.5 cm
(iii) Parallelogram MORE
OR = 6 cm
RE = 4.5 cm
EO = 7.5 cm
(iv) Rhombus BEST
BE = 4.5 cm
ET = 6 cm
4.2.2 When two diagonals and three sides are given
When four sides and a diagonal were given, we first drew a triangle with the available data and then tried to locate the fourth point. The same technique is used here.
Example 2: Construct a quadrilateral ABCD, given that BC = 4.5 cm, AD = 5.5 cm, CD = 5 cm the diagonal AC = 5.5 cm and diagonal BD = 7 cm.
Solution:
Here is the rough sketch of the quadrilateral ABCD (Fig 4.10). Studying this sketch, we can easily see that it is possible to draw ∆ ACD first (How?).
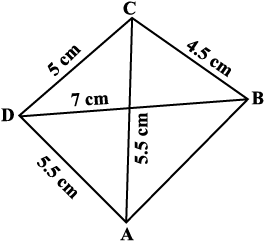
Fig 4.10
Step 1 Draw ∆ ACD using SSS construction (Fig 4.11).
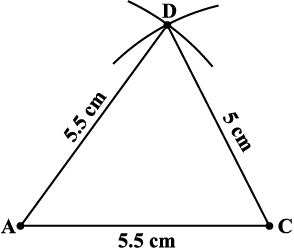
Fig 4.11
(We now need to find B at a distance of 4.5 cm from C and 7 cm from D).
Step 2 With D as centre, draw an arc of radius 7 cm. (B is somewhere on this arc) (Fig 4.12).
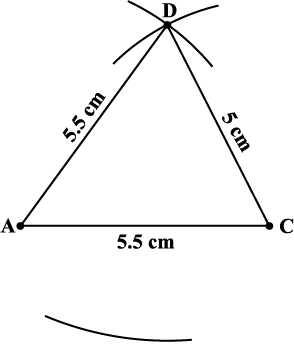
Fig 4.12
Step 3 With C as centre, draw an arc of radius 4.5 cm (B is somewhere on this arc also) (Fig 4.13).
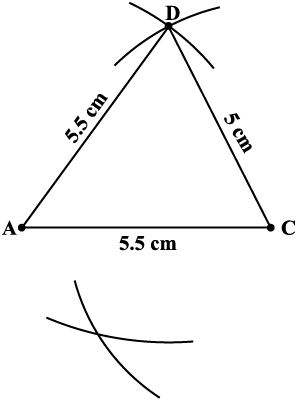
Fig 4.13
Step 4 Since B lies on both the arcs, B is the point intersection of the two arcs. Mark B and complete ABCD.
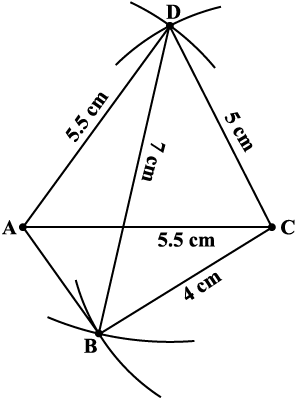
Fig 4.14
ABCD is the required quadrilateral (Fig 4.14).

THINK, DISCUSS AND WRITE
1. In the above example, can we draw the quadrilateral by drawing ∆ ABD first and then find the fourth point C?
Exercise 4.2
1. Construct the following quadrilaterals.
(i) quadrilateral LIFT
LI = 4 cm
IF = 3 cm
TL = 2.5 cm
LF = 4.5 cm
IT = 4 cm
(ii) Quadrilateral GOLD
OL = 7.5 cm
GL = 6 cm
GD = 6 cm
LD = 5 cm
OD = 10 cm
(iii) Rhombus BEND
BN = 5.6 cm
DE = 6.5 cm
4.2.3 When two adjacent sides and three angles are known
As before, we start with constructing a triangle and then look for the fourth point to complete the quadrilateral.
Example 3: Construct a quadrilateral MIST where MI = 3.5 cm, IS = 6.5 cm,
∠M = 75°, ∠I = 105° and ∠S = 120°.
Solution:
Here is a rough sketch that would help us in deciding our steps of construction. We give only hints for various steps (Fig 4.15).
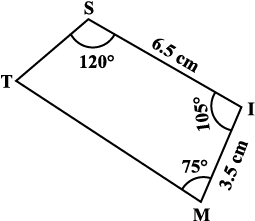
Fig 4.15
Step 1 How do you locate the points? What choice do you make for the base and what is the first step? (Fig 4.16)
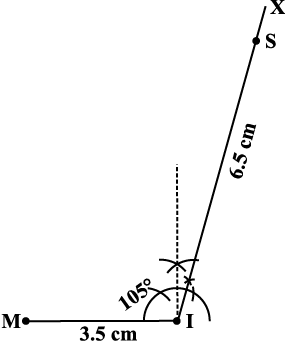
Fig 4.16

Step 2 Make ∠ISY = 120° at S (Fig 4.17).
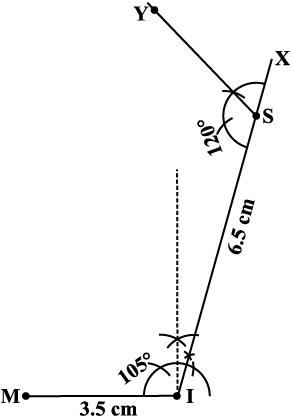
Fig 4.17
Step 3 Make ∠IMZ = 75° at M. (where will SY and MZ meet?) Mark that point as T.
We get the required quadrilateral MIST (Fig 4.18).
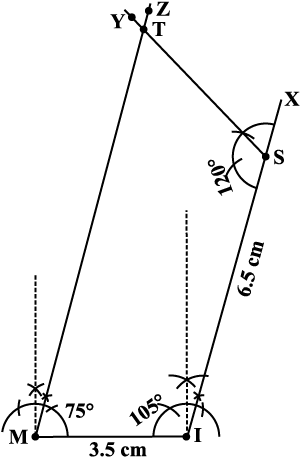
Fig 4.18

THINK, DISCUSS AND WRITE
1. Can you construct the above quadrilateral MIST if we have 100° at M instead of 75°?
3. In a parallelogram, the lengths of adjacent sides are known. Do we still need measures of the angles to construct as in the example above?

Exercise 4.3
1. Construct the following quadrilaterals.
(i) Quadrilateral MORE
MO = 6 cm
OR = 4.5 cm
∠M = 60°
∠O = 105°
∠R = 105°
(ii) Quadrilateral PLAN
PL = 4 cm
LA = 6.5 cm
∠P = 90°
∠A = 110°
∠N = 85°
(iii) Parallelogram HEAR
HE = 5 cm
EA = 6 cm
∠R = 85°
(iv) Rectangle OKAY
OK = 7 cm
KA = 5 cm
4.2.4 When three sides and two included angles are given
Under this type, when you draw a rough sketch, note carefully the “included” angles in particular.
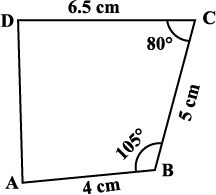
Fig 4.19
Example 4: Construct a quadrilateral ABCD, where
AB = 4 cm, BC = 5 cm, CD = 6.5 cm and ∠B = 105° and
∠C = 80°.
Solution:
We draw a rough sketch, as usual, to get an idea of how we can start off. Then we can devise a plan to locate the four points (Fig 4.19).
Step 1 Start with taking BC = 5 cm on B. Draw an angle of 105° along BX. Locate A 4 cm away on this. We now have B, C and A (Fig 4.20).
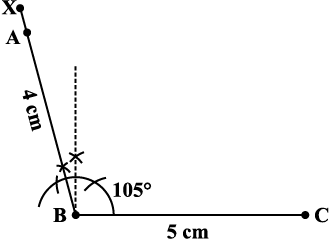
Fig 4.20

Step 2 The fourth point D is on CY which is inclined at 80° to BC. So make ∠BCY = 80° at C on BC (Fig 4.21).
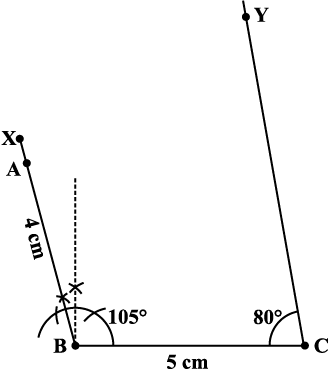
Fig 4.21
Step 3 D is at a distance of 6.5 cm on CY. With C as centre, draw an arc of length 6.5 cm. It cuts CY at D (Fig 4.22).
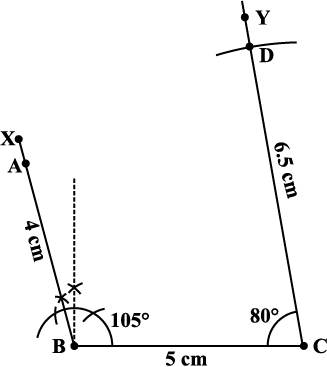
Fig 4.22
Step 4 Complete the quadrilateral ABCD. ABCD is the required quadrilateral (Fig 4.23).
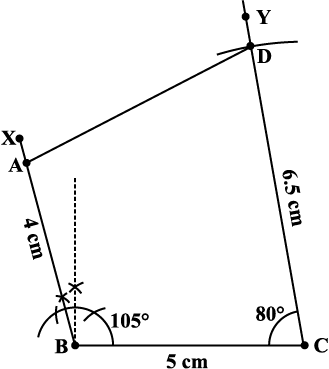
Fig 4.23

THINK, DISCUSS AND WRITE
1. In the above example, we first drew BC. Instead, what could have been be the other starting points?
2. We used some five measurements to draw quadrilaterals so far. Can there be different sets of five measurements (other than seen so far) to draw a quadrilateral? The following problems may help you in answering the question.
(i) Quadrilateral ABCD with AB = 5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm and ∠B = 80°.
(ii) Quadrilateral PQRS with PQ = 4.5 cm, ∠P = 70°, ∠Q = 100°, ∠R = 80° and ∠S = 110°.
Construct a few more examples of your own to find sufficiency/insufficiency of the data for construction of a quadrilateral.

Exercise 4.4
1. Construct the following quadrilaterals.
(i) Quadrilateral DEAR
DE = 4 cm
EA = 5 cm
AR = 4.5 cm
∠E = 60°
∠A = 90°
(ii) Quadrilateral TRUE
TR = 3.5 cm
RU = 3 cm
UE = 4 cm
∠R = 75°
∠U = 120°
4.3 Some Special Cases
To draw a quadrilateral, we used 5 measurements in our work. Is there any quadrilateral which can be drawn with less number of available measurements? The following examples examine such special cases.
Example 5: Draw a square of side 4.5 cm.
Solution: Initially it appears that only one measurement has been given. Actually we have many more details with us, because the figure is a special quadrilateral, namely a square. We now know that each of its angles is a right angle. (See the rough figure) (Fig 4.24)
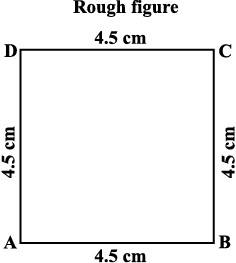
Fig 4.24
This enables us to draw ∆ ABC using SAS condition. Then D can be easily located. Try yourself now to draw the square with the given measurements.
Example 6: Is it possible to construct a rhombus ABCD where AC = 6 cm and BD = 7 cm? Justify your answer.
Solution: Only two (diagonal) measurements of the rhombus are given. However, since it is a rhombus, we can find more help from its properties.
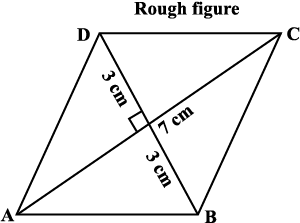
Fig 4.25
The diagonals of a rhombus are perpendicular bisectors of one another.
So, first draw AC = 7 cm and then construct its perpendicular bisector. Let them meet at 0. Cut off 3 cm lengths on either side of the drawn bisector. You now get B and D.
Draw the rhombus now, based on the method described above (Fig 4.25).
Try These
1. How will you construct a rectangle PQRS if you know only the lengths PQ and QR?
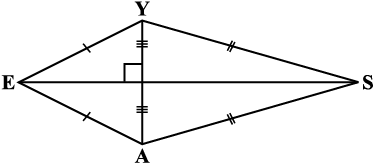
Fig 4.26
2. Construct the kite EASY if AY = 8 cm, EY = 4 cm and SY = 6 cm (Fig 4.26). Which properties of the kite did you use in the process?

Exercise 4.5
Draw the following.
1. The square READ with RE = 5.1 cm.
2. A rhombus whose diagonals are 5.2 cm and 6.4 cm long.
3. A rectangle with adjacent sides of lengths 5 cm and 4 cm.
4. A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm. Is it unique?
What have we Discussed?
1. Five measurements can determine a quadrilateral uniquely.
2. A quadrilateral can be constructed uniquely if the lengths of its four sides and a diagonal is given.
3. A quadrilateral can be constructed uniquely if its two diagonals and three sides are known.
4. A quadrilateral can be constructed uniquely if its two adjacent sides and three angles are known.
5. A quadrilateral can be constructed uniquely if its three sides and two included angles are given.

