Table of Contents
10.1 Introduction
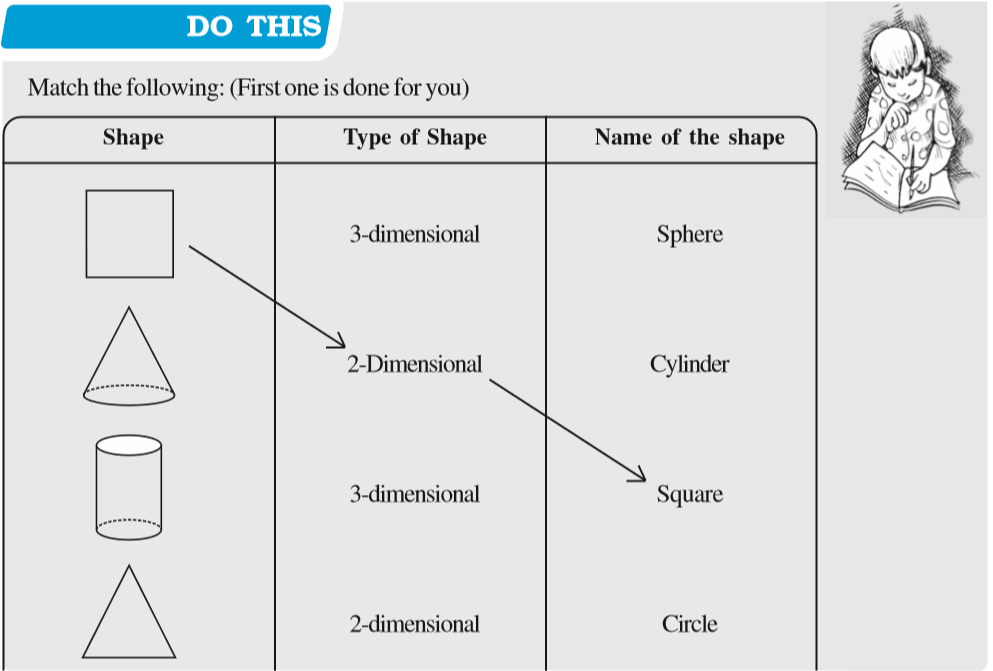
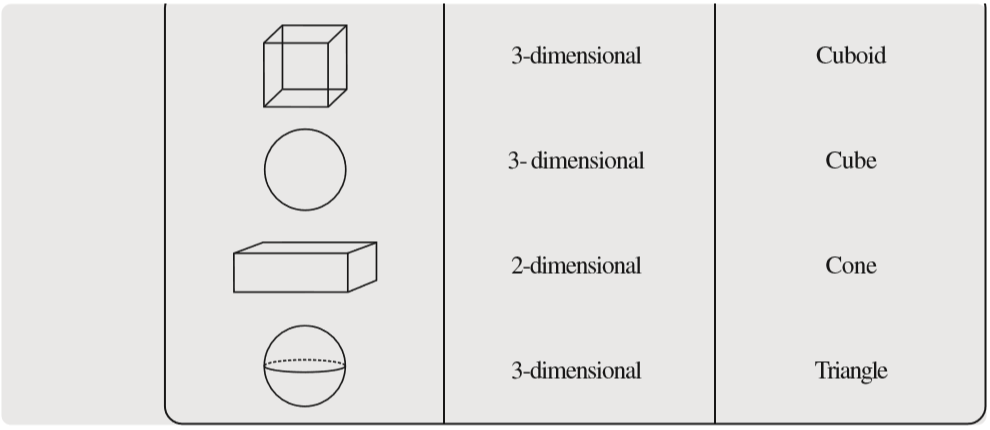
In Class VII, you have learnt about plane shapes and solid shapes. Plane shapes have two measurements like length and breadth and therefore they are called two-dimensional shapes whereas a solid object has three measurements like length, breadth, height or depth. Hence, they are called three-dimensional shapes. Also, a solid object occupies some space.
Two-dimensional and three-dimensional figures can also be briefly named as 2-D and 3-D figures. You may recall that triangle, rectangle, circle etc., are 2-D figures while cubes, cylinders, cones, spheres etc. are three-dimensional figures.
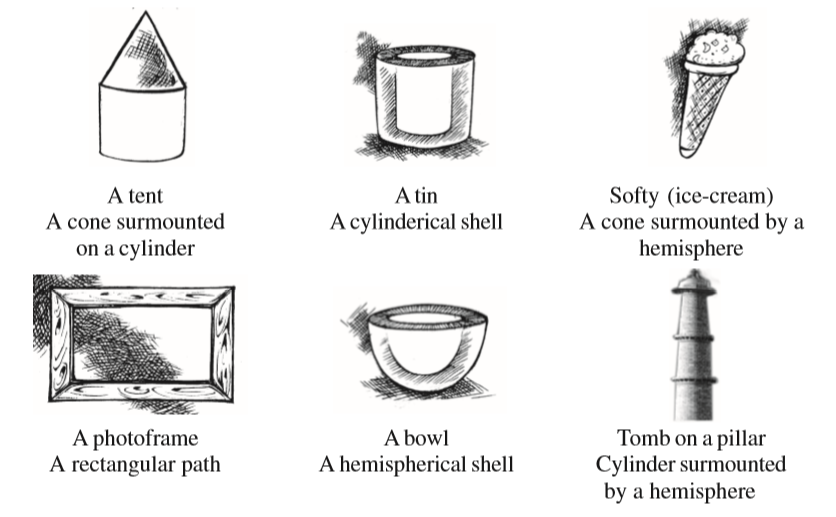
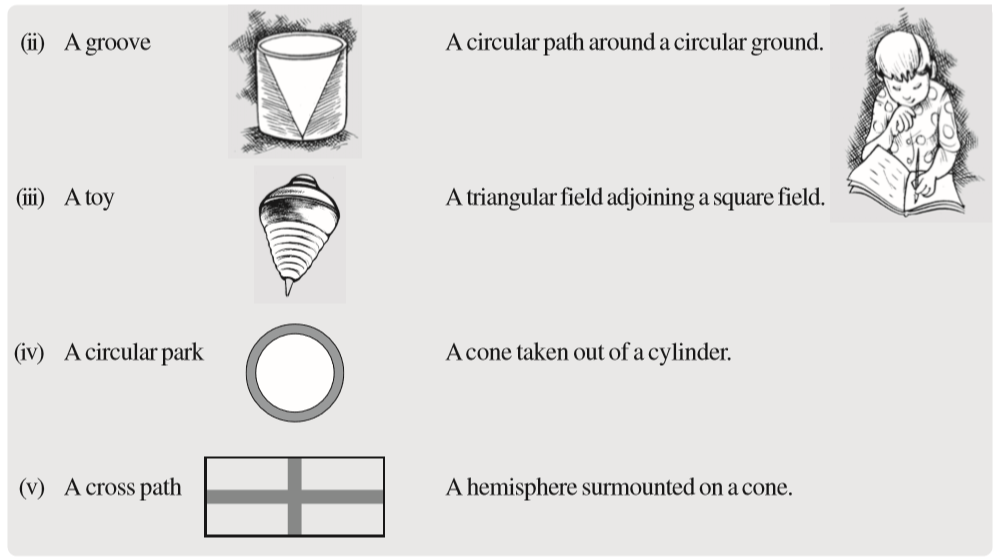
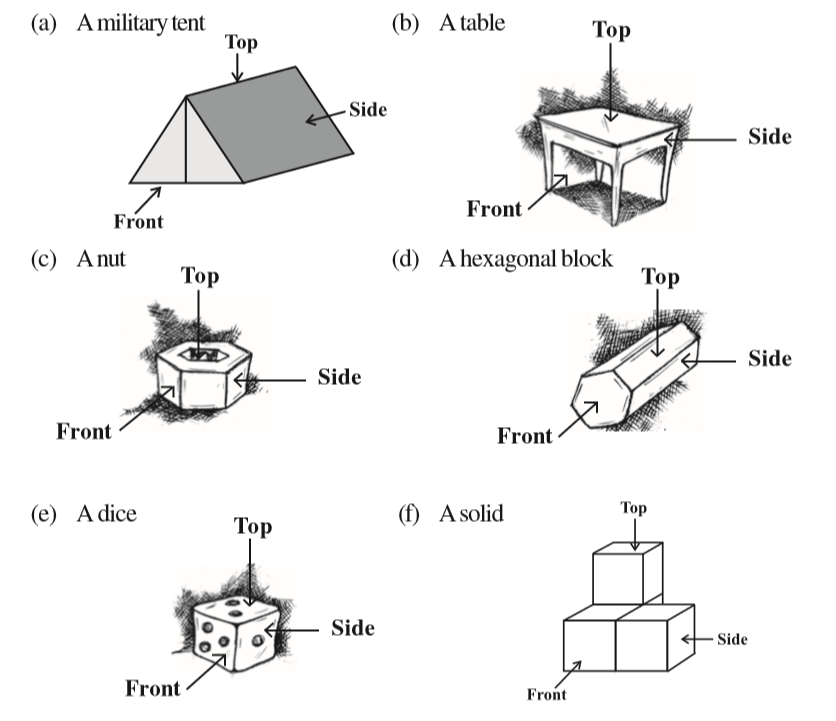
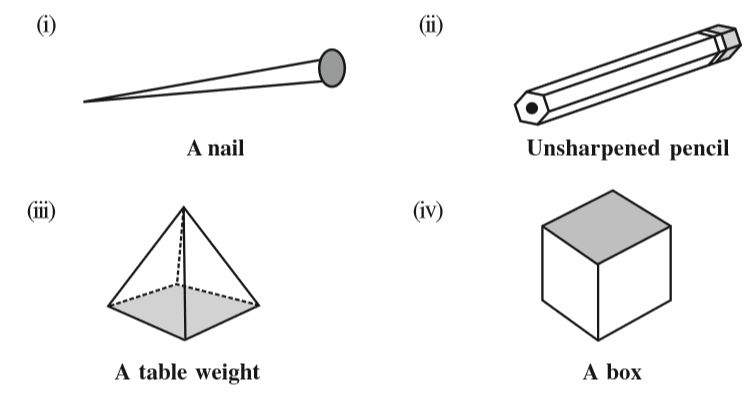
Note that all the above shapes are single. However, in our practical life, many a times, we come across combinations of different shapes. For example, look at the following objects.
10.2 Views of 3D-Shapes
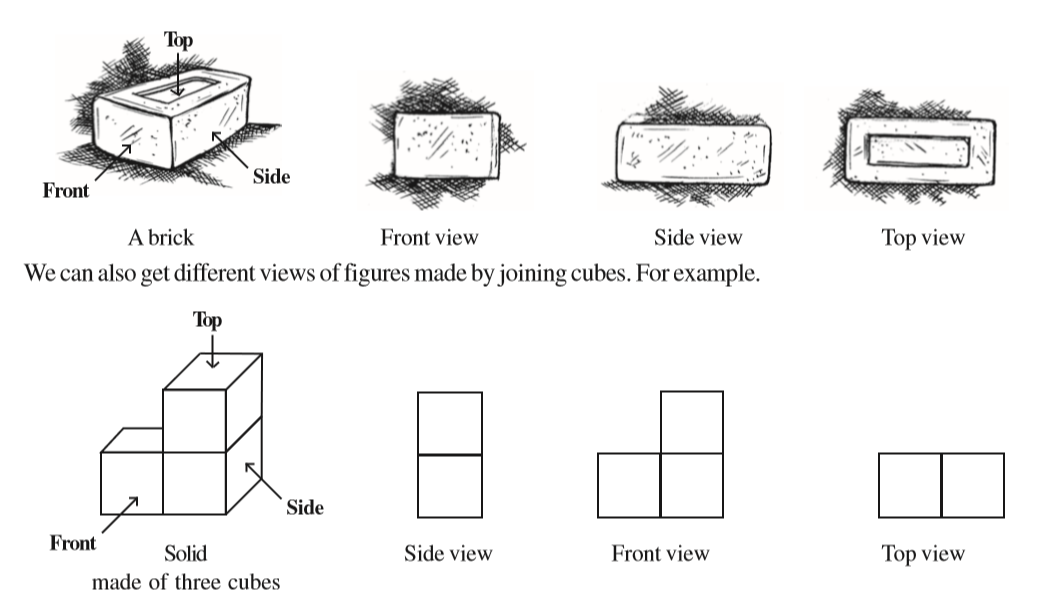
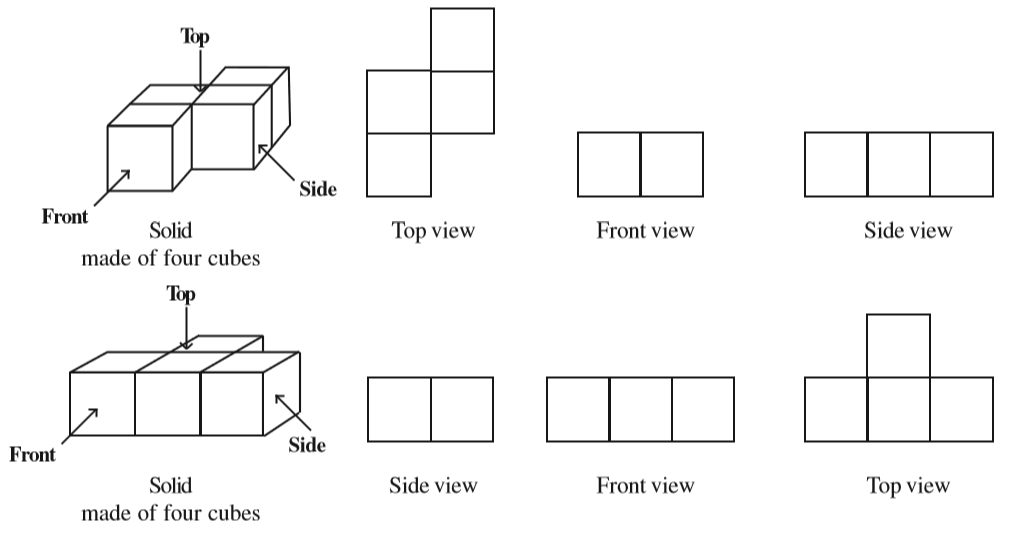
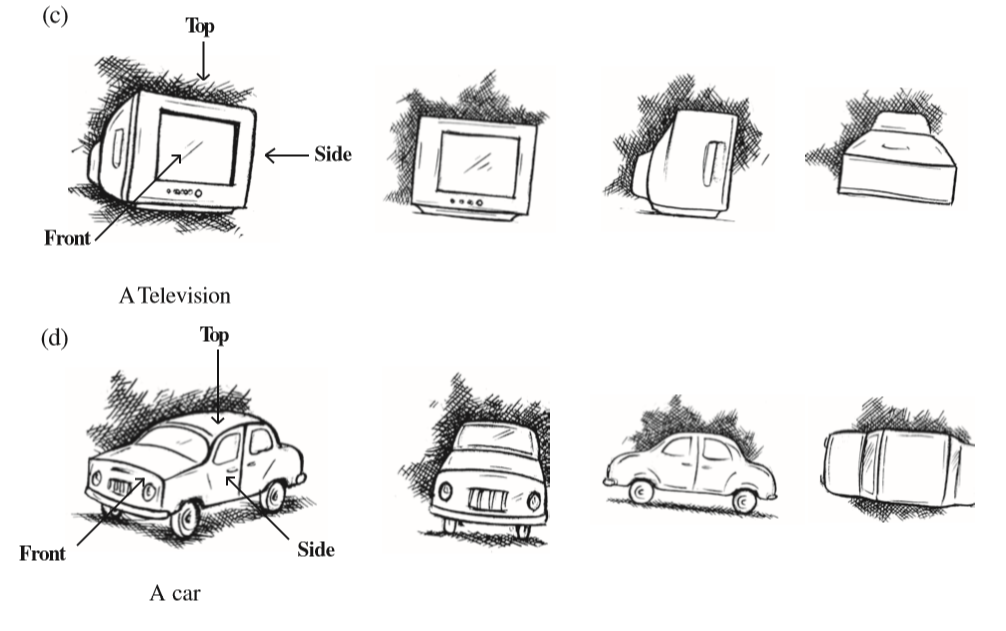
You have learnt that a 3-dimensional object can look differently from different positions so they can be drawn from different perspectives. For example, a given hut can have the following views.
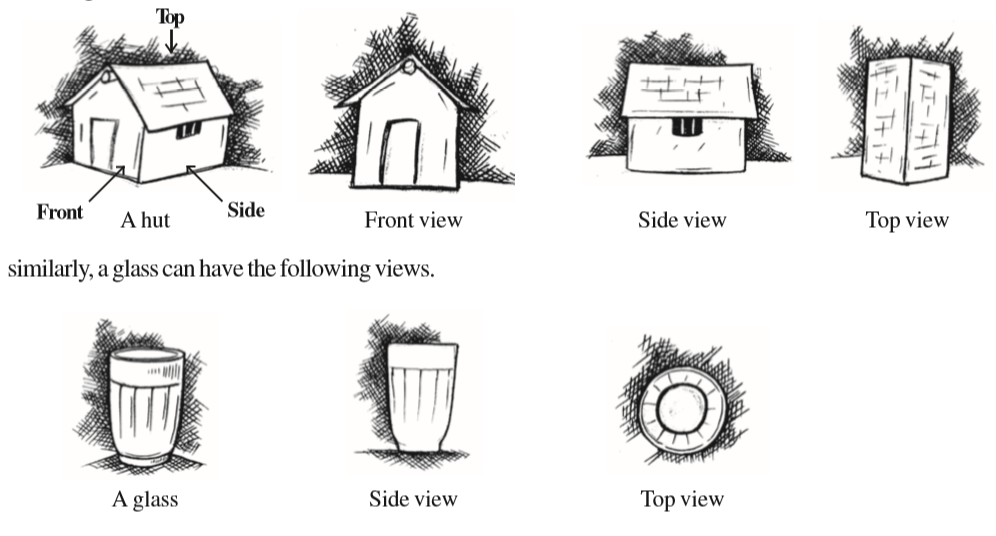
Why is the top view of the glass a pair of concentric circles? Will the side view appear different if taken from some other direction? Think about this! Now look at the different views of a brick.
Do This
Observe different things around you from different positions. Discuss with your friends their various views.
Exercise 10.1
1. For each of the given solid, the two views are given. Match for each solid the corresponding top and front views. The first one is done for you.
Container
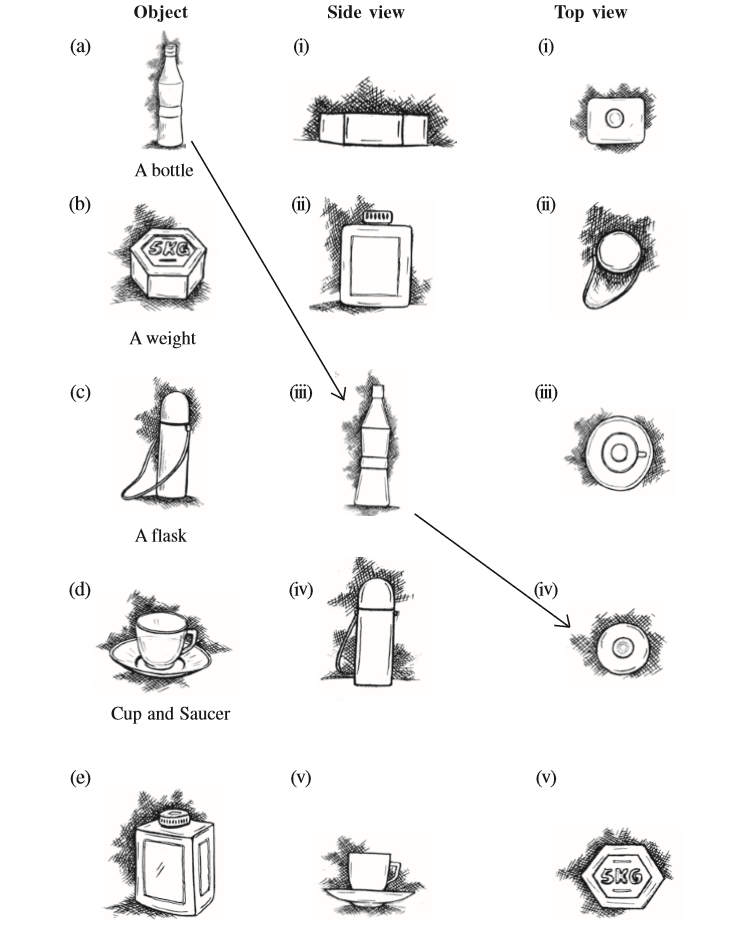
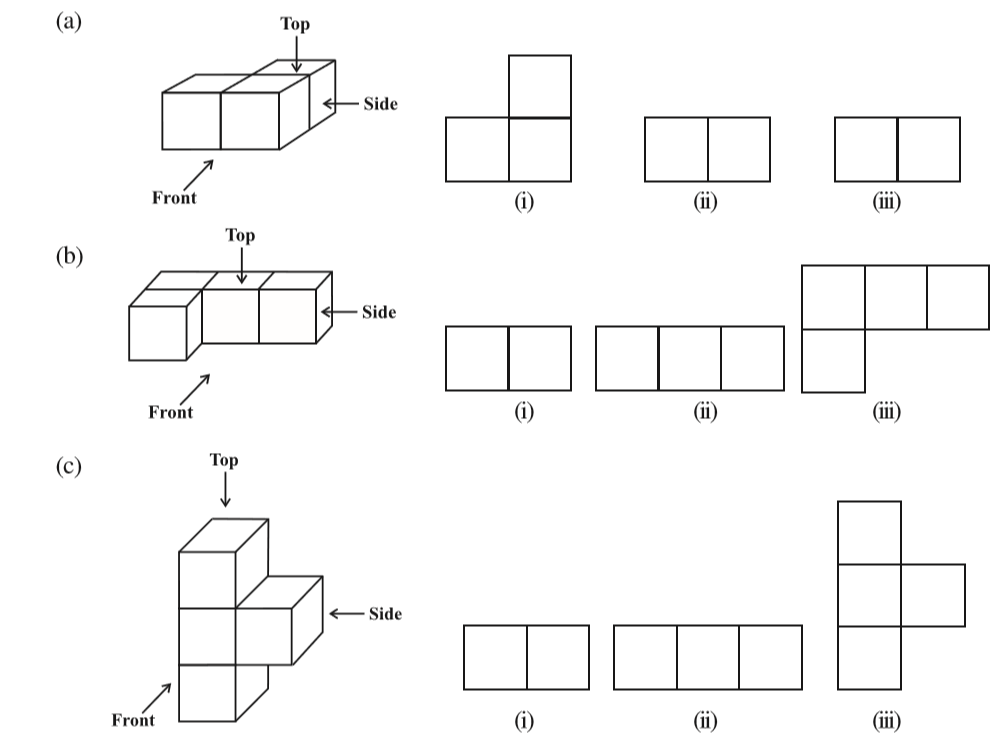
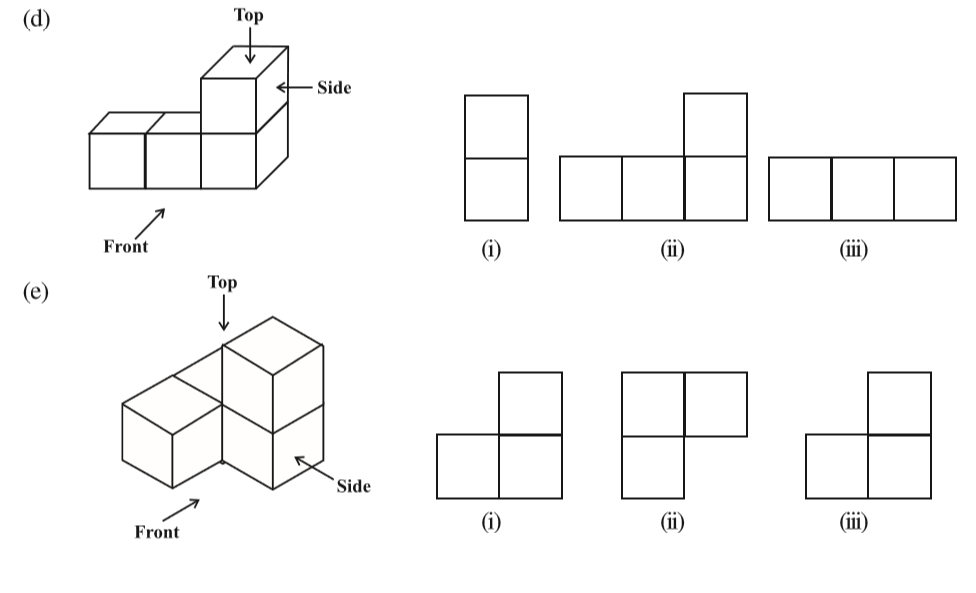
2. For each of the given solid, the three views are given. Identify for each solid the corresponding top, front and side views.
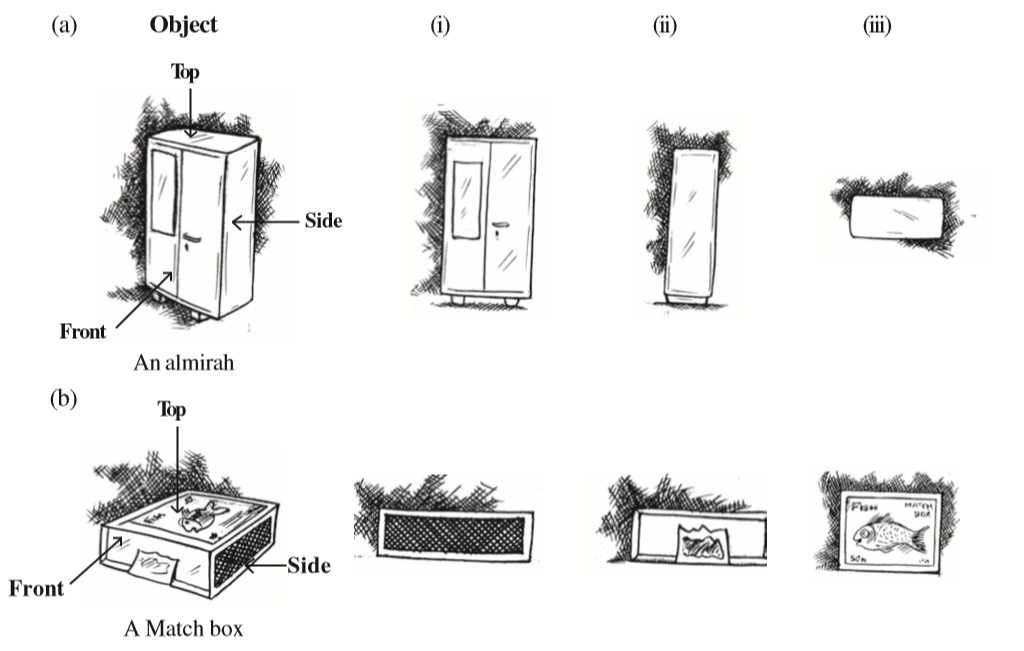
3. For each given solid, identify the top view, front view and side view.
4. Draw the front view, side view and top view of the given objects.
10.3 Mapping Space Around Us
You have been dealing with maps since you were in primary, classes. In Geography, you have been asked to locate a particular State, a particular river, a mountain etc., on a map. In History, you might have been asked to locate a particular place where some event had occured long back. You have traced routes of rivers, roads, railwaylines, traders and many others.
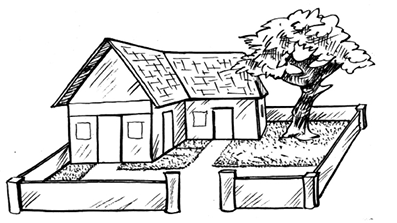
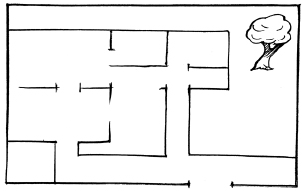
Fig 10.1
What can we conclude from the above illustration? When we draw a picture, we attempt to represent reality as it is seen with all its details, whereas, a map depicts only the location of an object, in relation to other objects. Secondly, different persons can give descriptions of pictures completely different from one another, depending upon the position from which they are looking at the house. But, this is not true in the case of a map. The map of the house remains the same irrespective of the position of the observer. In other words, perspective is very important for drawing a picture but it is not relevant for a map.
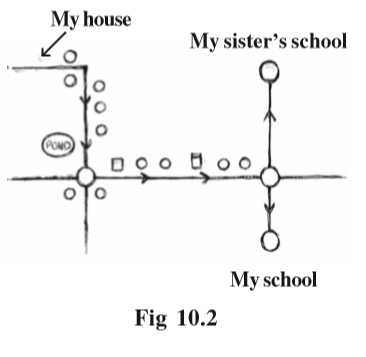
Now, look at the map (Fig 10.2), which has been drawn by seven year old Raghav, as the route from his house to his school:
From this map, can you tell –
(i) how far is Raghav’s school from his house?
(ii) would every circle in the map depict a round about?
(iii) whose school is nearer to the house, Raghav’s or his sister’s?
It is very difficult to answer the above questions on the basis of the given map. Can you tell why?
Now look at another map drawn by his sister, ten year old Meena, to show the route from her house to her school (Fig 10.3).
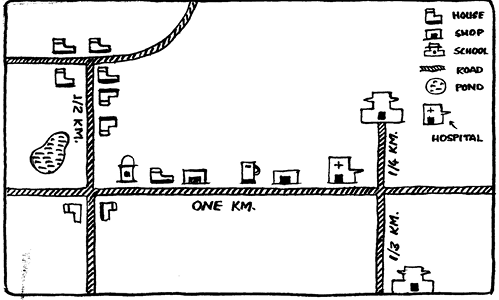
Fig 10.3
This map is different from the earlier maps. Here, Meena has used different symbols for different landmarks. Secondly, longer line segments have been drawn for longer distances and shorter line segments have been drawn for shorter distances, i.e., she has drawn the map to a scale.
Now, you can answer the following questions:
• How far is Raghav’s school from his residence?
• Whose school is nearer to the house, Raghav’s or Meena’s?
• Which are the important landmarks on the route?
Thus we realise that, use of certain symbols and mentioning of distances has helped us read the map easily. Observe that the distances shown on the map are proportional to the actual distances on the ground. This is done by considering a proper scale. While drawing (or reading) a map, one must know, to what scale it has to be drawn (or has been drawn), i.e., how much of actual distance is denoted by 1mm or 1cm in the map. This means, that if one draws a map, he/she has to decide that 1cm of space in that map shows a certain fixed distance of say 1 km or 10 km. This scale can vary from map to map but not within a map. For instance, look at the map of India alongside the map of Delhi.
You will find that when the maps are drawn of same size, scales and the distances in the two maps will vary. That is 1 cm of space in the map of Delhi will represent smaller distances as compared to the distances in the map of India.
The larger the place and smaller the size of the map drawn, the greater is the distance represented by 1 cm.
Thus, we can summarise that:
Fig 10.4
1. A map depicts the location of a particular object/place in relation to other objects/places.
2. Symbols are used to depict the different objects/places.
4. Maps use a scale which is fixed for a particular map. It reduces the real distances proportionately to distances on the paper.
DO THIS
1. Look at the following map of a city (Fig 10.5).
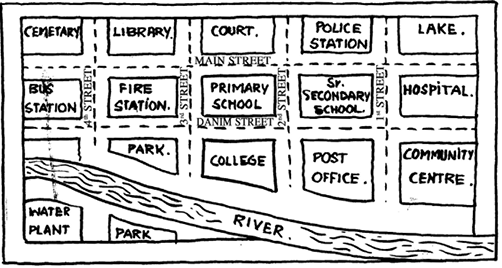
Fig 10.5
(a) Colour the map as follows: Blue-water, Red-fire station, Orange-Library, Yellow-schools, Green-Parks, Pink-Community Centre, Purple-Hospital, Brown-Cemetry.
(b) Mark a Green ‘X’ at the intersection of 2nd street and Danim street. A Black ‘Y’ where the river meets the third street. A red ‘Z’ at the intersection of main street and 1st street.
(c) In magenta colour, draw a short street route from the college to the lake.
Exercise 10.2
1. Look at the given map of a city.
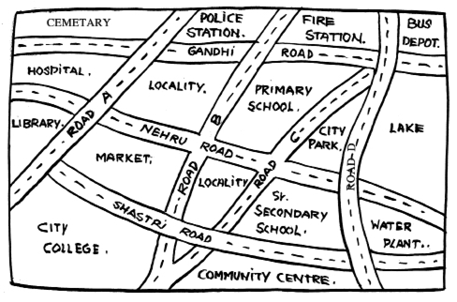
Answer the following.
(a) Colour the map as follows: Blue-water, red-fire station, orange-library, yellow - schools, Green - park, Pink - College, Purple - Hospital, Brown - Cemetery.
(b) Mark a green ‘X’ at the intersection of Road ‘C’ and Nehru Road, Green ‘Y’ at the intersection of Gandhi Road and Road A.
(c) In red, draw a short street route from Library to the bus depot.
(d) Which is further east, the city park or the market?
(e) Which is further south, the primary school or the Sr. Secondary School?
2. Draw a map of your class room using proper scale and symbols for different objects.
4. Draw a map giving instructions to your friend so that she reaches your house without any difficulty.
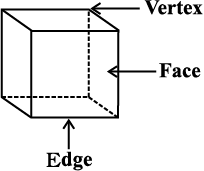
10.4 Faces, Edges and Vertices
Look at the following solids!
Riddle
I have no vertices.
I have no flat faces. Who am I?

Each of these solids is made up of polygonal regions which are called its faces;
these faces meet at edges which are line segments; and the edges meet at vertices which are points. Such solids are called polyhedrons.

These are polyhedrons These are not polyhedrons
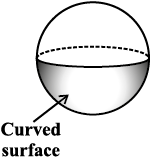

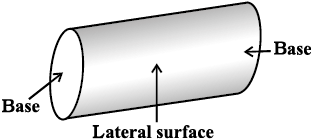
Sphere Cone Cylinder
Convex polyhedrons: You will recall the concept of convex polygons. The idea of convex polyhedron is similar.
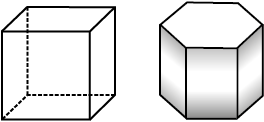

These are convex polyhedrons These are not convex polyhedrons
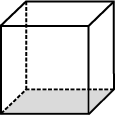

Regular polyhedrons: A polyhedron is said to be regular if its faces are made up of regular polygons and the same number of faces meet at each vertex.
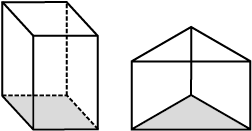
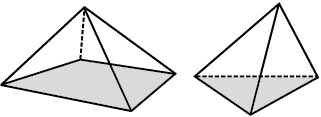
These are prisms These are pyramids
Two important members of polyhedron family around are prisms and pyramids.
On the other hand, a pyramid is a polyhedron whose base is a polygon (of any number of sides) and whose lateral faces are triangles with a common vertex. (If you join all the corners of a polygon to a point not in its plane, you get a model for pyramid).
A prism or a pyramid is named after its base. Thus a hexagonal prism has a hexagon as its base; and a triangular pyramid has a triangle as its base. What, then, is a rectangular prism? What is a square pyramid? Clearly their bases are rectangle and square respectively.

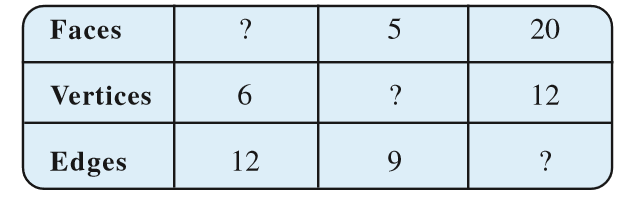
What do you infer from the last two columns? In each case, do you find
F + V = E + 2, i.e., F + V – E = 2? This relationship is called Euler’s formula.
In fact this formula is true for any polyhedron.
THINK, DISCUSS AND WRITE
What happens to F, V and E if some parts are sliced off from a solid? (To start with, you may take a plasticine cube, cut a corner off and investigate).
Exercise 10.3
1. Can a polyhedron have for its faces
(i) 3 triangles? (ii) 4 triangles?
(iii) a square and four triangles?
2. Is it possible to have a polyhedron with any given number of faces? (Hint: Think of a pyramid).
3. Which are prisms among the following?
(ii) How are pyramids and cones alike?
5. Is a square prism same as a cube? Explain.
6. Verify Euler’s formula for these solids.
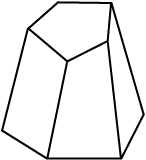
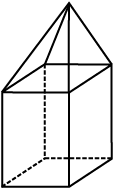
(i) (ii)
7. Using Euler’s formula find the unknown.
8. Can a polyhedron have 10 faces, 20 edges and 15 vertices?
WHAT HAVE WE DISCUSSED?
1. Recognising 2D and 3D objects.
2. Recognising different shapes in nested objects.
3. 3D objects have different views from different positions.
4. A map is different from a picture.
5. A map depicts the location of a particular object/place in relation to other objects/places.
6. Symbols are used to depict the different objects/places.
7. There is no reference or perspective in a map.
8. Maps involve a scale which is fixed for a particular map.
9. For any polyhedron,
F + V – E = 2
where ‘F’ stands for number of faces, V stands for number of vertices and E stands for number of edges. This relationship is called Euler’s formula.