Table of Contents
Chapter 11
Mensuration
11.1 Introduction
We have learnt that for a closed plane figure, the perimeter is the distance around its boundary and its area is the region covered by it. We found the area and perimeter of various plane figures such as triangles, rectangles, circles etc. We have also learnt to find the area of pathways or borders in rectangular shapes.
In this chapter, we will try to solve problems related to perimeter and area of other plane closed figures like quadrilaterals.
We will also learn about surface area and volume of solids such as cube, cuboid and cylinder.
11.2 Let us Recall
Let us take an example to review our previous knowledge.
This is a figure of a rectangular park (Fig 11.1) whose length is 30 m and width is 20 m.
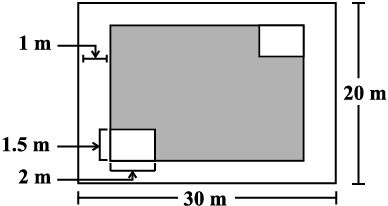
Fig 11.1
(i) What is the total length of the fence surrounding it? To find the length of the fence we need to find the perimeter of this park, which is 100 m. (Check it)
(ii) How much land is occupied by the park? To find the land occupied by this park we need to find the area of this park which is 600 square meters (m2) (How?).
(iii) There is a path of one metre width running inside along the perimeter of the park that has to be cemented.
If 1 bag of cement is required to cement 4 m2 area, how many bags of cement would be required to construct the cemented path?
We can say that the number of cement bags used =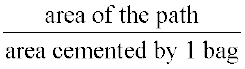 
.
Area of cemented path = Area of park – Area of park not cemented.
Path is 1 m wide, so the rectangular area not cemented is (30 – 2) × (20 – 2) m2. That is 28 × 18 m2.
Hence number of cement bags used = ------------------
(iv) There are two rectangular flower beds of size 1.5 m × 2 m each in the park as shown in the diagram (Fig 11.1) and the rest has grass on it. Find the area covered by grass.
Area of rectangular beds = ------------------
Area of park left after cementing the path = ------------------
Area covered by the grass = ------------------
We can find areas of geometrical shapes other than rectangles also if certain measurements are given to us . Try to recall and match the following:
TRY THESE
(a) Match the following figures with their respective areas in the box.
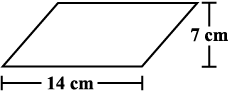
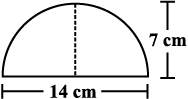
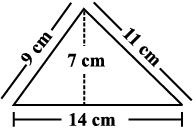
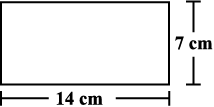
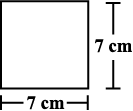
49 cm2
77 cm2
98 cm2
(b) Write the perimeter of each shape.
Exercise 11.1
1. A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
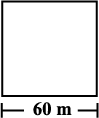
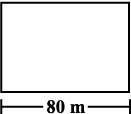
(a) (b)
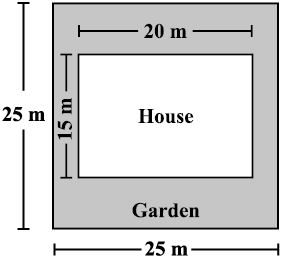
2. Mrs. Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of ` 55 per m2.
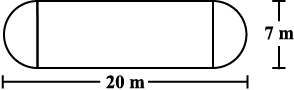
3. The shape of a garden is rectangular in the middle and semi circular at the ends as shown in the diagram. Find the area and the perimeter of this garden [Length of rectangle is
20 – (3.5 + 3.5) metres].
4. A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? (If required you can split the tiles in whatever way you want to fill up the corners).
5. An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c = 2πr, where r is the radius of the circle.
(a)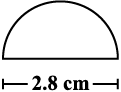 
(b) 
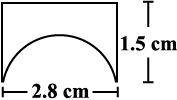(c)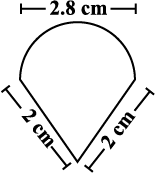 
11.3 Area of Trapezium
Nazma owns a plot near a main road (Fig 11.2). Unlike some other rectangular plots in her neighbourhood, the plot has only one pair of parallel opposite sides. So, it is nearly a trapezium in shape. Can you find out its area?
Let us name the vertices of this plot as shown in Fig 11.3.
By drawing EC || AB, we can divide it into two parts, one of rectangular shape and the other of triangular shape, (which is right angled at C), as shown in Fig 11.3.
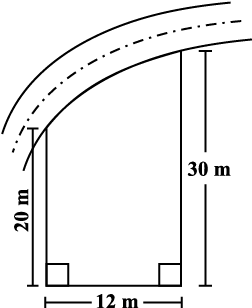
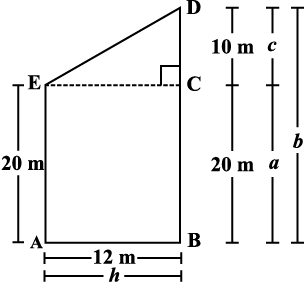
Fig 11.2 Fig 11.3
(b = c + a = 30 m)
Area of ∆ ECD =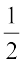 
h × c = 
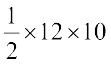= 60 m2.
Area of rectangle ABCE = h × a = 12 × 20 = 240 m2.
Area of trapezium ABDE = area of ∆ ECD + Area of rectangle ABCE = 60 + 240 = 300 m2.
We can write the area by combining the two areas and write the area of trapezium as
area ofABDE =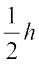 
× c + h × a = h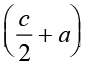 
= h 
= 
= 
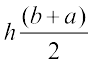By substituting the values of h, b and a in this expression, we find 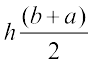= 300 m2.
TRY THESE
1. Nazma’s sister also has a trapezium shaped plot. Divide it into three parts as shown (Fig 11.4). Show that the area of trapezium WXYZ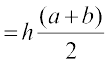 
.
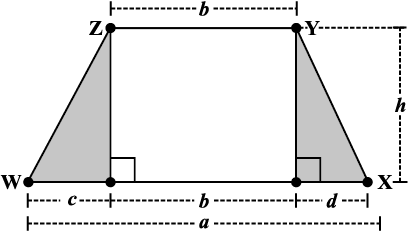
Fig 11.4
2. If h = 10 cm, c = 6 cm, b = 12 cm, d = 4 cm, find the values of each of its parts separetely and add to find the area WXYZ. Verify it by putting the values of h, a and b in the expression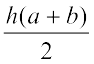 
.
Do This
1. Draw any trapezium WXYZ on a piece of graph paper as shown in the figure and cut it out (Fig 11.5).
Fig 11.5
Fig 11.6
2. Find the mid point of XY by folding the side and name it A (Fig 11.6).
3. Cut trapezium WXYZ into two pieces by cutting along ZA. Place ∆ ZYA as shown in Fig 11.7, where AY is placed on AX.
What is the length of the base of the larger triangle? Write an expression for the area of this triangle (Fig 11.7).
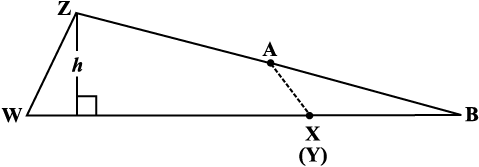
Fig 11.7
4. The area of this triangle and the area of the trapezium WXYZ are same (How?).
Get the expression for the area of trapezium by using the expression for the area of triangle.
So to find the area of a trapezium we need to know the length of the parallel sides and the perpendicular distance between these two parallel sides. Half the product of the sum of the lengths of parallel sides and the perpendicular distance between them gives the area of trapezium.
TRY THESE
Find the area of the following trapeziums (Fig 11.8).
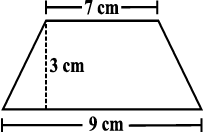(ii)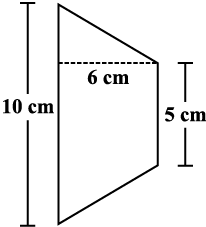 
DO THIS
Fig 11.9
We know that all congruent figures are equal in area. Can we say figures equal in area need to be congruent too? Are these figures congruent?
Draw at least three trapeziums which have different areas but equal perimeters on a squared sheet.
11.4 Area of a General Quadrilateral
A general quadrilateral can be split into two triangles by drawing one of its diagonals. This “triangulation” helps us to find a formula for any general quadrilateral. Study the Fig 11.10.
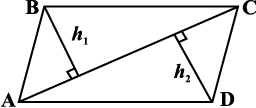
Fig 11.10
Area of quadrilateral ABCD
= (area of ∆ ABC) + (area of ∆ ADC)
= (
AC × h1) + (AC × h2)
= AC × ( h1 + h2)
= d ( h1 + h2) where d denotes the length of diagonal AC.
Example 1: Find the area of quadrilateral PQRS shown in Fig 11.11.
Area = d ( h1 + h2)
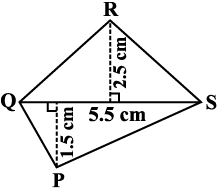
Fig 11.11
= × 5.5 × (2.5 + 1.5) cm2
= × 5.5 × 4 cm2 = 11 cm2
TRY THESE
We know that parallelogram is also a quadrilateral. Let us also split such a quadrilateral into two triangles, find their areas and hence that of the parallelogram. Does this agree with the formula that you know already? (Fig 11.12)
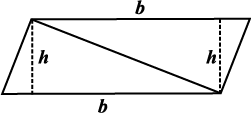
Fig 11.12
11.4.1 Area of special quadrilaterals
We can use the same method of splitting into triangles (which we called “triangulation”) to find a formula for the area of a rhombus. In Fig 11.13 ABCD is a rhombus. Therefore, its diagonals are perpendicular bisectors of each other.
Area of rhombus ABCD = (area of ∆ ACD) + (area of ∆ ABC)
= (
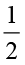× AC × OD) + (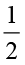× AC × OB) = 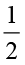AC × (OD + OB)
= AC × BD = d1 × d2 where AC = d1 and BD = d2
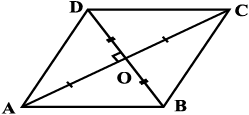
Fig 11.13
In other words, area of a rhombus is half the product of its diagonals.
Example 2: Find the area of a rhombus whose diagonals are of lengths 10 cm and 8.2 cm.
Solution: Area of the rhombus = 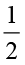d1 d2 where d1, d2 are lengths of diagonals.
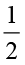= × 10 × 8.2 cm2 = 41 cm2.
THINK, DISCUSS AND WRITE
A parallelogram is divided into two congruent triangles by drawing a diagonal across it. Can we divide a trapezium into two congruent triangles?
TRY THESE
Find the area of these quadrilaterals (Fig 11.14).
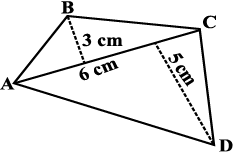
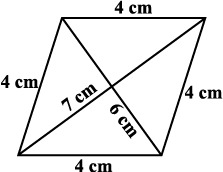
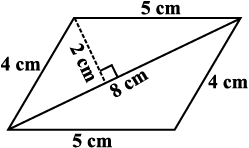
(i) (ii) (iii)
Fig 11.14
11.5 Area of a Polygon
We split a quadrilateral into triangles and find its area. Similar methods can be used to find the area of a polygon. Observe the following for a pentagon: (Fig 11.15, 11.16)
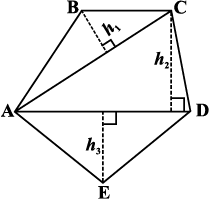
Fig 11.15
By constructing two diagonals AC and AD the pentagon ABCDE is divided into three parts. So, area ABCDE = area of ∆ABC + area of ∆ ACD + area of ∆ AED.
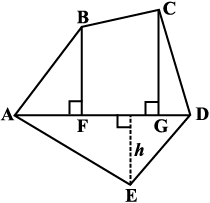
Fig 11.16
By constructing one diagonal AD and two perpendiculars BF and CG on it, pentagon ABCDE is divided into four parts. So, area of ABCDE = area of right angled ∆ AFB + area of trapezium BFGC + area of right angled ∆ CGD + area of ∆ AED. (Identify the parallel sides of trapezium BFGC.)
TRY THESE
(i) Divide the following polygons (Fig 11.17) into parts (triangles and trapezium) to find out its area.
Fig 11.17
Area of Polygon ABCDE = area of ∆ AFB + ....
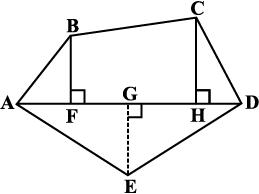
Fig 11.18
Area of ∆ AFB = 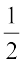× AF × BF = 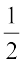× 3 × 2 = ....
Area of trapezium FBCH = FH ×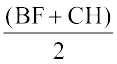
= 3 ×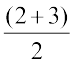 
[FH = AH – AF]
Area of ∆CHD = 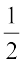× HD× CH = ....; Area of ∆ADE = 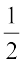× AD × GE = ....
So, the area of polygon ABCDE = ....
(iii) Find the area of polygon MNOPQR (Fig 11.19) if
Fig 11.19
MP = 9 cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2 cm
NA, OC, QD and RB are perpendiculars to diagonal MP.
Example 1: The area of a trapezium shaped field is 480 m2, the distance between two parallel sides is 15 m and one of the parallel side is 20 m. Find the other parallel side.
Solution: One of the parallel sides of the trapezium is a = 20 m, let another parallel side be b, height h = 15 m.
The given area of trapezium = 480 m2.
Area of a trapezium = 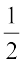h (a + b) So 480 = 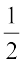× 15 × (20 + b) or 
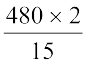= 20 + b
or 64 = 20 + b or b = 44 m
Hence the other parallel side of the trapezium is 44 m.
Example 2: The area of a rhombus is 240 cm2 and one of the diagonals is 16 cm. Find the other diagonal.
Solution: Let length of one diagonal d1 = 16 cm
and length of the other diagonal = d2
Area of the rhombus = 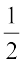d1 . d2 = 240
So,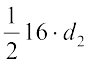 
= 240
Therefore, d2 = 30 cm
Hence the length of the second diagonal is 30 cm.
Example 3: There is a hexagon MNOPQR of side 5 cm (Fig 11.20). Aman and Ridhima divided it in two different ways (Fig 11.21).
Find the area of this hexagon using both ways.
Solution: Aman’s method:
Since it is a hexagon so NQ divides the hexagon into two congruent trapeziums. You can verify it by paper folding (Fig 11.22).
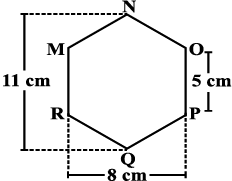
Fig 11.20
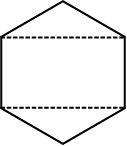
Fig 11.21
Now area of trapezium MNQR =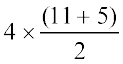 
= 2 × 16 = 32 cm2.
So the area of hexagon MNOPQR = 2 × 32 = 64 cm2.
Ridhima’s method:
∆ MNO and ∆ RPQ are congruent triangles with altitude 3 cm (Fig 11.23).
You can verify this by cutting off these two triangles and placing them on one another.
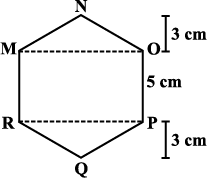
Fig 11.23
Area of ∆ MNO = 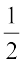× 8 × 3 = 12 cm2 = Area of ∆ RPQ
Area of rectangle MOPR = 8 × 5 = 40 cm2.
Now, area of hexagon MNOPQR = 40 + 12 + 12 = 64 cm2.
Exercise 11.2
2. The area of a trapezium is 34 cm2 and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.
3. Length of the fence of a trapezium shaped field ABCD is 120 m. If
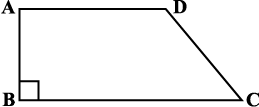
BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.
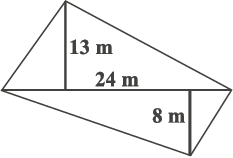
4. The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
5. The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
6. Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm.
If one of its diagonals is 8 cm long, find the length of the other diagonal.
7. The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2 is ` 4.
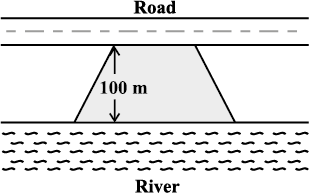
8. Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
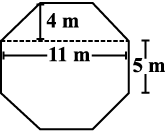
9. Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
10. There is a pentagonal shaped park as shown in the figure.
For finding its area Jyoti and Kavita divided it in two different ways.
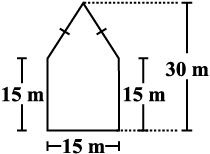
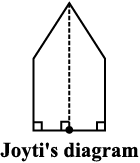
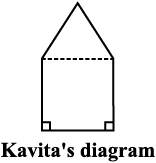
Find the area of this park using both ways. Can you suggest some other way of finding its area?
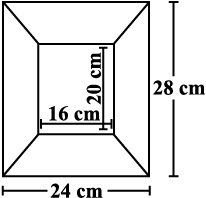
11. Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.
11.6 Solid Shapes
In your earlier classes you have studied that two dimensional figures can be identified as the faces of three dimensional shapes. Observe the solids which we have discussed so far (Fig 11.24).
Observe that some shapes have two or more than two identical (congruent) faces. Name them. Which solid has all congruent faces?
Fig 11.24
DO THIS
Soaps, toys, pastes, snacks etc. often come in the packing of cuboidal, cubical or cylindrical boxes. Collect, such boxes (Fig 11.25).
Fig 11.25
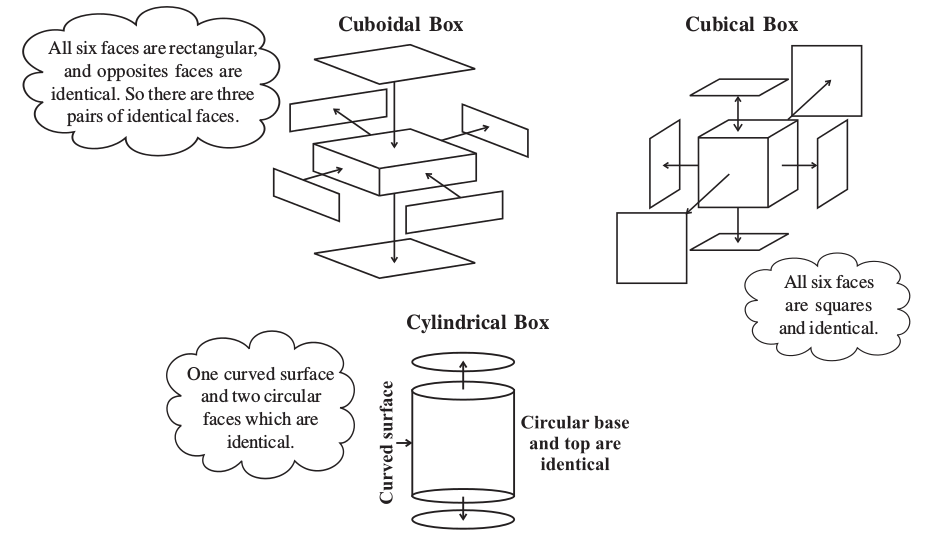
Now take one type of box at a time. Cut out all the faces it has. Observe the shape of each face and find the number of faces of the box that are identical by placing them on each other. Write down your observations.
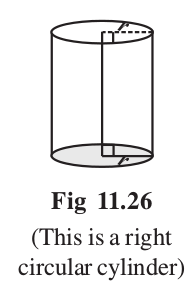
The cylinder has congruent circular faces that are parallel to each other (Fig 11.26). Observe that the line segment joining the center of circular faces is perpendicular to the base. Such cylinders are known as right circular cylinders. We are only going to study this type of cylinders, though there are other types of cylinders as well (Fig 11.27).
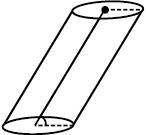
Fig 11.27
(This is not a right circular cylinder)
THINK, DISCUSS AND WRITE
Why is it incorrect to call the solid shown here a cylinder?
11.7 Surface Area of Cube, Cuboid and Cylinder
Imran, Monica and Jaspal are painting a cuboidal, cubical and a cylindrical box respectively of same height (Fig 11.28).
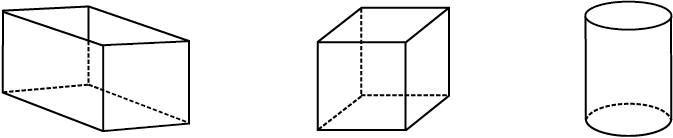
Fig 11.28
They try to determine who has painted more area. Hari suggested that finding the surface area of each box would help them find it out.
To find the total surface area, find the area of each face and then add. The surface area of a solid is the sum of the areas of its faces. To clarify further, we take each shape one by one.
11.7.1 Cuboid
Suppose you cut open a cuboidal box and lay it flat (Fig 11.29). We can see a net as shown below (Fig 11.30).
Write the dimension of each side. You know that a cuboid has three pairs of identical faces. What expression can you use to find the area of each face?
Find the total area of all the faces of the box. We see that the total surface area of a cuboid is area I + area II + area III + area IV +area V + area VI
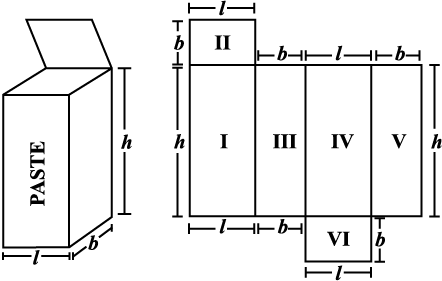
Fig 11.29 Fig 11.30
= h × l + b × l + b × h + l × h + b × h + l × b
So total surface area = 2 (h × l + b × h + b × l) = 2(lb + bh + hl)
where h, l and b are the height, length and width of the cuboid respectively.
Suppose the height, length and width of the box shown above are 20 cm, 15 cm and 10 cm respectively.
Then the total surface area = 2 (20 × 15 + 20 × 10 + 10 × 15)
= 2 ( 300 + 200 + 150) = 1300 m2.
TRY THESE
Find the total surface area of the following cuboids (Fig 11.31):
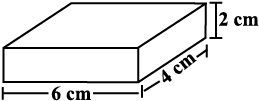
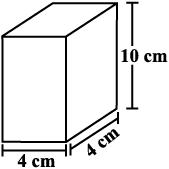
Fig 11.31
• The side walls (the faces excluding the top and bottom) make the lateral surface area of the cuboid. For example, the total area of all the four walls of the cuboidal room in which you are sitting is the lateral surface area of this room (Fig 11.32). Hence, the lateral surface area of a cuboid is given by 2(h × l + b × h) or 2h (l + b).
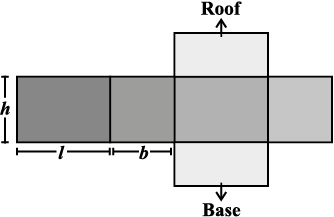
Fig 11.32
Do This
(i) Cover the lateral surface of a cuboidal duster (which your teacher uses in the class room) using a strip of brown sheet of paper, such that it just fits around the surface. Remove the paper. Measure the area of the paper. Is it the lateral surface area of the duster?
(ii) Measure length, width and height of your classroom and find
(b) the lateral surface area of this room.
(c) the total area of the room which is to be white washed.
THINK, DISCUSS AND WRITE
1. Can we say that the total surface area of cuboid = lateral surface area + 2 × area of base?
2. If we interchange the lengths of the base and the height of a cuboid (Fig 11.33(i)) to get another cuboid
(Fig 11.33(ii)), will its lateral surface area change?
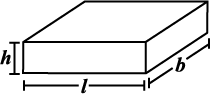
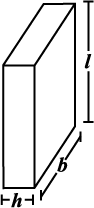
(i) (ii)
11.7.2 Cube
DO THIS
Draw the pattern shown on a squared paper and cut it out [Fig 11.34(i)]. (You know that this pattern is a net of a cube. Fold it along the lines [Fig 11.34(ii)] and tape the edges to form a cube [Fig 11.34(iii)].
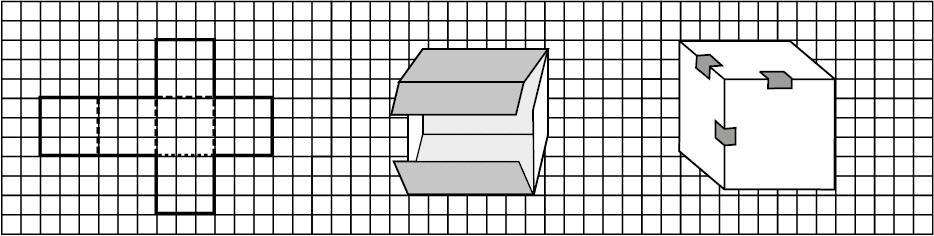
Fig 11.34
(i) 
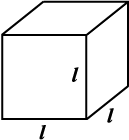(ii)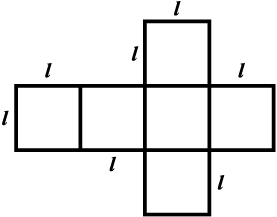 
Fig 11.35
(a) What is the length, width and height of the cube? Observe that all the faces of a cube are square in shape. This makes length, height and width of a cube equal (Fig 11.35(i)).
(b) Write the area of each of the faces. Are they equal?
(c) Write the total surface area of this cube.
(d) If each side of the cube is l, what will be the area of each face? (Fig 11.35(ii)).
Can we say that the total surface area of a cube of side l is 6l2 ?
TRY THESE
Find the surface area of cube A and lateral surface area of cube B (Fig 11.36).
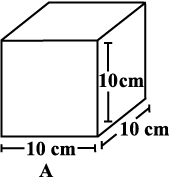
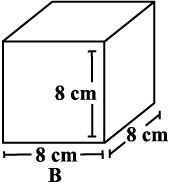
Fig 11.36
THINK, DISCUSS AND WRITE
(i) Two cubes each with side b are joined to form a cuboid (Fig 11.37). What is the surface area of this cuboid? Is it 12b2? Is the surface area of cuboid formed by joining three such cubes, 18b2? Why?
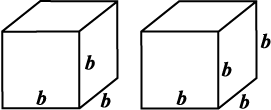
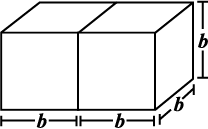
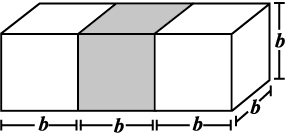
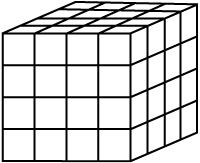
Fig 11.38
(ii) How will you arrange 12 cubes of equal length to form a cuboid of smallest surface area?
(iii) After the surface area of a cube is painted, the cube is cut into 64 smaller cubes of same dimensions (Fig 11.38).
How many have no face painted? 1 face painted? 2 faces painted? 3 faces painted?
11.7.3 Cylinders
DO THIS
(i) (ii) (iii) (iv)
Fig 11.39
Of course it is rectangular in shape. When you tape the parts of this cylinder together, the length of the rectangular strip is equal to the circumference of the circle. Record the radius (r) of the circular base, length (l) and width (h) of the rectangular strip. Is 2πr = length of the strip. Check if the area of rectangular strip is 2πrh. Count how many square units of the squared paper are used to form the cylinder.
Check if this count is approximately equal to 2πr (r + h).
(ii) We can deduce the relation 2πr (r + h) as the surface area of a cylinder in another way. Imagine cutting up a cylinder as shown below (Fig 11.40).
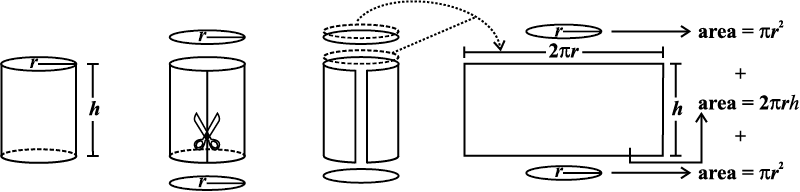
Fig 11.40
Note: We take π to be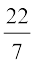 
unless otherwise stated
The lateral (or curved) surface area of a cylinder is 2πrh.
The total surface area of a cylinder = πr2 + 2πrh + πr2
= 2πr2 + 2πrh or 2πr (r + h)
TRY THESE
Find total surface area of the following cylinders (Fig 11.41)
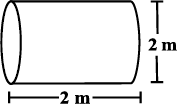
THINK, DISCUSS AND WRITE
Note that lateral surface area of a cylinder is the circumference of base × height of cylinder. Can we write lateral surface area of a cuboid as perimeter of base × height of cuboid?
Example 4: An aquarium is in the form of a cuboid whose external measures are
80 cm × 30 cm × 40 cm. The base, side faces and back face are to be covered with a coloured paper. Find the area of the paper needed?
Solution: The length of the aquarium = l = 80 cm
Width of the aquarium = b = 30 cm
Height of the aquarium = h = 40 cm
Area of the base = l × b = 80 × 30 = 2400 cm2
Area of the back face = l × h = 80 × 40 = 3200 cm2
Required area = Area of the base + area of the back face
+ (2 × area of a side face)
= 2400 + 3200 + (2 × 1200) = 8000 cm2
Hence the area of the coloured paper required is 8000 cm2.
Example 5: The internal measures of a cuboidal room are 12 m × 8 m × 4 m. Find the total cost of whitewashing all four walls of a room, if the cost of white washing is ` 5 per m2. What will be the cost of white washing if the ceiling of the room is also whitewashed.
Solution: Let the length of the room = l = 12 m
Width of the room = b = 8 m
Height of the room = h = 4 m
Area of the four walls of the room = Perimeter of the base × Height of the room
= 2 (l + b) × h = 2 (12 + 8) × 4
= 2 × 20 × 4 = 160 m2.
Cost of white washing per m2 = ` 5
Hence the total cost of white washing four walls of the room = ` (160 × 5) = ` 800
Area of ceiling is 12 × 8 = 96 m2
Cost of white washing the ceiling = ` (96 × 5) = ` 480
So the total cost of white washing = ` (800 + 480) = ` 1280
Example 6: In a building there are 24 cylindrical pillars. The radius of each pillar is 28 cm and height is 4 m. Find the total cost of painting the curved surface area of all pillars at the rate of ` 8 per m2.
Solution: Radius of cylindrical pillar, r = 28 cm = 0.28 m
height, h = 4 m
curved surface area of a cylinder = 2πrh
curved surface area of a pillar =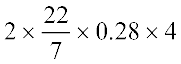 
= 7.04 m2
curved surface area of 24 such pillar = 7.04 × 24 = 168.96 m2
cost of painting an area of 1 m2 = ` 8
Therefore, cost of painting 1689.6 m2 = 168.96 × 8 = ` 1351.68
Example 7: Find the height of a cylinder whose radius is 7 cm and the total surface area is 968 cm2.
Solution: Let height of the cylinder = h, radius = r = 7cm
Total surface area = 2πr (h + r)
i.e., 2 ×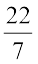 
× 7 × (7 + h) = 968
h = 15 cm
Hence, the height of the cylinder is 15 cm.
Exercise 11.3
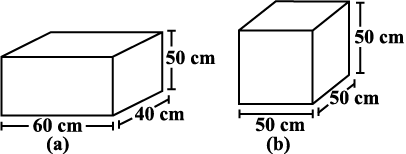
1. There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
2. A suitcase with measures 80 cm ×
48 cm × 24 cm is to be covered with a tarpaulin cloth. How many metres of tarpaulin of width 96 cm is required to cover 100 such suitcases?
3. Find the side of a cube whose surface area is 600 cm2.
4. Rukhsar painted the outside of the cabinet of measure 1 m × 2 m × 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet.
5. Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 m2 of area is painted.
How many cans of paint will she need to paint the room?
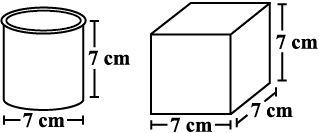
6. Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?
7. A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How much sheet of metal is required?
8. The lateral surface area of a hollow cylinder is 4224 cm2. It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of rectangular sheet?
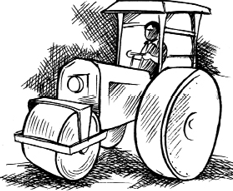
9. A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1 m.
10. A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label.
11.8 Volume of Cube, Cuboid and Cylinder
Amount of space occupied by a three dimensional object is called its volume. Try to compare the volume of objects surrounding you. For example, volume of a room is greater than the volume of an almirah kept inside it. Similarly, volume of your pencil box is greater than the volume of the pen and the eraser kept inside it. Can you measure volume of either of these objects?
Remember, we use square units to find the area of a region. Here we will use cubic units to find the volume of a solid, as cube is the most convenient solid shape (just as square is the most convenient shape to measure area of a region).
For finding the area we divide the region into square units, similarly, to find the volume of a solid we need to divide it into cubical units.
Observe that the volume of each of the adjoining solids is 8 cubic units (Fig 11.42 ).
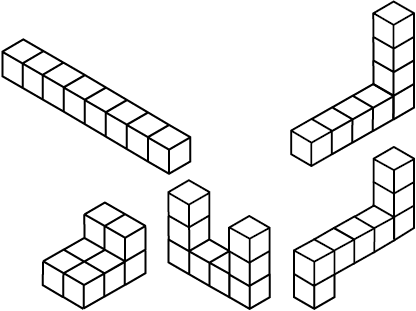
Fig 11.42
We can say that the volume of a solid is measured by counting the number of unit cubes it contains. Cubic units which we generally use to measure volume are
1 cubic cm = 1 cm × 1 cm × 1 cm = 1 cm3
= 10 mm × 10 mm × 10 mm = ............... mm3
1 cubic m = 1 m × 1 m × 1 m = 1 m3
= ............................... cm3
1 cubic mm = 1 mm × 1 mm × 1 mm = 1 mm3
= 0.1 cm × 0.1 cm × 0.1 cm = ...................... cm3
We now find some expressions to find volume of a cuboid, cube and cylinder. Let us take each solid one by one.
11.8.1 Cuboid
Take 36 cubes of equal size (i.e., length of each cube is same). Arrange them to form a cuboid. You can arrange them in many ways. Observe the following table and fill in the blanks.
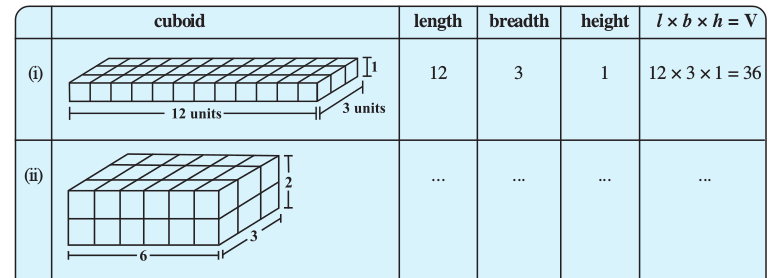
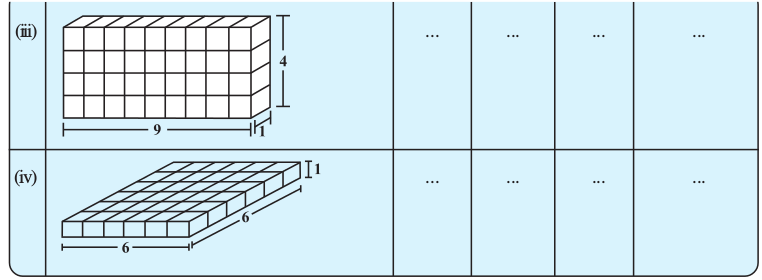
What do you observe?
Since we have used 36 cubes to form these cuboids, volume of each cuboid is 36 cubic units. Also volume of each cuboid is equal to the product of length, breadth and height of the cuboid. From the above example we can say volume of cuboid = l × b × h. Since l × b is the area of its base we can also say that,
Volume of cuboid = area of the base × height
DO THIS
Take a sheet of paper. Measure its area. Pile up such sheets of paper of same size to make a cuboid
(Fig 11.43). Measure the height of this pile. Find the volume of the cuboid by finding the product of the area of the sheet and the height of this pile of sheets.
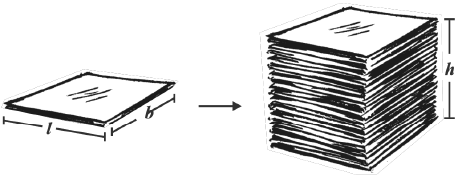
Fig 11.43
This activity illustrates the idea that volume of a solid can be deduced by this method also (if the base and top of the solid are congruent and parallel to each other and its edges are perpendicular to the base). Can you think of such objects whose volume can be found by using this method?
TRY THESE
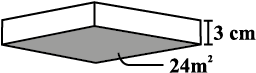
Find the volume of the following cuboids (Fig 11.44).
11.8.2 Cube
The cube is a special case of a cuboid, where l = b = h.
Hence, volume of cube = l × l × l = l3
TRY THESE
Find the volume of the following cubes
(a) with a side 4 cm (b) with a side 1.5 m
DO THIS
Arrange 64 cubes of equal size in as many ways as you can to form a cuboid.
Find the surface area of each arrangement. Can solid shapes of same volume have same surface area?
THINK, DISCUSS AND WRITE
A company sells biscuits. For packing purpose they are using cuboidal boxes:
box A →3 cm × 8 cm × 20 cm, box B → 4 cm × 12 cm × 10 cm. What size of the box will be economical for the company? Why? Can you suggest any other size (dimensions) which has the same volume but is more economical than these?
11.8.3 Cylinder
We know that volume of a cuboid can be found by finding the product of area of base and its height. Can we find the volume of a cylinder in the same way?
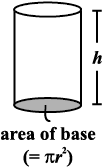
Just like cuboid, cylinder has got a top and a base which are congruent and parallel to each other. Its lateral surface is also perpendicular to the base, just like cuboid.
So the Volume of a cuboid = area of base × height
= l × b × h = lbh
think, discuss and write
Volume of cylinder = area of base × height
= πr2 × h = πr2h
TRY THESE
Find the volume of the following cylinders.
(i) 
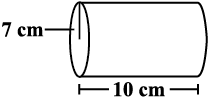(ii)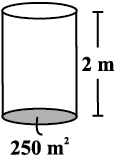 
11.9 Volume and Capacity
(a) Volume refers to the amount of space occupied by an object.
(b) Capacity refers to the quantity that a container holds.
Note: If a water tin holds 100 cm3 of water then the capacity of the water tin is 100 cm3.
Capacity is also measured in terms of litres. The relation between litre and cm3 is,
1 mL = 1 cm3,1 L = 1000 cm3. Thus, 1 m3 = 1000000 cm3 = 1000 L.
Example 8: Find the height of a cuboid whose volume is 275 cm3 and base area is 25 cm2 .
Solution: Volume of a cuboid = Base area × Height
Hence height of the cuboid =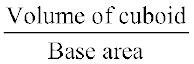 
= 
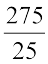= 11 cm
Height of the cuboid is 11 cm.
Example 9: A godown is in the form of a cuboid of measures 60 m × 40 m × 30 m. How many cuboidal boxes can be stored in it if the volume of one box is 0.8 m3 ?
Solution: Volume of one box = 0.8 m3
Volume of godown = 60 × 40 × 30 = 72000 m3
Number of boxes that can be stored in the godown =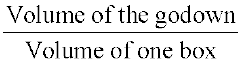 
= 
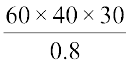= 90,000
Hence the number of cuboidal boxes that can be stored in the godown is 90,000.
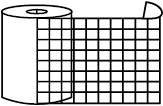
Example 10: A rectangular paper of width 14 cm is rolled along its width and a cylinder of radius 20 cm is formed. Find the volume of the cylinder (Fig 11.45). (Take 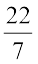for π)
Solution: A cylinder is formed by rolling a rectangle about its width. Hence the width of the paper becomes height and radius of the cylinder is 20 cm.
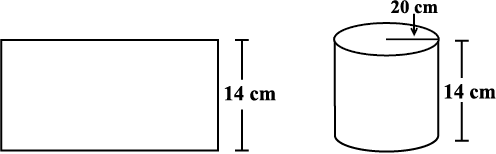
Fig 11.45
Height of the cylinder = h = 14 cm
Radius = r = 20 cm
Volume of the cylinder = V = π r2 h
= 
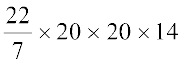= 17600 cm3
Hence, the volume of the cylinder is 17600 cm3.
Example 11: A rectangular piece of paper 11 cm × 4 cm is folded without overlapping to make a cylinder of height 4 cm. Find the volume of the cylinder.
Solution: Length of the paper becomes the perimeter of the base of the cylinder and width becomes height.
Let radius of the cylinder = r and height = h
Perimeter of the base of the cylinder = 2πr = 11
or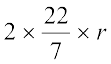 
= 11
Therefore, r =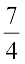 
cm
Volume of the cylinder = V = πr2h
= 
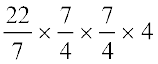cm3 = 38.5 cm3.
Hence the volume of the cylinder is 38.5 cm3.
Exercise 11.4
1. Given a cylindrical tank, in which situation will you find surface area and in which situation volume.
(a) To find how much it can hold.
(b) Number of cement bags required to plaster it.
(c) To find the number of smaller tanks that can be filled with water from it.
2. Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?
A B
5. Find the height of the cylinder whose volume is 1.54 m3 and diameter of the base is 140 cm ?
6. A milk tank is in the form of cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in litres that can be stored in the tank?
7. If each edge of a cube is doubled,
(ii) how many times will its volume increase?
8. Water is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108 m3, find the number of hours it will take to fill the reservoir.
WHAT HAVE WE DISCUSSED?
1. Area of
(i) a trapezium = half of the sum of the lengths of parallel sides × perpendicular distance between them.
(ii) a rhombus = half the product of its diagonals.
3. Surface area of
a cuboid = 2(lb + bh + hl)
a cube = 6l2
a cylinder = 2πr(r + h)
4. Amount of region occupied by a solid is called its volume.
5. Volume of
a cuboid = l × b × h
a cube = l3
a cylinder = πr2h
6. (i) 1 cm3 = 1 mL
(ii) 1L = 1000 cm3
(iii) 1 m3 = 1000000 cm3 = 1000L
