Table of Contents
Chapter 14
Factorisation
14.1 Introduction
14.1.1 Factors of natural numbers
You will remember what you learnt about factors in Class VI. Let us take a natural number, say 30, and write it as a product of other natural numbers, say
30 = 2 × 15
We know that 30 can also be written as 30 = 1 × 30
Thus, 1 and 30 are also factors of 30.
You will notice that 1 is a factor of any number. For example, 101 = 1 × 101. However, when we write a number as a product of factors, we shall not write 1 as a factor, unless it is specially required.
= 3 × 10 = 5 × 6
Thus, 1, 2, 3, 5, 6, 10, 15 and 30 are the factors of 30. Of these, 2, 3 and 5 are the prime factors of 30 (Why?)
A number written as a product of prime factors is said to be in the prime factor form; for example, 30 written as 2 × 3 × 5 is in the prime factor form.
The prime factor form of 70 is 2 × 5 × 7.
The prime factor form of 90 is 2 × 3 × 3 × 5, and so on.
Similarly, we can express algebraic expressions as products of their factors. This is what we shall learn to do in this chapter.
14.1.2 Factors of algebraic expressions
We have seen in Class VII that in algebraic expressions, terms are formed as products of factors. For example, in the algebraic expression 5xy + 3x the term 5xy has been formed by the factors 5, x and y, i.e.,
Note 1 is a factor of 5xy, since
5xy = 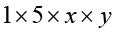
In fact, 1 is a factor of every term. As in the case of natural numbers, unless it is specially required, we do not show 1 as a separate factor of any term.
5xy = 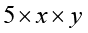
Observe that the factors 5, x and y of 5xy cannot further be expressed as a product of factors. We may say that 5,
x and y are ‘prime’ factors of 5xy. In algebraic expressions, we use the word ‘irreducible’ in place of ‘prime’. We say that 5 × x × y is the irreducible form of 5xy. Note 5 × (xy) is not an irreducible form of 5xy, since the factor xy can be further expressed as a product of x and y, i.e., xy = x × y.
Next consider the expression 3x (x + 2). It can be written as a product of factors.
3, x and (x + 2)
3x(x + 2) =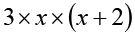
The factors 3, x and (x +2) are irreducible factors of 3x (x + 2).
Similarly, the expression 10x (x + 2) (y + 3) is expressed in its irreducible factor form as 10x (x + 2) (y + 3) = 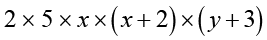 .
.
14.2 What is Factorisation?
When we factorise an algebraic expression, we write it as a product of factors. These factors may be numbers, algebraic variables or algebraic expressions.
Expressions like 3xy, 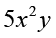 , 2x (y + 2), 5 (y + 1) (x + 2) are already in factor form. Their factors can be just read off from them, as we already know.
, 2x (y + 2), 5 (y + 1) (x + 2) are already in factor form. Their factors can be just read off from them, as we already know.
On the other hand consider expressions like 2x + 4, 3x + 3y, x2 + 5x, x2 + 5x + 6.
It is not obvious what their factors are. We need to develop systematic methods to factorise these expressions, i.e., to find their factors. This is what we shall do now.
14.2.1 Method of common factors
• We begin with a simple example: Factorise 2x + 4.
We shall write each term as a product of irreducible factors;
2x = 2 × x
4 = 2 × 2
Hence 2x + 4 = (2 × x) + (2 × 2)
Notice that factor 2 is common to both the terms.
Observe, by distributive law
2 × (x + 2) = (2 × x) + (2 × 2)
Therefore, we can write
2x + 4 = 2 × (x + 2) = 2 (x + 2)
Thus, the expression 2x + 4 is the same as 2 (x + 2). Now we can read off its factors: they are 2 and (x + 2). These factors are irreducible.
Next, factorise 5xy + 10x.
The irreducible factor forms of 5xy and 10x are respectively,
5xy = 5 × x × y
10x = 2 × 5 × x
Observe that the two terms have 5 and x as common factors. Now,
5xy + 10x = (5 × x × y) + (5 × x × 2)
= (5x × y) + (5x × 2)
We combine the two terms using the distributive law,
(5x× y) + (5x× 2) = 5x × ( y + 2)
Therefore, 5xy + 10x = 5 x (y + 2). (This is the desired factor form.)
Example 1: Factorise 12a2b + 15ab2
Solution: We have 12a2b = 2 × 2 × 3 × a × a × b
15ab2 = 3 × 5 × a × b × b
The two terms have 3, a and b as common factors.
Therefore, 12a2b + 15ab2 = (3 × a × b × 2 × 2 × a) + (3 × a × b × 5 × b)
= 3 × a × b × [(2 × 2 × a) + (5 × b)]
(combining the terms)
= 3ab × (4a + 5b)
= 3ab (4a + 5b) (required factor form)
Example 2: Factorise 10x2 – 18x3 + 14x4
Solution: 10x2 = 2 × 5 × x × x
18x3 = 2 × 3 × 3 × x × x × x
14x4 = 2 × 7 × x × x × x × x
The common factors of the three terms are 2, x and x.
Therefore, 10x2 – 18x3 + 14x4 = (2 × x × x × 5) – (2 × x × x × 3 × 3 × x)
(combining the three terms)
+ (2 × x × x × 7 × x × x)
= 2 × x × x ×[(5 – (3 × 3 × x) + (7 × x × x)]
= 2x2 × (5 – 9x + 7x2) = 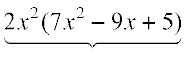
TRY THESE
Factorise: (i) 12x + 36 (ii) 22y – 33z (iii) 14pq + 35pqr
14.2.2 Factorisation by regrouping terms
Look at the expression 2xy + 2y + 3x + 3. You will notice that the first two terms have common factors 2 and y and the last two terms have a common factor 3. But there is no single factor common to all the terms. How shall we proceed?
Let us write (2xy + 2y) in the factor form:
2xy + 2y = (2 × x × y) + (2 × y)
= (2 × y × x) + (2 × y × 1)
= (2y × x) + (2y × 1) = 2y (x + 1)
Similarly, 3x + 3 = (3 × x) + (3 × 1)
= 3 × (x + 1) = 3 ( x + 1)
Hence, 2xy + 2y + 3x + 3 = 2y (x + 1) + 3 (x +1)
Observe, now we have a common factor (x + 1) in both the terms on the right hand side. Combining the two terms,
2xy + 2y + 3x + 3 = 2y (x + 1) + 3 (x + 1) = (x + 1) (2y + 3)
The expression 2xy + 2y + 3x + 3 is now in the form of a product of factors. Its factors are (x + 1) and (2y + 3). Note, these factors are irreducible.
What is regrouping?
Suppose, the above expression was given as 2xy + 3 + 2y + 3x; then it will not be easy to see the factorisation. Rearranging the expression, as 2xy + 2y + 3x + 3, allows us to form groups (2xy + 2y) and (3x + 3) leading to factorisation. This is regrouping.
Regrouping may be possible in more than one ways. Suppose, we regroup the expression as: 2xy + 3x + 2y + 3. This will also lead to factors. Let us try:
2xy + 3x + 2y + 3 = 2 × x × y + 3 × x + 2 × y + 3
= x × (2y + 3) + 1 × (2y + 3)
= (2y + 3) (x + 1)
The factors are the same (as they have to be), although they appear in different order.
Example 3: Factorise 6xy – 4y + 6 – 9x.
Solution:
Step 1 Check if there is a common factor among all terms. There is none.
Step 2 Think of grouping. Notice that first two terms have a common factor 2y;
6xy – 4y = 2y (3x – 2) (a)
What about the last two terms? Observe them. If you change their order to
– 9x + 6, the factor ( 3x – 2) will come out;
–9x + 6 = –3 (3x) + 3 (2)
= – 3 (3x – 2) (b)
Step 3 Putting (a) and (b) together,
6xy – 4y + 6 – 9x = 6xy – 4y – 9x + 6
= 2y (3x – 2) – 3 (3x – 2)
= (3x – 2) (2y – 3)
The factors of (6xy – 4y + 6 – 9 x) are (3x – 2) and (2y – 3).

Exercise 14.1
1. Find the common factors of the given terms.
(i) 12x, 36 (ii) 2y, 22xy (iii) 14 pq, 28p2q2
(iv) 2x, 3x2, 4 (v) 6 abc, 24ab2, 12 a2b
(vi) 16 x3, – 4x2, 32x (vii) 10 pq, 20qr, 30rp
(viii) 3x2 y3, 10x3 y2,6 x2 y2z
2. Factorise the following expressions.
(i) 7x – 42 (ii) 6p – 12q (iii) 7a2 + 14a
(iv) – 16 z + 20 z3 (v) 20 l2 m + 30 a l m
(vi) 5 x2 y – 15 xy2 (vii) 10 a2 – 15 b2 + 20 c2
(viii) – 4 a2 + 4 ab – 4 ca (ix) x2 y z + x y2z + x y z2
(x) a x2 y + b x y2 + c x y z
3. Factorise.
(i) x2 + x y + 8x + 8y (ii) 15 xy – 6x + 5y – 2
(iii) ax + bx – ay – by (iv) 15 pq + 15 + 9q + 25p
(v) z – 7 + 7 x y – x y z
14.2.3 Factorisation using identities
We know that (a + b)2 = a2 + 2ab + b2 (I)
(a – b)2 = a2 – 2ab + b2 (II)
(a + b) (a – b) = a2 – b2 (III)
The following solved examples illustrate how to use these identities for factorisation. What we do is to observe the given expression. If it has a form that fits the right hand side of one of the identities, then the expression corresponding to the left hand side of the identity gives the desired factorisation.
Example 4: Factorise x2 + 8x + 16
Identity III. Also, it’s first and third terms are perfect squares with a positive sign before the middle term. So, it is of the form a2 + 2ab + b2 where a = x and b = 4
such that a2 + 2ab + b2 = x2 + 2 (x) (4) + 42
= x2 + 8x + 16
Observe here the given expression is of the form a2 – 2ab + b2.
Where a = 2y, and b = 3 with 2ab = 2 × 2y × 3 = 12y.
Since a2 + 2ab + b2 = (a + b)2,
by comparison x2 + 8x + 16 = ( x + 4)2 (the required factorisation)
Example 5: Factorise 4y2 – 12y + 9
Solution: Observe 4y2 = (2y)2, 9 = 32 and 12y = 2 × 3 × (2y)
Therefore, 4y2 – 12y + 9 = (2y)2 – 2 × 3 × (2y) + (3)2
= ( 2y – 3)2 (required factorisation)
Example 6: Factorise 49p2 – 36
Solution: There are two terms; both are squares and the second is negative. The expression is of the form (a2 – b2). Identity III is applicable here;
49p2 – 36 = (7p)2 – ( 6 )2
= (7p – 6 ) ( 7p + 6) (required factorisation)
Example 7: Factorise a2 – 2ab + b2 – c2
Solution: The first three terms of the given expression form (a – b)2. The fourth term is a square. So the expression can be reduced to a difference of two squares.
Thus, a2 – 2ab + b2 – c2 = (a – b)2– c2 (Applying Identity II)
= [(a – b) – c) ((a – b) + c)] (Applying Identity III)
= (a – b – c) (a – b + c) (required factorisation)
Notice, how we applied two identities one after the other to obtain the required factorisation.
Example 8: Factorise m4 – 256
Solution: We note m4 = (m2)2 and 256 = (16) 2
Thus, the given expression fits Identity III.
Therefore, m4 – 256 = (m2)2 – (16) 2
= (m2 –16) (m2 +16) [(using Identity (III)]
Now, (m2 + 16) cannot be factorised further, but (m2 –16) is factorisable again as per Identity III.
m2–16 = m2 – 42
= (m – 4) (m + 4)
Therefore, m4 – 256 = (m – 4) (m + 4) (m2 +16)
14.2.4 Factors of the form ( x + a) ( x + b)
Let us now discuss how we can factorise expressions in one variable, like x2 + 5x + 6,
y2 – 7y + 12, z2 – 4z – 12, 3m2 + 9m + 6, etc. Observe that these expressions are not of the type (a + b) 2 or (a – b) 2, i.e., they are not perfect squares. For example, in
x2 + 5x + 6, the term 6 is not a perfect square. These expressions obviously also do not fit the type (a2 – b2) either.
They, however, seem to be of the type x2 + (a + b) x + a b. We may therefore, try to use Identity IV studied in the last chapter to factorise these expressions:
(x + a) (x + b) = x2 + (a + b) x + ab (IV)
For that we have to look at the coefficients of x and the constant term. Let us see how it is done in the following example.
Example 9: Factorise x2 + 5x + 6
Solution: If we compare the R.H.S. of Identity (IV) with x2 + 5x + 6, we find ab = 6, and a + b = 5. From this, we must obtain a and b. The factors then will be
(x + a) and (x + b).
If a b = 6, it means that a and b are factors of 6. Let us try a = 6, b = 1. For these values a + b = 7, and not 5, So this choice is not right.
Let us try a = 2, b = 3. For this a + b = 5 exactly as required.
The factorised form of this given expression is then (x +2) (x + 3).
In general, for factorising an algebraic expression of the type x2 + px + q, we find two factors a and b of q (i.e., the constant term) such that
ab = q and a + b = p
Then, the expression becomes x2 + (a + b) x + ab
or x2 + ax + bx + ab
or x(x + a) + b(x + a)
or (x + a) (x + b) which are the required factors.
Example 10: Find the factors of y2 –7y +12.
Solution: We note 12 = 3 × 4 and 3 + 4 = 7. Therefore,
y2 – 7y+ 12 = y2 – 3y – 4y + 12
= y (y –3) – 4 (y –3) = (y –3) (y – 4)
Note, this time we did not compare the expression with that in Identity (IV) to identify a and b. After sufficient practice you may not need to compare the given expressions for their factorisation with the expressions in the identities; instead you can proceed directly as we did above.
Example 11: Obtain the factors of z2 – 4z – 12.
Solution: Here a b = –12 ; this means one of a and b is negative. Further, a + b = – 4, this means the one with larger numerical value is negative. We try a = – 4, b = 3; but
this will not work, since a + b = –1. Next possible values are a = – 6, b = 2, so that
a + b = – 4 as required.
Hence, z2 – 4z –12 = z2 – 6z + 2z –12
= z(z – 6) + 2(z – 6 )
= (z – 6) (z + 2)
Example 12: Find the factors of 3m2 + 9m + 6.
Solution: We notice that 3 is a common factor of all the terms.
Therefore, 3m2 + 9m + 6 = 3(m2 + 3m + 2)
Now, m 2 + 3m + 2 = m2 + m + 2m + 2 (as 2 = 1 × 2)
= m(m + 1)+ 2( m + 1)
= (m + 1) (m + 2)
Therefore, 3m2 + 9m + 6 = 3(m + 1) (m + 2)

Exercise 14.2
1. Factorise the following expressions.
(i) a2 + 8a + 16 (ii) p2 – 10 p + 25 (iii) 25m2 + 30m + 9
(iv) 49y2 + 84yz + 36z2 (v) 4x2 – 8x + 4
(vi) 121b2 – 88bc + 16c2
(vii) (l + m)2 – 4lm (Hint: Expand ( l + m)2 first)
(viii) a4 + 2a2b2 + b4
2. Factorise.
(i) 4p2 – 9q2 (ii) 63a2 – 112b2 (iii) 49x2 – 36
(iv) 16x5 – 144x3 (v) (l + m)2 – (l – m)2
(vi) 9x2 y2 – 16 (vii) (x2 – 2xy + y2) – z2
(viii) 25a2 – 4b2 + 28bc – 49c2
3. Factorise the expressions.
(i) ax2 + bx (ii) 7p2 + 21q2 (iii) 2x3 + 2xy2 + 2xz2
(iv) am2 + bm2 + bn2 + an2 (v) (lm + l) + m + 1
(vi) y (y + z) + 9 (y + z) (vii) 5y2 – 20y – 8z + 2yz
(viii) 10ab + 4a + 5b + 2 (ix) 6xy – 4y + 6 – 9x
4. Factorise.
(i) a4 – b4 (ii) p4 – 81 (iii) x4 – (y + z)4
(iv) x4 – (x – z)4 (v) a4 – 2a2b2 + b4
5. Factorise the following expressions.
(i) p2 + 6p + 8 (ii) q2 – 10q + 21 (iii) p2 + 6p – 16
14.3 Division of Algebraic Expressions
We have learnt how to add and subtract algebraic expressions. We also know how to multiply two expressions. We have not however, looked at division of one algebraic expression by another. This is what we wish to do in this section.
We recall that division is the inverse operation of multiplication. Thus, 7 × 8 = 56 gives 56 ÷ 8 = 7 or 56 ÷ 7 = 8.
We may similarly follow the division of algebraic expressions. For example,
(i) 2x × 3x2 = 6x3
Therefore, 6x3 ÷ 2x = 3x2
and also, 6x3 ÷ 3x2 = 2x.
(ii) 5x (x + 4) = 5x2 + 20x
Therefore, (5x2 + 20x) ÷ 5x = x + 4
and also (5x2 + 20x) ÷ (x + 4) = 5x.
We shall now look closely at how the division of one expression by another can be carried out. To begin with we shall consider the division of a monomial by another monomial.
14.3.1 Division of a monomial by another monomial
Consider 6x3 ÷ 2x
We may write 2x and 6x3 in irreducible factor forms,
2x = 2 × x
6x3 = 2 × 3 × x × x × x
Now we group factors of 6x3 to separate 2x,
6x3 = 2 × x × (3 × x × x) = (2x) × (3x2)
Therefore, 6x3 ÷ 2x = 3x2.
A shorter way to depict cancellation of common factors is as we do in division of numbers:
77 ÷ 7 = 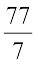 =
= 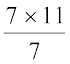 = 11
= 11
Similarly, 6x3 ÷ 2x = 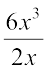
= 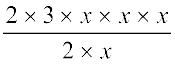 = 3 × x × x = 3x2
= 3 × x × x = 3x2
Example 13: Do the following divisions.
(i) –20x4 ÷ 10x2 (ii) 7x2y2z2 ÷ 14xyz
Solution:
(i) –20x4 = –2 × 2 × 5 × x × x × x × x
10x2 = 2 × 5 × x × x
Therefore, (–20x4) ÷ 10x2 = 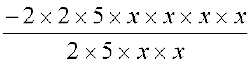 = –2 × x × x = –2x2
= –2 × x × x = –2x2
(ii) 7x2y2z2 ÷ 14xyz = 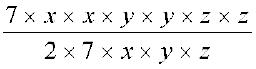
= 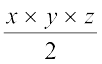 =
= 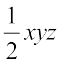

TRY THESE
Divide.
(i) 24xy2z3 by 6yz2 (ii) 63a2b4c6 by 7a2b2c3
14.3.2 Division of a polynomial by a monomial
Let us consider the division of the trinomial 4y3 + 5y2 + 6y by the monomial 2y.
4y3 + 5y2 + 6y = (2 × 2 × y × y × y) + (5 × y × y) + (2 × 3 × y)
(Here, we expressed each term of the polynomial in factor form) we find that 2 × y is common in each term. Therefore, separating 2 × y from each term. We get
4y3 + 5y2 + 6y = 2 × y × (2 × y × y) + 2 × y × 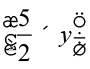 + 2 × y × 3
+ 2 × y × 3
= 2y (2y2) + 2y  + 2y (3)
+ 2y (3)
= 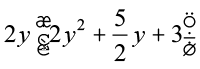 (The common factor 2y is shown separately.
(The common factor 2y is shown separately.
Therefore, (4y3 + 5y2 + 6y) ÷ 2y
=  = 2y2 +
= 2y2 +  y + 3
y + 3
Alternatively, we could divide each term of the trinomial by the monomial using the cancellation method.
(4y3 + 5y2 + 6y) ÷ 2y = 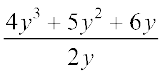
= 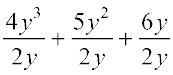 = 2y2 +
= 2y2 + 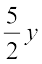 + 3
+ 3
Example 14: Divide 24(x2yz + xy2z + xyz2) by 8xyz using both the methods.
Solution: 24 (x2yz + xy2z + xyz2)
(By taking out the common factor)
= 2 × 2 × 2 × 3 × [(x × x × y × z) + (x × y × y × z) + (x × y × z × z)]
= 2 × 2 × 2 × 3 × x × y × z × (x + y + z) = 8 × 3 × xyz × (x + y + z)
Therefore, 24 (x2yz + xy2z + xyz2) ÷ 8xyz
= 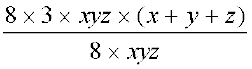 = 3 × (x + y + z) = 3 (x + y + z)
= 3 × (x + y + z) = 3 (x + y + z)
Alternately, 24(x2yz + xy2z + xyz2) ÷ 8xyz = 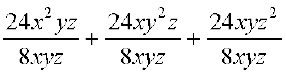
= 3x + 3y + 3z = 3(x + y + z)
14.4 Division of Algebraic Expressions Continued (Polynomial ÷ Polynomial)
We shall factorise (7x2 + 14x) first to check and match factors with the denominator:
7x2 + 14x = (7 × x × x) + (2 × 7 × x)
= 7 × x × (x + 2) = 7x(x + 2)
Will it help here to divide each term of the numerator by the binomial in the denominator?
Now (7x2 + 14x) ÷ (x + 2) = 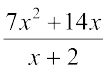
= 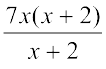 = 7x (Cancelling the factor (x + 2))
= 7x (Cancelling the factor (x + 2))
Example 15: Divide 44(x4 – 5x3 – 24x2) by 11x (x – 8)
Solution: Factorising 44(x4 – 5x3 – 24x2), we get
44(x4 – 5x3 – 24x2) = 2 × 2 × 11 × x2(x2 – 5x – 24)
(taking the common factor x2 out of the bracket)
= 2 × 2 × 11 × x2(x2 – 8x + 3x – 24)
We cancel the factors 11, x and (x – 8) common to both the numerator and denominator.
= 2 × 2 × 11 × x2 [x (x – 8) + 3(x – 8)]
= 2 × 2 × 11 × x2 (x + 3) (x – 8)
Therefore, 44(x4 – 5x3 – 24x2) ÷ 11x(x – 8)
= 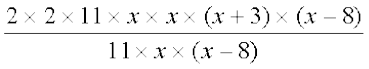
= 2 × 2 × x (x + 3) = 4x(x + 3)
Example 16: Divide z(5z2 – 80) by 5z(z + 4)
Solution: Dividend = z(5z2 – 80)
= z[(5 × z2) – (5 × 16)]
= z × 5 × (z2 – 16)
= 5z × (z + 4) (z – 4) [using the identity
a2 – b2 = (a + b) (a – b)]
Thus, z(5z2 – 80) ÷ 5z(z + 4) = 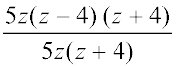 = (z – 4)
= (z – 4)

Exercise 14.3
(i) 28x4 ÷ 56x (ii) –36y3 ÷ 9y2 (iii) 66pq2r3 ÷ 11qr2
(iv) 34x3y3z3 ÷ 51xy2z3 (v) 12a8b8 ÷ (– 6a6b4)
2. Divide the given polynomial by the given monomial.
(i) (5x2 – 6x) ÷ 3x (ii) (3y8 – 4y6 + 5y4) ÷ y4
(iii) 8(x3y2z2 + x2y3z2 + x2y2z3) ÷ 4x2y2z2 (iv) (x3 + 2x2 + 3x) ÷ 2x
(v) (p3q6 – p6q3) ÷ p3q3
3. Work out the following divisions.
(i) (10x – 25) ÷ 5 (ii) (10x – 25) ÷ (2x – 5)
(iii) 10y(6y + 21) ÷ 5(2y + 7) (iv) 9x2y2(3z – 24) ÷ 27xy(z – 8)
(v) 96abc(3a – 12) (5b – 30) ÷ 144(a – 4) (b – 6)
4. Divide as directed.
(i) 5(2x + 1) (3x + 5) ÷ (2x + 1) (ii) 26xy(x + 5) (y – 4) ÷ 13x(y – 4)
(iii) 52pqr (p + q) (q + r) (r + p) ÷ 104pq(q + r) (r + p)
(iv) 20(y + 4) (y2 + 5y + 3) ÷ 5(y + 4) (v) x(x + 1) (x + 2) (x + 3) ÷ x(x + 1)
5. Factorise the expressions and divide them as directed.
(i) (y2 + 7y + 10) ÷ (y + 5) (ii) (m2 – 14m – 32) ÷ (m + 2)
(iii) (5p2 – 25p + 20) ÷ (p – 1) (iv) 4yz(z2 + 6z – 16) ÷ 2y(z + 8)
(v) 5pq(p2 – q2) ÷ 2p(p + q)
(vi) 12xy(9x2 – 16y2) ÷ 4xy(3x + 4y) (vii) 39y3(50y2 – 98) ÷ 26y2(5y + 7)
14.5 Can you Find the Error?
3x + x + 5x = 72
Therefore 8x = 72
and so, x = 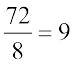
Coefficient 1 of a term is usually not shown. But while adding like terms, we include it in the sum.
Where has she gone wrong? Find the correct answer.
Task 2 Appu did the following:
For x = –3 , 5x = 5 – 3 = 2
Remember to make use of brackets, while substituting a negative value.
Is his procedure correct? If not, correct it.
Task 3 Namrata and Salma have done the multiplication of algebraic expressions in the following manner.
Namrata Salma
(a) 3(x – 4) = 3x – 4 3(x – 4) = 3x – 12
Remember, when you multiply the expression enclosed in a bracket by a constant (or a variable) outside, each term of the expression has to be multiplied by the constant (or the variable).
(b) (2x)2 = 2x2 (2x)2 = 4x2
(c) (2a – 3) (a + 2) (2a – 3) (a + 2)
= 2a2 – 6 = 2a2 + a – 6
Make sure, before applying any formula, whether the formula is really applicable.
(d) (x + 8)2 = x2 + 64 (x + 8)2
= x2 + 16x + 64
(e) (x – 5)2 = x2 – 25 (x – 5)2 = x2 – 10x + 25
Is the multiplication done by both Namrata and Salma correct? Give reasons for your answer.
Task 4 Joseph does a division as : 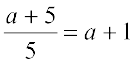
While dividing a polynomial by a monomial, we divide each term of the polynomial in the numerator by the monomial in the denominator.
His friend Sirish has done the same division as: 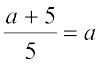
And his other friend Suman does it this way: 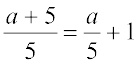
Who has done the division correctly? Who has done incorrectly? Why?
Some fun!
Atul always thinks differently. He asks Sumathi teacher, “If what you say is true, then why do I get the right answer for 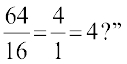 The teacher explains, “ This is so because 64 happens to be 16 × 4;
The teacher explains, “ This is so because 64 happens to be 16 × 4; 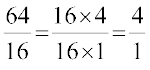 . In reality, we cancel a factor of 16 and not 6, as you can see. In fact, 6 is not a factor of either 64 or of 16.” The teacher adds further, “Also,
. In reality, we cancel a factor of 16 and not 6, as you can see. In fact, 6 is not a factor of either 64 or of 16.” The teacher adds further, “Also, 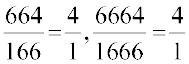 , and so on”. Isn’t that interesting? Can you help Atul to find some other examples like
, and so on”. Isn’t that interesting? Can you help Atul to find some other examples like 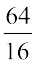 ?
?

Exercise 14.4
1. 4(x – 5) = 4x – 5 2. x(3x + 2) = 3x2 + 2 3. 2x + 3y = 5xy
4. x + 2x + 3x = 5x 5. 5y + 2y + y – 7y = 0 6. 3x + 2x = 5x2
7. (2x)2 + 4(2x) + 7 = 2x2 + 8x + 7 8. (2x)2 + 5x = 4x + 5x = 9x
9. (3x + 2)2 = 3x2 + 6x + 4
10. Substituting x = – 3 in
(a) x2 + 5x + 4 gives (– 3)2 + 5 (– 3) + 4 = 9 + 2 + 4 = 15
(b) x2 – 5x + 4 gives (– 3)2 – 5 ( – 3) + 4 = 9 – 15 + 4 = – 2
(c) x2 + 5x gives (– 3)2 + 5 (–3) = – 9 – 15 = – 24
11. (y – 3)2 = y2 – 9 12. (z + 5)2 = z2 + 25
13. (2a + 3b) (a – b) = 2a2 – 3b2 14. (a + 4) (a + 2) = a2 + 8
15. (a – 4) (a – 2) = a2 – 8 16. 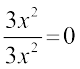
17. 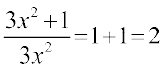 18.
18. 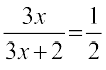 19.
19. 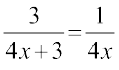
20. 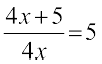 21.
21. 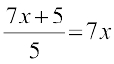
WHAT HAVE WE DISCUSSED?
1. When we factorise an expression, we write it as a product of factors. These factors may be numbers, algebraic variables or algebraic expressions.
2. An irreducible factor is a factor which cannot be expressed further as a product of factors.
3. A systematic way of factorising an expression is the common factor method. It consists of three steps: (i) Write each term of the expression as a product of irreducible factors (ii) Look for and separate the common factors and (iii) Combine the remaining factors in each term in accordance with the distributive law.
4. Sometimes, all the terms in a given expression do not have a common factor; but the terms can be grouped in such a way that all the terms in each group have a common factor. When we do this, there emerges a common factor across all the groups leading to the required factorisation of the expression. This is the method of regrouping.
5. In factorisation by regrouping, we should remember that any regrouping (i.e., rearrangement) of the terms in the given expression may not lead to factorisation. We must observe the expression and come out with the desired regrouping by trial and error.
6. A number of expressions to be factorised are of the form or can be put into the form : a2 + 2 ab + b2, a2 – 2ab + b2, a2 – b2 and x2 + (a + b) + ab. These expressions can be easily factorised using Identities I, II, III and IV, given in Chapter 9,
a2 + 2 ab + b2 = (a + b)2
a2 – 2ab + b2 = (a – b)2
a2 – b2 = (a + b) (a – b)
x2 + (a + b) x + ab = (x + a) (x + b)
7. In expressions which have factors of the type (x + a) (x + b), remember the numerical term gives ab. Its factors, a and b, should be so chosen that their sum, with signs taken care of, is the coefficient of x.
8. We know that in the case of numbers, division is the inverse of multiplication. This idea is applicable also to the division of algebraic expressions.
9. In the case of division of a polynomial by a monomial, we may carry out the division either by dividing each term of the polynomial by the monomial or by the common factor method.
10. In the case of division of a polynomial by a polynomial, we cannot proceed by dividing each term in the dividend polynomial by the divisor polynomial. Instead, we factorise both the polynomials and cancel their common factors.
11. In the case of divisions of algebraic expressions that we studied in this chapter, we have
Dividend = Divisor × Quotient.
In general, however, the relation is
Dividend = Divisor × Quotient + Remainder
Thus, we have considered in the present chapter only those divisions in which the remainder is zero.
12. There are many errors students commonly make when solving algebra exercises. You should avoid making such errors.

