Table of Contents
Chapter 16
Playing with Numbers
16.1 Introduction
You have studied various types of numbers such as natural numbers, whole numbers, integers and rational numbers. You have also studied a number of interesting properties about them. In Class VI, we explored finding factors and multiples and the relationships among them.
In this chapter, we will explore numbers in more detail. These ideas help in justifying tests of divisibility.

16.2 Numbers in General Form
Let us take the number 52 and write it as
52 = 50 + 2 = 10 × 5 + 2
Similarly, the number 37 can be written as
37 = 10 × 3 + 7
In general, any two digit number ab made of digits a and b can be written as
ab = 10 × a + b = 10a + b
What about ba? ba = 10 × b + a = 10b + a
Let us now take number 351. This is a three digit number. It can also be written as
351 = 300 + 50 + 1 = 100 × 3 + 10 × 5 + 1 × 1
Similarly 497 = 100 × 4 + 10 × 9 + 1 × 7
In general, a 3-digit number abc made up of digits a, b and c is written as
abc = 100 × a + 10 × b + 1 × c
= 100a + 10b + c
In the same way,
cab = 100c + 10a + b
bca = 100b + 10c + a and so on.

TRY THESE
1. Write the following numbers in generalised form.
2. Write the following in the usual form.
(i) 10 × 5 + 6 (ii) 100 × 7 + 10 × 1 + 8 (iii) 100 × a + 10 × c + b
16.3 Games with Numbers
(i) Reversing the digits – two digit number
Minakshi asks Sundaram to think of a 2-digit number, and then to do whatever she asks him to do, to that number. Their conversation is shown in the following figure. Study the figure carefully before reading on.
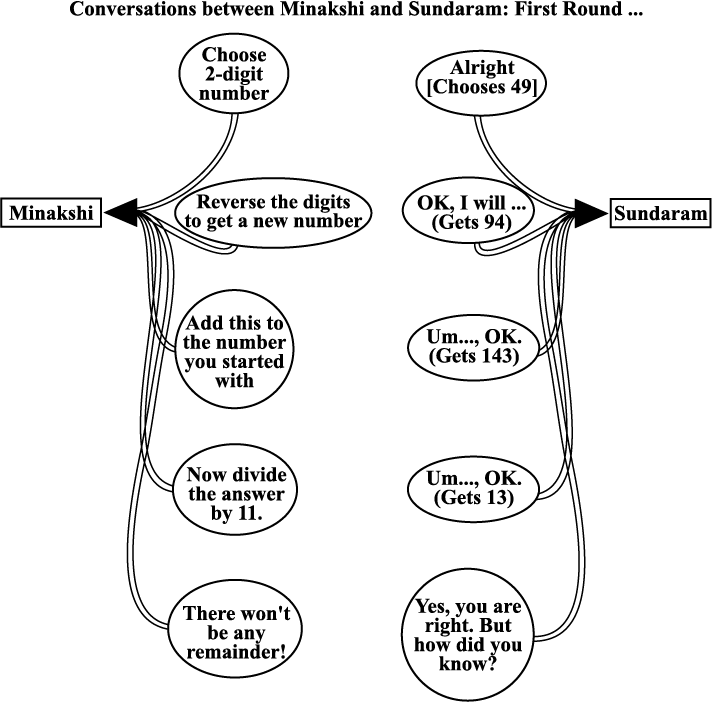
It so happens that Sundaram chose the number 49. So, he got the reversed number 94; then he added these two numbers and got 49 + 94 = 143. Finally he divided this number by 11 and got 143 ÷ 11 = 13, with no remainder. This is just what Minakshi had predicted.

TRY THESE
Check what the result would have been if Sundaram had chosen the numbers shown below.
1. 27 2. 39 3. 64 4. 17
Now, let us see if we can explain Minakshi’s “trick”.
Suppose Sundaram chooses the number ab, which is a short form for the 2-digit number 10a + b. On reversing the digits, he gets the number ba = 10b + a. When he adds the two numbers he gets:
(10a + b) + (10b + a) = 11a + 11b
= 11 (a + b).
So, the sum is always a multiple of 11, just as Minakshi had claimed.
Observe here that if we divide the sum by 11, the quotient is a + b, which is exactly the sum of the digits of chosen number ab.
You may check the same by taking any other two digit number.
The game between Minakshi and Sundaram continues!
Minakshi: Think of another 2-digit number, but don’t tell me what it is.
Sundaram: Alright.
Minakshi: Now reverse the digits of the number, and subtract the smaller number from the larger one.
Sundaram: I have done the subtraction. What next?
Minakshi: Now divide your answer by 9. I claim that there will be no remainder!
Sundaram: Yes, you are right. There is indeed no remainder! But this time I think I know how you are so sure of this!
In fact, Sundaram had thought of 29. So his calculations were: first he got the number 92; then he got 92 – 29 = 63; and finally he did (63 ÷ 9) and got 7 as quotient, with no remainder.

TRY THESE
Check what the result would have been if Sundaram had chosen the numbers shown below.
1. 17 2. 21 3. 96 4. 37
Let us see how Sundaram explains Minakshi’s second “trick”. (Now he feels confident of doing so!)
Suppose he chooses the 2-digit number ab = 10a + b. After reversing the digits, he gets the number ba = 10b + a. Now Minakshi tells him to do a subtraction, the smaller number from the larger one.
• If the tens digit is larger than the ones digit (that is, a > b), he does:
(10a + b) – (10b + a) = 10a + b – 10b – a
= 9a – 9b = 9(a – b).
• If the ones digit is larger than the tens digit (that is, b > a), he does:
(10b + a) – (10a + b) = 9(b – a).
• And, of course, if a = b, he gets 0.
In each case, the resulting number is divisible by 9. So, the remainder is 0. Observe here that if we divide the resulting number (obtained by subtraction), the quotient is a – b or b – a according as a > b or a < b. You may check the same by taking any other two digit numbers.
(ii) Reversing the digits – three digit number.
Now it is Sundaram’s turn to play some tricks!
Sundaram: Think of a 3-digit number, but don’t tell me what it is.
Minakshi: Alright.
Sundaram: Now make a new number by putting the digits in reverse order, and subtract the smaller number from the larger one.
Minakshi: Alright, I have done the subtraction. What next?
Sundaram: Divide your answer by 99. I am sure that there will be no remainder!
In fact, Minakshi chose the 3-digit number 349. So she got:
• Reversed number: 943; • Difference: 943 – 349 = 594;
• Division: 594 ÷ 99 = 6, with no remainder.

TRY THESE
Check what the result would have been if Minakshi had chosen the numbers shown below. In each case keep a record of the quotient obtained at the end.
1. 132 2. 469 3. 737 4. 901
Let us see how this trick works.
Let the 3-digit number chosen by Minakshi be abc = 100a + 10b + c.
After reversing the order of the digits, she gets the number cba = 100c + 10b + a. On subtraction:
• If a > c, then the difference between the numbers is
(100a + 10b + c) – (100c + 10b + a) = 100a + 10b + c – 100c – 10b – a
= 99a – 99c = 99(a – c).
• If c > a, then the difference between the numbers is
(100c + 10b + a) – (100a + 10b + c) = 99c – 99a = 99(c – a).
• And, of course, if a = c, the difference is 0.
In each case, the resulting number is divisible by 99. So the remainder is 0. Observe that quotient is a – c or c – a. You may check the same by taking other 3-digit numbers.
(iii) Forming three-digit numbers with given three-digits.
Now it is Minakshi’s turn once more.
Minakshi: Think of any 3-digit number.
Sundaram: Alright, I have done so.
Minakshi: Now use this number to form two more 3-digit numbers, like this: if the number you chose is abc, then
• ‘the first number is cab (i.e., with the ones digit shifted to the “left end” of the number);
• the other number is bca (i.e., with the hundreds digit shifted to the “right end” of the number).
Now add them up. Divide the resulting number by 37. I claim that there will be no remainder.
Sundaram: Yes. You are right!
In fact, Sundaram had thought of the 3-digit number 237. After doing what Minakshi had asked, he got the numbers 723 and 372. So he did:
2 3 7
+ 7 2 3
+ 3 7 2
1 3 3 2
Then he divided the resulting number 1332 by 37:
1332 ÷ 37 = 36, with no remainder.

TRY THESE
Check what the result would have been if Sundaram had chosen the numbers shown below.
1. 417 2. 632 3. 117 4. 937
Will this trick always work?
Let us see. abc = 100a + 10b + c
cab = 100c + 10a + b
bca = 100b + 10c + a
abc + cab + bca = 111(a + b + c)
= 37 × 3(a + b + c), which is divisible by 37
16.4 Letters for Digits
Here we have puzzles in which letters take the place of digits in an arithmetic ‘sum’, and the problem is to find out which letter represents which digit; so it is like cracking a code. Here we stick to problems of addition and multiplication.
Here are two rules we follow while doing such puzzles.
1. Each letter in the puzzle must stand for just one digit. Each digit must be represented by just one letter.
2. The first digit of a number cannot be zero. Thus, we write the number “sixty three” as 63, and not as 063, or 0063.
A rule that we would like to follow is that the puzzle must have just one answer.
Example 1: Find Q in the addition.
3 1 Q
+ 1 Q 3
5 0 1
Solution:
There is just one letter Q whose value we have to find.
Study the addition in the ones column: from Q + 3, we get ‘1’, that is, a number whose ones digit is 1.
For this to happen, the digit Q should be 8. So the puzzle can be solved as shown below.

3 1 8
+ 1 8 3
5 0 1
That is, Q = 8
Example 2: Find A and B in the addition.
A
+ A
+ A
B A
Solution: This has two letters A and B whose values are to be found.
Study the addition in the ones column: the sum of three A’s is a number whose ones digit is A. Therefore, the sum of two A’s must be a number whose ones digit is 0.
This happens only for A = 0 and A = 5.
If A = 0, then the sum is 0 + 0 + 0 = 0, which makes B = 0 too. We do not want this (as it makes A = B, and then the tens digit of BA too becomes 0), so we reject this possibility. So, A = 5.
Therefore, the puzzle is solved as shown below.
5
+ 5
+ 5
That is, A = 5 and B = 1. 1 5
Example 3: Find the digits A and B.
B A
× B 3
5 7 A
Solution:
This also has two letters A and B whose values are to be found.
Since the ones digit of 3 × A is A, it must be that A = 0 or A = 5.
Now look at B. If B = 1, then BA × B3 would at most be equal to 19 × 19; that is, it would at most be equal to 361. But the product here is 57A, which is more than 500. So we cannot have B = 1.
If B = 3, then BA × B3 would be more than 30 × 30; that is, more than 900. But 57A is less than 600. So, B can not be equal to 3.
Putting these two facts together, we see that B = 2 only. So the multiplication is either
20 × 23, or 25 × 23.
The first possibility fails, since 20 × 23 = 460. But, the second one works out correctly, since 25 × 23 = 575.
So the answer is A = 5, B = 2.
2 5
× 2 3
5 7 5

DO THIS
Write a 2-digit number ab and the number obtained by reversing its digits i.e., ba. Find their sum. Let the sum be a 3-digit number dad
i.e., ab + ba = dad
(10a + b) + (10b + a) = dad
11(a + b) = dad
The sum a + b can not exceed 18 (Why?).
Is dad a multiple of 11?
Is dad less than 198?
Write all the 3-digit numbers which are multiples of 11 upto 198.
Find the values of a and d.

Exercise 16.1
1.
3 A
+ 2 5
B 2
+ 9 8
C B 3
1 A
× A
9 A
4.
A B
+ 3 7
6 A
5.
A B
× 3
C A B
A B
× 5
C A B
7.
× 6
B B B
8.
A 1
+ 1 B
B 0
2 A B
+ A B 1
B 1 8
10.
+ 6 A B
A 0 9
16.5 Tests of Divisibility
In Class VI, you learnt how to check divisibility by the following divisors.
10, 5, 2, 3, 6, 4, 8, 9, 11.
You would have found the tests easy to do, but you may have wondered at the same time why they work. Now, in this chapter, we shall go into the “why” aspect of the above.
16.5.1 Divisibility by 10
This is certainly the easiest test of all! We first look at some multiples of 10.
10, 20, 30, 40, 50, 60, ... ,
and then at some non-multiples of 10.
13, 27, 32, 48, 55, 69,
From these lists we see that if the ones digit of a number is 0, then the number is a multiple of 10; and if the ones digit is not 0, then the number is not a multiple of 10. So, we get a test of divisibility by 10.
Of course, we must not stop with just stating the test; we must also explain why it “works”. That is not hard to do; we only need to remember the rules of place value.
Take the number. ... cba; this is a short form for
... + 100c + 10b + a
Here a is the one’s digit, b is the ten’s digit, c is the hundred’s digit, and so on. The dots are there to say that there may be more digits to the left of c.
Since 10, 100, ... are divisible by 10, so are 10b, 100c, ... . And as for the number a is concerned, it must be a divisible by 10 if the given number is divisible by 10. This is possible only when a = 0.
Hence, a number is divisible by 10 when its one’s digit is 0.
16.5.2 Divisibility by 5
Look at the multiples of 5.
5, 10, 15, 20, 25, 30, 35, 40, 45, 50,
We see that the one’s digits are alternately 5 and 0, and no other digit ever appears in this list.
So, we get our test of divisibility by 5.
If the ones digit of a number is 0 or 5, then it is divisible by 5.
Let us explain this rule. Any number ... cba can be written as:
... + 100c + 10b + a
Since 10, 100 are divisible by 10 so are 10b, 100c, ... which in turn, are divisible by 5 because 10 = 2 × 5. As far as number a is concerned it must be divisible by 5 if the number is divisible by 5. So a has to be either 0 or 5.

TRY THESE
(The first one has been done for you.)
1. If the division N ÷ 5 leaves a remainder of 3, what might be the ones digit of N?
(The one’s digit, when divided by 5, must leave a remainder of 3. So the one’s digit must be either 3 or 8.)
2. If the division N ÷ 5 leaves a remainder of 1, what might be the one’s digit of N?
3. If the division N ÷ 5 leaves a remainder of 4, what might be the one’s digit of N?
16.5.3 Divisibility by 2
Here are the even numbers.
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, ... ,
and here are the odd numbers.
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, ... ,
We see that a natural number is even if its one’s digit is
2, 4, 6, 8 or 0
A number is odd if its one’s digit is
1, 3, 5, 7 or 9
Recall the test of divisibility by 2 learnt in Class VI, which is as follows.
If the one’s digit of a number is 0, 2, 4, 6 or 8 then the number is divisible by 2.
The explanation for this is as follows.

Any number cba can be written as 100c + 10b + a
First two terms namely 100c, 10b are divisible by 2 because 100 and 10 are divisible by 2. So far as a is concerned, it must be divisible by 2 if the given number is divisible by 2. This is possible only when a = 0, 2, 4, 6 or 8.

TRY THESE
(The first one has been done for you.)
1. If the division N ÷ 2 leaves a remainder of 1, what might be the one’s digit of N?
(N is odd; so its one’s digit is odd. Therefore, the one’s digit must be 1, 3, 5, 7 or 9.)
2. If the division N ÷ 2 leaves no remainder (i.e., zero remainder), what might be the one’s digit of N?
3. Suppose that the division N ÷ 5 leaves a remainder of 4, and the division N ÷ 2 leaves a remainder of 1. What must be the one’s digit of N?
16.5.4 Divisibility by 9 and 3
Look carefully at the three tests of divisibility found till now, for checking division by 10, 5 and 2. We see something common to them: they use only the one’s digit of the given number; they do not bother about the ‘rest’ of the digits. Thus, divisibility is decided just by the one’s digit. 10, 5, 2 are divisors of 10, which is the key number in our place value.
But for checking divisibility by 9, this will not work. Let us take some number say 3573.
Its expanded form is: 3 × 1000 + 5 × 100 + 7 × 10 + 3
This is equal to 3 × (999 + 1) + 5 × (99 + 1) + 7 × (9 + 1) + 3
= 3 × 999 + 5 × 99 + 7 × 9 + (3 + 5 + 7 + 3) ... (1)
We see that the number 3573 will be divisible by 9 or 3 if (3 + 5 + 7 + 3) is divisible by 9 or 3.
We see that 3 + 5 + 7 + 3 = 18 is divisible by 9 and also by 3. Therefore, the number 3573 is divisible by both 9 and 3.
Now, let us consider the number 3576. As above, we get
3576 = 3 × 999 + 5 × 99 + 7 × 9 + (3 + 5 + 7 + 6) ... (2)
Since (3 + 5 + 7 + 6) i.e., 21 is not divisible by 9 but is divisible by 3,
therefore 3576 is not divisible by 9. However 3576 is divisible by 3. Hence,
(i) A number N is divisible by 9 if the sum of its digits is divisible by 9. Otherwise it is not divisible by 9.
(ii) A number N is divisible by 3 if the sum of its digits is divisible by 3. Otherwise it is not divisible by 3.
If the number is ‘cba’, then, 100c + 10b + a = 99c + 9b + (a + b + c)
= 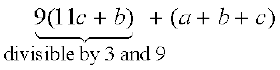
Example 4: Check the divisibility of 21436587 by 9.
Solution: The sum of the digits of 21436587 is 2 + 1 + 4 + 3 + 6 + 5 + 8 + 7 = 36. This number is divisible by 9 (for 36 ÷ 9 = 4). We conclude that 21436587 is divisible by 9.
We can double-check:
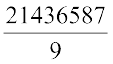 = 2381843 (the division is exact).
= 2381843 (the division is exact).
Example 5: Check the divisibility of 152875 by 9.
Solution: The sum of the digits of 152875 is 1 + 5 + 2 + 8 + 7 + 5 = 28. This number is not divisible by 9. We conclude that 152875 is not divisible by 9.

TRY THESE
Check the divisibility of the following numbers by 9.
1. 108 2. 616 3. 294 4. 432 5. 927
Example 6: If the three digit number 24x is divisible by 9, what is the value of x?
Solution: Since 24x is divisible by 9, sum of it’s digits, i.e., 2 + 4 + x should be divisible by 9, i.e., 6 + x should be divisible by 9.
This is possible when 6 + x = 9 or 18, ....
But, since x is a digit, therefore, 6 + x = 9, i.e., x = 3.

THINK, DISCUSS AND WRITE
1. You have seen that a number 450 is divisible by 10. It is also divisible by 2 and 5 which are factors of 10. Similarly, a number 135 is divisible 9. It is also divisible by 3 which is a factor of 9.
Can you say that if a number is divisible by any number m, then it will also be divisible by each of the factors of m?
2. (i) Write a 3-digit number abc as 100a + 10b + c
= 99a + 11b + (a – b + c)
= 11(9a + b) + (a – b + c)
If the number abc is divisible by 11, then what can you say about
(a – b + c)?
Is it necessary that (a + c – b) should be divisible by 11?
(ii) Write a 4-digit number abcd as 1000a + 100b + 10c + d
= (1001a + 99b + 11c) – (a – b + c – d)
= 11(91a + 9b + c) + [(b + d) – (a + c)]
If the number abcd is divisible by 11, then what can you say about
[(b + d) – (a + c)]?
(iii) From (i) and (ii) above, can you say that a number will be divisible by 11 if the difference between the sum of digits at its odd places and that of digits at the even places is divisible by 11?
Example 7: Check the divisibility of 2146587 by 3.
Example 8: Check the divisibility of 15287 by 3.
Solution: The sum of the digits of 15287 is 1 + 5 + 2 + 8 + 7 = 23. This number is not divisible by 3. We conclude that 15287 too is not divisible by 3.

TRY THESE
Check the divisibility of the following numbers by 3.
1. 108 2. 616 3. 294 4. 432 5. 927
Exercise 16.2
1. If 21y5 is a multiple of 9, where y is a digit, what is the value of y?
2. If 31z5 is a multiple of 9, where z is a digit, what is the value of z?
You will find that there are two answers for the last problem. Why is this so?
3. If 24x is a multiple of 3, where x is a digit, what is the value of x?
(Since 24x is a multiple of 3, its sum of digits 6 + x is a multiple of 3; so 6 + x is one of these numbers: 0, 3, 6, 9, 12, 15, 18, ... . But since x is a digit, it can only be that 6 + x = 6 or 9 or 12 or 15. Therefore, x = 0 or 3 or 6 or 9. Thus, x can have any of four different values.)
4. If 31z5 is a multiple of 3, where z is a digit, what might be the values of z?
What have we Discussed?
1. Numbers can be written in general form. Thus, a two digit number ab will be written as
ab = 10a + b.
2. The general form of numbers are helpful in solving puzzles or number games.
3. The reasons for the divisibility of numbers by 10, 5, 2, 9 or 3 can be given when numbers are written in general form.

