Table of Contents
गणित में हमें प्राय: साधारण समीकरण दिखाई देते हैं। उदाहरणार्थ समीकरण
x + 2 = 13
(1)
को x = 11 के लिए हल किया जाता है क्योंकि x का यह मान इस समीकरण को संतुष्ट करता है। हल 11, एक प्राकृत संख्या है। दूसरी तरफ समीकरण
x + 5 = 5
(2)
का हल शून्य है जो एक पूर्ण संख्या है। यदि हम केवल प्राकृत संख्याओं तक सीमित रहें तो समीकरण (2) को हल नहीं किया जा सकता। समीकरण (2) जैसे समीकरणों को हल करने के लिए हमने प्राकृत संख्याओं के समूह में शून्य को शामिल किया और इस नए समूह को पूर्ण संख्याओं का नाम दिया। यद्यपि
x + 18 = 5
(3)
जैसे समीकरणों को हल करने के लिए पूर्ण संख्याएँ भी पर्याप्त नहीं हैं। क्या आप जानते हैं ‘क्यों’? हमें संख्या –13 की आवश्यकता है जो कि पूर्ण संख्या नहीं है। इसने हमें पूर्णांकों (धनात्मक एवं ऋणात्मक) के बारे में सोचने के लिए प्रेरित किया। ध्यान दीजिए धनात्मक पूर्णांक प्राकृत संख्याओं के अनुरूप हैं। आप सोच सकते हैं कि सभी साधारण समीकरणों को हल करने के लिए हमारे पास उपलब्ध पूर्णांकों की सूची में पर्याप्त संख्याएँ हैं। निम्नलिखित समीकरणों के बारे में विचार करते हैं:
2x = 3
(4)
5x + 7 = 0
(5)
इनका हल हम पूर्णांकों में ज्ञात नहीं कर सकते (इसकी जाँच कीजिए)।
समीकरण (4) को हल करने के लिए संख्या
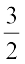 और समीकरण (5) को हल करने के लिए संख्या
और समीकरण (5) को हल करने के लिए संख्या 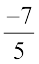 की आवश्यकता है। इससे हम परिमेय संख्याओं के समूह की तरफ अग्रसर होते हैं। हम पहले ही परिमेय संख्याओं पर मूल संक्रियाएँ पढ़ चुके हैं। अभी तक हमने जितनी भी विभिन्न प्रकार की संख्याएँ पढ़ी हैं उनकी संक्रियाओं के कुछ गुणधर्म खोजने का अब हम प्रयत्न करते हैं।
की आवश्यकता है। इससे हम परिमेय संख्याओं के समूह की तरफ अग्रसर होते हैं। हम पहले ही परिमेय संख्याओं पर मूल संक्रियाएँ पढ़ चुके हैं। अभी तक हमने जितनी भी विभिन्न प्रकार की संख्याएँ पढ़ी हैं उनकी संक्रियाओं के कुछ गुणधर्म खोजने का अब हम प्रयत्न करते हैं।1.2 परिमेय संख्याओं के गुणधर्म
1.2.1 संवृत
(i) पूर्ण संख्याएँ
| संक्रिया | संख्याएँ | टिप्पणी |
| योग | 0 + 5 = 5, एक पूर्णसंख्या है। 4 + 7 = ...क्या यह एक पूर्ण संख्या है? व्यापक रूप से किन्हीं दो पूर्ण संख्याओं a तथा b के लिए a + b एक पूर्ण संख्या है। | पूर्ण संख्याएँ योग के अंतर्गत संवृत हैं। |
| व्यवकलन | 5 – 7 = – 2, जो कि एक पूर्ण संख्या नहीं है। | पूर्ण संख्याएँ व्यवकलन के अंतर्गत संवृत नहीं हैं। |
| गुणन | 0 × 3 = 0, एक पूर्ण संख्या है। 3 × 7 = ... . क्या यह एक पूर्ण संख्या है? व्यापक रूप से यदि a तथा b कोई भी दो पूर्ण संख्याएँ हैं तो उनका गुणनफल ab एक पूर्ण संख्या है। | पूर्ण संख्याएँ गुणन के अंतर्गत संवृत हैं। |
| भाग | 5 ÷ 8 = , यह एक पूर्ण संख्या नहीं है। | पूर्ण संख्याएँ भाग के अंतर्गत संवृत नहीं हैं। |
प्राकृत संख्याओं के लिए सभी चार संक्रियाओं के अंतर्गत संवृत गुण की जाँच कीजिए।
(ii) पूर्णांक
आइए, अब हम उन संक्रियाओं का स्मरण करते हैं जिनके अंतर्गत पूर्णांक संवृत हैं।
| संक्रिया | संख्याएँ | टिप्पणी |
| योग | – 6 + 5 = – 1, एक पूर्णांक है। क्या – 7 + (–5) एक पूर्णांक है ? क्या 8 + 5 एक पूर्णांक है ? व्यापक रूप से किन्हीं दो पूर्णांकाें a तथा b के लिए a + b एक पूर्णांक है। | पूर्णांक योग के अंतर्गत संवृत हैं। |
| व्यवकलन | 7 – 5 = 2, एक पूर्णांक है। क्या 5 – 7 एक पूर्णांक है ? – 6 – 8 = – 14, एक पूर्णांक है। – 6 – (– 8) = 2, एक पूर्णांक है क्या 8 – (– 6) एक पूर्णांक है ? व्यापक रूप से किन्हीं दो पूर्णांकों a तथा b के लिए a – b भी एक पूर्णांक है। जाँच कीजिए कि क्या b – a भी एक पूर्णांक है। | पूर्णांक व्यवकलन के अंतर्गत संवृत हैं। |
| गुणन | 5 × 8 = 40, एक पूर्णांक है। क्या – 5 × 8 एक पूर्णांक है? – 5 × (– 8) = 40, एक पूर्णांक है। व्यापक रूप से किन्हीं दो पूर्णांकों a तथा b के लिए a × b भी एक पूर्णांक है। | पूर्णांक गुणन के अंतर्गत संवृत हैं। |
| भाग | 5 ÷ 8 = , यह एक पूर्णांक नहीं हैं। | पूर्णांक भाग के अंतर्गत संवृत नहीं हैं। |
आपने देखा कि पूर्ण संख्याएँ योग और गुणन के अंतर्गत संवृत हैं परंतु भाग और व्यवकलन के अंतर्गत संवृत नहीं हैं। तथापि पूर्णांक योग, व्यवकलन एवं गुणन के अंतर्गत संवृत हैं लेकिन भाग के अंतर्गत संवृत नहीं हैं।
(iii) परिमेय संख्याएँ
स्मरण कीजिए कि एेसी संख्या परिमेय संख्या कहलाती है जिसे 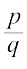 के रूप में लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है। उदाहरणार्थ
के रूप में लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है। उदाहरणार्थ 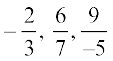 परिमेय संख्याएँ हैं। क्योंकि संख्याएँ 0, –2, 4,
परिमेय संख्याएँ हैं। क्योंकि संख्याएँ 0, –2, 4, 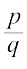 , के रूप में लिखी जा सकती हैं इसलिए ये भी परिमेय संख्याएँ हैं। (इसकी जाँच कीजिए।)
, के रूप में लिखी जा सकती हैं इसलिए ये भी परिमेय संख्याएँ हैं। (इसकी जाँच कीजिए।)
(a) आप जानते हैं कि परिमेय संख्याओं को कैसे जोड़ा जाता है। आइए कुछ युग्मों का योग ज्ञात करते हैं
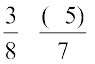 =
= 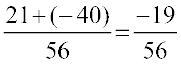 (एक परिमेय संख्या)
(एक परिमेय संख्या)
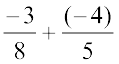 =
= 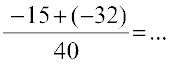 (क्या यह एक परिमेय संख्या है?)
(क्या यह एक परिमेय संख्या है?)
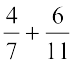 = ... (क्या यह एक परिमेय संख्या है?)
= ... (क्या यह एक परिमेय संख्या है?)
हम देखते हैं कि दो परिमेय संख्याओं का योग भी एक परिमेय संख्या है। कुछ और परिमेय संख्याओं के युग्मों के लिए इसकी जाँच कीजिए। इस प्रकार हम कहते हैं कि परिमेय संख्याएँ योग के अंतर्गत संवृत हैं। अर्थात् किन्हीं दो परिमेय संख्याओं a तथा b के लिए a + b भी एक परिमेय संख्या है।
(b) क्या दो परिमेय संख्याओं का अंतर भी एक परिमेय संख्या होगा?
हम प्राप्त करते हैं, 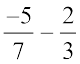 =
= 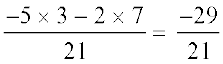 (एक परिमेय संख्या है?)
(एक परिमेय संख्या है?)
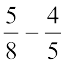 =
= 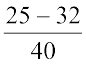 = ... (क्या यह एक परिमेय संख्या है?)
= ... (क्या यह एक परिमेय संख्या है?)
 = ... (क्या यह एक परिमेय संख्या है?)
= ... (क्या यह एक परिमेय संख्या है?)
परिमेय संख्याओं के कुछ और युग्मों के लिए इसकी जाँच कीजिए। इस प्रकार हम पाते हैं कि परिमेय संख्याएँ व्यवकलन के अंतर्गत संवृत हैं। अर्थात् किन्हीं दो परिमेय संख्याओं a तथा b के लिए a – b भी एक परिमेय संख्या है।
(c) आइए, अब हम दो परिमेय संख्याओं के गुणनफल की चर्चा करते हैं।
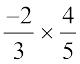 =
= 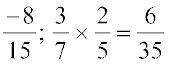 (दोनों गुणनफल परिमेय संख्याएँ हैं)
(दोनों गुणनफल परिमेय संख्याएँ हैं)
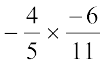 = ... (क्या यह एक परिमेय संख्या है?)
= ... (क्या यह एक परिमेय संख्या है?)
परिमेय संख्याओं के कुछ और युग्म लीजिए और जाँच कीजिए कि उनका गुणनफल भी एक परिमेय संख्या है। अत: हम कह सकते हैं कि परिमेय संख्याएँ गुणन के अंतर्गत संवृत हैं। अर्थात् किन्हीं दो परिमेय संख्याओं a तथा b के लिए a × b भी एक परिमेय संख्या है।
(d) हम नोट करते हैं कि 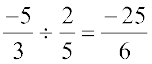 (एक परिमेय संख्या है)
(एक परिमेय संख्या है)
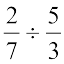 = ... (क्या यह एक परिमेय संख्या है?)
= ... (क्या यह एक परिमेय संख्या है?)
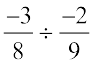 = ... (क्या यह एक परिमेय संख्या है?)
= ... (क्या यह एक परिमेय संख्या है?)
क्या आप कह सकते हैं कि परिमेय संख्याएँ भाग के अंतर्गत संवृत हैं? हम जानते हैं कि किसी भी परिमेय संख्या a के लिए a ÷ 0 परिभाषित नहीं है। अत: परिमेय संख्याएँ भाग के अंतर्गत संवृत नहीं हैं। तथापि, यदि हम शून्य को शामिल नहीं करें तो दूसरी सभी परिमेय संख्याओं का समूह, भाग के अंतर्गत संवृत है।
प्रयास कीजिए
| संख्याएँ | अंतर्गत संवृत हैं | |||
| योग के | व्यवकलन के | गुणन के | भाग के | |
| परिमेय संख्याएँ पूर्णांक पूर्ण संख्याएँ प्राकृत संख्याएँ | हाँ ... ... ... | हाँ हाँ ... नहीं | ... ... हाँ ... | नहीं नहीं ... ... |
1.2.2 क्रमविनिमेयता
(i) पूर्ण संख्याएँ
निम्नलिखित सारणी के रिक्त स्थानों को भरते हुए विभिन्न संक्रियाओं के अंतर्गत पूर्ण संख्याओं की क्रमविनिमेयता का स्मरण कीजिए:
| संक्रिया | संख्याएँ | टिप्पणी |
| योग | 0 + 7 = 7 + 0 = 7 2 + 3 = ... + ... = .... किन्हीं दो पूर्ण संख्याओं a तथा b के लिए a + b = b + a | योग क्रमविनिमेय है। |
| व्यवकलन(घटाना) | ......... | व्यवकलन क्रमविनिमेय नहीं है। |
| गुणन | ......... | गुणन क्रमविनिमेय है। |
| भाग | ......... | भाग क्रमविनिमेय नहीं है |
जाँच कीजिए कि क्या प्राकृत संख्याओं के लिए भी ये संक्रियाएँ क्रम विनिमेय हैं।
(ii) पूर्णांक
निम्नलिखित सारणी के रिक्त स्थानों को भरिए और पूर्णांकों के लिए विभिन्न संक्रियाओं की क्रम विनिमेयता जाँचिए:
| संक्रिया | संख्याएँ | टिप्पणी |
| योग व्यवकलन गुणन भाग | ......... क्या 5 – (–3) = – 3 – 5? ......... ......... | योग क्रमविनिमेय है। व्यवकलन क्रमविनिमेय नहीं है। गुणन क्रमविनिमेय है। भाग क्रमविनिमेय नहीं है। |
(iii) परिमेय संख्याएँ
(a) योग
आप जानते हैं कि दो परिमेय संख्याओं को कैसे जोड़ा जाता है। आइए, हम यहाँ कुछ युग्मों को जोड़ते हैं।
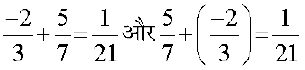
इसलिए, 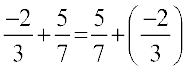
इसके अतिरिक्त 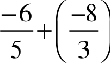 = ...
= ... 
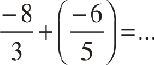
क्या 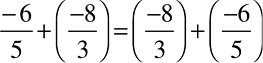 ?
?
क्या 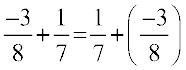 ?
?
आप पाते हैं कि दो परिमेय संख्याओं को किसी भी क्रम में जोड़ा जा सकता है। हम कहते हैं कि परिमेय संख्याओं के लिए योग क्रम विनिमेय है। अर्थात् किन्हीं दो परिमेय संख्याओं a तथा b के लिए a + b = b + a ।
(b) व्यवकलन
क्या 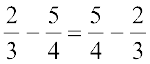 है?
है?
क्या 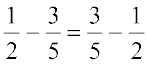 है?
है?
आप पाएँगे कि परिमेय संख्याओं के लिए व्यवकलन क्रम विनिमेय नहीं है।
ध्यान दीजिए कि पूर्णांकों के लिए व्यवकलन क्रम विनिमेय नहीं है तथा पूर्णांक परिमेय संख्याएँ भी हैं। अत: व्यवकलन परिमेय संख्याओं के लिए भी क्रम विनिमेय नहीं होता है।
(c) गुणन
हम पाते हैं, 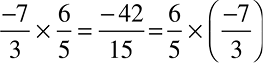
क्या 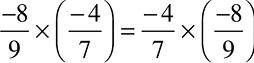 है?
है?
एेसे कुछ और गुणनफलों के लिए भी जाँच कीजिए।
(d) भाग
क्या 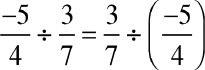 है?
है?
आप पाएँगे कि दोनों पक्षों के व्यंजक समान नहीं हैं।
इसलिए परिमेय संख्याओं के लिए भाग क्रम विनिमेय नहीं है।
प्रयास कीजिए
निम्नलिखित सारणी को पूरा कीजिए:
| संख्याएँ | क्रमविनिमेय | |||
| योगके लिए | व्यवकलन के लिए | गुणन के लिए | भाग के लिए | |
| परिमेयसंख्याएँ पूर्णांक पूर्णसंख्याएँ प्राकृत संख्याएँ | हाँ ... ... ... | ... नहीं ... ... | ... ... हाँ ... | ... ... ... नहीं |
1.2.3 साहचर्यता (सहचारिता)
(i) पूर्ण संख्याएँ
निम्नलिखित सारणी के माध्यम से पूर्ण संख्याओं के लिए चार संक्रियाओं की साहचर्यता को स्मरण कीजिए।
| संक्रिया | संख्याएँ | टिप्पणी |
| योग | ......... | योग साहचर्य है। |
| व्यवकलन | ......... | व्यवकलन साहचर्य नहीं है। |
| गुणन | क्या 7 × (2 × 5) = (7 × 2) × 5? क्या 4 × (6 × 0) = (4 × 6) × 0? किन्हीं तीन पूर्ण संख्याओं a, b तथा c के लिए a × (b × c) = (a × b) × c | गुणन साहचर्य है। |
| भाग | ......... | भाग साहचर्य नहीं है। |
इस सारणी को भरिए और अंतिम स्तंभ में दी गई टिप्पणियों को सत्यापित कीजिए।
प्राकृत संख्याओं के लिए विभिन्न संक्रियाओं की साहचर्यता की स्वयं जाँच कीजिए।
(ii) पूर्णांक
पूर्णांकों के लिए चार संक्रियाओं की साहचर्यता निम्नलिखित सारणी से देखी जा सकती है :
| संक्रिया | संख्याएँ | टिप्पणी |
| योग | क्या (–2) + [3 + (– 4)] = [(–2) + 3)] + (– 4) है? क्या (– 6) + [(– 4) + (–5)] = [(– 6) +(– 4)] + (–5)है? किन्हीं तीन पूर्ण संख्याओं a, b तथा c के लिए a + (b + c) = (a + b) + c | योग साहचर्य है। |
| व्यवकलन | क्या 5 – (7 – 3) = (5 – 7) – 3 है? | व्यवकलन साहचर्य नहीं है। |
| गुणन | क्या 5 × [(–7) × (– 8) = [5 × (–7)] × (– 8) है? क्या (– 4) × [(– 8) × (–5)] = [(– 4) × (– 8)] × (–5)है? किन्हीं तीन पूर्ण संख्याओं a, b तथा c के लिए a × (b × c) = (a × b) × c | गुणन साहचर्य है। |
| भाग | क्या [(–10) ÷ 2] ÷ (–5) = (–10) ÷ [2 ÷ (– 5)] है? | भाग साहचर्य नहीं है। |
(iii) परिमेय संख्याएँ
(a) योग
हम पाते हैं : 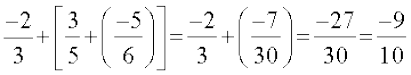
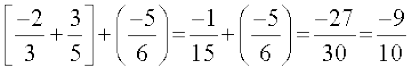
इसलिए, 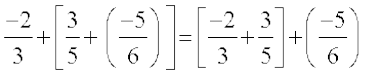
ज्ञात कीजिए 
कुछ और परिमेय संख्याएँ लीजिए, उपर्युक्त उदाहरणों की तरह उन्हें जोड़िए और देखिए कि क्या दोनों योग समान हैं। हम पाते हैं कि परिमेय संख्याओं के लिए योग साहचर्य है, अर्थात् किन्हीं तीन परिमेय संख्याओं a, b तथा c के लिए a + (b + c) = (a + b) + c ।
(b) व्यवकलन
आप पहले से जानते हैं कि व्यवकलन पूर्णांकोंें के लिए सहचारी नहीं है। परिमेय संख्याओं के बारे में आप क्या कह सकते हैैं?
क्या 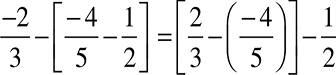 है?
है?
स्वयं जाँच कीजिए।
परिमेय संख्याओं के लिए व्यवकलन साहचर्य नहीं है।
(c) गुणन
आइए, हम गुणन के लिए साहचर्यता की जाँच करते हैं।
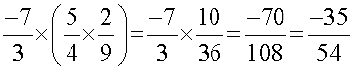
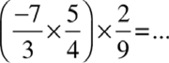
हम पाते हैं कि 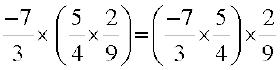
क्या 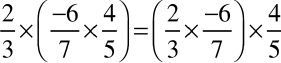 है?
है?
(d) भाग
याद कीजिए कि पूर्णांकों के लिए विभाजन सहचारी नहीं है। परिमेय संख्याओं के बारे में आप क्या कह सकते हैं? आइए, देखते हैं कि यदि
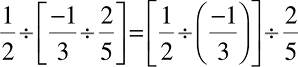 है? हम पाते हैं,
है? हम पाते हैं,
बायाँ पक्ष (L.H.S) = 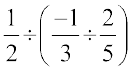
= 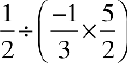 (
( का व्युत्क्रम
का व्युत्क्रम 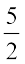 है)
है)
= 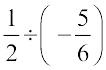
= ...
पुन: दायाँ पक्ष (R.H.S) = 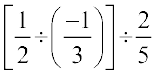
= 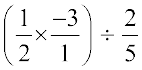
= 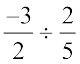 = ...
= ...
क्या L.H.S. = R.H.S. है? स्वयं जाँच कीजिए। आप पाएँगे कि परिमेय संख्याओं के लिए भाग साहचर्य नहीं है।
प्रयास कीजिए
निम्नलिखित सारणी को पूरा कीजिए:
| संख्याएँ | साहचर्य | |||
| योग के लिए | व्यवकलन के लिए | गुणन के लिए | भाग के लिए | |
| परिमेय संख्याएँ पूर्णांक पूर्ण संख्याएँ प्राकृत संख्याएँ | ... ... हाँ ... | ... ... ... नहीं | ... हाँ ... ... | नहीं ... ... ... |
उदाहरण 1 : ज्ञात कीजिए 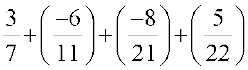
हल : 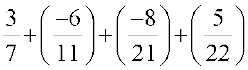
प्रयास कीजिए
= 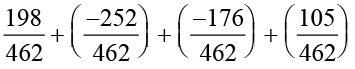
(नोट कीजिए कि 7, 11, 21 तथा 22 का ल.स.प. 462 है।)
= 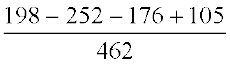 =
= 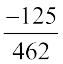
हम इसे निम्नलिखित प्रकार से भी हल कर सकते हैं:
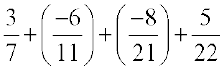
= 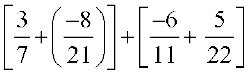 (क्रम विनिमेयता और साहचर्यता के उपयोग से)
(क्रम विनिमेयता और साहचर्यता के उपयोग से)
= 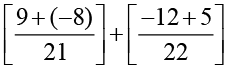
(7 और 21 का ल.स.प. 21 है। 11 और 22 का ल.स.प. 22 है।)
= 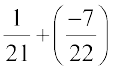 =
= 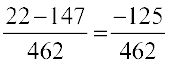
क्या आप सोचते हैं कि क्रमविनिमेयता और साहचर्यता के गुणधर्मों की सहायता से परिकलन आसान हो गया है?
उदाहरण 2 : ज्ञात कीजिए 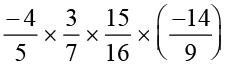
हल : हमें प्राप्त है,
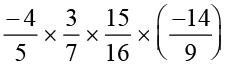
= 
= 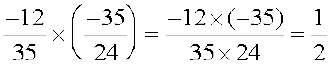
हम इसे निम्नलिखित प्रकार से भी हल कर सकते हैं:
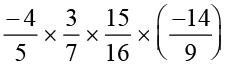
= 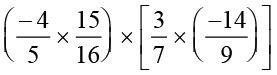 (क्रमविनिमेयता और साहचर्यता के उपयोग से)
(क्रमविनिमेयता और साहचर्यता के उपयोग से)
= 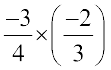 =
= 
निम्नलिखित पर विचार कीजिए:
2 + 0 = 0 + 2 = 2 (शून्य को पूर्ण संख्या में जोड़ना)
– 5 + 0 = ... + ... = – 5 (शून्य को पूर्णांक में जोड़ना)
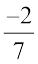 + ... = 0 +
+ ... = 0 + 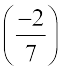 =
= 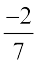 (शून्य को परिमेय संख्या में जोड़ना)
(शून्य को परिमेय संख्या में जोड़ना)
आप पहले भी इस प्रकार के योग ज्ञात कर चुके हैं।
एेसे कुछ और योग ज्ञात कीजिए। आप क्या देखते हैं? आप पाएँगे कि जब किसी पूर्ण संख्या में शून्य जोड़ा जाता है तो योग फिर से वही पूर्ण संख्या होती है। यह तथ्य पूर्णांकों और परिमेय संख्याओं के लिए भी सत्य है।
व्यापक रूप से
a + 0 = 0 + a = a, (जहाँ a एक पूर्ण संख्या है)
b + 0 = 0 + b = b, (जहाँ b एक पूर्णांक है)
c + 0 = 0 + c = c, (जहाँ c एक परिमेय संख्या है)
परिमेय संख्याओं के योग के लिए शून्य एक तत्समक कहलाता है। यह पूर्णांकों और पूर्ण संख्याओं के लिए भी योज्य तत्समक है।
1.2.5 1 की भूमिका
हम प्राप्त करते हैं कि
5 × 1 = 5 = 1 × 5 (पूर्ण संख्या के साथ 1 का गुणन)
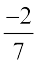 × 1 = ... × ... =
× 1 = ... × ... = 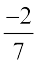
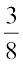 × ... = 1 ×
× ... = 1 × 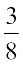 =
= 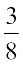
आप क्या पाते हैं?
आप पाएँगे कि जब आप किसी भी परिमेय संख्या के साथ 1 से गुणा करते हैं तो आप उसी परिमेय संख्या को गुणनफल के रूप में पाते हैं। कुछ और परिमेय संख्याओं के लिए इसकी जाँच कीजिए। आप पाएँगे कि किसी भी परिमेय संख्या a के लिए, a × 1 = 1 × a = a है। हम कहते हैं कि 1 परिमेय संख्याओं के लिए गुणनात्मक तत्समक है। क्या 1 पूर्णांकों और पूर्ण संख्याओं के लिए भी गुणनात्मक तत्समक हैं?
यदि कोई गुणधर्म परिमेय संख्याओं के लिए सत्य है तो क्या वह गुणधर्म, पूर्णांकों, पूर्ण संख्याओं के लिए भी सत्य होगा? कौन-से गुणधर्म इनके लिए सत्य होंगे और कौन-से सत्य नहीं होंगे?
1.2.6 एक संख्या का ऋणात्मक
पूर्णांकों का अध्ययन करते समय आपने पूर्णांकों के ऋणात्मक पाए हैं। 1 का ऋणात्मक क्या है? यह – 1 है, क्योंकि 1 + (– 1) = (–1) + 1 = 0 है।
अत: (–1) का ऋणात्मक क्या होगा? यह 1 होगा।
इसके अतिरिक्त, 2 + (–2) = (–2) + 2 = 0 है। इस प्रकार हम कहते हैं कि –2 का ऋणात्मक अथवा योज्य प्रतिलोम 2 है जो विलोमत: भी सत्य है। व्यापक रूप से किसी भी पूर्णांक a के लिए a + (– a) = (– a) + a = 0; इस प्रकार – a का ऋणात्मक a है और a का ऋणात्मक – a है।
किसी परिमेय संख्या 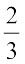 के लिए, हम पाते हैं,
के लिए, हम पाते हैं,
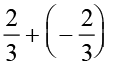 =
= 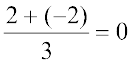
सोचिए, चर्चा कीजिए और लिखिए
इसके अतिरिक्त  = 0 (कैसे ?)
= 0 (कैसे ?)
इसी प्रकार 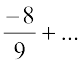 =
= 
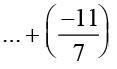 =
= 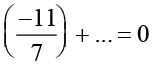
व्यापक रूप से किसी परिमेय संख्या 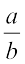 के लिए
के लिए  प्राप्त है।
प्राप्त है।
हम कहते हैं कि 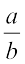 का योज्य प्रतिलोम
का योज्य प्रतिलोम 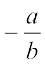 है और
है और  का योज्य प्रतिलोम
का योज्य प्रतिलोम 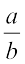 है।
है।
1.2.7 व्युत्क्रम
आप 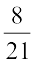 को किस परिमेय संख्या से गुणा करेंगे ताकि गुणनफल 1 हो जाए? स्पष्ट रूप से
को किस परिमेय संख्या से गुणा करेंगे ताकि गुणनफल 1 हो जाए? स्पष्ट रूप से 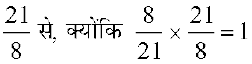 है।
है।
इसी प्रकार, 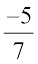 को
को 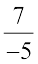 से गुणा करना चाहिए ताकि गुणनफल 1 प्राप्त हो सके।
से गुणा करना चाहिए ताकि गुणनफल 1 प्राप्त हो सके।
हम कहते हैं कि 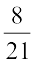 का व्युत्क्रम
का व्युत्क्रम 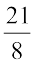 है और
है और 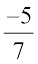 का व्युत्क्रम
का व्युत्क्रम 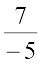 है।
है।
क्या आप बता सकते हैं कि शून्य का व्युत्क्रम क्या है? क्या कोई एेसी परिमेय संख्या है जिसे शून्य से गुणा करने पर 1 प्राप्त हो जाए। अत: शून्य का कोई व्युत्क्रम नहीं है। हम कहते हैं कि– एक परिमेय संख्या 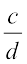 दूसरी शून्येतर संख्या
दूसरी शून्येतर संख्या 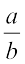 का व्युत्क्रम अथवा गुणात्मक प्रतिलोम कहलाती है यदि
का व्युत्क्रम अथवा गुणात्मक प्रतिलोम कहलाती है यदि 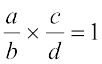 है।
है।
1.2.8 परिमेय संख्याओं के लिए गुणन की योग पर वितरकता
इस तथ्य को समझने के लिए परिमेय संख्याएँ 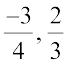 और
और 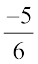 को लीजिए:
को लीजिए:
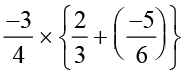 =
= 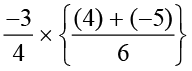
= 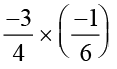 =
= 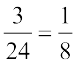
इसके अतिरिक्त 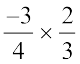 =
= 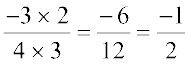
और 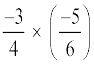 =
= 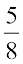
इसलिए,  =
= 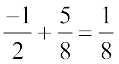
अत: 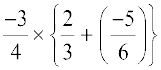 =
= 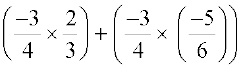
योग एवं व्यवकलन पर गुणन की वितरकता
सभी परिमेय संख्याओं a, b और c के लिए
a (b + c) = ab + ac
a (b – c) = ab – ac
वितरकता के उपयोग से निम्नलिखित का मान ज्ञात कीजिए:
(i)  (ii)
(ii) 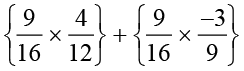
उदाहरण 3 : निम्नलिखित के योज्य प्रतिलोम लिखिए:
(i) 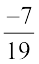 (ii)
(ii) 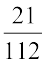
हल :
(i) 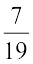 का योज्य प्रतिलोम
का योज्य प्रतिलोम 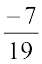 है क्योंकि
है क्योंकि 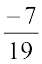 +
+ 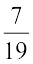 =
= 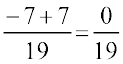 = 0 है।
= 0 है।
(ii) 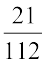 का योज्य प्रतिलोम
का योज्य प्रतिलोम 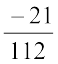 है। (जाँच कीजिए )
है। (जाँच कीजिए )
उदाहरण 4 : सत्यापित कीजिए कि निम्न के लिए – (– x) और x समान हैं।
(i) x = 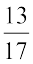 (ii)
(ii) 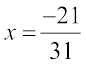
हल :
(i) हमें प्राप्त है x = 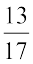
x = 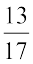 का योज्य प्रतिलोम – x =
का योज्य प्रतिलोम – x = 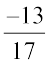 है, क्योंकि
है, क्योंकि 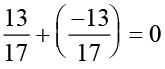 है।
है।
समिका 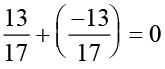 , दर्शाती है कि
, दर्शाती है कि 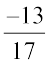 का योज्य प्रतिलोम
का योज्य प्रतिलोम 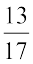 है,
है,
अथवा 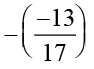 =
= 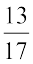 , अर्थात्् – (– x) = x
, अर्थात्् – (– x) = x
(ii) 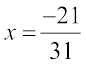 का योज्य प्रतिलोम – x =
का योज्य प्रतिलोम – x = 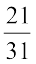 है, क्योंकि
है, क्योंकि 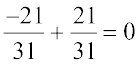 है।
है।
समिका 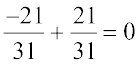 , दर्शाती है कि
, दर्शाती है कि 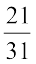 का योज्य प्रतिलोम
का योज्य प्रतिलोम 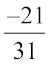 है, अर्थात्
है, अर्थात्
– (– x) = x है।
उदाहरण 5 : ज्ञात कीजिए 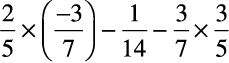
हल : 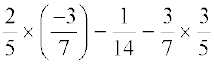 =
= 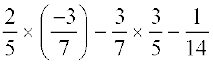 (क्रमविनिमेयता से )
(क्रमविनिमेयता से )
= 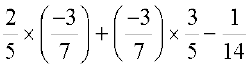 =
= 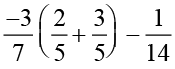 (वितरकता से)
(वितरकता से)
= 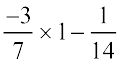 =
= 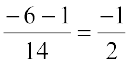
प्रश्नावली 1.1
1. उचित गुणधर्मोंं के उपयोग से निम्नलिखित का मान ज्ञात कीजिए:
(i) 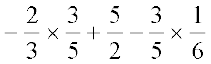 (ii)
(ii) 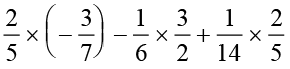
2. निम्नलिखित में से प्रत्येक के योज्य प्रतिलोम लिखिए:
(i) 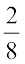 (ii)
(ii) 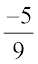 (iii)
(iii) 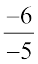 (iv)
(iv) 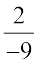 (v)
(v) 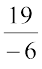
3. (i) x = 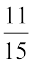 (ii)
(ii) 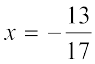 के लिए सत्यापित कीजिए कि – (– x) = x
के लिए सत्यापित कीजिए कि – (– x) = x
4. निम्नलिखित के गुणनात्मक प्रतिलोम ज्ञात कीजिए:
(i) – 13 (ii) 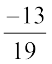 (iii)
(iii) 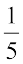 (iv)
(iv) 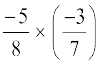
(v) – 1 × 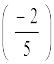 (vi) – 1
(vi) – 1
5. निम्नलिखित प्रत्येक में गुणन के अंतर्गत उपयोग किए गए गुणधर्म (गुण) का नाम लिखिए:
(i) 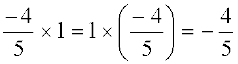 (ii)
(ii) 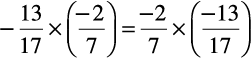
(iii) 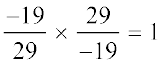
6. 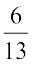 को
को 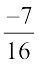 के व्युत्क्रम से गुणा कीजिए।
के व्युत्क्रम से गुणा कीजिए।
7. बताइए कौन से गुणधर्म (गुण) की सहायता से आप  के रूप में अभिकलन करते हैं।
के रूप में अभिकलन करते हैं।
8. क्या 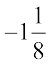 का गुणात्मक प्रतिलोम
का गुणात्मक प्रतिलोम 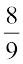 है? क्यों अथवा क्यों नहीं?
है? क्यों अथवा क्यों नहीं?
9. क्या 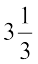 का गुणनात्मक प्रतिलोम 0.3 है? क्यों अथवा क्यों नहीं?
का गुणनात्मक प्रतिलोम 0.3 है? क्यों अथवा क्यों नहीं?
10. लिखिए:
(i) एेसी परिमेय संख्या जिसका कोई व्युत्क्रम नहीं है।
(ii) परिमेय संख्याएँ जो अपने व्युत्क्रम के समान है।
(iii) परिमेय संख्या जो अपने ऋणात्मक के समान है।
11. रिक्त स्थानों की पूर्ति कीजिए:
(i) शून्य का व्युत्क्रम ________ है।
(ii) संख्याएँ ________ तथा ________ स्वयं के व्युत्क्रम हैं।
(iii) – 5 का व्युत्क्रम ________ है।
(iv) 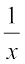 (x ≠ 0) का व्युत्क्रम ________ है।
(x ≠ 0) का व्युत्क्रम ________ है।
(v) दो परिमेय संख्याओं का गुणनफल हमेशा _______ है।
(vi) किसी धनात्मक परिमेय संख्या का व्युत्क्रम ________ है।
1.3 परिमेय संख्याओं का संख्या रेखा पर निरूपण
आप प्राकृत संख्याओं, पूर्ण संख्याओं, पूर्णांकों और परिमेय संख्याओं को संख्या रेखा पर निरूपित करना सीख चुके हैं। हम उनकी पुनरावृत्ति करेंगे।
प्राकृत संख्याएँ
(i) 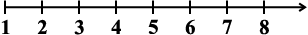
पूर्ण संख्याएँ
(ii) 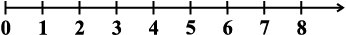
पूर्णांक
(iii) 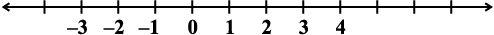
परिमेय संख्याएँ
(iv) 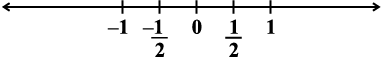
(v) 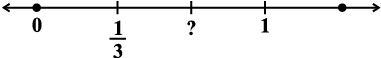
संख्या रेखा (iv) पर वह बिंदु जो 0 और 1 के मध्य स्थित है उसे 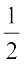 के रूप में अंकित किया गया है। संख्या रेखा (v) पर 0 और 1 के बीच की दूरी को तीन बराबर भागों में बाँटने वाले समदूरस्थ बिंदुओं में से प्रथम बिंदु को
के रूप में अंकित किया गया है। संख्या रेखा (v) पर 0 और 1 के बीच की दूरी को तीन बराबर भागों में बाँटने वाले समदूरस्थ बिंदुओं में से प्रथम बिंदु को 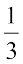 के रूप में अंकित किया जा सकता है। संख्या रेखा (v) पर भाजक बिंदुओं में से दूसरे बिंदु को आप कैसे अंकित करेंगे?
के रूप में अंकित किया जा सकता है। संख्या रेखा (v) पर भाजक बिंदुओं में से दूसरे बिंदु को आप कैसे अंकित करेंगे?
अंकित किए जाने वाला यह बिंदु शून्य के दाईं तरफ़ 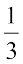 के रूप में अंकित बिंदु से दुगुनी दूरी पर है, इस प्रकार यह
के रूप में अंकित बिंदु से दुगुनी दूरी पर है, इस प्रकार यह 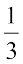 से दुगुना है, अर्थात्
से दुगुना है, अर्थात् 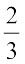 है। आप इसी प्रकार संख्या रेखा पर समदूरस्थ बिंदुओं को अंकित कर सकते हैं। इस शृंखला में अगला चिह्न 1 है। आप देख सकते हैं कि 1 और
है। आप इसी प्रकार संख्या रेखा पर समदूरस्थ बिंदुओं को अंकित कर सकते हैं। इस शृंखला में अगला चिह्न 1 है। आप देख सकते हैं कि 1 और 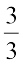 एक समान हैं।
एक समान हैं।
जैसा की संख्या रेखा (vi) पर दर्शाया गया है इसके पश्चात् 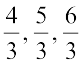 (अथवा 2),
(अथवा 2), 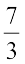 आते हैं।
आते हैं।
(vi) 
इसी प्रकार, 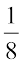 को निरूपित करने के लिए संख्या रेखाखंड को आठ बराबर भागों में बाँटा जा सकता है जैसा कि निम्न आकृति में दर्शाया गया है:
को निरूपित करने के लिए संख्या रेखाखंड को आठ बराबर भागों में बाँटा जा सकता है जैसा कि निम्न आकृति में दर्शाया गया है:

इस विभाजन के प्रथम बिंदु को नाम देने के लिए हम संख्या 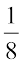 का उपयोग करते हैं। विभाजन का दूसरा बिंदु
का उपयोग करते हैं। विभाजन का दूसरा बिंदु 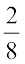 के रूप में अंकित किया जाएगा, तीसरा बिंदु
के रूप में अंकित किया जाएगा, तीसरा बिंदु 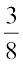 के रूप में और इसी प्रकार आगे भी, जैसा कि संख्या रेखा (vii) पर दर्शाया गया है।
के रूप में और इसी प्रकार आगे भी, जैसा कि संख्या रेखा (vii) पर दर्शाया गया है।
(vii) 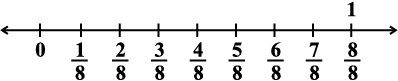
इसी प्रकार संख्या रेखा पर किसी भी परिमेय संख्या को निरूपित किया जा सकता है। एक परिमेय संख्या में रेखा के नीचे का संख्यांक अर्थात् हर, यह दर्शाता है कि प्रथम इकाई को कितने समान भागों में बाँटा गया है। रेखा के ऊपर का संख्यांक अर्थात् अंश, यह दर्शाता है कि इन समान भागों में से कितने भागों को शामिल किया गया है। इस प्रकार परिमेय संख्या  का अर्थ है कि शून्य के दाईं तरफ़ नौ समान भागों में से चार को लिया गया है (संख्या रेखा viii) और
का अर्थ है कि शून्य के दाईं तरफ़ नौ समान भागों में से चार को लिया गया है (संख्या रेखा viii) और 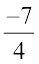 , के लिए हम शून्य से शुरू करते हुए बाईं तरफ़ 7 चिह्न लगाते हैं जिनमें से प्रत्येक की दूरी
, के लिए हम शून्य से शुरू करते हुए बाईं तरफ़ 7 चिह्न लगाते हैं जिनमें से प्रत्येक की दूरी 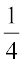 है। सातवाँ चिह्न
है। सातवाँ चिह्न 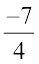 है [संख्या रेखा (ix)]।
है [संख्या रेखा (ix)]।
(viii) 
(ix) 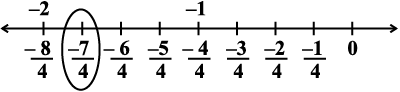
प्रयास कीजिए
अक्षर द्वारा अंकित प्रत्येक बिंदु के लिए परिमेय संख्या लिखिए:
(i) 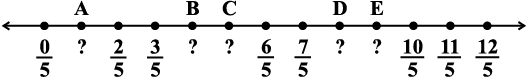
(ii) 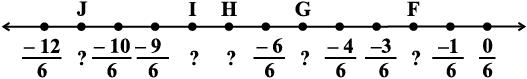
1.4 दो परिमेय संख्याओं के बीच परिमेय संख्याएँ
क्या आप 1 और 5 के बीच प्राकृत संख्याएँ बता सकते हैं? वे प्राकृत संख्याएँ 2, 3 और 4 हैं।
7 और 9 के बीच में कितनी प्राकृत संख्याएँ हैं? केवल एक, और वह है 8
10 और 11 के बीच कितनी प्राकृत संख्याएँ हैं? स्पष्ट रूप से एक भी नहीं।
–5 और 4 के बीच स्थित पूर्णांकों की सूची बनाइए। यह है, – 4, – 3, –2, –1, 0, 1, 2, 3.
–1 और 1 के बीच कितने पूर्णांक हैं?
–9 और –10 के बीच कितने पूर्णांक हैं?
आप दो प्राकृत संख्याओं (पूर्णांकों) के बीच निश्चित प्राकृत संख्याएँ (पूर्णांक) पाएँगे।
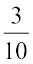 और
और 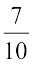 के बीच कितनी परिमेय संख्याएँ हैं? शायद आप सोच सकते हैं कि ये संख्याएँ
के बीच कितनी परिमेय संख्याएँ हैं? शायद आप सोच सकते हैं कि ये संख्याएँ 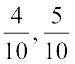 और
और 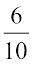 हैं। परंतु आप
हैं। परंतु आप 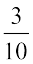 को
को 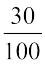 और
और 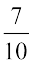 को
को 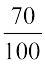 लिख सकते हैं।
लिख सकते हैं।
अब संख्याएँ, 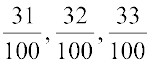
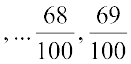 , सभी
, सभी 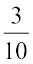 और
और 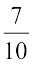 के बीच में हैं। इन परिमेय संख्याओं की संख्या 39 है।
के बीच में हैं। इन परिमेय संख्याओं की संख्या 39 है।
इसके अतिरिक्त 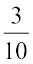 को
को  तथा
तथा 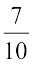 को
को  के रूप में लिखा जा सकता है। अब हम पाते हैं कि परिमेय संख्याएँ
के रूप में लिखा जा सकता है। अब हम पाते हैं कि परिमेय संख्याएँ 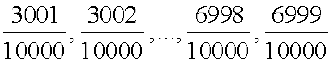 सभी
सभी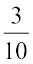 और
और 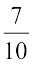 के बीच में हैं। ये कुल 3999 संख्याएँ हैं।
के बीच में हैं। ये कुल 3999 संख्याएँ हैं।
इस प्रकार हम 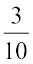 और
और 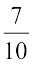 के बीच में अधिक से अधिक संख्याओं का समावेश कर सकते हैं। इसलिए प्राकृत संख्याओं और पूर्णांकों की तरह दो परिमेय संख्याओं के बीच पाई जाने वाली परिमेय संख्याएँ परिमित नहीं हैं। एक और उदाहरण पर विचार करते हैं।
के बीच में अधिक से अधिक संख्याओं का समावेश कर सकते हैं। इसलिए प्राकृत संख्याओं और पूर्णांकों की तरह दो परिमेय संख्याओं के बीच पाई जाने वाली परिमेय संख्याएँ परिमित नहीं हैं। एक और उदाहरण पर विचार करते हैं। 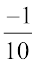 और
और 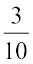 के बीच में कितनी परिमेय संख्याएँ हैं? स्पष्ट रूप से दी हुई संख्याओं के बीच में
के बीच में कितनी परिमेय संख्याएँ हैं? स्पष्ट रूप से दी हुई संख्याओं के बीच में 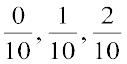 परिमेय संख्याएँ हैं।
परिमेय संख्याएँ हैं।
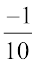 को
को  तथा
तथा 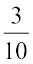 को
को 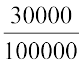 के रूप में लिखते हैं तो हम
के रूप में लिखते हैं तो हम 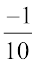 और
और 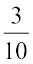 के बीच में
के बीच में 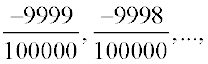
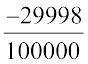 ,
, 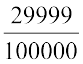 , परिमेय संख्याएँ प्राप्त करते हैं।
, परिमेय संख्याएँ प्राप्त करते हैं।आप कोई भी दो परिमेय संख्याओं के बीच में अपरिमित परिमेय संख्याएँ प्राप्त करेंगे।
उदाहरण 6 : –2 और 0 के मध्य 3 परिमेय संख्याएँ ज्ञात कीजिए।
हल : –2 को 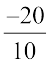 और 0 को
और 0 को 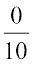 के रूप में लिखा जा सकता है। अत: हम –2 और 10 के बीच में
के रूप में लिखा जा सकता है। अत: हम –2 और 10 के बीच में 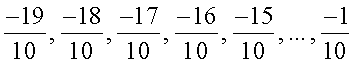 परिमेय संख्याएँ प्राप्त करते हैं। आप इनमें से कोई भी तीन संख्याएँ ले सकते हैं।
परिमेय संख्याएँ प्राप्त करते हैं। आप इनमें से कोई भी तीन संख्याएँ ले सकते हैं।
उदाहरण 7 : 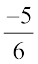 और
और 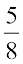 के बीच में दस परिमेय संख्याएँ ज्ञात कीजिए।
के बीच में दस परिमेय संख्याएँ ज्ञात कीजिए।
हल : सर्वप्रथम हम 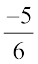 और
और 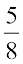 को समान हर वाली परिमेय संख्याओं के रूप में परिवर्तित करते हैं।
को समान हर वाली परिमेय संख्याओं के रूप में परिवर्तित करते हैं।
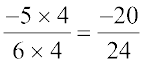 और
और 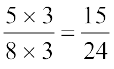
इसी प्रकार हम 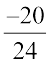 और
और 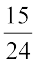 के मध्य निम्नलिखित परिमेय संख्याएँ प्राप्त करते हैं। आप इनमें से कोई भी दस संख्याएँ ले सकते हैं
के मध्य निम्नलिखित परिमेय संख्याएँ प्राप्त करते हैं। आप इनमें से कोई भी दस संख्याएँ ले सकते हैं 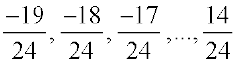
अन्य विधि
आइए 1 और 2 के बीच में परिमेय संख्याएँ ज्ञात करते हैं। उनमें से एक संख्या 1.5 अथवा 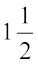 अथवा
अथवा 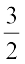 है। यह 1 और 2 का माध्य है। आपने कक्षा VII में माध्य के बारे में पढ़ा है।
है। यह 1 और 2 का माध्य है। आपने कक्षा VII में माध्य के बारे में पढ़ा है।
इस प्रकार हम पाते हैं कि दी हुई दो संख्याओं के बीच में पूर्णांक प्राप्त होना आवश्यक नहीं है परंतु दी हुई दो संख्याओं के बीच में एक परिमेय संख्या हमेशा स्थित होती है। हम दी हुई दो परिमेय संख्याओं के बीच में परिमेय संख्याएँ ज्ञात करने के लिए माध्य की अवधारणा का उपयोग कर सकते हैं।
उदाहरण 8 : 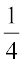 और
और 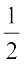 के मध्य एक परिमेय संख्या ज्ञात कीजिए।
के मध्य एक परिमेय संख्या ज्ञात कीजिए।
हल : हम दी हुई परिमेय संख्याओं का माध्य ज्ञात करते हैं  =
= 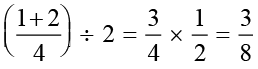
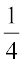 और
और 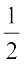 के मध्य
के मध्य 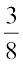 स्थित है।
स्थित है।
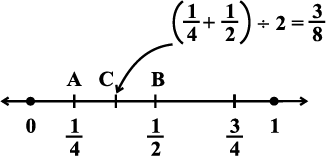
इसे संख्या रेखा पर भी देखा जा सकता है।
हम AB का मध्य बिंदु C प्राप्त करते हैं जो 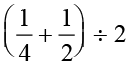 =
= 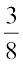 द्वारा निरूपित है। हम पाते हैं कि
द्वारा निरूपित है। हम पाते हैं कि 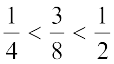 है।
है।
यदि a और b कोई दो परिमेय संख्याएँ हैं तो a और b के मध्य 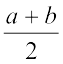 एक परिमेय संख्या इस प्रकार है कि a <
एक परिमेय संख्या इस प्रकार है कि a < 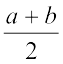 < b
< b
इससे यह भी प्रदर्शित होता है कि दी हुई दो परिमेय संख्याओं के बीच अपरिमित परिमेय संख्याएँ होती हैं।
उदाहरण 9 : 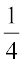 और
और 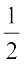 के मध्य तीन परिमेय संख्याएँ ज्ञात कीजिए।
के मध्य तीन परिमेय संख्याएँ ज्ञात कीजिए।
हल : हम दी हुई संख्याओं का माध्य ज्ञात करते हैं। जैसा कि उपर्युक्त उदाहरण में दिया हुआ है इन संख्याओं का माध्य 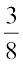 है और
है और 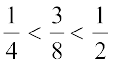 है।
है। 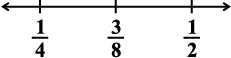
अब 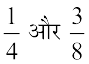 के बीच में एक और परिमेय संख्या ज्ञात करते हैं। इसके लिए हम पुन:
के बीच में एक और परिमेय संख्या ज्ञात करते हैं। इसके लिए हम पुन: 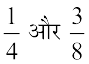 का माध्य ज्ञात करते हैं। अर्थात्
का माध्य ज्ञात करते हैं। अर्थात् 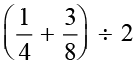 =
= 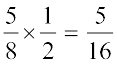 है।
है।
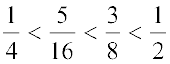
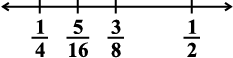
अब 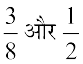 का माध्य ज्ञात कीजिए। हम
का माध्य ज्ञात कीजिए। हम 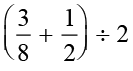 =
= 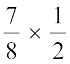 =
= 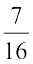 प्राप्त करते हैं।
प्राप्त करते हैं।
इस प्रकार हमें 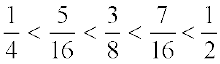 प्राप्त होता है।
प्राप्त होता है।
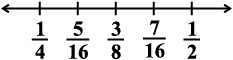
इस प्रकार 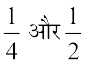 के मध्य तीन परिमेय संख्याएँ
के मध्य तीन परिमेय संख्याएँ 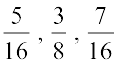 हैं।
हैं।
इसे स्पष्ट रूप से संख्या रेखा पर निम्न रूप में दर्शाया जा सकता है:
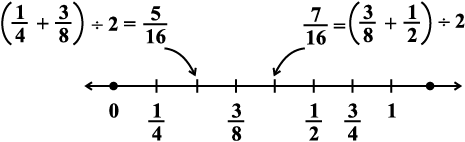
इसी प्रकार हम दी हुई दो परिमेय संख्याओं के बीच में अपनी इच्छानुसार कितनी भी परिमेय संख्याएँ ज्ञात कर सकते हैं। आप देख चुके हैं कि दी हुई दो परिमेय संख्याओं के बीच में अपरिमित परिमेय संख्याएँ होती हैं।
प्रश्नावली 1.2
1. निम्नलिखित संख्याओं को संख्या रेखा पर निरूपित कीजिए: (i) 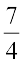 (ii)
(ii) 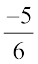
2. 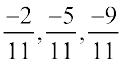 को संख्या रेखा पर निरूपित कीजिए।
को संख्या रेखा पर निरूपित कीजिए।
3. एेसी पाँच परिमेय संख्याएँ लिखिए जो 2 से छोटी हों।
4. 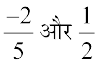 के मध्य दस परिमेय संख्याएँ ज्ञात कीजिए।
के मध्य दस परिमेय संख्याएँ ज्ञात कीजिए।
5. (i) 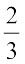

 (ii)
(ii) 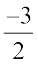

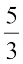
(iii) 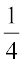

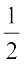 के मध्य पाँच परिमेय संख्याएँ ज्ञात कीजिए।
के मध्य पाँच परिमेय संख्याएँ ज्ञात कीजिए।
6. –2 से बड़ी पाँच परिमेय संख्याएँ लिखिए।
7. 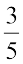

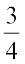 के बीच में दस परिमेय संख्याएँ ज्ञात कीजिए।
के बीच में दस परिमेय संख्याएँ ज्ञात कीजिए।
हमने क्या चर्चा की?
1. परिमेय संख्याएँ योग व्यवकलन और गुणन की संक्रियाओं के अंतर्गत संवृत हैं।
2. परिमेय संख्याओं के लिए योग और गुणन की संक्रियाएँ
(i) क्रमविनिमेय हैं।
(ii) साहचर्य हैं।
3. परिमेय संख्याओं के लिए परिमेय संख्या शून्य योज्य तत्समक है।
4. परिमेय संख्याओं के लिए परिमेय संख्या 1 गुणनात्मक तत्समक है।
5. परिमेय संख्या 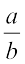 का योज्य प्रतिलोम
का योज्य प्रतिलोम 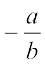 है और विलोमत: भी सत्य है।
है और विलोमत: भी सत्य है।
6. यदि 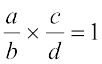 तो परिमेय संख्या
तो परिमेय संख्या 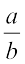 का व्युत्क्रम अथवा गुणनात्मक प्रतिलोम
का व्युत्क्रम अथवा गुणनात्मक प्रतिलोम 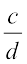 है।
है।
7. परिमेय संख्याओं की वितरकता : परिमेय संख्याएँ a, b और c के लिए
a(b + c) = ab + ac और a(b – c) = ab – ac है।
8. परिमेय संख्याओं को संख्या रेखा पर निरूपित किया जा सकता है।
9. दी हुई दो परिमेय संख्याओं के मध्य अपरिमित परिमेय संख्याएँ होती हैं। दो परिमेय संख्याओं के मध्य परिमेय संख्याएँ ज्ञात करने में माध्य की अवधारणा सहायक है।
