Table of Contents
अध्याय 2
एक चर वाले रैखिक समीकरण
2.1 भूमिका
पिछली कक्षाओं में, आपने अनेक बीजीय व्यंजकों और समीकरणों के बारे में जानकारी प्राप्त की है। एेसे व्यंजक जो हमने देखे, उनके कुछ उदाहरण हैं–
5x, 2x – 3, 3x + y, 2xy + 5, xyz + x + y + z, x2 + 1, y + y2
समीकरणों के कुछ उदाहरण हैंः 5x = 25, 2x – 3 = 9,
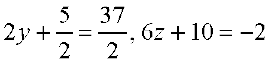
आपको याद होगा कि समीकरणों में सदैव समता ‘=’ का चिह्न प्रयोग होता है, जो व्यंजकों में नहीं होता।
इन व्यंजकों में, कुछ में एक से अधिक चर प्रयोग हुए हैं। उदाहरण के लिए, 2xy + 5 में दो चर हैं। तथापि, हम अब समीकरण बनाने में केवल एक चर वाले व्यंजक ही प्रयोग करेंगे और जो व्यंजक समीकरण बनाने में लिखे जाएँगे वे रैखिक ही होंगे। इससे तात्पर्य है कि व्यंजकों में प्रयोग होने वाले चर की अधिकतम घात एक होगी।
कुछ रैखिक व्यंजक हैं–
2x, 2x + 1, 3y – 7, 12 – 5z, 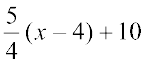
ये रैखिक व्यंजक नहीं हैंः x2 + 1, y + y2, 1 + z + z2 + z3
(ध्यान दीजिए चर की अधिकतम घात 1 से अधिक है)
अब हम समीकरणों में, केवल एक चर वाले व्यंजकों का ही प्रयोग करेंगे। एेसे समीकरण, एक चर वाले रैखिक समीकरण कहलाते हैं। पिछली कक्षाओं में जिन सरल समीकरणों को आपने हल करना सीखा वे इसी प्रकार के थे।
आइए, जो हम जानते हैं, उसे संक्षिप्त में दोहरा लें–
2x – 3 = 7. इस समीकरण का हल है–
x = 5 क्योंकि x = 5 होने पर बाएँ पक्ष का मान होगा 2 × 5 – 3 = 7 जो दाएँ पक्ष का मान है लेकिनx = 10 इसका हल नहीं है, क्योंकि x = 10 होने पर बाएँ पक्ष का मान होगा, 2 × 10 –3 = 17 जो दाएँ पक्ष के बराबर नहीं है।
(b) एक समीकरण में बाएँ पक्ष में व्यंजक का मान, दाएँ पक्ष में व्यंजक के मान के बराबर होता है। एेसा, चर के कुछ मानों के लिए ही संभव होता है और चर के एेसे मानों को ही चर के हल कहते हैं।
(c) किसी समीकरण का हल कैसे ज्ञात करें?
हम मानते हैं कि समीकरण के दोनों पक्ष, तुला के पलड़ों की तरह संतुलन में हैं। अतः हम समीकरण के दोनों पक्षों पर एक जैसी ही गणितीय संक्रियाएँ करते हैं जिससे समीकरण का संतुलन बना रहे; बिगड़े नहीं, लेकिन समीकरण सरल, अधिक सरल होता जाए। इस प्रकार कुछ चरणों के बाद समीकरण का हल प्राप्त हो जाता है।
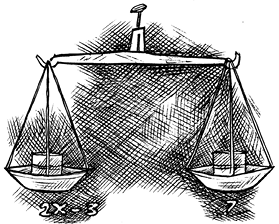
2.2 समीकरणों को हल करना, जिनके एक पक्ष में रैε क व्यंजक तथा दूसरे में केवल संख्या हो
कुछ उदाहरण लेकर, समीकरणों को हल करने की विधि फिर ध्यान में लाते हैं। हलों पर ध्यान दीजिए। हल के रूप में कोई भी परिमेय संख्या प्राप्त हो सकती है।
उदाहरण 1 : हल ज्ञात कीजिए 2x – 3 = 7
हल :
चरण 1 दोनों पक्षों में 3 जोड़ने पर
2x – 3 + 3 = 7 + 3 (संतुलन नहीं बिगड़ा)
या 2x = 10
चरण 2 दोनों पक्षों को 2 से भाग करने पर
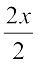 =
= 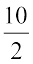
या x = 5 (अपेक्षित हल)
उदाहरण 2 : हल कीजिए 2y + 9 = 4
हल : 9 का, दाएँ पक्ष में पक्षांतरण करने पर
2y = 4 – 9
या 2y = – 5
दोनों पक्षों को 2 से भाग करने पर, y = 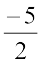 (हल)
(हल)
हल की जाँच: बायाँ पक्ष = 2 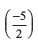 + 9 = – 5 + 9 = 4 = दायाँ पक्ष (जैसा चाहिए)
+ 9 = – 5 + 9 = 4 = दायाँ पक्ष (जैसा चाहिए)
क्या आपने ध्यान दिया कि संख्या 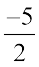 एक परिमेय संख्या है? सातवीं कक्षा में जो समीकरण हल किए गए उनके हल एेसी संख्याएँ नहीं थीं।
एक परिमेय संख्या है? सातवीं कक्षा में जो समीकरण हल किए गए उनके हल एेसी संख्याएँ नहीं थीं।
उदाहरण 3 : हल कीजिए 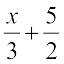 =
= 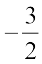
हल : 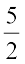 को दाएँ पक्ष में पक्षांतरण करने पर
को दाएँ पक्ष में पक्षांतरण करने पर 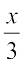 =
= 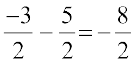
या 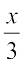 = – 4
= – 4
दोनों पक्षों को 3 से गुणा करने पर x = – 4 × 3
या x = – 12 (हल)
जाँच: बायाँ पक्ष = 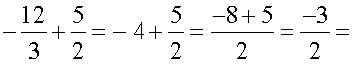 दायाँ पक्ष (जैसा चाहिए)
दायाँ पक्ष (जैसा चाहिए)
ध्यान दीजिए कि समीकरण में चर का गुणांक आवश्यक नहीं कि सदैव एक पूर्णांक ही हो।
उदाहरण 4 : हल कीजिए 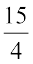 – 7x = 9
– 7x = 9
हल : ज्ञात है 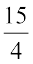 – 7x = 9
– 7x = 9
या – 7x = 9 – 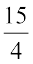 (
(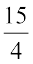 दाएँ पक्ष में पक्षांतरण करने पर)
दाएँ पक्ष में पक्षांतरण करने पर)
या – 7x = 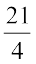
या x = 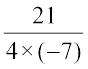 (दोनों पक्षों को -7 से भाग करने पर)
(दोनों पक्षों को -7 से भाग करने पर)
या x = 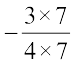
या x = 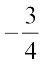 (अपेक्षित हल)
(अपेक्षित हल)
जाँच: बायाँ पक्ष =  =
= 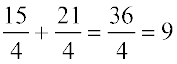 = दायाँ पक्ष (जैसा चाहिए)
= दायाँ पक्ष (जैसा चाहिए)
प्रश्नावली 2.1
निम्न समीकरणों को हल कीजिए:
1. x – 2 = 7 2. y + 3 = 10 3. 6 = z + 2
4. 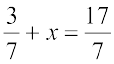 5. 6x = 12 6.
5. 6x = 12 6. 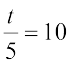
7. 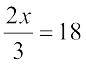 8. 1.6 =
8. 1.6 = 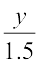 9. 7x – 9 = 16
9. 7x – 9 = 16
10. 14y – 8 = 13 11. 17 + 6p = 9 12. 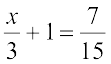
2.3 कुछ अनुप्रयोग
हम एक सरल उदाहरण से आरंभ करते हैं:
दो संख्याओं का योग 74 है। उनमें एक संख्या दूसरी से 10 अधिक है। वे संख्याएँ कौन-सी हैं? यह एक पहेली की तरह है। हमें दोनों में कोई भी संख्या पता नहीं और उन्हें ज्ञात करना है। हमें दो शर्तें दी गई हैं:
(i) एक संख्या दूसरी से 10 अधिक है, तथा
(ii) उनका योग 74 है।
हम कक्षा VII में सीख चुके हैं कि इस तरह की समस्या कैसे आरंभ करते हैं। हम मानते हैं कि छोटी संख्या x है। तब बड़ी संख्या है x से 10 अधिक अर्थात् x + 10 ।
दूसरी शर्त है कि संख्याओं का योग 74 है।
अतः x + (x + 10) = 74
या 2x + 10 = 74
10 को दाएँ पक्ष में पक्षांतरण करने पर 2x = 74 – 10
या 2x = 64
दोनों पक्षों को 2 से भाग करने पर x = 32
अर्थात् छोटी संख्या है 32 तथा दूसरी बड़ी संख्या है x + 10 = 32 + 10 = 42
अर्थात् अपेक्षित संख्याएँ 32 तथा 42 हैं, जो दोनों शर्तें भी पूरी करती हैं। इस विधि की उपयोगिता दिखाने के लिए हम कुछ और उदाहरणों पर विचार करते हैं।
उदाहरण 5 : परिमेय संख्या 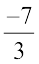 के दुगुने में क्या जोड़ा जाए जिससे
के दुगुने में क्या जोड़ा जाए जिससे 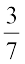 प्राप्त हो?
प्राप्त हो?
हल : परिमेय संख्या 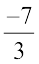 का दुगुना है
का दुगुना है 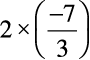 =
= 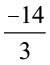 .
.
माना इसमें x जोड़ने पर 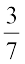 प्राप्त होता है। अतः
प्राप्त होता है। अतः  =
= 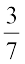
या 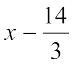 =
= 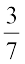
या x = 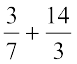 (
(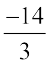 को दाएँ पक्ष में पक्षांतरण करने पर)
को दाएँ पक्ष में पक्षांतरण करने पर)
= 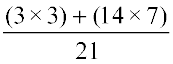 =
= 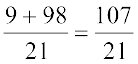 .
.
इस प्रकार 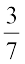 प्राप्त करने के लिए
प्राप्त करने के लिए 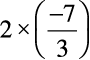 में
में 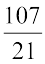 जोड़ा जाना चाहिए।
जोड़ा जाना चाहिए।
उदाहरण 6 : एक आयत का परिमाप 13 cm है और उसकी चौड़ाई 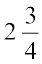 cm है। उसकी लंबाई ज्ञात कीजिए।
cm है। उसकी लंबाई ज्ञात कीजिए।
हल : मान लेते हैं कि आयत की लंबाई x cm है।
आयत का परिमाप = 2 × (लंबाई + चौड़ाई)
= 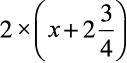 =
= 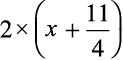
परिमाप 13 cm दिया गया है।
अतः 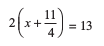
या 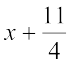 =
= 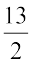 (दोनों पक्षों को 2 से भाग करने पर)
(दोनों पक्षों को 2 से भाग करने पर)
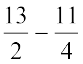 (
( को दाएँ पक्ष में पक्षांतरण करने पर)
को दाएँ पक्ष में पक्षांतरण करने पर) = 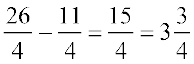
आयत की लंबाई 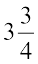 cm है।
cm है।
उदाहरण 7 : साहिल की माँ की वर्तमान आयु साहिल की वर्तमान आयु की तीन गुनी है। 5 वर्ष बाद उन दोनों की आयु का योग 66 वर्ष हो जाएगा। उनकी वर्तमान आयु ज्ञात कीजिए।
हल : माना साहिल की वर्तमान आयु = x वर्ष
| साहिल | माँ | योग | |
| वर्तमान आयु | x | 3x | |
| 5 वर्ष बाद आयु | x+5 | 3x+5 | 4x+10 |
अतः 4x + 10 = 66
इस समीकरण में x साहिल की वर्तमान आयु है। समीकरण हल करने के लिए 10 दाएँ पक्ष में पक्षांतरित करते हैं।
4x = 66 – 10
या 4x = 56
या x = 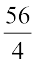 = 14 (हल)
= 14 (हल)
इस प्रकार साहिल की वर्तमान आयु 14 वर्ष है तथा उसकी माँ की आयु 42 वर्ष है। आप जाँच कर सकते हैं कि 5 वर्ष बाद उन दोनों की आयु का योग 66 वर्ष हो जाएगा।
उदाहरण 8 : बंसी के पास कुछ सिक्के ₹ 2 वाले तथा कुछ ₹ 5 वाले हैं। यदि ₹ 2 वाले सिक्कों की संख्या ₹ 5 वाले सिक्कों की संख्या की तिगुनी है और उनके मूल्यों का कुल योग ₹ 77 है तो दोनों प्रकार के सिक्कों की संख्या ज्ञात कीजिए।
हल : माना बंसी के पास ₹ 5 वाले सिक्कों की संख्या x है।
तब ₹ 2 वाले सिक्कों की संख्या = 3x
अतः (i) ₹ 5 वाले x सिक्कों का मूल्य = 5 × x = ₹ 5x
तथा (ii) ₹ 2 वाले 3x सिक्कों का मूल्य = 2 × 3x = ₹ 6x
अतः कुल मूल्य = 5x + 6x = ₹ 11x
कुल मूल्य दिया है ₹ 77
अतः 11x = 77
या x = 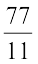 = 7 (दोनों पक्षों को 11 से भाग करने पर)
= 7 (दोनों पक्षों को 11 से भाग करने पर)
अर्थात् ₹ 5 वाले सिक्कों की संख्या = x = 7
तथा ₹ 2 वाले सिक्कों की संख्या = 3x = 21 (हल)
आप जाँच कर सकते हैं कि इन दोनों का मूल्य ₹ 77 ही होता है।
₹ 5
₹ 2
उदाहरण 9 : यदि 11 के तीन लगातार गुणजों का योग 363 है तो उन्हें ज्ञात कीजिए।
हल : यदि 11 का एक गुणज x है तब अगला गुणज होगा x + 11
और उससे अगला गुणज होगा x + 11 + 11 या x + 22
दिया है कि 11 के इन तीनों लगातार
गुणजों का योग 363 है। इससे हमें
निम्न समीकरण प्राप्त होता है –
x + (x + 11) + (x + 22) = 363
या x + x + 11 + x + 22 = 363
या 3x + 33 = 363

या 3x = 363 – 33
या 3x = 330
या x = 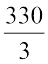 = 110
= 110
अर्थात् ये तीन लगातार गुणज हैं 110, 121 तथा 132 ।
हम यहाँ देखते हैं कि समस्या को विभिन्न प्रकार से कैसे हल किया जा सकता है।
वैकल्पिक हल: 11 के तीनों लगातार गुणजों में हम मध्य वाला x मानते हैं। इसके पहले वाला गुणजहोगा x – 11 और इसके बाद वाला गुणज होगा x + 11
अतः समीकरण होगा –
(x – 11) + x + (x + 11) = 363
या 3x = 363
दोनों पक्षों को 3 से भाग करने पर
x = 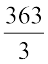 = 121
= 121
इस प्रकार x = 121, x – 11 = 110, x + 11 = 132
अतः 11 के तीन लगातार गुणज हैं 110, 121 व 132
उदाहरण 10 : दो पूर्ण संख्याओं का अंतर 66 है। यदि उनमें 2 : 5 का अनुपात है तो वे संख्याएँ ज्ञात कीजिए।
हल : क्योंकि दोनों संख्याएँ 2 : 5 के अनुपात में हैं, अतः हम एक संख्या 2x और दूसरी 5x मान सकते हैं। (ध्यान दीजिए 2x : 5x में 2 : 5 का अनुपात है।)
इनमें अंतर है, 5x – 2x जो 66 के बराबर दिया है।
अतः 5x – 2x = 66
या 3x = 66
या x = 22
क्योंकि संख्याएँ 2x तथा 5x हैं। अतः संख्याएँ हुईं 2 × 22 तथा 5 × 22 अर्थात् 44 तथा 110 और इनका अंतर 110 – 44 = 66 ही है जो वांछित है।
उदाहरण 11 : देवेशी के पास ₹ 50, ₹ 20 तथा ₹ 10 वाले कुल मिलाकर 25 नोट हैं जिनका मूल्य ₹ 590 बनता है। यदि ₹ 50 तथा ₹ 20 वाले नोटों की संख्या में अनुपात 3 : 5 है तो प्रत्येक प्रकार के नोटों की संख्या ज्ञात कीजिए।
हल : मानते हैं कि ₹ 50 तथा ₹ 20 वाले नोटों की संख्या क्रमशः 3x तथा 5x है।
लेकिन कुल नोटों की संख्या 25 है।
अतः ₹ 10 वाले नोटों की संख्या = 25 – (3x + 5x) = 25 – 8x
इन नोटों से उसके पास धन हुआ
₹ 50 वाले नोटों से: 3x × 50 = ₹ 150x
₹ 20 वाले नोटों में: 5x × 20 = ₹ 100x
₹ 10 वाले नोटों में (25 – 8x) × 10 = ₹ (250 – 80x)
और कुल धन हुआ = 150x + 100x + (250 – 80x)
= ₹ (170x + 250)
यह धन ₹ 590 के बराबर दिया है। अतः 170x + 250 = 590
या 170x = 590 – 250 = 340
या x = 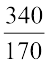 = 2
= 2
अर्थात् देवेशी के पास ₹ 50 वाले नोट = 3x
= 3 × 2 = 6 नोट
₹ 20 वाले नोट = 5x = 5 × 2 = 10 नोट
तथा ₹ 10 वाले नोट = 25 – 8x
= 25 – (8 × 2) = 25 – 16 = 9
प्रश्नावली 2.2
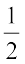 घटाने और परिणाम को
घटाने और परिणाम को 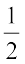 से गुणा करने पर
से गुणा करने पर 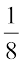 प्राप्त होता है तो वह संख्या क्या है?
प्राप्त होता है तो वह संख्या क्या है?2. एक आयताकार तरण-ताल (swimming pool) की लंबाई उसकी चौड़ाई के दुगुने से 2 मीटर अधिक है। यदि इसका परिमाप 154 मीटर है तो इसकी लंबाई व चौड़ाई ज्ञात कीजिए।
3. एक समद्विबाहु त्रिभुज का आधार  cm तथा उसका परिमाप
cm तथा उसका परिमाप  cm है। उसकी दो बराबर भुजाओं की माप ज्ञात कीजिए।
cm है। उसकी दो बराबर भुजाओं की माप ज्ञात कीजिए।
4. दो संख्याओं का योग 95 है। यदि एक संख्या दूसरी से 15 अधिक है तो दोनों संख्याएँ ज्ञात कीजिए।
5. दो संख्याओं में अनुपात 5 : 3 है। यदि उनमें अंतर 18 है तो संख्याएँ ज्ञात कीजिए।
7. 8 के तीन लगातार गुणजों का योग 888 है। गुणजों को ज्ञात कीजिए।
8. तीन लगातार पूर्णांक बढ़ते क्रम में लेकर उन्हें क्रमशः 2, 3 तथा 4 से गुणा कर योग करने पर योगफल 74 प्राप्त होता है। तीनों पूर्णांक ज्ञात कीजिए।
9. राहुल और हारुन की वर्तमान आयु में अनुपात 5 : 7 है। 4 वर्ष बाद उनकी आयु का योग 56 वर्ष हो जाएगा। उनकी वर्तमान आयु क्या है?
10. किसी कक्षा में बालक और बालिकाओं की संख्याओं में अनुपात 7 : 5 है। यदि बालकों की संख्या बालिकाओं की संख्या से 8 अधिक है तो कक्षा में कुल कितने विद्यार्थी हैं?
11. बाइचुंग के पिताजी उसके दादाजी से 26 वर्ष छोटे हैं और उससे 29 वर्ष बड़े हैं। यदि उन तीनों की आयु का योग 135 वर्ष है तो उनकी आयु अलग-अलग ज्ञात कीजिए।
12. 15 वर्ष बाद रवि की आयु, उसकी वर्तमान आयु से चार गुनी हो जाएगी। रवि की वर्तमान आयु क्या है?
13. एक परिमेय संख्या को 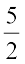 से गुणा कर
से गुणा कर 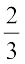 जोड़ने पर
जोड़ने पर 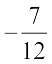 प्राप्त होता है। वह संख्या क्या है?
प्राप्त होता है। वह संख्या क्या है?
14. लक्ष्मी एक बैंक में खजांची है। उसके पास नगदी के रूप में ₹ 100, ₹ 50 व ₹ 10 वाले नोट हैं। उनकी संख्याओं में क्रमशः 2 : 3 : 5 का अनुपात है और उनका कुल मूल्य ₹ 4,00,000 है। उसके पास प्रत्येक प्रकार के कितने-कितने नोट हैं?
15. मेरे पास ₹ 300 मूल्य के, ₹ 1, ₹ 2 और ₹ 5 वाले सिक्के हैं। ₹ 2 वाले सिक्कों की संख्या ₹ 5 वाले सिक्कों की संख्या की तिगुनी है और सिक्कों की कुल संख्या 160 है। मेरे पास प्रत्येक प्रकार के कितने-कितने सिक्के हैं?
16. एक निबंध प्रतियोगिता में आयोजकों ने तय किया कि प्रत्येक विजेता को ₹ 100 और विजेता को छोड़कर प्रत्येक प्रतिभागी को ₹ 25 पुरस्कार के रूप में दिए जाएँगे। यदि पुरस्कारों में बाँटी गई राशि ₹ 3,000 थी तो कुल 63 प्रतिभागियों में विजेताओं की संख्या ज्ञात कीजिए।
2.4 समीकरण हल करना जब दोनों ही पक्षों में चर उपस्थित हो
एक समीकरण, दो बीजीय व्यंजकों के मानों में समता होती है। समीकरण 2x – 3 = 7 में एक व्यंजक है 2x – 3 तथा दूसरा है 7। अभी तक लिए गए लगभग सभी उदाहरणों में दाएँ पक्ष में एक ही संख्या थी। लेकिन एेसा होना सदैव आवश्यक नहीं है। चर राशि दोनों पक्षों में भी हो सकती है। उदाहरण के लिए, समीकरण 2x – 3 = x + 2 में, दोनों ही पक्षों में चर वाले व्यंजक हैं। बाएँ पक्ष में व्यंजक है (2x – 3) तथा दाएँ में है (x + 2)।
• अब हम एेसे ही समीकरणों के हल करने की चर्चा करेंगे जिनके दोनों ही पक्षों में चर वाले व्यंजक हों।
उदाहरण 12 : हल कीजिए 2x – 3 = x + 2
हल : दिया हैः 2x – 3 = x + 2 या 2x = x + 2 + 3
या 2x = x + 5
या 2x – x = x + 5 – x (दोनों पक्षों से x घटाने पर)
या x = 5 (हल)
यहाँ, हमने समीकरण के दोनों पक्षों से, एक संख्या या स्थिरांक ही नहीं, बल्कि चर वाला पद घटाया। हम एेसा कर सकते हैं क्योंकि चर का मान भी कोई संख्या ही है। ध्यान दीजिए कि x दोनों पक्षों से घटाने से तात्पर्य है x को बाएँ पक्ष में पक्षांतरण करना।
उदाहरण 13 : हल कीजिए 5x + 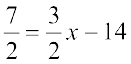
हल : दोनों पक्षों को 2 से गुणा करने पर प्राप्त होता है
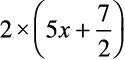 =
= 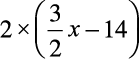
या (2 × 5x) + 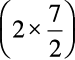 =
= 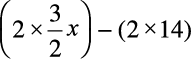
या 10x + 7 = 3x – 28
या 10x – 3x + 7 = – 28 (3x को बाएँ पक्ष में पक्षांतरण करने पर)
या 7x + 7 = – 28
या 7x = – 28 – 7
या 7x = – 35
या x = 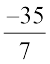
या x = – 5 (हल)
प्रश्नावली 2.3
निम्न समीकरणों को हल कीजिए और अपने उत्तर की जाँच कीजिए।
1. 3x = 2x + 18 2. 5t – 3 = 3t – 5 3. 5x + 9 = 5 + 3x
4. 4z + 3 = 6 + 2z 5. 2x – 1 = 14 – x 6. 8x + 4 = 3 (x – 1) + 7
7. x =  (x + 10) 8.
(x + 10) 8. 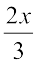 + 1 =
+ 1 =  9. 2y +
9. 2y + 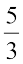 =
= 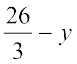
10. 3m = 5 m – 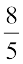
2.5 कुछ और उदाहरण
उदाहरण 14 : दो अंकों वाली एक संख्या के दोनों अंकों में 3 का अंतर है। इस संख्या में, इसके अंकों को बदलकर प्राप्त संख्या को जोड़ने पर 143 प्राप्त होता है। संख्या ज्ञात कीजिए।
हल : उदाहरण के तौर पर दो अंकों वाली कोई एक संख्या, जैसे 56 लेते हैं।
इसे इस प्रकार भी लिखा जा सकता है, 56 = (10 × 5) + 6
हम दो अंकों वाली संख्या में इकाई का अंक b मानते हैं। क्योंकि दोनों अंकों का अंतर 3 है। अतः दहाई का अंक = b + 3
अर्थात् दो अंकों वाली संख्या = 10 (b + 3) + b = 10b + 30 + b = 11b + 30
अंकों के बदलने पर संख्या होगी 10b + (b + 3) = 11b + 3
इन दोनों संख्याओं को जोड़ने पर मिलता है 143
अतः (11b + 30) + (11b + 3) = 143
या 11b + 11b + 30 + 3 = 143
या 22b + 33 = 143
या 22b = 143 – 33
या 22b = 110
या b = 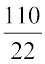
या b = 5
अर्थात् इकाई का अंक = 5
तब दहाई का अंक = 5 + 3 = 8
अतः संख्या = 85
जाँच: अंक बदलने पर संख्या 58 मिलती है। और 58 तथा 85 का योग है 143 जैसा कि दिया है।
उदाहरण 15 : अर्जुन की आयु श्रीया की आयु की दुगुनी है। 5 वर्ष पहले उसकी आयु श्रीया की आयु की तिगुनी थी। दोनों की आयु ज्ञात कीजिए।
तब अर्जुन की वर्तमान आयु = 2x वर्ष
श्रीया की 5 वर्ष पहले आयु थी (x – 5) वर्ष
तथा अर्जुन की 5 वर्ष पहले आयु थी (2x – 5) वर्ष
दिया है कि 5 वर्ष पहले अर्जुन की आयु श्रीया की आयु की तिगुनी थी
अतः 2x – 5 = 3(x – 5)
या 2x – 5 = 3x – 15
या 15 – 5 = 3x – 2x
या 10 = x
अतः श्रीया की वर्तमान आयु = x = 10 वर्ष
तथा अर्जुन की वर्तमान आयु = 2x = 2 × 10 = 20 वर्ष
प्रश्नावली 2.4
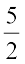 घटाकर परिणाम को 8 से गुणा करती है। अब जो परिणाम मिलता है वह सोची गई संख्या की तिगुनी है। वह सोची गई संख्या
घटाकर परिणाम को 8 से गुणा करती है। अब जो परिणाम मिलता है वह सोची गई संख्या की तिगुनी है। वह सोची गई संख्या ज्ञात कीजिए।
2. दो संख्याओं में पहली संख्या दूसरी की पाँच गुनी है। प्रत्येक संख्या में 21 जोड़ने पर पहली संख्या दूसरी की दुगुनी हो जाती है। संख्याएँ ज्ञात कीजिए।
3. दो अंकों वाली दी गई एक संख्या के अंकों का योग 9 है। इस संख्या के अंकों के स्थान बदलकर प्राप्त संख्या, दी गई संख्या से 27 अधिक है। दी गई संख्या ज्ञात कीजिए।
4. दो अंकों वाली दी गई एक संख्या में एक अंक दूसरे का तीन गुना है। इसके अंकों के स्थान बदलकर प्राप्त संख्या को, दी गई संख्या में जोड़ने पर 88 प्राप्त होता है। दी गई संख्या
ज्ञात कीजिए।
5. शोबो की माँ की आयु, शोबो की आयु की छः गुनी है। 5 वर्ष बाद शोबो की आयु, उसकी माँ की वर्तमान आयु की एक तिहाई हो जाएगी। उनकी आयु ज्ञात कीजिए।
6. महूली गाँव में, एक तंग आयताकार भूखंड विद्यालय बनाने के लिए सुरक्षित है। इस भूखंड की लंबाई और चौड़ाई में 11 : 4 का अनुपात है। गाँव पंचायत को इस भूखंड की बाड़ (fence) कराने में, ₹ 100 प्रति मीटर की दर से ₹ 75000 व्यय करने होंगे। भूखंड की माप (dimension) ज्ञात कीजिए।
7. हसन, स्कूल वर्दी बनाने के लिए दो प्रकार का कपड़ा खरीदता है। इसमें कमीज़ के कपड़े का भाव ₹ 50 प्रति मीटर तथा पतलून के कपड़े का भाव ₹ 90 प्रति मीटर है। वह कमीज़ के प्रत्येक 3 मीटर कपड़े के लिए पतलून का 2 मीटर कपड़ा खरीदता है। वह इस कपड़े को क्रमशः 12% तथा 10% लाभ पर बेचकर ₹ 36,600 प्राप्त करता है। उसने पतलूनों के लिए कितना कपड़ा खरीदा?
8. हिरणों के एक झुंड का आधा भाग मैदान में चर रहा है और शेष का तीन चौथाई पड़ोस में ही खेलकूद रहा है। शेष बचे 9 हिरण एक तालाब में पानी पी रहे हैं। झुंड में हिरणों की संख्या ज्ञात कीजिए।
9. दादाजी की आयु अपनी पौत्री की आयु की दस गुनी है। यदि उनकी आयु पौत्री की आयु से 54 वर्ष अधिक है तो उन दोनों की आयु ज्ञात कीजिए।
2.6 समीकरणों को सरल रूप में बदलना
उदाहरण 16 : हल कीजिए: 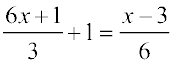
6 से ही क्यों?
ध्यान दीजिए हरों का ल.स.प. (L.C.M.) 6 है।
हल : दोनों पक्षों को 6 से गुणा करने पर
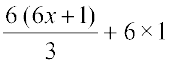 =
= 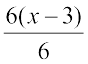
या 2 (6x + 1) + 6 = x – 3
या 12x + 2 + 6 = x – 3 (कोष्ठक हटाने पर)
या 12x + 8 = x – 3
या 12x – x + 8 = – 3
या 11x + 8 = – 3
या 11x = –3 – 8
या 11x = –11
या x = – 1 (वांछित हल)
जाँच: बायाँ पक्ष (LHS) = 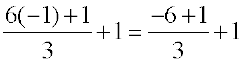 =
=
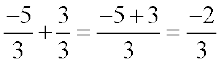
दायाँ पक्ष (RHS) = 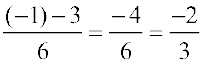
बायाँ पक्ष (LHS) = दायाँ पक्ष (RHS) (जैसा वांछित था)
उदाहरण 17 : हल कीजिए: 5x – 2 (2x – 7) = 2 (3x – 1) + 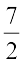
हल : कोष्ठक हटाने पर
बायाँ पक्ष (LHS) = 5x – 4x + 14 = x + 14
दायाँ पक्ष (RHS) = 6x – 2 + 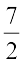 =
= 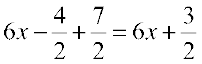
अतः समीकरण x + 14 = 6x + 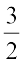 हुआ
हुआ
या 14 = 6x – x + 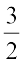
या 14 = 5x + 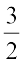
या 14 – 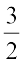 = 5x (
= 5x (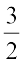 का पक्षांतरण करने पर)
का पक्षांतरण करने पर)
या 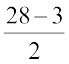 = 5x
= 5x
या 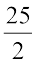 = 5x
= 5x
या x = 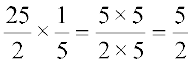
अतः वांछित हल है x = 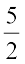
जाँच: बायाँ पक्ष (LHS) = 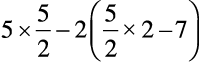
= 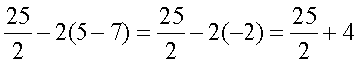 =
= 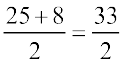
दायाँ पक्ष (RHS) = 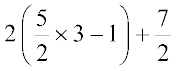
= 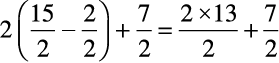
=  = LHS (यथावांछित)
= LHS (यथावांछित)
निम्न रैखिक समीकरणों को हल कीजिए:
1. 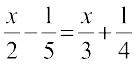 2.
2. 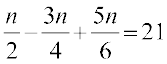 3.
3. 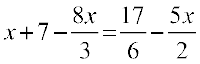
4. 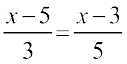 5.
5. 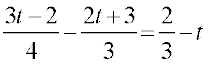
6. 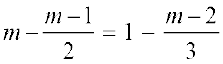
निम्न समीकरणों को सरल रूप में बदलते हुए हल कीजिए:
7. 3(t – 3) = 5(2t + 1) 8. 15(y – 4) –2(y – 9) + 5(y + 6) = 0
9. 3(5z – 7) – 2(9z – 11) = 4(8z – 13) – 17
10. 0.25(4f – 3) = 0.05(10f – 9)
2.7 रैखिक रूप में बदल जाने वाले समीकरण
उदाहरण 18 : हल कीजिए: 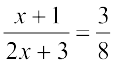
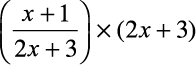 =
= 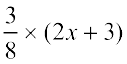
2x + 3 ≠ 0 (क्यों?)
(2x + 3) बाएँ पक्ष में निरस्त (cancel) हो जाता है और हमें प्राप्त होता है:
x + 1 = 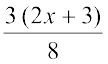
अब हमें एक रैखिक समीकरण मिला जिसे हम हल करना जानते हैं।
यह चरण वज्र-गुणन की प्रक्रिया से भी प्राप्त हो सकता है:
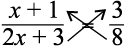
दोनों पक्षों को 8 से गुणा करने पर
8 (x + 1) = 3 (2x + 3)
या 8x + 8 = 6x + 9
या 8x = 6x + 9 – 8
या 8x = 6x + 1
या 8x – 6x = 1
या 2x = 1
या x = 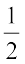
अतः हल x = 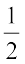 है।
है।
जाँच: बाएँ पक्ष में अंश = 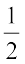 + 1 =
+ 1 =  है।
है।
बाएँ पक्ष में हर = 2x + 3 = 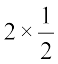 + 3 = 1 + 3 = 4 है।
+ 3 = 1 + 3 = 4 है।
अतः बायाँ पक्ष = अंश ÷ हर = 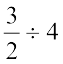 =
= 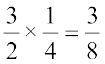
अर्थात् बायाँ पक्ष (LHS) = दायाँ पक्ष (RHS)
हल : माना कि अनु तथा राज की वर्तमान आयु क्रमशः 4x तथा 5x हैं।
8 वर्ष बाद अनु की आयु = (4x + 8) वर्ष
8 वर्ष बाद राज की आयु = (5x + 8) वर्ष
उनकी आयु का अनुपात = 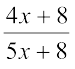 , जो दिया है 5 : 6
, जो दिया है 5 : 6
अतः 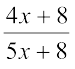 =
= 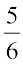
वज्र-गुणन करने पर 6 (4x + 8) = 5 (5x + 8)
या 24x + 48 = 25x + 40
या 24x + 48 – 40 = 25x
या 24x + 8 = 25x
या 8 = 25x – 24x
या 8 = x
अतः अनु की वर्तमान आयु 4x = 4 × 8 = 32 वर्ष
तथा राज की वर्तमान आयु 5x = 5 × 8 = 40 वर्ष
प्रश्नावली 2.6
निम्न समीकरणों को हल कीजिए:
1.  2.
2. 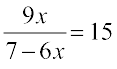 3.
3. 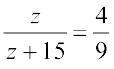
4. 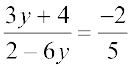 5.
5. 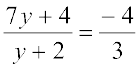
6. हरी और हैरी की वर्तमान आयु का अनुपात 5 : 7 है। अब से 4 वर्ष बाद उनकी आयु का अनुपात 3 : 4 हो जाएगा। उनकी वर्तमान आयु ज्ञात कीजिए।
7. एक परिमेय संख्या का हर उसके अंश से 8 अधिक है। यदि अंश में 17 जोड़ दिया जाए तथा हर में से 1 घटा दिया जाए तब हमें 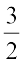 प्राप्त होता है। वह परिमेय संख्या ज्ञात कीजिए।
प्राप्त होता है। वह परिमेय संख्या ज्ञात कीजिए।
हमने क्या चर्चा की?
1. एक बीजीय समीकरण, चरों में एक समता होती है। यह प्रकट करती है कि समता के चिह्न के एक ओर वाले व्यंजक का मान उसके दूसरी ओर वाले व्यंजक के मान के बराबर होता है।
2. कक्षा VI, VII तथा VIII में सीखे जाने वाले समीकरण, एक चर वाले रैखिक समीकरण हैं। इन समीकरणों में, समीकरण बनाने वाले व्यंजकों में एक ही चर प्रयोग होता है। इसके अतिरिक्त, ये समीकरण रैखिक होते हैं अर्थात् प्रयोग किए गए चर की अधिकतम घात 1 होती है।
3. एक रैखिक समीकरण का हल कोई भी परिमेय संख्या हो सकती है।
4. समीकरण के दोनों पक्षों में कोई रैखिक व्यंजक हो सकते हैं। जो समीकरण हमने कक्षा VI तथा VII में सीखे, उनमें किसी एक पक्ष में केवल संख्या ही होती थी।
5. संख्याओं की भाँति ही चरों को भी एक पक्ष से दूसरे पक्ष में पक्षांतरित किया जा सकता है।
6. प्रायः समीकरण बनाने वाले व्यंजकों को, उसे हल करने से पहले, सरल बना लिया जाता है। आरंभ में कुछ समीकरण रैखिक नहीं होते। लेकिन उसके दोनों पक्षों को उपयुक्त व्यंजकों से गुणा कर रैखिक समीकरण के रूप में बदला जा सकता है।
7. रैखिक समीकरणों की उपयोगिता, उनके विविध अनुप्रयोगों में है। संख्याओं, आयु, परिमापों तथा मुद्रा के रूप में प्रयोग होने वाले सिक्के व नोटों पर आधारित अनेक प्रकार की समस्याएँ रैखिक समीकरणों का उपयोग कर हल की जा सकती हैं।
