Table of Contents
आप जानते हैं कि कागज़, समतल का एक प्रतिरूप है। जब आप कागज़ से पेंसिल को हटाए बिना बिंदुओं को आपस में जोड़ते हैं (अकेले बिंदुओं को छोड़कर आकृति के किसी भी भाग को अनुरेखित किए बिना) तो आप एक समतलीय वक्र प्राप्त करते हैं।
पिछली कक्षाओं में अलग-अलग प्रकार के देखे गए वक्रों को स्मरण करने का प्रयास कीजिए।
निम्न आकृतियों का सुमेलन कीजिए: (ध्यान रखिए! एक आकृति का एक से अधिक आकृतियों से सुमेलन हो सकता है।)
| आकृति | नमूना |
(1)  | (a) सरल बंद वक्र है। |
(2)  | (b) बंद वक्र जो सरल नहीं है। |
(3)  | (c) सरल वक्र जो बंद नहीं है। |
(4) 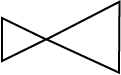 | (d) सरल वक्र नहीं है। |
अपने मित्रों से इस मिलान की तुलना कीजिए, क्या वे सहमत हैं?
3.2 बहुभुज
केवल रेखाखंडों से बना सरल बंद वक्र बहुभुज कहलाता है।


वक्र जो बहुभुज हैं

वक्र जो बहुभुज नहीं हैं
कुछ और बहुभुजों के उदाहरण देने का प्रयास कीजिए तथा कुछ और एेसे उदाहरण दीजिए जो बहुभुज न हों। एक बहुभुज की एक कच्ची (Rough) आकृति खींचिए और उसकी भुजाओं और शीर्षों की पहचान कीजिए।
3.2.1 बहुभुजों का वर्गीकरण
हम बहुभुजों का वर्गीकरण उनकी भुजाओं (या शीर्षों) के अनुसार करते हैं।
| भुजाओं या शीर्षों की संख्या | वर्गीकरण | आकृति नमूना |
| 3 | त्रिभुज |  |
| 4 | चतुर्भुज |  |
| 5 | पंचभुज |  |
| 6 | षड्भुज |  |
| 7 | सप्तभुज |  |
| 8 | अष्टभुज |  |
| 9 | नवभुज |  |
| 10 | दसभुज |  |
 |  |  |
| n | n-भुज |
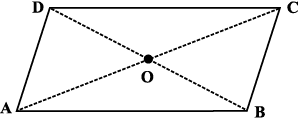
3.2.2 विकर्ण
किसी बहुभुज का विकर्ण उसके किन्हीं दो शीर्षों (आसन्न शीर्षों को छोड़कर) को जोड़ने से प्राप्त रेखाखंड होता है। (आकृति 3.1)
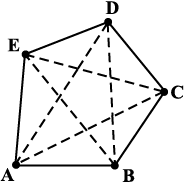
आकृति 3.1


अभ्यंतर आकृति 3.2 बहिर्भाग
अभ्यंतर की एक परिसीमा होती है। क्या बहिर्भाग की परिसीमा होती है? अपने दोस्तों के साथ चर्चा कीजिए।
3.2.3 उत्तल और अवतल बहुभुज
यहाँ पर कुछ उत्तल (convex) बहुभुज और कुछ अवतल (cocave) बहुभुज दिए गए हैं: (आकृति 3.3)
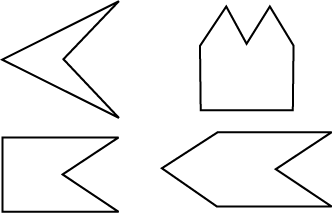
एक सम बहुभुज, समभुज तथा समकोणिक होता है। उदाहरणार्थ, एक वर्ग में भुजाएँ तथा कोण बराबर माप के होते हैं। इसलिए यह एक सम बहुभुज है। एक आयत समकोणिक तो होता है परंतु समभुज नहीं होता है। क्या एक आयत एक सम बहुभुज है? क्या एक समबाहु त्रिभुज एक सम बहुभुज है? क्यों?
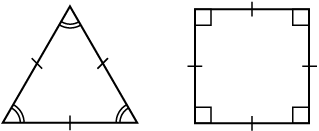
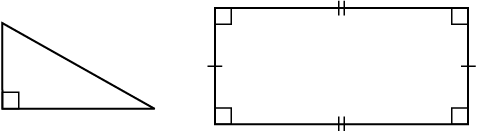
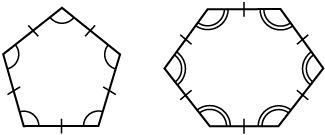
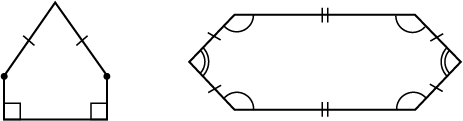
सम बहुभुज (Regular polygons) विषम बहुभुज (Irregular polygons)
[संकेत:  या
या  का उपयोग बराबर लंबाई वाले रेखाखंडों को दर्शाता है]
का उपयोग बराबर लंबाई वाले रेखाखंडों को दर्शाता है]
पिछली कक्षाओं में, क्या आप किसी एेसे चतुर्भुज के बारे में पढ़ा है जो समभुज तो हो परंतु समकोणिक न हो? पिछली कक्षाओं में देखे गए चतुर्भुजों की आकृतियों का स्मरण कीजिए जैसे आयत, वर्ग, सम चतुर्भुज इत्यादि।
क्या कोई एेसा त्रिभुज है जो समभुज तो हो परंतु समकोणिक न हो?
3.2.5 कोण-योग गुणधर्म
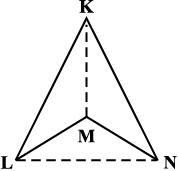
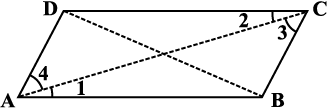
1. कोई एक चतुर्भुज, माना ABCD, लीजिए (आकृति 3.4)। एक विकर्ण खींचकर, इसे दो त्रिभुजों में बाँटिए। आप छ: कोण 1, 2, 3, 4, 5 और 6 प्राप्त करते हैं।
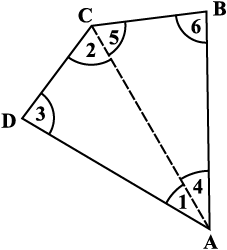
आकृति 3.4
त्रिभुज के कोण-योग वाले गुणधर्म का उपयोग कीजिए और तर्क कीजिए कि कैसे ∠A, ∠B, ∠C तथा ∠D के मापों का योगफल 180° + 180° = 360° हो जाता है।
2. किसी चतुर्भुज ABCD, की गत्ते वाली चार सर्वांगसम प्रतिलिपियाँ लीजिए जिनके कोण दर्शाए गए हैं (आकृति 3.5 (i)). इन प्रतिलिपियों को इस प्रकार से व्यवस्थित कीजिए जिससे ∠1, ∠2, ∠3, ∠4 एक ही बिंदु पर मिलें जैसा कि आकृति में दर्शाया गया है (आकृति 3.5 (ii))।
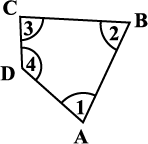
(i)
(ii)
आकृति 3.5
आप ∠1, ∠2, ∠3 तथा ∠4 के योगफल के बारे में क्या कह सकते हैं?
[टिप्पणी : हम कोणों को ∠1, ∠2, ∠3 इत्यादि से तथा उनकी मापों को m∠1, m∠2, m∠3 इत्यादि से दर्शाते हैं]
आप इस परिणाम पर अन्य कई तरीकों से भी पहुँच सकते हैं।
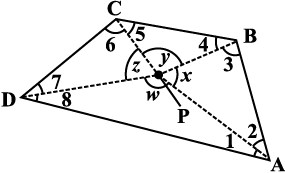
आकृति 3.6
3. चतुर्भुज ABCD पर पुन: विचार कीजिए (आकृति 3.6)। माना इसके अभ्यंतर में कोई बिंदु P स्थित है। P को शीर्षों A, B, C तथा D से जोड़िए। आकृति में, ∆PAB पर विचार कीजिए। हम देखते हैं कि x = 180° – m∠2 – m∠3; इसी प्रकार, ∆PBC, से y = 180° – m ∠4 – m∠5, ∆PCD से z = 180º – m∠6 – m∠7 और ∆PDA, w = 180º – m∠8 – m∠1 इसका उपयोग करके कुल माप m∠1 + m∠2 + ... + m∠8, ज्ञात कीजिए। क्या यह आप को परिणाम तक पहुँचाने में सहायता करता है? याद रखिए, ∠x + ∠y + ∠z + ∠w = 360° है।
आकृति 3.7
प्रश्नावली 3.1


(i) (ii) (iii) (iv)
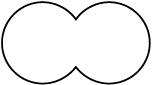

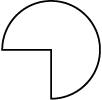
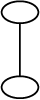
(v) (vi) (vii) (viii)
प्रत्येक का वर्गीकरण निम्नलिखित आधार पर कीजिए:
(a) साधारण वक्र (b) साधारण बंद वक्र (c) बहुभुज
(d) उत्तल बहुभुज (e) अवतल बहुभुज
2. निम्नलिखित प्रत्येक में कितने विकर्ण हैं?
(a) एक उत्तल चतुर्भुज (b) एक समषड्भुज (c) एक त्रिभुज
3. उत्तल चतुर्भुज के कोणों के मापों का योगफल क्या है? यदि चतुर्भुज, उत्तल न हो तो क्या यह गुण लागू होगा? (एक चतुर्भुज बनाइए जो उत्तल न हो और प्रयास कीजिए।)
4. तालिका की जाँच कीजिए: (प्रत्येक आकृति को त्रिभुजों में बाँटिए और कोणों का योगफल ज्ञात कीजिए)
| आकृति | 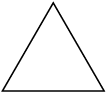 | 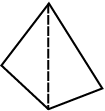 | 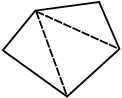 | 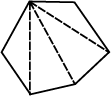 |
| भुजा | 3 | 4 | 5 | 6 |
| कोणों का योगफल | 180º | 2 × 180° = (4 – 2) × 180° | 3 × 180° = (5 – 2) × 180° | 4 × 180° = (6 – 2) × 180° |
एक बहुभुज के कोणों के योग के बारे में आप क्या कह सकते हैं जिसकी भुजाओं की संख्या निम्नलिखित हो?
(a) 7 (b) 8 (c) 10 (d) n
5. सम बहुभुज क्या है?
एक सम बहुभुज का नाम बताइए जिसमें
(i) 3 भुजाएँ (ii) 4 भुजाएँ (iii) 6 भुजाएँ हों।
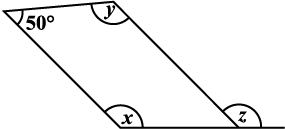
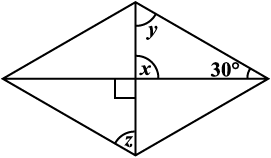
6. निम्नलिखित आकृतियों में x (कोण की माप) ज्ञात कीजिए:
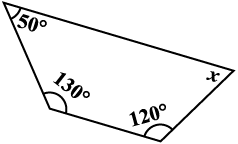
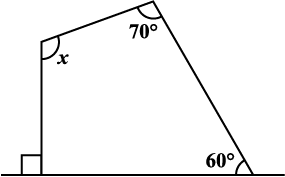
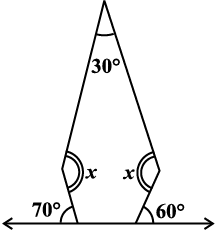
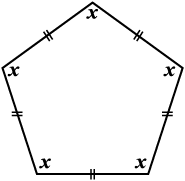
7.
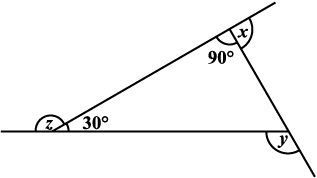
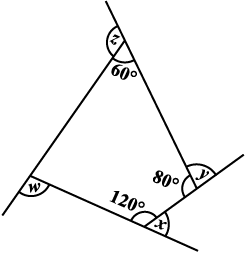
(b) x + y + z + w ज्ञात कीजिए।
3.3 एक बहुभुज के बाह्य कोणों की मापों का योग
कई अवसरों पर बाह्य कोणों की जानकारी अंत: कोणों और भुजाओं की प्रकृति पर प्रकाश डालती है।
इन्हें कीजिए
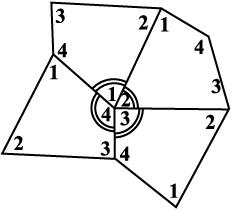
एक चॉक के टुकड़े से फर्श पर एक बहुभुज बनाइए। (आकृति में, एक पंचभुज ABCDE दर्शाया गया है ) (आकृति 3.8)। हम सभी कोणों के मापों का योग जानना चाहते हैं, अर्थात् m∠1 + m∠2 + m∠3 + m∠4 + m∠5 है। A से आरंभ कीजिए और  के अनुदिश चलिए। B पर पहुँचने के उपरांत, आपको कोण m∠1 पर घूमने की आवश्यकता है जिससे आप
के अनुदिश चलिए। B पर पहुँचने के उपरांत, आपको कोण m∠1 पर घूमने की आवश्यकता है जिससे आप  के अनुदिश चल सकें। C पर पहुँचने के उपरांत,
के अनुदिश चल सकें। C पर पहुँचने के उपरांत,  के अनुदिश चलने के लिए आपको m∠2 पर घूमने की आवश्यकता है। आप इसी तरीके से चलना जारी रखें जब तक आप A पर नहीं पहुँच जाते। वास्तव में, इस तरह से आपने एक पूरा चक्कर घूम लिया है।
के अनुदिश चलने के लिए आपको m∠2 पर घूमने की आवश्यकता है। आप इसी तरीके से चलना जारी रखें जब तक आप A पर नहीं पहुँच जाते। वास्तव में, इस तरह से आपने एक पूरा चक्कर घूम लिया है।
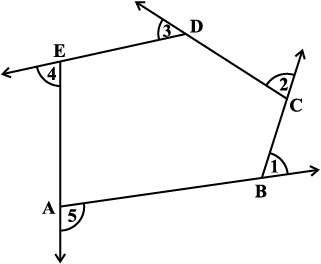
आकृति 3.8
इसलिए, m∠1 + m∠2 + m∠3 + m∠4 + m∠5 = 360° है।
एक बहुभुज की चाहे कितनी भी भुजाएँ हों उन सबके लिए यह सही है।
अत: किसी बहुभुज के बाह्य कोणों के मापों का योग 360° होता है।
उदाहरण 1 : आकृति 3.9 में माप x ज्ञात कीजिए।
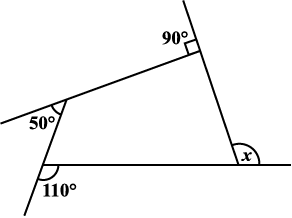
आकृति 3.9
हल : x + 90° + 50° + 110° = 360° (क्यों ?)
x + 250° = 360°
x = 110°
प्रयास कीजिए
एक सम षड्भुज लीजिए (आकृति 3.10)।
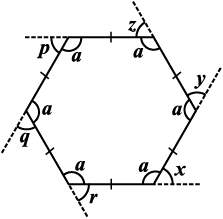
(i) बाह्य कोणों x, y, z, p, q तथा r के मापों का योग क्या है?
(ii) क्या x = y = z = p = q = r है? क्यों?
(iii) प्रत्येक का माप क्या है?
(i) बाह्य कोण (ii) अंत: कोण
(iv) इस क्रियाकलाप को निम्नलिखित के लिए दोहराएँ
(i) एक सम अष्टभुज (ii) एक सम 20 भुज
उदाहरण 2 : एक सम बहुभुज की भुजाओं की संख्या ज्ञात कीजिए जिसके प्रत्येक बाह्य कोण का माप 45° है।
हल : सभी बाह्य कोणों की कुल माप = 360°
प्रत्येक बाह्य कोण का माप = 45°
इसलिए, बाह्य कोणों की संख्या = 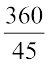 = 8
= 8
अत: बहुभुज की 8 भुजाएँ हैं।
प्रश्नावली 3.2
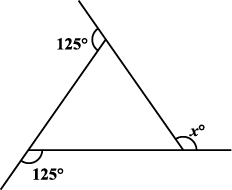
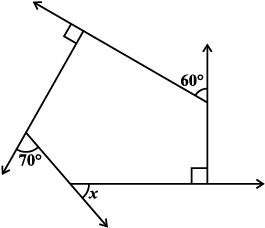
1. निम्नलिखित आकृतियों में x का मान ज्ञात कीजिए:
2. एक सम बहुभुज के प्रत्येक बाह्य कोण का माप ज्ञात कीजिए जिसकी
(i) 9 भुजाएँ (ii) 15 भुजाएँ हों।
3. एक सम बहुभुज की कितनी भुजाएँ हाेंगी यदि एक बाह्य कोण का माप 24° हो?
4. एक सम बहुभुज की भुजाओं की संख्या ज्ञात कीजिए यदि इसका प्रत्येक अंत:कोण 165° का हो?
5. (a) क्या एेसा सम बहुभुज संभव है जिसके प्रत्येक बाह्य कोण का माप 22° हो?
(b) क्या यह किसी सम बहुभुज का अंत:कोण हो सकता है? क्यों?
6. (a) किसी सम बहुभुज में कम से कम कितने अंश का अंत:कोण संभव है? क्यों?
3.4 चतुर्भुजों के प्रकार
एक चतुर्भुज की भुजाओं व कोणों की प्रकृति के आधार पर इसे विशेष नाम दिए जाते हैं।
3.4.1 समलंब
समलंब एक एेसा चतुर्भुज होता है जिसमें भुजाओं का एक युग्म समांतर होता है।
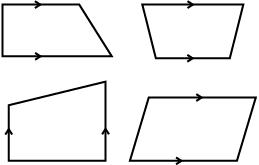
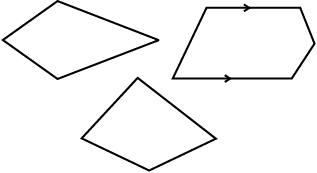
ये समलंब हैं ये समलंब नहीं हैं
उपरोक्त आकृतियों का अध्ययन कीजिए और अपने मित्रों के साथ चर्चा कीजिए कि क्यों इनमें से कुछ समलंब हैं और कुछ समलंब नहीं हैं। (संकेत: तीर का निशान समांतर रेखाओं को दर्शाता है।)
इन्हें कीजिए
1. समान सर्वांगसम त्रिभुजों के कटे हुए भाग लीजिए जिनकी भुजाएँ 3 cm, 4 cm, 5 cm हैं। इन्हें व्यवस्थित कीजिए जैसा कि आकृति में दर्शाया गया है (आकृति 3.11)।
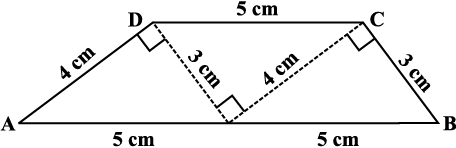
आकृति 3.11
आपको एक समलंब प्राप्त होता है। (निरीक्षण कीजिए)
यहाँ पर कौन सी भुजाएँ समांतर हैं? क्या असमांतर भुजाएँं बराबर माप की होनी चाहिए?
इन समान त्रिभुजों के समूह का उपयोग कर आप दो और समलंब प्राप्त कर सकते हैं। उनको ढूँढिए और उनकी आकृतियों की चर्चा कीजिए।
2. अपने तथा अपने मित्रों के ज्यामितीय बॉक्स से चार सेटस्क्वेयर लीजिए। इन्हें अलग-अलगसंख्याओं में उपयोग कर साथ-साथ रखिए और अलग-अलग किस्म के समलंब प्राप्त कीजिए।
यदि समलंब की असमांतर भुजाएँ बराबर लंबाई की हों तो हम इसे समद्विबाहु समलंब कहते हैं।
क्या आपने ऊपर किए गए अपने किसी निरीक्षण में कोई समद्विबाहु समलंब प्राप्त किया है?
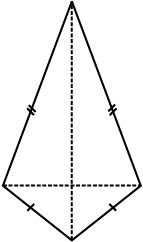
3.4.2 पतंग
पतंग विशिष्ट प्रकार का एक चतुर्भुज है। प्रत्येक आकृति में एक जैसे चिह्न बराबर भुजाओं को दर्शाते हैं। उदाहरणार्थ AB = AD और BC = CD
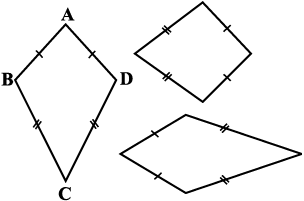
ये पतंग हैं ये पतंग नहीं हैं
इन आकृतियों का अध्ययन कीजिए और यह बताने का प्रयास कीजिए कि पतंग क्या है। निरीक्षण कीजिए कि:
(i) एक पतंग में 4 भुजाएँ होती हैं (यह एक चतुर्भुज है)।
(ii) इसमें अलग-अलग आसन्न भुजाओं के दो युग्म होते हैं जिनकी लंबाई बराबर होती है। जाँच कीजिए कि क्या वर्ग एक पतंग है।
इन्हें कीजिए
एक मोटे कागज़ की शीट लीजिए।
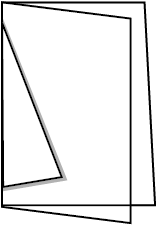
आकृति 3.12
इसे दोहरा मोड़िए।
दो अलग-अलग लंबाई वाले रेखाखंडों को खींचिए जैसाकि आकृति 3.12 में दर्शाया गया है।
इन रेखाखंडों के अनुदिश काटकर खोलिए।
आपको एक पतंग की आकृति प्राप्त होती है (आकृति 3.13)।
क्या पतंग में कोई सममित रेखा है?
पतंग को दोनों विकर्णों पर मोड़िए। सेट-स्क्वेयर के उपयोग से जाँचिए कि क्या वे एक दूसरे को समकोण पर काटते हैं। क्या विकर्ण बराबर लंबाई के हैं?
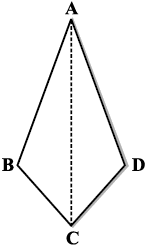
आकृति 3.13
जाँचिए (पेपर को मोड़ने या मापने द्वारा) कि क्या विकर्ण एक दूसरे को समद्विभाजित करते हैं?
पतंग के एक कोण को एक विकर्ण के अनुदिश विपरीत मोड़ने पर, बराबर माप वाले कोणों को जाँचिए।
अपनी जानकारी को साथियों में बाँटिए और उनकी सूची बनाइए। इन परिणामों का सारांश अध्याय में कहीं पर आपके लिए दिया गया है।
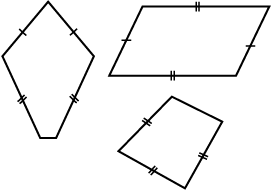
समांतर चतुर्भुज एक चतुर्भुज ही है। जैसा कि नाम संकेत करता है इसका संबंध समांतर रेखाओं से है।
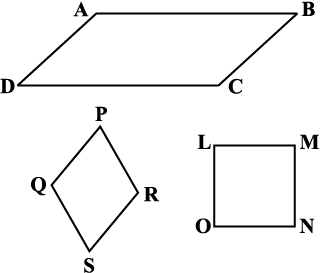
ये समांतर चतुर्भुज हैं ये समांतर चतुर्भुज नहीं हैं
इन आकृतियों का अध्ययन कीजिए और अपने शब्दों में बताने का प्रयास कीजिए कि समांतर चतुर्भुज क्या है। अपने निष्कर्ष अपने मित्रों के साथ बाँटिए।
जाँच कीजिए कि क्या आयत एक समांतर चतुर्भुज है।
इन्हें कीजिए
दो अलग-अलग चौड़ाई वाली गत्ते की आयताकार पट्टियाँ लीजिए (आकृति 3.14)।


पट्टी 1 आकृति 3.14 पट्टी 2
एक गत्ते की पट्टी को समतल पर रखिए और इसके किनारों के अनुदिश रेखाएँ खींचिए जैसा कि आकृति में दर्शाया गया है (आकृति 3.15)।

आकृति 3.15
अब दूसरी पट्टी को खींची गई रेखाओं के ऊपर तिरछी दिशा में रखिए और इसका उपयोग करते हुए दो और रेखाओं को खींचिए जैसा कि आकृति में दर्शाया गया है (आकृति 3.16)।
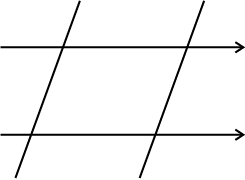
आकृति 3.16
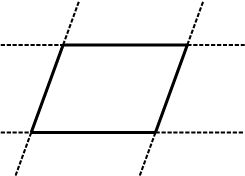
आकृति 3.17
इन चार रेखाओं से बनी बंद आकृति चतुर्भुज है (आकृति 3.17)।
यह समांतर रेखाओं के दो युग्मों से मिलकर बनी है। यह एक समांतर चतुर्भुज है।
समांतर चतुर्भुज एक चतुर्भुज होता है जिसकी सम्मुख भुजाएँ समांतर होती हैं।
3.4.4 समांतर चतुर्भुज के अवयव
एक समांतर चतुर्भुज में चार भुजाएँ और चार कोण होते हैं। इनमें से कुछ बराबर माप के होते हैं। आपको इन अवयवों से संबंधित कुछ तथ्यों को याद रखने की आवश्यकता है।

आकृति 3.18
एक समांतर चतुर्भुज ABCD दिया गया है (आकृति 3.18)।
 और
और  , इसकी सम्मुख भुजाएँ हैं।
, इसकी सम्मुख भुजाएँ हैं।  तथा
तथा  सम्मुख भुजाओं का दूसरा युग्म बनाते हैं।
सम्मुख भुजाओं का दूसरा युग्म बनाते हैं।
∠A और ∠C सम्मुख कोणों का एक युग्म है और इसी प्रकार ∠B तथा ∠D सम्मुख कोणों का एक दूसरा युग्म है।
 और
और  समांतर चतुर्भुज की आसन्न भुजाएँ हैं। अर्थात् जहाँ पर एक भुजा समाप्त होती है वहीं से दूसरी भुजा प्रारंभ होती है। क्या
समांतर चतुर्भुज की आसन्न भुजाएँ हैं। अर्थात् जहाँ पर एक भुजा समाप्त होती है वहीं से दूसरी भुजा प्रारंभ होती है। क्या  और
और  भी आसन्न भुजाएँ हैं? दो और आसन्न भुजाओं के युग्मों को ढूँढने का प्रयास कीजिए।
भी आसन्न भुजाएँ हैं? दो और आसन्न भुजाओं के युग्मों को ढूँढने का प्रयास कीजिए।
∠A और ∠B समांतर चतुर्भुज के आसन्न कोण हैं। दोनों ही कोण उभयनिष्ठ भुजा के अंत बिंदुओं पर बने हैं। ∠B तथा ∠C भी आसन्न कोण हैं। समांतर चतुर्भुज के आसन्न कोणों के दूसरे युग्मों की पहचान कीजिए।
इन्हें कीजिए
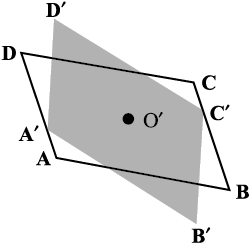
दो समान समांतर चतुर्भुजों के कटे हुए भाग ABCD तथा A′B′C′D′ लीजिए (आकृति 3.19).


आकृति 3.19
यहाँ पर भुजा  , भुजा
, भुजा 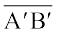 के समान है परंतु इनके नाम अलग-अलग हैं। इसी प्रकार, दूसरी संगत भुजाएँ भी समान हैं।
के समान है परंतु इनके नाम अलग-अलग हैं। इसी प्रकार, दूसरी संगत भुजाएँ भी समान हैं।
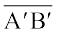 को
को  के ऊपर रखिए। क्या वे एक दूसरे को पूर्णतया ढकती हैं? अब आप
के ऊपर रखिए। क्या वे एक दूसरे को पूर्णतया ढकती हैं? अब आप
 तथा
तथा  की लंबाई के बारे में क्या कह सकते हैं?
की लंबाई के बारे में क्या कह सकते हैं?
इसी प्रकार  तथा
तथा  की लंबाई की जाँच कीजिए। आप क्या पाते हैं?
की लंबाई की जाँच कीजिए। आप क्या पाते हैं?
आप  तथा
तथा  को माप कर इस परिणाम पर पहुँच सकते हैं।
को माप कर इस परिणाम पर पहुँच सकते हैं।
गुण: समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर माप की होती हैं।
प्रयास कीजिए
आकृति 3.20
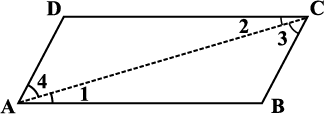
आप तर्क-वितर्क के द्वारा इस अवधारणा को प्रभावी बना सकते हैं। एक समांतर चतुर्भुज ABCD पर विचार कीजिए (आकृति 3.21)। एक विकर्ण, 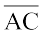 खींचिए।
खींचिए।
आकृति 3.21
हम देखते हैं कि ∠1 = ∠2 और ∠3 = ∠4 (क्यों?)
क्योंकि त्रिभुज ABC और ADC में ∠1 = ∠2, ∠3 = ∠4 और  उभयनिष्ठ है इसलिए, ASA सर्वांगसमता कसौटी द्वारा
उभयनिष्ठ है इसलिए, ASA सर्वांगसमता कसौटी द्वारा
∆ ABC ≅ ∆ CDA (यहाँ ASA कसौटी कैसे प्रयोग हुई?)
अत: AB = DC और BC = AD.
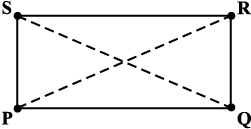
उदाहरण 3 : समांतर चतुर्भुज PQRS का परिमाप ज्ञात कीजिए (आकृति 3.22)
हल : समांतर चतुर्भुज में, सम्मुख भुजाएँ बराबर लंबाई की होती हैं।
इसलिए, PQ = SR = 12 cm और QR = PS = 7 cm
अत: परिमाप = PQ + QR + RS + SP
= 12 cm + 7 cm + 12 cm + 7 cm = 38 cm
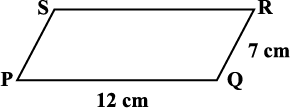
आकृति 3.22
3.4.5 समांतर चतुर्भुज के कोण
हमने समांतर चतुर्भुज की सम्मुख भुजाओं से संबंधित एक गुण का अध्ययन किया। हम कोणों के बारे में क्या कह सकते हैं?
इन्हें कीजिए
माना ABCD एक समांतर चतुर्भुज है (आकृति 3.23)। ट्रेसिंग शीट पर इसकी प्रतिलिपि बनाइए। इस प्रतिलिपि को A′B′C′D′ से प्रदर्शित कीजिए। A′B′C′D′ को ABCD पर आच्छादित कीजिए। दोनों चतुर्भुजों को आपस में मिलाकर उस बिंदु पर पिन लगाइए जहाँ पर उनके विकर्ण प्रतिच्छेद करते हाें, ट्रेसिंग शीट को 180° घुमाइए। समांतर चतुर्भुज अभी भी एक दूसरे को पूर्णतया ढक लेते हैं; परंतु अब आप देखते हैं कि A′ पूर्ण रूप से C पर और C पूर्ण रूप से B′ पर आ जाता है। इसी प्रकार B′ बिंदु D पर जाता है और विलोम रूप से भी सत्य है।
आकृति 3.23
क्या यह कोण A तथा कोण C के मापों के बारे में आपको कुछ बताता है? कोण B तथा D के मापों के लिए जाँच कीजिए। अपने निष्कर्ष की चर्चा कीजिए।
गुण : समांतर चतुर्भुज के सम्मुख कोण बराबर माप के होते हैं।
प्रयास कीजिए
30° – 60° – 90° कोणों वाले दो समान सेट-स्क्वेयर लेकर पहले की तरह ही एक समांतर चतुर्भुज बनाइए। क्या प्राप्त आकृति ऊपर बताए गए गुण की पुष्टि करने में आपकी सहायता करती है?
यदि  और
और  समांतर चतुर्भुज के विकर्ण हाें (आकृति 3.24) तो आप देखेंगे कि
समांतर चतुर्भुज के विकर्ण हाें (आकृति 3.24) तो आप देखेंगे कि
∠1 =∠2 और ∠3 = ∠4 (क्यों?)
आकृति 3.24
∆ ABC तथा ∆ ADC का अलग-अलग अध्ययन करने पर आप देखेंगे कि (आकृति 3.25) ASA सर्वांगसम कसौटी के द्वारा
∆ ABC ≅ ∆ CDA (कैसे?)
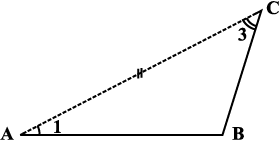
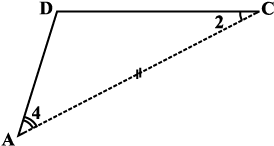
आकृति 3.25
यह दर्शाता है कि ∠B और ∠D समान माप के हैं। इस प्रकार आप प्राप्त करते हैं
m∠A = m∠C
उदाहरण 4 : आकृति 3.26 में BEST एक समांतर चतुर्भुज है। x, y तथा z के मान ज्ञात कीजिए।
हल : बिंदु S, बिंदु B के विपरीत है।
अत: x = 100° (सम्मुख कोण गुण)
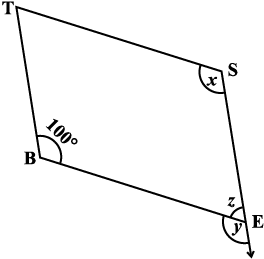
आकृति 3.26
y = 100° (∠x के संगत कोण का माप)
अब हम अपना ध्यान एक समांतर चतुर्भुज के आसन्न कोणों पर केंद्रित करते हैं।
समांतर चतुर्भुज ABCD में (आकृति 3.27) ∠A और ∠D संपूरक कोण हैं,

आकृति 3.27
क्योंकि  और
और  , एक तिर्यक रेखा है। अत: दोनाें कोण अंत: सम्मुख कोण हैं।
, एक तिर्यक रेखा है। अत: दोनाें कोण अंत: सम्मुख कोण हैं।
∠A और ∠B भी संपूरक कोण हैं। क्या आप बता सकते हैं ‘क्याें’?
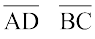 और
और  एक तिर्यक रेखा है जो ∠A तथा ∠B को अंत: सम्मुख कोण बनाती है। आकृति से दो और संपूरक कोणों के युग्मों की पहचान कीजिए।
एक तिर्यक रेखा है जो ∠A तथा ∠B को अंत: सम्मुख कोण बनाती है। आकृति से दो और संपूरक कोणों के युग्मों की पहचान कीजिए।
गुण: समांतर चतुर्भुज के आसन्न कोण संपूरक होते हैं।
उदाहरण 5 : समांतर चतुर्भुज RING में ( आकृति 3.28) यदि m∠R = 70° हो तो दूसरे सभी कोण ज्ञात कीजिए।
हल : दिया है m∠R = 70°

आकृति 3.28
क्योंकि ∠R तथा ∠I संपूरक कोण हैं
m∠I = 180° – 70° = 110°
और m∠G = 110° क्योंकि ∠G, ∠I का सम्मुख कोण है।
अत: m∠R = m∠N = 70° और m∠I = m∠G = 110°
सोचिए, चर्चा कीजिए और लिखिए
m∠R = m∠N = 70°, दर्शाने के उपरांत क्या आप किसी अन्य विधि से m∠I और m∠G को ज्ञात कर सकते हैं?
3.4.6 समांतर चतुर्भुज के विकर्ण
साधारणतया समांतर चतुर्भुज के विकर्ण बराबर माप के नहीं होते।
(क्या आपने अपने पूर्व क्रियाकलाप में इसे जाँचा?)
यद्यपि समांतर चतुर्भुज के विकर्णों में एक रोचक गुण होता है।
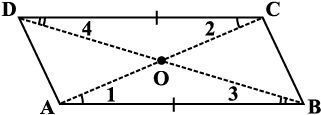
समांतर चतुर्भुज, (मान लीजिए ABCD,) का एक कटा हुआ भाग लीजिए (आकृति 3.29)। माना इसके विकर्ण 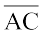 तथा
तथा  एक दूसरे को 'O' पर प्रतिच्छेद करते हैं।
एक दूसरे को 'O' पर प्रतिच्छेद करते हैं।
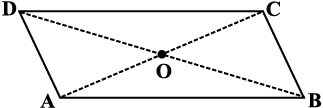
आकृति 3.29
C को A पर रखकर एक तह (Fold) के द्वारा 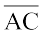 का मध्य बिंदु ज्ञात कीजिए। क्या मध्य बिंदु O ही है? क्या यह दर्शाता है कि विकर्ण
का मध्य बिंदु ज्ञात कीजिए। क्या मध्य बिंदु O ही है? क्या यह दर्शाता है कि विकर्ण  , विकर्ण
, विकर्ण  को बिंदु 'O' पर समद्विभाजित करता है? अपने मित्रों के साथ इसकी चर्चा कीजिए। इस क्रियाकलाप को यह ज्ञात करने के लिए दोहराएँ कि
को बिंदु 'O' पर समद्विभाजित करता है? अपने मित्रों के साथ इसकी चर्चा कीजिए। इस क्रियाकलाप को यह ज्ञात करने के लिए दोहराएँ कि  का मध्य बिंदु कहाँ पर स्थित होगा।
का मध्य बिंदु कहाँ पर स्थित होगा।
गुण: समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं। (अवश्य ही उनके प्रतिच्छेदी बिंदु पर।)
आकृति 3.30
इस गुण का तर्क-वितर्क तथा पुष्टि करना मुश्किल नहीं है। आकृति 3.30 से, ASA सर्वांगसमता प्रतिबंध द्वारा बड़ी आसानी से देखा जा सकता है कि
∆ AOB ≅ ∆ COD (यहाँ पर ASA प्रतिबंध का कैसे प्रयोग हुआ ?)
अत: AO = CO तथा BO = DO
उदाहरण 6 : आकृति 3.31 में, HELP एक समांतर चतुर्भुज है। दिया है (लंबाई cm में है):
OE = 4 और HL, PE से 5 अधिक है। OH ज्ञात कीजिए।
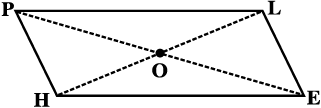
आकृति 3.31
हल : यदि OE = 4 तब OP = 4 (क्यों?)
अत: PE = 8, (क्यों?)
इसलिए HL = 8 + 5 = 13
अत: OH = 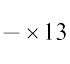 = 6.5 cm
= 6.5 cm
इन्हें कीजिए
1. ABCD एक समांतर चतुर्भुज है। प्रत्येक कथन को परिभाषा या प्रयोग किए गए गुण द्वारा पूरा कीजिए:
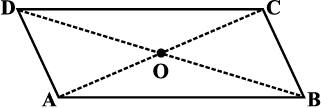
(i) AD = ...... (ii) ∠ DCB = ......
(iii) OC = ...... (iv) m ∠DAB + m ∠CDA = ......
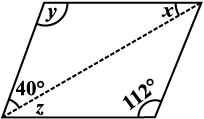
2. निम्न समांतर चतुर्भुजों में अज्ञात x, y, z के मानों को ज्ञात कीजिए:

(i) (ii)

(iii) (iv) (v)
(iii) ∠A = 70° और ∠C = 65°?
4. एक चतुर्भुज की कच्ची (Rough) आकृति खींचिए जो समांतर चतुर्भुज न हो परंतु जिसके दो सम्मुख कोणों के माप बराबर हों।
5. किसी समांतर चतुर्भुज के दो आसन्न कोणों का अनुपात 3: 2 है। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
6. किसी समांतर चतुर्भुज के दो आसन्न कोणों के माप बराबर हैं। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
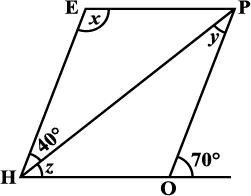
7. संलग्न आकृति HOPE एक समांतर चतुर्भुज है। x, y और z कोणों की माप ज्ञात कीजिए। ज्ञात करने में प्रयोग किए गए गुणों को बताइए।
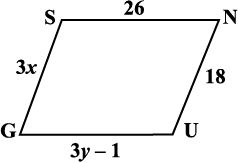
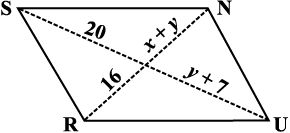
8. निम्न आकृतियाँ GUNS और RUNS समांतर चतुर्भुज हैं। x तथा y ज्ञात कीजिए (लंबाई cm में है):
(ii)
9. दी गई आकृति में RISK तथा CLUE दोनों समांतर चतुर्भुज हैं, x का मान ज्ञात कीजिए।
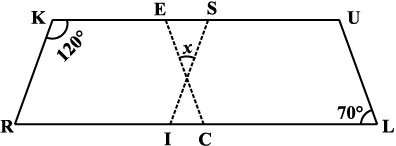
10. बताइए कैसे यह आकृति एक समलंब है। इसकी कौन सी दो भुजाएँ समांतर हैं?
(आकृति 3.32)
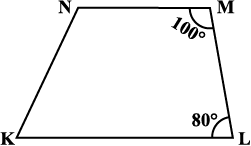
आकृति 3.32
11. आकृति 3.33 में m∠C ज्ञात कीजिए यदि 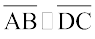 है।
है।
आकृति 3.33
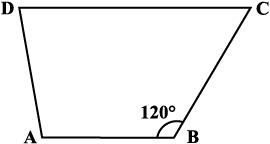
12. आकृति 3.34 में ∠P तथा ∠S की माप ज्ञात कीजिए यदि  है। (यदि आप m∠R, ज्ञात करते हैं, तो क्या m∠P को ज्ञात करने की एक से अधिक विधि है?)
है। (यदि आप m∠R, ज्ञात करते हैं, तो क्या m∠P को ज्ञात करने की एक से अधिक विधि है?)
आकृति 3.34
3.5 कुछ विशिष्ट समांतर चतुर्भुज
3.5.1 समचतुर्भुज
पतंग (जो कि एक समांतर चतुर्भुज नहीं है) की विशेष स्थिति के रूप में हमें एक समचतुर्भुज (Rhombus) जो एक समांतर चतुर्भुज भी है, प्राप्त होता है।
इन्हें कीजिए
आपके द्वारा कागज़ से काटकर पहले बनाई गई पतंग का स्मरण करें।
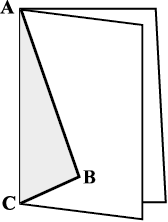
पतंग-काट (Kite-cut) समचतुर्भुज-काट (Rhombus-cut)
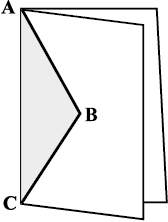
जब आप ABC के अनुदिश काटकर खोलते हैं तो आप एक पतंग प्राप्त करते हैं। यहाँ पर लंबाई AB और BC अलग-अलग थीं। यदि आप AB = BC खींचते हैं तो प्राप्त की गई पतंग एक समचतुर्भुज कहलाता है।
पतंग
सम चतुर्भुज
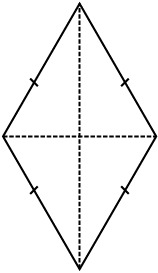
समचतुर्भुज एक चतुर्भुज है जिसकी सभी भुजाएँ बराबर लंबाई की होती हैं।
गुण : एक समचतुर्भुज के विकर्ण परस्पर लंब समद्विभाजक होते हैं।
इन्हें कीजिए
तर्क-पूर्ण चरणों का उपयोग कर यहाँ एक खाका दिया गया है जो इस गुण की पुष्टि करता है।
ABCD एक समचतुर्भुज है (आकृति 3.35)। अत: यह एक समांतर चतुर्भुज भी है।
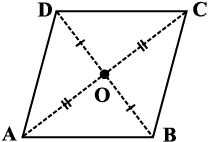
आकृति 3.35
चूँकि विकर्ण एक दूसरे को समद्विभाजित करते हैं,
अत: OA = OC और OB = OD
चूँकि AO = CO (क्यों?)
AD = CD (क्यों?)
OD = OD
हमें यह दर्शाना है कि m∠AOD = m∠COD = 90° है।
SSS सर्वांगसमता प्रतिबंध से यह देखा जा सकता है कि
∆ AOD ≅ ∆ COD
अत: m ∠AOD = m ∠COD
क्योंकि ∠AOD और ∠COD रैखिक युग्म बनाते हैं,
उदाहरण 7 :
RICE एक समचतुर्भुज है (आकृति 3.36)। x, y, तथा z का
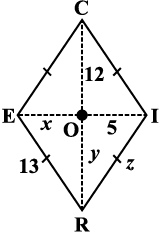
आकृति 3.36
मान ज्ञात कीजिए और अपने उत्तर की पुष्टि कीजिए।
हल :
x = OE y = OR z = समचतुर्भुज की भुजा
= OI (विकर्ण = OC (विकर्ण = 13 (समचतुर्भुज की सभी
समद्विभाजित करते हैं) समद्विभाजित करते है ) भुजाएँ बराबर माप की होती हैं)
3.5.2 एक आयत
आयत एक समांतर चतुर्भुज है जिसके सभी कोण समान माप के होते हैं (आकृति 3.37)।

आकृति 3.37
इस परिभाषा का पूर्ण अर्थ क्या है? इसकी चर्चा अपने मित्रों के साथ कीजिए। यदि आयत समकोणिक हो तो प्रत्येक कोण की माप क्या होगी? माना प्रत्येक कोण का माप x° होगी।
तब 4x° = 360° (क्यों )?
अत: आयत का प्रत्येक कोण समकोण होता है।
अत: एक आयत समांतर चतुर्भुज होता है जिसमें प्रत्येक कोण समकोण होता है।

आकृति 3.37
एक समांतर चतुर्भुज होने के कारण आयत की सम्मुख भुजाएँ बराबर लंबाई की होती हैं और विकर्ण एक दूसरे को समद्विभाजित करते हैं। समांतर चतुर्भुज में विकर्ण अलग-अलग लंबाई के हो सकते हैं (जाँच कीजिए) : परंतु आयत (विशेष स्थिति में) के विकर्ण बराबर माप (लंबाई) के होते हैं।
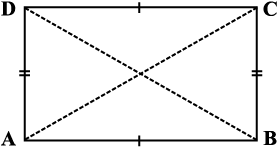
आकृति 3.38
आकृति 3.39
आकृति 3.40
गुण : आयत के विकर्ण बराबर लंबाई के होते हैं।
∆ ABC ≅ ∆ ABD
क्योंकि AB = AB (उभयनिष्ठ)
BC = AD (क्यों?)
m ∠A = m ∠B = 90° (क्यों?)
SAS प्रतिबंध से सर्वांगसमता होती है।
और एक आयत में विकर्ण बराबर लंबाई के होने के अतिरिक्त एक दूसरे को समद्विभाजित करते हैं। (क्यों?)
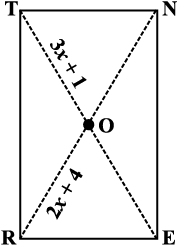
उदाहरण 8 : RENT एक आयत है (आकृति 3.41)। इसके विकर्ण एक दूसरे को 'O' पर प्रतिच्छेद करते हैं। x, का मान ज्ञात कीजिए यदि OR = 2x + 4 और OT = 3x + 1 हैं।
हल :  , विकर्ण
, विकर्ण  का आधा है।
का आधा है।  , विकर्ण
, विकर्ण  का आधा है।
का आधा है।
यहाँ पर विकर्ण बराबर लंबाई के हैं। (क्यों?) अत: उनके आधे भी आपस में बराबर हैं।
इसलिए 3x + 1 = 2x + 4
अर्थात् x = 3
3.5.3 वर्ग
वर्ग एक आयत होता है जिसकी भुजाएँ बराबर होती हैं।
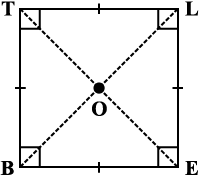
BELT एक वर्ग है जिसमें,
BE = EL = LT = TB
∠B, ∠E, ∠L तथा ∠T समकोण हैं।
BL = ET और
OB = OL और OE = OT
इसका मतलब यह है कि एक वर्ग में एक आयत के सभी गुण होने के साथ-साथ एक अतिरिक्त गुण भी होता है कि इसकी भुजाएँ बराबर लंबाई की होती हैं।
वर्ग के विकर्ण, आयत के विकर्णों की तरह ही, बराबर लंबाई के होते हैं।
एक आयत में विकर्णों का एक दूसरे पर लंब होना आवश्यक
नहीं होता है (जाँचिए)। किसी वर्ग में विकर्ण
(i) एक दूसरे को समद्विभाजित करते हैं (वर्ग एक समांतर चतुर्भुज है)।
(ii) बराबर लंबाई के होते हैं। (वर्ग एक आयत है।) और
(iii) एक दूसरे को समकोण पर समद्विभाजित करते हैं।
इस प्रकार, हमें निम्नलिखित गुणधर्म प्राप्त होता है।
आकृति 3.41
गुण : वर्ग के विकर्ण एक दूसरे को समकोण पर समद्विभाजित करते हैं।
इन्हें कीजिए
एक वर्गाकार शीट, माना PQRS लीजिए (आकृति 3.42)।
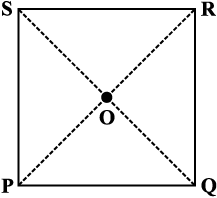
आकृति 3.42
दोनों विकर्णों के अनुदिश तह (fold) लगाइए। क्या उनके मध्य बिंदु समान ही हैं।
सेट-स्क्वेयर का उपयोग करके जाँच कीजिए, क्या 'O' पर बना कोण 90° का है। यह ऊपर बताए गए गुणधर्म को सिद्ध करता है।
तर्क-वितर्क की सहायता से हम इसकी पुष्टि कर सकते हैं।
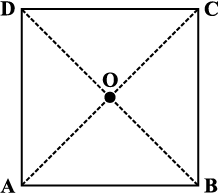
आकृति 3.43
ABCD एक वर्ग है जिसके विकर्ण एक दूसरे को 'O' पर प्रतिच्छेद
करते हैं (आकृति 3.43)।
OA = OC (क्योंकि वर्ग एक समांतर चतुर्भुज है )
SSS सर्वांगसमता प्रतिबंध के अनुसार
∆ AOD ≅ ∆ COD (कैसे?)
अत: m∠AOD = m∠COD
ये कोण रैखिक युग्म बनाते हैं। अत: प्रत्येक कोण समकोण है।
प्रश्नावली 3.4
1. बताइए, कथन सत्य है या असत्य :
(a) सभी आयत वर्ग होते हैं (e) सभी पतंगें सम चतुर्भुज होती हैं
(b) सभी सम चतुर्भुज समांतर चतुर्भुज होते हैं (f) सभी सम चतुर्भुज पतंग होते हैं
(c) सभी वर्ग सम चतुर्भुज और आयत भी होते हैं (g) सभी समांतर चतुर्भुज समलंब होते हैं
2. उन सभी चतुर्भुजों की पहचान कीजिए जिनमें
(a) चारों भुजाएँ बराबर लंबाई की हों (b) चार समकोण हों
3. बताइए कैसे एक वर्ग
(iv) एक आयत है।
4. एक चतुर्भुज का नाम बताइए जिसके विकर्ण
(i) एक दूसरे को समद्विभाजित करते हैं (ii) एक दूसरे पर लंब समद्विभाजक हो
(iii) बराबर हों।
5. बताइए एक आयत उत्तल चतुर्भुज कैसे है।
सोचिए, चर्चा कीजिए और लिखिए
1. एक राजमिस्त्री एक पत्थर की पट्टी बनाता है। वह इसे आयताकार बनाना चाहता है। कितने अलग-अलग तरीकों से उसे यह विश्वास हो सकता है कि यह आयताकार है।
2. वर्ग को आयत के रूप में परिभाषित किया गया था जिसकी सभी भुजाएँ बराबर होती हैं। क्या हम इसे समचतुर्भुज के रूप में परिभाषित कर सकते हैं जिसके कोण बराबर माप के हाें? इस विचार को स्पष्ट कीजिए।
3. क्या एक समलंब के सभी कोण बराबर माप के हो सकते हैं? क्या इसकी सभी भुजाएँ बराबर हो सकती हैं? वर्णन कीजिए।
हमने क्या चर्चा की?
| चतुर्भुज | गुण |
समांतर चतुर्भुज : एक चतुर्भुज जिसमें सम्मुख भुजाओं का प्रत्येक युग्म समांतर होता है।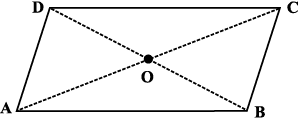 | (1) सम्मुख भुजाएँ बराबर होती हैं। (2) सम्मुख कोण बराबर होते हैैं। (3) विकर्ण एक दूसरे को समद्विभाजित करते हैैं। |
समचतुर्भुज : एक चतुर्भुज जिसकी सभी भुजाएँ बराबर माप की होती हैं।
| (1) समांतर चतुर्भुज के सभी गुण होते हैं। (2) विकर्ण परस्पर लंब होते हैैं। |
आयत :एक समांतर चतुर्भुज जिसमें एक कोण समकोण होता है।
| (1) समांतर चतुर्भुज के सभी गुण होते हैैं। (2) प्रत्येक कोण समकोण होता हैं। (3) विकर्ण बराबर माप के होते हैैं। |
वर्ग :एक आयत जिसकी सभी भुजाएँ बराबर होती हैं।
| समांतर चतुर्भुज, समचतुर्भुज तथा आयत सभी के गुण होते हैं। |
पतंग : एक चतुर्भुज जिसमें दो आसन्न भुजाओं के युग्म बराबर होते हैं।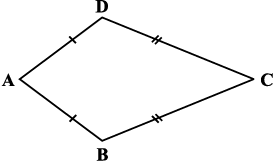 | (1) विकर्ण एक दूसरे पर लंब होते हैं। (2) एक विकर्ण दूसरे विकर्ण को समद्विभाजित (3) आकृति में, m∠B = m∠D परंतु m∠A ≠ m∠C |