Table of Contents
अध्याय 4
प्रायोगिक ज्यामिति
4.1 भूमिका
आप कक्षा VII में त्रिभुजों की रचना करना सीख चुके हैं। हमेें एक अद्वितीय त्रिभुज की रचना के लिए तीन मापों (भुजाओें और कोणों) की आवश्यकता होती है।
चूँकि एक त्रिभुज की रचना करने के लिए तीन मापों का होना पर्याप्त है, एक स्वाभाविक प्रश्न उठता है कि क्या एक अद्वितीय चार भुजाओं वाली बंद आकृति की जिसे चतुर्भुज कहते हैं, रचना के लिए चार मापें पर्याप्त होंगी।
इन्हें कीजिए

समान लंबाई (मान लीजिए 10 cm) वाली तीलियों (Sticks) का एक युग्म लीजिए। अब एक दूसरा समान लंबाई, (माना 8 cm) वाली तीलियों का युग्म लीजिए। इन्हें आपस में इस प्रकार जोड़िए (Hinge) जिससे 10 cm लंबाई तथा 8 cm चौड़ाई वाला एक आयत प्राप्त हो जाए। इस आयत का निर्माण 4 मापों के उपयोग से किया गया है। (आकृति 4.1)
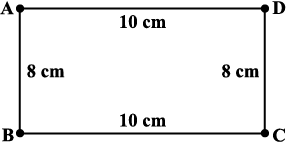
आकृति 4.1
अब आयत की चौड़ाई के अनुदिश दबाव डालिए। क्या नयी प्राप्त आकृति अभीभी एक आयत है (आकृति 4.2)? ध्यान दीजिए कि अब आयत एक समांतर चतुर्भुज बन गया है। क्या आपने तीलियों कीलंबाइयों को बदला है? नहीं, भुजाओं की माप वही रहती है।
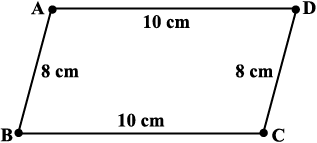
आकृति 4.2
नयी प्राप्त आकृति को दूसरी दिशा में दबाव डालिए। आपको क्या प्राप्त होता है? आप पुनः एक समांतर चतुर्भुज प्राप्त करते हैं जो बिल्कुल अलग है (आकृति 4.3)। अभीभी चारों माप वही रहती हैं।
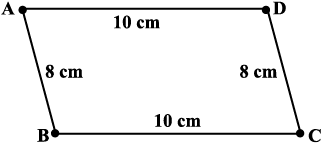
आकृति 4.3
यह दर्शाता है कि एक चतुर्भुज की चार मापों से एक अद्वितीय चतुर्भुज प्राप्त नहीं हो सकता है। क्या पाँच मापों से एक अद्वितीय चतुर्भुज प्राप्त हो सकता है?
आइए, इस क्रियाकलाप पर पुनः विचार करें। आप, प्रत्येक 10 cm लंबाई की दो तीलियों एवं प्रत्येक 8 cm लंबाई की दो तीलियों की सहायता से एक आयत की रचना कर चुके हैं। अब BD के बराबर लंबाई वाली एक दूसरी तीली को BD के अनुदिश बाँधिए (आकृति 4.4)। यदि आप अब चौड़ाई की ओर दबाव डालते हैं तो क्या आकृति में परिवर्तन होता है? नहीं, आकृति को खोले बिना परिवर्तन संभव नहीं हो सकता है। पाँचवीं तीली के प्रवेश ने आयत को अद्वितीय रूप से स्थिर कर दिया है, अर्थात्, कोई दूसरा चतुर्भुज (दी गई भुजाओं की लंबाई के बराबर) अब संभव नहीं है।
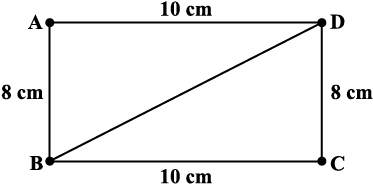
आकृति 4.4
अतः हमने देखा कि पाँच मापों से हमें एक अद्वितीय चतुर्भुज प्राप्त होता है।
परंतु क्या एक अद्वितीय चतुर्भुज की रचना करने के लिए कोई भी पाँच माप (भुजाओं और कोणों की) पर्याप्त हैं?

सोचिए, चर्चा कीजिए और लिखिए
4.2 एक चतुर्भुज की रचना
अब हम सीखेंगे कि दी हुई निम्नलिखित मापों से एक अद्वितीय चतुर्भुज की रचना कैसे की जा सकती है।
• जब चार भुजाएँ और एक विकर्ण दिया हुआ है।
• जब दो विकर्ण और तीन भुजाएँ दी हुई हैं।
• जब दो आसन्न भुजाएँ और तीन कोण दिए हुए हैं।
• जब तीन भुजाएँ और उनके बीच के दो कोण दिए हुए हैं।
• जब अन्य विशिष्ट गुण ज्ञात हैं।
आइए, एक-एक करके इन रचनाओं को लें:
4.2.1 एक चतुर्भुज की रचना जब चारों भुजाएँ और एक विकर्ण की लंबाई दी हो
हम इस रचना को एक उदाहरण की सहायता से समझाएँगे।
उदाहरण 1 : एक चतुर्भुज PQRS की रचना कीजिए जिसमें
PQ = 4 cm, QR = 6 cm, RS = 5 cm, PS = 5.5 cm और
PR = 7 cm हो।
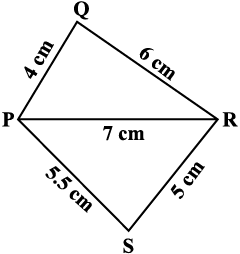
आकृति 4.5
हल : एक कच्ची (rough) आकृति चतुर्भुज को समझने में हमारी सहायता करेगी। हम पहले कच्ची आकृति खींचते हैं और मापों को चिह्नित करते हैं (आकृति 4.5)।
चरण 1 कच्ची आकृति से बड़ी आसानी से देखा जा सकता है कि SSS रचना कसौटी से ∆ PQR की रचना की जा सकती है। ∆ PQR की रचना कीजिए (आकृति 4.6)।
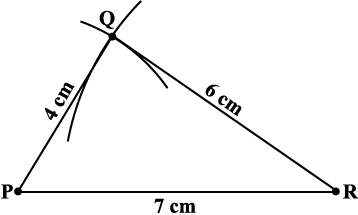
आकृति 4.6
चरण 2 अब हमें चौथे बिंदु 'S' का पता लगाना है। यह बिंदु S, PR के संदर्भ में, बिंदु Q के विपरीत दिशा में होगा। उसके लिए हमारे पास दो माप हैं। बिंदु P से, बिंदु S, 5.5 cm की दूरी पर स्थित है। अतः P को केंद्र मानकर 5.5 cm त्रिज्या की एक चाप खींचिए। (बिंदु S इस चाप पर ही कहीं स्थित होगा।) (आकृति 4.7)
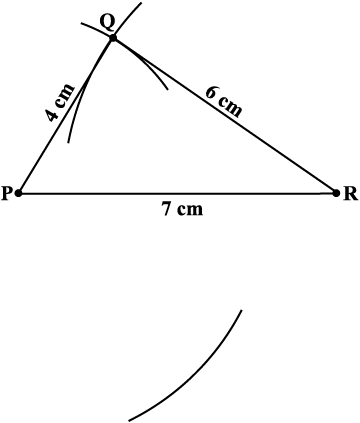
आकृति 4.7
चरण 3 R से बिंदु S, 5 cm दूरी पर है। अतः R को केंद्र मानकर और 5 cm त्रिज्या लेकर एक चाप खींचिए। (बिंदु 'S' इस चाप पर कहीं स्थित होगा!) (आकृति 4.8)
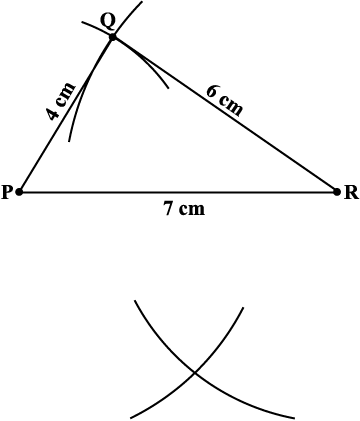
आकृति 4.8
चरण 4 बिंदु S को खींचे गए दोनों चापों पर स्थित होना चाहिए। अतः यह इन दोनों चापों का प्रतिच्छेद बिंदु है। इस बिंदु को 'S' से अंकित कीजिए और PQRS को पूरा कीजिए, अर्थात्, PS तथा RS को जोड़िए। PQRS अभीष्ट चतुर्भुज है। (आकृति 4.9)
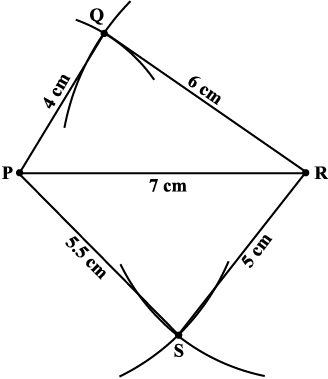
आकृति 4.9

सोचिए, चर्चा कीजिए और लिखिए
(i) हमने देखा कि एक चतुर्भुज की पाँच मापों से एक अद्वितीय चतुर्भुज की रचना की जा सकती है। क्या आप सोचते हैं कि चतुर्भुज की किन्हीं पाँच मापाें से एेसी रचना की जा सकती है?
(ii) क्या आप एक समांतर चतुर्भुज BATS की रचना कर सकते हैं जिसमें BA = 5 cm, AT = 6 cm, और AS = 6.5 cm हो? क्यों?
(iii) क्या आप एक सम चतुर्भुज (Rhombus) ZEAL की रचना कर सकते हैं जिसमें ZE = 3.5 cm, विकर्ण EL = 5 cm है? क्यों?
(iv) एक विद्यार्थी एक चतुर्भुज PLAY की रचना करने का प्रयास करता है जिसमें PL = 3 cm, LA = 4 cm, AY = 4.5 cm, PY = 2 cm और LY = 6 cm है, परंतु वह इसकी रचना नहीं कर सका। कारण बताइए?
[संकेतः एक कच्ची आकृति की सहायता से चर्चा कीजिए]

प्रश्नावली 4.1
1. निम्नलिखित चतुर्भुजों की रचना कीजिए:
(i) चतुर्भुज ABCD जिसमें
AB = 4.5 cm
BC = 5.5 cm
CD = 4 cm
AD = 6 cm
AC = 7 cm है।
(ii) चतुर्भुज JUMP जिसमें
JU = 3.5 cm
UM = 4 cm
MP = 5 cm
PJ = 4.5 cm
PU = 6.5 cm है।
(iii) समांतर चतुर्भुज MORE जिसमें
OR = 6 cm
EO = 7.5 cm
MO = 7.5 cm है।
(iv) सम चतुर्भुज BEST जिसमें
BE = 4.5 cm और
ET = 6 cm है।
4.2.2 एक चतुर्भुज की रचना करना जब दो विकर्ण और तीन भुजाओं की लंबाइयाँ दी हों
जब चतुर्भुज की चार भुजाएँ और एक विकर्ण दिया हुआ था तो हमने पहले दी हुई मापों से एक त्रिभुज की रचना की और तदुपरांत चतुर्थ बिंदु का पता लगाने का प्रयास किया था। इसी विधि का उपयोग हम यहाँ पर करेंगे।
उदाहरण 2 : एक चतुर्भुज ABCD की रचना कीजिए, जिसमें BC = 4.5 cm, AD = 5.5 cm, CD = 5 cm, विकर्ण AC = 5.5 cm और विकर्ण BD = 7 cm है।
हल : यहाँ पर चतुर्भुज ABCD की कच्ची आकृति दी गई है (आकृति 4.10)। इस कच्ची आकृति का अध्ययन करके हम आसानी से देख सकते हैं कि सबसे पहले ∆ ACD की रचना करना संभव है (क्यों?)
चरण 1 SSS कसौटी का उपयोग करके ∆ ACD की रचना कीजिए। (आकृति 4.11) (अब हमें बिंदु B का पता लगाने की आवश्यकता है जो बिंदु C से 4.5 cm तथा बिंदु D से 7 cm दूरी पर स्थित है)।
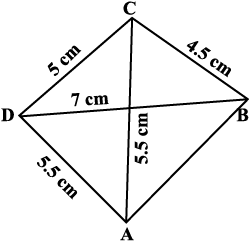
आकृति 4.10
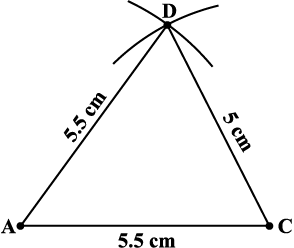
आकृति 4.11
चरण 2 D को केंद्र मानकर, 7 cm त्रिज्या वाली एक चाप खींचिए।
(बिंदु B इस चाप पर कहीं स्थित होगा।) (आकृति 4.12)।
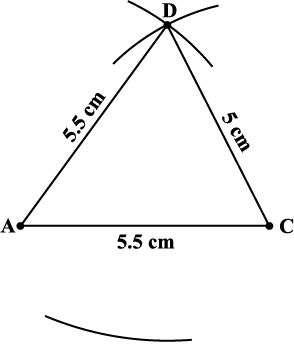
आकृति 4.12
चरण 3 C को केंद्र मानकर और 4.5 cm त्रिज्या लेकर एक चाप खींचिए। (बिंदु B इस चाप पर कहीं स्थित होगा) (आकृति 4.13)।
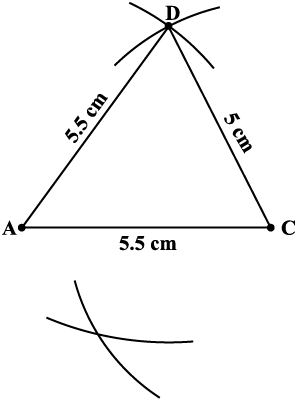
आकृति 4.13
चरण 4 क्योंकि बिंदु B इन दोनों चापों पर स्थित है। अतः बिंदु B इन दोनों चापों का प्रतिच्छेद बिंदु है। बिंदु B को अंकित कीजिए और ABCD को पूरा कीजिए। ABCD एक अभीष्ट चतुर्भुज है (आकृति 4.14)।
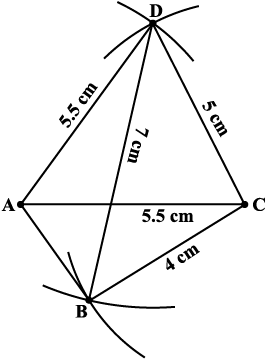
आकृति 4.14
सोचिए, चर्चा कीजिए और लिखिए
1. उपर्युक्त उदाहरण में क्या हम पहले ∆ ABD खींचकर उसके बाद चतुर्थ बिंदु C को ज्ञात करके चतुर्भुज की रचना कर सकते हैं?
2. क्या आप एक चतुर्भुज PQRS की रचना कर सकते हैं जिसमें PQ = 3 cm, RS = 3 cm, PS = 7.5 cm, PR = 8 cm, और SQ = 4 cm है? अपने उत्तर की पुष्टि कीजिए।

प्रश्नावली 4.2
1. निम्नलिखित चतुर्भुजों की रचना कीजिए:
(i) चतुर्भुज LIFT जिसमें (ii) चतुर्भुज GOLD जिसमें
LI = 4 cm OL = 7.5 cm
IF = 3 cm GL = 6 cm
TL = 2.5 cm GD = 6 cm
LF = 4.5 cm LD = 5 cm
IT = 4 cm है। OD = 10 cm है।
(iii) समचतुर्भुज BEND जिसमें
BN = 5.6 cm
DE = 6.5 cm है।
4.2.3 एक चतुर्भुज की रचना जब दो आसन्न भुजाएँ और तीन कोणों की माप दी हो
पहले की तरह ही, हम त्रिभुज की रचना से ही प्रारंभ करते हैं तदुपरांत चतुर्भुज को पूर्ण करने के लिए चतुर्थ बिंदु का पता लगाते हैं।
उदाहरण 3 : एक चतुर्भुज MIST की रचना कीजिए, जहाँ MI = 3.5 cm,
IS = 6.5 cm, ∠M = 75° cm, ∠I = 105° cm और ∠S = 120° cm है।
हल : यहाँ पर एक कच्ची आकृति दी गई है जो हमारी रचना के चरणों को निश्चित करने में हमारी सहायता करेगी। हम भिन्न चरणों के लिए केवल संकेत देंगे (आकृति 4.15)।
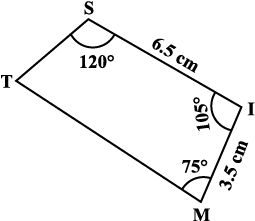
आकृति 4.15
चरण 1 आप बिंदुओं का कैसे पता लगाएँगे? आप आधार के लिए किसका चयन करते हैं और आपका पहला चरण क्या होगा (आकृति 4.16)।
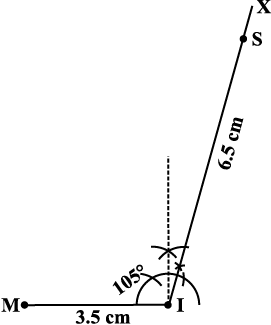
आकृति 4.16
चरण 2 बिंदु S पर ∠ISY = 120° बनाइए (आकृति 4.17)।
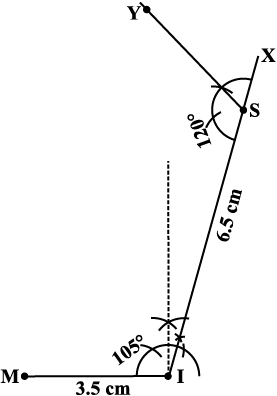
आकृति 4.17
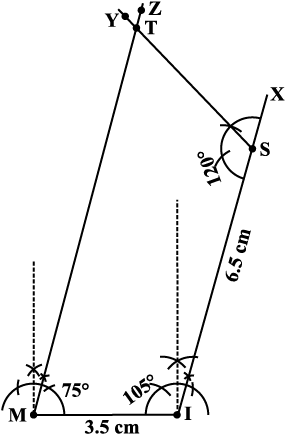
आकृति 4.18
चरण 3 बिंदु M पर ∠IMZ = 75° बनाइए।
SY तथा MZ कहाँ पर प्रतिच्छेद करेंगे? उस बिंदु को T से अंकित कीजिए। हमें अभीष्ट चतुर्भुज MIST प्राप्त होता है (आकृति 4.18)।
सोचिए, चर्चा कीजिए और लिखिए

1. यदि हमें M पर 75° माप के स्थान पर 100° की माप दी हुई हो तो क्या आप ऊपर बताए गए चतुर्भुज MIST की रचना कर सकते हैं?
2. क्या आप एक चतुर्भुज PLAN की रचना कर सकते हैं, यदि PL = 6 cm, LA = 9.5 cm, ∠P = 75° cm, ∠L = 150° cm और ∠A = 140°है?
(संकेत: कोण-योगफल गुण को स्मरण कीजिए।)
3. एक समांतर चतुर्भुज में दो आसन्न भुजाओं की लंबाइयाँ दी हुई हैं। क्या हमें रचना करने के लिए अभी भी कोणों की मापों की आवश्यकता है जैसा कि उपरोक्त उदाहरण में दिया है?
प्रश्नावली 4.3
1. निम्नलिखित चतुर्भुजों की रचना कीजिए:
(i) चतुर्भुज MORE जिसमें
MO = 6 cm
OR = 4.5 cm
∠M = 60°
∠O = 105°
∠R = 105° है।
(ii) चतुर्भुज PLAN जिसमें
PL = 4 cm
LA = 6.5 cm
∠P = 90°
∠A = 110°
∠N = 85° है।
(iii) समांतर चतुर्भुज HEAR जिसमें
HE = 5 cm
EA = 6 cm और ∠R = 85° है।
(iv) आयत OKAY जिसमें
OK = 7 cm
KA = 5 cm है।
4.2.4 एक चतुर्भुज की रचना करना जब तीन भुजाएँ और उनके बीच के दो कोणों की माप दी हो
इस प्रकार के चतुर्भुज के अंतर्गत जब आप एक रफ़ आकृति बनाते हैं तो विशेष रूप से उनके बीच के कोणों को विशेष रूप से ध्यानपूर्वक देखेंगे।
उदाहरण 4 : एक चतुर्भुज ABCD की रचना कीजिए जहाँ AB = 4 cm, BC = 5 cm, CD = 6.5 cm और ∠B = 105° तथा ∠C = 80° है।
हल : साधारणतया, हम एक कच्ची आकृति खींचते हैं जिससे हमें यह पता चल सके कि रचना को हम कैसे प्रारंभ कर सकते हैं। तब हम चारों बिंदुओं का पता लगाने की योजना बना सकते हैं (आकृति 4.19)।
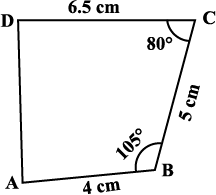
आकृति 4.19
चरण 1 बिंदु B पर BC = 5 cm लेकर प्रारंभ कीजिए। BX के अनुदिश 105° का कोण बनाइए। इससे 4 cm की दूरी पर बिंदु A को अंकित कीजिए। अब हमें बिंदु B, C और A प्राप्त हो गए हैं (आकृति 4.20)।
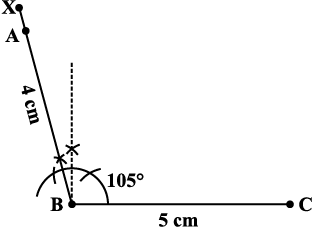
आकृति 4.20
चरण 2 चतुर्थ बिंदु D, CY पर कहीं स्थित है जो भुजा BC के साथ 80° का कोण बनाता है। BC पर स्थित बिंदु C पर
∠BCY = 80° बनाइए (आकृति 4.21)।
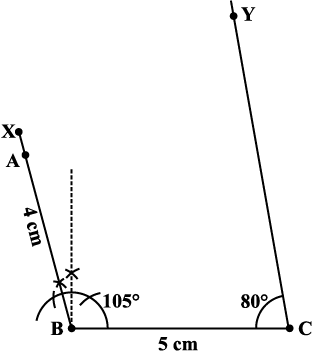
आकृति 4.21
चरण 3 बिंदु D, CY पर 6.5 cm की दूरी पर स्थित है। C को केंद्र मानकर और 6.5 cm त्रिज्या लेकर एक चाप खींचिए। यह CY को D पर प्रतिच्छेद करती है (आकृति 4.22)।
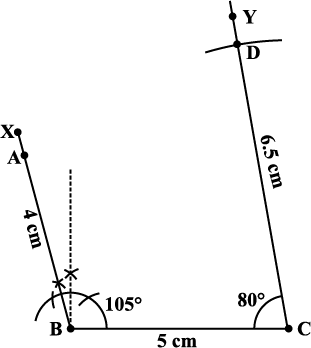
आकृति 4.22
चरण 4 चतुर्भुज ABCD को पूर्ण कीजिए। ABCD अभीष्ट चतुर्भुज है
(आकृति 4.23)।
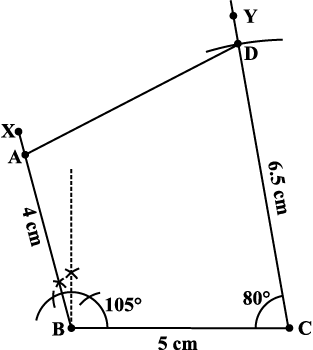
आकृति 4.23
सोचिए, चर्चा कीजिए और लिखिए

1. उपरोक्त उदाहरण में, हमने सर्वप्रथम BC खींची। इसके स्थान पर दूसरे अन्य प्रारंभ बिंदु और कौन से हो सकते हैं?
2. हमने अभी तक चतुर्भुजों की रचना के लिए कोई पाँच मापों का प्रयोग किया। क्या एक चतुर्भुज की रचना करने के लिए पाँच मापों के अलग-अलग समुच्चय (अभी तक देखें गए मापों के अतिरिक्त) हो सकते हैं?
निम्नलिखित समस्याएँ प्रश्नों के उत्तर देने में आपकी सहायता कर सकती हैं।
(i) चतुर्भुज ABCD जिसमें AB = 5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm और ∠B = 80° है।
(ii) चतुर्भुज PQRS जिसमें PQ = 4.5 cm, ∠P = 70°, ∠Q = 100°, ∠R = 80° और ∠S = 110° है।
आप स्वयं कुछ और उदाहरणों की रचना कीजिए और एक चतुर्भुज की रचना के लिए आँकड़ों की पर्याप्तता/अपर्याप्तता ज्ञात कीजिए।
प्रश्नावली 4.4

1. निम्नलिखित चतुर्भुजों की रचना कीजिए:
(i) चतुर्भुज DEAR जिसमें
DE = 4 cm
EA = 5 cm
AR = 4.5 cm
∠E = 60°
और ∠A = 90° है।
(ii) चतुर्भुज TRUE जिसमें
TR = 3.5 cm
RU = 3 cm
UE = 4 cm
∠R = 75°
और ∠U = 120° है।
4.3 कुछ विशिष्ट स्थितियाँ
एक चतुर्भुज की रचना के लिए हमने पाँच मापों का प्रयोग किया। क्या किसी एेसे चतुर्भुज कीरचना की जा सकती है जिसकी मापों की संख्या इन मापों की संख्या से कम हो? निम्नलिखित उदाहरण एेसी ही विशिष्ट स्थितियों को जाँचते हैं।
उदाहरण 5 : 4.5 cm भुजा वाले वर्ग की रचना कीजिए।
हल : सर्वप्रथम एेसा प्रतीत होता है कि केवल एक ही माप दी हुई है। वास्तव में हमारे पास और बहुत सी जानकारियाँ हैं क्योंकि यह आकृति एक विशेष चतुर्भुज है जिसका नाम वर्ग है। अब हम जानते हैं कि इसका प्रत्येक कोण एक समकोण है। (रफ़ आकृति देखिए) (आकृति 4.24)
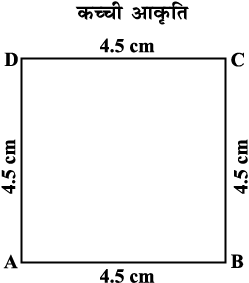
आकृति 4.24
यह SAS कसौटी के उपयोग से ∆ ABC खींचने में हमें सहायता करता है। तदुपरांत बिंदु D का बड़ी आसानी से पता लगाया जा सकता है। दी हुई मापों से अब आप स्वयं एक वर्ग की रचना कीजिए।
उदाहरण 5 : क्या एक सम चतुर्भुज ABCD की रचना करना संभव है जहाँ AC = 6 cm और BD = 7 cm हो? अपने उत्तर की पुष्टि कीजिए।
हल : सम चतुर्भुज की केवल दो मापें (विकर्ण) दी हुई हैं। चूँकि यह एक सम चतुर्भुज है, इसके गुणों से हम और सहायता प्राप्त कर सकते हैं।
सम चतुर्भुज के विकर्ण एक दूसरे के लंब समद्विभाजक होते हैं।
अतः सर्वप्रथम AC = 7 cm खींचिए और तदुपरांत इसके लंब समद्विभाजक की रचना कीजिए। दोनों एक दूसरे को O पर प्रतिच्छेद करते हैं। खींचे गए समद्विभाजक को बिंदु O से दोनों ओर लंबाई वाली त्रिज्या लेकर काटिए। अब आप बिंदु B तथा बिंदु D प्राप्त करते हैं।
ऊपर बताई गई विधि पर आधारित अब एक सम समचतुर्भुज की रचना कीजिए (आकृति 4.25)।
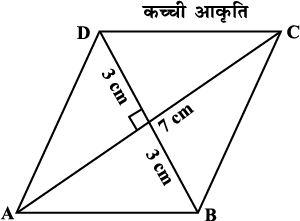
आकृति 4.25

प्रयास कीजिए
1. आप एक आयत PQRS की रचना कैसे करेंगे यदि आप केवल PQ और QR की लंबाई जानते हैं?
2. एक पतंग EASY की रचना कीजिए यदि AY = 8 cm, EY = 4 cm और SY = 6 cm है (आकृति 4.26)। रचना के दौरान आपने पतंग के कौन से गुणों का प्रयोग किया?
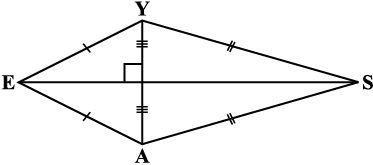
आकृति 4.26
प्रश्नावली 4.5

निम्नलिखित की रचना कीजिए:
1. एक वर्ग READ जिसमें RE = 5.1 cm है।
2. एक सम चतुर्भुज जिनके विकर्णों की लंबाई 5.2 cm और 6.4 cm हैै।
3. एक आयत जिसकी आसन्न भुजाओं की लंबाइयाँ 5 cm और 4 cm है।
4. एक समांतर चतुर्भुज OKAY जहाँ OK = 5.5 cm और KA = 4.2 cm है। क्या यह अद्वितीय है?
हमने क्या चर्चा की?
1. पाँच मापों से एक अद्वितीय चतुर्भुज प्राप्त हो सकता है।
2. एक अद्वितीय चतुर्भुज की रचना की जा सकती है यदि उसकी चार भुजाओं की लंबाइयाँ और एक विकर्ण दिया हुआ हो।
3. एक अद्वितीय चतुर्भुज की रचना की जा सकती है यदि उसके दो विकर्ण और तीन भुजाएँ दी हों।
4. एक अद्वितीय चतुर्भुज की रचना की जा सकती है यदि उसकी दो आसन्न भुजाएँ और तीन कोणों की माप ज्ञात हो।
5. एक अद्वितीय चतुर्भुज की रचना की जा सकती है यदि उसकी तीन भुजाएँ और दो बीच के कोण दिए हुए हों।
