Table of Contents
अध्याय 5
आँकड़ों का प्रबंधन
5.1 सूचनाओं की खोज में
आपके दैनिक जीवन में आपके सम्मुख निम्नलिखित प्रकार की सूचनाएँ आई होंगी :
(a) पिछले 10 टेस्ट मैचों में एक बल्लेबाज द्वारा बनाए गए कुल रन।

(b) पिछले 10 एक दिवसीय अंतर्राष्ट्रीय मैचों (ODI) में एक गेंदबाज द्वारा लिए गए कुल विकेट।
(c) आपकी कक्षा के विद्यार्थियों द्वारा गणित के यूनिट टेस्ट में प्राप्त किए गए अंक।
(d) आपके मित्रों में से प्रत्येक द्वारा पढ़ी गई कहानियों की पुस्तकों की संख्या, इत्यादि।
इन सभी स्थितियों में एकत्रित की गई सूचनाएँ आँकड़े (data) कहलाती हैं। आँकड़े प्राय: एक एेसी स्थिति के संदर्भ में एकत्रित किए जाते हैं जिसका हम अध्ययन करना चाहते हैं। उदाहरणार्थ, एक अध्यापिका की अपनी कक्षा के विद्यार्थियों की औसत ऊँचाई जानने में रुचि हो सकती है। इसे ज्ञात करने के लिए, वह अपनी कक्षा के सभी विद्यार्थियों की ऊँचाइयाँ लिखेगी, इन आँकड़ों को एक क्रमबद्ध रूप से संगठित करेगी और तदनुसार उनकी व्याख्या करेगी।
कभी-कभी आँकड़ों को, यह सुस्पष्ट करने के लिए कि वे क्या निरूपित करते हैं, आलेखीय रूप से (graphically) निरूपित किया जाता है। क्या आपको उन विभिन्न प्रकारों के आलेखों के बारे में कुछ याद है जो हमने पिछली कक्षाओं में पढ़े थे?
1. एक चित्रालेख (pictograph) : संकेतों का प्रयोग करते हुए, आँकड़ों का चित्रीय निरूपण :
 = 100 कार
= 100 कार  एक संकेत 100 कारों को प्रदर्शित करता है।
एक संकेत 100 कारों को प्रदर्शित करता है।
जुलाई 

 = 250
= 250  100 को
100 को  व्यक्त करता है
व्यक्त करता है
अगस्त 

 = 300
= 300
सितंबर 


 = ?
= ?
(i) जुलाई के महीने में कितनी कारों का उत्पादन हुआ?
(ii) किस महीने में कारों का अधिकतम उत्पादन हुआ?
2. एक दंड आलेख (bar graph): एक समान चौड़ाई के दंडों का प्रयोग करते हुए, सूचना का प्रदर्शन, जिसमें दंडों की लंबाइयाँ (ऊँचाइयाँ) क्रमश: उनके मानों के समानुपातिक होती हैं।
(i) इस दंड आलेख द्वारा क्या सूचना दी गई है?
(ii) किस वर्ष में विद्यार्थियों की संख्या में अधिकतम वृद्धि हुई?
(iii) किस वर्ष में विद्यार्थियों की संख्या अधिकतम है?
(iv) बताइए कि यह सत्य है या असत्य : ‘‘2005-06 में विद्यार्थियों की संख्या 2003-04 की संख्या की दुगुनी है।’’
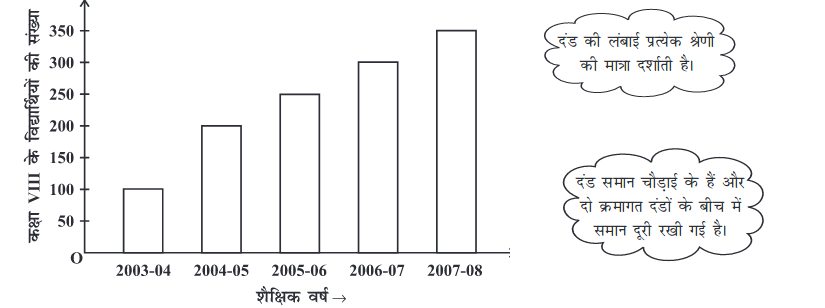
3. द्वि-दंड आलेख (double bar graph) : आँकड़ों के दो समूहों को एक साथ दर्शाने वाला दंड आलेख
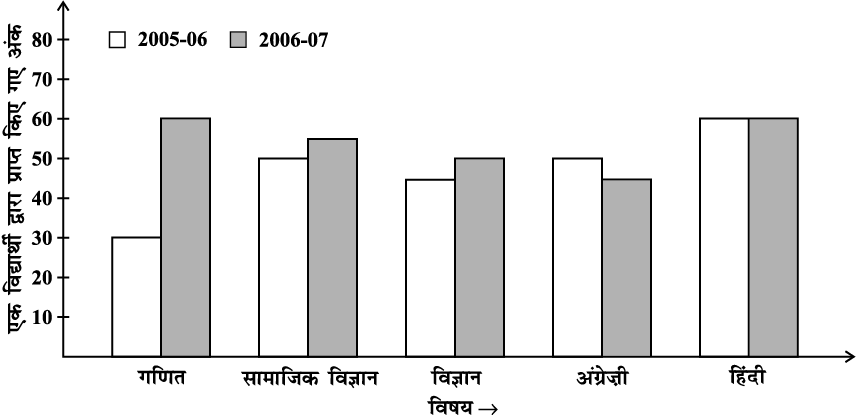
(i) इस द्वि-दंड आलेख द्वारा क्या सूचना दी गई है?
(ii) किस विषय में विद्यार्थी के प्रदर्शन में सबसे अधिक सुधार हुआ है?
(iii) किस विषय में प्रदर्शन में गिरावट आई है?
(iv) किस विषय में प्रदर्शन समान रहा है?
सोचिए, चर्चा कीजिए और लिखिए

यदि हम एक दंड आलेख के दंडों में से किसी एक की स्थिति बदल दें, तो क्या प्रदर्शित जानकारी में कोई बदलाव या परिवर्तन होगा? क्यों?
प्रयास कीजिए
1. महीना जुलाई अगस्त सितंबर अक्टूबर नवंबर दिसंबर
.png)
3. 8 सर्वश्रेष्ठ क्रिकेट टीमों द्वारा ODI में जीतने का प्रतिशत
.png)
5.2 आँकड़ों का संगठन (Organising Data)
प्राय: हमें उपलब्ध आँकड़े असंगठित रूप में प्राप्त होते हैं, जिन्हें यथाप्राप्त आँकड़े (raw data) कहा जाता है। अर्थपूर्ण निष्कर्ष निकालने के लिए, हमें आँकड़ों को एक क्रमबद्ध रूप में संगठित करने की आवश्यकता होती है। उदाहरणार्थ, विद्यार्थियों के एक समूह से उनके मनपसंद विषयों के बारे में पूछा गया। इसके परिणामों की सूची नीचे दी गई है :
कला, गणित, विज्ञान, अंग्रेज़ी, गणित, कला, अंग्रेज़ी, गणित अंग्रेज़ी, कला, विज्ञान, कला, विज्ञान, विज्ञान, गणित, कला, अंग्रेज़ी, कला, विज्ञान, गणित, विज्ञान, कला।
कौन-सा विषय सबसे अधिक पसंद किया गया और कौन-सा विषय सबसे कम पसंद किया गया?
आकस्मिक रूप से लिखी गई रुचियों या पसंदों को देखकर इस प्रश्न का उत्तर देना सरल नहीं है। हम मिलान चिह्नों (tally marks) का प्रयोग करते हुए, इन आँकड़ों को सारणी 5.1 के रूप में व्यवस्थित करते हैं :
.png)
प्रत्येक विषय के सम्मुख लिखी मिलान चिह्नों की संख्या से हम विशिष्ट विषय को पसंद करने वाले विद्यार्थियों की संख्या प्राप्त करते हैं।
यह संख्या उस विषय की बारंबारता (frequency) कहलाती है।
किसी प्रविष्टि की बारंबारता वह संख्या है जितनी बार वह प्रविष्टि आँकड़ों में आती है।
सारणी 5.1 से, अंग्रेज़ी को पसंद करने वाले विद्यार्थियों की बारंबारता 4 है।
गणित को पसंद करने वाले विद्यार्थियों की बारंबारता 5 है।
उपरोक्त रूप से बनाई गई सारणी एक बारंबारता बंटन सारणी (frequency distribution table) कहलाती है, क्योंकि इससे पता चलता है कि एक प्रविष्टि कितनी बार आई है।

प्रयास कीजिए
1. विद्यार्थियों के एक समूह से यह बताने को कहा गया कि वे किस पशु को सबसे अधिक घर में पालना पसंद करेंगे। इसके परिणाम नीचे दिए गए हैं :
कुत्ता, बिल्ली, बिल्ली, मछली, बिल्ली, खरगोश, कुत्ता, बिल्ली, खरगोश, कुत्ता, बिल्ली, कुत्ता, कुत्ता, कुत्ता, बिल्ली, गाय, मछली, खरगोश, कुत्ता, बिल्ली, कुत्ता, बिल्ली, बिल्ली, कुत्ता, खरगोश, बिल्ली, मछली, कुत्ता। उपरोक्त के लिए एक बारंबारता बंटन सारणी बनाइए।
5.3 आँकड़ों का वर्गीकरण
विषयों की पसंद से संबंधित आँकड़े प्रत्येक प्रविष्टि के अनेक बार आने को दर्शाते हैं। उदाहरणार्थ, कला को 7 विद्यार्थी पसंद करते हैं, गणित को 5 विद्यार्थी पसंद करते हैं इत्यादि (सारणी 5.1)। इस सूचना को आलेखीय रूप से एक चित्रालेख या एक दंड आलेख द्वारा प्रदर्शित किया जा सकता है। परंतु कभी-कभी हमें बड़े आँकड़ों के साथ कार्य करना पड़ता है। उदाहरणार्थ, कक्षा VIII के 60 विद्यार्थियों द्वारा गणित में प्राप्त किए गए (50 में से) निम्नलिखित अंकों पर विचार कीजिए :
21, 10, 30, 22, 33, 5, 37, 12, 25, 42, 15, 39, 26, 32, 18, 27, 28, 19, 29, 35, 31, 24, 36, 18, 20, 38, 22, 44, 16, 24, 10, 27, 39, 28, 49, 29, 32, 23, 31, 21, 34, 22, 23, 36, 24, 36, 33, 47, 48, 50, 39, 20, 7, 16, 36, 45, 47, 30, 22, 17.
यदि हम प्रत्येक प्रेक्षण के लिए एक बारंबारता बंटन सारणी बनाएँ, तो वह बहुत लंबी होगी। अत:, हम सुविधा के लिए प्रेक्षणों के कुछ समूह या वर्ग बनाते हैं, जैसे 0-10, 10-20 इत्यादि तथा प्रत्येक समूह या वर्ग में आने वाले प्रेक्षणों की संख्या के आधार पर एक बारंबारता बंटन (frequency distribution) प्राप्त करते हैं। इस प्रकार, उपरोक्त आँकड़ों के लिए, बारंबारता बंटन सारणी निम्नलिखित हो सकती है :
.png)
उपरोक्त प्रकार से प्रस्तुत आँकड़े वर्गीकृत आँकड़े (grouped data) कहलाते हैं तथा प्राप्त बंटन वर्गीकृत बारंबारता बंटन कहलाता है। इससे अर्थपूर्ण निष्कर्ष निकालने में सहायता मिलती है, जैसे :
(1) अधिकांश विद्यार्थियों ने 20 और 40 के बीच अंक प्राप्त किए हैं।
(2) 8 विद्यार्थियों ने 50 में से 40 से अधिक अंक प्राप्त किए हैं।
समूहों 0-10, 10-20, 20-30 इत्यादि में से प्रत्येक एक वर्ग अंतराल (class interval) [या संक्षेप में एक वर्ग (class)] कहलाता है।
ध्यान दीजिए कि प्रेक्षण 10 दोनों ही वर्गों 0-10 और 10-20 में सम्मिलित है। इसी प्रकार, 20 वर्गों 10-20 और 20-30 दोनों में ही सम्मिलित है। परंतु एक प्रेक्षण (10 या 20) दो वर्गों में एक साथ सम्मिलित नहीं हो सकता। इससे बचने के लिए, हम यह परिपाटी अपनाते हैं कि उभयनिष्ठ प्रेक्षण उच्चतर वर्ग में सम्मिलित होगा। अर्थात् प्रेक्षण 10 वर्ग अंतराल 10-20 में सम्मिलित है (0-10 में नहीं)। इसी प्रकार, 20 वर्ग अंतराल 20-30 में सम्मिलित है (10-20 में नहीं)। वर्ग अंतराल 10-20 में, 10 निम्न वर्ग सीमा (lower class limit) कहलाती है तथा 20 उपरि या उच्च वर्ग सीमा (upper class limit) कहलाती है। इसी प्रकार, वर्ग अंतराल 20-30 में, 20 निम्न वर्ग सीमा है तथा 30 उच्च वर्ग सीमा है। ध्यान दीजिए कि वर्ग अंतरालों 0-10, 10-20, 20-30 इत्यादि में से प्रत्येक की उच्च वर्ग सीमा और निम्न वर्ग सीमा का अंतर बराबर है (इस स्थिति में 10)। उपरि (या उच्च) वर्ग सीमा और निम्न वर्ग सीमा का यह अंतर वर्ग अंतराल की चौड़ाई (width) या माप (size) कहलाती है।
![]() प्रयास कीजिए
प्रयास कीजिए
1. निम्नलिखित बारंबारता बंटन सारणी का अध्ययन कीजिए और उसके नीचे दिए हुए प्रश्नों के उत्तर दीजिए :
.png)
(i) वर्ग अंतरालों की माप क्या है?
(ii) किस वर्ग की सबसे अधिक बारंबारता है?
(iii) किस वर्ग की सबसे कम बारंबारता है?
(iv) वर्ग अंतराल 250-275 की उच्च सीमा क्या है?
(v) किन दो वर्गों की बारंबारता एक ही है?
2. अंतरालों 30-35, 35-40 इत्यादि का प्रयोग करते हुए, एक कक्षा के 20 विद्यार्थियों के भारों (kg में) के निम्नलिखित आँकड़ों के लिए एक बारंबारता बंटन सारणी बनाइए :
40, 38, 33, 48, 60, 53, 31, 46, 34, 36, 49, 41, 55, 49, 65, 42, 44, 47, 38, 39
5.3.1 एक विभिन्नता के साथ दंड
आइए, 60 विद्यार्थियों द्वारा गणित टेस्ट में प्राप्त किए गए अंकों के वर्गीकृत बारंबारता बंटन पर पुन: विचार करें (सारणी 5.4)।
.png)
उपरोक्त को संलग्न आलेख के रूप में निरूपित करके प्रदर्शित किया जाता है (आकृति 5.1)।
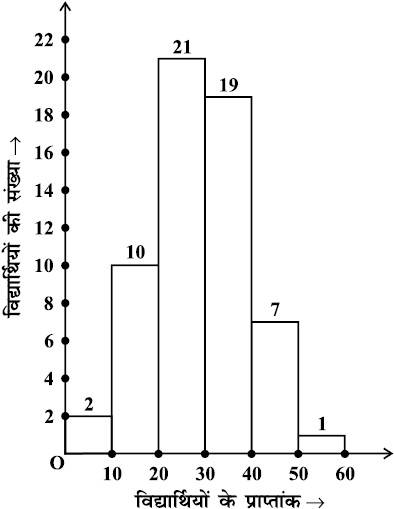
आकृति 5.1
क्या यह आलेख उन दंड आलेखों से किसी रूप में भिन्न है जो आपने कक्षा VII में खींचे थे? ध्यान दीजिए कि यहाँ हमने क्षैतिज अक्ष पर प्रेक्षणों के समूहों (अर्थात् वर्ग अंतरालों) को निरूपित किया है। दंड की लंबाई वर्ग अंतराल की बारंबारता दर्शाती है। साथ ही, यहाँ दंडों के बीच में कोई रिक्तता नहीं है, क्योंकि वर्ग अंतरालों के बीच में कोई रिक्तता नहीं है।
आँकड़ों का इस प्रकार का आलेखीय निरूपण एक आयतचित्र (histogram) कहलाता है। निम्नलिखित आलेख एक अन्य आयतचित्र है (आकृति 5.2):
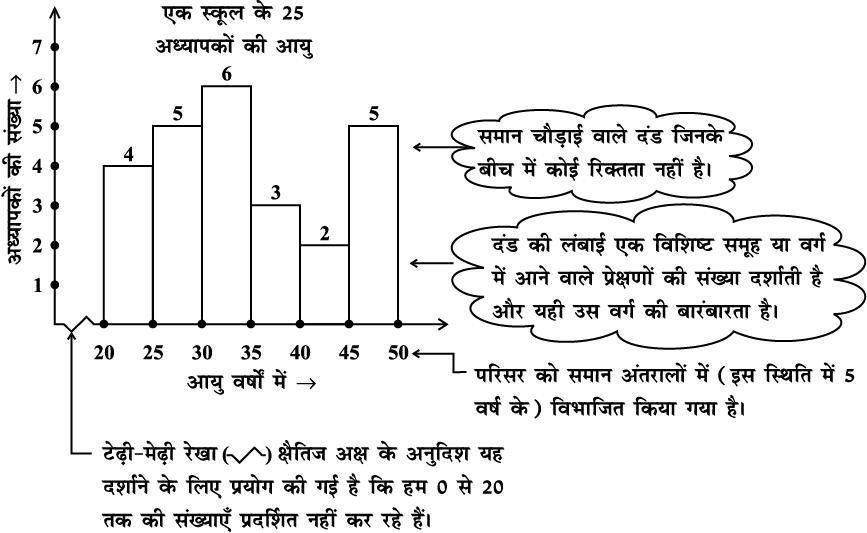
आकृति 5.2
इस आयतचित्र के दंडों से हम निम्नलिखित प्रश्नों के उत्तर दे सकते हैं :
(i) कितने अध्यापकों की आयु 45 वर्ष या उससे अधिक है परंतु 50 वर्ष से कम है?
(ii) 35 वर्ष से कम आयु वाले अध्यापकों की संख्या कितनी है?

प्रयास कीजिए
1. आयतचित्र (आकृति 5.3) को देखिए और उसके नीचे दिए गए प्रश्नों के उत्तर दीजिए:
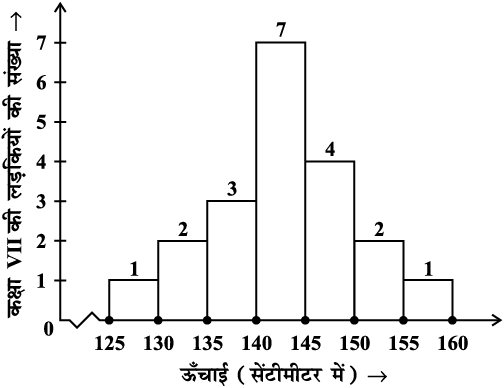
आकृति 5.3
(i) इस आयतचित्र द्वारा क्या सूचना दी जा रही है?
(ii) किस वर्ग में अधिकतम लड़कियाँ हैं?
(iii) कितनी लड़कियों की लंबाई 145 cm या उससे अधिक है?
(iv) यदि हम लड़कियों को निम्नलिखित तीन श्रेणियों में विभाजित करें, तो प्रत्येक में कितनी लड़कियाँ होंगी?
150 cm या उससे अधिक — समूह A
140 cm या उससे अधिक परंतु 150 cm से कम — समूह B
140 cm से कम — समूह C

प्रश्नावली 5.1
1. निम्नलिखित में से किन आँकड़ों को दर्शाने के लिए आप एक आयतचित्र का प्रयोग करेंगे?
(a) एक डाकिए के थैले में विभिन्न क्षेत्रों के पत्रों की संख्या।
(b) किसी खेलकूद प्रतियोगिता में प्रत्याशियों की ऊँचाइयाँ।
(c) 5 कंपनियों द्वारा निर्मित कैसेटों की संख्या।
(d) किसी स्टेशन पर प्रात: 7 बजे से सायं 7 बजे तक रेलगाड़ियों से जाने वाले यात्रियों की संख्या।
प्रत्येक के लिए, कारण भी दीजिए।
2. किसी विभागीय स्टोर पर खरीदारी करने आए व्यक्तियों को इस प्रकार अंकित किया जाता है : पुरुष (M), महिला (W), लड़का (B) या लड़की (G)। निम्नलिखित सूची उन खरीदारों को दर्शाती है, जो प्रात:काल पहले घंटे में आए हैं :
W W W G B W W M G G M M W W W W G B M W B G G M W W M M W W W M W B W G M W W W W G W M M W W M W G W M G W M M B G G W
मिलान चिह्नों का प्रयोग करते हुए एक बारंबारता बंटन सारणी बनाइए। इसे प्रदर्शित करने के लिए एक दंड आलेख खींचिए।
3. किसी फैक्ट्री के 30 श्रमिकों की साप्ताहिक मजदूरी (रुपयों में) निम्नलिखित है :
830, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 835, 836, 878, 840, 868, 890, 806, 840
मिलान चिह्नों का प्रयोग करते हुए, अंतरालों 800-810, 810-820 इत्यादि वाली एक बारंबारता सारणी बनाइए।
4. प्रश्न 3 में दिए आँकड़ों से प्राप्त सारणी के लिए एक आयतचित्र बनाइए और निम्नलिखित प्रश्नों के उत्तर दीजिए :
(i) किस समूह में श्रमिकों की संख्या सबसे अधिक है?
(ii) कितने श्रमिक ₹ 850 या उससे अधिक अर्जित करते हैं?
(iii) कितने श्रमिक ₹ 850 से कम अर्जित करते हैं?
5. अवकाश के दिनों में एक विशिष्ट कक्षा के विद्यार्थियों द्वारा प्रतिदिन टेलीविज़न (टी.वी.) देखने के समय (घंटों में), दिए हुए आलेख में दर्शाए गए हैं :
निम्नलिखित प्रश्नों के उत्तर दीजिए :
(i) अधिकतम विद्यार्थियों ने कितने घंटों तक टी.वी. देखा?
(ii) 4 घंटों से कम समय तक कितने विद्यार्थियों ने टी.वी. देखा?
(iii) कितने विद्यार्थियों ने टी.वी. देखने में 5 घंटे से अधिक का समय व्यतीत किया?

5.4 वृत्त आलेख या पाई चार्ट
क्या आपके सम्मुख कभी वृत्तीय रूप में निरूपित आँकड़े प्रस्तुत हुए हैं, जैसे आकृति 5.4 में दर्शाए गए हैं?
.png)
ये निरूपण वृत्त आलेख (circle graphs) कहलाते हैं। एक वृत्त आलेख एक संपूर्ण (whole) और उसके भागों में संबंध दर्शाता है। यहाँ संपूर्ण वृत्त को त्रिज्यखंडों (sectors) में विभाजित किया जाता है। प्रत्येक त्रिज्यखंड का साइज़ या आमाप उसके द्वारा निरूपित क्रियाकलाप या सूचना के समानुपाती होता है।
उदाहरणार्थ, उपरोक्त आलेख में, सोने की क्रिया में व्यतीत किए गए घंटों में त्रिज्यखंड का आनुपातिक भाग
= 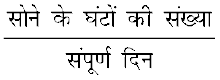 =
= 
इसीलिए, इस त्रिज्यखंड को पूरे वृत्त के 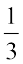 वें भाग के रूप में खींचा गया है। इसी प्रकार, स्कूल में व्यतीत किए गए घंटों के त्रिज्यखंड का आनुपातिक भाग
वें भाग के रूप में खींचा गया है। इसी प्रकार, स्कूल में व्यतीत किए गए घंटों के त्रिज्यखंड का आनुपातिक भाग
= 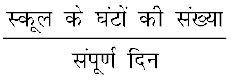 =
= 
इसीलिए, इस त्रिज्यखंड को वृत्त के 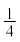 भाग के रूप में खींचा गया है। इसी प्रकार, अन्य त्रिज्यखंडों के माप ज्ञात किए जा सकते हैं।
भाग के रूप में खींचा गया है। इसी प्रकार, अन्य त्रिज्यखंडों के माप ज्ञात किए जा सकते हैं।
सभी क्रियाकलापों की भिन्नों को जोड़िए। क्या आपको योग एक प्राप्त होता है?
वृत्त आलेख पाई चार्ट (pie दैनिक आय श्रमिकों की संख्या
75-100 45
100-125 35
125-150 55
150-175 30
175-200 50
200-225 125
225-250 140
योग 480chart) भी कहलाता है।
प्रयास कीजिए
1. निम्नलिखित पाई चार्टों में से प्रत्येक (आकृति 5.5) आपकी कक्षा के बारे में एक भिन्न प्रकार की सूचना देता है। इनमें से प्रत्येक सूचना को निरूपित करने वाला वृत्त का भाग ज्ञात कीजिए।
.png)
आकृति 5.5
2. दिए हुए पाई चार्ट (आकृति 5.6) के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए :
प्रयास कीजिए
(i) किस प्रकार के कार्यक्रम सबसे अधिक देखे जाते हैं?
(ii) किन दो प्रकार के कार्यक्रमों को देखने वालों की कुल संख्या खेलों के कार्यक्रमों को देखने वालों की संख्या के बराबर है?
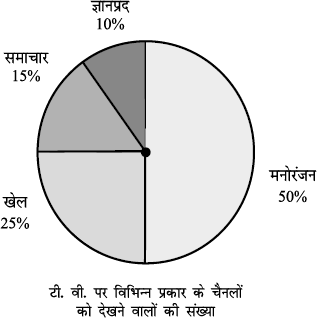
आकृति 5.6
5.4.1 पाई चार्टों का खींचना
किसी स्कूल के विद्यार्थियों द्वारा पसंद किए जाने वाली आइसक्रीमों की महक या स्वाद (प्रतिशतों में) नीचे दिए गए हैं :
.png)
आइए, इन आँकड़ों को एक पाई चार्ट के रूप में निरूपित करें।
वृत्त के केंद्र पर पूरा कोण 360° है। त्रिज्यखंडों के केंद्रीय कोण (central angles) 360° के भाग या कोई भिन्न होंगे। हम त्रिज्यखंडों के केंद्रीय कोणों को ज्ञात करने के लिए एक सारणी बनाएँगे (सारणी 5.5)।
सारणी 5.5
.png)
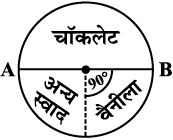
1. किसी सुविधाजनक त्रिज्या का एक वृत्त खींचिए। इसका केंद्र (O) और एक त्रिज्या (OA) अंकित कीजिए।

2. चॉकलेट के त्रिज्यखंड का कोण 180° है। चाँदे का प्रयोग करके, ∠ AOB=180° खींचिए।

3. बचे हुए त्रिज्यखंडों को भी इसी प्रकार अंकित करते रहिए।
उदाहरण 1 : संलग्न पाई चार्ट (आकृति 5.7) एक महीने में एक परिवार के विभिन्न मदों में व्यय और उसकी बचत (प्रतिशतों में) को दर्शाता है।
(i) किस मद में व्यय सबसे अधिक है?
(ii) किस मद पर हुआ व्यय परिवार की कुल बचत के बराबर है?
(iii) यदि परिवार की मासिक बचत ₹ 3000 है, तो कपड़ों पर हुआ मासिक व्यय क्या है?
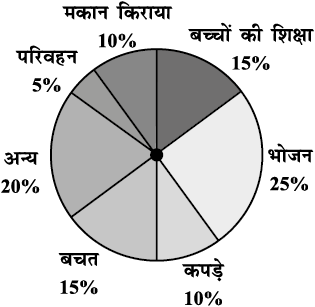
आकृति 5.7
हल :
(i) भोजन पर व्यय सबसे अधिक है।
(ii) बच्चों की शिक्षा पर हुआ व्यय (15%) परिवार की कुल बचत के बराबर है।
(iii) 15% निरूपित करता है, ₹ 3000।
अत:, 10% निरूपित करता है, ₹ 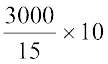 = ₹ 2000।
= ₹ 2000।
उदाहरण 2 : एक विशेष दिन किसी बेकरी की दुकान में हुई विभिन्न वस्तुओं की बिक्री (रुपयों में) नीचे दी गई है:.png)
हल : हम प्रत्येक त्रिज्यखंड का केंद्रीय कोण ज्ञात करते हैं। यहाँ कुल बिक्री ₹ 720 है। इससे हमें निम्नलिखित सारणी प्राप्त होती है:
.png)
उपरोक्त का प्रयोग करके, अब हम पाई चार्ट बनाते हैं (आकृति 5.8)।
प्रयास कीजिए
नीचे दिए आँकड़ों के लिए एक पाई चार्ट खींचिए :
एक बच्चे द्वारा एक दिन में व्यतीत किया गया समय इस प्रकार है:
सोना — 8 घंटे
स्कूल — 6 घंटे
गृह कार्य — 4 घंटे
खेल — 4 घंटे
अन्य — 2 घंटे
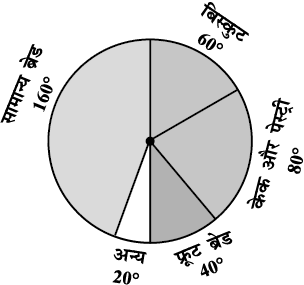
आकृति 5.8
सोचिए, चर्चा कीजिए और लिखिए
निम्नलिखित आँकड़ों को दर्शाने के लिए, किस प्रकार का आलेख उपयुक्त रहेगा?
1. किसी राज्य के खाद्यान्न का उत्पादन :
.png)
2. व्यक्तियों के एक समूह के भोजन की पसंद :
.png)
3. किसी फैक्ट्री के श्रमिकों के एक समूह की दैनिक आय :
.png)
प्रश्नावली 5.2
1. किसी शहर के युवा व्यक्तियों के एक समूह का यह जानने के लिए एक सर्वे किया गया कि वे किस प्रकार का संगीत पसंद करते हैं। इनसे प्राप्त आँकड़ों को संलग्न पाई चार्ट में दर्शाया गया है। इस पाई चार्ट से निम्नलिखित प्रश्नों के उत्तर दीजिए :
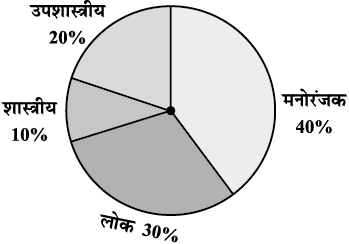
(i) यदि 20 व्यक्ति शास्त्रीय संगीत पसंद करते हैं, तो कुल कितने युवा व्यक्तियों का सर्वे किया गया था?
(ii) किस प्रकार का संगीत सबसे अधिक व्यक्तियों द्वारा पसंद किया जाता है?
(iii) यदि कोई कैसेट कंपनी 1000 सी.डी. (C.D.) बनाए, तो वह प्रत्येक प्रकार की कितनी सी.डी. बनाएगी?
2. 360 व्यक्तियों के एक समूह से तीन ऋतुओं – वर्षा, सर्दी और गर्मी में से अपनी मनपसंद ऋतु के लिए मतदान करने को कहा गया। इनसे प्राप्त आँकड़ों को संलग्न चित्र में दर्शाया गया है :
(i) किस ऋतु को सबसे अधिक मत मिले?
(ii) प्रत्येक त्रिज्यखंड का केंद्रीय कोण ज्ञात कीजिए।
(iii) इस सूचना को दर्शाने के लिए, एक पाई चार्ट खींचिए।
.png)
3. निम्नलिखित सूचना को दर्शाने वाला एक पाई चार्ट खींचिए। यह सारणी व्यक्तियों के एक समूह द्वारा पसंद किए जाने वाले रंगों को दर्शाती है।
.png)
4. संलग्न पाई चार्ट एक विद्यार्थी द्वारा किसी परीक्षा में हिंदी, अंग्रेज़ी, गणित, सामाजिक विज्ञान और विज्ञान में प्राप्त किए गए अंकों को दर्शाता है। यदि उस विद्यार्थी द्वारा प्राप्त किए गए कुल अंक 540 थे, तो निम्नलिखित प्रश्नों के उत्तर दीजिए :
(i) किस विषय में उस विद्यार्थी ने 105 अंक प्राप्त किए?
(संकेत : 540 अंकों के लिए केंद्रीय कोण 360° है। अत:, 105 अंकों के लिए केंद्रीय कोण क्या होगा?)
(iii) जाँच कीजिए कि क्या सामाजिक विज्ञान और गणित में प्राप्त किए गए अंकों का योग विज्ञान और हिंदी में प्राप्त किए गए अंकों के योग से अधिक है। (संकेत : केवल केंद्रीय कोणों पर ध्यान दीजिए।)
.png)
5. किसी छात्रावास में, विभिन्न भाषाएँ बोलने वाले विद्यार्थियों की संख्या नीचे दी गई है। इन आँकड़ों को एक पाई चार्ट द्वारा प्रदर्शित कीजिए।
.png)
5.5 संयोग और प्रायिकता
कभी-कभी एेसा होता है कि वर्षा ऋतु में, हम प्रत्येक दिन बरसाती लेकर बाहर निकलते हैं और कई दिनों तक कोई वर्षा नहीं होती है। परंतु संयोग से एक दिन आप बरसाती ले जाना भूल जाते हैं और उसी दिन भारी वर्षा हो जाती है।
.png)
कभी-कभी एेसा हो जाता है कि एक विद्यार्थी एक टेस्ट के लिए 5 में से 4 अध्याय अच्छी प्रकार से तैयार कर लेता है। परंतु एक बड़ा प्रश्न उस अध्याय में से पूछ लिया जाता है जिसे उसने अच्छी प्रकार से तैयार नहीं किया था।
प्रत्येक व्यक्ति जानता है कि एक विशेष रेलगाड़ी सही समय से चलती है, परंतु जिस दिन आप सही समय पर पहुँचते हैं, उसी दिन वह देरी से आती है।
आपको उपरोक्त प्रकार की अनेक स्थितियों का सामना करना पड़ता है, जहाँ आप संयोग (chance) का सहारा लेकर कार्य करना चाहते हैं, परंतु वह उस प्रकार से नहीं होता जैसा आप चाहते हैं। क्या आप एेसे कुछ और उदाहरण दे सकते हैं? ये एेसे उदाहरण हैं जहाँ किसी बात के होने या न होने के संयोग बराबर (समान) नहीं हैं।
एक रेलगाड़ी के समय पर आने या न आने के संयोग बराबर नहीं हैं। जब आप कोई टिकट खरीदते हैं और यदि वह प्रतीक्षा सूची में है, तो आप निश्चय ही संयोग का सहारा लेते हैं। आप यह आशा करते हैं कि जब आप यात्रा करेंगे तब संभवत: इस टिकट पर आपकी सीट आरक्षित हो जाएगी। परंतु यहाँ हम कुछ एेसे प्रयोगों (experiments) पर विचार करेंगे जिनमें परिणामों के घटित होने के संयोग बराबर हैं।
5.5.1 कोई परिणाम प्राप्त करना
आपने संभवत: यह देखा होगा कि एक क्रिकेट मैच के प्रारंभ होने से पहले, दोनों टीमों के कप्तान बाहर जाकर यह निर्णय करने के लिए सिक्का (coin) उछालते (toss) हैं कि कौन-सी टीम पहले बल्लेबाजी करेगी।
जब एक सिक्के को उछाला जाता है, तो आपको क्या संभव परिणाम प्राप्त होते हैं? नि:संदेह, चित (Head) या पट (Tail)।
कल्पना कीजिए कि आप एक टीम के कप्तान हैं और आपका मित्र दूसरी टीम का कप्तान है। आप एक सिक्का उछालते हैं और अपने मित्र से चित या पट बोलने को कहते हैं। क्या आप इस उछाल के परिणाम पर कोई नियंत्रण रख सकते हैं? क्या आपको चित प्राप्त हो सकता है, यदि आप एेसा चाहते हैं? अथवा क्या आपको पट प्राप्त हो सकता है, यदि आप एेसा चाहते हैं? नहीं, एेसा संभव नहीं है। इस प्रकार का प्रयोग एक यादृच्छ या यादृच्छिक प्रयोग (random experiment) कहलाता है। चित और पट इस प्रयोग के दो परिणाम (outcomes) हैं।
प्रयास कीजिए
1. यदि आप एक स्कूटर चलाना प्रारंभ करें, तो संभव परिणाम क्या हैं?
2. जब एक पासे (die) को फेंका जाता है, तो संभव छह परिणाम क्या हैं?
3. जब आप पहिए को घुमाएँगे, तो संभावित परिणाम क्या होंगे (आकृति 5.9)? इनकी सूची बनाइए।
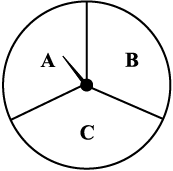
आकृति 5.9
(यहाँ परिणाम का अर्थ है कि वह त्रिज्यखंड जहाँ पर सूचक (pointer) घुमाने पर रुकेगा।)
4. आपके पास एक थैला है और उसमें भिन्न-भिन्न रंगों की पाँच एक जैसी गेंदें हैं (आकृति 5.10)। आप बिना देखे इसमें से एक गेंद निकालते हैं। प्राप्त होने वाले परिणामों को लिखिए।
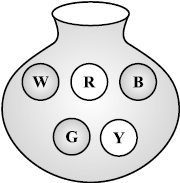
आकृति 5.10
सोचिए, चर्चा कीजिए और लिखिए
एक पासे को फेंकने पर :
• क्या पहले खिलाड़ी के 6 प्राप्त करने का संयोग अधिक है?
• क्या उसके बाद खेलने वाले खिलाड़ी के 6 प्राप्त करने का संयोग कम है?
• मान लीजिए कि दूसरा खिलाड़ी 6 प्राप्त कर लेता है। क्या इसका अर्थ यह है कि तीसरे खिलाड़ी द्वारा 6 प्राप्त करने का कोई संयोग नहीं है?
5.5.2 सम संभावित परिणाम
एक सिक्के को अनेक बार उछाला जाता है तथा जितनी बार चित या पट आते हैं उन्हें लिख लिया जाता है। आइए अपनी परिणाम शीट (तालिका) को देखें, जहाँ हम उछालों की संख्या में वृद्धि करते जा रहे हैं :
.png)
ध्यान दीजिए कि जब आप उछालों की संख्या अधिकाधिक बढ़ाते जाते हैं, तब चितों की संख्या और पटों की संख्या परस्पर अधिकाधिक निकट आते जाते हैं।
एेसा ही एक पासे के साथ भी हो सकता है, जब उसे एक बड़ी संख्या में फेंका जाता है। छह परिणामों में से प्रत्येक की संख्या परस्पर लगभग बराबर हो जाती हैं।
एेसी स्थितियों में, हम कह सकते हैं कि प्रयोग के विभिन्न परिणाम सम संभावित या समप्रायिक (equally likely) हैं। इसका अर्थ यह है कि सभी में से प्रत्येक परिणाम के आने का संयोग (chance) एक ही है।
.png)
5.5.3 संयोग को प्रायिकता से जोड़ना
एक सिक्के को एक बार उछालने के प्रयोग पर विचार कीजिए। परिणाम क्या हैं? यहाँ केवल दो परिणाम हैं– चित या पट। दोनों ही परिणाम समप्रायिक (equally likely) हैं। एक चित प्राप्त करने की संभावना 2 परिणामों में से 1, अर्थात्  है। दूसरे शब्दों में, हम कहते हैं कि एक चित प्राप्त करने की प्रायिकता (probability) =
है। दूसरे शब्दों में, हम कहते हैं कि एक चित प्राप्त करने की प्रायिकता (probability) =  है। एक पट प्राप्त करने की प्रायिकता क्या है?
है। एक पट प्राप्त करने की प्रायिकता क्या है?
अब एक पासे को फेंकने के उदाहरण पर विचार कीजिए, जिसके फलकों (faces) पर 1, 2, 3, 4, 5, 6 (एक फलक पर एक संख्या) अंकित हैं। यदि आप इसे एक बार फेंके, तो परिणाम क्या प्राप्त होंगे?
परिणाम हैं : 1, 2, 3, 4, 5, 6 । इस प्रकार, यहाँ छह समप्रायिक परिणाम हैं।
परिणाम 2 प्राप्त करने की प्रायिकता क्या है?
.png)
संख्या 5 प्राप्त करने की प्रायिकता क्या है? संख्या 7 प्राप्त करने की प्रायिकता क्या है? 1 से 6 तक की संख्या प्राप्त करने की प्रायिकता क्या है?
5.5.4 घटनाओं के रूप में परिणाम
एक प्रयोग के प्रत्येक परिणाम या परिणामों के संग्रह से एक घटना (event) बनती है। उदाहरणार्थ, एक सिक्के को उछालने के प्रयोग में, एक ‘चित’ प्राप्त करना एक घटना है तथा एक ‘पट’ प्राप्त करना भी एक घटना है।
एक पासे को फेंकने की स्थिति में, परिणामों 1, 2, 3, 4, 5 और 6 में से प्रत्येक परिणाम प्राप्त करना एक घटना है।
क्या एक सम संख्या प्राप्त करना एक घटना है? क्योंकि एक सम संख्या 2, 4 या 6 हो सकती है, इसलिए एक सम संख्या प्राप्त करना भी एक घटना है। एक सम संख्या प्राप्त करने की प्रायिकता क्या होगी?
.png)
उदाहरण 3 : एक थैले में 4 लाल गेंदें और 2 पीली गेंदें हैं। (ये गेंदें रंग के अतिरिक्त सभी प्रकार से एक जैसी, अर्थात् सर्वसम (identical) हैं।) थैले के अंदर से बिना देखे एक गेंद निकाली जाती है। एक लाल गेंद प्राप्त करने की क्या प्रायिकता है? क्या यह एक पीली गेंद प्राप्त करने की प्रायिकता से अधिक है या कम?
हल : यहाँ घटना के कुल (4 + 2 =) 6 परिणाम हैं। लाल गेंद प्राप्त करने के लिए 4 परिणाम हैं। (क्यों?)
अत:, लाल गेंद प्राप्त करने की प्रायिकता 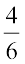 =
= 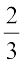 है।
है।
इसी प्रकार, पीली गेंद प्राप्त करने की प्रायिकता  =
= 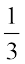 है। (क्यों?)
है। (क्यों?)
अत:, लाल गेंद प्राप्त करने की प्रायिकता पीली गेंद प्राप्त करने की प्रायिकता से अधिक है।
प्रयास कीजिए
1. मान लीजिए कि आप पहिए को घुमाते हैं (आकृति 5.11)।
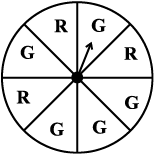
आकृति 5.11
(i) इस पहिए पर एक हरा त्रिज्यखंड प्राप्त करने के परिणामों की संख्या और हरा त्रिज्यखंड प्राप्त न होने के परिणामों की संख्या लिखिए।
(ii) एक हरा त्रिज्यखंड प्राप्त करने की प्रायिकता ज्ञात कीजिए।
(iii) एक हरा त्रिज्यखंड प्राप्त न होने की प्रायिकता ज्ञात कीजिए।
5.5.5 वास्तविक जीवन से संबंधित संयोग और प्रायिकता
हमने उस संयोग की बात की थी जिसमें केवल उसी दिन वर्षा हुई जब हम बरसाती लेकर नहीं चले थे। आप प्रायिकता के पदों में संयोग के बारे में क्या कह सकते थे? क्या यह वर्षा ऋतु में 10 दिन में 1 दिन हो सकता था?
तब वर्षा होने की प्रायिकता 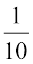 है। वर्षा न होने की प्रायिकता
है। वर्षा न होने की प्रायिकता 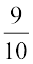 है।
है।
(यह कल्पना करते हुए कि किसी दिन वर्षा होना या न होना सम संभावित या समप्रायिक है।) वास्तविक जीवन की विभिन्न स्थितियों में प्रायिकता का प्रयोग किया जाता है।
1. एक बड़े समूह के अभिलक्षणों या विशेषताओं को उस समूह के एक छोटे भाग का प्रयोग करते हुए ज्ञात करना। उदाहरणार्थ, चुनाव के समय ‘एक्जिट पोल’ (exit poll) किया जाता है। इसमें संपूर्ण क्षेत्र में बंटित केंद्रों में से यदृच्छ रूप से (बिना किसी पूर्वाग्रह के) कुछ केंद्र चुनकर मतदान करके आने वाले व्यक्तियों से यह पूछा जाता है कि उन्होंने किसे मत दिया है। इससे प्रत्येक प्रत्याशी के जीतने की संभावना का अनुमान लग जाता है तथा इसी आधार पर प्रागुक्तियाँ (भविष्यवाणियाँ) की जाती हैं।
2. मौसम विभाग बीते हुए अनेक वर्षों के आँकड़ों की प्रवृत्तियों को देखकर मौसम के बारे में भविष्यवाणी (प्रागुक्तियाँ) करता है।
प्रश्नावली 5.3
1. इन प्रयोगों में आप जो परिणाम देख सकते हैं उन्हें लिखिए :
(a) पहिए को घुमाना

(b) दो सिक्कों को एक साथ उछालना
2. जब एक पासे को फेंका जाता है, तब निम्नलिखित प्रत्येक घटना से प्राप्त होने वाले परिणामों को लिखिए :
(i) (a) एक अभाज्य संख्या (b) एक अभाज्य संख्या नहीं
(ii) (a) 5 से बड़ी एक संख्या (b) 5 से बड़ी संख्या नहीं
3. ज्ञात कीजिए :
(a) (प्रश्न 1(a) में) सूचक के D पर रुकने की प्रायिकता।
(b) अच्छी प्रकार से फेटी हुई 52 ताशों की एक गड्डी में से 1 इक्का प्राप्त करने की प्रायिकता।
(c) एक लाल सेब प्राप्त करने की प्रायिकता (दी हुई आकृति से देखिए)।

4. 10 पृथक् पर्चियों पर 1 से 10 तक संख्याएँ लिखी हुई हैं (एक पर्ची पर एक संख्या), उन्हें एक बक्स में रखकर अच्छी प्रकार से मिला दिया जाता है। बक्स के अंदर से बिना देखे एक पर्ची निकाली जाती है। निम्नलिखित की प्रायिकता क्या है?
(i) संख्या 6 प्राप्त करना।
(ii) 6 से छोटी एक संख्या प्राप्त करना।
(iii) 6 से बड़ी एक संख्या प्राप्त करना।
(iv) 1 अंक की एक संख्या प्राप्त करना।
5. यदि आपके पास 3 हरे त्रिज्यखंड, 1 नीला त्रिज्यखंड और 1 लाल त्रिज्यखंड वाला एक घूमने वाला पहिया है तो एक हरा त्रिज्यखंड प्राप्त करने की प्रायिकता क्या है? एेसा त्रिज्यखंड प्राप्त करने की प्रायिकता क्या है, जो नीला न हो?
6. प्रश्न 2 में दी हुई घटनाओं की प्रायिकताएँ ज्ञात कीजिए।
हमने क्या चर्चा की?
1. हमारे पास अधिकतर उपलब्ध आँकड़े जो असंगठित रूप में होते हैं जिन्हें यथाप्राप्त आँकड़े कहा जाता है।
2. किन्हीं भी आँकड़ों से अर्थपूर्ण निष्कर्ष निकालने के लिए हमें उन्हें क्रमबद्ध रूप में संगठित करने की आवश्यकता पड़ती है।
3. बारंबारता वह संख्या दर्शाती है जितनी बार कोई एक विशिष्ट प्रविष्टि आँकड़ों में आती है।
4. यथाप्राप्त आँकड़ों के समूह बनाए जा सकते हैं और उन्हें एक क्रमबद्ध प्रकार से ‘वर्गीकृत बारंबारता बंटन’ के रूप में प्रस्तुत किया जा सकता है।
5. वर्गीकृत आँकड़ों को आयतचित्र का प्रयोग करते हुए प्रदर्शित किया जा सकता है। आयतचित्र एक प्रकार का दंड आलेख है, जिसमें क्षैतिज अक्ष पर वर्ग अंतरालों को दर्शाया जाता है तथा दंडों की लंबाइयाँ वर्ग अंतरालों की बारंबारताएँ दर्शाती हैं। साथ ही, दंडों के बीच में कोई रिक्तता नहीं होती, क्योंकि वर्ग अंतरालों के बीच में कोई रिक्तता नहीं है।
6. आँकड़ों को वृत्त आलेख या पाई चार्ट का प्रयोग करके भी प्रस्तुत किया जा सकता है। एक वृत्त आलेख एक संपूर्ण और उसके भागों में संबंध को दर्शाता है।
7. कुछ एेसे प्रयोग होते हैं जिनमें परिणामों के आने के संयोग बराबर होते हैं।
8. एक यदृच्छ प्रयोग वह प्रयोग है जिसमें परिणामों की ठीक-ठीक प्रागुक्ति (भविष्यवाणी) पहले से नहीं की जा सकती है।
9. किसी प्रयोग के परिणाम सम संभावित या समप्रायिक कहलाते हैं, यदि उनके आने के संयोग बराबर हों।
10..png)
जब परिणाम समप्रायिक हैं।
11. किसी प्रयोग के एक या अधिक परिणामों से एक घटना बनती है।
12. संयोग और प्रायिकता वास्तविक जीवन से संबंधित हैं।

 प्रयास कीजिए
प्रयास कीजिए