Table of Contents
अध्याय 6
वर्ग और वर्गमूल
6.1 भूमिका
आप जानते हैं कि वर्ग का क्षेत्रफल = भुजा × भुजा (जहाँ ‘भुजा’ का अर्थ एक भुजा की लंबाई) होता हैै। निम्न सारणी का अध्ययन कीजिए:
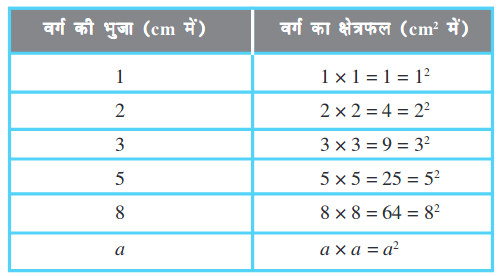
संख्याओं 4, 9, 25, 64 और इस प्रकार की दूसरी संख्याओं में क्या विशेष है? चूँकि 4 को 2 × 2 = 22, 9 को 3 × 3 = 32 के रूप में व्यक्त कर सकते हैं अतः हम पाते हैं कि इस प्रकार की सभी संख्याओं को उसी संख्या के गुणनफल के रूप में व्यक्त किया जा सकता है।
इस प्रकार की संख्याएँ जैसे 1, 4, 9, 16, 25, ... को वर्ग संख्याएँ कहते हैं।
साधारणतया, यदि एक प्राकृत संख्या m को n2 से व्यक्त किया जाता है, जहाँ n भी एक प्राकृत संख्या है, तब m एक वर्ग संख्या है। क्या 32 एक वर्ग संख्या है?
हम जानते हैं कि 52 = 25 और 62 = 36 होता है। यदि 32 एक वर्ग संख्या है, तो यह एक प्राकृत संख्या का वर्ग होना चाहिए जो 5 और 6 के बीच हो। परंतु यहाँ 5 और 6 के बीच कोई प्राकृत संख्या नहीं है। निम्न संख्याओं और उनके वर्गों के बारे में विचार कीजिए:

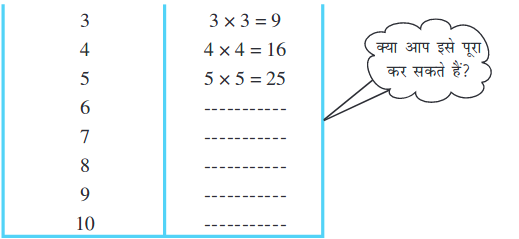
उपरोक्त सारणी से क्या आप 1 से 100 के बीच की वर्ग संख्याओं को लिख सकते हैं?
क्या 100 तक कोई प्राकृत वर्ग संख्या छूट गई है? आप पाएँगे कि शेष सभी संख्याएँ, वर्ग
संख्याएँ नहीं हैं। संख्याएँ 1, 4, 9, 16 वर्ग संख्याएँ हैं। ये संख्याएँ पूर्ण वर्ग संख्याएँ भी
कहलाती हैं।
प्रयास कीजिए
1. दी गई संख्याओं के बीच की पूर्ण वर्ग संख्याएँ ज्ञात कीजिए।
(i) 30 और 40 (ii) 50 और 60
6.2 वर्ग संख्याओं के गुणधर्म
निम्नलिखित सारणी में 1 से 20 तक की वर्ग संख्याओं को दिखाया गया है।
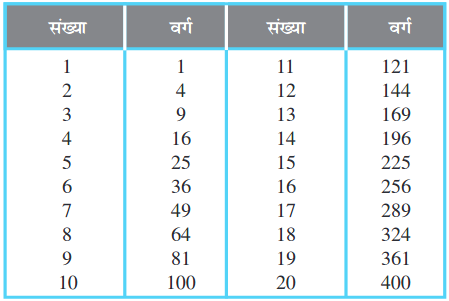
उपरोक्त सारणी में वर्ग संख्याओं का अध्ययन कीजिए। वर्ग संख्याओं का अंतिम अंक (यानी वर्ग संख्याओं के इकाई स्थान का अंक) क्या है? ये सभी संख्याएँ इकाई स्थान पर 0, 1, 4, 5, 6 या 9 पर समाप्त होती हैं। इनमें से किसी भी संख्या के इकाई स्थान पर 2, 3, 7 या 8 नहीं आता है।
क्या हम कह सकते हैं कि यदि एक संख्या 0, 1, 4, 5, 6 या 9 पर समाप्त होती है, तो वह एक वर्ग संख्या होगी? इस बारे में सोचिए।
प्रयास कीजिए
1. क्या हम कह सकते हैं कि निम्न संख्याएँ पूर्ण वर्ग संख्याएँ हैं? हम कैसे जानते हैं?
(i) 1057 (ii) 23453 (iii) 7928 (iv) 222222
(v) 1069 (vi) 2061
पाँच एेसी संख्याएँ लिखिए जिनके इकाई स्थान को देखकर आप बता सकें कि ये संख्याएँ वर्ग संख्याएँ नहीं हैं।
2. पाँच एेसी संख्याएँ लिखिए जिनके इकाई स्थान को देखकर आप नहीं बता सकते कि वे वर्ग संख्याएँ हैं या नहीं।
• निम्न सारणी में कुछ संख्याओं एवं उनके वर्गों का अध्ययन कीजिए और दोनों में इकाई स्थान का निरीक्षण कीजिए:
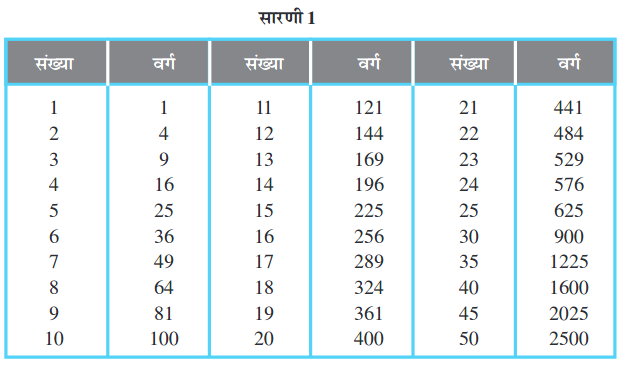
निम्नलिखित वर्ग संख्याएँ अंक 1 पर समाप्त होती हैं:
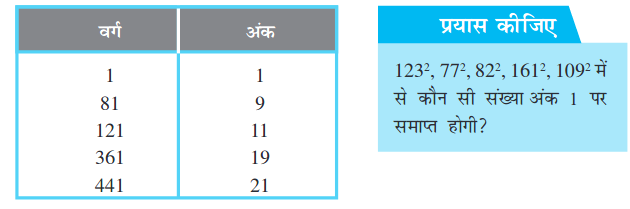
इनके अलावा अगली दो वर्ग संख्याएँ लिखिए जो 1 पर उनकी संगत संख्याओं पर समाप्त होती है।
आप देखेंगे कि यदि एक संख्या के इकाई स्थान पर 1 या 9 आता है तब इसकी वर्ग संख्या के अंत में 1 आता है।
• अब 6 पर समाप्त होने वाली संख्या पर विचार कीजिए:

हम देखते हैं कि जब कोई वर्ग संख्या 6 पर समाप्त होती है तो वह जिस संख्या का वर्ग हेै, उसका इकाई अंक या तो 4 या 6 होगा।
क्या आप इस प्रकार के कुछ और नियम, सारणी में लिखी गई संख्याओं एवं उनके वर्गों के अवलोकन से ज्ञात कर सकते हैं (सारणी 1)?
निम्नलिखित संख्याओं के वर्ग करने पर उनके इकाई स्थान पर क्या होगा?
(i) 1234 (ii) 26387 (iii) 52698 (iv) 99880
(v) 21222 (vi) 9106
• निम्नलिखित संख्याओं और उनके वर्गों पर विचार कीजिए:
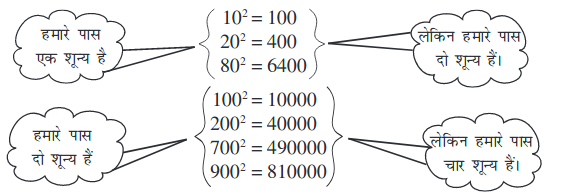
यदि एक संख्या के अंत में तीन शून्य हों, तो उसके वर्ग में कितने शून्य होंगे? क्या आपने, संख्या के अंत में शून्यों की संख्या और उसके वर्ग के अंत में शून्यों की संख्या पर ध्यान दिया?
क्या आप कह सकते हैं कि वर्ग संख्याओं के अंत में शून्यों की संख्या केवल सम संख्या होती है?
• संख्या और उनके वर्गों के लिए सारणी 1 देखिए।
सम संख्याओं के वर्गों एवं विषम संख्याओं के वर्गों के बारे में आप क्या कह सकते हैं?
प्रयास कीजिए
1. निम्नलिखित में से किन संख्याओं के वर्ग विषम संख्या/सम संख्या होंगे। क्यों?
(i) 727 (ii) 158 (iii) 269 (iv) 1980
2. निम्नलिखित संख्याओं के वर्ग में शून्यों की संख्या क्या होगी?
(i) 60 (ii) 400
6.3 कुछ और रोचक प्रतिरूप
1. त्रिकोणीय संख्याओं के जोड़
क्या आपको त्रिकोणीय संख्याएँ (संख्याएँ जिनके बिंदु प्रतिरूप त्रिभुजों के रूप में व्यवस्थित किए जा सकते हैं) याद हैं?
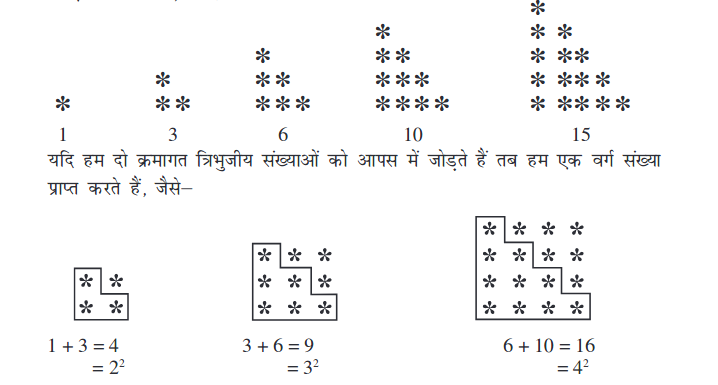
2. वर्ग संख्याओं के बीच की संख्याएँ
अब हम देखेंगे कि क्या हम दो क्रमागत वर्ग संख्याओं के बीच कुछ रुचिकर प्रतिरूप प्राप्त कर सकते हैं।

12(=1) और 22(= 4) के बीच में दो (अर्थात् 2 × 1) संख्याएँ 2, 3, हैं जो वर्ग संख्याएँ नहीं हैं।
22(= 4) और 32(= 9) के बीच में चार (अर्थात् 2 × 2) संख्याएँ 5, 6, 7, 8, है जो वर्ग संख्याएँ नहीं हैं।
अब 32 = 9, 42 = 16
अतः 42 – 32 = 16 – 9 = 7
यहाँ 9(=32) और 16(= 42) के बीच में छः संख्याएँ 10, 11, 12, 13, 14, 15 हैं जो वर्ग संख्याएँ नहीं हैं, उनकी संख्या दोनों वर्गों के अंतर से 1 कम है।
हमारे पास 42 = 16 और 52 = 25 है।
अतः 52 – 42 = 9
यहाँ 16(= 42) और 25(= 52) के बीच 17, 18, ... , 24 आठ संख्याएँ हैं जो वर्ग संख्याएँ नहीं हैं। उनकी संख्या दो वर्गों के अंतर से 1 कम है
72 और 62 को देखिए। क्या तुम कह सकते हो कि 62 और 72 के बीच कितनी संख्याएँ हैं?
यदि हम कोई प्राकृत संख्याएँ n और (n + 1) लेते हैं तब
(n + 1)2 – n2 = (n2 + 2n + 1) – n2 = 2n + 1
हम n2 और (n + 1)2 के बीच 2n संख्याएँ पाते हैं जो दो वर्ग संख्याओं के अंतर से 1 कम है।
व्यापक रूप से हम कह सकते हैं कि दो वर्ग संख्याओं n और (n + 1) के बीच 2n संख्याएँ हैं जो वर्ग संख्याएँ नहीं हैं। जाँच के लिए n = 5, n = 6 इत्यादि लें और इन्हें सत्यापित कीजिए।
प्रयास कीजिए
1. 92 और 102 के बीच कितनी प्राकृत संख्याएँ हैं? 112 और 122 के बीच भी प्राकृत संख्याओं की संख्या बताइए।
2. निम्नलिखित संख्याओं के युग्मों के बीच की संख्या बताइए जो वर्ग संख्याएँ नहीं हैं।
(i) 1002 और 1012 (ii) 902 और 912 (iii) 10002 और 10012
3. विषम संख्याओं का जोड़
निम्न पर विचार कीजिए।
1 [एक विषम संख्या] = 1 = 12
1 + 3 [पहली दो विषम संख्याओं का योग] = 4 = 22
1 + 3 + 5 [पहली तीन विषम संख्याओं का योग] = 9 = 32
1 + 3 + 5 + 7 [... ] = 16 = 42
1 + 3 + 5 + 7 + 9 [... ] = 25 = 52
1 + 3 + 5 + 7 + 9 + 11 [... ] = 36 = 62
अतः हम कह सकते हैं कि पहली n विषम प्राकृत संख्याओं का योग n2 है।
इसे अलग ढ़ंग से देखते हुए हम कह सकते हैं कि यदि एक संख्या, वर्ग संख्या है तो वह 1 से प्रारंभ होने वाली क्रमागत विषम संख्याओं का योग है।
अब इन संख्याओं पर विचार कीजिए जो पूर्ण वर्ग संख्याएँ नहीं हैं जैसे 2, 3, 5, 6, ... । क्या आप इन संख्याओं को 1 से प्रारंभ कर सभी क्रमागत विषम प्राकृत संख्याओं के योग के रूप में लिख सकते हैं?
आप पाएँगे कि इन संख्याओं को इस प्रकार नहीं लिख सकते हैं। संख्या 25 को लीजिए और इसमें से 1, 3, 5, 7, 9, ... को क्रम में घटाएँ:
(i) 25 – 1 = 24 (ii) 24 – 3 = 21 (iii) 21 – 5 = 16 (iv) 16 – 7 = 9
(v) 9 – 9 = 0
अर्थात् यहाँ 25 = 1 + 3 + 5 + 7 + 9 है, अतः 25 एक पूर्ण वर्ग संख्या है।
अब एक दूसरी संख्या 38 को लीजिए और पुनः ऊपर जैसा कीजिए।
(i) 38 – 1 = 37 (ii) 37 – 3 = 34 (iii) 34 – 5 = 29 (iv) 29 – 7 = 22
(v) 22 – 9 = 13 (vi) 13 – 11 = 2 (vii) 2 – 13 = – 11
अतः यह दर्शाता है कि 38 को 1 से प्रारंभ होने वाली क्रमागत विषम संख्याओं के रूप में हम नहीं लिख सकते हैं और 38 एक पूर्ण वर्ग संख्या नहीं है।
अतः हम यह भी कह सकते हैं कि यदि कोई प्राकृत संख्या 1 से प्रारंभ होने वाली क्रमागत विषम संख्याओं के योग के रूप में व्यक्त नहीं हो सकती तो वह संख्या पूर्ण वर्ग संख्या नहीं है।
एक संख्या पूर्ण है या नहीं यह जानने के लिए इस परिणाम का उपयोग कर सकते हैं।
प्रयास कीजिए
निम्नलिखित संख्याओं में प्रत्येक पूर्ण वर्ग संख्याएँ हैं या नहीं?
(i) 121 (ii) 55 (iii) 81
(iv) 49 (v) 69
4. क्रमागत प्राकृत संख्याओं का योग
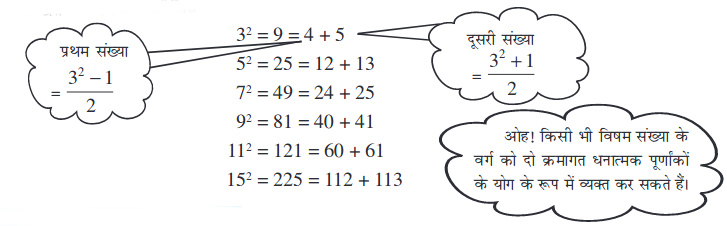
प्रयास कीजिए
1. निम्नलिखित संख्याओं को दो क्रमागत पूर्णांकों के योग के रूप में लिखिए:
(i) 212 (ii) 132 (iii) 112 (iv) 192
2. क्या आप सोचते हैं कि इसका विलोम सत्य है अर्थात् क्या दो क्रमागत धनात्मक पूर्णांकों का योग एक पूर्ण वर्ग होता है? अपने उत्तर के पक्ष में अपने एक उदाहरण दीजिए।
5. दो क्रमागत सम या विषम प्राकृत संख्याओं का गुणनफल
11 × 13 = 143 = 122 – 1
इस प्रकार 11 × 13 = (12 – 1) × (12 + 1)
अतः 11 × 13 = (12 – 1) × (12 + 1) = 122 – 1
इसी तरह 13 × 15 = (14 – 1) × (14 + 1) = 142 – 1
29 × 31 = (30 – 1) × (30 + 1) = 302 – 1
44 × 46 = (45 – 1) × (45 + 1) = 452 – 1
अतः सामान्यतः हम कह सकते हैं कि (a + 1) × (a – 1) = a2 – 1
6. वर्ग संख्याओं के कुछ और प्रतिरूप
संख्याओं के वर्गों का अवलोकन कीजिए 1, 11, 111 ... इत्यादि। ये एक सुंदर प्रतिरूप देते हैं।
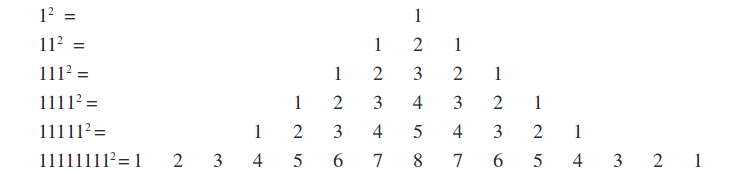
अन्य रोचक प्रतिरूप
72 = 49
672 = 4489
6672 = 444889
66672 = 44448889
666672 = 4444488889
6666672 = 444444888889
प्रयास कीजिए
उपरोक्त प्रतिरूप का उपयोग करते हुए वर्ग संख्याएँ लिखिए:
(i) 1111112 (ii) 11111112
एेसा क्यों होता है, यह जानना आपके लिए मनोरंजन पूर्ण हो सकता है। आपके लिए इस तरह के प्रश्नों के बारे में खोजना और सोचना रुचिकर होगा। भले ही एेसे उत्तर कुछ समय बाद मिलें।
प्रयास कीजिए
उपरोक्त प्रतिरूप का उपयोग करते हुए क्या आप निम्नलिखित संख्याओं का वर्ग ज्ञात कर सकते हैं?
(i) 66666672 (ii) 666666672
प्रश्नावली 6.1
1. निम्नलिखित संख्याओं के वर्गों के इकाई के अंक क्या होंगे?
(i) 81 (ii) 272 (iii) 799 (iv) 3853
(v) 1234 (vi) 26387 (vii) 52698 (viii) 99880
(ix) 12796 (x) 55555
2. निम्नलिखित संख्याएँ स्पष्ट रूप से पूर्ण वर्ग संख्याएँ नहीं हैं, इसका कारण दीजिए।
(i) 1057 (ii) 23453 (iii) 7928 (iv) 222222
(v) 64000 (vi) 89722 (vii) 222000 (viii) 505050
3. निम्नलिखित संख्याओं में से किस संख्या का वर्ग विषम संख्या होगा?
(i) 431 (ii) 2826 (iii) 7779 (iv) 82004
4. निम्न प्रतिरूप का अवलोकन कीजिए और रिक्त स्थान भरिए।
112 = 121
1012 = 10201
10012 = 1002001
1000012 = 1 ......... 2 ......... 1
100000012 = ...........................
5. निम्न प्रतिरूप का अवलोकन कीजिए और रिक्त स्थान भरिए:
112 = 1 2 1
1012 = 1 0 2 0 1
101012 = 102030201
10101012 = ...........................
............2 = 10203040504030201
प्रतिरूप प्राप्त कीजिए:
तीसरी संख्या पहली और दूसरी से संबंधित है। कैसे? चौथी संख्या तीसरी संख्या से संबंधित है। कैसे?
6. दिए गए प्रतिरूप का उपयोग करते हुए लुप्त संख्याओं को प्राप्त कीजिए:
12 + 22 + 22 = 32
22 + 32 + 62 = 72
32 + 42 + 122 = 132
42 + 52 + _2 = 212
52 + _2 + 302 = 312
62 + 72 + _2 = __2
7. योग संक्रिया किए बिना योगफल ज्ञात कीजिए:
(i) 1 + 3 + 5 + 7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + I1 + 13 + 15 + 17 +19
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23
8. (i) 49 को 7 विषम संख्याओं के योग के रूप में लिखिए।
(ii) 121 को 11 विषम संख्याओं के योग के रूप में लिखिए।
9. निम्नलिखित संख्याओं के वर्ग के बीच में कितनी संख्याएँ हैं?
(i) 12 और 13 (ii) 25 और 26 (iii) 99 और 100
6.4 संख्याओं का वर्ग ज्ञात करना
छोटी संख्याएँ जैसे 3, 4, 5, 6, 7, ... इत्यादि का वर्ग ज्ञात करना सरल है। लेकिन क्या हम 23 का वर्ग इतनी शीघ्रता से प्राप्त कर सकते हैं?
इसका उत्तर इतना आसान नहीं है और हमें 23 को 23 से गुणा करने की आवश्यकता है।
इसे प्राप्त करने का एक तरीका है जो 23 × 23 को बिना गुणा किए प्राप्त होता है।
हम जानते हैं कि 23 = 20 + 3
इसलिए 232 = (20 + 3)2 = 20(20 + 3) + 3(20 + 3)
= 202 + 20 × 3 + 3 × 20 + 32
= 400 + 60 + 60 + 9 = 529
उदाहरण 1 : निम्नलिखित संख्याओं का वर्ग गुणा किए बिना ज्ञात कीजिए:
(i) 39 (ii) 42
हल : (i) 392 = (30 + 9)2 = 30(30 + 9) + 9(30 + 9)
= 302 + 30 × 9 + 9 × 30 + 92
= 900 + 270 + 270 + 81 = 1521
(ii) 422 = (40 + 2)2 = 40(40 + 2) + 2(40 + 2)
= 402 + 40 × 2 + 2 × 40 + 22
= 1600 + 80 + 80 + 4 = 1764
एक एेसी संख्या लीजिए जिसके इकाई स्थान पर अंक 5 हो, अर्थात् a5 ।
(a5)2 = (10a + 5)2
= 10a(10a + 5) + 5(10a + 5)
= 100a2 + 50a + 50a + 25
= 100a(a + 1) + 25
= a(a + 1) सैंकड़ा + 25
6.4.1 वर्ग के अन्य प्रतिरूप
निम्न प्रतिरूप को देखिए
252 = 625 = (2 × 3) सैकड़े + 25
352 = 1225 = (3 × 4) सैकड़े + 25
752 = 5625 = (7 × 8) सैकड़े + 25
1252 = 15625 = (12 × 13) सैकड़े + 25
अब क्या आप 95 का वर्ग प्राप्त कर सकते हैं?
प्रयास कीजिए
निम्नलिखित संख्याआें के वर्ग ज्ञात कीजिए जिनके इकाई अंक 5 हैं।
(i) 15 (ii) 95 (iii) 105 (iv) 205
6.4.2 पाइथागोरस त्रिक
निम्न को लीजिए
32 + 42 = 9 + 16 = 25 = 52
संख्या 3, 4, 5 के समूह को पाइथागोरस त्रिक कहते हैं। 6, 8, 10 भी एक पाइथागोरस त्रिक है। इसी प्रकार
62 + 82 = 36 + 64 = 100 = 102
पुनः अवलोकन करें कि
52 + 122 = 25 + 144 = 169 = 132 । इसी प्रकार संख्याएँ 5, 12, 13 एेसी ही दूसरी त्रिक है। क्या आप इस प्रकार के कुछ और त्रिक प्राप्त कर सकते हैं?
किसी प्राकृत संख्या m > 1 के लिए, हम पाते हैं (2m)2 + (m2 – 1)2 = (m2 + 1)2। अतः
2m, m2 – 1 और m2 + 1 पाइथागोरस त्रिक के रूप में हैं।
इस रूप का उपयोग करते हुए कुछ और पाइथागोरस त्रिक ज्ञात कीजिए।
उदाहरण 2 : एक पाइथागोरस त्रिक लिखिए जिसकी सबसे छोटी संख्या 8 है।
हल : साधारण रूप 2m, m2 – 1, m2 + 1 से हम पाइथागोरस त्रिक पा सकते हैं।
पहले हम लेते हैं m2 – 1 = 8
अतः m2 = 8 + 1 = 9
m = 3
इसलिए 2m = 6 और m2 + 1 = 10
अतः 6, 8, 10 एक त्रिक है लेकिन 8 सबसे छोटी संख्या नहीं है।
इसलिए हम लेते हैं 2m = 8
तब m = 4
m2 – 1 = 16 – 1 = 15
और m2 + 1 = 16 + 1 = 17
अतः 8, 15, 17 एक एेसा त्रिक है जहांँ 8 सबसे छोटी संख्या है।
उदाहरण 3 : एक पाइथागोरस त्रिक ज्ञात कीजिए जिसकी एक संख्या 12 है।
हल : यदि हम लेते हैं m2 – 1 = 12
तब, m2 = 12 + 1 = 13
यहाँ m का मान पूर्णांक नहीं होगा।
अतः हम कोशिश करते हैं m2 + 1 = 12 । पुनः m2 = 11 जो m के लिए पूर्णांक मान नहीं देगा।
अतः हमें लेना चाहिए 2m = 12
तब, m = 6
इस प्रकार m2 – 1 = 36 – 1 = 35 और m2 + 1 = 36 + 1 = 37
अतः आवश्यक त्रिक है 12, 35, 37
नोट : इस रूप का उपयोग करते हुए सभी पाइथागोरस त्रिक प्राप्त नहीं कर सकते हैं। उदाहरण के लिए दूसरी त्रिक 5, 12, 13 में भी 12 एक सदस्य हैं।
प्रश्नावली 6.2
1. निम्न संख्याओं का वर्ग ज्ञात कीजिए।
(i) 32 (ii) 35 (iii) 86 (iv) 93
(v) 71 (vi) 46
2. पाइथागोरस त्रिक लिखिए जिसका एक सदस्य है,
(i) 6 (ii) 14 (iii) 16 (iv) 18
6.5 वर्गमूल
निम्न स्थितियाें का अध्ययन कीजिए:
(a) वर्ग का क्षेत्रफल 144 cm2 है। वर्ग की भुजा क्या होगी?
हम जानते हैं कि वर्ग का क्षेत्रफल = भुजा2 होता है।
यदि हम भुजा की लंबाई का मान 'a' लेते हैं, तब 144 = a2
भुजा की लंबाई ज्ञात करने के लिए आवश्यक है कि एक एेसी संख्या ज्ञात करें जिसका वर्ग 144 है।
(b) एक वर्ग जिसकी भुजा 8 cm है, उसके विकर्ण की लंबाई क्या होगी (चित्र 6.1)?
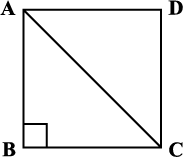
आकृति 6.1
इसको हल करने के लिए क्या हम पाइथागोरस प्रमेय का उपयोग कर सकते हैं?
हम जानते हैं AB2 + BC2 = AC2
अर्थात् 82 + 82 = AC2
या 64 + 64 = AC2
या 128 = AC2
पुनः AC प्राप्त करने के लिए हमें एक एेसी संख्या सोचनी है जिसका वर्ग 128 हो।
(c) एक समकोण त्रिभुज में कर्ण और एक भुजा क्रमशः 5 cm और 3 cm हैं। (चित्र 6.2) क्या आप तीसरी भुजा प्राप्त कर सकते हैं?
माना कि तीसरी भुजा की लंबाई x cm है।
पाइथागोरस प्रमेय के उपयोग से 52 = x2 + 32
25 – 9 = x2
16 = x2
पुनः x का मान प्राप्त करने के लिए हमें एक संख्या की आवश्यकता है जिसका वर्ग 16 है। उपरोक्त सभी स्थितियों में हमें एक संख्या की आवश्यकता है, जिसका वर्ग ज्ञात हो, और उस संख्या को वर्गमूल के रूप में जाना जाता हो।
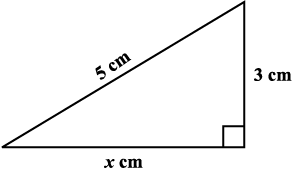
आकृति 6.2
6.5.1 वर्गमूल ज्ञात करना
योग की प्रतिलोम (विपरीत) संक्रिया घटाना है और गुणा की प्रतिलोम संक्रिया भाग है। इसी तरह वर्गमूल प्राप्त करना भी वर्ग की प्रतिलोम संक्रिया है।
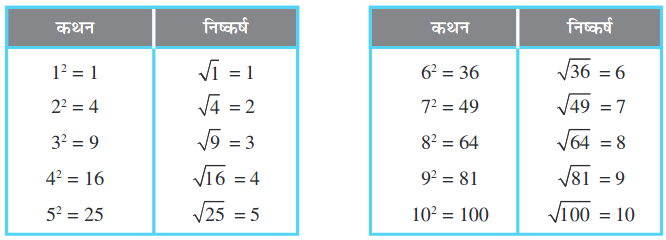
हमें ज्ञात है 12 = 1, अतः 1 का वर्गमूल 1 है।
22 = 4, अतः 4 का वर्गमूल 2 है।
32 = 9, अतः 9 का वर्गमूल 3 है।
इसी प्रकार 92 = 81,
और (–9)2 = 81
हम कह सकते है कि 81 के वर्गमूल 9 और – 9
प्रयास कीजिए
(i) 112 = 121. 121 का वर्गमूल क्या है? (ii) 142 = 196. 196 का वर्गमूल क्या है?
सोचिए, चर्चा कीजिए और लिखिए
(–1)2 = 1. क्या 1 का वर्गमूल है –1?
(–2)2 = 4. क्या 4 का वर्गमूल है –2?
(–9)2 = 81. क्या 81 का वर्गमूल है –9?
उपरोक्त के अनुसार आप कह सकते हैं कि किसी पूर्ण वर्ग संख्या के दो समाकलित (एक साथ) वर्गमूल होते हैं। इस अध्याय में हम किसी प्राकृत संख्या के केवल धनात्मक वर्गमूल ही लेंगे। धनात्मक वर्गमूल संख्या को 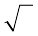 संकेत से व्यक्त करते हैं।
संकेत से व्यक्त करते हैं।
उदाहरणार्थ, 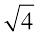 = 2 (–2 नहीं );
= 2 (–2 नहीं ); 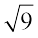 = 3 (–3 नहीं) इत्यादि।
= 3 (–3 नहीं) इत्यादि।
6.5.2 घटाने की संक्रिया के द्वारा वर्गमूल ज्ञात करना
क्या आपको याद है कि प्रथम n विषम प्राकृत संख्याओं का योग n2 है? अतः प्रत्येक वर्ग संख्या को 1 से प्रारंभ कर क्रमागत प्राकृत संख्याओं के योग के रूप में व्यक्त किया जा सकता है। 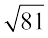 को लीजिए
को लीजिए
(i) 81 – 1 = 80 (ii) 80 – 3 = 77 (iii) 77 – 5 = 72 (iv) 72 – 7 = 65
(v) 65 – 9 = 56 (vi) 56 – 11 = 45 (vii) 45 – 13 = 32 (viii) 32 – 15 = 17
(ix) 17 – 17 = 0
प्रयास कीजिए
1 से प्रारंभ होने वाली विषम संख्याओं को बार-बार घटाने पर प्राप्त निम्नलिखित संख्याएँ पूर्ण वर्ग हैं या नहीं? यदि यह संख्या पूर्ण वर्ग हैं तो इसके वर्गमूल ज्ञात कीजिए।
(i) 121 (ii) 55 (iii) 36
(iv) 49 (v) 90
संख्या 1 से क्रमागत विषम संख्याओं को 81 में रूप घटाने पर 9वाँ पद 0 प्राप्त होता है अतः 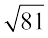 = 9। इस नियम का उपयोग करते हुए क्या आप 729 का वर्गमूल ज्ञात कर सकते हैं? हाँ, लेकिन इसमें समय अधिक लगता है। अब हम एक सरल तरीके से वर्गमूल प्राप्त करने की कोशिश करते हैं।
= 9। इस नियम का उपयोग करते हुए क्या आप 729 का वर्गमूल ज्ञात कर सकते हैं? हाँ, लेकिन इसमें समय अधिक लगता है। अब हम एक सरल तरीके से वर्गमूल प्राप्त करने की कोशिश करते हैं।
6.5.3 अभाज्य गुणनखंडन के द्वारा वर्गमूल ज्ञात करना
निम्न संख्याओं एवं उनके वर्गों को अभाज्य गुणनखंडन के रूप में लिखिए:
.png)
6 के अभाज्य गुणनखंड में 2 कितनी बार आता है? एक बार । 36 के अभाज्य गुणनखंडन में 2 कितनी बार आता है? दो बार । इसी तरह 6 और 36 में 3 बार तथा 8 और 64 इत्यादि में 2 कितनी बार है?
.png)
आप पाएँगे कि किसी संख्या के वर्ग के अभाज्य गुणनखंडों की संख्या उस संख्या के अभाज्य गुणनखंडों की संख्या की दुगुना होती है। आइए, हम एक दी गई वर्ग संख्या 324 का वर्गमूल ज्ञात करते हैं।
हम जानते हैं कि 324 का अभाज्य गुणनखंडन
324 = 2 × 2 × 3 × 3 × 3 × 3
अभाज्य गुणनखंड के युग्म बनाने पर हम प्राप्त करते हैं,
324 = 2 × 2 × 3 × 3 × 3 × 3 = 22 × 32 × 32 = (2 × 3 × 3)2
अतः 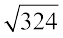 = 2 × 3 × 3 = 18
= 2 × 3 × 3 = 18
इसी तरह क्या आप 256 का वर्गमूल ज्ञात कर सकते हैं? 256 का अभाज्य गुणनखंड है,
.png)
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
अभाज्य गुणनखंड में युग्म बनाने से हम पाते हैं?
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = (2 × 2 × 2 × 2)2
अतः 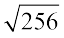 = 2 × 2 × 2 × 2 = 16
= 2 × 2 × 2 × 2 = 16
क्या 48 एक पूर्ण वर्ग संख्या है?
हम जानते हैं, 48 = 2 × 2 × 2 × 2 × 3
यहाँ सारे गुणनखंड युग्म में नहीं हैं, अतः 48 एक पूर्ण वर्ग संख्या नहीं है। कल्पना कीजिए कि हम 48 के सबसे छोटे गुणज ज्ञात करना चाहते हैं जो कि एक पूर्ण वर्ग संख्या हो। इसे कैसे करेंगे? 48 के अभाज्य गुणनखंड के युग्म बनाने पर देखते हैं कि केवल 3 एक संख्या है जो युग्म में नहीं बन पाती है अतः हमें युग्म को पूरा करने में 3 से गुणा करने की आवश्यकता है।
अतः 48 × 3 = 144 एक पूर्ण वर्ग है।
क्या आप कह सकते हैं कि 48 को किस संख्या से भाग दें कि पूर्ण वर्ग संख्या प्राप्त हो?
गुणज 3, युग्म में नहीं है। अतः हम 48 को यदि 3 से भाग दें तो हम 48 ÷ 3 = 16 =
2 × 2 × 2 × 2 प्राप्त करेंगे और यह संख्या पूर्ण वर्ग भी है।
उदाहरण 4 : 6400 का वर्गमूल ज्ञात कीजिए?
हल : लिखिए 6400 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5
.png)
अतः 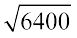 = 2 × 2 × 2 × 2 × 5 = 80
= 2 × 2 × 2 × 2 × 5 = 80
उदाहरण 5 : क्या 90 एक पूर्ण वर्ग है?
हल : हम 90 = 2 × 3 × 3 × 5 रखते हैं।
अभाज्य गुणनखंड में 2 और 5 युग्म में नहीं हैं।
.png)
अतः 90 एक पूर्ण वर्ग संख्या नहीं है। जिसे यथार्थ रूप में हम इस प्रकार भी देख सकते हैं क्योंकि इसमें केवल 1 शून्य है।
उदाहरण 6 : क्या 2352 एक पूर्ण वर्ग संख्या है? यदि नहीं तो 2352 का सबसे छोटा गुणज प्राप्त कीजिए जो कि पूर्ण वर्ग संख्या हो तथा नयी संख्या का वर्गमूल ज्ञात कीजिए।
हल : हम जानते हैं कि 2352 = 2 × 2 × 2 × 2 × 3 × 7 × 7
.png)
अभाज्य गुणनखंड के अनुसार 3 के युग्म नहीं हैं अतः 2352 एक पूर्ण वर्ग नहीं है। यदि 3 का एक जोड़ा बनाते हैं तब संख्या पूर्ण वर्ग हो जाएगी। अतः 2352 को 3 से गुणा करने पर हम पाएंँगेः
2352 × 3 = 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
अब प्रत्येक अभाज्य गुणनखंड युग्म में हैं। अतः 2352 × 3 = 7056 एक पूर्ण वर्ग संख्या है। और 2352 का सबसे छोटा गुणज 7056 है जो एक पूर्ण वर्ग संख्या है।
और  = 2 × 2 × 3 × 7 = 84
= 2 × 2 × 3 × 7 = 84
उदाहरण 7 : सबसे छोटी संख्या प्राप्त कीजिए जिसे 9408 से भाग देने पर भागफल एक पूर्ण वर्ग संख्या हो जाए। उस भागफल का वर्गमूल ज्ञात कीजिए।
हल : 9408 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 7 × 7
यदि हम 9408 को 3 से भाग देते हैं तब
9408 ÷ 3 = 3136 = 2 × 2 × 2 × 2 × 2 × 2 × 7 × 7 जो कि एक पूर्ण वर्ग संख्या हैं। (क्यों?) अतः सबसे छोटी वांछित संख्या 3 है।
और 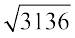 = 2 × 2 × 2 × 7 = 56
= 2 × 2 × 2 × 7 = 56
उदाहरण 8 : सबसे छोटी वर्ग संख्या ज्ञात कीजिए जो प्रत्येक संख्या 6, 9 और 15 से विभाजित हो जाए।
हल : इसे दो चरण में हल कर सकते हैं। सबसे पहले छोटे उभयनिष्ठ गुणज को ज्ञात कीजिए और तब उसके बाद आवश्यक वर्ग संख्या ज्ञात कीजिए। वह सबसे छोटी संख्या जिसमें 6, 9, 15 का भाग जाएगा, इनकी ल.स. है। 6, 9 और 15 का ल.स. है 2 × 3 × 3 × 5 = 90 ।
.png)
90 का अभाज्य गुणनखंडन 90 = 2 × 3 × 3 × 5 है।
हम देखते हैं कि अभाज्य गुणनखंड 2 और 5 के युग्म नहीं हैं। अतः 90 एक पूर्ण वर्ग संख्या नहीं है।
पूर्ण वर्ग संख्या प्राप्त करने के लिए 90 के प्रत्येक गुणनखंड युग्म में होने चाहिए अतः हमें 2 और 5 का जोड़ा बनाने की आवश्यकता होगी। इसलिए 90 को 2 × 5, अर्थात् 10 से गुणा करना चाहिए। अतः वह वर्ग संख्या 90 × 10 = 900 है।
प्रश्नावली 6.3

1. निम्नलिखित संख्याओं के वर्गमूल ज्ञात करने में इकाई अंक की क्या संभावना है।
(i) 9801 (ii) 99856 (iii) 998001 (iv) 657666025
2. बिना गणना किए वह संख्या बताएँ जो वास्तव में पूर्ण वर्ग नहीं है।
(i) 153 (ii) 257 (iii) 408 (iv) 441
3. बार-बार घटाने की विधि से 100 और 169 का वर्गमूल ज्ञात कीजिए।
4. अभाज्य गुणनखंड विधि से निम्न संख्याओं का वर्गमूल ज्ञात कीजिए:
(i) 729 (ii) 400 (iii) 1764 (iv) 4096
(v) 7744 (v) 9604 (vii) 5929 (viii) 9216
(ix) 529 (x) 8100
5. निम्नलिखित संख्याओं में प्रत्येक के लिए वह सबसे छोटी पूर्ण संख्या ज्ञात कीजिए जिससे इस संख्या को गुणा करने पर यह एक पूर्ण वर्ग संख्या बन जाए। इस पूर्ण वर्ग संख्या का वर्गमूल भी ज्ञात कीजिए।
(i) 252 (ii) 180 (iii) 1008 (iv) 2028
(v) 1458 (vi) 768
6. निम्नलिखित संख्याओं में प्रत्येक के लिए वह सबसे छोटी पूर्ण संख्या ज्ञात कीजिए जिससेे इस संख्या को भाग देने पर वह एक पूर्ण वर्ग संख्या बन जाए। इस तरह ज्ञात की गई संख्या का वर्गमूल भी ज्ञात कीजिए।
(i) 252 (ii) 2925 (iii) 396 (iv) 2645
(v) 2800 (vi) 1620
7. एक विद्यालय में कक्षा VIII के सभी विद्यार्थियों ने प्रधानमंत्री राष्ट्रीय राहत कोष में
2401 रु दान में दिए। प्रत्येक विद्यार्थी ने उतने ही रुपये दान में दिए जितने कक्षा में विद्यार्थी थे। कक्षा के विद्यार्थियों की संख्या ज्ञात कीजिए।
8. एक बाग में 2025 पौधे इस प्रकार लगाए जाने हैं कि प्रत्येक पंक्ति में उतने ही पौधे हों, जितनी पंक्तियों की संख्या हो। पंक्तियों की संख्या और प्रत्येक पंक्ति में पौधों कि संख्या ज्ञात कीजिए।
9. वह सबसे छोटी वर्ग संख्या ज्ञात कीजिए जो 4, 9 और 10 प्रत्येक से विभाजित हो जाए।
10. वह सबसे छोटी वर्ग संख्या ज्ञात कीजिए जो प्रत्येक 8, 15 और 20 से विभाजित हो जाए।
6.5.4 भागफल विधि से वर्गमूल ज्ञात करना
जब संख्याएँ बड़ी हों तब अभाज्य गुणनखंड विधि से वर्गमूल ज्ञात करना लंबा और कठिन होता है। इस समस्या से निकलने के लिए हम दीर्घ विभाजन विधि का प्रयोग करते हैं।
इसके लिए हमें वर्गमूल में अंकों की संख्या को ज्ञात करने की आवश्यकता है।
निम्नलिखित सारणी को देखिए:
.png)
अतः वर्गमूल में अंकों की संख्या के बारे में हम क्या कह सकते हैं यदि एक पूर्ण वर्ग संख्या 3 अंकों या 4 अंकों की हो?
हम कह सकते हैं कि यदि एक पूर्ण वर्ग संख्या 3 अंकों की या 4 अंकों की है तब इसका वर्गमूल 2 अंकों का होगा। क्या आप हमें 5 या 6 अंकों वाली संख्या के वर्गमूल में अंकों की संख्या बता सकते हैं?
सबसे छोटी 3 अंकों की पूर्ण वर्ग संख्या 100 है जो कि 10 का वर्ग है और 3 अंकों की सबसे बड़ी पूर्ण वर्ग संख्या 961 है जो कि 31 का वर्ग है। सबसे छोटी 4 अंकों की पूर्ण वर्ग संख्या 1024 है जो 32 का वर्ग है और सबसे बड़ी 4 अंकों की संख्या 9801 है जो 99 का वर्ग है।
![]() सोचिए, चर्चा कीजिए और लिखिए
सोचिए, चर्चा कीजिए और लिखिए
क्या हम कह सकते हैं कि एक पूर्ण वर्ग संख्या में यदि n अंक है तो उसके वर्गमूल में 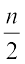 अंक होंगे यदि n सम है या
अंक होंगे यदि n सम है या 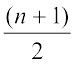 होंगे यदि n विषम हैं?
होंगे यदि n विषम हैं?
निम्न विधि किसी संख्या के वर्गमूल में अंकों की संख्या ज्ञात करने में उपयोगी होगी।
• 529 का वर्गमूल ज्ञात करने के लिए निम्नलिखित चरणों पर विचार कीजिए।
क्या आप इस संख्या के वर्गमूल में अंकों की संख्या का अनुमान लगा सकते हैं?
चरण 1 इकाई स्थान से प्रारंभ करते हुए प्रत्येक युग्म पर बार लगाइए। यदि अंकों की संख्या विषम है तब बाएँ तरफ़ एक अंक पर बार लगाइए। 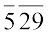 इस प्रकार लिखते हैं।
इस प्रकार लिखते हैं।
चरण 2 वह सबसे बड़ी संख्या ज्ञात कीजिए जिसका वर्ग सबसे बाईं तरफ़ के बार के नीचे लिखी संख्या से कम या बराबर हो (22 < 5 < 32)। सबसे बाईं बार के नीचे भाज्य (यहाँ 5) के साथ भाजक और भागफल के रूप में इस संख्या को लीजिए। भाग कीजिए और शेषफल ज्ञात कीजिए (इस स्थिति में 1 है।)
.png)
चरण 3 अगली बार के नीचे की संख्या को शेषफल के दाएँ लिखिए। (अर्थात् इस स्थिति में 29 है।) अतः अगली भाज्य 129 होगी।
.png)
चरण 4 भाजक को दुगुना कीजिए और इसे इसके दाएँ में खाली स्थान के साथ लिखिए।
.png)
चरण 5 रिक्त स्थान को भरने के लिए सबसे बड़े संभावित अंक का अनुमान लगाइए जो कि भागफल में नया अंक होगा और नए भाजक को नए भागफल से गुणा करने पर गुणनफल भाज्य से कम या बराबर होगी।
इस स्थिति में 42 × 2 = 84
चूँकि 43 × 3 = 129, अतः शेषफल प्राप्त करने के लिए नया अंक 3 चुनते हैं
.png)
चरण 6 क्योंकि शेषफल 0 है और दी गई संख्या में कोई अंक शेष नहीं है,
अतः  = 23
= 23
• अब 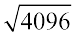 को हल कीजिए:
को हल कीजिए:
चरण 1 इकाई स्थान से प्रारंभ करते हुए प्रत्येक युग्म के ऊपर बार लगाइए (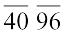 )।
)।
.png)
चरण 2 एक सबसे बड़ी संख्या ज्ञात कीजिए जो सबसे बाईं तरफ़ के बार के नीचे लिखी संख्या से कम या बराबर हो (62 < 40 < 72)। इस संख्या को भाजक और सबसे बाईं तरफ बार के नीचे संख्या को भाज्य के रूप में लीजिए। भाग दीजिए और शेषफल (इस स्थिति में अर्थात् 4) ज्ञात कीजिए।
.png)
चरण 3 अगली बार के नीचे लिखी संख्या (अर्थात् 96) को शेषफल के दाएँ लिखिए। नया भाज्य 496 होगा।
.png)
चरण 4 भाजक का दुगुना कीजिए और दाईं तरफ़ के रिक्त स्थान में लिखिए।
.png)
चरण 5 रिक्त स्थान को भरने के लिए सबसे बड़े संभावित अंक का अनुमान लगाइए जो अंक भागफल में नया होगा इस प्रकार नया अंक जब भागफल से गुणा होता है तब गुणनफल भाज्य से छोटा या बराबर होगा। इस स्थिति में हम देखते हैं कि 124 × 4 = 496 अतः भागफल में नया अंक 4 है। शेषफल ज्ञात कीजिए।
चरण 6 चूँकि शेषफल शून्य है और कोई बार नहीं है अतः 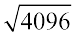 = 64 है।
= 64 है।
संख्या का अनुमान
पूर्ण वर्ग संख्या के वर्गमूल में अंकों की संख्या ज्ञात करने के लिए बार का उपयोग करते हैं।
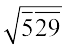 = 23 और
= 23 और 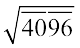 = 64
= 64
इन दोनों संख्याओं 529 और 4096 में बार की संख्या 2 है, और उनके वर्गमूल में अंकों की संख्या 2 है।
क्या आप 14400 के वर्गमूल में अंकों की संख्या बता सकते हैं? बार लगाने पर हम 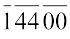 प्राप्त करते हैं। यद्यपि यहाँ पर बार की संख्या 3 है। अतः वर्गमूल 3 अंक का होगा।
प्राप्त करते हैं। यद्यपि यहाँ पर बार की संख्या 3 है। अतः वर्गमूल 3 अंक का होगा।

प्रयास कीजिए
निम्नलिखित संख्याओं के वर्गमूल में अंकों की संख्या को गणना के बिना ज्ञात कीजिए।
(i) 25600 (ii) 100000000 (iii) 36864
उदाहरण 9 : वर्गमूल ज्ञात कीजिए : (i) 729 (ii) 1296
हल :
(i).png)
उदाहरण 10 : वह सबसे छोटी संख्या ज्ञात कीजिए जिसे 5607 में से घटाने पर वह पूर्ण वर्ग संख्या बन जाए। इस पूर्ण वर्ग संख्या का वर्गमूल भी ज्ञात कीजिए।
.png)
हल : आइए, दीर्घ विभाजन विधि से  ज्ञात करने का प्रयास करें। हमें 131 शेषफल प्राप्त होता है। यह दर्शाता है कि 742,5607 से 131 कम है।
ज्ञात करने का प्रयास करें। हमें 131 शेषफल प्राप्त होता है। यह दर्शाता है कि 742,5607 से 131 कम है।
अर्थात् यदि हम किसी संख्या में से उसका शेषफल घटा देते हैं तो हमें एक पूर्ण वर्ग संख्या प्राप्त होती है। अतः वांछित पूर्ण वर्ग संख्या है 5607 – 131 = 5476 और  = 74
= 74
उदाहरण 11 : चार अंकों की सबसे बड़ी संख्या बताइए, जो पूर्ण वर्ग हो।
.png)
हल : चार अंकों की सबसे बड़ी संख्या = 9999 है। हम दीर्घ विभाजन विधि द्वारा 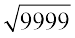 ज्ञात करते हैं, जिसका शेषफल 198 है। यह दर्शाता है 992, 9999 से 198 कम है।
ज्ञात करते हैं, जिसका शेषफल 198 है। यह दर्शाता है 992, 9999 से 198 कम है।
इसका अर्थ है कि यदि हम किसी संख्या में से शेषफल घटाते हैं तो हमें एक पूर्ण वर्ग संख्या प्राप्त होती है। अतः वांछित पूर्ण वर्ग संख्या है 9999 – 198 = 9801
और  = 99
= 99
उदाहरण 12 : वह सबसे छोटी संख्या ज्ञात कीजिए जिसे 1300 में जोड़ने पर एक पूर्ण वर्ग संख्या प्राप्त हो। उस पूर्ण वर्ग संख्या का वर्गमूल भी ज्ञात कीजिए।
.png)
हल : दीर्घ विभाजन विधि से  ज्ञात करते हैं। यहाँ पर शेषफल 4 है। यह दर्शाता है कि 362 < 1300
ज्ञात करते हैं। यहाँ पर शेषफल 4 है। यह दर्शाता है कि 362 < 1300
अगली पूर्ण वर्ग संख्या 372 = 1369
अतः अभीष्ट संख्या = 372 – 1300 = 1369 – 1300 = 69
6.6 दशमलव का वर्गमूल
संख्या 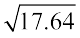 पर विचार कीजिए
पर विचार कीजिए
चरण 1 दशमलव संख्या का वर्गमूल ज्ञात करने के लिए हम पूर्ण संख्या पर सामान्य रूप से बार लगाते हैं। (अर्थात् 17) दशमलव भाग पर भी पहले दशमलव स्थान से प्रारंभ करके बार लगाते हैं और सामान्य रूप से आगे बढ़ते जाते हैं। हम 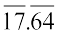 पाते हैं।
पाते हैं।
.png)
चरण 2 अब इसी तरह से आगे बढ़ते हैं। 17 पर बार सबसे बाईं ओर है और 42 < 17 < 52, इस संख्या को भाजक के रूप में लीजिए और सबसे बाईं बार के नीचे की संख्या भाज्य के रूप मे लीजिए (अर्थात् 17)। भाग दीजिए और शेषफल ज्ञात कीजिए।
.png)
चरण 3 शेषफल 1 है। अगली बार के नीचे की संख्या अर्थात् 64 शेषफल के दाएँ लिखिए, 164 प्राप्त कीजिए।
.png)
चरण 4 भाजक को दुगुना कीजिए और दाईं तरफ़ लिखिए। पहले 64 दशमलव भाग में था अतः भागफल में दशमलव रखिए।
.png)
चरण 5 हम जानते हैं कि 82 × 2 = 164, अतः नई संख्या 2 है। भाग दीजिए और शेषफल ज्ञात कीजिए।
चरण 6 अतः शेषफल 0 है। अब शेष कोई बार नहीं है, अतः 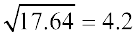
उदाहरण 13 : 12.25 का वर्गमूल ज्ञात कीजिए।
हल : .png)
किस तरफ़ बढ़ें
संख्या 176.341 पर ध्यान दीजिए। पूर्ण संख्या और दशमलव संख्या के दोनों भागों पर बार लगाइये। दशमलव भाग में क्या तरीका है, जो पूर्ण भाग से भिन्न है? 176 पर ध्यान दीजिए हम दशमलव के पास के इकाई स्थान से प्रारंभ करके बाईं तरफ़ जाते हैं। प्रथम बार 76 के ऊपर और दूसरा बार 1 के उपर है। .341 के लिए, हम दशमलव से प्रारंभ करके दाईं तरफ़ जाते हैं। पहला बार 34 के उपर और दूसरा बार लगाने के लिए हम 1 के बाद 0 रखते हैं और इस प्रकार 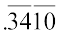 बनाते हैं।
बनाते हैं।
उदाहरण 14 : एक वर्गाकार क्षेत्र का क्षेत्रफल 2304 m2 है। इस वर्गाकार क्षेत्र की भुजा
ज्ञात कीजिए।
हल : वर्गाकार क्षेत्र का क्षेत्रफल = 2304 m2
.png)
इसलिए, वर्गाकार क्षेत्र की भुजा = 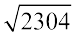 m2
m2
हम पाएंगे कि 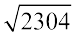 = 48 m
= 48 m
इस प्रकार वर्गाकार क्षेत्र की भुजा 48 m है।
उदाहरण 15 : एक विद्यालय में 2401 विद्यार्थी हैं। पी.टी. अध्यापक उन्हें पंक्ति एवं स्तंभ में इस प्रकार खड़ा रखना चाहते हैं कि पंक्तियों की संख्या स्तंभ की संख्या के बराबर हो। पंक्तियों की संख्या ज्ञात करो।
हल : माना कि पंक्तियों की संख्या x है।
.png)
अतः स्तंभ की संख्या = x
इसलिए, विद्यार्थियों की संख्या = x × x = x2
अतः x2 = 2401 अर्थात् x = 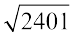 = 49 होता है।
= 49 होता है।
पंक्तियों की संख्या = 49
6.7 वर्गमूल का अनुमान लगाना
निम्न स्थितियों पर विचार कीजिए:
1. देवेशी के पास कपड़े का एक वर्गाकार टुकड़ा है। जिसका क्षेत्रफल 125 cm2 है। वह जानना चाहती है कि क्या वह 15 cm भुजा का रुमाल बना सकती है। यदि यह संभव है तो वह जानना चाहती है कि इस टुकड़े से अधिक से अधिक कितनी लंबाई का रुमाल बनाया जा सकता है।
2. मीना और शोभा ने एक खेल खेला। पहली संख्या देती है एवं दूसरी उसका वर्गमूल देती है। मीना ने पहले प्रारंभ किया। उसने 25 कहा और शोभा ने तुरंत 5 उत्तर दिया तब शोभा ने कहा 81 और मीना ने 9 उत्तर दिया। यह तब तक चलता रहा जब तक मीना की संख्या 250 तक पहुँच गई। अब शोभा उत्तर नहीं दे सकी। तब मीना ने कहा शोभा तुम कम से कम एक एेसी संख्या बताओ जिसका वर्ग 250 के नज़दीक हो।
इन सभी स्थितियों में वर्गमूल अनुमान करने की ज़रूरत होती है।
हम जानते हैं कि 100 < 250 < 400 और 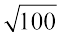 = 10 तथा
= 10 तथा 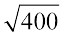 = 20
= 20
अतः 10 < 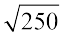 < 20
< 20
लेकिन फिर भी हम वर्ग संख्या के करीब नहीं हैं।
हम जानते हैं कि 152 = 225 और 162 = 256
अतः 15 < 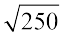 < 16 और 250, 225 की अपेक्षा 256 के बहुत पास है।
< 16 और 250, 225 की अपेक्षा 256 के बहुत पास है।
अतः 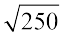 लगभग 16 है।
लगभग 16 है।

प्रयास कीजिए
निम्नलिखित संख्याओं के निकटतम पूर्ण संख्याओं का अनुमान लगाइए:
(i) 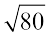 (ii)
(ii)  (iii)
(iii)  (iv)
(iv) 
![]() प्रश्नावली 6.4
प्रश्नावली 6.4
1. निम्नलिखित संख्याओं का वर्गमूल, भाग विधि से ज्ञात कीजिए:
(i) 2304 (ii) 4489 (iii) 3481 (iv) 529
(v) 3249 (vi) 1369 (vii) 5776 (viii) 7921
(ix) 576 (x) 1024 (xi) 3136 (xii) 900
2. निम्नलिखित संख्याओं में से प्रत्येक के वर्गमूल के अंको की संख्या ज्ञात कीजिए:
(बिना गणना के)
(i) 64 (ii) 144 (iii) 4489 (iv) 27225
(v) 390625
3. निम्नलिखित दशमलव संख्याओं के वर्गमूल ज्ञात कीजिए:
(i) 2.56 (ii) 7.29 (iii) 51.84 (iv) 42.25
(v) 31.36
4. निम्नलिखित संख्याओं में से प्रत्येक में न्यूनतम संख्या क्या घटाई जाए कि एक पूर्ण वर्ग संख्या प्राप्त हो जाए। इस प्रकार प्राप्त पूर्ण वर्ग संख्याओं का वर्गमूल भी ज्ञात कीजिए:
(i) 402 (ii) 1989 (iii) 3250 (iv) 825
(v) 4000
5. निम्नलिखित संख्याओं में से प्रत्येक में कम से कम कितना जोड़ा जाए कि एक पूर्ण वर्ग संख्या प्राप्त हो जाए। इस प्रकार प्राप्त पूर्ण वर्ग संख्याओं का वर्गमूल भी ज्ञात कीजिए:
(i) 525 (ii) 1750 (iii) 252 (iv) 1825
(v) 6412
6. किसी वर्ग की भुजा की लंबाई ज्ञात कीजिए जिसका क्षेत्रफल 441 m2 है।
7. किसी समकोण त्रिभुज ABC में, ∠B = 90°
(a) यदि AB = 6 cm, BC = 8 cm, है तो AC ज्ञात कीजिए।
(b) यदि AC = 13 cm, BC = 5 cm, है तो AB ज्ञात कीजिए।
8. एक माली के पास 1000 पौधे हैं। इन पौधों को वह इस प्रकार लगाना चाहता है कि पंक्तियों की संख्या और कॉलम की संख्या समान रहे। इसके लिए कम से कम पौधों की संख्या ज्ञात कीजिए जिसकी उसे आवश्यकता हो।
9. एक विद्यालय में 500 विद्यार्थी हैं। पी.टी. के अभ्यास के लिए इन्हें इस तरह से खड़ा किया गया कि पंक्तियों की संख्या कॉलम की संख्या के समान रहे। इस व्यवस्था को बनाने में कितने विद्यार्थियों को बाहर जाना होगा?
हमने क्या चर्चा की?
1. यदि एक प्राकृत संख्या m को n2 के रूप में व्यक्त कर सकते हैं, जहाँ n भी एक प्राकृत संख्या है, तब m एक वर्ग संख्या है।
2. सभी वर्ग संख्याओं के अंत में इकाई स्थान पर 0, 1, 4, 5, 6 या 9 होता है।
3. वर्ग संख्याओं के अंत में शून्यों की संख्या केवल सम होती है।
4. वर्गमूल, वर्ग की प्रतिलोम संक्रिया है।
5. एक पूर्ण वर्ग संख्या के दो पूर्ण वर्गमूल होते हैं।
धनात्मक वर्गमूल को संकेत 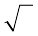 द्वारा व्यक्त किया जाता है।
द्वारा व्यक्त किया जाता है।
उदाहरणार्थ, 32 = 9, 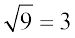 होता है।
होता है।


 सोचिए, चर्चा कीजिए और लिखिए
सोचिए, चर्चा कीजिए और लिखिए प्रश्नावली
प्रश्नावली